Bamboo Garden Trimming Problem: Priority Schedulings †
Abstract
:1. Introduction
1.1. Related Work
1.2. Achieved Results
2. Notation
3. Theoretical Results
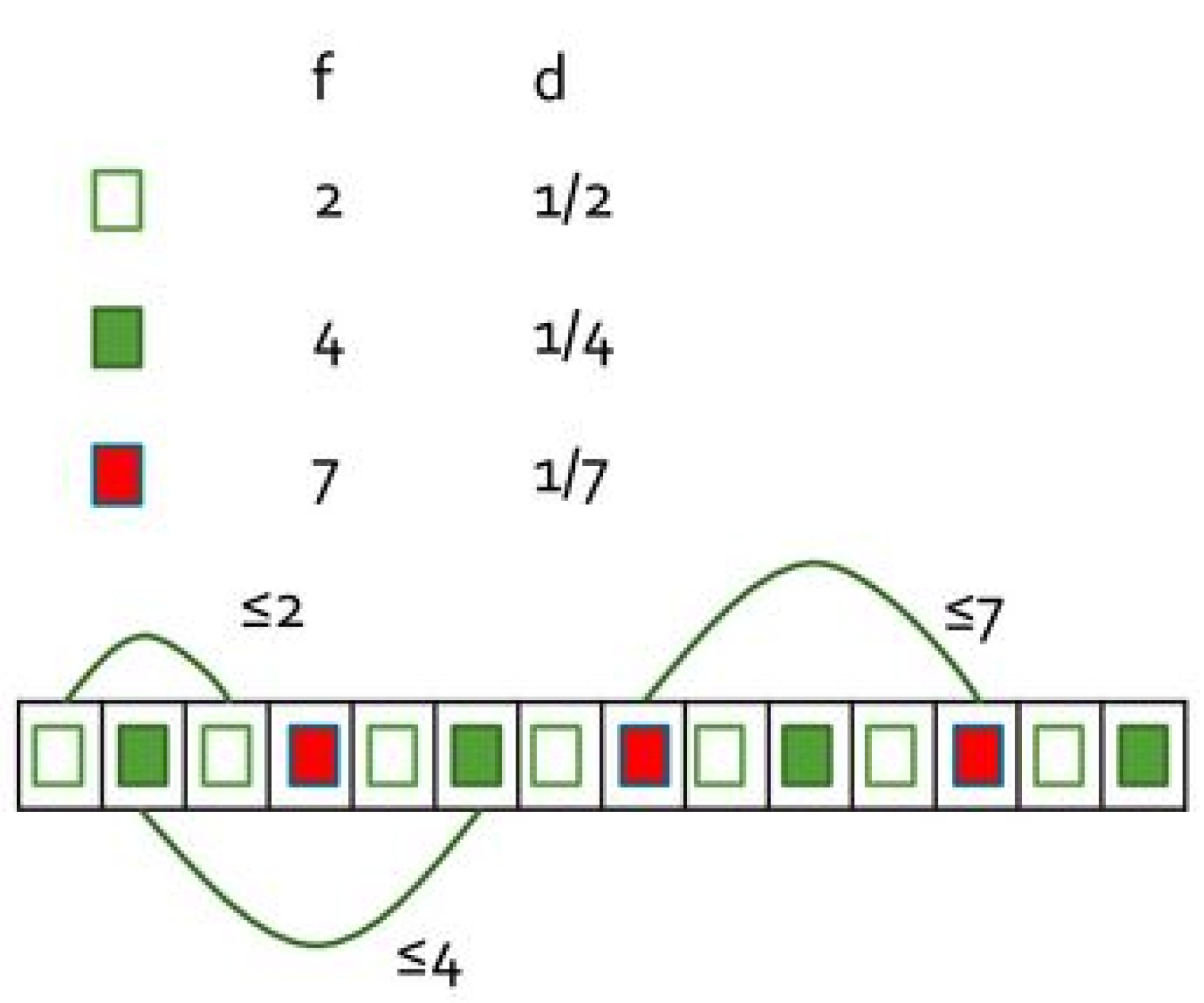
3.1. Priority Schedulings
- , where is the first configuration belonging to , reached from , and is the length of the cycle, i.e., the number of configurations in .
- is the height of the bamboo cut in . It is assumed if no bamboo is cut.
- is the number of times bamboo is cut in , for each , which is equal to the number of relative maximum heights reached by in the cycle.
- is the relative maximum height reached by in the cycle just before the jth cut, for and . Note that, by definition, during day t, for some values of i and j.
- is the sum of the relative maximum heights reached by .
3.2. Scheduling
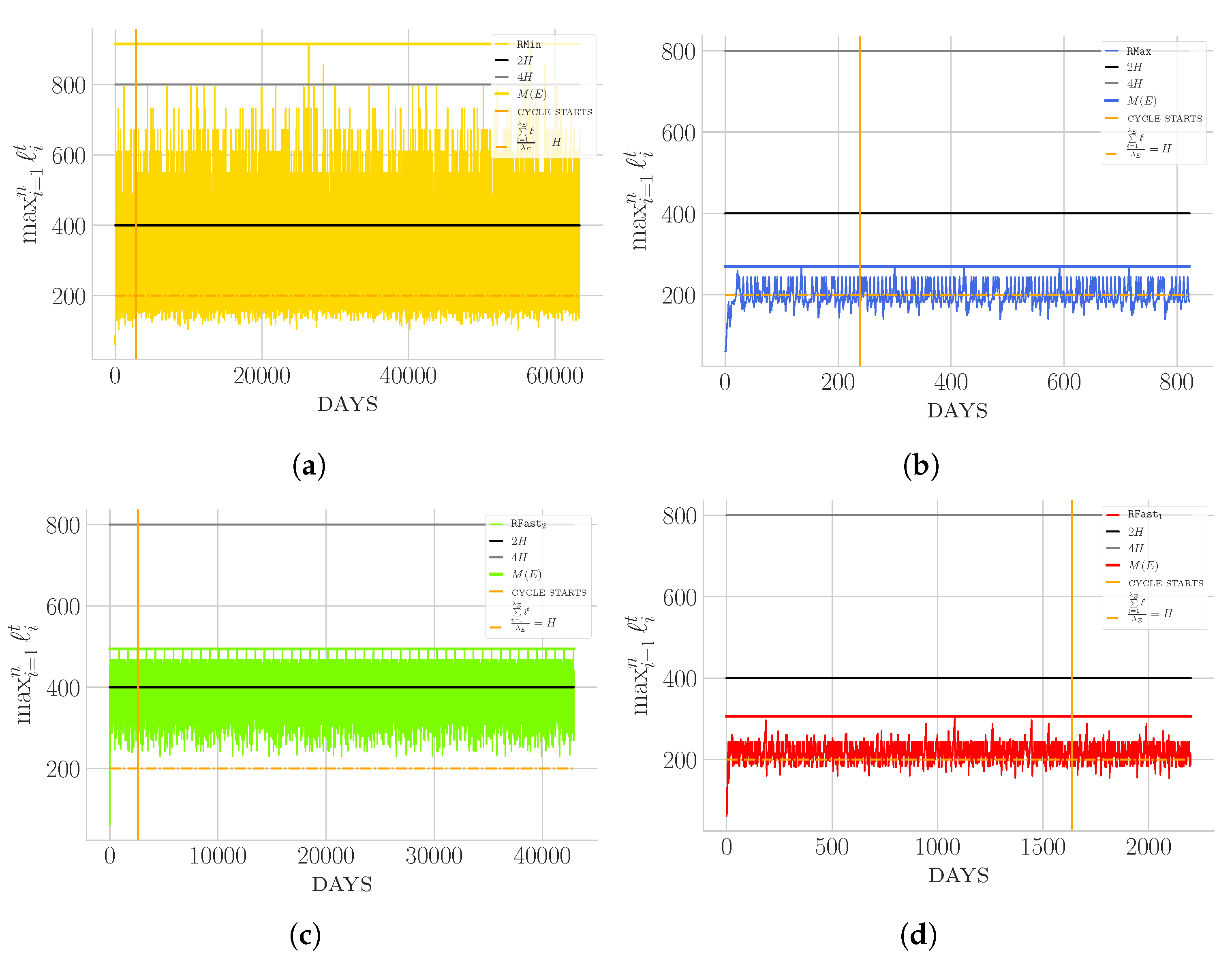
4. Experimental Results
- (, for short): This is the heuristic which performance is the most relevant to the experiments. In particular, in [1], based on [27], a -approximation guarantee has been established. However, the interest is in determining whether such a bound is tight in practice, i.e., whether the logarithmic factor is an accurate estimation. The strategy works in a greedy fashion by cutting each day the tallest bamboo.
- (, for short): This is another greedy strategy introduced in [1]. It guarantees 4-approximation. However, this method requires ordering the input configurations according to the non-increasing order of the bamboos’ growth rates. In fact, each day it cuts the fastest growing bamboo (the one having the biggest ) among those whose height exceeds threshold . If none of the bamboos is taller than , no cuts are performed.
- (, for short): This is a variant of , introduced here for the first time, obtained by decreasing the threshold from to H, and by allowing the cut of the fastest growing bamboo also below the threshold. Basically, if none of the bamboos has reached height H, the fastest growing bamboo is cut. This is a natural extension of , and the aim of defining it is to check whether there are chances to obtain better performance with respect to and . Note that is an ordered H-priority scheduling.
- (, for short): This priority algorithm cuts each day the shortest bamboo, giving priorities to those above H. The aim of defining this strategy is to evaluate performance of counter-intuitive methods, i.e., to see whether even in an adversarial approach one may obtain acceptable performances. is a H-priority scheduling.
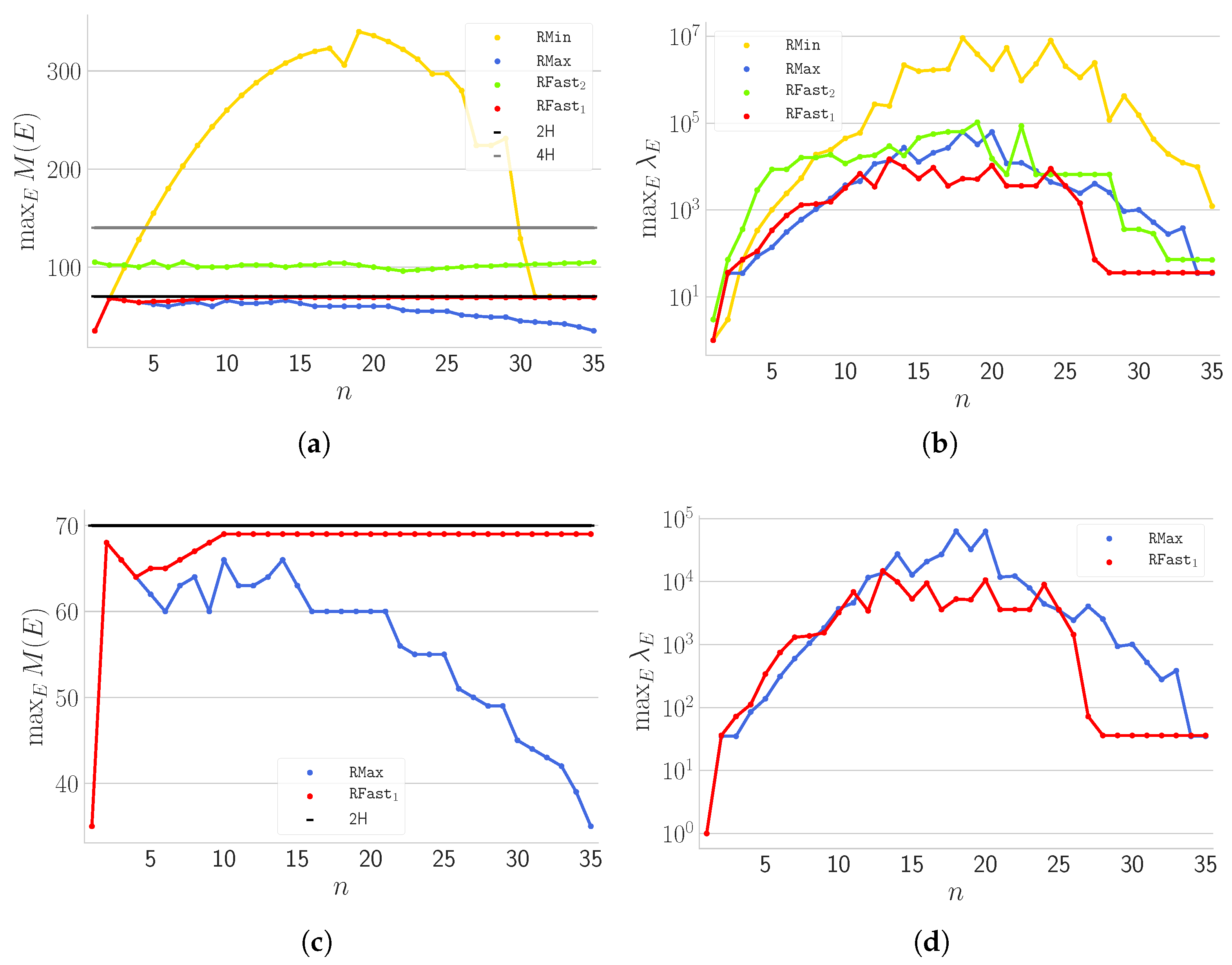
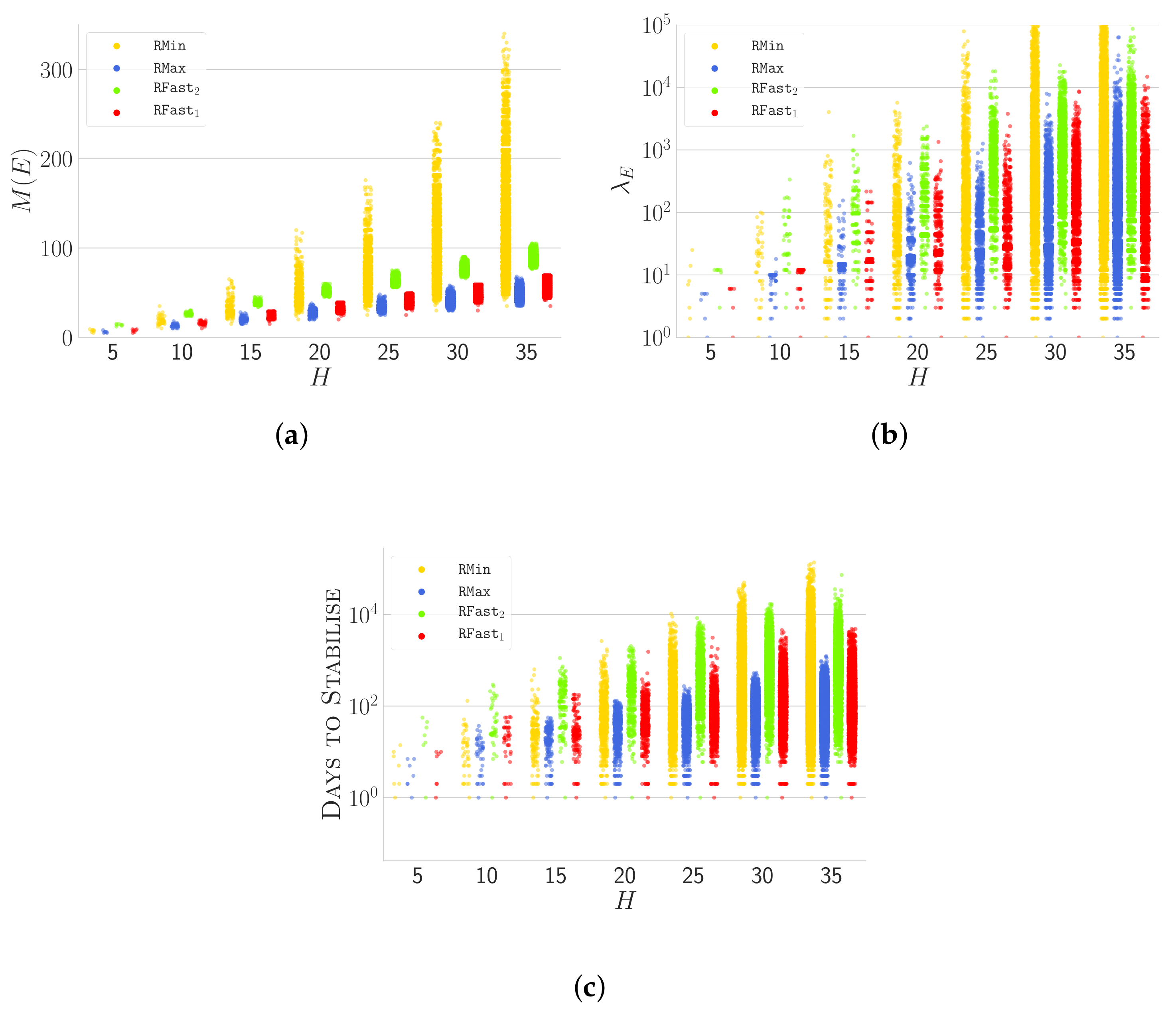
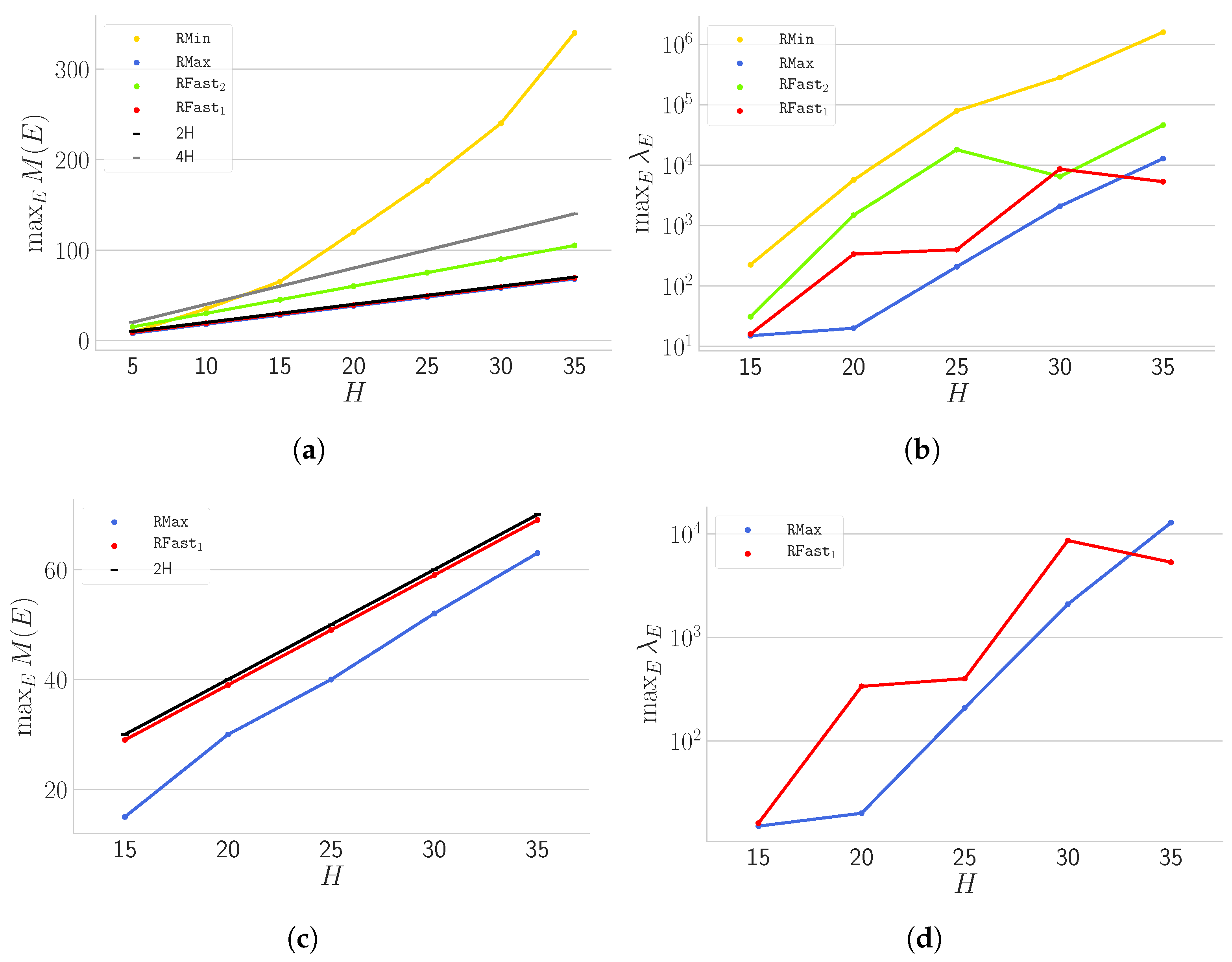
4.1. Fixed H Experimentation
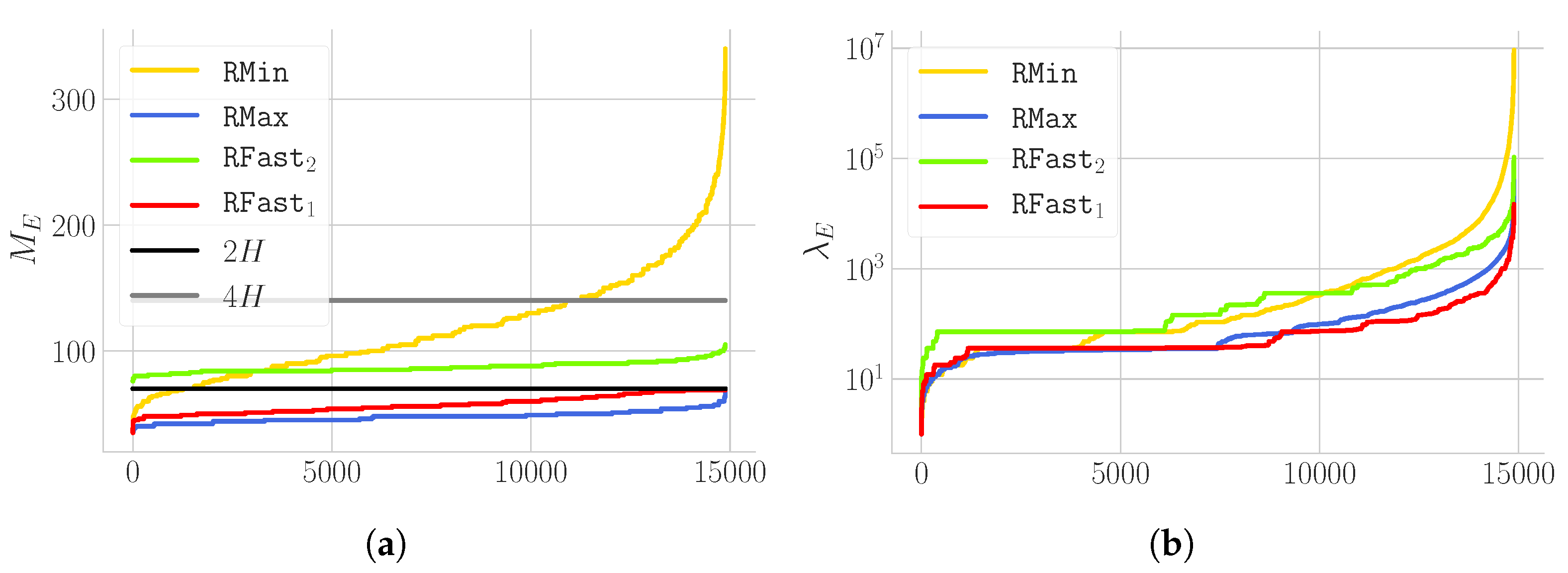
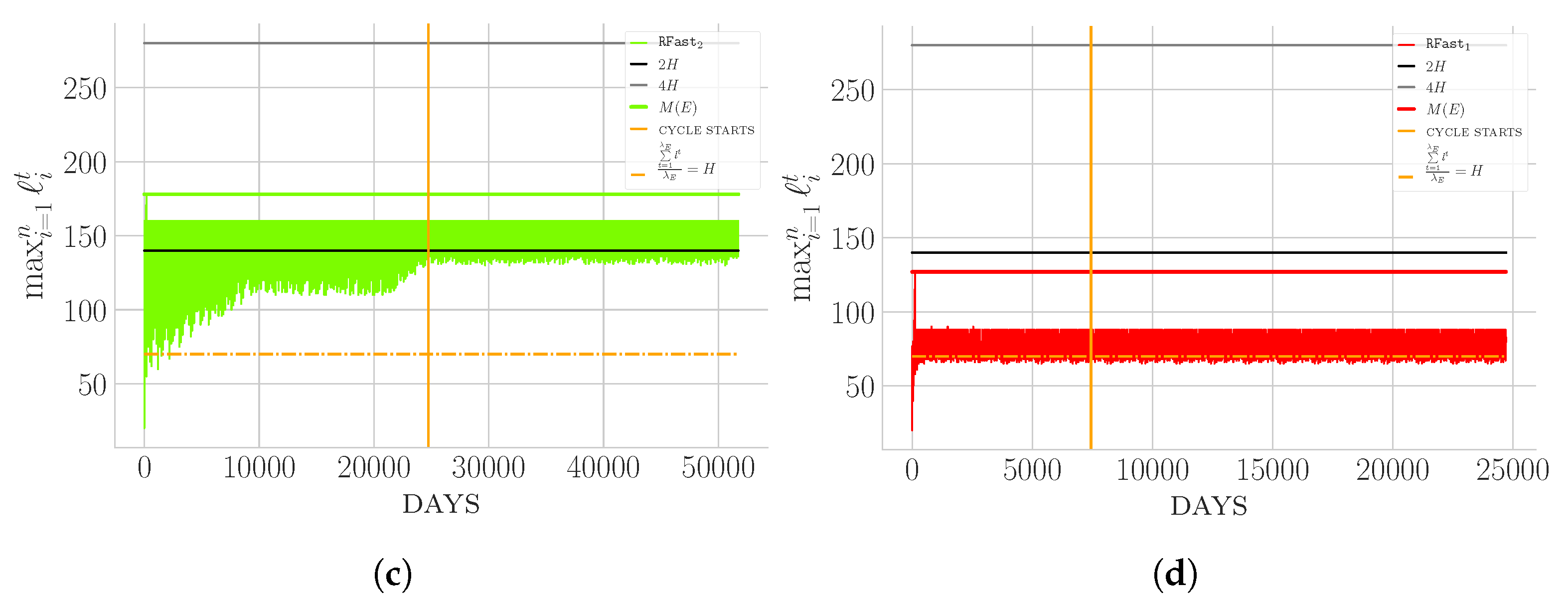
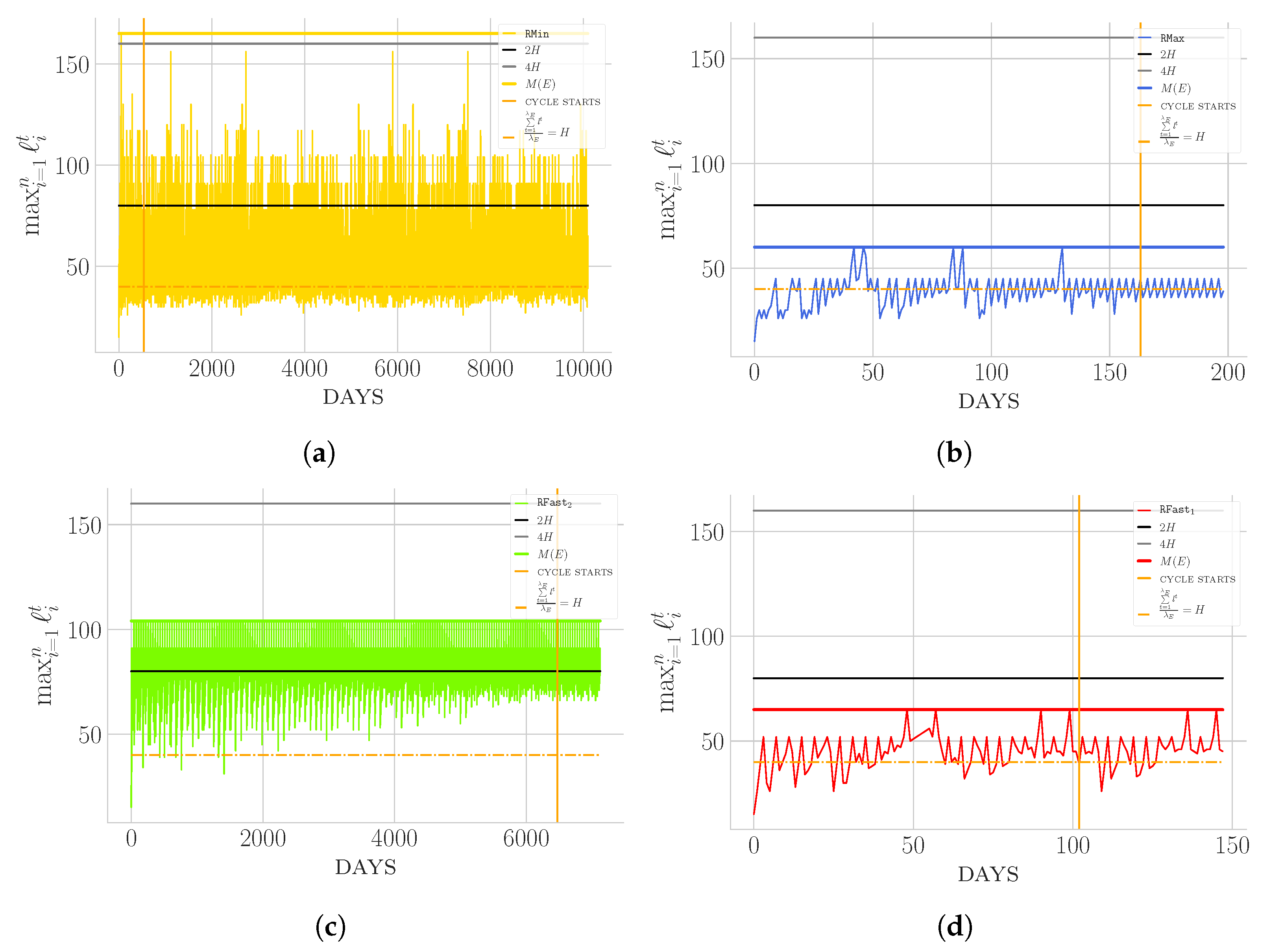
4.2. Fixed n Experimentation
- bamboos with ; and
- with .
- (i) Some strategies exhibit a very small variance in terms of height (e.g., ) with respect to others (e.g., ).
- (ii) Some strategies (e.g., ) are able to stabilise very quickly to a cycle, which is a clearly desirable behaviour in a stabilisation perspective. On top of that, they also exhibit a small .
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gąsieniec, L.; Klasing, R.; Levcopoulos, C.; Lingas, A.; Min, J.; Radzik, T. Bamboo Garden Trimming Problem (Perpetual Maintenance of Machines with Different Attendance Urgency Factors). In SOFSEM 2017: Theory and Practice of Computer Science, Proceedings of the 43rd International Conference on Current Trends in Theory and Practice of Computer Science, Limerick, Ireland, 16–20 January 2017; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2017; Volume 10139, pp. 229–240. [Google Scholar]
- Holte, R.; Mok, A.; Rosier, L.; Tulchinsky, I.; Varvel, D. The pinwheel: A real-time scheduling problem. In Proceedings of the 22nd Annual Hawaii International Conference on System Sciences, Kailua-Kona, HI, USA, 3–6 January 1989; Volume 2, pp. 693–702. [Google Scholar]
- Fishburn, P.C.; Lagarias, J.C. Pinwheel Scheduling: Achievable Densities. Algorithmica 2002, 34, 14–38. [Google Scholar] [CrossRef]
- Alshamrani, S.; Kowalski, D.R.; Gąsieniec, L. How Reduce Max Algorithm Behaves with Symptoms Appearance on Virtual Machines in Clouds. In Proceedings of the 2015 International Conference on Cloud Computing (ICCC), Riyadh, Saudi Arabia, 26–29 April 2015; pp. 1703–1710. [Google Scholar]
- Gąsieniec, L.; Klasing, R.; Martin, R.; Navarra, A.; Zhang, X. Fast periodic graph exploration with constant memory. J. Comput. Syst. Sci. 2008, 74, 802–822. [Google Scholar] [CrossRef]
- Kosowski, A.; Navarra, A. Graph Decomposition for Memoryless Periodic Exploration. Algorithmica 2012, 63, 26–38. [Google Scholar] [CrossRef]
- D’Emidio, M.; Di Stefano, G.; Frigioni, D.; Navarra, A. Characterizing the computational power of mobile robots on graphs and implications for the Euclidean plane. Inf. Comput 2018, 263, 57–74. [Google Scholar] [CrossRef]
- D’Emidio, M.; Frigioni, D.; Navarra, A. Explore and repair graphs with black holes using mobile entities. Theor. Comput. Sci. 2015, 605, 129–145. [Google Scholar] [CrossRef]
- Ntafos, S. On gallery watchmen in grids. Inf. Process. Lett. 1986, 23, 9–102. [Google Scholar] [CrossRef]
- Urrutia, J. Art gallery and illumination problems. In Handbook of Computational Geometry; Elsevier: Amsterdam, The Netherlands, 2000; pp. 973–1027. [Google Scholar]
- Collins, A.; Czyzowicz, J.; Gąsieniec, L.; Kosowski, A.; Kranakis, E.; Krizanc, D.; Martin, R.; Morales Ponce, O. Optimal Patrolling of Fragmented Boundaries. In Proceedings of the 25th Annual ACM Symposium on Parallelism in Algorithms and Architectures, Montréal, QC, Canada, 23–25 July 2013; ACM: New York, NY, USA, 2013; pp. 241–250. [Google Scholar]
- Czyzowicz, J.; Gąsieniec, L.; Kosowski, A.; Kranakis, E. Boundary Patrolling by Mobile Agents with Distinct Maximal Speeds. In Algorithms—ESA 2011, Proceedings of the 19th Annual European Symposium, Saarbrücken, Germany, 5–9 September 2011; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2011; Volume 6942, pp. 701–712. [Google Scholar]
- Chuangpishit, H.; Czyzowicz, J.; Gąsieniec, L.; Georgiou, K.; Jurdzinski, T.; Kranakis, E. Patrolling a Path Connecting a Set of Points with Unbalanced Frequencies of Visits. In SOFSEM 2018: Theory and Practice of Computer Science, Proceedings of the 44th International Conference on Current Trends in Theory and Practice of Computer Science, Krems, Austria, 29 January–2 February 2018; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2018; Volume 10706, pp. 367–380. [Google Scholar]
- Serafini, P.; Ukovich, W. A Mathematical Model for Periodic Scheduling Problems. SIAM J. Discret. Math. 1989, 2, 550–581. [Google Scholar] [CrossRef]
- Chan, M.Y.; Chin, F.Y.L. General schedulers for the pinwheel problem based on double-integer reduction. IEEE Trans. Comput. 1992, 41, 755–768. [Google Scholar] [CrossRef]
- Chan, M.Y.; Chin, F.Y.L. Schedulers for larger classes of pinwheel instances. Algorithmica 1993, 9, 425–462. [Google Scholar] [CrossRef]
- Hsueh, C.; Lin, K. An Optimal Pinwheel Scheduler Using the Single-number Reduction Technique. In Proceedings of the 17th IEEE Real-Time Systems Symposium, Washington, DC, USA, 4–6 December 1996; pp. 196–205. [Google Scholar]
- Holte, R.; Rosier, L.; Tulchinsky, I.; Varvel, D. Pinwheel scheduling with two distinct numbers. Theor. Comput. Sci. 1992, 100, 105–135. [Google Scholar] [CrossRef]
- Lin, S.S.; Lin, K.J. A Pinwheel Scheduler for Three Distinct Numbers with a Tight Schedulability Bound. Algorithmica 1997, 19, 411–426. [Google Scholar] [CrossRef]
- Romer, T.H.; Rosier, L.E. An algorithm reminiscent of euclidean-gcd for computing a function related to pinwheel scheduling. Algorithmica 1997, 17, 1–10. [Google Scholar] [CrossRef]
- Baruah, S.K.; Lin, S.-S. Pfair scheduling of generalized pinwheel task systems. IEEE Trans. Comput. 1998, 47, 812–816. [Google Scholar] [CrossRef]
- Baruah, S.K.; Cohen, N.K.; Plaxton, C.G.; Varvel, D.A. Proportionate progress: A notion of fairness in resource allocation. Algorithmica 1996, 15, 600–625. [Google Scholar] [CrossRef]
- Mok, A.; Rosier, L.; Tulchinski, I.; Varvel, D. Algorithms and complexity of the periodic maintenance problem. Microprocess. Microprogram. 1989, 27, 657–664. [Google Scholar] [CrossRef]
- Anily, S.; Glass, C.A.; Hassin, R. The scheduling of maintenance service. Discret. Appl. Math. 1998, 82, 27–42. [Google Scholar] [CrossRef]
- Anily, S.; Glass, C.A.; Hassin, R. Scheduling maintenance services to three machines. Ann. Oper. Res. 1999, 86, 375–391. [Google Scholar] [CrossRef]
- Bender, M.A.; Fekete, S.P.; Kröller, A.; Mitchell, J.S.B.; Liberatore, V.; Polishchuk, V.; Suomela, J. The Minimum Backlog Problem. Theor. Comput. Sci. 2015, 605, 51–61. [Google Scholar] [CrossRef]
- Bodlaender, M.H.L.; Hurkens, C.A.J.; Kusters, V.J.J.; Staals, F.; Woeginger, G.J.; Zantema, H. Cinderella versus the Wicked Stepmother. In TCS 2012: Theoretical Computer Science, Proceedings of the IFIP Theoretical Computer Science Conference, Amsterdam, The Netherlands, 26–28 September 2012; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2012; Volume 6942, pp. 57–71. [Google Scholar]
- Chrobak, M.; Csirik, J.; Imreh, C.; Noga, J.; Sgall, J.; Woeginger, G.J. The Buffer Minimization Problem for Multiprocessor Scheduling with Conflicts. In Automata, Languages and Programming, Proceedings of the 28th International Colloquium on Automata, Languages, and Programming, Crete, Greece, 8–12 July 2001; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2001; Volume 2076, pp. 862–874. [Google Scholar]
- D’Emidio, M.; Di Stefano, G.; Navarra, A. Priority Scheduling in the Bamboo Garden Trimming Problem. In SOFSEM 2019: Theory and Practice of Computer Science, Proceedings of the 45th International Conference on Current Trends in Theory and Practice of Computer Science, Nový Smokovec, Slovakia, 27–30 January 2019; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2019; Volume 11376, pp. 136–149. [Google Scholar]
- Hardy, G.H.; Ramanujan, S. Asymptotic formulas in combinatorial analysis. Proc. Lond. Math. Soc. 1918, 17, 75–115. [Google Scholar] [CrossRef]
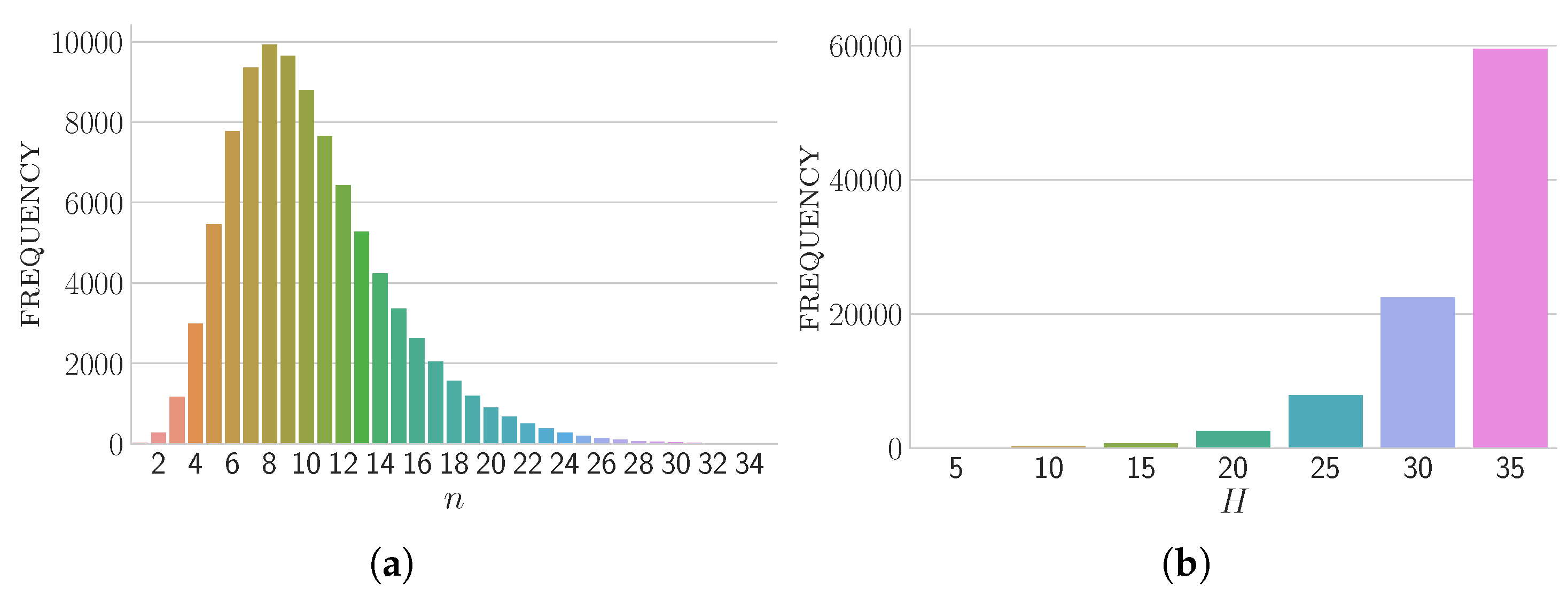




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Emidio, M.; Di Stefano, G.; Navarra, A. Bamboo Garden Trimming Problem: Priority Schedulings. Algorithms 2019, 12, 74. https://doi.org/10.3390/a12040074
D’Emidio M, Di Stefano G, Navarra A. Bamboo Garden Trimming Problem: Priority Schedulings. Algorithms. 2019; 12(4):74. https://doi.org/10.3390/a12040074
Chicago/Turabian StyleD’Emidio, Mattia, Gabriele Di Stefano, and Alfredo Navarra. 2019. "Bamboo Garden Trimming Problem: Priority Schedulings" Algorithms 12, no. 4: 74. https://doi.org/10.3390/a12040074
APA StyleD’Emidio, M., Di Stefano, G., & Navarra, A. (2019). Bamboo Garden Trimming Problem: Priority Schedulings. Algorithms, 12(4), 74. https://doi.org/10.3390/a12040074




