Triplet Loss Network for Unsupervised Domain Adaptation
Abstract
1. Introduction
- We implement a novel DUDA technique for image classification. Deep (D) because it consists of an auto-encoder, a discriminator, and a classifier—all of which are simple deep networks. Unsupervised (U) because we do not use the actual annotations of the target domain. Domain adaptation (DA) because, while learning the model using source data, we adapt it such that it performs well on the target domain, too.
- Our approach obtains a domain adaptive model by introducing separability loss, discrimination loss, and classification loss, which works by generating a latent representation that is both domain-invariant and class informative, by pushing samples from the same classes and different domains to share similar distributions.
- We compare the performance of our model against several existing state-of-the-art works in DA on different image classification tasks.
- Through extensive experimentation, we show that our model, despite its simplicity, either surpasses or achieves similar performance to that of the state-of-the-art in DA.
2. Related Work
2.1. Discriminator
2.2. Image Reconstruction
2.3. Generative Models
2.4. Pseudo-labeling
3. Architecture and Methodology
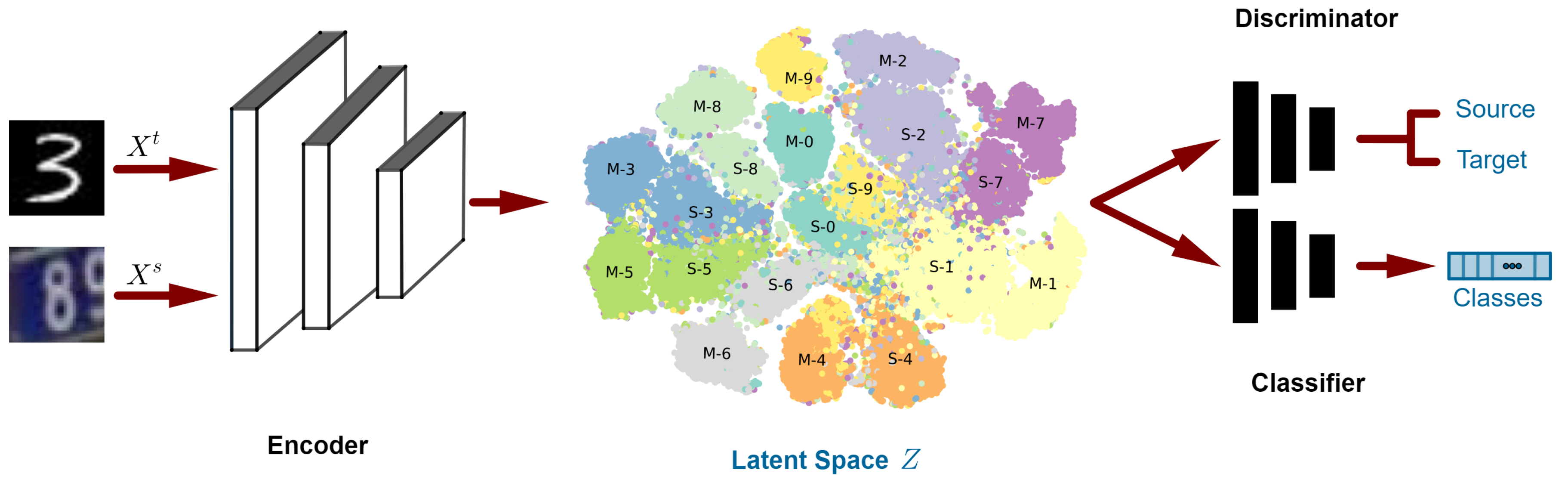
3.1. Overview
3.2. Architecture
3.3. Losses
3.4. Optimization
| Algorithm 1: The training process of TripNet |
 |
3.5. Novelty
4. Experiments and Results
4.1. Target Accuracy Comparison
4.1.1. Digit Classification
4.1.2. Object Recognition using OFFICE31
4.1.3. SYN-SIGNS to GTSRB
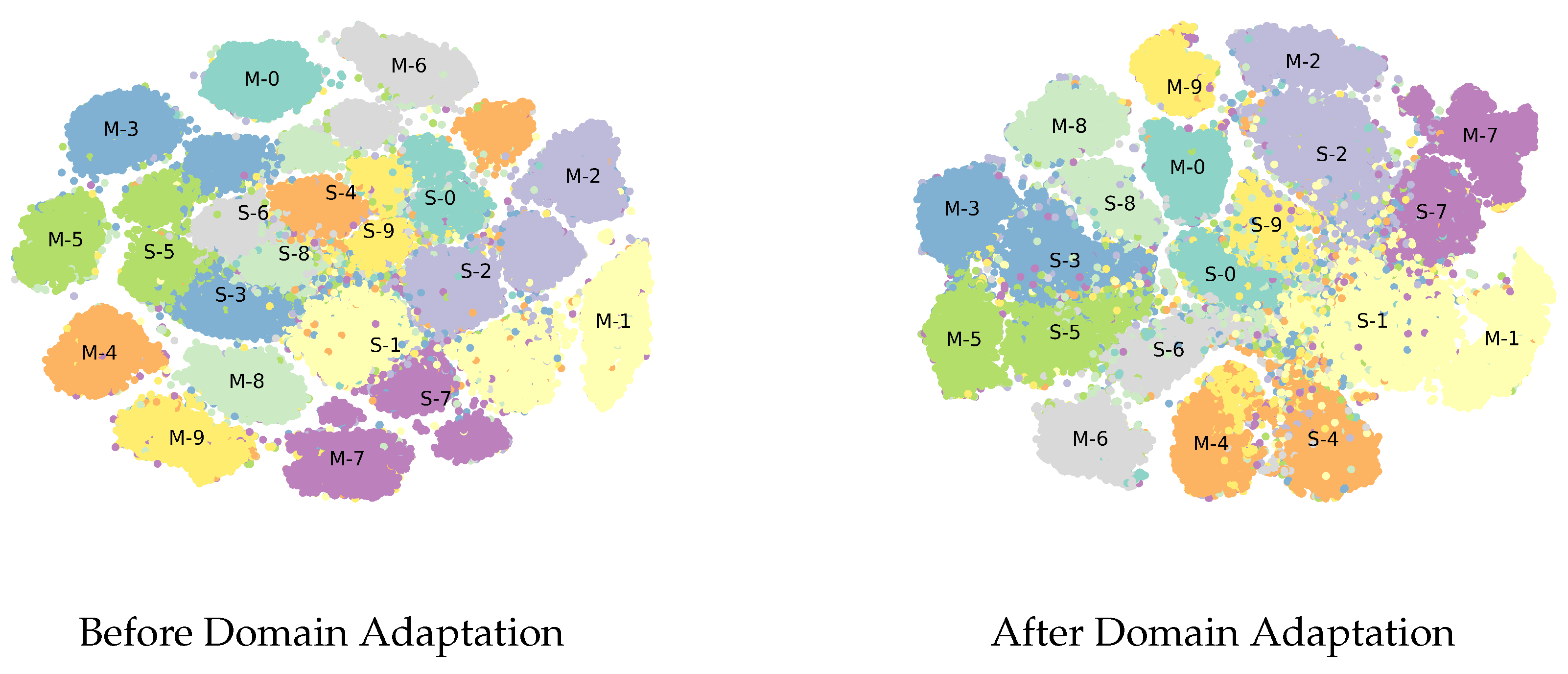
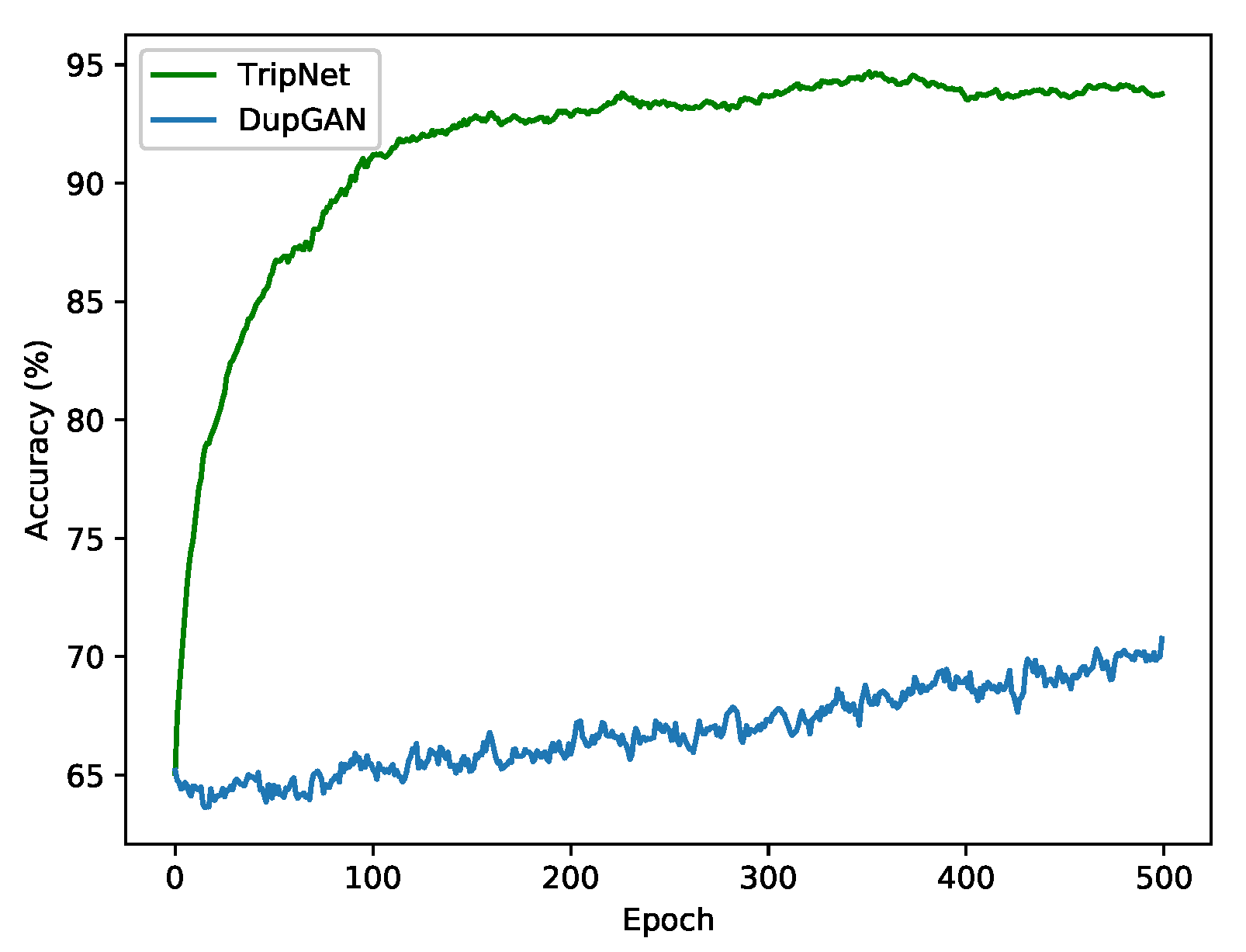
4.2. Comparison of TripNet and DupGAN
4.3. Ablation Study
4.4. Implementation Details
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Hoffman, J.; Tzeng, E.; Park, T.; Zhu, J.Y.; Isola, P.; Saenko, K.; Efros, A.A.; Darrell, T. CyCADA: Cycle-Consistent Adversarial Domain Adaptation. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Saito, K.; Yamamoto, S.; Ushiku, Y.; Harada, T. Open Set Domain Adaptation by Backpropagation. arXiv 2018, arXiv:1804.10427. [Google Scholar]
- Busto, P.P.; Gall, J. Open Set Domain Adaptation. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 754–763. [Google Scholar]
- Motiian, S.; Piccirilli, M.; Adjeroh, D.A.; Doretto, G. Unified Deep Supervised Domain Adaptation and Generalization. arXiv 2017, arXiv:1709.10190. [Google Scholar]
- Yao, T.; Pan, Y.; Ngo, C.; Li, H.; Mei, T. Semi-supervised Domain Adaptation with Subspace Learning for visual recognition. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 2142–2150. [Google Scholar]
- Cai, G.; Wang, Y.; Zhou, M.; He, L. Unsupervised Domain Adaptation with Adversarial Residual Transform Networks. arXiv 2018, arXiv:1804.09578. [Google Scholar]
- Russo, P.; Carlucci, F.M.; Tommasi, T.; Caputo, B. From source to target and back: Symmetric bi-directional adaptive GAN. arXiv 2017, arXiv:1705.08824. [Google Scholar]
- Deshmukh, A.A.; Bansal, A.; Rastogi, A. Domain2Vec: Deep Domain Generalization. arXiv 2018, arXiv:1807.02919. [Google Scholar]
- Li, Z.; Ko, B.; Choi, H. Pseudo-Labeling Using Gaussian Process for Semi-Supervised Deep Learning. In Proceedings of the 2018 IEEE International Conference on Big Data and Smart Computing (BigComp), Shanghai, China, 15–17 January 2018; pp. 263–269. [Google Scholar]
- Ren, Z.; Lee, Y.J. Cross-Domain Self-Supervised Multi-task Feature Learning Using Synthetic Imagery. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 762–771. [Google Scholar]
- Hu, L.; Kan, M.; Shan, S.; Chen, X. Duplex Generative Adversarial Network for Unsupervised Domain Adaptation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Pinheiro, P.O. Unsupervised Domain Adaptation with Similarity Learning. arXiv 2017, arXiv:1711.08995. [Google Scholar]
- Xie, S.; Zheng, Z.; Chen, L.; Chen, C. Learning Semantic Representations for Unsupervised Domain Adaptation. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Dy, J., Krause, A., Eds.; PMLR: Stockholmsmässan, Stockholm, Sweden, 2018; Volume 80, pp. 5423–5432. [Google Scholar]
- Teng, Y.; Choromanska, A.; Bojarski, M. Invertible Autoencoder for domain adaptation. arXiv 2018, arXiv:1802.06869. [Google Scholar]
- Kan, M.; Shan, S.; Chen, X. Bi-Shifting Auto-Encoder for Unsupervised Domain Adaptation. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 3846–3854. [Google Scholar]
- Zhang, H.; Liu, L.; Long, Y.; Shao, L. Unsupervised Deep Hashing With Pseudo Labels for Scalable Image Retrieval. IEEE Trans. Image Process. 2018, 27, 1626–1638. [Google Scholar] [CrossRef]
- Wei, J.; Liang, J.; He, R.; Yang, J. Learning Discriminative Geodesic Flow Kernel for Unsupervised Domain Adaptation. In Proceedings of the 2018 IEEE International Conference on Multimedia and Expo (ICME), San Diego, CA, USA, 23–27 July 2018; pp. 1–6. [Google Scholar]
- Zhu, J.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks. arXiv 2017, arXiv:1703.10593. [Google Scholar]
- Sener, O.; Song, H.O.; Saxena, A.; Savarese, S. Learning Transferrable Representations for Unsupervised Domain Adaptation. In Advances in Neural Information Processing Systems 29; Lee, D.D., Sugiyama, M., Luxburg, U.V., Guyon, I., Garnett, R., Eds.; Curran Associates, Inc.: Nice, France, 2016; pp. 2110–2118. [Google Scholar]
- Murez, Z.; Kolouri, S.; Kriegman, D.; Ramamoorthi, R.; Kim, K. Image to Image Translation for Domain Adaptation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4500–4509. [Google Scholar]
- Hong, W.; Wang, Z.; Yang, M.; Yuan, J. Conditional Generative Adversarial Network for Structured Domain Adaptation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1335–1344. [Google Scholar]
- Almahairi, A.; Rajeswar, S.; Sordoni, A.; Bachman, P.; Courville, A.C. Augmented CycleGAN: Learning Many-to-Many Mappings from Unpaired Data. arXiv 2018, arXiv:1802.10151. [Google Scholar]
- Lv, F.; Zhu, J.; Yang, G.; Duan, L. TarGAN: Generating target data with class labels for unsupervised domain adaptation. Knowl.-Based Syst. 2019. [Google Scholar] [CrossRef]
- Sankaranarayanan, S.; Balaji, Y.; Castillo, C.D.; Chellappa, R. Generate To Adapt: Aligning Domains using Generative Adversarial Networks. arXiv 2017, arXiv:1704.01705. [Google Scholar]
- Chen, M.; Weinberger, K.Q.; Blitzer, J.C. Co-training for Domain Adaptation. In Proceedings of the 24th International Conference on Neural Information Processing Systems, Granada, Spain, 12–15 December 2011; Curran Associates Inc.: Redhook, NY, USA, 2011; pp. 2456–2464. [Google Scholar]
- Saito, K.; Ushiku, Y.; Harada, T. Asymmetric Tri-training for Unsupervised Domain Adaptation. arXiv 2017, arXiv:1702.08400. [Google Scholar]
- Khan, A.M.; Lee, Y.K.; Lee, S.Y.; Kim, T.S. A triaxial accelerometer-based physical-activity recognition via augmented-signal features and a hierarchical recognizer. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 1166–1172. [Google Scholar] [CrossRef] [PubMed]
- Saito, K.; Watanabe, K.; Ushiku, Y.; Harada, T. Maximum Classifier Discrepancy for Unsupervised Domain Adaptation. arXiv 2017, arXiv:1712.02560. [Google Scholar]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-Adversarial Training of Neural Networks. J. Mach. Learn. Res. 2016, 17, 1–35. [Google Scholar]
- Ganin, Y.; Lempitsky, V. Unsupervised domain adaptation by backpropagation. arXiv 2014, arXiv:1409.7495. [Google Scholar]
- Tzeng, E.; Hoffman, J.; Saenko, K.; Darrell, T. Adversarial Discriminative Domain Adaptation. arXiv 2017, arXiv:1702.05464. [Google Scholar]
- Bousmalis, K.; Trigeorgis, G.; Silberman, N.; Krishnan, D.; Erhan, D. Domain Separation Networks. arXiv 2016, arXiv:1608.06019. [Google Scholar]
- Ghifary, M.; Kleijn, W.B.; Zhang, M.; Balduzzi, D.; Li, W. Deep Reconstruction-Classification Networks for Unsupervised Domain Adaptation. arXiv 2016, arXiv:1607.03516. [Google Scholar]
- Liu, M.; Tuzel, O. Coupled Generative Adversarial Networks. arXiv 2016, arXiv:1606.07536. [Google Scholar]
- Liu, M.; Breuel, T.; Kautz, J. Unsupervised Image-to-Image Translation Networks. arXiv 2017, arXiv:1703.00848. [Google Scholar]
- Bousmalis, K.; Silberman, N.; Dohan, D.; Erhan, D.; Krishnan, D. Unsupervised Pixel-Level Domain Adaptation with Generative Adversarial Networks. arXiv 2016, arXiv:1612.05424. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading Digits in Natural Images with Unsupervised Feature Learning. 2011. Available online: http://ufldl.stanford.edu/housenumbers/nips2011_housenumbers.pdf (accessed on 2 May 2019).
- Denker, J.S.; Gardner, W.R.; Graf, H.P.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D.; Baird, H.S.; Guyon, I. Neural Network Recognizer for Hand-Written Zip Code Digits. In Advances in Neural Information Processing Systems 1; Touretzky, D.S., Ed.; Morgan-Kaufmann: San Francisco, CA, USA, 1989; pp. 323–331. [Google Scholar]
- van der Maaten, L.; Hinton, G.E. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Saenko, K.; Kulis, B.; Fritz, M.; Darrell, T. Adapting Visual Category Models to New Domains. In Proceedings of the 11th European Conference on Computer Vision: Part IV; Springer: Berlin/Heidelberg, Germany, 2010; pp. 213–226. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems–Volume 1, Lake Tahoe, NV, USA, 3–6 December 2012; Curran Associates Inc.: New York, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics; Teh, Y.W., Titterington, M., Eds.; PMLR: Sardinia, Italy, 2010; Volume 9, pp. 249–256. [Google Scholar]
| Method | SVHN → MNIST | MNIST → USPS | USPS → MNIST | SVHNextra → MNIST |
|---|---|---|---|---|
| DCNN-TargetOnly | 98.97 | 95.02 | 98.96 | 98.97 |
| DCNN-SourceOnly | 62.19 | 86.75 | 75.52 | 73.67 |
| ADDA | 76.0 | 92.87 | 93.75 | 86.37 |
| RevGrad | - | 89.1 | 89.9 | - |
| PixelDA | - | 95.9 | - | - |
| DSN | - | 91.3 | 73.2 | - |
| DANN | 73.85 | 85.1 | 73.0 | - |
| DRCN | 81.97 | 91.8 | 73.0 | - |
| KNN-Ad | 78.8 | - | - | - |
| ATDA | 85.8 | 93.17 | 84.14 | 91.45 |
| UNIT | - | 95.97 | 93.58 | 90.53 |
| CoGAN | - | 95.65 | 93.15 | - |
| SimNet | - | 96.4 | 95.6 | - |
| Gen2Adpt | 92.4 | 92.8 | 90.8 | - |
| MCD | 93.6 | - | - | - |
| Image2Image | 90.1 | 98.8 | 97.6 | - |
| TarGAN | 98.1 | 93.8 | 94.1 | - |
| DupGAN | 92.46 | 96.01 | 98.75 | 96.42 |
| TripNet (Ours) | 94.70 | 97.63 | 97.94 | 98.57 |
| Methods | W -> A | W ->D | D ->A | D ->W |
|---|---|---|---|---|
| AlexNet before DA | 32.6 | 70.8 | 35.0 | 77.3 |
| DANN | 52.7 | - | 54.5 | - |
| DRCN | 54.9 | - | 56.0 | - |
| DCNN | 49.8 | - | 51.1 | - |
| DupGan | 59.1 | - | 61.5 | - |
| TripNet | 55.6 | 99.3 | 57.3 | 98.5 |
| TCA - ResNet | 60.9 | 99.6 | 61.7 | 96.9 |
| RevGrad - ResNet | 67.4 | 99.1 | 68.2 | 96.9 |
| Gen2Apdt - ResNet | 71.4 | 99.8 | 72.8 | 97.9 |
| ResNet before DA | 60.7 | 99.3 | 62.5 | 96.7 |
| Methods | Before DA | DANN | DDC | DSN | TarGAN | Tri-Training | TripNet (ours) |
|---|---|---|---|---|---|---|---|
| SYN-SIGNS to GTSRB | 56.4 | 78.9 | 80.3 | 93.1 | 95.9 | 96.2 | 88.7 |
| Experiments | MNIST → USPS | SVHNextra → MNIST |
|---|---|---|
| Training and testing on target labels | 95.02 | 98.97 |
| Training on source and testing on target | 86.75 | 73.67 |
| TripNet-WD | 96.07 | 81.4 |
| TripNet-WPL | 90.42 | 71.06 |
| TripNet-WSL | 90.86 | 71.33 |
| TripNet-WBF | 96.71 | 92.83 |
| TripNet (Full) | 97.63 | 98.57 |
| Experiments | PLThresh | |||||
|---|---|---|---|---|---|---|
| SVHN → MNIST | 1.5 | 1 | 4 | 0.5 | 0.8 | 0.999 |
| MNIST → USPS | 1.5 | 2.5 | 1 | 0.2 | 1 | 0.995 |
| USPS → MNIST | 2.5 | 3 | 1.5 | 0.6 | 1 | 0.995 |
| SVHNextra → MNIST | 3 | 0.5 | 2 | 0.5 | 1 | 0.9999 |
| W → A | 2 | 1.5 | 3 | 0.5 | 1 | 0.999 |
| W → D | 1.5 | 1 | 2.5 | 0.7 | 1 | 0.999 |
| D → A | 2 | 1.5 | 2.5 | 0.5 | 1.5 | 0.999 |
| D → W | 1.5 | 2 | 3 | 0.5 | 1 | 0.999 |
| SYS-SIGNS → GTSRB | 2 | 2 | 1.5 | 0.5 | 1 | 0.99 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bekkouch, I.E.I.; Youssry, Y.; Gafarov, R.; Khan, A.; Khattak, A.M. Triplet Loss Network for Unsupervised Domain Adaptation. Algorithms 2019, 12, 96. https://doi.org/10.3390/a12050096
Bekkouch IEI, Youssry Y, Gafarov R, Khan A, Khattak AM. Triplet Loss Network for Unsupervised Domain Adaptation. Algorithms. 2019; 12(5):96. https://doi.org/10.3390/a12050096
Chicago/Turabian StyleBekkouch, Imad Eddine Ibrahim, Youssef Youssry, Rustam Gafarov, Adil Khan, and Asad Masood Khattak. 2019. "Triplet Loss Network for Unsupervised Domain Adaptation" Algorithms 12, no. 5: 96. https://doi.org/10.3390/a12050096
APA StyleBekkouch, I. E. I., Youssry, Y., Gafarov, R., Khan, A., & Khattak, A. M. (2019). Triplet Loss Network for Unsupervised Domain Adaptation. Algorithms, 12(5), 96. https://doi.org/10.3390/a12050096







