A Source Domain Extension Method for Inductive Transfer Learning Based on Flipping Output

Abstract

Transfer learning aims for high accuracy by applying knowledge of source domains for which data collection is easy in order to target domains where data collection is difficult, and has attracted attention in recent years because of its significant potential to enable the application of machine learning to a wide range of real-world problems. However, since the technique is user-dependent, with data prepared as a source domain which in turn becomes a knowledge source for transfer learning, it often involves the adoption of inappropriate data. In such cases, the accuracy may be reduced due to “negative transfer.” Thus, in this paper, we propose a novel transfer learning method that utilizes the flipping output technique to provide multiple labels in the source domain. The accuracy of the proposed method is statistically demonstrated to be significantly better than that of the conventional transfer learning method, and its effect size is as high as 0.9, showing high performance.

1. Introduction

In recent years, machine learning has attracted attention, while the need to utilize data that can be acquired from various sites is increasing. For example, at manufacturing sites, the manufacturing data collected during a given process, the operation history of a given machine, and the like can all be acquired as data as a result of innovations in sensor technology. In supervised learning, learning using supervised data (a set of signals acquired using sensors and their affiliated class labels) makes it possible to acquire abilities comparable to humans in the fields of speech and object recognition [1,2]. However, many of the proposed algorithms are designed for training situations, showing excellent performance under conditions typically encountered during training, but often weaker performance in other situations. What is required in the real world is not algorithms that show high performance only in limited, training situations, but those which demonstrate general-purpose high performance in a wide range of situations similar to these. The generalization of such algorithms to various conditions remains underdeveloped. Real-world datasets are typically messy, and inappropriate predictions are often made based on models developed from carefully constructed datasets.

One means of addressing this problem is to utilize transfer learning [3,4] to apply learned knowledge to a new problem domain. Transfer learning deals with situations where two types of datasets are available: A source domain and a target domain. The target domain contains data related to the task which we wish to accomplish, while the source domain contains data related to tasks similar to, but not including, the task of the target domain. Due to real-world limitations, such as difficulty in protecting a sufficient amount of data, the target domain often has an insufficient number of data items. However, the source domain can easily prepare abundant data, and the task of the source domain can be efficiently accomplished. The purpose of transfer learning is to show high accuracy in tasks to be accomplished using the data not only of the target domain, but of the source domain, and it aims at the acquisition of new knowledge based on the two types of data sets. As such, it is a valuable technique not only in the manufacturing process, but also in many fields, such as natural science experimentation and financial strategies.

When using transfer learning, it is not necessary to prepare a large number of target domain items, typically involving high collection costs. Instead, it is possible to obtain complementary data from the source domain, which can be easily collected in large quantities. Inductive transfer learning is a transfer learning method in which different labels are given to the respective data of the target and source domains. The technique is utilized in situations where the respective distributions of the target and source domains are different, as well as in situations where the label definitions differ in the two domains. In inductive transfer learning, it is possible to learn independently in each domain, taking advantage of the fact that labels are given to both domains. In one example of the method, Kamishima proposed TrBagg [5], an algorithm with applied bagging [6]. TrBagg employs only weak learners that are effective for learning in the target domain, selected from the weak learners learned from the original domain.

The key issue in applying transfer learning to real environments is that it is not known how much data among the data collected in the source domain can be used for transfer learning. Furthermore, we cannot know which data items are available. If the source domain contains many inappropriate data items for accomplishing the task of the target domain, “negative transfer” [7] may occur, and the target domain learning may not be successful. In order to suppress negative transfer, it is desirable that the data in the source domain should fit the target domain as much as possible, but a trade-off between the quality of the source domain data and the data collection cost cannot be avoided. Since the similarity between the source domain and target domain is generally unmeasurable, it is up to the user to decide what source domain to prepare. In order to increase the effectiveness of transfer learning, to lower the data collection cost, a general-purpose algorithm that can show a high discrimination rate is desirable, even if the source domain contains many data items that are inappropriate for learning the target domain.

In this study, we developed a novel transfer learning method that utilizes more data contained in the source domain than conventional transfer learning methods. The proposed method is based on TrBagg, which selectively utilizes source domain data. The selective use of data lessens the likelihood of negative transfer, but essentially uses only data assigned labels on the same basis as the target domain. If there are only a few items that can be transferred to the target domain, the benefits of learning are small. We thus utilize flipping output [8] as an important tool in the proposed method. We apply the flipping output technique to the source domain and newly generate the inverted label data as the inverted source domain, then selectively utilize data from a combined set of source domain and inverted source domain data items. With the flipping output, even items originally assigned a label different from the target domain can be used. In theory, by utilizing data-based acceptance algorithms typified by TrBagg, we can make use of all the data of the source domain. Among the key features of the proposed method:

• By applying label flipping to the source domain, all data items have multiple labels at the same time;
• Verification experiments using benchmark datasets confirmed that the proposed method performs significantly better than TrBagg.

The paper is organized as follows. In Section 2, we outline the salient features of transfer learning and TrBagg. Section 3 describes the flipping output technique utilized in the proposed method, and details the algorithm. Section 4 compares the proposed and conventional methods, through experiments using the benchmark dataset from UCI. In Section 5, we discuss related research, and in Section 6, conclude the paper.

2. Transfer Learning

In this section, we outline the salient features of transfer learning and TrBagg, which is its solution method.

2.1. Inductive Transfer Learning for Classification

Transfer learning deals with data in two domains: A source domain and a target domain. Transfer learning, in which labels are assigned to both source and target domains, is commonly referred to as inductive transfer learning. The two main differences between the source and target domains in inductive transfer learning are the different data distribution and label definition in each domain. Inductive transfer learning often deals with situations in which there is a difference in distribution between the target domain and the source domain. In this study, we focused on inductive transfer learning and the classification problem. When the feature vector representing an object is described by $x$, and the class is labeled by $c$, the data can be expressed as $\left(x,c\right)$. The solution to the classification problem involves prediction of the appropriate class label $c_i$ for the feature vector $x_i$. In this paper, we denote the target domain as $D_T$ and the source domain as $D_S$. The data of the target domain can be expressed as $D_T={\left\{\left(x_i,c_i\right)\right\}}_{i=1}^{N_T}$, where $N_T=\left|D_T\right|$. Similarly, the data of the source domain can be expressed as $D_S={\left\{\left(x_i,c_i\right)\right\}}_{i=1}^{N_S}$, where, $N_S=\left|D_S\right|$. Since the source domain is sufficiently larger than the target domain, $N_T\ll N_S$ is satisfied. All cases included in the target domain are generated from the simultaneous distribution $P_T\left[x,c\right]$, representing the target concept, but the source domain is not limited to this distribution. The purpose of inductive transfer learning is to express $P_T\left[x,c\right]$ more accurately than by learning using only $D_T\left[x,c\right]$ by including the two domains $D_T\left[x,c\right]$ and $D_S\left[x,c\right]$.

2.2. TrBagg: Conventional Inductive Transfer Method

TrBagg was utilized in the proposed method because bagging offers a solution for inductive transfer learning. TrBagg is an example-based approach to transferring knowledge based on data. That is, among the item of the source domain, the item that is effective for classification of the target domain is selectively used. Since the respective data items in the two domains have different distributions and/or definitions, it is impossible to directly compare data items with each other. Therefore, TrBagg determines whether the classifier learned from part of the source domain has enough classification accuracy for the target domain, and the data to be used is selected via the classifier.

Specifically, the TrBagg’s algorithm is as follows (Algorithm 1). First, $T$ training datasets $d_1,d_2,\cdots ,d_T$ are generated from $D_S$ by bootstrap sampling. Learning from the generated individual datasets, $T$ classifiers $C_1,C_2,\cdots ,C_T$ are generated. Among $C_1,C_2,\cdots ,C_T$ the classifiers whose experience error $ac{c}_1,ac{c}_2,\cdots ,ac{c}_T$ are less than the threshold $th$ with respect to $D_T$ are adopted as $C_i^{ad}$. If the experience error of a classifier is higher than $th$, the classifier is discarded. This determination is made for all the classifiers, and the result is calculated using only the adopted classifiers. The above flow is shown in Figure 1.

Algorithm 1: Algorithms of TrBagg.

$i=1$

$\mathrm{for} n\mathrm{in}1:T$:

Bootstrap sampling from $D_s$ as $d_n$

Create classifier $C_n$ learning from $d_n$

Calculate experience error for $D_T$ as $ac{c}_n$

If $ac{c}_n<th:$

Save classifier $C_n$ as $C_i^{ad}$

$i=i+1$

Else:

Discard classifier $C_n$

n = n + 1

Calculate result using $C_1^{ad}\cdots C_i^{ad}$

3. Proposed Method

As described in Section 2, TrBagg selectively uses data from the source domain. However, it is generally unknown how much data among the data contained in the source domain can be utilized. One example may be seen in the sensory testing commonly employed for quality control at manufacturing sites. Although such sensory testing enables quality determination based on the examiner’s vision and hearing, the determination criteria is often difficult to quantify. Therefore, large numbers of samples must be labeled by multiple inspectors, and variations in examiner criteria and judgment are inevitable. In this case, since it is not known by which criteria a plurality of inspectors is making decisions, it becomes unclear which samples are labeled according to the desired criteria; and if there are few available data items, the benefits of metastatic learning cannot be expected. Therefore, in this paper we propose a method that is effective even when there are few available data items in the source domain. We address situations with different label criteria, as described above, and utilize flipping output, whereby different labels are given to the source domain at the same time. Further, we propose a method based on TrBagg, aiming to increase the number of usable data items, as well as the generalization of the method, using flipping output.

3.1. Flipping Output

In this section, we outline the flipping output employed in the study. Flipping output is a method used to improve generalization through ensemble learning. With flipping output, several data items are randomly selected from the learning dataset and given different labels. We obtain classifiers that show better generalization performance by learning from data with different labels. The reason why flipping output works well is explained by bias-variance theory [9]. The generalization error $Err$ of ensemble learning of $T$ classifiers can be expressed as:

$$Err=bias+variance+noise,$$

(1)

where $bias$ is error derived from the learning algorithm, $variance$ is error derived from the learning data to be used, and $noise$ is the lower bound of the expected error of an arbitrary learning algorithm, a form of error that cannot be reduced. In ensemble learning, we attempt to reduce variance by learning using various training examples; while, through the use of flipping output, we aim to reduce the generalization error by further reducing the variance through varying the label. In general, flipping output assumes that all the data used for learning is correctly labeled according to the target concept. However, in the transfer learning focused on in this study, the source domain contains data that is correctly labeled according to the target concept, as well as data that is not. Therefore, we expect two effects from the use of flipping output: One is reduced variance, and the other is that labels describing the target concept will be assigned to data already assigned labels differing from the concept. As a result, the number of data items labeled according to the target concept is increased, and the number of available data items is increased.

3.2. Algorithm of the Proposed Method

Here we describe the proposed method involving flipping output. The method is based on TrBagg. First, a source domain $D_S^f$, including data with different labels, is generated using flipping output. Then the two source domains $D_S$ and $D_S^f$ are combined to generate a new source domain $D_S^{\prime }$. Next, $T$ training datasets $d_1,d_2,\cdots ,d_T$ are generated from $D_S^{\prime }$ by bootstrap sampling. Learning from the generated individual datasets, $T$ classifiers $C_1,C_2,\cdots ,C_T$ are generated. Among $C_1,C_2,\cdots ,C_T$, classifiers whose experience error $ac{c}_1,ac{c}_2,\cdots ,ac{c}_T$ is less than the threshold $th$ with respect to $D_T$ are adopted as $C_i^{ad}$. If the experience error of a classifier is higher than $th$, the classifier is discarded.

This determination is made for all classifiers, and the result is calculated using only the adopted classifiers. The above algorithm is shown in Algorithm 2 and the flow chart in Figure 2.

Algorithm 2: Algorithm of the proposed method.

$i=1$

Create $D_s$ using flipping output

Prepare a new source domain $D_S^{\prime } (D_S+D_S^f)$

$\mathrm{for}n\mathrm{in}1:T$:

Bootstrap sampling from $D_S^{\prime }$ as $d_n$

Create classifier $C_n$ learning from $d_n$

Calculate experience error for $D_T$ as $ac{c}_n$

If $ac{c}_n<th:$

Save classifier $C_n$ as $C_i^{ad}$

$i=i+1$

Else:

Discard classifier $C_n$

$n=n+1$

Calculate result using $C_1^{ad}\cdots C_i^{ad}$

4. Experimental

In order to confirm the effectiveness of the proposed method, verification experiments were conducted using benchmark datasets and focusing on a binary classification problem.

4.1. Datasets

We conducted a verification experiment using two datasets described in the UCI benchmark dataset: The “abalone dataset” [10] and the “wine quality dataset” [11]. The abalone dataset summarizes measurements of physical characteristics of the abalone (eight dimensions) and the age of each. The wine quality dataset summarizes the measured values of the chemical composition of wine (11 dimensions) and the quality determined by sensory evaluation by wine experts (10 levels). In this experiment, in order to consider it as a binary classification problem, the age of the abalone was used as a target variable in the abalone dataset, and the quality of wine was used as a target variable in wine quality dataset. In the abalone dataset, data under 10 years old was assigned class label #1, and data of 10 years and older was assigned class label #2. In the wine quality dataset, data with quality level 5 or lower was assigned class label # 1, and data with quality level 6 or more was assigned class label #2.

Table 1. Abalone dataset.

Label	Original Label	Number of Data Items
#1	1~9	2096
#2	10~29	2081

shows the abalone dataset and

Table 2. Wine quality dataset.

Label	Original Label	Number of Data Items
#1	3~5	1640
#2	6~9	3258

the wine quality dataset used in this experiment. As shown in Table 1 and Table 2, the abalone dataset was a balanced problem with approximately the same number of data items in each class, and the wine quality dataset was an imbalanced problem with a class ratio of about 1:2.

4.2. Experimental Conditions

From the datasets prepared in Section 4.1, we created the target and source domains randomly so that they were disjointed. As a specific procedure, first, $N_T$ data are extracted from the data set and used as a target domain. Then, let the remaining data be the source domain. Since transfer learning is usually employed in situations where sufficient data for the target domain cannot be secured, we set $N_T=\left\{40,60,80,100\right\}$, to reproduce such situations. In addition, since the source domain contains data labeled with a standard different from the target concept, we intentionally included data with an erroneous label, in this paper referred to as non-target data. 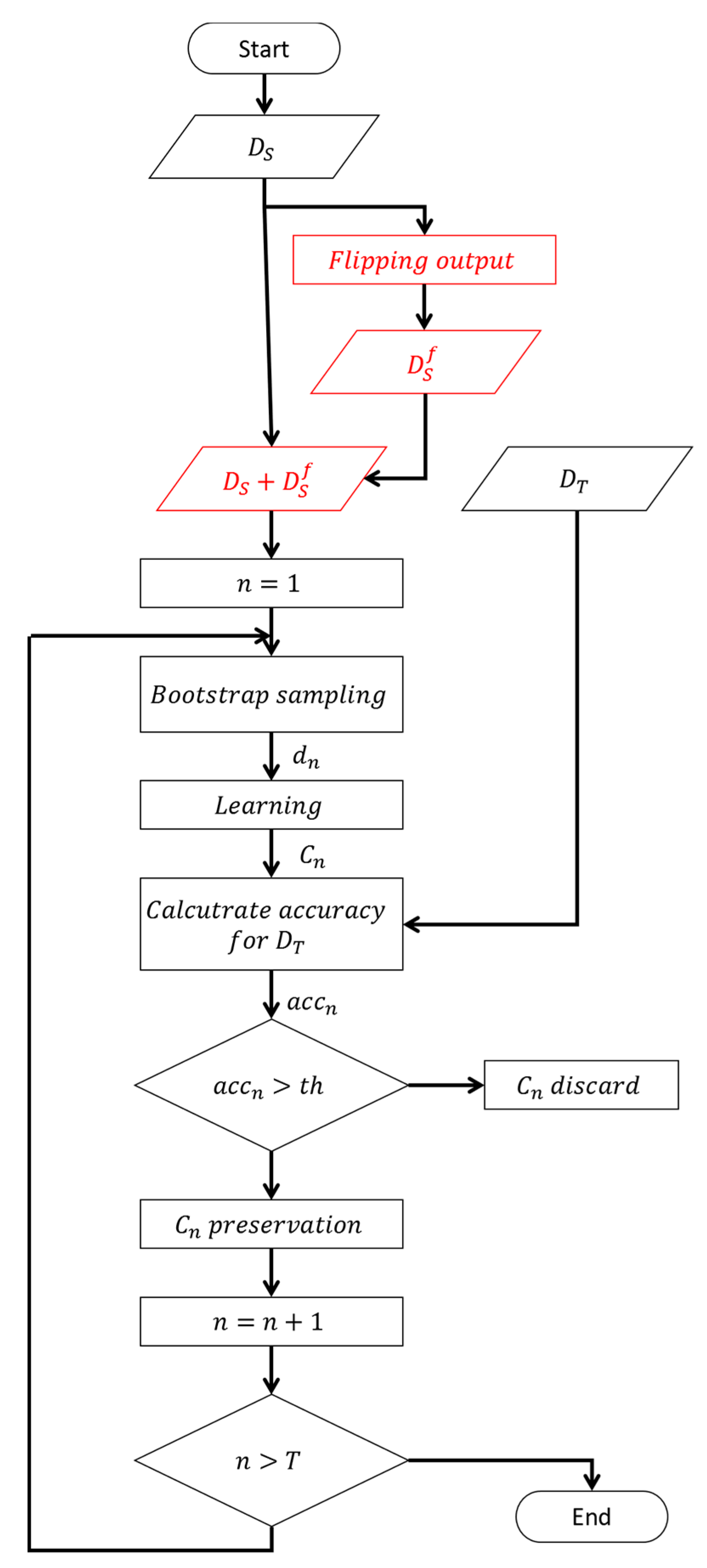The number of non-target data items was determined based on the size of the source domain, that is, we set the percentage of non-target data contained in the source domain at α$=\left\{0.2,0.4,0.6\right\}$, and α × $N_T$ data items were mislabeled in the source domain. In this study, we used a decision tree commonly used in ensemble learning, and generated multiple classifiers using bootstrap sampling. We set the amount of data extracted by bootstrap sampling at 50% of the $N_T$. In addition, the accuracy rate for the target domain of the base classifiers learned from the target domain was calculated using five-fold cross validation, and used as the adoption standard for the classifiers. In order to evaluate each method, five-fold cross validation was used.

4.3. Experimental Results

In this section, the results of experiments using the proposed method are reported. One of the merits of the proposed method is the extension of the source domain by using flipping output. Using the proposed method, which enables learning from the expanded source domain, we demonstrated that the accuracy could be improved in comparison with the conventional TrBagg transfer learning method.

4.3.1. Abalone Dataset

The experimental results for the abalone dataset are shown in

Table 3. Accuracy of test data using the abalone dataset.

${\mathit{N}}_{\mathit{T}}$	$\mathit{\alpha }$	$\mathbf{Bagging}\mathbf{Using}{\mathit{D}}_{\mathit{T}}$	$\mathbf{Bagging}\mathbf{Using}{\mathit{D}}_{\mathit{S}}$	TrBagg	Proposed Method
40	0.2	68.18	69.17	76.73	82.92
	0.4	72.55	66.58	75.89	76.73
	0.6	69.31	65.50	71.47	76.81
60	0.2	70.67	68.31	72.48	77.76
	0.4	70.01	66.96	73.83	74.74
	0.6	69.52	66.57	76.10	76.30
80	0.2	71.62	67.42	76.98	77.01
	0.4	71.22	65.50	76.90	78.36
	0.6	70.85	65.26	73.95	75.14
100	0.2	72.87	71.92	78.35	81.74
	0.4	72.99	66.14	74.88	80.91
	0.6	72.52	65.78	71.53	78.67

. The table shows the accuracy for test data of the proposed method, and additionally, the accuracy of TrBagg, a conventional transfer learning method, bagging for learning using only the target domain, and bagging for learning using only the source domain. We can see that the accuracy of bagging is low. This is considered to be due to the fact that the number of data items contained in the target domain is too small for sufficient learning. In most cases, TrBagg showed a higher accuracy than bagging, but when $\alpha =0.6$, the accuracy was sometimes lower than bagging. On the other hand, the proposed method showed higher accuracy than TrBagg under all conditions, and higher accuracy than bagging even when TrBagg’s accuracy was lower ($N_T=100,\alpha =0.6$).

4.3.2. Wine Quality Dataset

The experimental results for the wine quality dataset are shown in

Table 4. Accuracy of test data using the wine quality dataset.

${\mathit{N}}_{\mathit{T}}$	$\mathit{\alpha }$	$\mathbf{Bagging}\mathbf{Using}{\mathit{D}}_{\mathit{T}}$	$\mathbf{Bagging}\mathbf{Using}{\mathit{D}}_{\mathit{S}}$	TrBagg	Proposed Method
40	0.2	58.02	62.71	64.41	66.84
	0.4	59.61	60.25	60.46	65.54
	0.6	53.31	59.46	60.03	64.43
60	0.2	59.97	63.71	64.44	66.05
	0.4	60.98	62.90	63.74	67.01
	0.6	61.89	61.83	62.95	68.92
80	0.2	63.55	62.71	66.21	70.34
	0.4	64.02	63.63	65.98	68.68
	0.6	63.51	62.44	62.64	70.35
100	0.2	64.45	62.71	67.69	69.87
	0.4	64.79	62.99	67.21	69.89
	0.6	64.52	61.98	61.29	68.96

, which is structured similarly to Table 3. Table 4 shows that, as in the abalone dataset, bagging has low accuracy, and in many cases, the TrBagg accuracy is better than that of bagging. However, even in this experiment, there were cases where the accuracy of TrBagg was inferior to that of bagging when $\alpha =0.6$. As in Table 3, the proposed method showed higher accuracy than TrBagg under all conditions, and higher accuracy than bagging even when TrBagg’s accuracy was worse ($N_T=100,\alpha =0.6$).

4.4. Discussion

Consider the experimental results described in Section 4.3. The target variable in the abalone dataset is a quantitative label because it is the age of the abalone, while the objective variable in the wine quality dataset is a qualitative label because it is based on sensory evaluation by a wine expert. Therefore, it is considered that the labels in the wine quality dataset had variation. First, we discuss the accuracy of the two bagging (learning using target domain and learning using source domain). In the bagging learned using the target domain, the accuracy is improved as the number of target domains increases. On the other hand, bagging learned using the source domain shows a stable accuracy. It is important to note that as α increases, the accuracy of bagging with the source domain tends to decrease. When there are many target domains, learning with source domains shows a worse accuracy than with target domains. Next, we discuss the accuracy of TrBagg, a conventional transfer learning method, under the conditions of this experiment. In the case of $N_T=40,60,80$, it can be seen that TrBagg exhibits higher accuracy than bagging learned using the target domain, under all conditions. However, when $N_T=100$ and $\alpha =0.6$, TrBagg exhibits lower accuracy than bagging. There are two possible causes. One is that when $\alpha =0.6$, there were few classifiers that could be adopted from the source domain. The data used for learning relies on random sampling by bootstrap sampling, because it is not known which data in the source domain is in accordance with the target concept. In a source domain in which more than half the data is erroneously labeled, it is considered that many data items with erroneous labels will inevitably be extracted. Therefore, it can be inferred from the results above that many classifiers could not properly learn the target concept. The other possible cause was the evaluation method for classifier adoption. Each classifier learned from data in the source domain is adopted or discarded based on its accuracy for the target domain. In this process, the target-domain accuracy of bagging learned from the target domain is used as the adoption criterion. In the case of $N_T=100$, the accuracy of bagging learning from the target domain is improved. As a result, the adoption criterion is also improved, and it is considered that it is difficult to adopt many classifiers. It can be said that TrBagg is not fully effective when there are a large number of data items in the target domain, and more than half the data in the source domain is erroneously labeled.

Next, we consider the proposed method. It can be seen that under all conditions of the validation experiments, the accuracy of the proposed method is higher than that of TrBagg. This shows the effect of extending the source domain by flipping output. There are two expected effects of the flipping output: 1) An increase in diversity as the number of data items increases, and 2) proper labeling of mislabeled data. Let us examine each of these effects. We will assume that all the data in the source domain is assigned a correct label (i.e., $\alpha =0$), and evaluate the improvement in accuracy in the proposed method.

Table 5. Accuracy of test data when $\alpha =0$.

	Abalone Dataset			Wine Quality Dataset
${\mathit{N}}_{\mathit{T}}$	Bagging	TrBagg	Proposed Method	Bagging	TrBagg	Proposed Method
40	74.87	79.40	79.08	60.10	63.07	64.37
60	69.76	76.68	76.54	60.86	65.16	66.00
80	74.78	79.56	79.54	62.06	68.96	69.71
100	64.27	69.86	69.86	66.27	72.41	72.73

shows the results. We can see that the accuracy in the proposed method is not improved, compared to TrBagg, in many cases. From this, it can be seen that the performance improvement due an increase in diversity cannot be expected very much. Therefore, it is judged that the improvement in performance of the proposed method is due to proper labeling of mislabeled data. Notably, even when the accuracy of TrBagg is worse than that of bagging ($N_T=100,\alpha =0.6$), the accuracy can be improved by using the proposed method.

In order to further verify the effectiveness of the proposed method, we introduce effect size, a statistical indication of the effectiveness of a proposed method. In this paper, we used $Cohe{n}^{’}s d$ [12], an effect size that represents the difference between two groups. $Cohe{n}^{’}s d$ between the two groups $g_1$ and $g_2$ is as follows:

$$Cohe{n}^{’}s d=\frac{\left|{\mu }_1-{\mu }_2\right|}{\sqrt{\frac{n_1{\sigma }_1^2+n_2{\sigma }_2^2}{n_1+n_2}}}$$

(2)

Here, the sample size of $g_1$ is $n_1$, the variance ${\sigma }_1^2$, and the sample average ${\mu }_1$. The sample size of $g_2$ is $n_2$, the variance ${\sigma }_2^2$, and the sample average ${\mu }_2$. The larger the value of $Cohe{n}^{’}s d$, the larger the difference between the average values of the two groups.

Table 6. $Cohe{n}^{’}s d$ using the proposed method and bagging.

${\mathit{N}}_{\mathit{T}}$	$\mathit{\alpha }$	Abalone Dataset	Wine Quality Dataset
40	0.2	0.551	0.555
	0.4	0.596	0.510
	0.6	0.578	1.019
60	0.2	0.508	0.432
	0.4	1.019	0.417
	0.6	1.103	1.038
80	0.2	0.973	0.779
	0.4	0.902	0.555
	0.6	1.092	0.788
100	0.2	0.548	0.888
	0.4	0.753	0.884
	0.6	0.705	0.603

shows the comparative effect size between the proposed method and bagging in each condition of the verification experiment, and

Table 7. $Cohe{n}^{’}s d$ using the proposed method and TrBagg.

${\mathit{N}}_{\mathit{T}}$	$\mathit{\alpha }$	Abalone Dataset	Wine Quality Dataset
40	0.2	0.141	0.155
	0.4	0.211	0.235
	0.6	0.252	0.531
60	0.2	0.178	0.091
	0.4	0.362	0.165
	0.6	0.399	0.620
80	0.2	0.178	0.174
	0.4	0.298	0.270
	0.6	1.053	0.916
100	0.2	0.161	0.095
	0.4	0.527	0.327
	0.6	1.243	0.603

shows the effect size between the proposed method and TrBagg. Table 6 and Table 7 clearly show that the proposed method has a large effect size. Table 6 shows that the effect size increases as $\alpha$ increases. In particular, when $\alpha =0.6$, the effect size compared with TrBagg is expected to be very large, 0.9 or more. Therefore, it can be seen that the proposed method is more effective as more data are incorrectly labeled in the source domain. However, when $\alpha$ is small, the effect size is as small as 0.2. This suggests that the proposed method is effective when the source domain contains many errors. Table 7 also shows that the proposed method is effective when $N_T$ is small.

5. Related Research

As in the case of transfer learning discussed in this paper, several machine learning approaches involving two types of data have been proposed. Semi-supervised learning [13] complements labeled data with unlabeled data to improve the generalization performance of the classifiers. However, in focusing on unlabeled data, the technique differs from inductive transfer learning, which focuses on labeled data. In self-training [14], one of the semi-supervised learning methods, the labels of unlabeled data are estimated using classifiers learned from labeled data, and these data are then employed for learning. Self-training is similar to the proposed method in its use of two types of labeled data, but it depends on the distribution of labeled data for label estimation. In inductive transfer learning, on the other hand, data is labeled according to each standard, so that it has the possibility of more diverse distribution than the target domain. As in the proposed method, TrAdaBoost [15] utilizes ensemble learning as part of transfer learning. However, TrAdaBoost is based on Adaboost [16], which updates the training case weights, and the sequential change in these weights marks a clear difference from the proposed method. Finally, unlike in the proposed method, some transfer learning methods [17,18] transfer knowledge based on features not case-dependent. However, in these methods, it is difficult to select data and to provide multiple labels for one feature vector, both of which are facilitated by the proposed method.

6. Conclusions

In order to make transfer learning work effectively in various situations, we proposed in this paper a transfer learning method that extends the source domain. The following key results were obtained through verification experiments using benchmark datasets.

• If much data in the source domain is incorrectly labeled, conventional transfer learning methods will tend to have reduced accuracy due to negative transfer.
• Negative transfer can be suppressed by extending the source domain using the proposed method.
• Even in situations where negative transfer does not occur, the accuracy of the proposed method is higher than the conventional transfer learning method, because the proposed method increases the amount of effective data for learning.

Overall, the results suggest that use of the proposed method can suppress negative transfer and improve accuracy in various situations.

There are many practical fields (manufacturing, scientific experimentation, etc.) in which exact labeling of data is difficult, and it is generally difficult to apply transfer learning to such fields. Use of the proposed method, however, enables the transfer of appropriate knowledge even in such situations, making it possible to construct systems that utilize more real-world data.

However, as noted in the discussion of the verification experiment in Section 4.4, if the data in the source domain is largely correctly labeled (data that can be labeled with the correct index, $\alpha =0.2$ in the experiment), the effect size of the proposed method (0.2) suggested that no significant improvement could be expected over the comparison methods.

In sum, the study suggests that the features of the method proposed in this paper are suitable for application to various real-world problems.

Future work will include refinement of the proposed learning technique, such as more efficient sampling and improvement in the adoption criteria, to improve the discrimination accuracy.