An INS-UWB Based Collision Avoidance System for AGV
Abstract
:1. Introduction
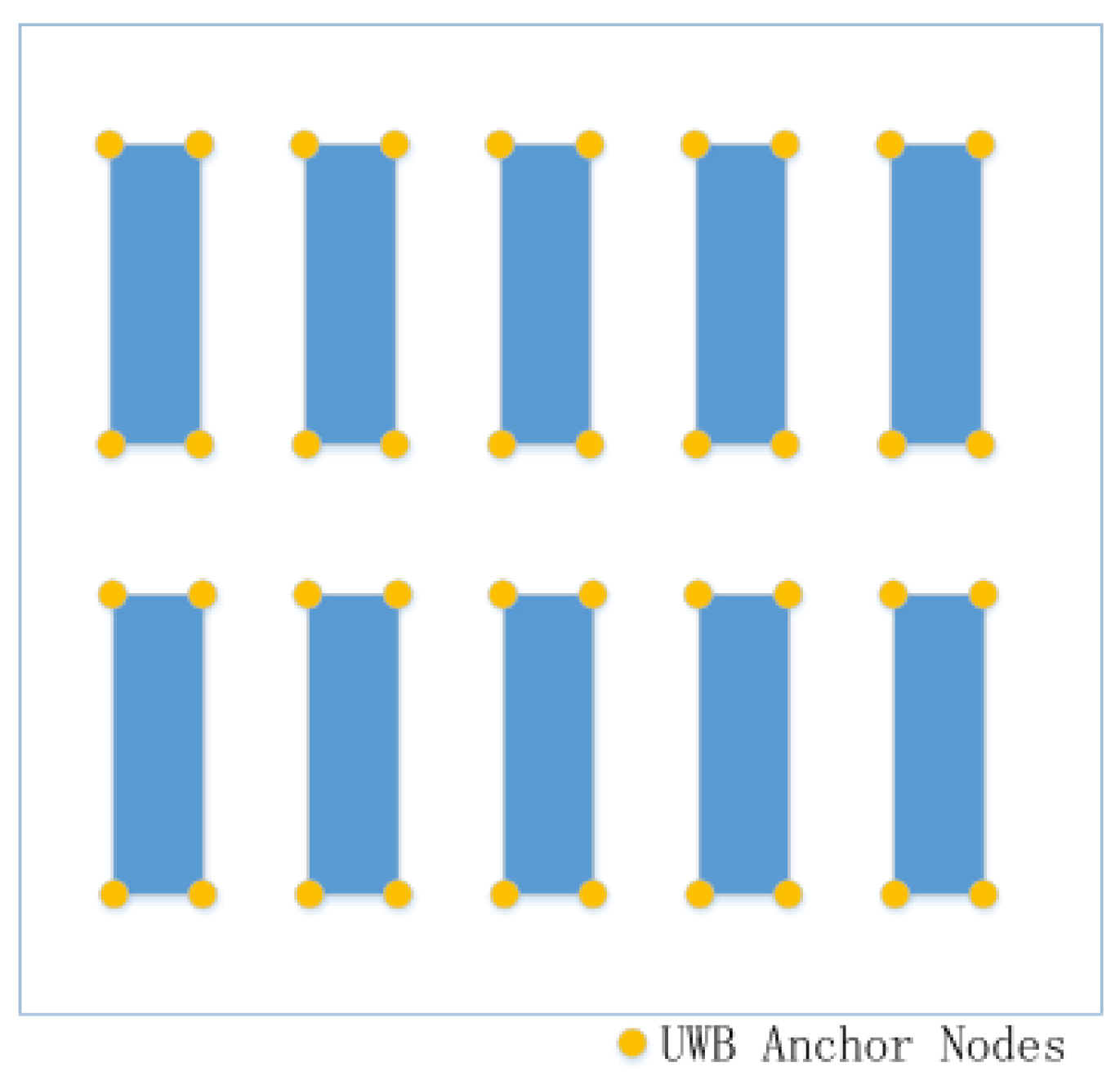
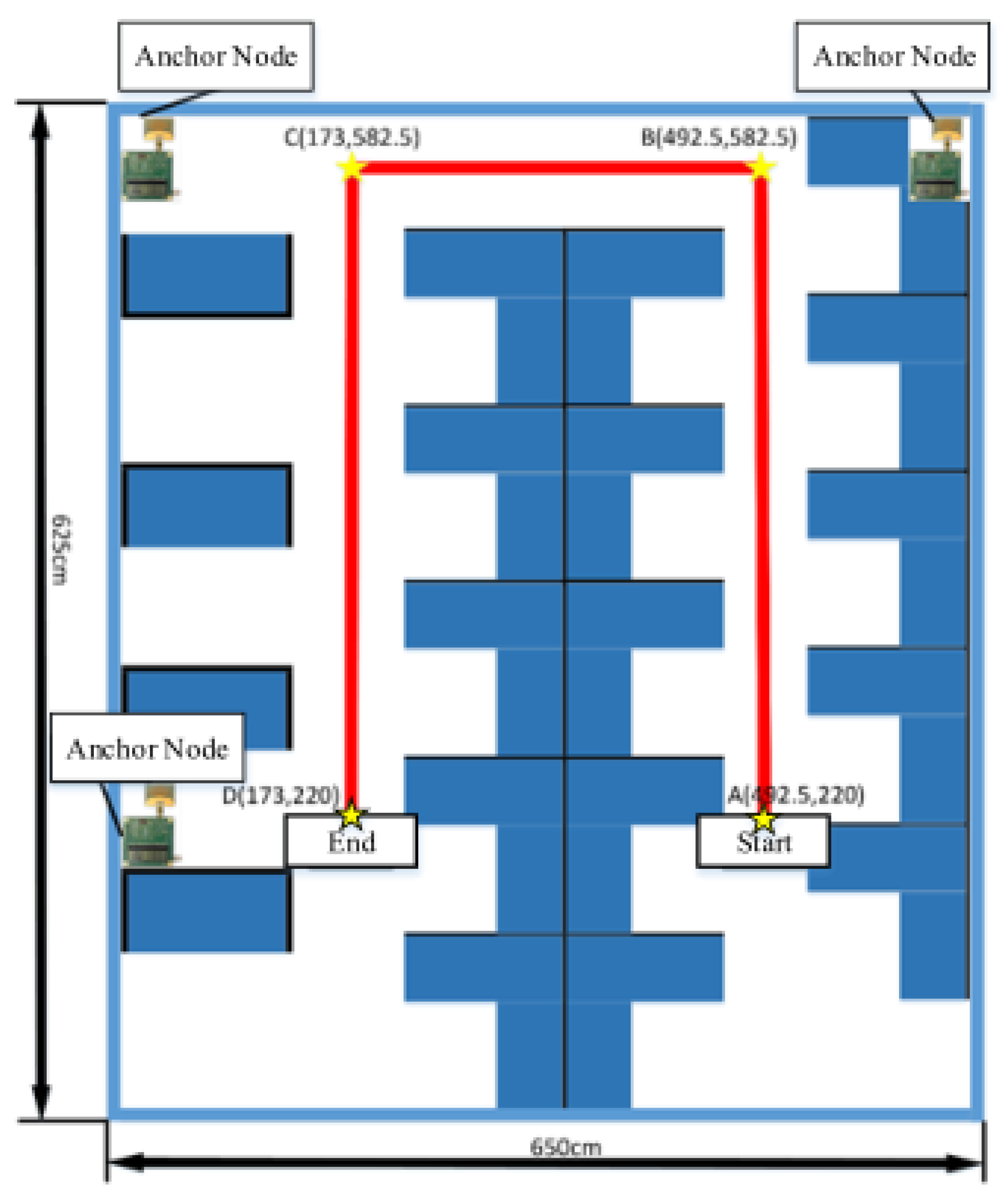
2. Factory Scenario of the Application
3. Collision Avoidance System Design
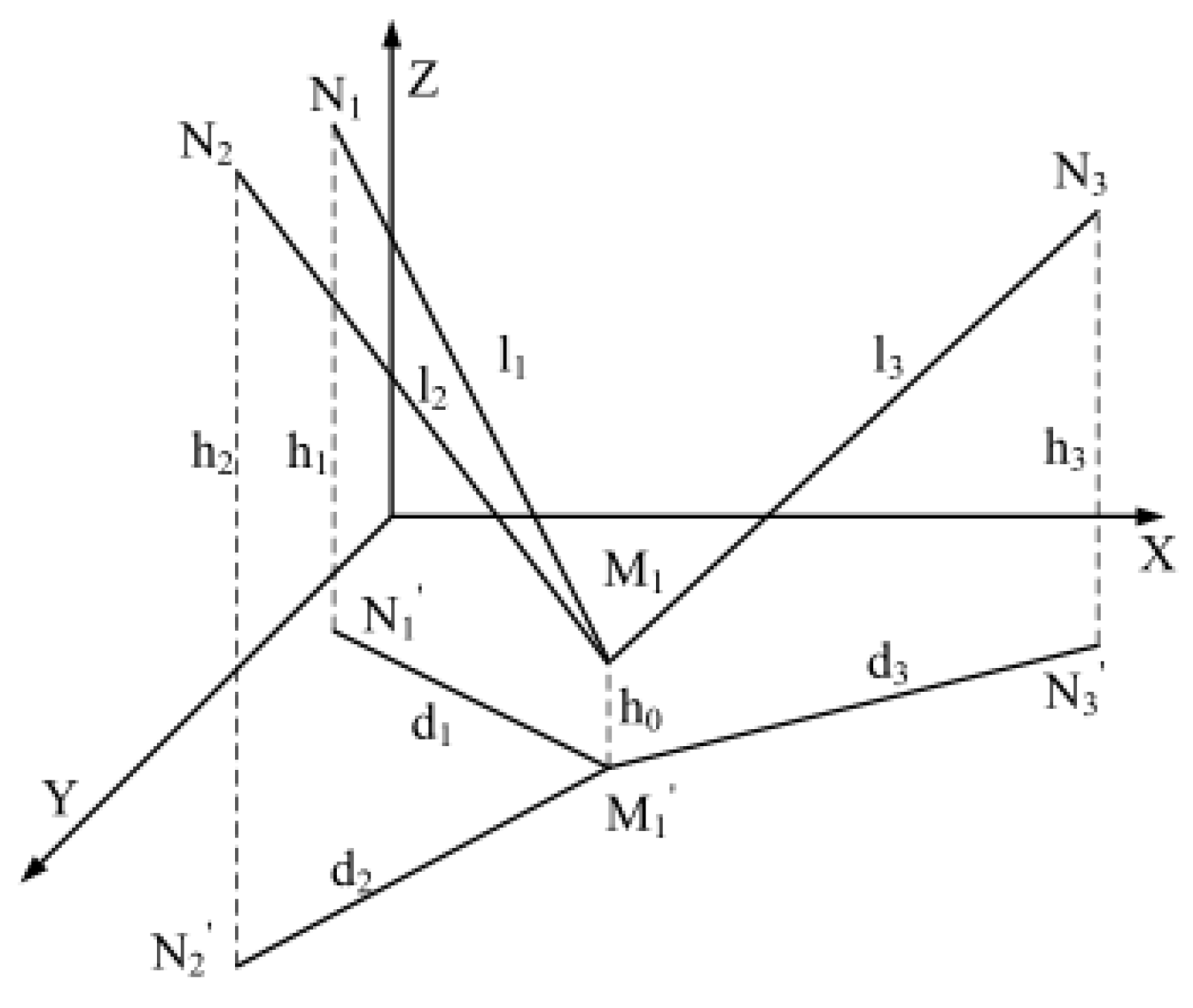
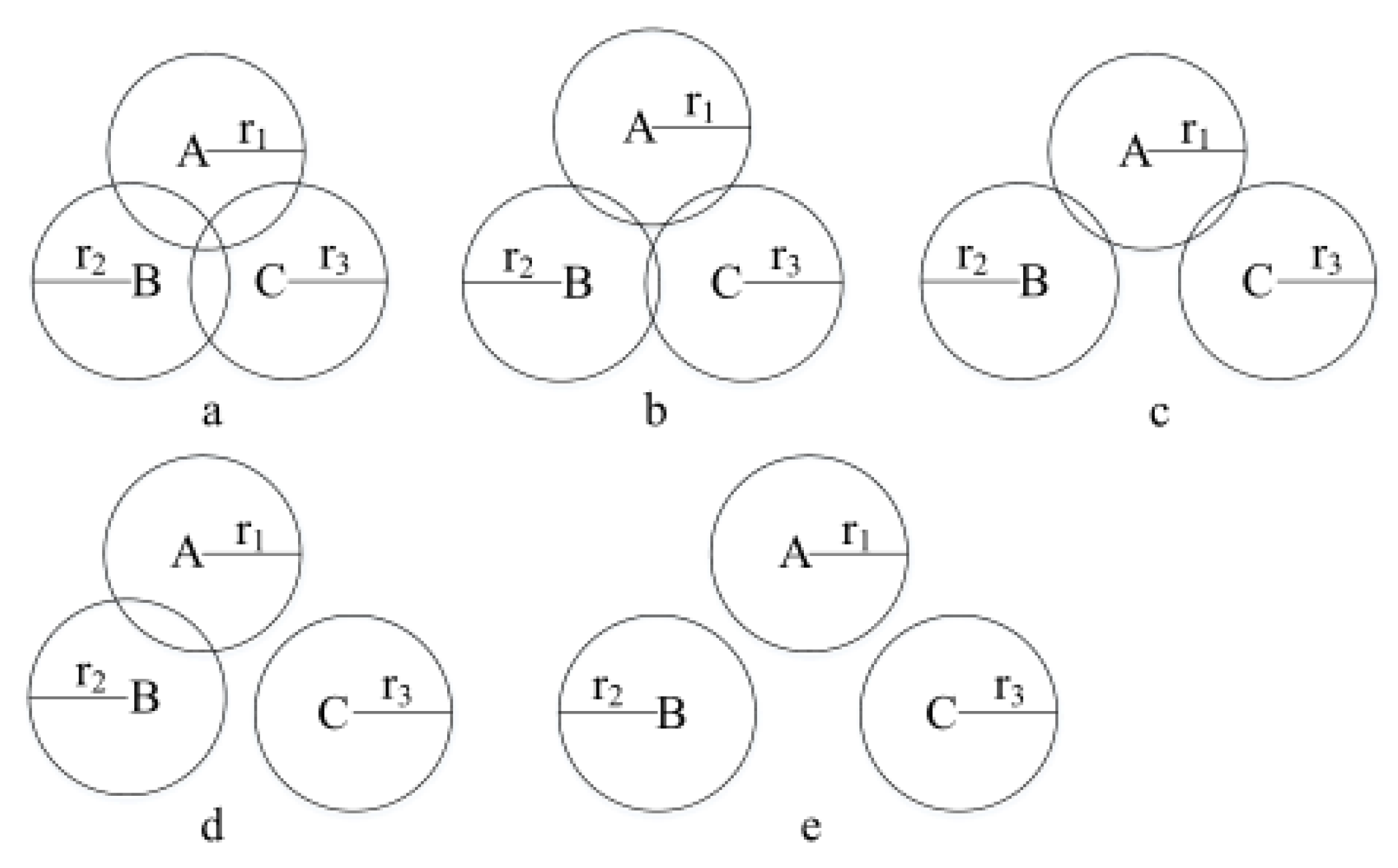
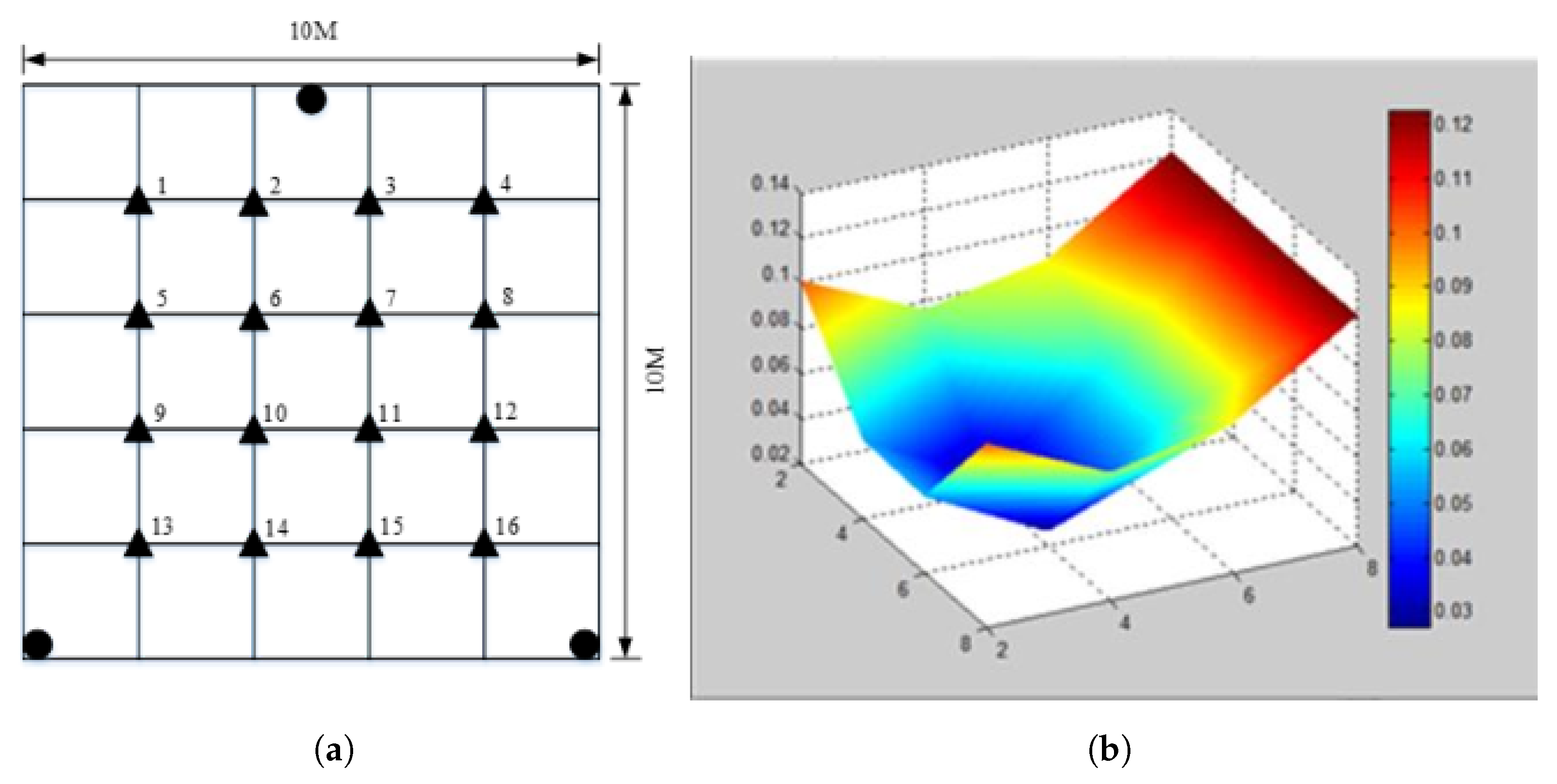
3.1. UWB Positioning
3.2. INS and UWB Integrated Positioning Method
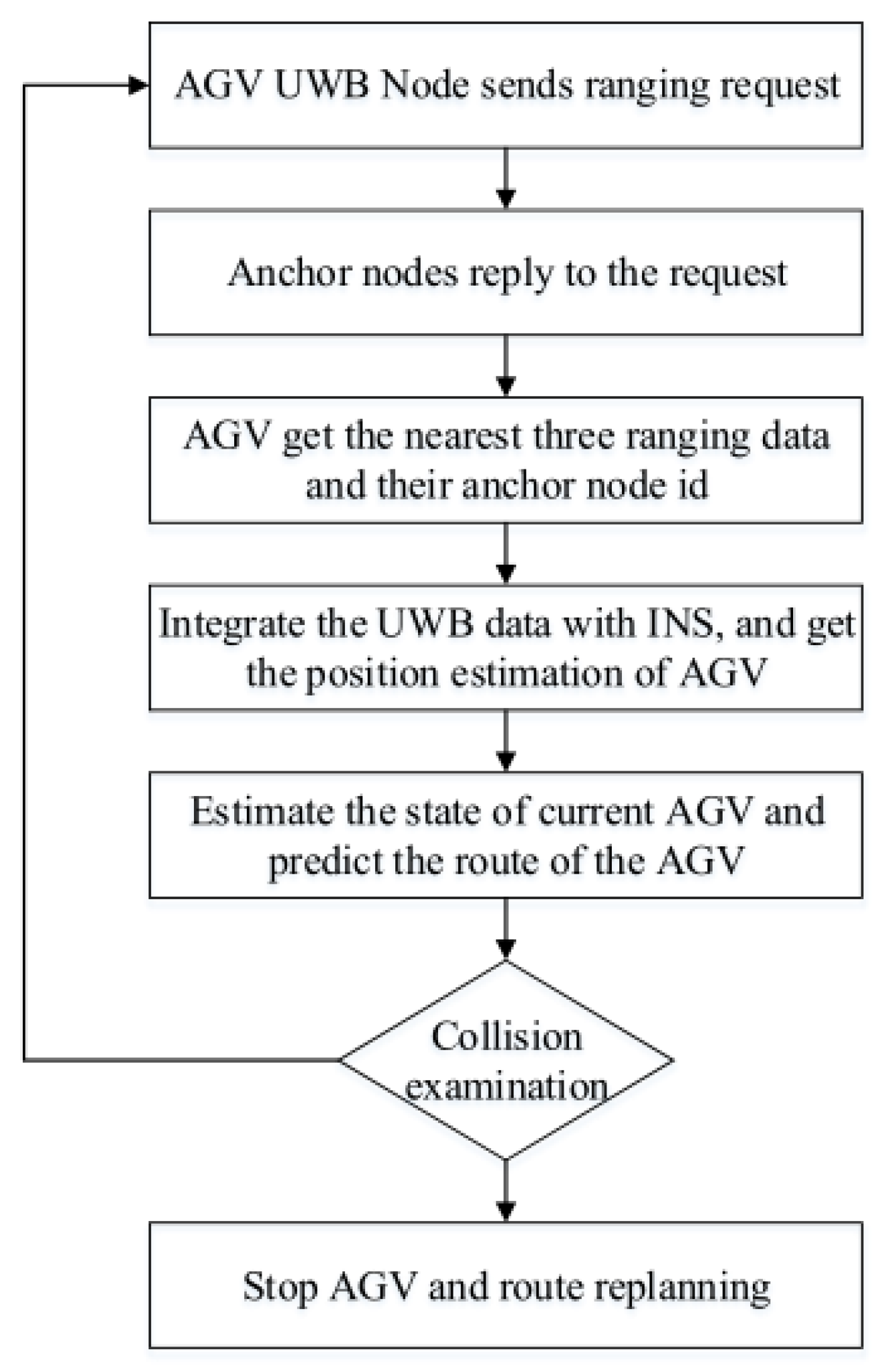
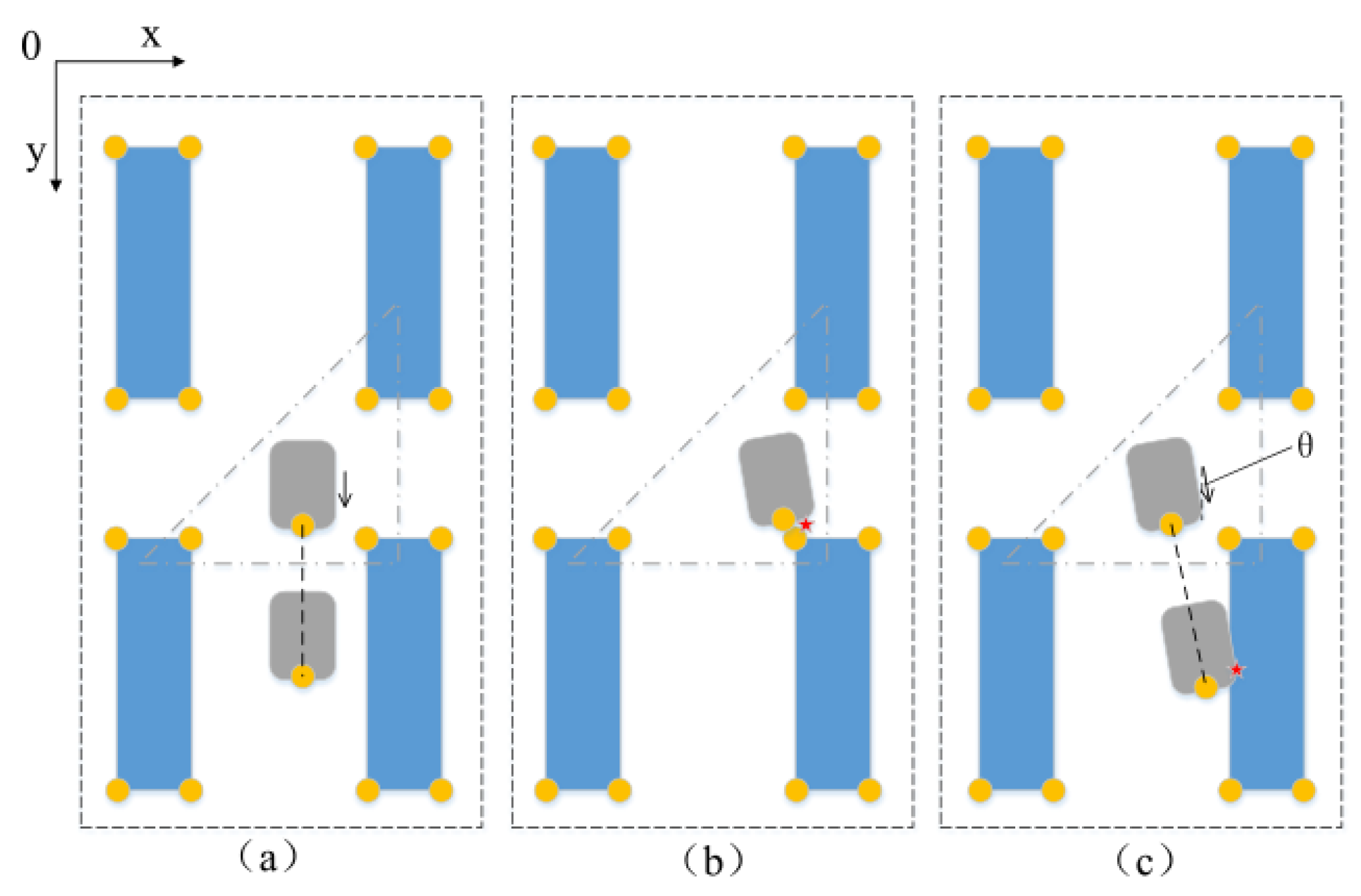
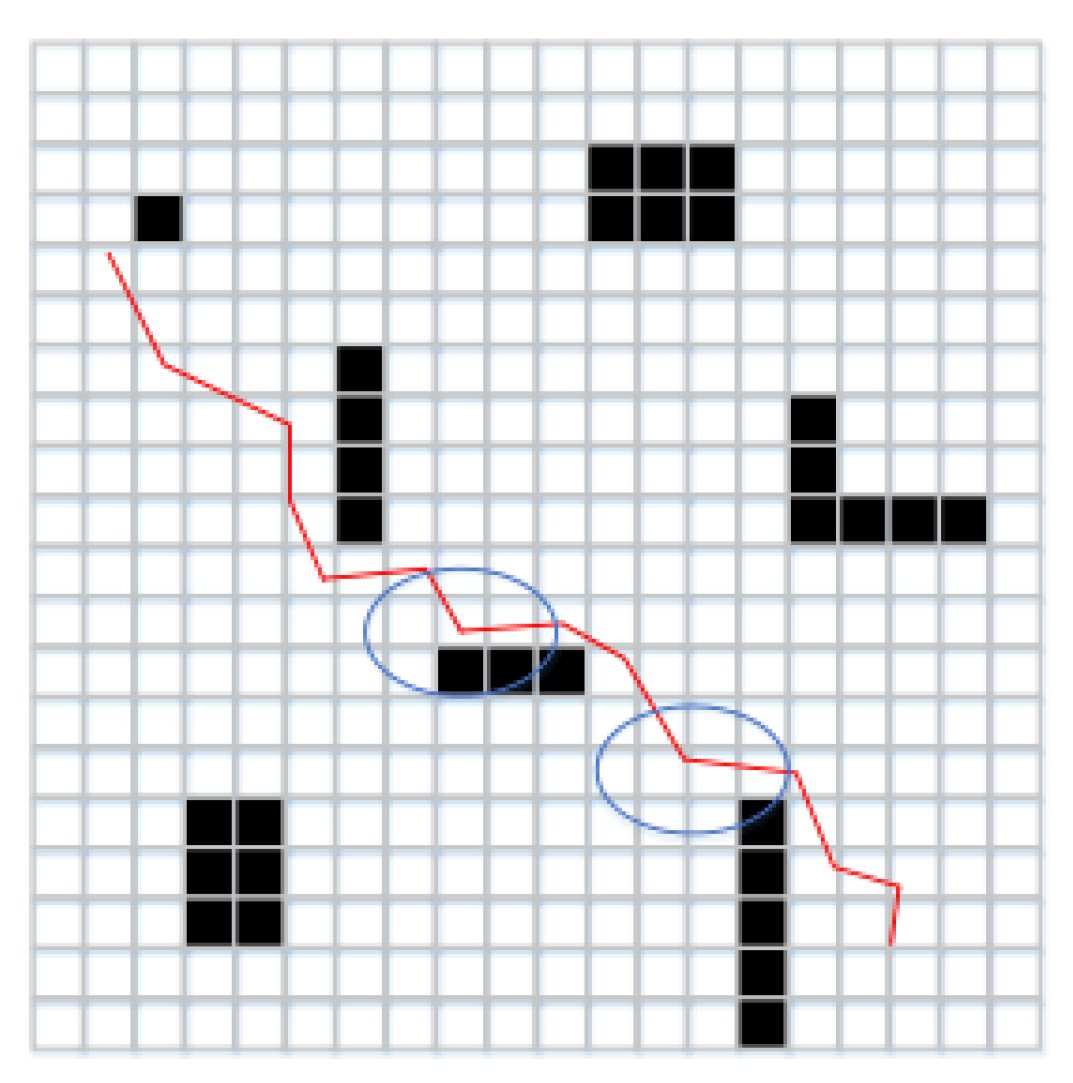
3.3. AGV Collision Avoidance System
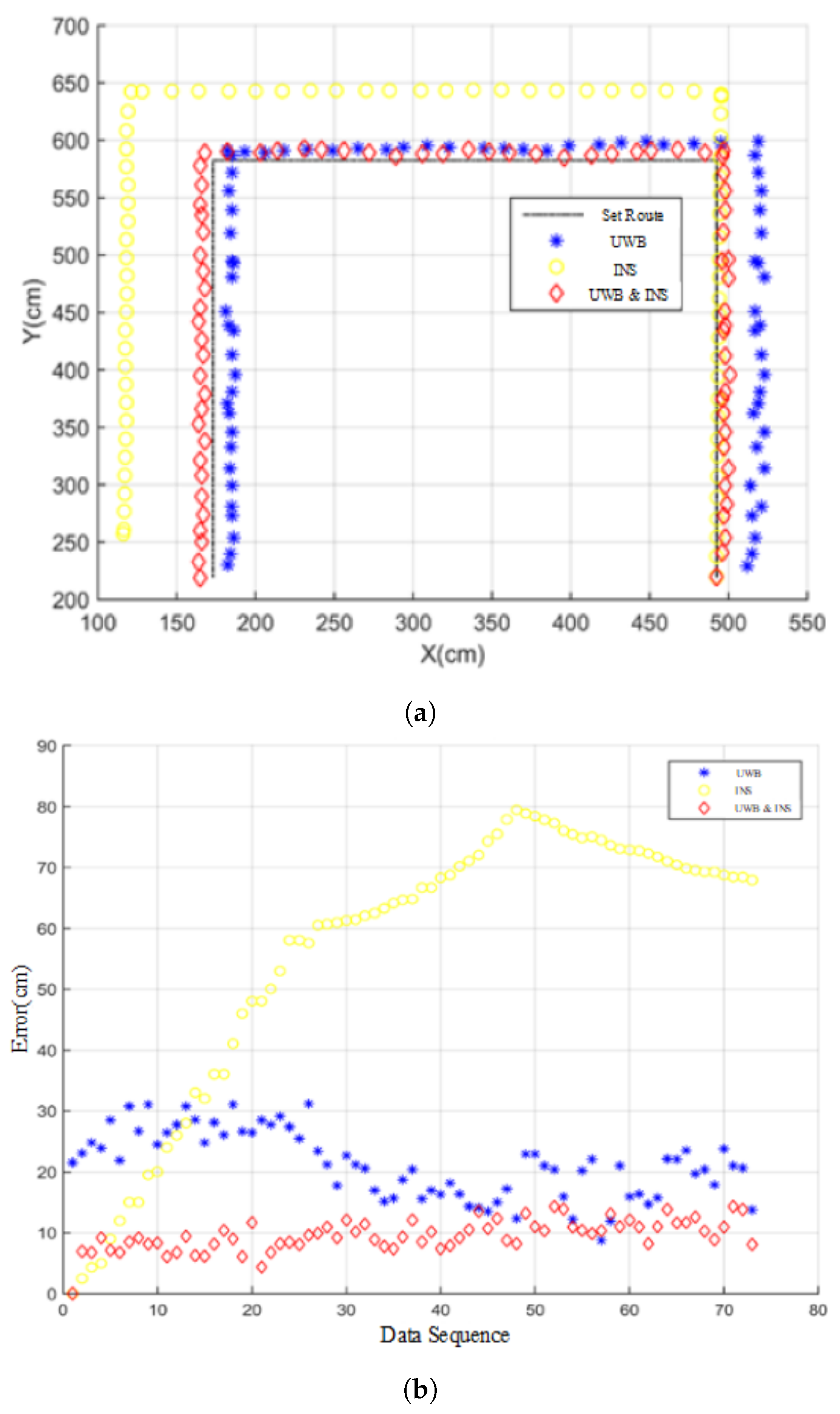
4. Experiment Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gotting, H.H. Automation and Steering of Vehicles in ports. Port Technol. Int. 2000, 10, 101–111. [Google Scholar]
- Vis, I.F. Survey of research in the design and control of automated guided vehicle systems. Eur. J. Oper. Res. 2006, 170, 677–709. [Google Scholar] [CrossRef]
- Zirkelbach, C. Integration of Automated Guided Vehicles into Manufacturing Plants. Intelligent Robots— Sensing, Modeling and Planning; World Scientific: Singapore, 1996; pp. 449–466. [Google Scholar]
- Yudanto, R.G.; Petre, F. Sensor fusion for indoor navigation and tracking of automated guided vehicles. In Proceedings of the 2015 International Conference on IEEE Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015; pp. 1–8. [Google Scholar]
- Zhan, Y.; Luo, Y. Guided and detecting technology of intelligent robot AGV and new-style AGV. In Proceedings of the International Conference on Sensors & Control Techniques, Wuhan, China, 9 May 2000; pp. 461–464. [Google Scholar]
- Cho, H.; Song, H.; Park, M.; Kim, J.; Woo, S.; Kim, S. Independence localization system for Mecanum wheel AGV. In Proceedings of the 2013 IEEE RO-MAN, Gyeongju, South Korea, 26–29 August 2013; pp. 192–197. [Google Scholar]
- Kim, J.; Cho, H.; Kim, S. Positioning and driving control of fork-type automatic guided vehicle with laser navigation. Int. J. Fuzzy Logic Intell. Syst. 2013, 13, 307–314. [Google Scholar] [CrossRef]
- Siagian, C.; Chang, C.K.; Itti, L. Mobile robot navigation system in outdoor pedestrian environment using vision-based road recognition. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 564–571. [Google Scholar]
- Saab, S.S.; Nakad, Z.S. A standalone RFID indoor positioning system using passive tags. IEEE Trans. Ind. Electron. 2011, 58, 1961–1970. [Google Scholar] [CrossRef]
- Fang, S.H.; Lin, T. Principal component localization in indoor WLAN environments. IEEE Trans. Mob. Comput. 2012, 11, 100–110. [Google Scholar] [CrossRef]
- Grossmann, R.; Golatowski, F.; Timmermann, D. Weighted centroid localization in zigbee-based sensor networks, In Proceedings of 2007 IEEE International Symposium on Intelligent Signal Processing WISP, Alcala de Henares, Spain, 3–5 October 2007; pp. 1–6. [Google Scholar]
- Pivarciova, E.; Csongrady, T. Tracer robot with a proportional control. MM Sci. J. 2016, 1277–1286. [Google Scholar] [CrossRef]
- Krishnan, S.; Sharma, P.; Guoping, Z.; Woon, O.H. A uwb based localization system for indoor robot navigation. In Proceedings of the IEEE International Conference on UltraWideband, Singapore, 24–26 September 2007; pp. 77–82. [Google Scholar]
- Zhao, S.Y.; Hua18ng, B.; Liu, F. Localization of Indoor Mobile Robot Using Minimum Variance Unbiased FIR Filter. IEEE Trans. Autom. Sci. Eng. 2018, 15, 410–419. [Google Scholar] [CrossRef]
- Huerta, J.M.; Vidal, J.; Giremus, A.; Tourneret, J.-Y. Joint particle filter and UKF position tracking in severe non-line-of-sight situations. IEEE J. Sel. Top. Signal Process 2009, 3, 874–888. [Google Scholar] [CrossRef]
- Derr, K.; Manic, M. Wireless sensor networks—Node localization for various industry problems. IEEE Trans. Ind. Inform. 2015, 11, 752–762. [Google Scholar] [CrossRef]
- DiGiampaolo, E.; Martinelli, F. Mobile robot localization using the phase of passive UHF RFID signals. IEEE Trans. Ind. Electron. 2014, 61, 365–376. [Google Scholar] [CrossRef]
- Benini, A.; Mancini, A.; Longhi, S. An imu/uwb/vision-based extended kalman filter for mini-uav localization in indoor environment using 802.15. 4a wireless sensor network. J. Intell. Robot. Syst. 2013, 70, 461–476. [Google Scholar] [CrossRef]


| Line 1 | 0.1226 | 0.1219 | 0.1222 | 0.1235 | 0.1226 |
| Line 2 | 0.0871 | 0.0664 | 0.0662 | 0.0861 | 0.0765 |
| Line 3 | 0.0773 | 0.0272 | 0.0291 | 0.0755 | 0.0528 |
| Line 4 | 0.1017 | 0.0546 | 0.0527 | 0.1001 | 0.0773 |
| Average | 0.0972 | 0.0675 | 0.0676 | 0.0963 | 0.0823 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Hu, J.; Li, J.; Liu, R.; Shu, M.; Yang, Y. An INS-UWB Based Collision Avoidance System for AGV. Algorithms 2019, 12, 40. https://doi.org/10.3390/a12020040
Sun S, Hu J, Li J, Liu R, Shu M, Yang Y. An INS-UWB Based Collision Avoidance System for AGV. Algorithms. 2019; 12(2):40. https://doi.org/10.3390/a12020040
Chicago/Turabian StyleSun, Shunkai, Jianping Hu, Jie Li, Ruidong Liu, Meng Shu, and Yang Yang. 2019. "An INS-UWB Based Collision Avoidance System for AGV" Algorithms 12, no. 2: 40. https://doi.org/10.3390/a12020040
APA StyleSun, S., Hu, J., Li, J., Liu, R., Shu, M., & Yang, Y. (2019). An INS-UWB Based Collision Avoidance System for AGV. Algorithms, 12(2), 40. https://doi.org/10.3390/a12020040




