Computation of Compact Distributions of Discrete Elements
Abstract
:1. Introduction
2. Related Work
3. Methods of This Paper
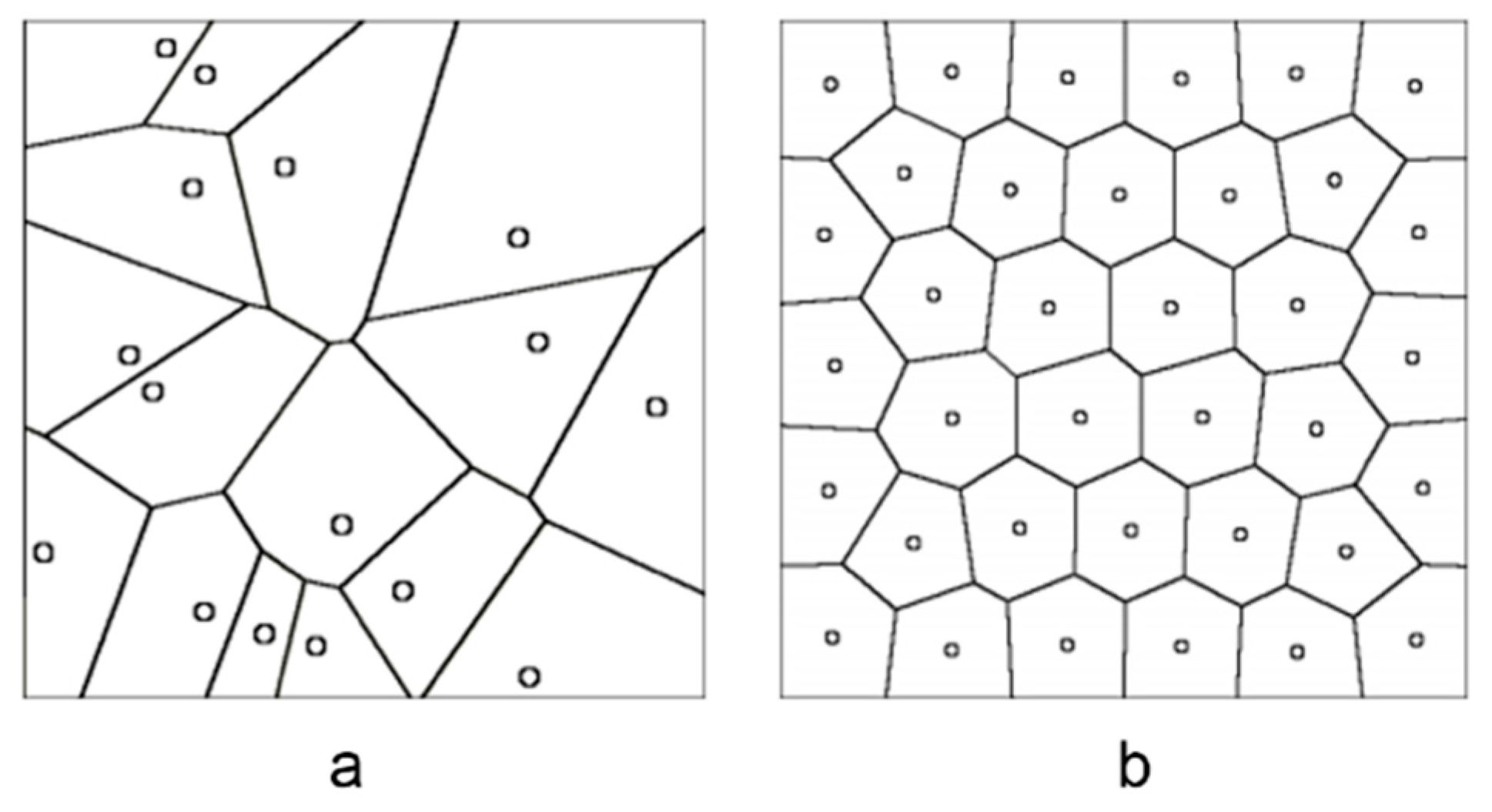
3.1. Voronoi Diagram Based on Several Distance Metrics
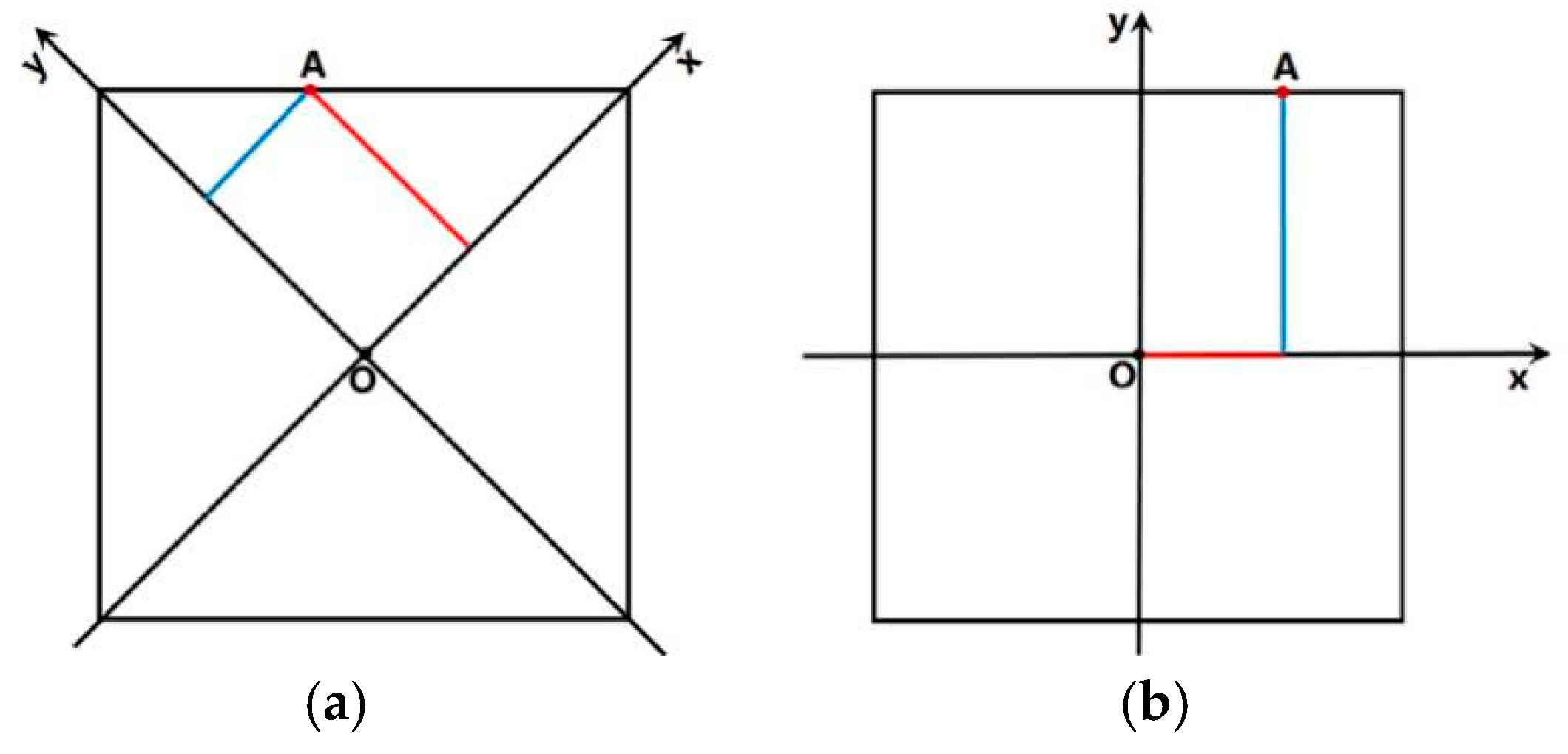
3.1.1. Chebyshev Distance
3.1.2. Chebyshev Distance with Axial Scale
3.1.3. L2-Metric Distance with Axial Scale
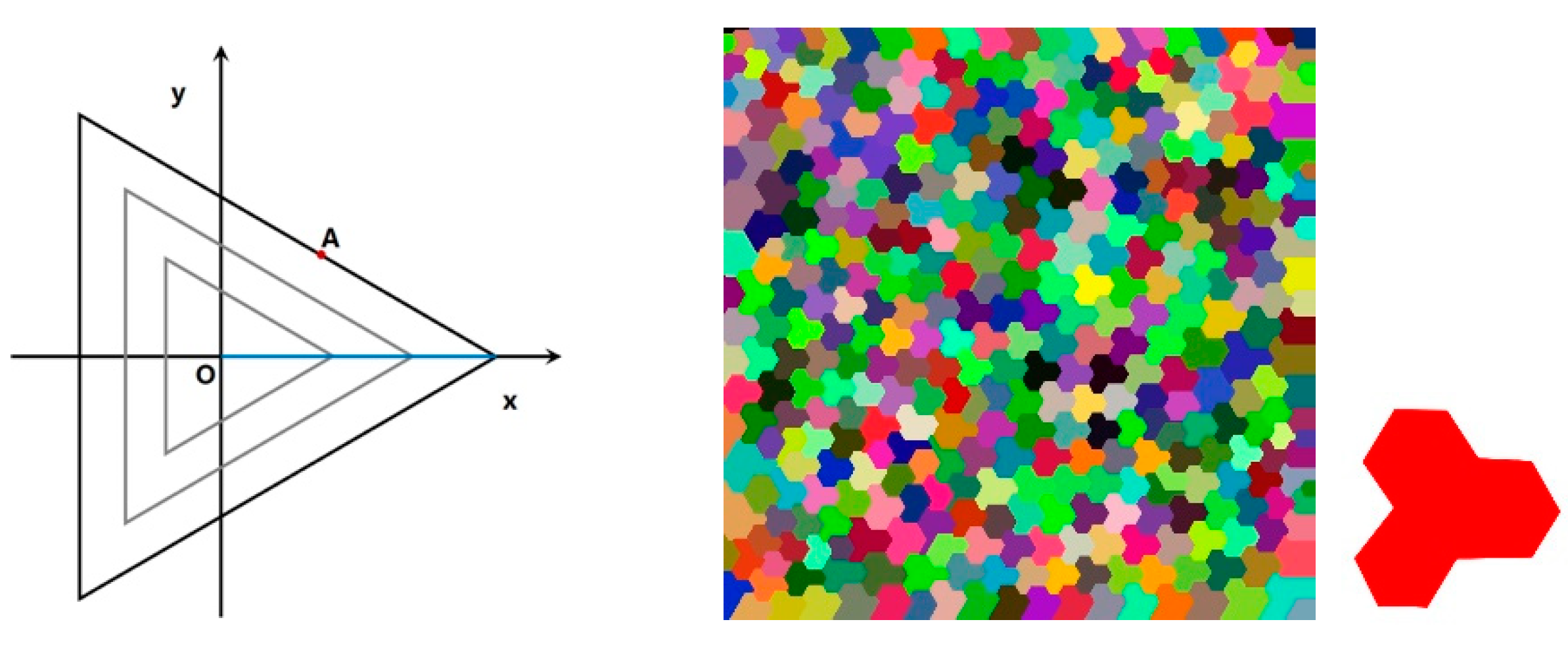
3.1.4. Equidistant Line Distance
3.2. Voronoi Diagram Generation Based on GPU Acceleration
3.3. Parametric Control of Element Distribution
3.3.1. Changing of Element Sizes
3.3.2. Changing of the Vector Field
3.4. Placement of the Elements
4. Results
4.1. Experimental Results
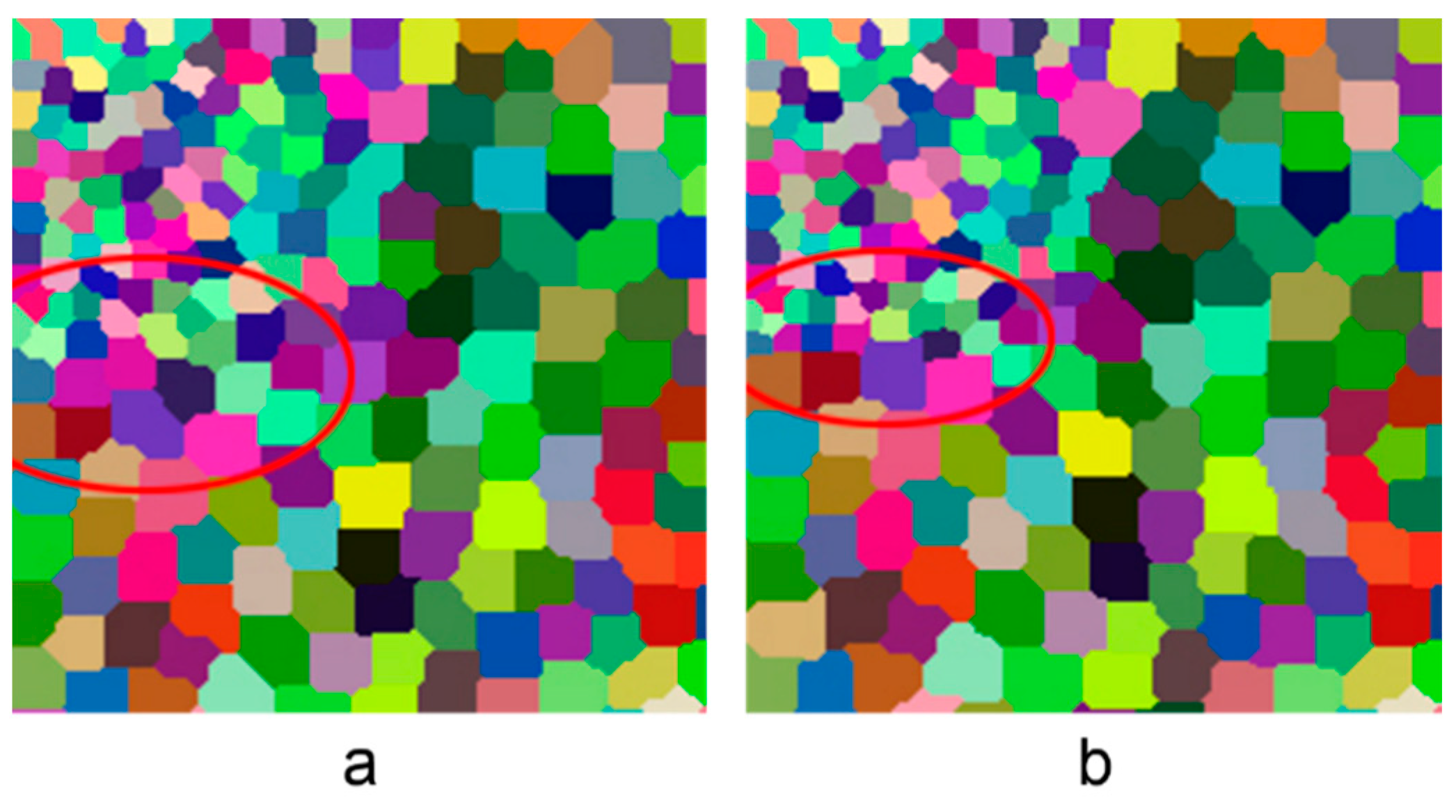
4.2. Synthesis Effect Comparison
5. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Cho, J.H.; Xenakis, A.; Gronsky, S. Course 6: Anyone can cook: inside Ratatouille’s kitchen. In Proceedings of the SIGGRAPH ‘07 ACM SIGGRAPH 2007 courses, San Diego, CA, USA, 5–9 August 2007; Available online: https://www.xuebuyuan.com/zh-hant/121918.html (accessed on 16 February 2019).
- Guendelman, E.; Bridson, R.; Fedkiw, R. Nonconvex rigid bodies with stacking. ACM Trans. Graphics 2003, 22, 871–878. [Google Scholar] [CrossRef]
- Barla, P.; Breslav, S.; Markosian, L.; Thollot, J. Interactive Hatching and Stippling by Example. Available online: https://arxiv.org/abs/cs/0607050 (accessed on 14 February 2019).
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Cook, R.L. Stochastic sampling in computer graphics. ACM Trans. Graphics 1986, 5, 51–72. [Google Scholar] [CrossRef]
- Hoff, K.; Keyser, J.; Lin, M.; Manocha, D.; Culver, T. Fast Computation of Generalized Voronoi Diagrams Using Graphics Hardware. In Proceedings of the 26th annual conference on Computer graphics and interactive techniques, Los Angeles, CA, USA, 8–13 August 1999; pp. 277–286. [Google Scholar]
- Smith, K.; Liu, Y.; Klein, A.W. Animosaics. In Proceedings of the 2005 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Los Angeles, CA, USA, 29–31 July 2005; pp. 201–208. [Google Scholar]
- Efros, A.A.; Leung, T.K. Texture synthesis by non-parametric sampling. In Proceedings of the International Conference on Computer Vision 1999, Kerkyra, Corfu, Greece, 20–25 September 1999; pp. 1033–1038. [Google Scholar]
- Wei, L.; Levoy, M. Fast texture synthesis using tree-structured vector quantization. In Proceedings of the 27th annual conference on Computer graphics and interactive techniques, New Orleans, LA, USA, 23–28 July 2000; pp. 479–488. [Google Scholar]
- Fritzsche, L.P.; Hellwig, H.; Hiller, S.; Deussen, O. Interactive design of authentic looking mosaics using Voronoi structures. In Proceedings of the 2nd international symposium on Voronoi diagrams in science and engineering VD 2005 conference, Seoul, Korea, 10–13 October 2005; pp. 1–11. [Google Scholar]
- Ijiri, T.; Mech, R.; Igarashi, T.; Miller, G. An example-based procedural system for element arrangement. Comput. Graphics Forum 2008, 27, 429–436. [Google Scholar] [CrossRef]
- Passos, V.A.; Waltery, M.; Sousa, M.C. Sample-Based Synthesis of Illustrative Patterns. In Proceedings of the Pacific Conference on Computer Graphics and Applications, Hangzhou, China, 25–27 September 2010; pp. 109–116. [Google Scholar]
- Xu, C.; Yang, G. Vector texture pattern synthesis based on neighborhood histogram matching. J. Image Graphics 2013, 18, 1703–1713. [Google Scholar]
- Hausner, A. Simulating decorative mosaics. In Proceedings of the 28th annual conference on Computer graphics and interactive techniques, Los Angeles, CA, USA, 12–17 August 2001; pp. 573–580. [Google Scholar]
- Barla, P.; Breslav, S.; Thollot, J.; Sillion, F.; Markosian, L. Stroke pattern analysis and synthesis. Comput. Graphics 2006, 25, 663–671. [Google Scholar]
- Hurtut, T.; Landes, P.E.; Thollot, J.; Gousseau, Y.; Drouillhet, R.; Coeurjolly, J.F. Appearance-guided synthesis of element arrangements by example. In Proceedings of the 7th International Symposium on Non-Photorealistic Animation and Rendering, New Orleans, LA, USA, 1–2 August 2009; pp. 51–60. [Google Scholar]
- Efros, A.A.; Freeman, W.T. Image quilting for texture synthesis and transfer. In Proceedings of the 28th annual conference on Computer graphics and interactive techniques, Los Angeles, CA, USA, 12–17 August 2001; pp. 341–346. [Google Scholar]
- Liang, L.; Liu, C.; Xu, Y.; Guo, B.; Shum, H.Y. Real-time texture synthesis by patch-based sampling. ACM Trans. Graphics 2001, 20, 127–150. [Google Scholar] [CrossRef]
- Hertzmann, A.; Jacobs, C.E.; Oliver, N.; Curless, B.; Salesin, D.H. Image Analogies. In Proceedings of the 28th annual conference on Computer graphics and interactive techniques, Los Angeles, CA, USA, 12–17 August 2001; pp. 327–340. [Google Scholar]
- Liu, Y.; Lin, W.C.; Hays, J. Near-regular texture analysis and manipulation. ACM Trans. Graphics 2004, 23, 368–376. [Google Scholar] [CrossRef]
- Hu, W.; Chen, Z.; Pan, H.; Yu, Y.; Grinspun, E.; Wang, W. Surface Mosaic Synthesis with Irregular Tiles. IEEE Trans. Visual. Comput. Graphics 2016, 22, 1302–1313. [Google Scholar] [CrossRef] [PubMed]
- Aurenhammer, F. Voronoi diagrams—A survey of a fundamental data structure. ACM Comput. Surv. 1991, 23, 345–405. [Google Scholar] [CrossRef]
- Lee, D.T. Two-dimensional Voronoi diagrams in the L_p-metric. J. ACM 1980, 27, 604–618. [Google Scholar] [CrossRef]
- Barequet, G.; Dickerson, M.T.; Goodrich, M.T. Voronoi diagrams for convex polygon-offset distance functions. Discrete Comput. Geom. 2001, 25, 271–291. [Google Scholar] [CrossRef]
- Klein, R. Voronoi Diagrams in the Moscow Metric; Springer: Heidelberg/Berlin, Germany, 2005. [Google Scholar]
- Labelle, F.; Shewchuk, J.R. Anisotropic voronoi diagrams and guaranteed-quality anisotropic mesh generation. In Proceedings of the nineteenth annual symposium on Computational geometry, San Diego, CA, USA, 8–10 June 2003; pp. 191–200. [Google Scholar]
- Augenbaum, J.M.; Peskin, C.S. On the construction of the Voronoi mesh on a sphere. J. Comput. Phys. 1985, 59, 177–192. [Google Scholar] [CrossRef]
- Aichholzer, O.; Aurenhammer, F.; Chen, D.Z.; Lee, D.T.; Papadopoulou, E. Skew Voronoi diagrams. Int. J. Comput. Geom. Appl. 1999, 9, 235–246. [Google Scholar] [CrossRef]
- Leibon, G.; Letscher, D. Delaunay triangulations and Voronoi diagrams for Riemannian manifolds. In Proceedings of the Sixteenth Annual Symposium on Computational Geometry, Kowloon, Hong Kong, China, 12–14 June 2000; pp. 341–349. [Google Scholar]
- Boissonnat, J.D.; Rouxel-Labbé, M.; Wintraecken, M. Anisotropic Triangulations Via Discrete Riemannian Voronoi Diagrams. Available online: https://arxiv.org/abs/1703.06487 (accessed on 14 February 2019).
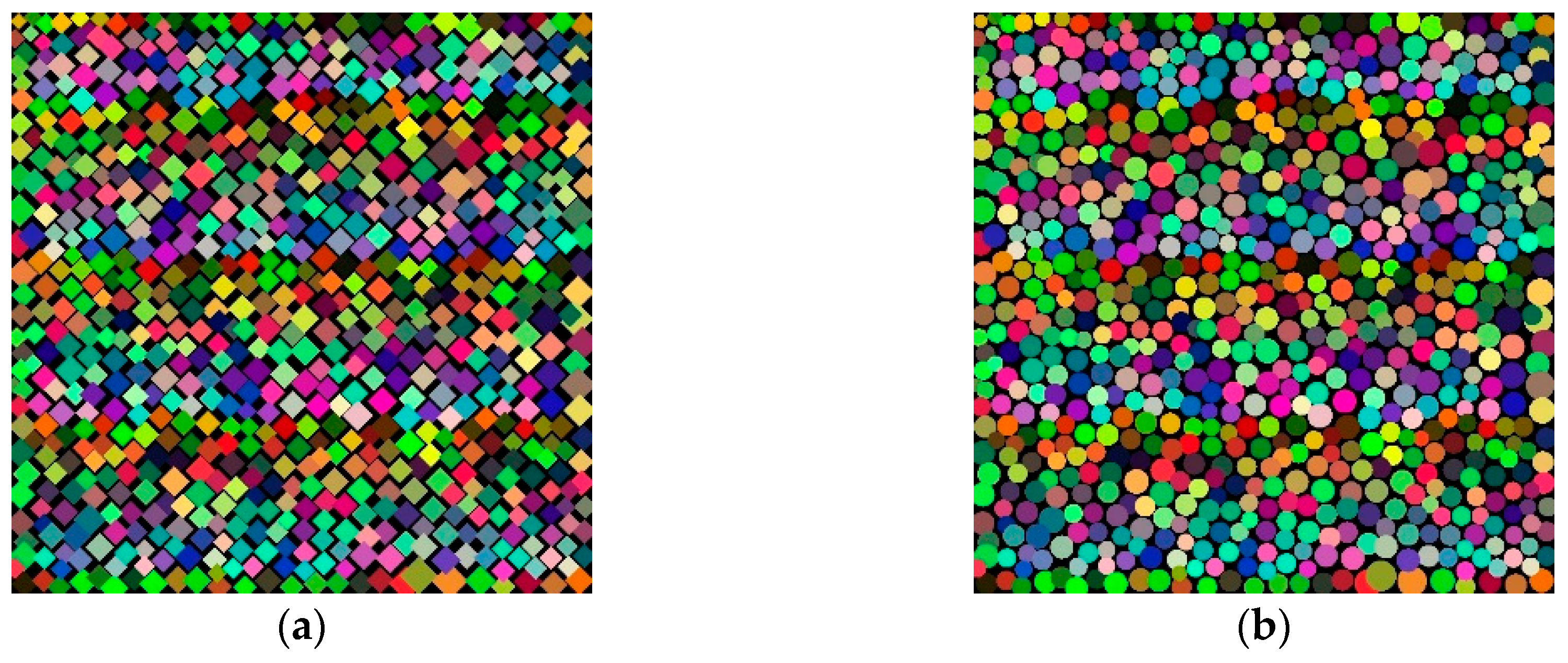



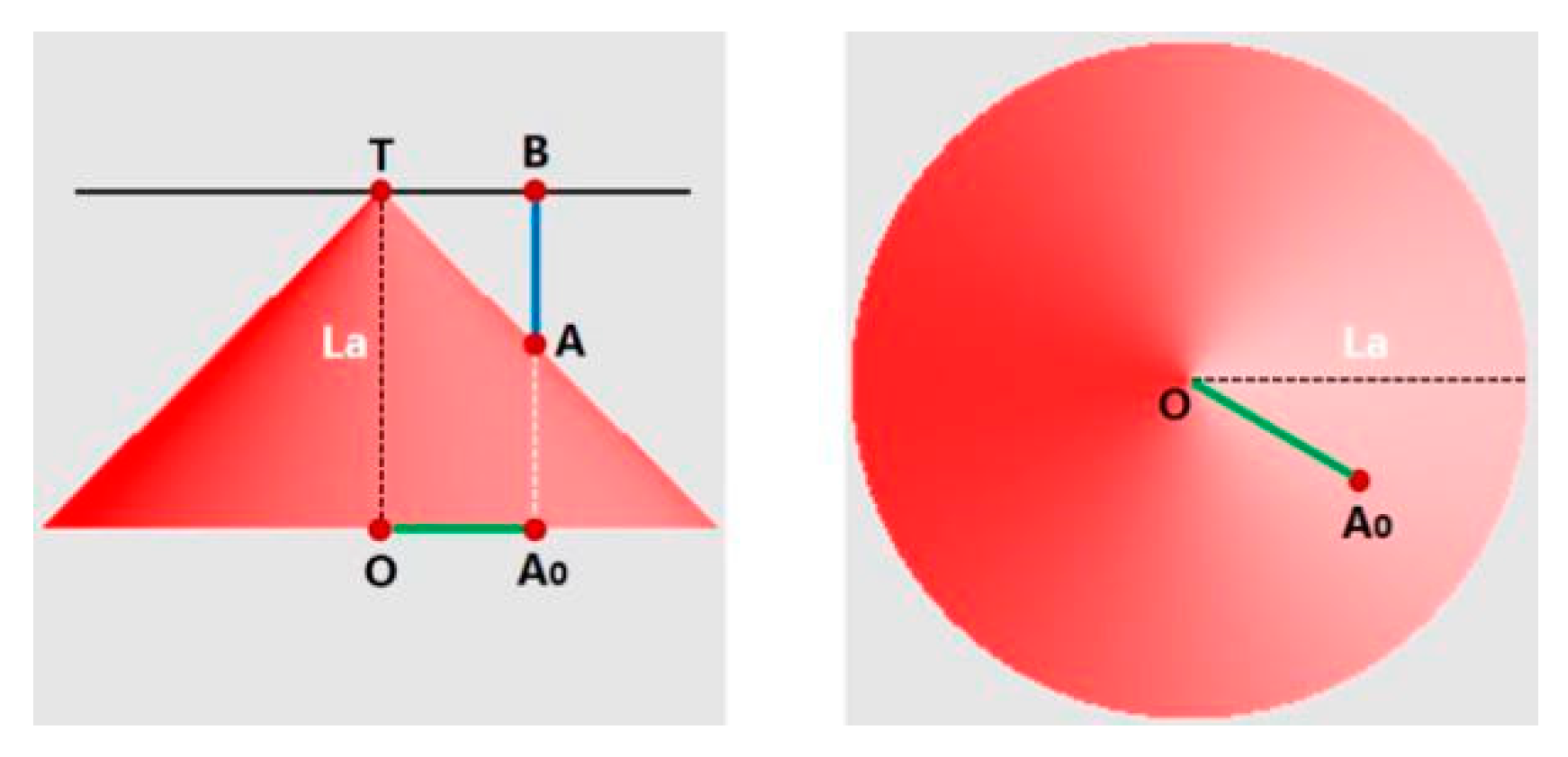










| Geometry | Distance Metric | Bottom Size | Height | |
|---|---|---|---|---|
| Circular cone |  | Euclidean distance | Radius = La | La |
| Square pyramid |  | Manhattan distance | Side length = La | |
| Square pyramid |  | Chebyshev distance | Side length = La | |
| Pyramid |  | Chebyshev distance with axial scale | Length = , width = | La |
| Elliptic cone |  | Euclidean distance with axial scale | axis = , minor axis | La |
| Triangular pyramid |  | Equidistant line distance | Side = La | |
| Effect Picture | Average Coverage Scale | Average Time | |
|---|---|---|---|
| Fritzsche L P |  | 64.8% | 1 min |
| K. Smith |  | 68.1% | 1 min |
| Hu W |  | 84.3% | 10 min |
| Author | 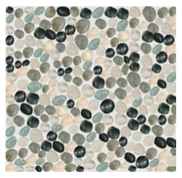 | 85.6% | 19 s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Yang, G.; Yang, M. Computation of Compact Distributions of Discrete Elements. Algorithms 2019, 12, 41. https://doi.org/10.3390/a12020041
Chen J, Yang G, Yang M. Computation of Compact Distributions of Discrete Elements. Algorithms. 2019; 12(2):41. https://doi.org/10.3390/a12020041
Chicago/Turabian StyleChen, Jie, Gang Yang, and Meng Yang. 2019. "Computation of Compact Distributions of Discrete Elements" Algorithms 12, no. 2: 41. https://doi.org/10.3390/a12020041
APA StyleChen, J., Yang, G., & Yang, M. (2019). Computation of Compact Distributions of Discrete Elements. Algorithms, 12(2), 41. https://doi.org/10.3390/a12020041




