Data Analysis, Simulation and Visualization for Environmentally Safe Maritime Data
Abstract
1. Introduction
1.1. ICT and Maritime Data Engineering
1.2. Factors That Raise Marine Traffic Engineering Awareness
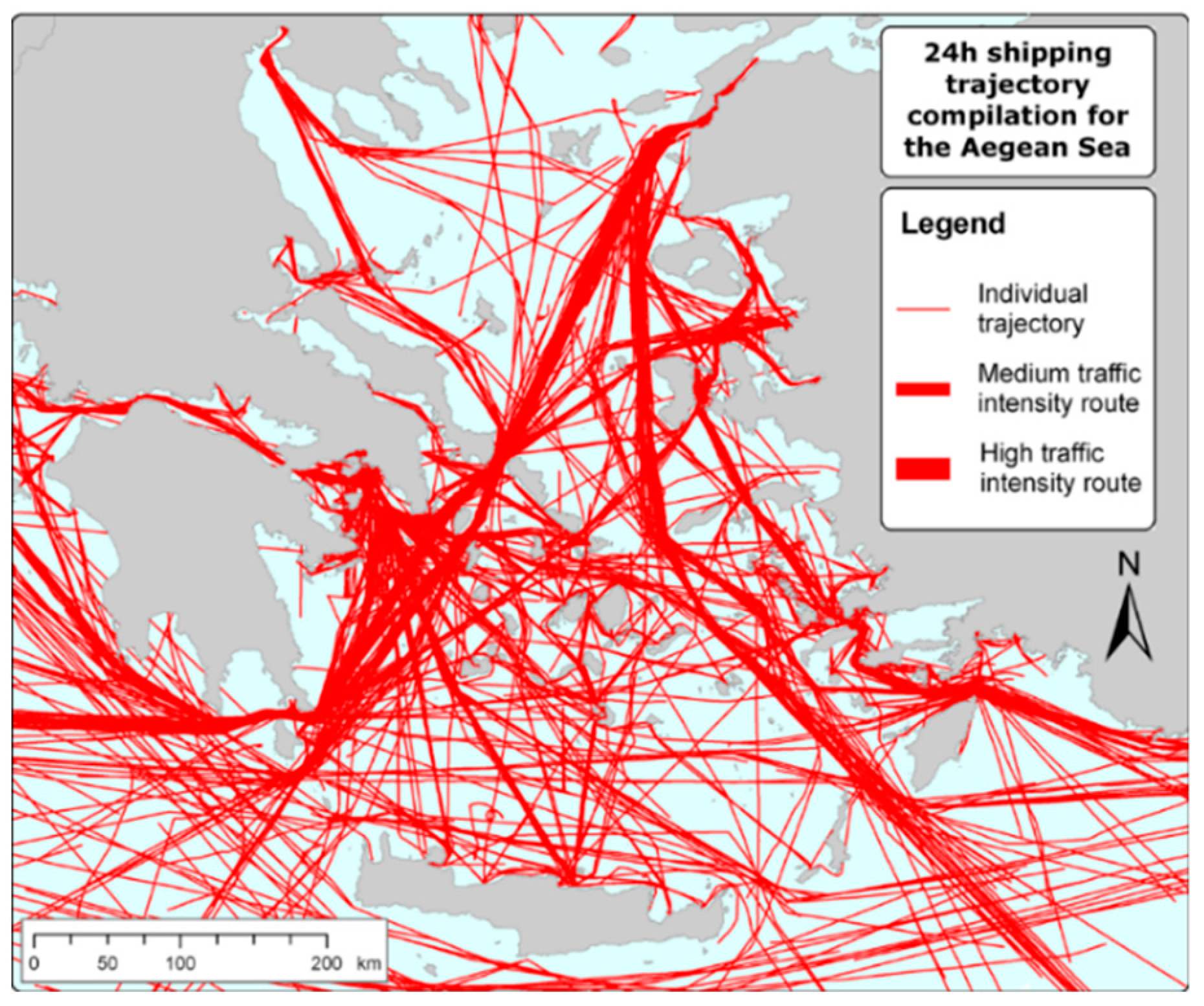
1.2.1. Sea Traffic
1.2.2. Accidents and Hazards
Lack of Designated Shipping Lanes
1.2.3. Impact of Maritime Accidents
1.3. Research Questions
- RQ1: How to incorporate various heterogeneous data sources about marine traffic, vessel information and sea conditions towards modeling and understanding potential hazardous situations.
- RQ2: How to exploit historical data towards creating a simulation tool for inferring about future situations under conditions of uncertainty.
- RQ3: How to create useful visualization and insights for the domain, in order to help experts formulate policies, regulations, reform emergency plans, etc.
2. Related Work
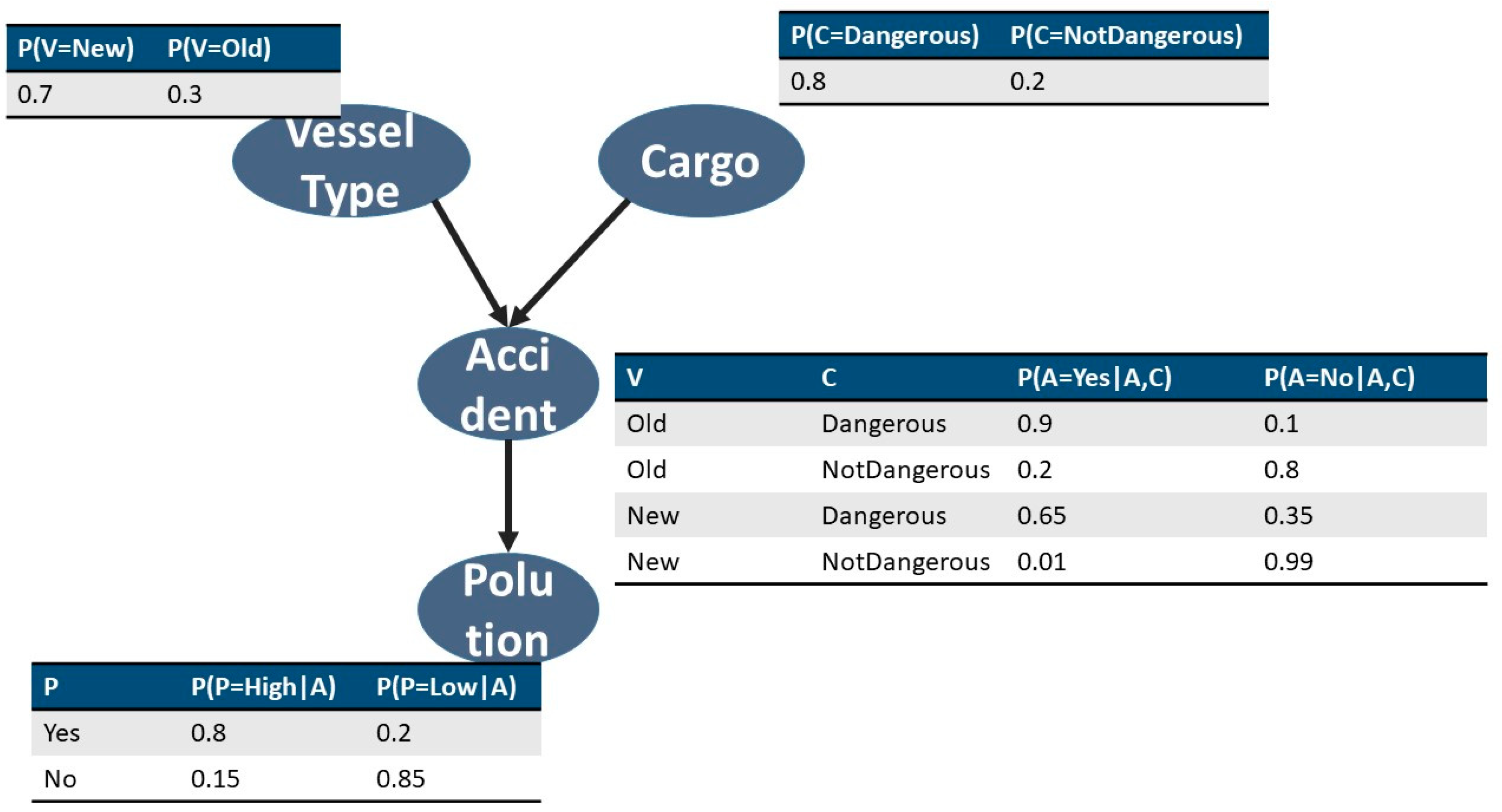
3. Theoretical Background
- VesselType:
- ○
- New
- ○
- Old
- Cargo:
- ○
- Dangerous
- ○
- Not Dangerous
- Accident:
- ○
- Yes
- ○
- No
- Pollution:
- ○
- High
- ○
- Low
- The variables VesselType and Cargo are marginally independent, but when Accident is observed (given) they are conditionally dependent. The type of this relation is often named as explaining away.
- When Accident is given, Pollution is conditionally independent of its ancestors VesselType and Cargo.
- Instead of factorizing the joint distribution of all variables using the chain rule, such as P(V,C,A,P) = P(V)P(C|V)P(A|C,V)P(P|A,C,V) the BN defines a compact JPD in a factored form, such as P(V,C,A,P) = P(V)P(C)P(A|V,C)P(P|A). Note that the BN structure reduces the number of model parameters (i.e., the number of rows in the JPD table) from 24 − 1 = 15 to only 8. This property is of major importance since it allows researchers to create a tractable model of domains with a plethora of attributes.
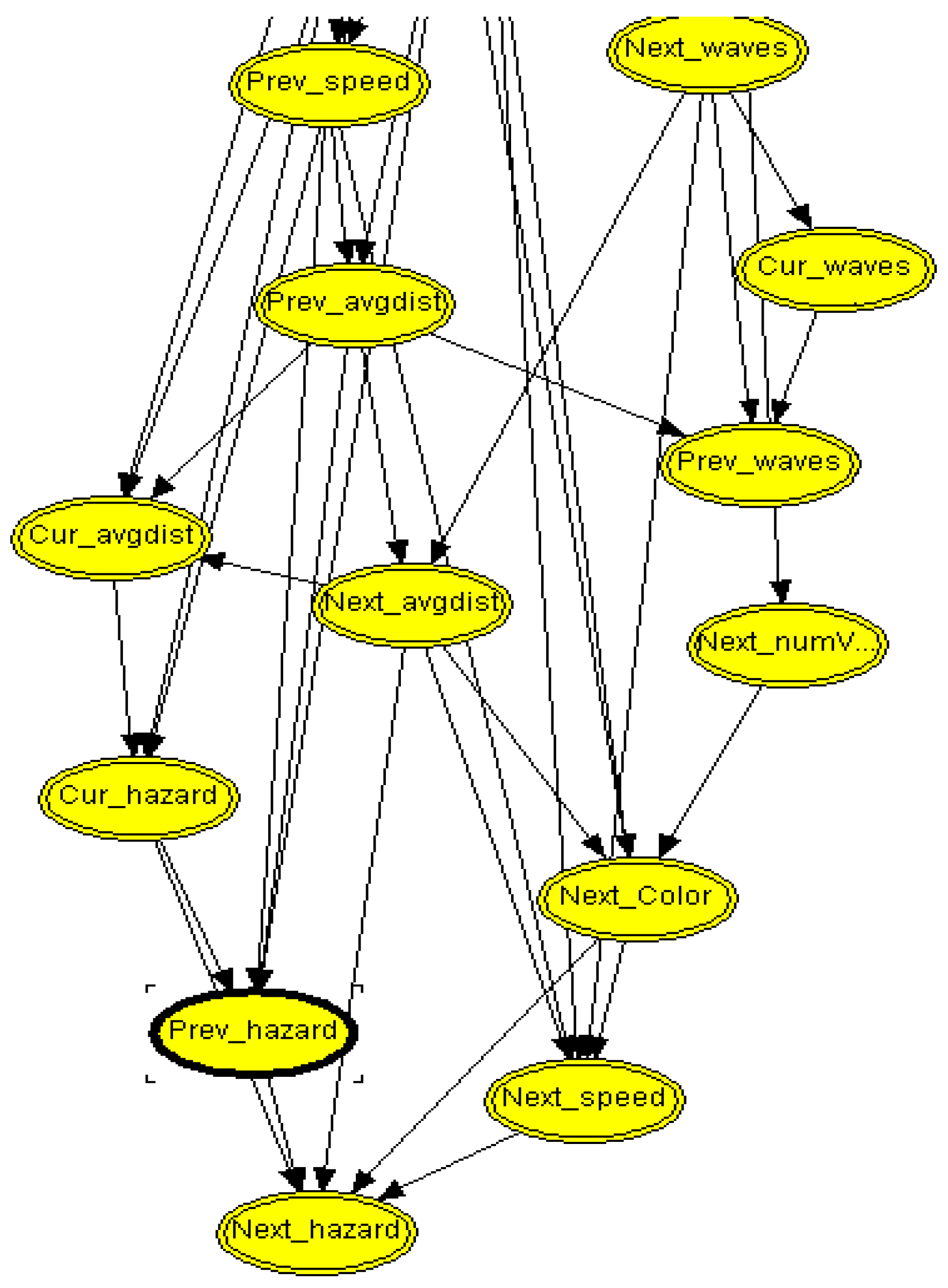
Hybrid Bayesian Networks
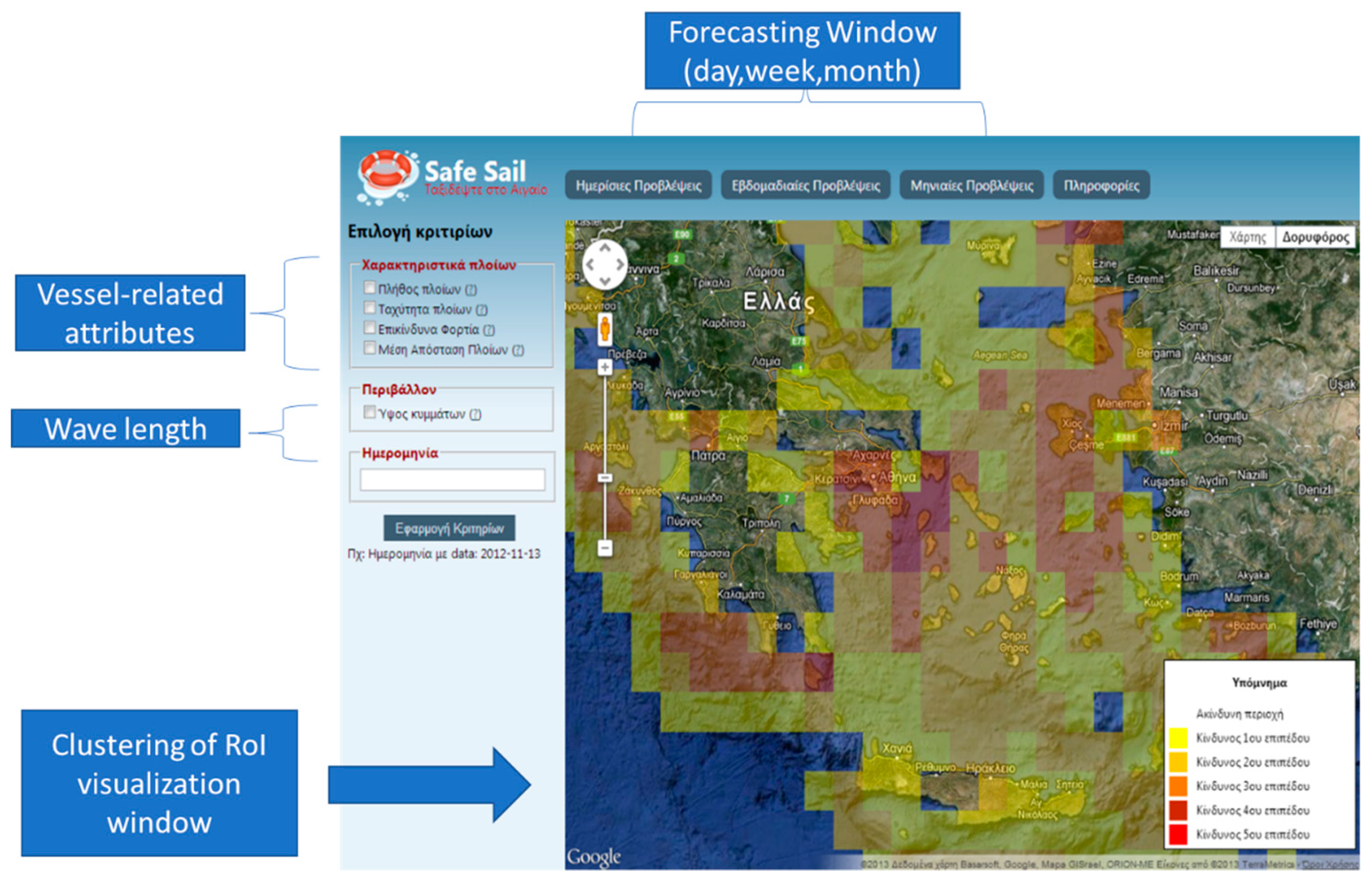
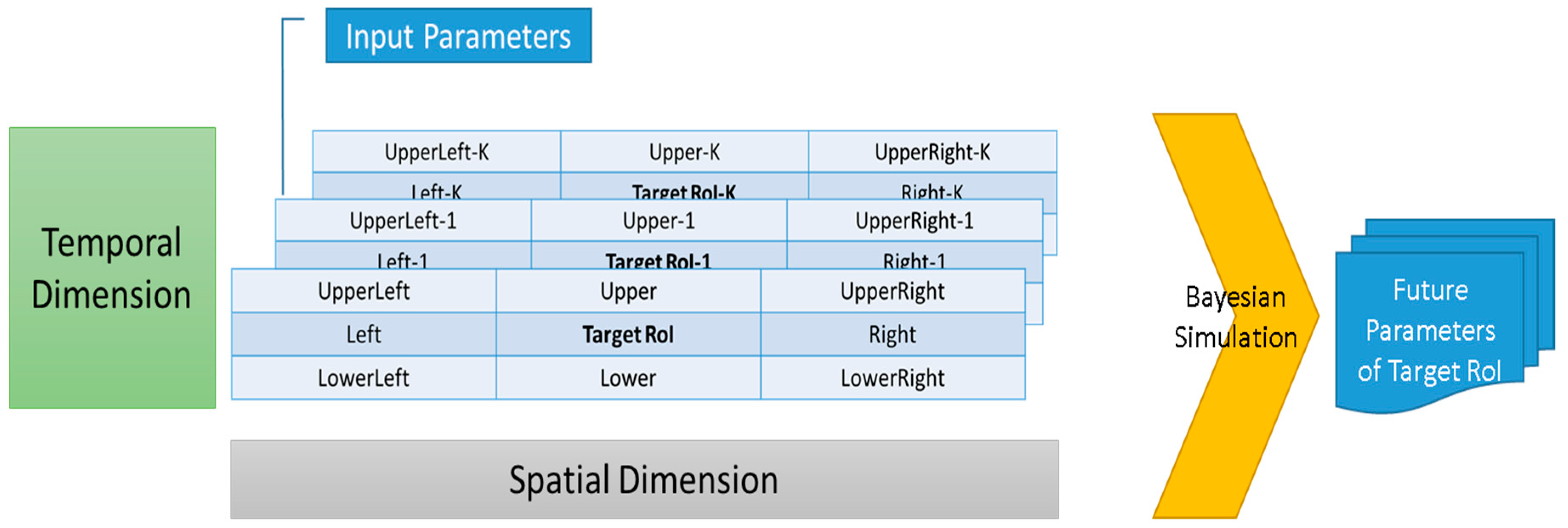
4. Marine Simulation System
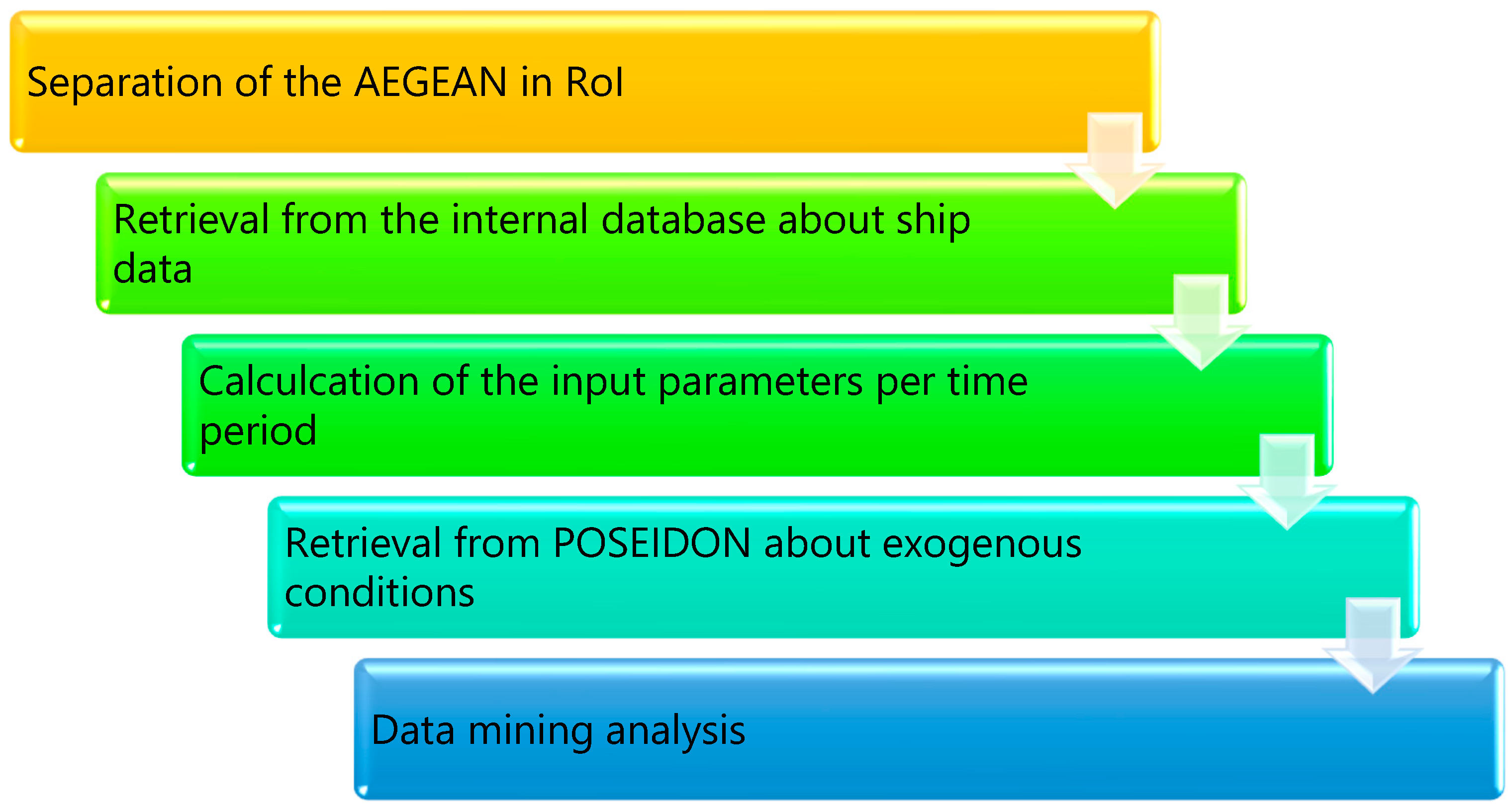
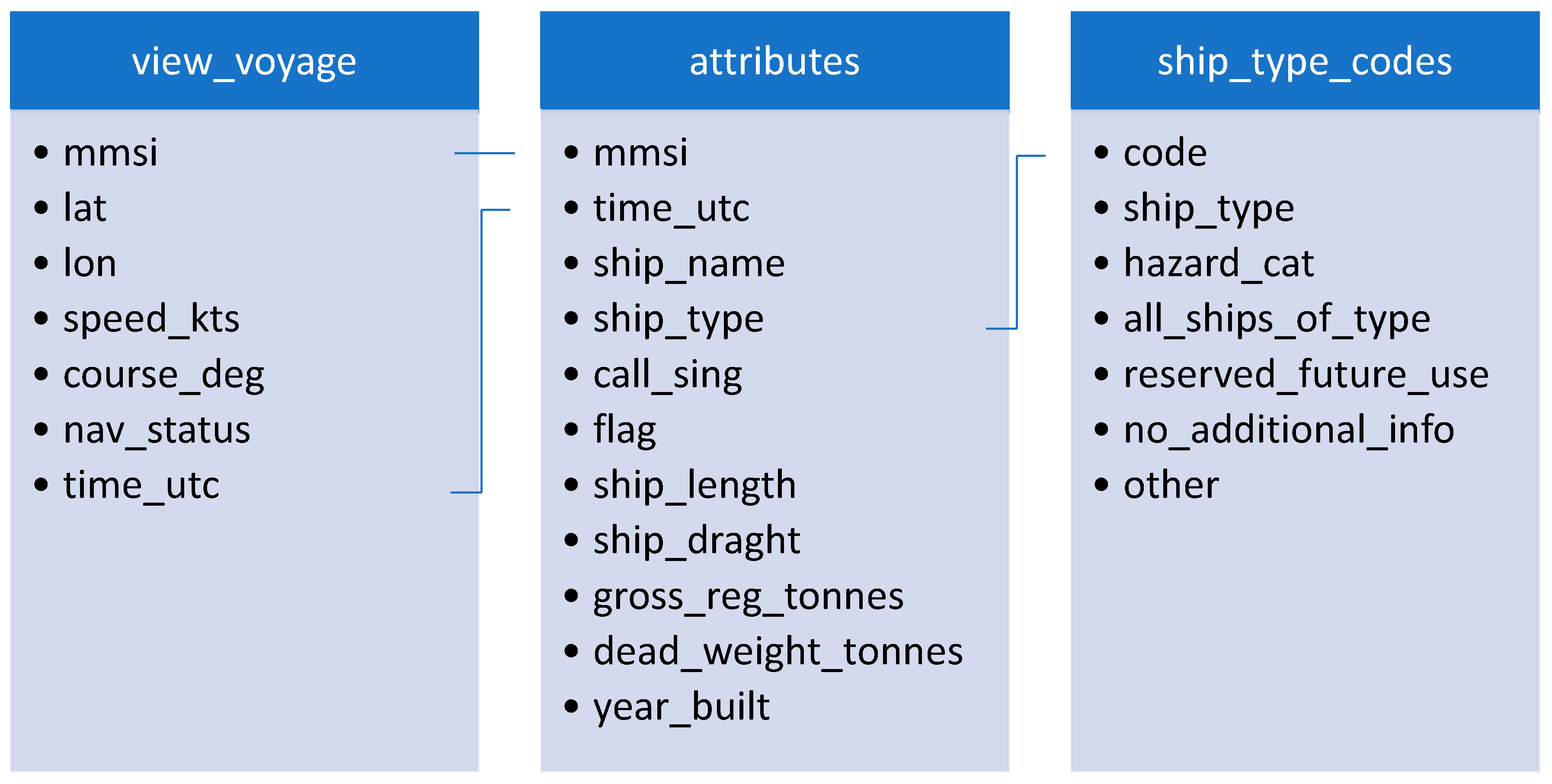
4.1. Data Description and Preprocessing
- Number of ships
- ○
- It represents the total number of ships that passed through that RoI in a whole time slot (day, week, month)
- Average speed
- ○
- For each RoI, the speed of each instance is averaged on the number of instances
- Hazardous cargo
- ○
- the most frequent hazard level, as extracted by looking at all cargos from ships that passed through this RoI (i.e., nominal value from A to D, A denoting the most hazardous situation). This is a weighted value in order to give more emphasis on the hazardous load.
- Ship density
- ○
- The average distance between all ships that passed through a RoI.
- Wave height
- ○
- As retrieved from the POSEIDON system
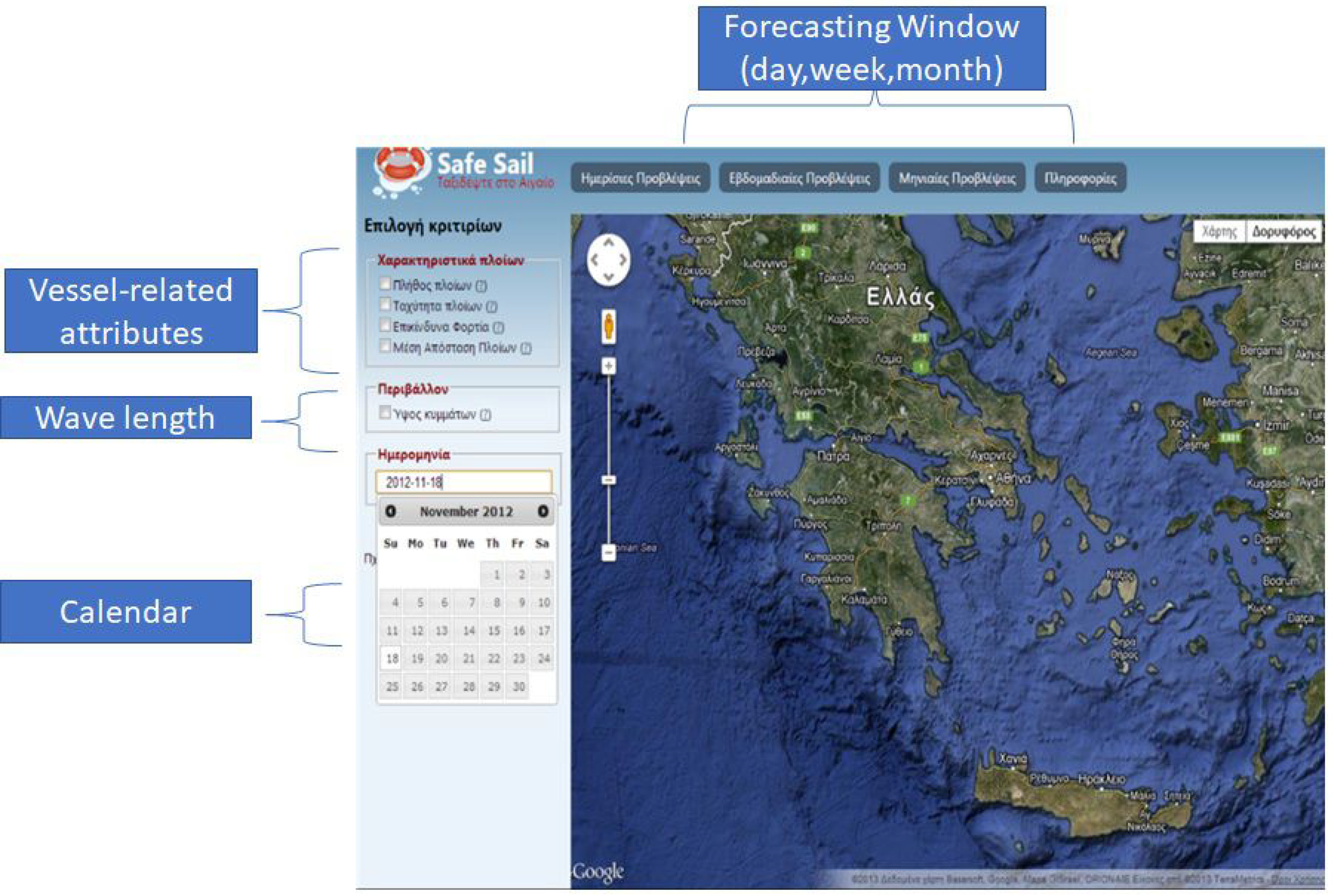
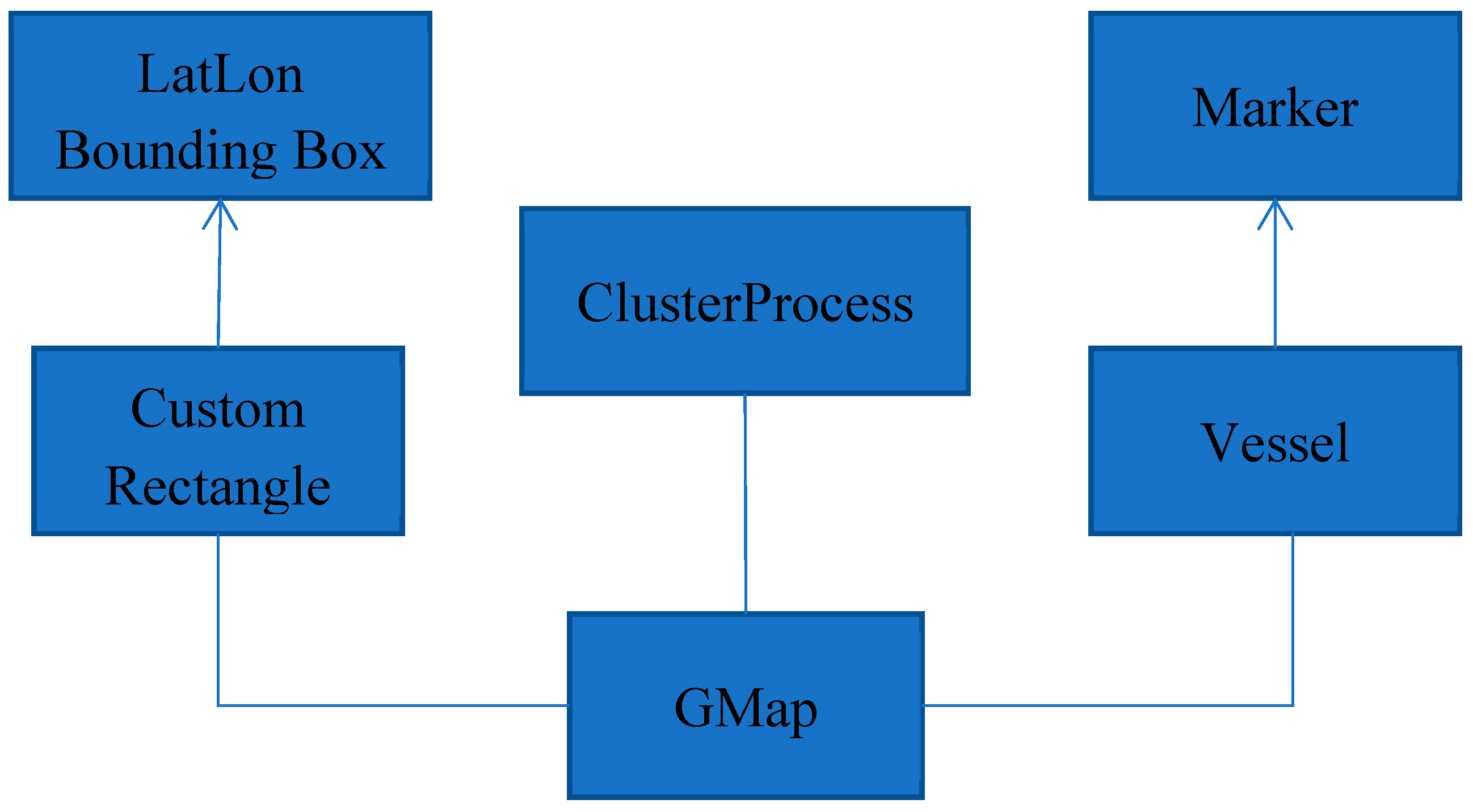
4.2. System Programming Details
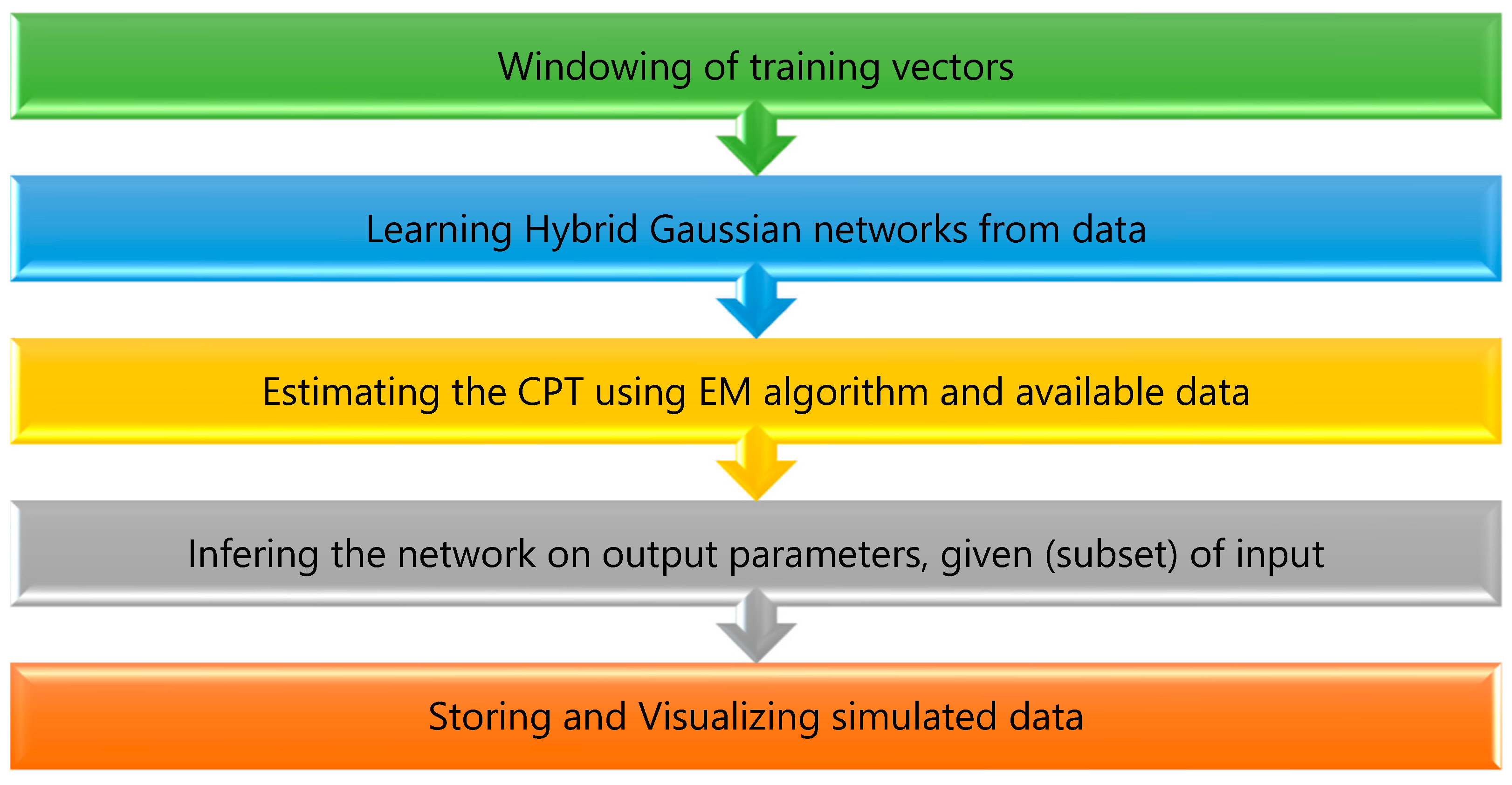
4.3. Simulation Phase
5. Experimental Evaluation
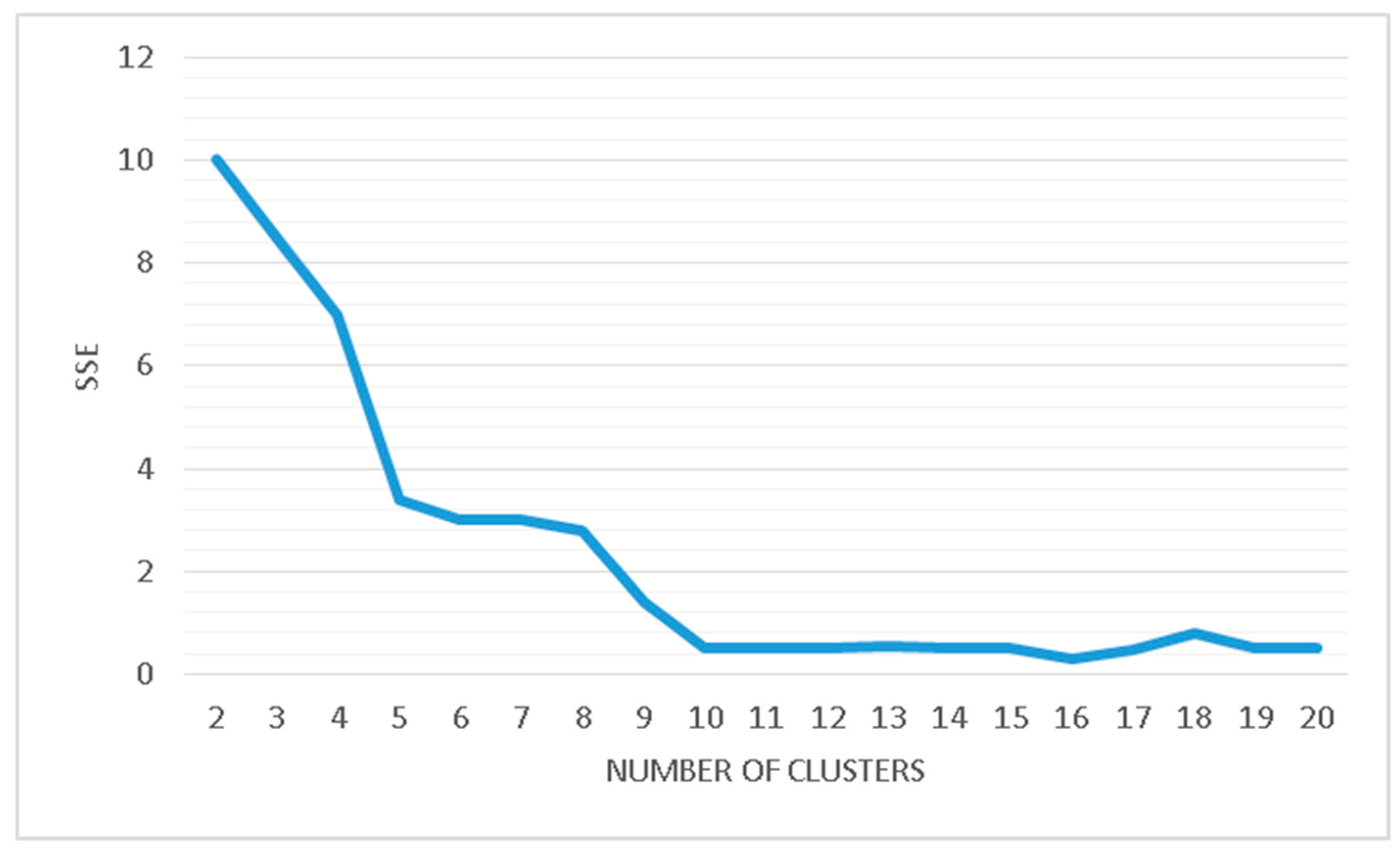
5.1. Measuring Clustering Validation
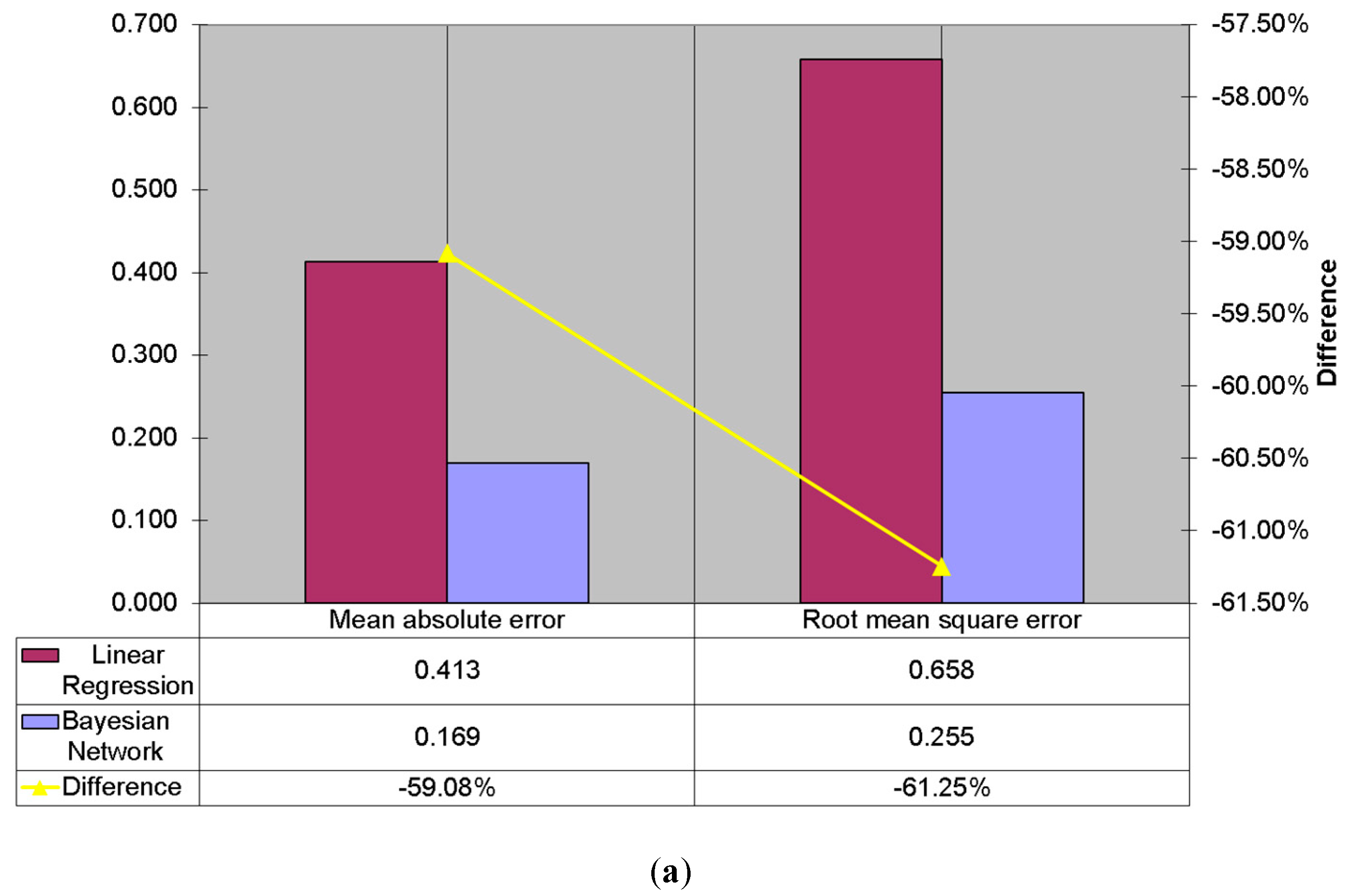
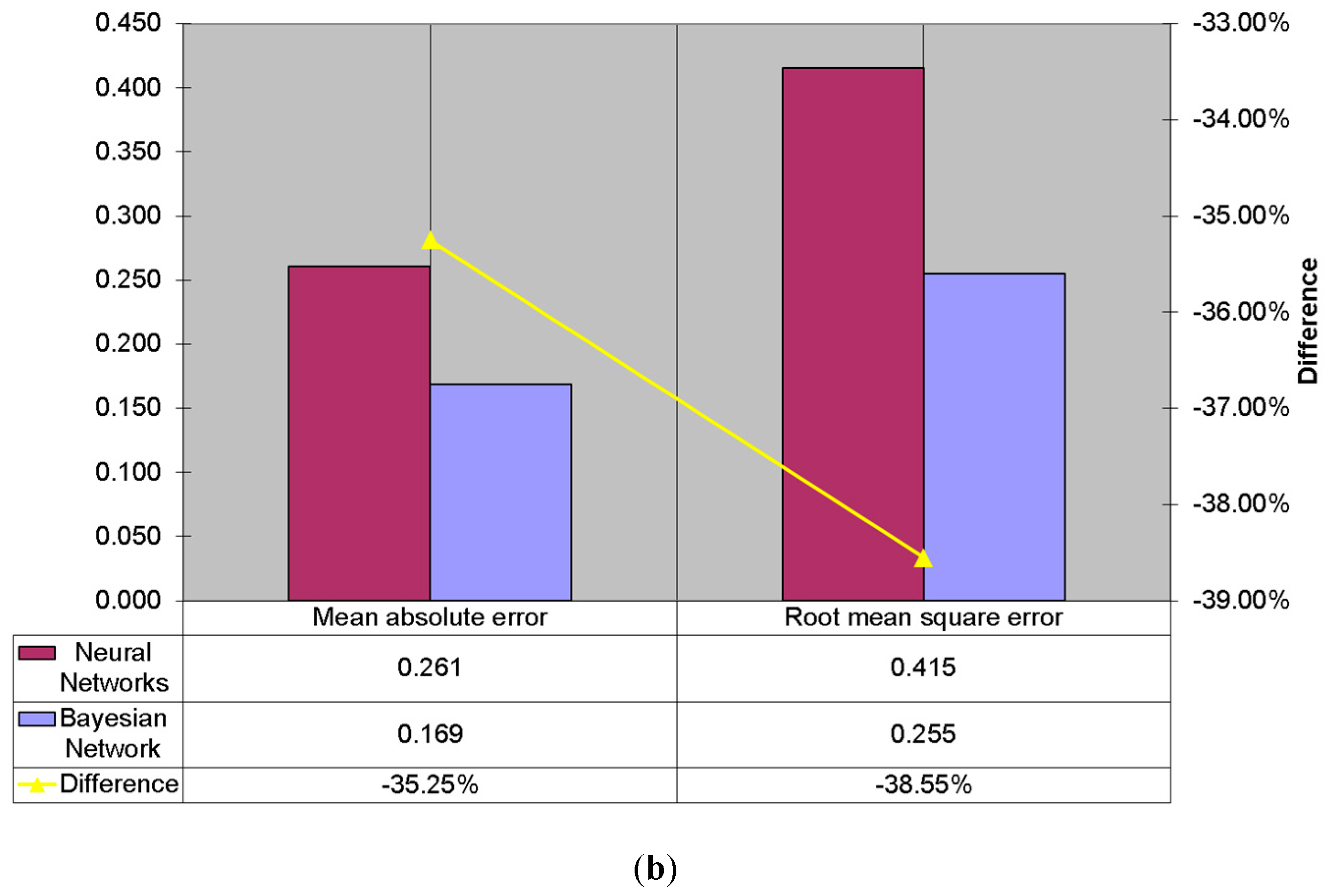
5.2. Evaluation of the Inference Performance
5.2.1. Mean Absolute Error
5.2.2. Root Mean Squared Error
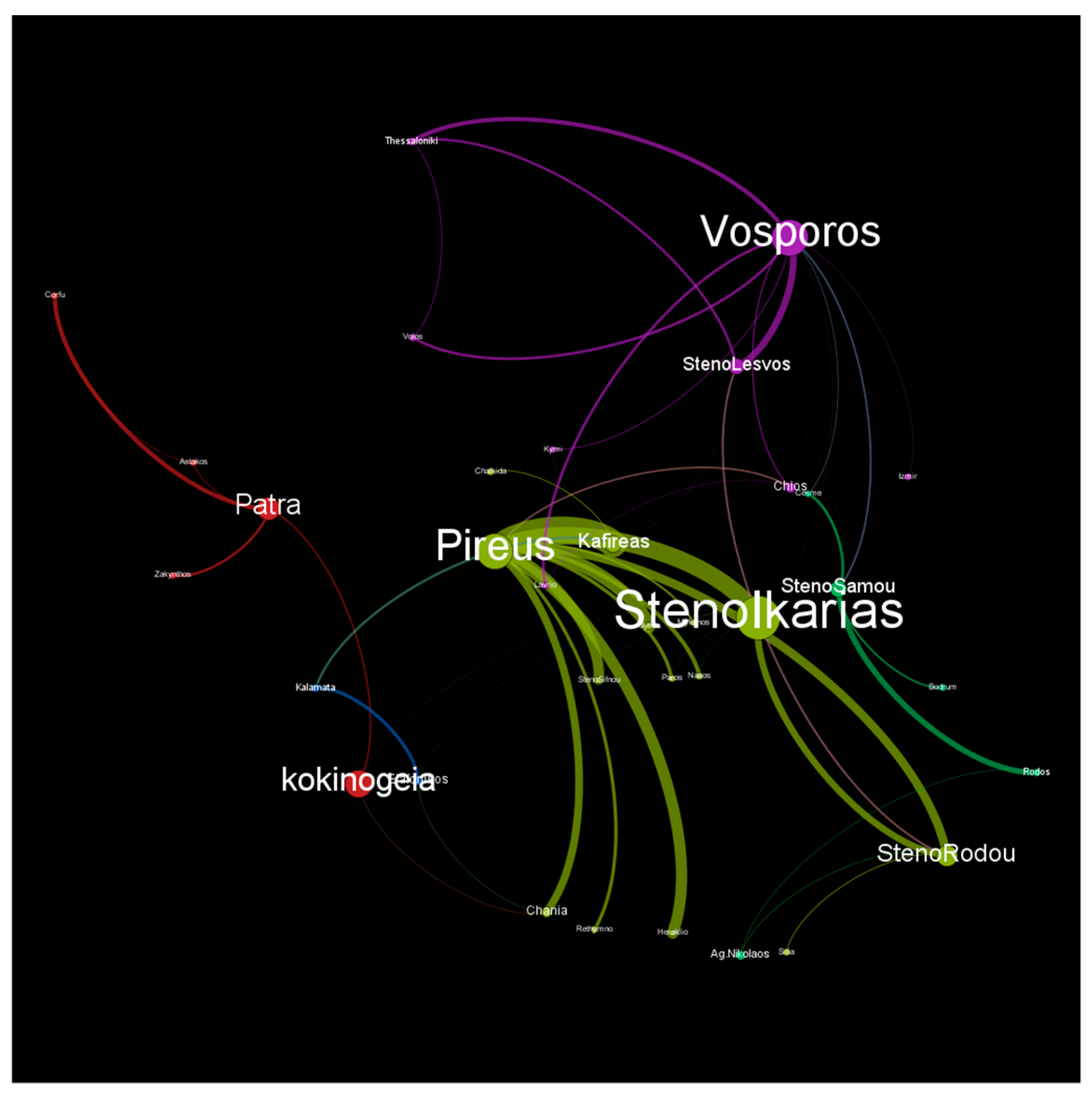
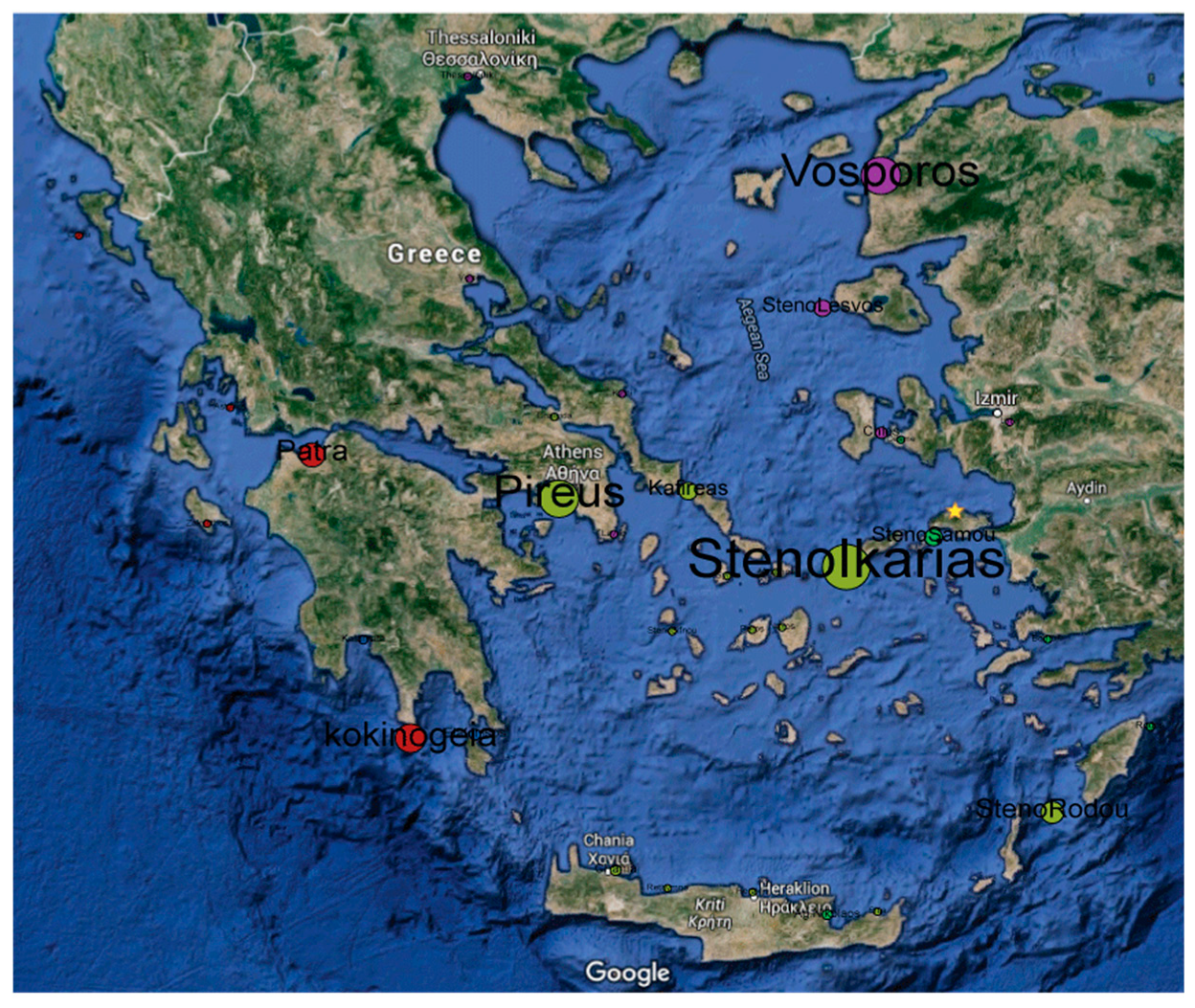
6. Modeling Marine Transportation as Social Network
6.1. Social Network Analysis Measures
6.2. Applying SNA to Marine Traffic Data
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guziewicz, G.; Ślączka, W. Methods for determining the maneuvering area of the vessel used in navigating simulation studies. In Proceedings of the VII MTE Conference, Szczecin, Poland, 1997. [Google Scholar]
- Papanikolaou, A.; Boulougouris, E.; Sklavenitis, A. The sinking of the Ro-Ro passenger ferry SS Heraklion. Int. Shipbuild. Prog. 2014, 61, 81–102. [Google Scholar] [CrossRef]
- MaritimeCyprus. Available online: https://maritimecyprus.com/2018/12/11/ireland-ro-ro-passenger-ferry-epsilon-8-feb-2016-incident-investigation-report/ (accessed on 18 January 2019).
- Kum, S.; Sahin, B. A root cause analysis for Arctic Marine accidents from 1993 to 2011. Saf. Sci. 2015, 74, 206–220. [Google Scholar] [CrossRef]
- Kiousis, G. Γιώργος Κιούσης, Ζητείται... τροχονόμος και για το Aιγαίο. Ελευθεροτυπία, X.K. Τεγόπουλος Εκδόσεις A.Ε. Available online: http://www.enet.gr/?i=news.el.article&id=135365 (accessed on 18 January 2019). (In Greek).
- Vafeiadis, N. Νίκος Βαφειάδης. Μια νάρκη στο βυθό της Σαντορίνης (SEA DIAMOND). Περιοδικό «Κ», τεύχος 236, σελ. 62-71. Available online: http://eyploia.epyna.eu/modules.php?name=News&file=article&sid=1454 (accessed on 18 January 2019). (In Greek).
- Aarsæther, G.; Moan, T. Estimating Navigation Patterns from AIS. J. Navig. 2009, 62, 587–607. [Google Scholar] [CrossRef]
- Chen, J.; Lu, F.; Peng, G. A quantitative approach for delineating principal fairways of ship passages through a strait. Ocean Eng. 2015, 103, 188–197. [Google Scholar] [CrossRef]
- Shelmerdine, R.L. Teasing out the detail: How our understanding of marine AIS data can better inform industries, developments, and planning. Mar. Policy 2015, 54, 17–25. [Google Scholar] [CrossRef]
- Tsou, M.-C. Online analysis process on Automatic Identification System data warehouse for application in vessel traffic service. Proc. Inst. Mech. Eng. M J. Eng. Marit. Environ. 2016, 230, 199–215. [Google Scholar] [CrossRef]
- Fournier, M.; Hilliard, R.C.; Rezaee, S.; Pelot, R. Past, present, and future of the satellite-based automatic identification system: Areas of applications (2004–2016). WMU J. Marit. Aff. 2018, 17, 1–35. [Google Scholar] [CrossRef]
- Goerlandt, F.; Goite, H.; Valdez Banda, O.A.; Höglund, A.; Ahonen-Rainio, P.; Lensu, M. An analysis of wintertime navigational accidents in the Northern Baltic Sea. Saf. Sci. 2017, 92, 66–84. [Google Scholar] [CrossRef]
- Rezaee, S.; Pelot, R.; Ghasemi, A. The effect of extreme weather conditions on commercial fishing activities and vessel incidents in Atlantic Canada. Ocean Coast. Manag. 2016, 130, 115–127. [Google Scholar] [CrossRef]
- Montewka, J.; Krata, P.; Goerlandt, F.; Mazaheri, A.; Kujala, P. Marine traffic risk modelling an innovative approach and a case study. Proc. Inst. Mech. Eng. O J. Risk Reliab. 2011, 225, 307–322. [Google Scholar] [CrossRef]
- Almaz, O.A.; Altiok, T. Simulation modeling of the vessel traffic in Delaware River: Impact of deepening on port performance. Simul. Model. Pract. Theory 2012, 22, 146–165. [Google Scholar] [CrossRef]
- Goerlandt, F.; Montewka, J. Maritime transportation risk analysis: Review and analysis in light of some foundational issues. Reliabil. Eng. Syst. Saf. 2015, 138, 115–134. [Google Scholar] [CrossRef]
- Ozbas, B. Safety Risk Analysis of Maritime Transportation: Review of the Literature. Transp. Res. Rec. 2013, 2326, 32–38. [Google Scholar] [CrossRef]
- Li, K.X.; Jingbo, Y.I.N.; Yang, Z.; Wang, J. The effect of shipowners’ effort in vessels accident: A Bayesian network approach. In Proceedings of the International Forum in Shipping, Ports and Airports (IFSPA2010), Chengdu, China, 15–18 October 2010. [Google Scholar]
- Jensen, V.F. An Introduction to Bayesian Networks; UCL Press: London, UK, 1996. [Google Scholar]
- Murphy, P.K. A variational approximation for bayesian networks with discrete and continuous latent variables. In Proceedings of the 15th Conference on Uncertainty in Artificial Intelligence; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1999. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-Means Clustering Al-gorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 100–108. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from In-complete Data via the EM Algorithm. J. R. Stat. Soc. Ser. B Methodol. 1977, 39, 1–38. [Google Scholar]
- Kriegel, H.P.; Kröger, P.; Sander, J.; Zimek, A. Density-based Clustering. WIREs Data Min. Knowl. Discov. 2011, 1, 231–240. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Tan, P.N.; Steinbach, M.; Kumar, V. Introduction to Data Mining; Ad-dison-Wesley: Boston, MA, USA, 2003. [Google Scholar]
- Diebold, F.X. Comparing predictive accuracy, twenty years later: A personal perspective on the use and abuse of Diebold-Mariano tests. J. Bus. Econ. Stat. 2015, 33, 1. [Google Scholar] [CrossRef]
- Jenson, D.; Neville, J. Data mining in networks. In Symposium on Dynamic Social Network Modelling and Analysis, National Academy of Sciences; National Academy Press: Washington, DC, USA, 2002. [Google Scholar]
- Lauritzen, S.; Jensen, F. Stable local computation with conditional Gaussian distributions. Stat. Comput. 2001, 11, 191–203. [Google Scholar] [CrossRef]
- Lauritzen, S. Propagation of probabilities, means, and variances in mixed graphical association models. J. Am. Stat. Assoc. 1992, 87, 1098–1108. [Google Scholar] [CrossRef]


| k-Means | DBSCAN | ΕΜ | |
|---|---|---|---|
| Day | −748.720 | −3582.824 | −1705.336 |
| Week | −769.273 | −3701.001 | −1715.009 |
| Month | −991.182 | −3717.501 | −2195.938 |
| k-Means | DBSCAN | ΕΜ | |
|---|---|---|---|
| Day | 0.741 | 0.343 | 0.610 |
| Week | 0.733 | 0.311 | 0.606 |
| Month | 0.681 | 0.303 | 0.588 |
| Null Hypothesis: Both Forecasts Have the Same Accuracy | |||
|---|---|---|---|
| p-value | LR | BN | NN |
| LR | 0.0073 | 0.6311 | |
| BN | 0.0088 | ||
| NN | |||
| DM statistic | LR | BN | NN |
| LR | 0.6264 | 0.4305 | |
| BN | −3.8733 | ||
| NN | |||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maragoudakis, M. Data Analysis, Simulation and Visualization for Environmentally Safe Maritime Data. Algorithms 2019, 12, 27. https://doi.org/10.3390/a12010027
Maragoudakis M. Data Analysis, Simulation and Visualization for Environmentally Safe Maritime Data. Algorithms. 2019; 12(1):27. https://doi.org/10.3390/a12010027
Chicago/Turabian StyleMaragoudakis, Manolis. 2019. "Data Analysis, Simulation and Visualization for Environmentally Safe Maritime Data" Algorithms 12, no. 1: 27. https://doi.org/10.3390/a12010027
APA StyleMaragoudakis, M. (2019). Data Analysis, Simulation and Visualization for Environmentally Safe Maritime Data. Algorithms, 12(1), 27. https://doi.org/10.3390/a12010027





