A Convex Optimization Algorithm for Electricity Pricing of Charging Stations
Abstract
1. Introduction
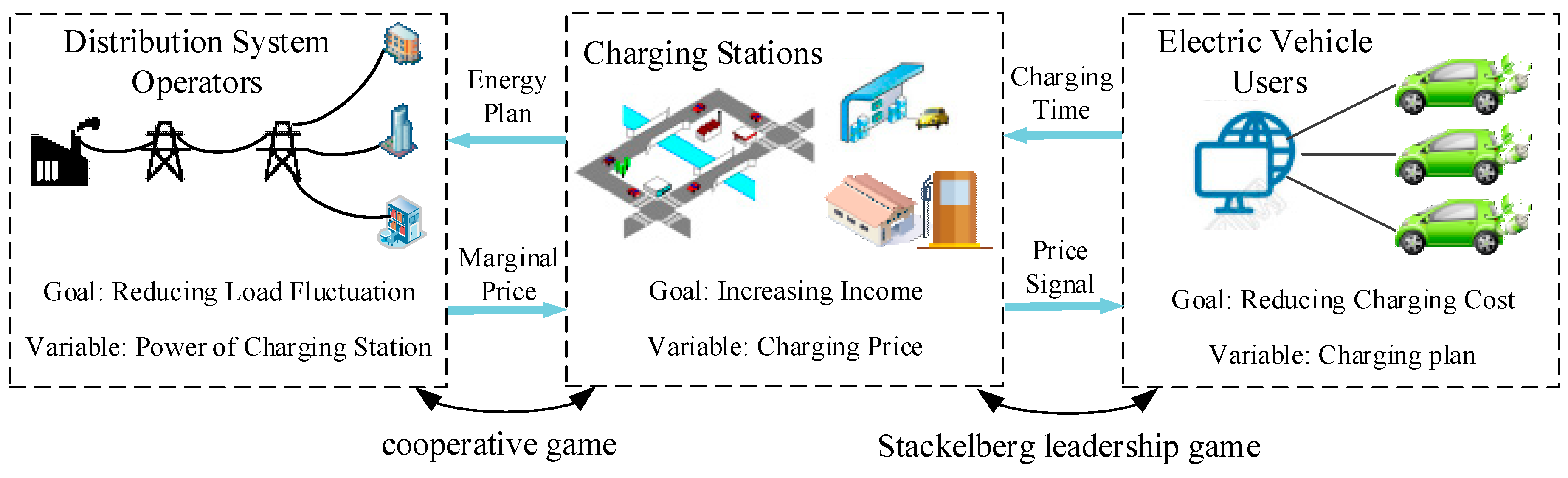
2. The Model of Electricity Pricing of Charging Stations
3. Convex Optimization Algorithm
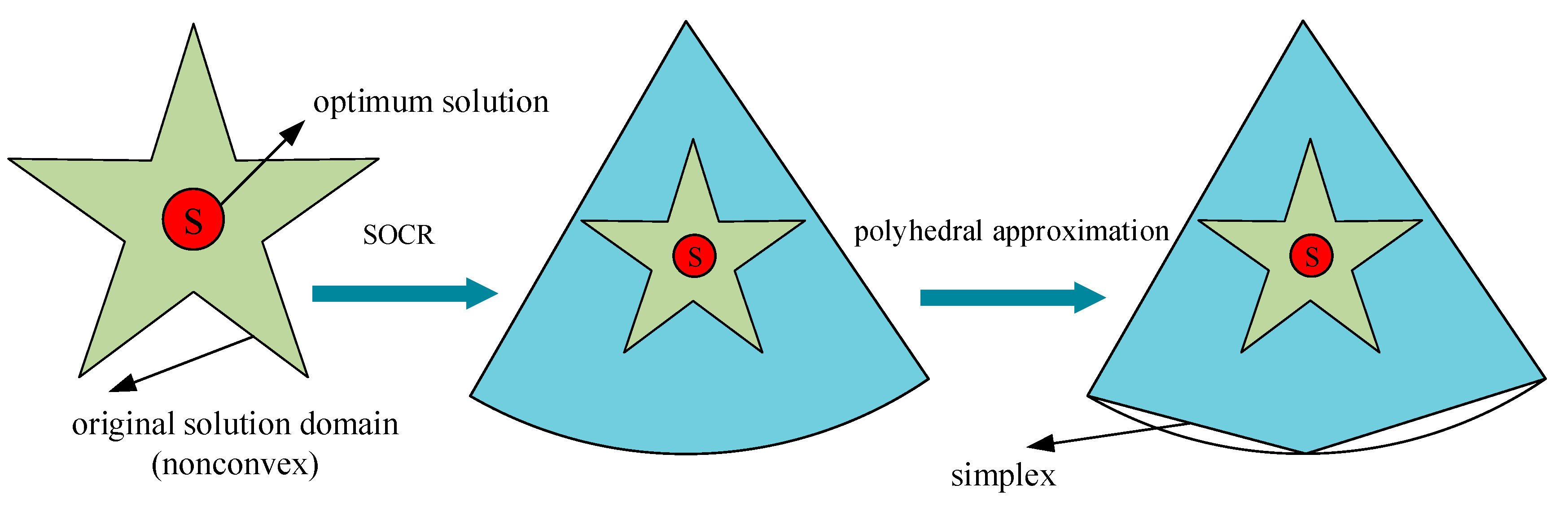
3.1. SOCR Method
| Algorithm 1: Polyhedral approximation algorithm |
| 1: υ: = 0, obtain ε by Equation (20), construct model by Equations (11), (12), and (14) |
| 2: while ε > 10−7 do |
| 3: υ++, obtain ε by Equation (20) |
| 4: end while |
| 5: for t = 1 to T do |
| 6: for ij = 1 to L do |
| 7: add Equations (21) and (23) into model |
| 8: for k = 1 to υ do |
| 9: add Equation (22) into model |
| 10: end do |
| 11: end do |
| 12: end do |
| 13: solve MILP by branch and bound method |
| 14: return PG,t, Pc,t, πc,t, Rij,t, Sij,t, Wi,t, fDSO, fCSs and fEV,n |
| Algorithm 2: Return mapping algorithm |
| 1: Rij,t, Sij,t, and Wi,t: calculated by Algorithm 1 |
| 2: for t = 1 to T do |
| 3: for i = 1 to N do |
| 4: Vi,t: calculated by Equation (24) |
| 5: end do |
| 6: θN0,t:=0 |
| 7: for ij = 1 to L do |
| 8: θi,t: calculated by Equation (26) |
| 9: end do |
| 10: end do |
| 11: return Vi,t and θi,t |
3.2. Scaling Algorithm
| Algorithm 3: Scaling algorithm |
| 1 DL: = +∞, PG,t: obtain by Algorithm 1, fDSO: obtain by Algorithm 1, fCSs: obtain by Algorithm 1 |
| 2 DL: = , t: = 0, obj1[t]: = fDSO, obj2[t]: = fCSs |
| 3 repeat |
| 4 solve MILP by algorithm 1, fDSO: obtain by Algorithm 1, fCSs: obtain by Algorithm 1 |
| 5 if fCSs == obj2[t] then |
| 6 break |
| 7 else then |
| 8 t: t++ |
| 9 obj1[t]: = fDSO, obj2[t]: = fCSs |
| 10 end if |
| 11 until the problem is infeasible |
| 12 return obj1 and obj2 |
4. Case Studies
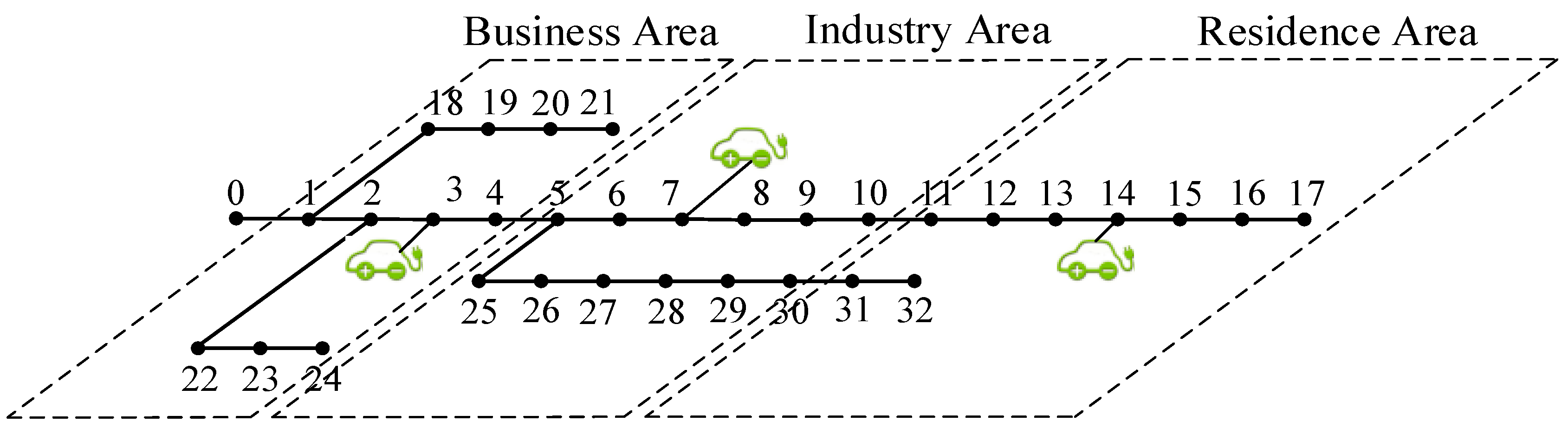
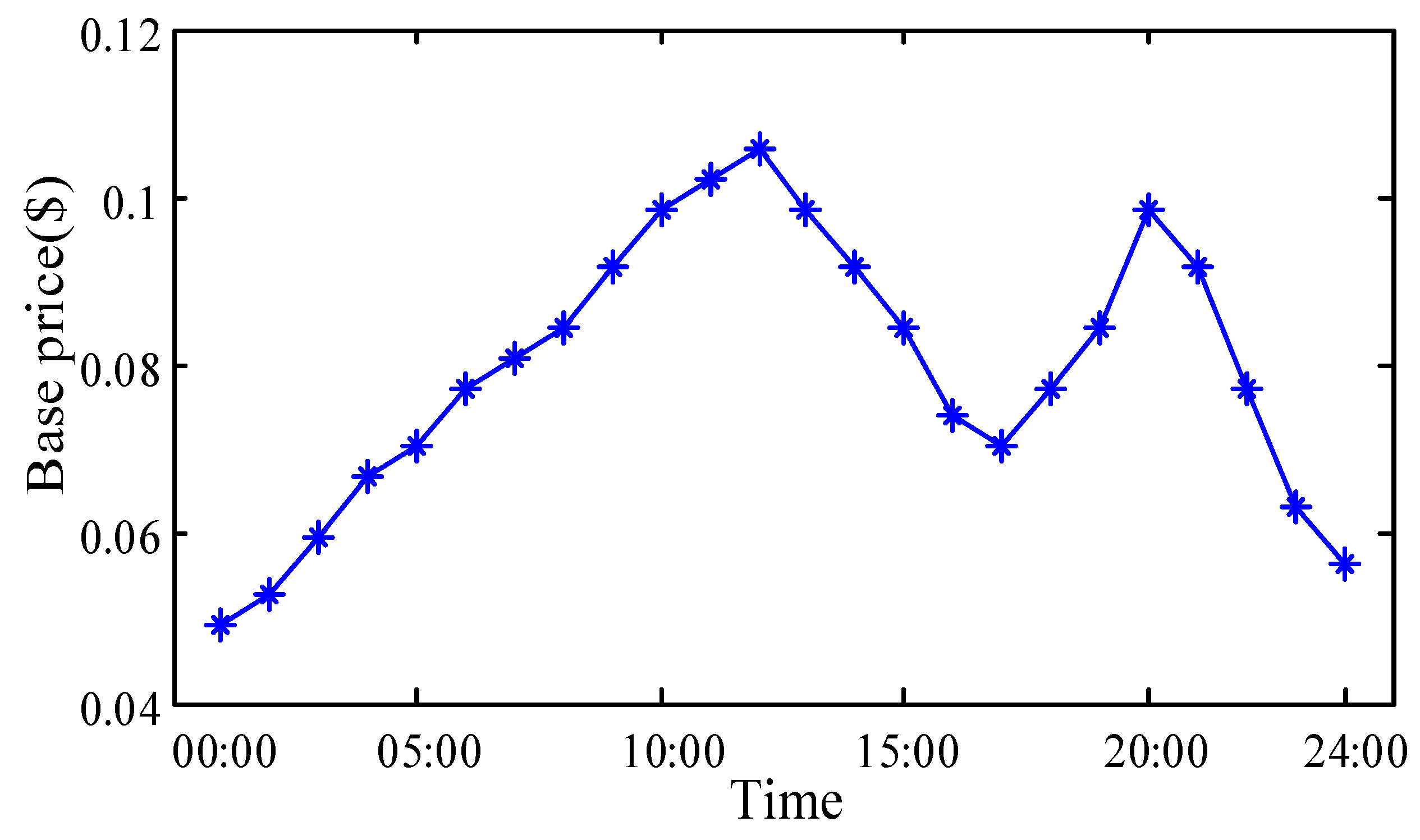
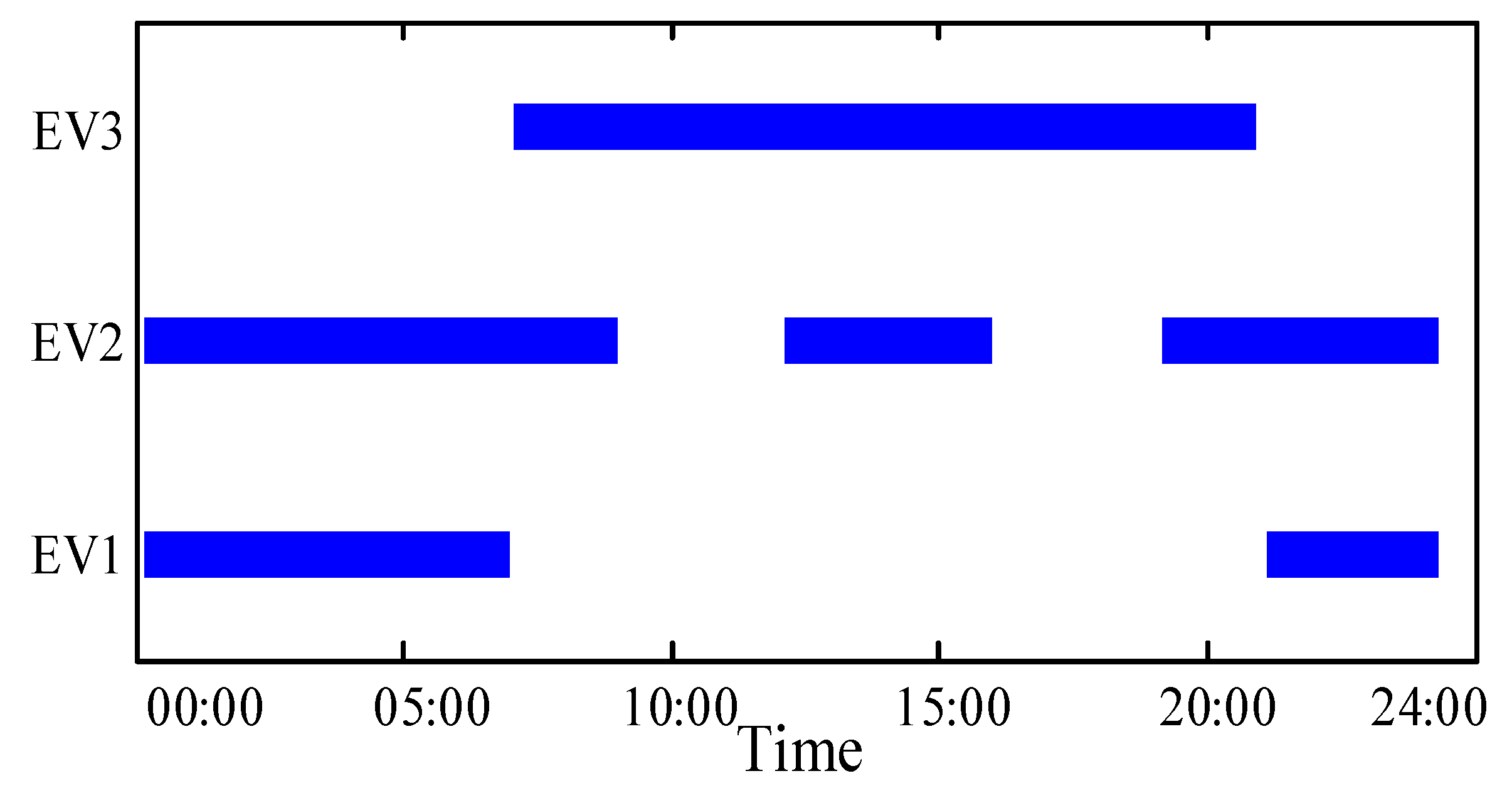
4.1. Data Generation
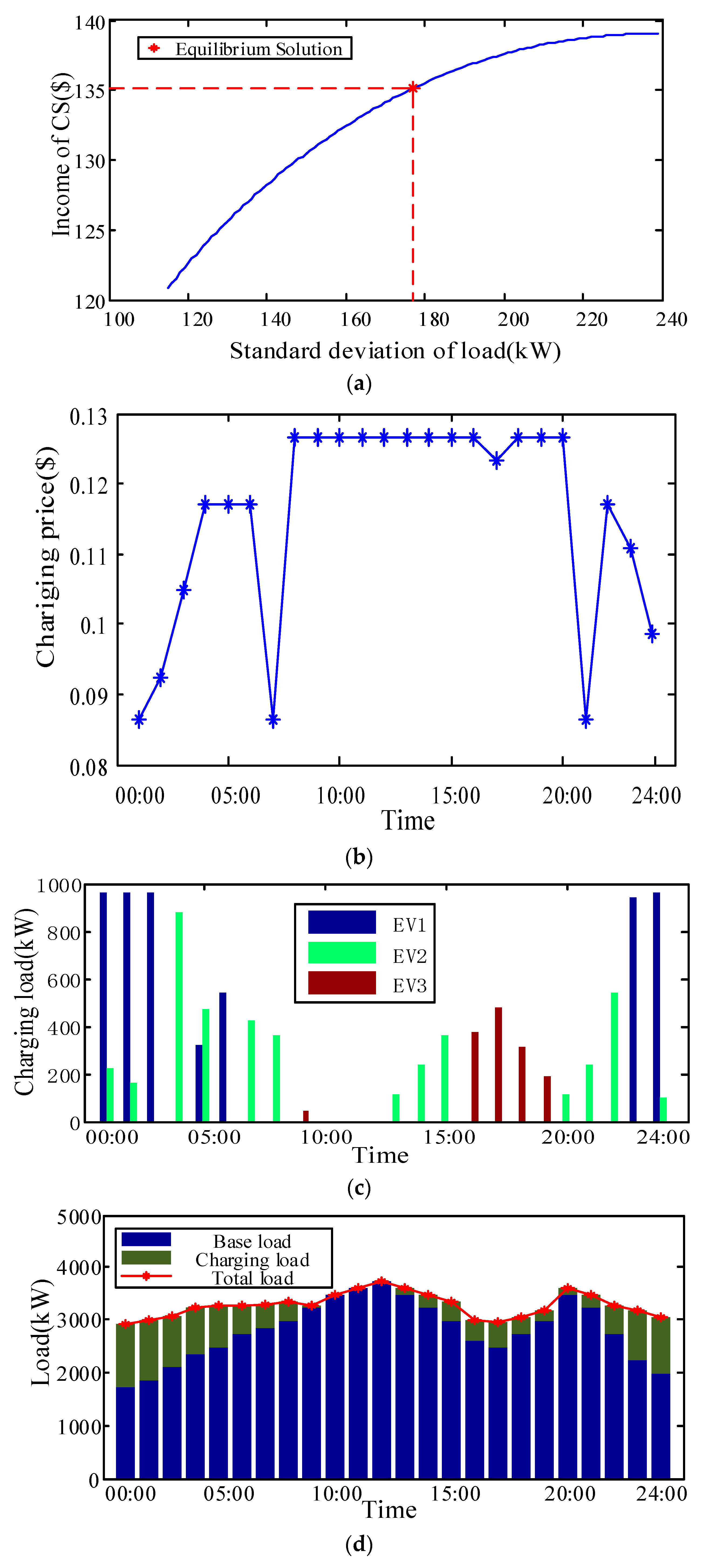
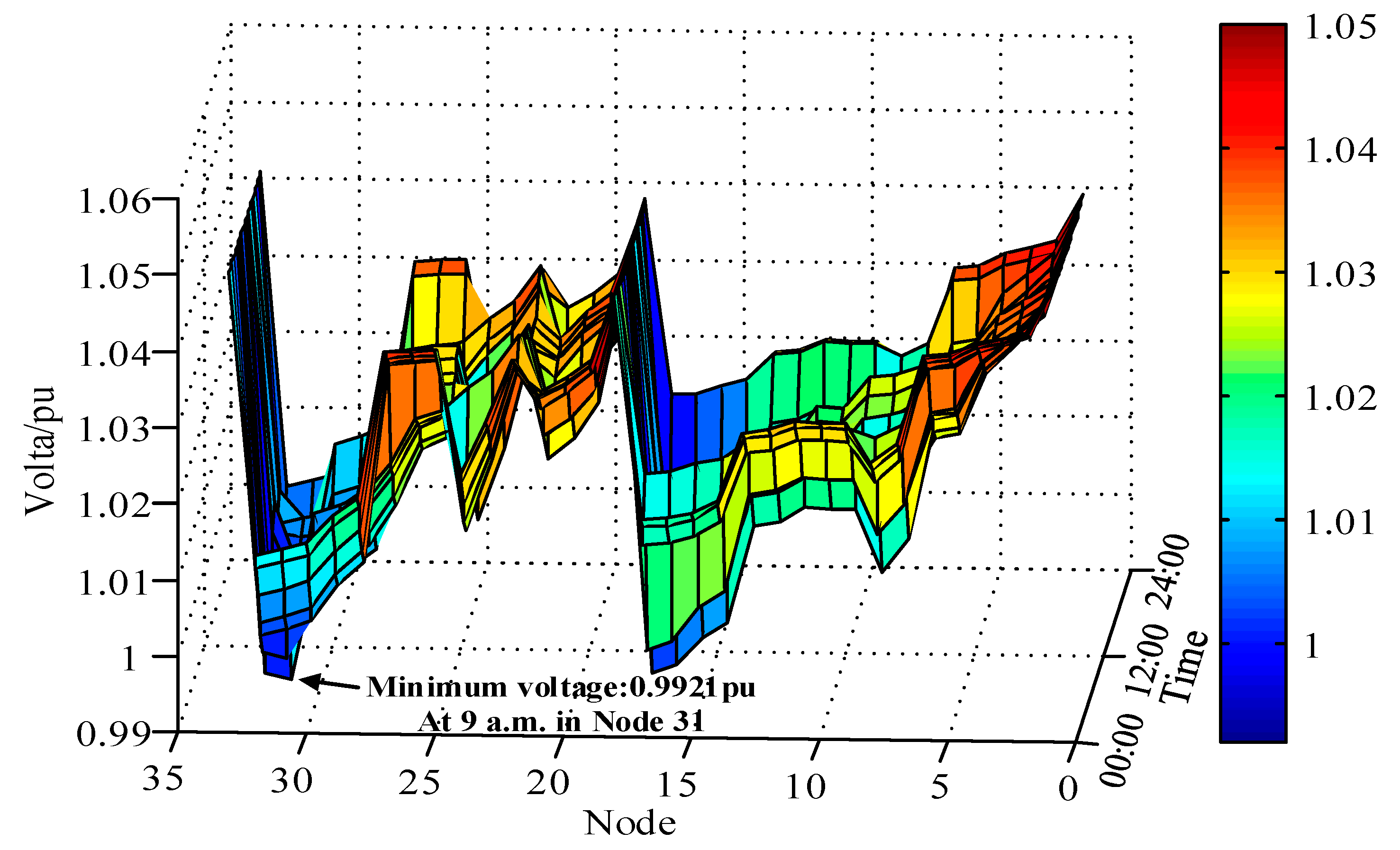
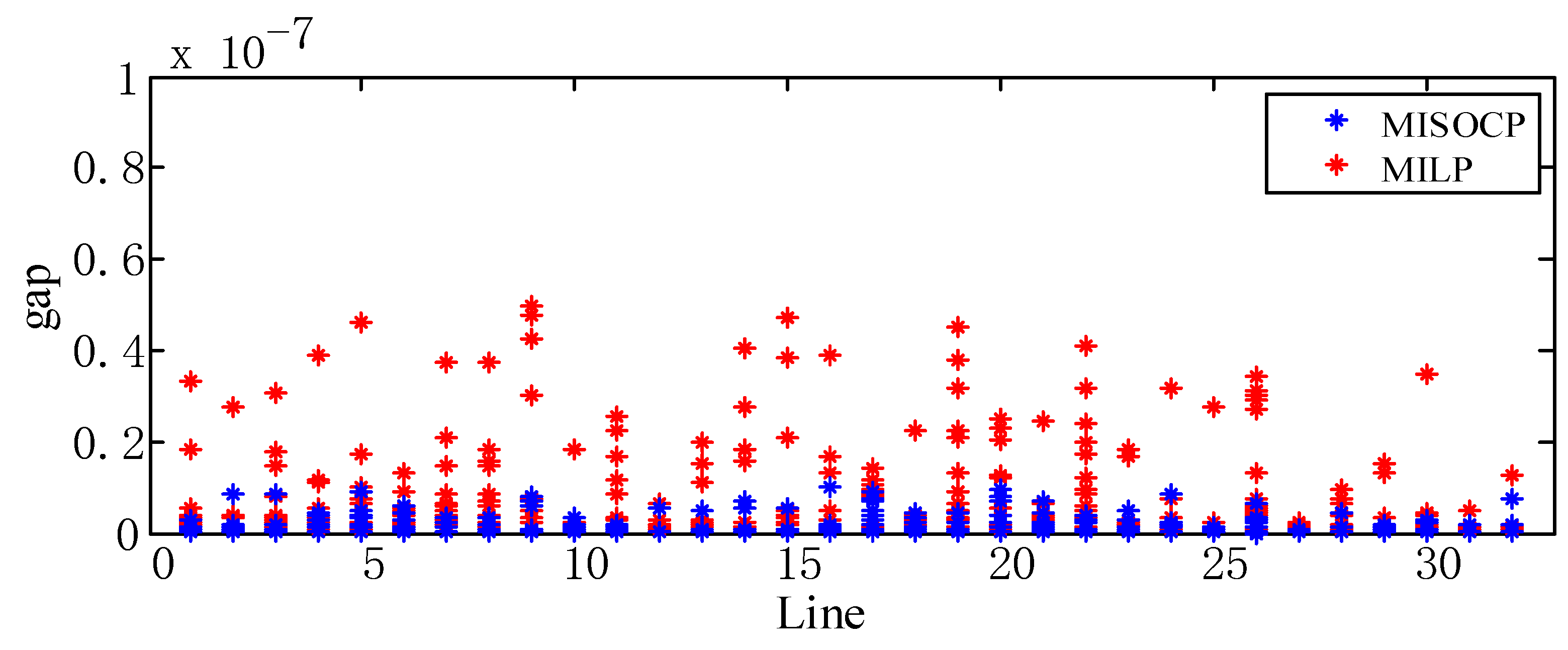
4.2. Discussion
5. Conclusions
- (1)
- The proposed second-order conic relaxation is accurate, which can transform the original model into a convex optimization model in order to obtain the global optimal solution. At the same time, the original variables can be easily restored.
- (2)
- The proposed polyhedral approximation method can speed up the solution of the model. Compared with other algorithms, the polyhedral approximation algorithm can get the global optimal solution with the minimum CPU time.
- (3)
- The proposed scaling algorithm can obtain the Pareto front by solving the problem iteratively, which can preserve the multi-solution of the model and obtain the equilibrium solution.
Author Contributions
Funding
Conflicts of Interest
References
- He, J.F.; Chen, J.J.; Huang, J.Q.; Xiong, W.; Yang, J.; Liu, Y. Research on electric vehicle orderly charging based on regional peak-valley time-of-use price. Electr. Meas. Instrum. 2018, 55, 23–29. [Google Scholar]
- Yang, J.; He, L.F.; Fu, S.Y. An improved PSO-based charging strategy of electric vehicles in electrical distribution grid. Appl. Energy 2014, 128, 82–92. [Google Scholar] [CrossRef]
- Tan, J.; Wang, L. Real-Time Charging Navigation of Electric Vehicles to Fast Charging Stations: A Hierarchical Game Approach. IEEE Trans. Smart Grid. 2015, 8, 846–856. [Google Scholar] [CrossRef]
- Song, Y.; Zheng, Y.; Hill, D. Optimal scheduling for EV charging stations in distribution networks: A convexified model. IEEE Trans. Power Syst. 2017, 32, 1574–1575. [Google Scholar] [CrossRef]
- Chen, J.; Yang, J.; Zhu, J.; Li, X.L.; Zeng, S.; Li, Y.X.; Wang, X.P.; Tang, Y.F. An optimal regional time-of-use charging price model for electric vehicles. In Proceedings of the IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar]
- Li, Y.; Feng, C.S.; Wen, F.S.; Wang, K.; Huang, Y.C. Energy Pricing and Management for Park-level Energy Internets with Electric Vehicles and Power-to-gas Devices. Autom. Electr. Power Syst. 2018, 42, 1–10. [Google Scholar]
- Huang, S.J.; Wu, Q.W.; Oren, S.S.; Li, R.Y.; Liu, Z.X. Distribution Locational Marginal Pricing Through Quadratic Programming for Congestion Management in Distribution Networks. IEEE Trans. Power Syst. 2015, 30, 2170–2178. [Google Scholar] [CrossRef]
- Liu, Z.X.; Wu, Q.W.; Oren, S.S.; Huang, S.J.; Li, R.Y.; Cheng, L. Distribution Locational Marginal Pricing for Optimal Electric Vehicle Charging through Chance Constrained Mixed-Integer Programming. IEEE Trans. Smart Grid 2016, 9, 644–654. [Google Scholar] [CrossRef]
- Li, R.Y.; Wu, Q.W.; Oren, S.S. Distribution Locational Marginal Pricing for Optimal Electric Vehicle Charging Management. IEEE Trans. Power Syst. 2014, 29, 203–211. [Google Scholar] [CrossRef]
- Bitencourt, L.D.A.; Borba, B.S.M.C.; Maciel, R.S.; Fortes, M.Z.; Ferreira, V.H. Optimal EV charging and discharging control considering dynamic pricing. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017. [Google Scholar]
- Yang, J.; Chen, J.J.; Chen, L.; Wang, F.; Xie, P.Y.; Zeng, C.L. A Regional Time-of-Use Electricity Price Based Optimal Charging Strategy for Electrical Vehicles. Energies 2016, 9, 670. [Google Scholar] [CrossRef]
- Yang, X.D.; Zhang, Y.B.; Ren, S.J.; Tong, S.F.; Qi, J.; Weng, G.Q. Optimal charging and discharging dispatching strategy for electric vehicle based on customer’s benefit. In Proceedings of the 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016. [Google Scholar]
- Zhang, G.; Wang, X.; Jiang, C.W. Stackelberg game based coordinated dispatch of virtual power plant considering electric vehicle management. Autom. Electr. Power Syst. 2018, 42, 48–55. [Google Scholar]
- Mao, T.; Lau, W.H.; Shum, C.; Chung, H.S.; Tsang, K.F.; Tse, N.C. A Regulation Policy of EV Discharging Price for Demand Scheduling. IEEE Trans. Power Syst. 2017, 33, 1275–1288. [Google Scholar] [CrossRef]
- Yang, J.W.; Gou, F.J.; Huang, Y.; He, Z.Y. Residential Area Electric Vehicle Charging Pricing Strategy Based on Uncertainty Measure. Power Syst. Technol. 2018, 42, 96–102. [Google Scholar]
- Li, J.Y.; Li, C.J.; Xu, Y.; Dong, Z.Y.; Wong, K.P.; Huang, T.W. Noncooperative Game-based Distributed Charging Control for Plug-In Electric Vehicles in Distribution Networks. IEEE Trans. Ind. Inform. 2016, 14, 301–310. [Google Scholar] [CrossRef]
- Zhang, J.; Yuan, R.M.; Yan, D.X.; Li, T.Y.; Jiang, Z.Y.; Ma, C.B.; Chen, T.J.; Luo, G.Y. A non-cooperative game based charging power dispatch in electric vehicle charging station and charging effect analysis. In Proceedings of the 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–6. [Google Scholar]
- Wei, W.; Liu, F.; Mei, S.W. Energy Pricing and Dispatch for Smart Grid Retailers Under Demand Response and Market Price Uncertainty. IEEE Trans. Smart Grid 2015, 6, 1364–1374. [Google Scholar] [CrossRef]
- Xi, X.; Sioshansi, R. Using Price-Based Signals to Control Plug-in Electric Vehicle Fleet Charging. IEEE Trans. Smart Grid 2014, 5, 1451–1464. [Google Scholar] [CrossRef]
- Wei, W.; Chen, Y.; Liu, F.; Mei, S.W.; Tian, F.; Zhang, X. Stachelberg game based retailer pricing scheme and ev charging management in smart residential area. Power Syst. Technol. 2015, 39, 939–945. [Google Scholar]
- Yurii, N. Lectures on Convex Optimization. IEEE Trans. Autom. Control 2006, 51, 1859. [Google Scholar]
- Jabr, R.A.; Singh, R.; Pal, B.C. Minimum Loss Network Reconfiguration Using Mixed-Integer Convex Programming. IEEE Trans. Power Syst. 2012, 27, 1106–1115. [Google Scholar] [CrossRef]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. Optimization 2004, 2004, 284–289. [Google Scholar]
- Brânzei, R.; Dimitrov, D.A.; Tijs, S.H. Models in Cooperative Game Theory; Springer: New York, NY, USA, 2005. [Google Scholar]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- He, L.F.; Yang, J.; Yan, J.; Tang, Y.F.; He, H.B. A bi-layer optimization based temporal and spatial scheduling for large-scale electric vehicles. Appl. Energy 2016, 168, 179–192. [Google Scholar] [CrossRef]
- Vilar, J.M.G.; Saiz, L. CplexA: A Mathematica package to study macromolecular-assembly control of gene expression. Bioinformatics 2010, 26, 2060–2061. [Google Scholar] [CrossRef] [PubMed]
- Lawler, E.L.; Wood, D.E. Branch-and-Bound Methods: A Survey. Oper. Res. 1966, 14, 699–719. [Google Scholar] [CrossRef]
| Algorithm | fDSO (kW) | fCSs ($) | The Sum of fEVs ($) | CPU Time (s) |
|---|---|---|---|---|
| GA | 183.5642 | 133.1157 | 1207.11 | 892.4 |
| PSO | 178.7535 | 127.5048 | 1244.34 | 411.5 |
| MISOCP | 177.1124 | 135.1261 | 1142.67 | 10.843 |
| MILP | 177.1121 | 135.1372 | 1143.12 | 0.172 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhan, X.; Li, T.; Jiang, L.; Yang, J.; Zhang, Y.; Diao, X.; Han, S. A Convex Optimization Algorithm for Electricity Pricing of Charging Stations. Algorithms 2019, 12, 208. https://doi.org/10.3390/a12100208
Zhang J, Zhan X, Li T, Jiang L, Yang J, Zhang Y, Diao X, Han S. A Convex Optimization Algorithm for Electricity Pricing of Charging Stations. Algorithms. 2019; 12(10):208. https://doi.org/10.3390/a12100208
Chicago/Turabian StyleZhang, Jing, Xiangpeng Zhan, Taoyong Li, Linru Jiang, Jun Yang, Yuanxing Zhang, Xiaohong Diao, and Sining Han. 2019. "A Convex Optimization Algorithm for Electricity Pricing of Charging Stations" Algorithms 12, no. 10: 208. https://doi.org/10.3390/a12100208
APA StyleZhang, J., Zhan, X., Li, T., Jiang, L., Yang, J., Zhang, Y., Diao, X., & Han, S. (2019). A Convex Optimization Algorithm for Electricity Pricing of Charging Stations. Algorithms, 12(10), 208. https://doi.org/10.3390/a12100208





