Abstract
The problem of electricity pricing for charging stations is a multi-objective mixed integer nonlinear programming. Existing algorithms have low efficiency in solving this problem. In this paper, a convex optimization algorithm is proposed to get the optimal solution quickly. Firstly, the model is transformed into a convex optimization problem by second-order conic relaxation and Karush–Kuhn–Tucker optimality conditions. Secondly, a polyhedral approximation method is applied to construct a mixed integer linear programming, which can be solved quickly by branch and bound method. Finally, the model is solved many times to obtain the Pareto front according to the scalarization basic theorem. Based on an IEEE 33-bus distribution network model, simulation results show that the proposed algorithm can obtain an exact global optimal solution quickly compared with the heuristic method.
1. Introduction
With the popularization of traffic electrification, the number of electric vehicles (EVs) is increasing year by year. It is estimated that the number of EVs will reach 11 million in 2025 and 30 million in 2030 [1]. In order to satisfy the charging demand of EVs, a large number of charging stations (CSs) have been built in the distribution network. Considering the charging behavior of EV closely related to people’s daily work and rest, EV users usually charge after work in the evening. In addition, the operation of the distribution network will be severely impacted by a large number of charging loads [2]. Therefore, the electric energy plan of CSs must be optimized to ensure the orderly charging of EVs [3]. Electric vehicle users are guided to change charging time by CSs setting charging prices [4]. The relationship among electric vehicle users, charging station operators, and distribution network operators (DSO), needs to be taken into consideration. However, existing algorithms are inefficient in solving this problem [5]. Therefore, it is very meaningful to develop the optimization algorithm for electric power planning of charging stations.
For the time being, the research on charging price of EVs mainly focuses on time-of-use price [6]. In [7,8,9], the distribution locational marginal pricing (DLMP) method is applied to optimize the charging price of EVs to reduce the impact of charging load on distribution network. In [10,11,12], the electricity demand and travel characteristics of EV users are considered, and charging price is optimized by the price demand elasticity coefficient. In [13], a Stackelberg leadership game model is applied to optimize the electricity prices for encouraging EV users to participate in the electricity market, improving their own interests, and promoting the development of smart energy systems. However, the problem of power planning for charging stations is a multi-objective mixed integer nonlinear programming (MINLP) and some constraints are nonconvex. Heuristic algorithms are usually used to solve this problem such as genetic algorithm (GA) in [14] and particle swarm optimization (PSO) in [15], which take a long time to solve and easily fall into local optimum.
Aiming at getting the global optimal solution quickly, the main contribution of this paper is to propose a convex optimization algorithm for electricity pricing of charging stations. Firstly, the model is transformed into a convex optimization problem by second-order conic relaxation and Karush–Kuhn–Tucker optimality conditions. Secondly, a polyhedral approximation method is applied to construct a mixed integer linear programming, which can be solved quickly by branch and bound method. Finally, the model is solved iteratively to obtain the Pareto front according to the scalarization basic theorem.
On the one hand, the optimal solution can be obtained in the strict sense provided with a convex optimization problem. The conic problem is approximated to a simple type based on polyhedral approximation in order to improve the speed of solution. In addition, the tripartite game problem is decomposed into a Stackelberg leadership game and a cooperative game. Besides, the multi-solution property of the multi-objective optimization problem is preserved under the scaling method.
The remainder of the paper is organized as follows. Section 2 introduces the model of charging station electric power planning. Section 3 proposes the convex optimization algorithm based on second order conic relaxation (SOCR) and polyhedral approximation method. Simulations and analysis are carried out in Section 4. Finally, a conclusion is drawn in Section 5.
2. The Model of Electricity Pricing of Charging Stations
The benefits of DSO and EVs should be taken into account when CSs set electricity prices. The relationship among DSO, CSs, and EVs is shown in Figure 1. Usually, optimizing the power plan of CSs can not only improve its own revenue, but also reduce the peak-valley difference of the distribution network. DSO and CSs can achieve a win-win situation, which constitutes a cooperative relationship [11]. In order to adjust the load curve, DSO guides CSs through marginal price to formulate an appropriate power plan. Charging fee is a cost for EVs but a revenue for CSs. Therefore, there is a conflict of benefits between EVs and CSs, which can be considered as a non-cooperative game relationship [16,17]. A more accurate description should be the Stackelberg game between EVs and CSs because there is a sequence of decisions between the two sides [18]. After charging station operators set charging service price, electric vehicle users decide charging mode according to the price. The goal of EVs is to reduce charging cost and thus EVs will charge when the charging price is low. When CSs formulate the power plan, guiding EVs to charge orderly by setting an appropriate charging price is necessary, and the revenue of CSs should also be maximized.
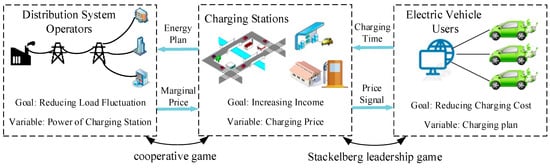
Figure 1.
The relationship among distribution network operators (DSO), charging stations (CSs), and electric vehicles (EVs).
The electricity pricing problem of charging stations is a classical problem in power systems [2,3,4,5,6,7,8,9,10,11], which can be decomposed into the security checking problem of DSO, charging pricing problem of CSs, and charging mode optimization problem of EVs. In the security checking problem of DSO, the objective function of DSO is shown in Equation (1) and the constraints are shown in Equation (2), including power demand equation constraints, bus power balance constraints, bus voltage safety constraints, and line power transmission capacity constraints. The variables in this problem are and the purpose of this problem is to ensure the security of the power system [11].
where fDSO is the deviation of load in distribution network; is the total active power of DSO in period t; is the average active power of DSO; is the basic active power at bus i in period t; is the basic reactive power at bus i in period t; is the charging power at bus i in period t; is the conductance of line ij; Line ij stands for transmission line from bus i to bus j; is the voltage at bus i in period t; is the power angle difference of line ij in period t; is the set of dispatching time; is the susceptance of line ij; is the bus set of distribution network; is the set of transmission lines of distribution network; and are the boundary of voltage.
In the charging pricing problem of CSs, the objective function of CSs is shown in Equation (3) and the constraints are shown in Equation (4), including price boundary constraints and average price equality constraints in order to ensure the fairness of the market when the competition between CSs is neglected [19]. The variables in this problem are and the purpose of this problem is to maximize the revenue of the CSs [18].
where fCSs is the income of CSs; is the charging price at period t; is the price of electricity purchase at period t; N is the set of electric vehicle users; is the charging power of EVn at period t; and are the boundary of charging price; is the average charging price.
In charging mode optimization problem of EVs, the objective function of EVs is shown in Equation (5) and the constraints are shown in Equation (6), including power demand equation constraints, maximum charging power constraints, and available charging time constraints. The variables in this problem are and the purpose of this problem is to minimize the charging cost of EVs [18].
where fEV,n is the charging cost of EVn; is the power demand of EVn; is the maximum charging power; Te(n) is the set of rechargeable time of EVn.
From the above formulas, there are three objective functions in the electricity pricing problem and there are correlations among variables, what lead to the complexity of the model. Hence a series of equivalent transformations must be applied to the model. According to the Stackelberg leadership game model, the game between CSs and EVs can be regarded as a bilevel optimization problem [20], and the subproblems can be expressed as Equation (7).
In order to obtain the optimal solution of the problem, the Lagrange function is shown in Equation (8).
where, Ln is the Lagrange function of Equations (5) and (6); is the dual variable of power demand equation constraints; and are dual variables of maximum charging power constraints; is the dual variable of available charging time constraints.
According to the linear duality theory [21], the dual expression of Equation (5) is shown in Equation (9). At the same time, the optimum condition is Equation (10). The optimization problem of electric vehicle users is transformed into a series of Karush–Kuhn–Tucker (KKT) optimality conditions.
However, Equation (10) includes some complementary constraints, which leads to the nonlinearity of the model. A big-M method is applied to relax the complementary constraints into mixed integer constraints, as Equation (11). At the same time, the main problem can be expressed as Equation (12) according to duality theory.
where M is a given big value; and are binary variables for relaxing Equation (10).
So far, the charging station power planning model is a MINLP with integer variables and non-linear expressions. Additionally, the quadratic equality constraints in Equation (2) make the model non-convex. At the same time, the benefits of DSO and CSs should be considered, which lead to multiple solutions of the model. In short, the problem of power planning for charging stations is a NP-hard problem and existing methods have difficulty in solving this problem.
3. Convex Optimization Algorithm
In this section, the second order conic relaxation method is proposed to transform the model into a convex optimization problem and the scaling algorithm is proposed to obtain the Pareto front.
3.1. SOCR Method
In [22], a method of equality transformation is proposed to promotion dimension of model like Equation (13).
where are temporary variables in order to replace the original variables, which have no practical physical significance.
After this transformation, decision variables have become in the security checking problem of DSO. Additionally, Equation (2) becomes a linear form like Equation (14). In this process, variables are projected into a higher dimensional space. In order to ensure the accuracy of the original problem, a new set of equality constraints need to be added as Equation (13), which constitutes a set of rotating conical spaces. In order to transform the model into convex optimization form, Equation (15) is applied to relax the feasible region to some second order cones.
So far, the original problem has been relaxed into a mixed integer second order conic programming (MISOCP). The existing commercial solver can solve this convex optimization problem. However, the existing convex optimization algorithms are weak in solving this problem because the problem contains a large number of variables [21]. In order to improve the efficiency of solving this problem, a polyhedral approximation method is proposed to construct a mixed integer linear programming (MILP), which can be solved quickly by general algorithms like the branch and bound method [23]. At the same time, the literature [22] has confirmed that the polyhedral approximation method can accurately control model errors and has high efficiency in power flow problems.
At first, Equation (15) is rewritten as Equation (16). And Equation (17) is applied to relax Equation (16) to a polyhedral space.
where is a relaxation scalar and .
Secondly, the rotating cones are equivalent to two standard cones like Equations (18) and (19).
Finally, the smooth edges of cones are replaced with polyhedrons by Equations (21)–(23). The dimensions of a polyhedron depend on the accuracy required in Equation (20).
The boundary of a polyhedron is calculated by recursion. The initial boundary can be calculated by Equation (21) and the recursive expression is shown in Equation (22). These expressions form a set of linear spaces when is given.
Finally, the upper bound of the polyhedron is defined by Equation (23).
The details of polyhedral approximation method are described in Algorithm 1.
| Algorithm 1: Polyhedral approximation algorithm |
| 1: υ: = 0, obtain ε by Equation (20), construct model by Equations (11), (12), and (14) |
| 2: while ε > 10−7 do |
| 3: υ++, obtain ε by Equation (20) |
| 4: end while |
| 5: for t = 1 to T do |
| 6: for ij = 1 to L do |
| 7: add Equations (21) and (23) into model |
| 8: for k = 1 to υ do |
| 9: add Equation (22) into model |
| 10: end do |
| 11: end do |
| 12: end do |
| 13: solve MILP by branch and bound method |
| 14: return PG,t, Pc,t, πc,t, Rij,t, Sij,t, Wi,t, fDSO, fCSs and fEV,n |
The relaxation process is shown in Figure 2. The original non-convex feasible region is first relaxed to a second order cone and then to a series of polyhedrons, which can be solved quickly by simplex method.
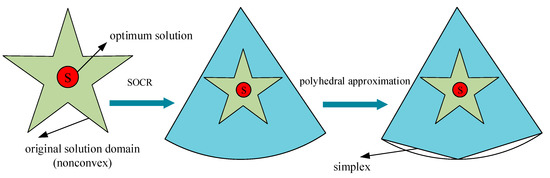
Figure 2.
Relaxation process.
The original solution variables are projected into high-dimensional space by SOCR, so it is necessary to get the original variables by returning the mapping. Firstly, the voltage can be returned by Equation (24).
Then the power angle difference of the line can be obtained by Equations (25) and (26). Based on the agreement of , all angles can be obtained by solving the matrix.
The details of return mapping method are described in Algorithm 2.
| Algorithm 2: Return mapping algorithm |
| 1: Rij,t, Sij,t, and Wi,t: calculated by Algorithm 1 |
| 2: for t = 1 to T do |
| 3: for i = 1 to N do |
| 4: Vi,t: calculated by Equation (24) |
| 5: end do |
| 6: θN0,t:=0 |
| 7: for ij = 1 to L do |
| 8: θi,t: calculated by Equation (26) |
| 9: end do |
| 10: end do |
| 11: return Vi,t and θi,t |
In order to verify the accuracy of relaxation, relaxation errors are defined as Equation (27) to check whether constraints are satisfied.
3.2. Scaling Algorithm
DSO and CSs are cooperative game relations, but both sides have their own benefits. The problem of power planning for charging stations is a multi-objective programming, and the Pareto front can balance the benefits of DSO and CSs well. According to the Pareto front, all the cooperation results can be obtained, and then the appropriate cooperation decision can be selected [24]. Therefore, the key to the problem is how to get the Pareto front of the model. According to the scalarization basic theorem [21], the Pareto front can be obtained by transforming the objective function into a set of constraints and solving the model many times. In this paper, the objective function of DSO is transformed into a constraint like Equation (28). By changing DL, the model is solved many times to obtain the Pareto front.
In order to simplify the model, standard deviation as Equation (29) is used to simplify Equation (28), which can be rewritten as a set of linear constraints.
The details of scaling method are described in Algorithm 3.
| Algorithm 3: Scaling algorithm |
| 1 DL: = +∞, PG,t: obtain by Algorithm 1, fDSO: obtain by Algorithm 1, fCSs: obtain by Algorithm 1 |
| 2 DL: = , t: = 0, obj1[t]: = fDSO, obj2[t]: = fCSs |
| 3 repeat |
| 4 solve MILP by algorithm 1, fDSO: obtain by Algorithm 1, fCSs: obtain by Algorithm 1 |
| 5 if fCSs == obj2[t] then |
| 6 break |
| 7 else then |
| 8 t: t++ |
| 9 obj1[t]: = fDSO, obj2[t]: = fCSs |
| 10 end if |
| 11 until the problem is infeasible |
| 12 return obj1 and obj2 |
4. Case Studies
4.1. Data Generation
The case uses an IEEE 33-bus system [25], and the urban area is divided into residential area, commercial area, and industry area [26]. The total load is 3715 kVA and there are three types of EVs in the distribution network. The structure of the distribution network and the location of the charging station are shown in Figure 3 and the electricity price of DSO is shown in Figure 4. The data of electric vehicles can be obtained in [20]. The battery capacity of EVs is assumed to be 42 kWh, and the initial state of charge (SOC) is 30%. There are 60 charging piles in the CS and the maximum charging power of each charging pile is 30 kW. In order to simplify the problem, this paper assumes that there are three types of EVs in distribution network and their parking time is shown in Figure 5. Additionally, the number of three types of electric vehicles is 200, 150, and 50 respectively. All simulations are implemented on a laptop with Intel® Core(TM) i5-7300HQ CPU@2.5 GHz, 8 GB memory, and the algorithms are compiled by MATLAB. YALMIP tools [23] are used to model and CPLEX [27] is called to solve the MILP model by branch and bound method. Branch and bound method is a common method, whose process only briefly described in this article can be seen in [28].
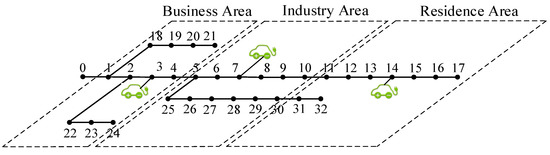
Figure 3.
IEEE 33-bus system.
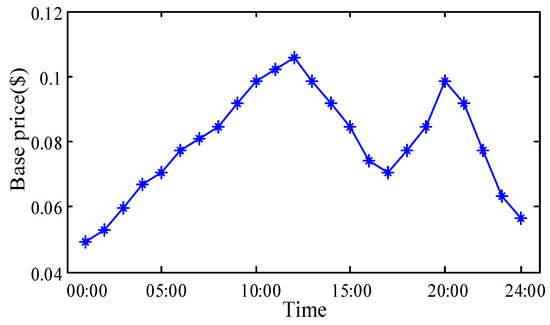
Figure 4.
The basic price of DSO.
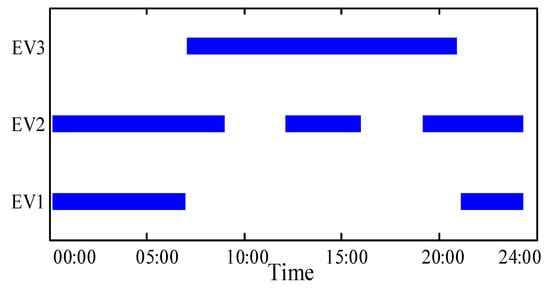
Figure 5.
The parking time of EVs.
4.2. Discussion
The Pareto front obtained is shown in Figure 6a, and an equilibrium solution is selected to show the results. As shown in Figure 6b, charging price is higher in the peak period and lower in the valley period, so as to guide electric vehicle users to charge in the valley period. However, charging prices are the same as in many periods of time, in order to avoid users concentrating on charging at the low price period, resulting in new load peaks. Under the guidance of charging price, the charging power of different electric vehicles is shown in Figure 6c. It can be seen that charging load is mainly concentrated in the night time and some electric vehicles charge in the afternoon, due to their parking characteristics. The load curve of distribution network after orderly charging of electric vehicles is shown in Figure 6d. Under the guidance of charging price, charging load mainly concentrates on the period of low power consumption, which greatly reduces the load fluctuation of the distribution network. It can be seen that the cooperative game between DSO and CSs can achieve win-win situation and maximize social welfare.
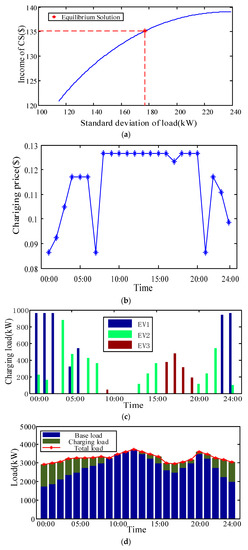
Figure 6.
Simulation results. (a) shows the Pareto front. (b) shows the charging prices. (c) shows the charging load of charging stations. (d) shows the total load of distribution system.
The voltage distribution in the distribution network is shown in Figure 7. It can be seen that the return mapping algorithm can correctly restore the original variables. At the same time, the minimum voltage of distribution network is 0.9921 pu, which occurs at 9 a.m. on bus 31. The minimum operating voltage allowed in the distribution network is 0.93 pu. In other words, the voltage security of the distribution network can be guaranteed under the scheduling strategy in this paper. As shown in Figure 8, the relaxation error of MILP is larger than that of MISOCP but both are less than 10−7. Compared with the numerical value of decision variables, this part of the error can be neglected. It can be seen that the second order cone relaxation has high accuracy. At the same time, polyhedral approximation will not greatly reduce the accuracy of the model.
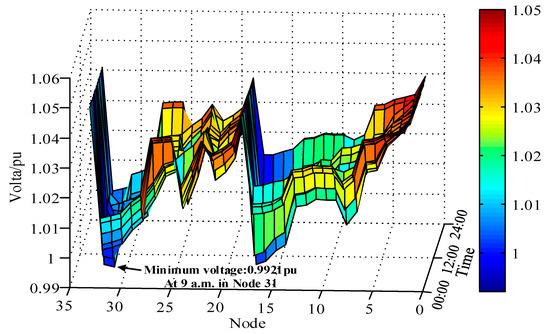
Figure 7.
Voltage distribution in the distribution network.
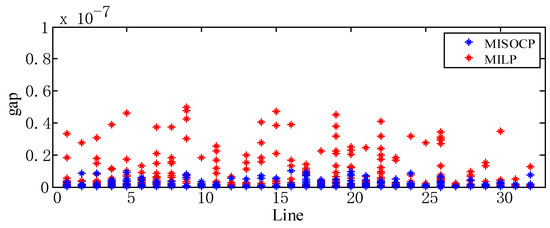
Figure 8.
Relaxation error of the model.
In this paper, the proposed algorithm was compared with GA [14] and PSO [15]. As can be seen from Table 1, the performance of GA and PSO is not ideal in solving this problem. In contrast, MISOCP and MILP can obtain the optimal solution in a very short time. Besides, MISOCP and MILP get the global optimal solution according to the convex optimization theory. Moreover, MILP is more efficient than MISOCP without losing accuracy. Therefore, the polyhedral approximation algorithm proposed in this paper can effectively improve the efficiency of solving this problem.

Table 1.
Comparisons of calculation results.
5. Conclusions
In this paper, a convex optimization algorithm was proposed to solve the problem of power planning for charging station. Second-order conic relaxation and Karush–Kuhn–Tucker optimality conditions were proposed to transform the model into a convex optimization problem. Further, a polyhedral approximation method was applied to construct a MILP and the model was solved iteratively to obtain the Pareto front according to the scalarization basic theorem. The simulation results of IEEE 33-bus test system show that some conclusions can be drawn as follows:
- (1)
- The proposed second-order conic relaxation is accurate, which can transform the original model into a convex optimization model in order to obtain the global optimal solution. At the same time, the original variables can be easily restored.
- (2)
- The proposed polyhedral approximation method can speed up the solution of the model. Compared with other algorithms, the polyhedral approximation algorithm can get the global optimal solution with the minimum CPU time.
- (3)
- The proposed scaling algorithm can obtain the Pareto front by solving the problem iteratively, which can preserve the multi-solution of the model and obtain the equilibrium solution.
However, this study ignores the competitive relationship between charging stations, which may lead to an unfair market. Therefore, the game between charging stations needs further consideration, which is the focus of our future work.
Author Contributions
Conceptualization, J.Z. and T.L.; Methodology, X.Z. and S.H.; Validation, L.J. and Y.Z.; Formal Analysis, J.Y. and X.D.
Funding
This research was funded by Open Fund of Beijing Engineering Technology Research Center of Electric Vehicle Charging/Battery Swap, China Electric Power Research Institute Co., Ltd. (YD83-19-003).
Conflicts of Interest
The authors declare no conflict of interest.
References
- He, J.F.; Chen, J.J.; Huang, J.Q.; Xiong, W.; Yang, J.; Liu, Y. Research on electric vehicle orderly charging based on regional peak-valley time-of-use price. Electr. Meas. Instrum. 2018, 55, 23–29. [Google Scholar]
- Yang, J.; He, L.F.; Fu, S.Y. An improved PSO-based charging strategy of electric vehicles in electrical distribution grid. Appl. Energy 2014, 128, 82–92. [Google Scholar] [CrossRef]
- Tan, J.; Wang, L. Real-Time Charging Navigation of Electric Vehicles to Fast Charging Stations: A Hierarchical Game Approach. IEEE Trans. Smart Grid. 2015, 8, 846–856. [Google Scholar] [CrossRef]
- Song, Y.; Zheng, Y.; Hill, D. Optimal scheduling for EV charging stations in distribution networks: A convexified model. IEEE Trans. Power Syst. 2017, 32, 1574–1575. [Google Scholar] [CrossRef]
- Chen, J.; Yang, J.; Zhu, J.; Li, X.L.; Zeng, S.; Li, Y.X.; Wang, X.P.; Tang, Y.F. An optimal regional time-of-use charging price model for electric vehicles. In Proceedings of the IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar]
- Li, Y.; Feng, C.S.; Wen, F.S.; Wang, K.; Huang, Y.C. Energy Pricing and Management for Park-level Energy Internets with Electric Vehicles and Power-to-gas Devices. Autom. Electr. Power Syst. 2018, 42, 1–10. [Google Scholar]
- Huang, S.J.; Wu, Q.W.; Oren, S.S.; Li, R.Y.; Liu, Z.X. Distribution Locational Marginal Pricing Through Quadratic Programming for Congestion Management in Distribution Networks. IEEE Trans. Power Syst. 2015, 30, 2170–2178. [Google Scholar] [CrossRef]
- Liu, Z.X.; Wu, Q.W.; Oren, S.S.; Huang, S.J.; Li, R.Y.; Cheng, L. Distribution Locational Marginal Pricing for Optimal Electric Vehicle Charging through Chance Constrained Mixed-Integer Programming. IEEE Trans. Smart Grid 2016, 9, 644–654. [Google Scholar] [CrossRef]
- Li, R.Y.; Wu, Q.W.; Oren, S.S. Distribution Locational Marginal Pricing for Optimal Electric Vehicle Charging Management. IEEE Trans. Power Syst. 2014, 29, 203–211. [Google Scholar] [CrossRef]
- Bitencourt, L.D.A.; Borba, B.S.M.C.; Maciel, R.S.; Fortes, M.Z.; Ferreira, V.H. Optimal EV charging and discharging control considering dynamic pricing. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017. [Google Scholar]
- Yang, J.; Chen, J.J.; Chen, L.; Wang, F.; Xie, P.Y.; Zeng, C.L. A Regional Time-of-Use Electricity Price Based Optimal Charging Strategy for Electrical Vehicles. Energies 2016, 9, 670. [Google Scholar] [CrossRef]
- Yang, X.D.; Zhang, Y.B.; Ren, S.J.; Tong, S.F.; Qi, J.; Weng, G.Q. Optimal charging and discharging dispatching strategy for electric vehicle based on customer’s benefit. In Proceedings of the 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016. [Google Scholar]
- Zhang, G.; Wang, X.; Jiang, C.W. Stackelberg game based coordinated dispatch of virtual power plant considering electric vehicle management. Autom. Electr. Power Syst. 2018, 42, 48–55. [Google Scholar]
- Mao, T.; Lau, W.H.; Shum, C.; Chung, H.S.; Tsang, K.F.; Tse, N.C. A Regulation Policy of EV Discharging Price for Demand Scheduling. IEEE Trans. Power Syst. 2017, 33, 1275–1288. [Google Scholar] [CrossRef]
- Yang, J.W.; Gou, F.J.; Huang, Y.; He, Z.Y. Residential Area Electric Vehicle Charging Pricing Strategy Based on Uncertainty Measure. Power Syst. Technol. 2018, 42, 96–102. [Google Scholar]
- Li, J.Y.; Li, C.J.; Xu, Y.; Dong, Z.Y.; Wong, K.P.; Huang, T.W. Noncooperative Game-based Distributed Charging Control for Plug-In Electric Vehicles in Distribution Networks. IEEE Trans. Ind. Inform. 2016, 14, 301–310. [Google Scholar] [CrossRef]
- Zhang, J.; Yuan, R.M.; Yan, D.X.; Li, T.Y.; Jiang, Z.Y.; Ma, C.B.; Chen, T.J.; Luo, G.Y. A non-cooperative game based charging power dispatch in electric vehicle charging station and charging effect analysis. In Proceedings of the 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–6. [Google Scholar]
- Wei, W.; Liu, F.; Mei, S.W. Energy Pricing and Dispatch for Smart Grid Retailers Under Demand Response and Market Price Uncertainty. IEEE Trans. Smart Grid 2015, 6, 1364–1374. [Google Scholar] [CrossRef]
- Xi, X.; Sioshansi, R. Using Price-Based Signals to Control Plug-in Electric Vehicle Fleet Charging. IEEE Trans. Smart Grid 2014, 5, 1451–1464. [Google Scholar] [CrossRef]
- Wei, W.; Chen, Y.; Liu, F.; Mei, S.W.; Tian, F.; Zhang, X. Stachelberg game based retailer pricing scheme and ev charging management in smart residential area. Power Syst. Technol. 2015, 39, 939–945. [Google Scholar]
- Yurii, N. Lectures on Convex Optimization. IEEE Trans. Autom. Control 2006, 51, 1859. [Google Scholar]
- Jabr, R.A.; Singh, R.; Pal, B.C. Minimum Loss Network Reconfiguration Using Mixed-Integer Convex Programming. IEEE Trans. Power Syst. 2012, 27, 1106–1115. [Google Scholar] [CrossRef]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. Optimization 2004, 2004, 284–289. [Google Scholar]
- Brânzei, R.; Dimitrov, D.A.; Tijs, S.H. Models in Cooperative Game Theory; Springer: New York, NY, USA, 2005. [Google Scholar]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- He, L.F.; Yang, J.; Yan, J.; Tang, Y.F.; He, H.B. A bi-layer optimization based temporal and spatial scheduling for large-scale electric vehicles. Appl. Energy 2016, 168, 179–192. [Google Scholar] [CrossRef]
- Vilar, J.M.G.; Saiz, L. CplexA: A Mathematica package to study macromolecular-assembly control of gene expression. Bioinformatics 2010, 26, 2060–2061. [Google Scholar] [CrossRef] [PubMed]
- Lawler, E.L.; Wood, D.E. Branch-and-Bound Methods: A Survey. Oper. Res. 1966, 14, 699–719. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).