1. Introduction
The machine learning techniques for Markov random fields (MRFs) are fundamental in various fields involving pattern recognition [
1,
2], image processing [
3], sparse modeling [
4], and Earth science [
5,
6], and a Boltzmann machine [
7,
8,
9] is one of the most important models in MRFs. The inference and learning problems in the Boltzmann machine are NP-hard, because they include intractable multiple summations over all the possible configurations of variables. Thus, one of the major challenges of the Boltzmann machine is the design of the efficient inference and learning algorithms that it requires.
Various effective algorithms for Boltzmann machine learning were proposed by many researchers, a few of which are mean-field learning algorithms [
10,
11,
12,
13,
14,
15], maximum pseudo-likelihood estimation (MPLE) [
16,
17], contrastive divergence (CD) [
18], ratio matching (RM) [
19], and minimum probability flow (MPF) [
20,
21]. In particular, the CD and MPLE methods are widely used. More recently, the author proposed an effective learning algorithm based on the spatial Monte Carlo integration (SMCI) method [
22]. The SMCI method is a Monte Carlo integration method that takes spatial information around the region of focus into account; it was proven that this method is more effective than the standard Monte Carlo integration method. The main target of this study is Boltzmann machine learning based on the first-order SMCI (1-SMCI) method, which is the simplest version of the SMCI method. We refer it to as the 1-SMCI learning method in this paper.
It was empirically shown through the numerical experiments that Boltzmann machine learning based on the 1-SMCI learning method is more effective than MPLE in the case where no model error exists, i.e., in the case where the learning model includes the generative model [
22]. However, the theoretical reason for this was not revealed at all. In this paper, theoretical insights into the effectiveness of the 1-SMCI learning method as compared to that of MPLE are given from an asymptotic point of view. The theoretical results obtained in this paper state that the gradients of the log-likelihood function obtained by the 1-SMCI learning method constitute a quantitatively better approximation of the exact gradients than those obtained by the MPLE method in the case where the generative model and the learning model are the same Boltzmann machine (in
Section 4.1). This is one of the contributions of this paper. In the previous paper [
22], the 1-SMCI learning method was compared with only the MPLE. In this paper, we compare the 1-SMCI learning method with other effective learning algorithms, RM and MPF, through numerical experiments, and show that the 1-SMCI learning method is superior to them (in
Section 5). This is the second contribution of this paper.
The remainder of this paper is organized as follows. The definition of Boltzmann machine learning and a briefly explanation of the MPLE method are given in
Section 2. In
Section 3, we explain Boltzmann machine learning based on the 1-SMCI method: reviews of the SMCI and 1-SMCI learning methods are presented in
Section 3.1 and
Section 3.2, respectively. In
Section 4, the 1-SMCI learning method and MPLE are compared using two different approaches, the theoretical approach (in
Section 4.1) and the numerical approach (in
Section 4.2), and the effectiveness of the 1-SMCI learning method as compared to the MPLE is shown. In
Section 5, we numerically compare the 1-SMCI method with other effective learning algorithms and observe that the 1-SMCI learning method yields the best approximation. Finally, the conclusion is given in
Section 6.
2. Boltzmann Machine Learning
Consider an undirected and connected graph,
, with
n nodes, where
is the set of labels of nodes and
E is the set of labels of undirected links; an undirected link between nodes
i and
j is labeled
. Since an undirected graph is now considered, labels
and
indicate the same link. On undirected graph
G, we define a Boltzmann machine with random variables
, where
is the sample space of the variable. It is expressed as [
7,
9]
where
is the partition function defined by
where
is the multiple summation over all the possible realizations of
; i.e.,
. Here and in the following, if
is continuous,
is replaced by integration.
represents the symmetric coupling parameters (
). Although a Boltzmann machine can include a bias term, e.g.,
, in its exponent, it is ignored in this paper for the sake of the simplicity of arguments.
Suppose that a set of
N data points corresponding to
,
where
, is obtained. The goal of Boltzmann machine learning is to maximize the log-likelihood
with respect to
, that is, the maximum likelihood estimation (MLE). The Boltzmann machine, with
that maximizes Equation (
2), yields the distribution most similar to the data distribution (also referred to as the empirical distribution) in the perspective of the measure based on Kullback–Leibler divergence (KLD). This fact can be easily seen in the following. The empirical distribution of
is expressed as
where
is the Kronecker delta function:
when
, and
when
. The KLD between the empirical distribution and the Boltzmann machine in Equation (
1),
can be rewritten as
, where
C is the constant unrelated to
. From this equation, we determine that
that maximizes the log-likelihood in Equation (
2) minimizes the KLD.
Since the log-likelihood in Equation (
2) is the concave function with respect to
[
8], in principle, we can optimize the log-likelihood using a gradient ascent method. The gradient of the log-likelihood with respect to
is
where
is the expectation of the assigned quantity over the Boltzmann machine in Equation (
1). In the optimal point of the MLE, all the gradients are zero, and therefore, from Equation (
5), the optimal
is the solution to the simultaneous equations
When the data points are generated independently from a Boltzmann machine,
, defined on the same graph as the Boltzmann machine we use in the learning, i.e., the case without the model error, the solution to the MLE,
, converges to
as
[
23]. In other words, the MLE is asymptotically consistent.
However, it is difficult to compute the second term in Equation (
5), because the computations of these expectations need the summation over
terms. Thus, the exact Boltzmann machine learning, i.e., the MLE, cannot be performed. As mentioned in
Section 1, various approximations for Boltzmann machine learning were proposed by many authors, such as the mean-field learning methods [
10,
11,
12,
13,
14,
15] and the MPLE [
16,
17], CD [
18], RM [
19], MPF [
20,
21] and SMCI [
22] methods. In the following, we briefly review the MPLE method.
In MPLE, we maximize the following pseudo-likelihood [
16,
17,
24] instead of the true log-likelihood in Equation (
2).
where
is the variables in
and
; i.e.,
. The conditional distribution in the above equation is the conditional distribution in the Boltzmann machine expressed by
where
where
is the set of labels of nodes directly connected to node
i; i.e.,
. The derivative of the pseudo-likelihood with respect to
is
is defined by
where
and where, for a set
,
is the
-th data point corresponding to
; i.e.,
. When
,
. In order to fit the magnitude of the gradient to that of the MLE, we use half of Equation (
10) as the gradient of the MPLE
The order of the total computational complexity of the gradients in Equation (
11) is
, where
is the number of links in
. The pseudo-likelihood is also the concave function with respect to
, and therefore, one can optimize it using a gradient ascent method. The typical performance of the MPLE method is almost the same as or slightly better than that of the CD method in Boltzmann machine learning [
24].
From Equation (
13), the optimal
in the MPLE is the solution to the simultaneous equations
By comparing Equation (
6) with Equation (
14), it can be seen that the MPLE is the approximation of the MLE such that
. Many authors proved that the MPLE is also asymptotically consistent (for example, [
24,
25,
26]), that is, in the case without model error, the solution to the MPLE,
, converges to
as
. However, the asymptotic variance of the MPLE is larger than that of the MLE [
25].
4. Comparison of 1-SMCI Learning Method and MPLE
It was empirically observed in some numerical experiments that the 1-SMCI learning method discussed in the previous section is better than MPLE in the case without model error [
22]. In this section, first we provide some theoretical insights into this observation, and then some numerical comparisons of the two methods in the cases with and without model error.
4.1. Comparison from Asymptotic Point of View
Suppose that we want to approximate the expectation
in a Boltzmann machine, and assume that the data points are generated independently from the same Boltzmann machine. Here, we re-express
in Equation (
11) and
in Equation (23) as
respectively, where
Since
s are the i.i.d. points sampled from
,
and
can also be regarded as i.i.d. sample points. Thus,
and
are the sample averages over the i.i.d. points. One can easily verify that the two equations
and
are justified (the former equation can also be justified by using the correlation equality [
27]). Therefore, from the law of large numbers,
in the limit of
. This implies that, in the case without model error, the 1-SMCI learning method has the same solution to the MLE in the limit of
.
From the central limit theorem, the distributions of
and
asymptotically converge to Gaussians with mean
and variances
respectively, for
. For the two variances, we obtain the following theorem.
Theorem 1. For a Boltzmann machine, , defined in Equation (1), the inequality is satisfied for all and for any N. The proof of this theorem is given in
Appendix A. Theorem 1 states that the variance in the distribution of
is always larger than (or equal to) that of
. This means that, when
, the distribution of
converges to a Gaussian around the mean value (i.e., the exact expectation) that is sharper than a Gaussian to which the distribution of
converges, and therefore, it is likely that
is closer to the exact expectation than
when
; that is,
is a better approximation of
than
.
Next, we consider the differences between the true gradient in Equation (
5) and the approximate gradients in Equations (
13) and (26) for
:
For the gradient differences in Equations (32) and (33), we obtain the following theorem.
Theorem 2. For a Boltzmann machine, , defined in Equation (1), the inequalityis satisfied for all when , where is the set of N data points generated independently from . The proof of this theorem is given in
Appendix B. Theorem 2 states that it is likely that the magnitude of
is smaller than (or equivalent to) that of
when the data points are generated independently from the same Boltzmann machine and when
.
Suppose that N data points are generated independently from a generative Boltzmann machine, , defined on , and that a learning Boltzmann machine, defined on the same graph as the generative Boltzmann machine, is trained using the generative data points. In this case, since there is no model error, the solutions of the MLE, the MPLE and the 1-SMCI learning methods are expected to approach as , that is , , and are expected to approach zero as . Consider the case in which N is very large and . From the statement in Theorem 2, is statistically closer to zero than . This implies that the solution of the 1-SMCI learning method converges to that of the MLE faster than the MPLE.
The theoretical results presented in this section have not reached a rigid justification of the effectiveness of the 1-SMCI learning method, because some issues still remain, for instance: (i) since we do not specify whether the problem of solving Equation (27), i.e., a gradient ascent method with the gradients in Equation (26), is a convex problem or not, we cannot remove the possibility of existence local optimal solutions which degrade the performance of the 1-SMCI learning method, (ii) although we discussed the asymptotic property of for each link separately, a joint analysis of them is necessary for a more rigid discussion, and (iii) a perturbative analysis around the optimal point is completely lacking. However, we can expect that they constitute evidence that is important for gaining insight into the effectiveness.
4.2. Numerical Comparison
We generated N data points from a generative Boltzmann machine, and then trained a learning Boltzmann machine of the same size as the generative Boltzmann machine using the generated data points. The coupling parameters in the generative Boltzmann machine, , were generated from a unique distribution, .
First, we consider the case where the graph structures of the generative Boltzmann machine and the learning Boltzmann machine are the same: a
square grid, that is the case “without” model error.
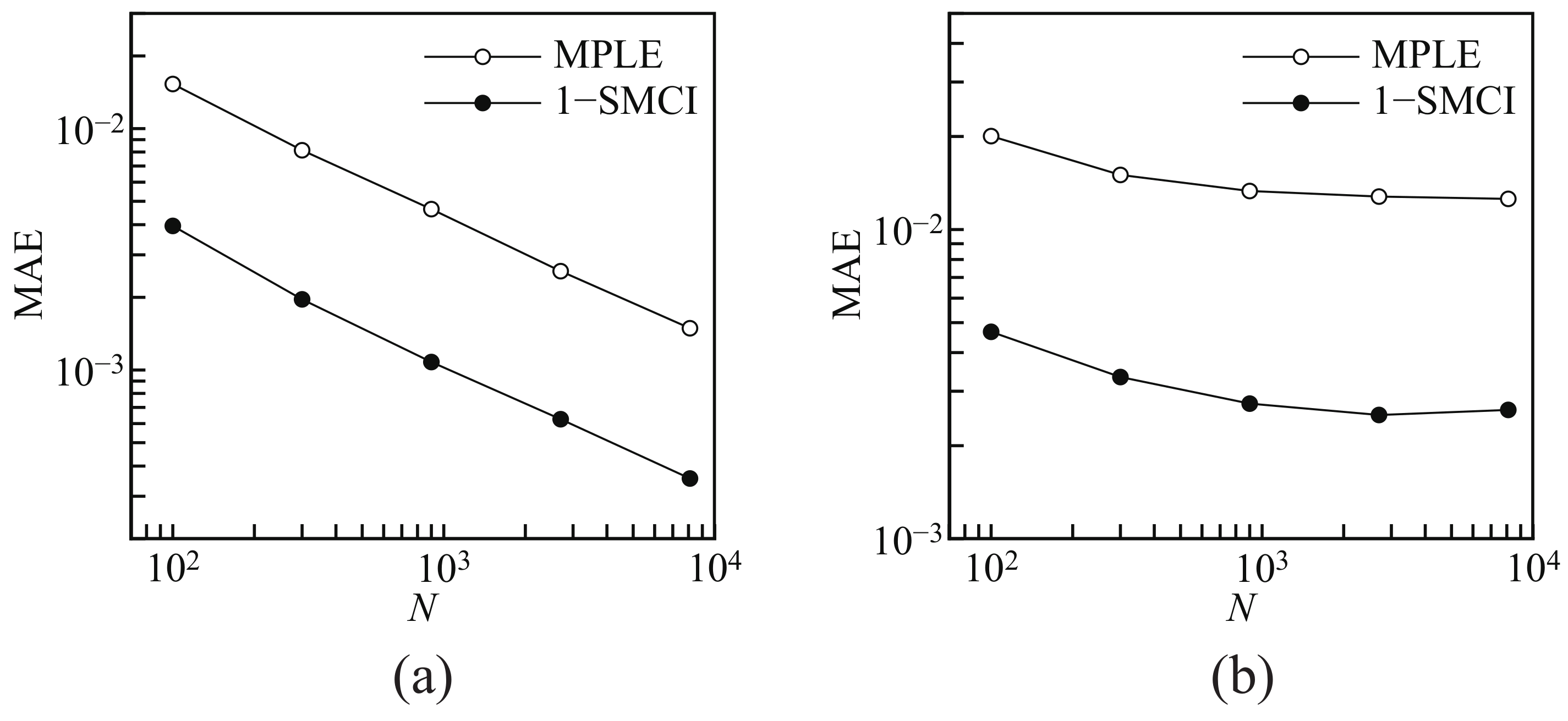
Figure 2a shows the mean absolute errors between the solutions to the MLE and the approximate methods (the MLPE and the 1-SMCI learning method),
, against
N. Here, we set
. Since the size of the Boltzmann machine used here is not large, we can obtain the solution to the MLE. We observe that the solutions to the two approximate methods converge to the solution to the MLE as
N increases, and the 1-SMCI learning method is better than the MPLE as the approximation of the MLE. These results are consistent with the results obtained in [
22] and the theoretical arguments in the previous section.
Next, we consider the case in which the graph structure of the generative Boltzmann machine is fully connected with
and that in which the learning Boltzmann machine is again a
square grid, namely the case “with” model error. Thus, this case is completely outside the theoretical arguments in the previous section.
Figure 2b shows the mean absolute errors between the solution to the MLE and that to the approximate methods against
N. Here, we set
. Unlike the above case, the solutions to the two approximate methods do not converge to the solution to the MLE because of the model error. The 1-SMCI learning method is again better than the MPLE as the approximation of the MLE in this case.
By comparing
Figure 2a,b, we observed that the 1-SMCI learning method in (b) is worse than in (a). The following reason can be considered. In
Section 3.2, we replaced
, which is the sample points drawn from the Boltzmann machine, by
in order to avoid the sampling cost. However, this replacement implies the assumption of the case “without” model error, and therefore, it is not justified in the case “with” model error.
5. Numerical Comparison with Other Methods
In this section, we demonstrate a numerical comparison of the 1-SMCI learning method with other approximation methods, RM [
19] and MPF [
20,
21]. The orders of the computational complexity of these two methods are the same as that of the MPLE and 1-SMCI learning methods. The four methods were implemented by a simple gradient ascent method,
, where
is the learning rate.
As described in
Section 4.2, we generated
N data points from a generative Boltzmann machine,
and then trained a learning Boltzmann machine of the same size as the generative Boltzmann machine using the generated data points. The coupling parameters in the generative Boltzmann machine,
, were generated from
. The graph structures of the generative Boltzmann machine and of the learning Boltzmann machine are the same: a
square grid.
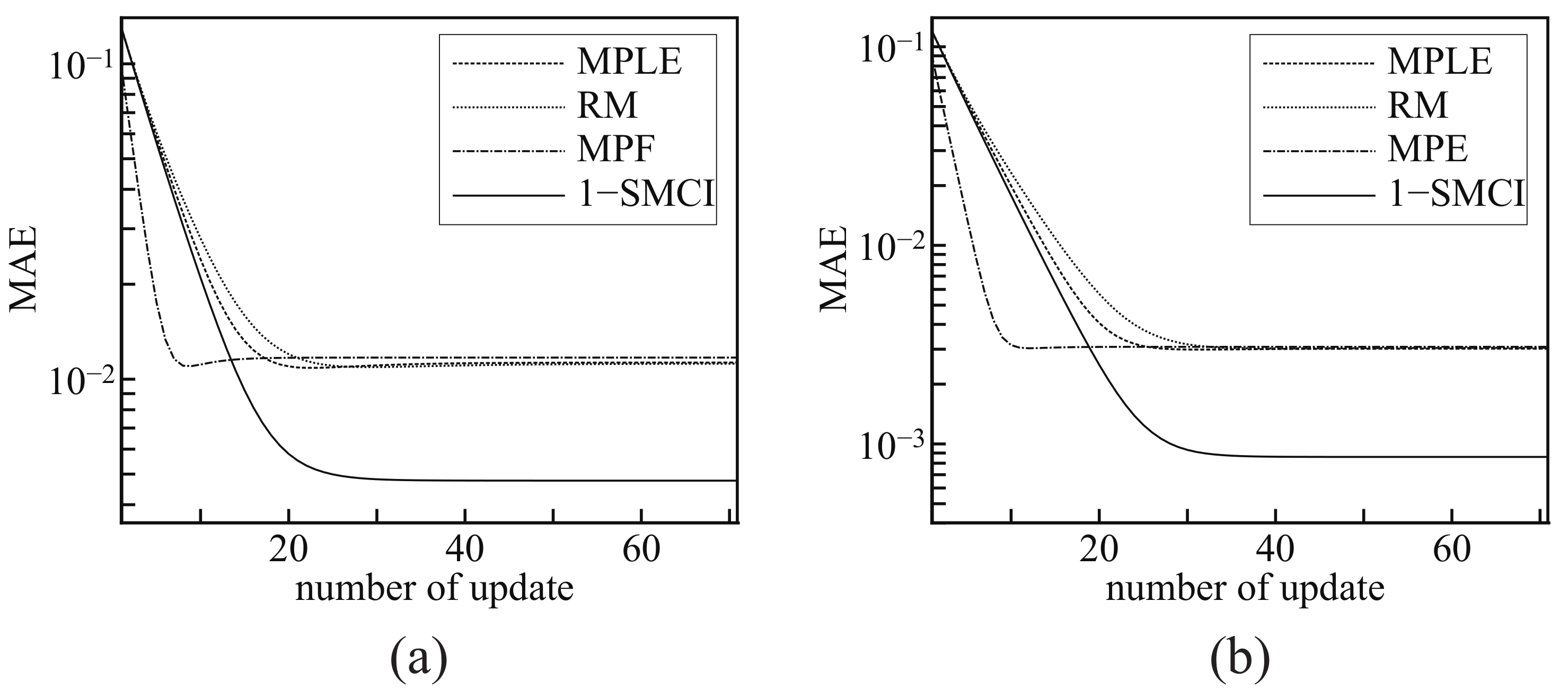
Figure 3 shows the learning curves of the four methods. The horizontal axis represents the number of the step,
t, of the gradient ascent method, and the vertical axis represents the mean absolute errors between the solution to the MLE,
, and the values of the coupling parameters at the step,
. In this experiment, we set
, and the values of
were initialized as zero.
Since the vertical axises in
Figure 3 represents the the mean absolute error from the solution to the MLE, the lower one is the better approximation of the MLE. We can observe that the MPF shows the fastest convergence and the MPLE, RM, and MPF converge to almost the same values, while the 1-SMCI learning method converges to the lowest values. This concludes that, among the four methods, the 1-SMCI learning method is the best as the approximation of the MLE. However, the 1-SMCI learning method has a drawback. The MPLE, RM, and MPF are convex optimization problems and they have unique solutions, whereas, we do not specify whether the 1-SMCI learning method is a convex problem or not in the present stage. We cannot eliminate the possibility of the existence of local optimal solutions that degrade the accuracy of approximation.
As mentioned above, the orders of the computational complexity of these four methods, the MPLE, RM, MPF, and 1-SMCI learning methods, are the same,
. However, it is important to check the real computational times of these methods.
Table 1 shows the total computational times needed for the one-time learning (until convergence), where the setting of the experiment is the same as that of
Figure 3b.
The MPF method is the fastest, and the 1-SMCI learning method is the slowest which is about 6–7 times slower than the MPF method.
6. Conclusions
In this paper, we examined the effectiveness of Boltzmann machine learning based on the 1-SMCI method proposed in [
22] where, by numerical experiments, it was shown that the 1-SMCI learning method is more effective than the MPLE in the case where no model error exists. In
Section 4.1, we gave the theoretical results for the empirical observation from the asymptotic point of view. The theoretical results improved our understanding of the advantage of the 1-SMCI learning method as compared to the MPLE. The numerical experiments in
Section 4.2 showed that the 1-SMCI learning method is a better approximation of the MPLE in the case with and without model error. Furthermore, we compared the 1-SMCI learning method with the other effective methods, RM and MPF, using the numerical experiments in
Section 5. The numerical results showed that the 1-SMCI learning method is the best method.
However, issues related to the 1-SMCI learning method still remain. Since the objective function of the 1-SMCI learning method, e.g., Equation (
7) for the MPLE, is not revealed, it is not straightforward to specify whether the problem of solving Equation (27), i.e., a gradient ascent method with the gradients in Equation (26), is a convex problem or not. This is one of the most challenging issues of the method. As shown in
Section 4.2, the performance of the 1-SMCI learning method decreases when model error exists, i.e., when the learning Boltzmann machine does not include the generative model. The decrease may be caused by the replacement of the sample points,
, by the data points,
, as discussed in the same section. It is expected that combining the 1-SMCI learning method with an effective sampling method, e.g., the persistent contrastive divergence [
28], relaxes the problem of the performance degradation.
The presented the 1-SMCI learning method can be applied to other types of Boltzmann machines, e.g., restricted Boltzmann machine [
1], deep Boltzmann machine [
2,
29]. Although we focused on the Boltzmann machine learning in this paper, the SMCI method can be applied to various MRFs [
22]. Hence, there are many future directions of application of the SMCI: for example, graphical LASSO problem [
4], Bayesian image processing [
3], Earth science [
5,
6] and brain-computer interface [
30,
31,
32,
33].