Abstract
The number of just-in-time jobs maximization in a permutation flow shop scheduling problem is considered. A mixed integer linear programming model to represent the problem as well as solution approaches based on enumeration and constructive heuristics were proposed and computationally implemented. Instances with up to 10 jobs and five machines are solved by the mathematical model in an acceptable running time (3.3 min on average) while the enumeration method consumes, on average, 1.5 s. The 10 constructive heuristics proposed show they are practical especially for large-scale instances (up to 100 jobs and 20 machines), with very good-quality results and efficient running times. The best two heuristics obtain near-optimal solutions, with only 0.6% and 0.8% average relative deviations. They prove to be better than adaptations of the NEH heuristic (well-known for providing very good solutions for makespan minimization in flow shop) for the considered problem.
1. Introduction
Permutation flow shop scheduling, a production system in which jobs follow the same flow for all machines in the same order, is one of the most important production planning problems [1]. This type of manufacturing environment is very often encountered in intermittent industrial production systems. In this context, the just-in-time scheduling aims to achieve a solution that minimizes the cost functions associated with the earliness and tardiness of jobs. Therefore, it is more common to find research addressing the sum of the earliness and tardiness of jobs or the penalties caused by a deviation from a previously established due date for the delivery of a product. In practice, these performance measures are very important for companies as both the earliness and tardiness of completing jobs entail relatively higher costs of production, such as increases in inventory levels, fines, cancellations of orders or even loss of customers.
A different approach is to consider an objective related to the number of early/tardy jobs rather than earliness/tardiness duration [2]. Lann and Mosheiov [3] introduced in 1996 a class of problems in the just-in-time area that aims to maximize the number of jobs completed exactly on their due dates, which are called just-in-time jobs. However, up to date, there are still few works in the literature that consider as an optimization criterion the maximization of the number of just-in-time jobs, despite its applicability. Examples of applications in which such structure may arise include: chemical or hi-tech industries, where parts need to be ready at specific times in order to meet certain required conditions (arrival of other parts, specific temperature, pressure, etc.); production of perishable items (e.g., food and drugs) under deterministic demand; maintenance services agencies which handle the preferable due date for customers; and rental agencies (hotels amd car rental), where reservations schedule must meet exactly the time requested by all clients.
In classical notation of three fields, the maximization of the number of just-in-time jobs in a permutation flow shop problem can be denoted by Fm|prmu, dj|nJIT, where Fm indicates a generic flow shop environment with m machines, prmu the permutation constraint, dj the existence of a due date for each job and nJIT the objective function that maximizes the number of jobs completed just-in-time. In some environments, such as a single-machine problem and permutation flow shop, the schedule is provided by only job sequencing. In others, it is also necessary to allocate jobs to machines, such as in the ones with parallel machines and in hybrid flow shop. Although this research addresses the problem of the permutation flow shop, in addition to sequencing, there is also the possibility of inserting idle time into some jobs to adjust their completions to the due dates (if there is slack). That is, the solution (schedule) comprises sequencing and timing phases; besides an order of jobs, it is also necessary to define the starting and ending stages of each operation. In the literature, it is known as a schedule with inserted idle time [4].
The purpose of this work is to provide insights for a theme in the area of scheduling that, despite its importance for several industrial contexts, is relatively unexplored. This study proposes a mathematical model to represent the permutation flow shop scheduling with the total number of just-in-time jobs being maximized and a set of heuristic solution approaches to solve it in a relatively short execution time. A comprehensive computational study is presented. As shown in the literature review, to the best of our knowledge, all but one of the papers dealing with the maximization of the total number of just-in-time jobs only present theoretical results. Thus, this research helps to fill the gap of computational results in the literature of scheduling problems. We are concerned with applications for which there is no interest in jobs that are finished before or after their due dates.
The remainder of this paper is organized as follows. A review of the just-in-time scheduling problems literature is presented in Section 2. A formal description of the problem considered and the mixed integer linear programming model developed is given in Section 3. The proposed constructive heuristics methods are discussed in Section 4. Analyses of the results from all the solution approaches computationally implemented in this study are presented in Section 5. Final remarks are given in Section 6.
2. Literature Review
Although the just-in-time philosophy involves broader concepts, until recent decades, scheduling problems in this area were considered variations of earliness and tardiness minimization, as can be seen in the review by [5]. Many problems are presented in [6,7]. The most common just-in-time objective functions found in the literature are related the total weighted earliness and tardiness, with equal, asymmetric or individual weights.
Recently, Shabtay and Steiner [8] published a review of the literature addressing the problem of maximizing the number of just-in-time jobs which demonstrates that this theme has been very little explored. The work presented in [7], which deals with various types of just-in-time scheduling problems, mentions only one paper that considers the number of just-in-time jobs, that is, the survey presented in [8] of single-, parallel- and two-machine flow shop environments.
There are some publications in the relevant literature that discuss the problem considering the criteria of maximizing the number of just-in-time jobs in different production systems, specifically with flow shops. Choi and Yoon [9] showed that a two-machine weighted problem is classified as NP-complete and a three-machine identical weights one as NP-hard. These authors proposed and demonstrated several dominance conditions for an identical weights problem. Based on these conditions, they presented an algorithm for a two-machine problem. In addition, they proved that an optimal solution to a two-machine problem is given by the earliest due date (EDD) priority rule.
Several two-machine weighted problems, a flow shop, job shop and open shop, are considered by [10]. They propose pseudo-polynomial time algorithms and a way of converting them to polynomial time approach schemes. Shabtay [11] examined four different scenarios for a weighted problem: firstly, two machines and identical weights for jobs; secondly, a proportional flow shop, which the processing times on all machines are the same; thirdly, a set of identical jobs to be produced for different clients (the processing times are equal but due dates different for each client); and, lastly, the no-wait flow shop with no waiting times between the operations of a job. A dynamic programming algorithm and, for a two-machine problem, an algorithm of less complexity than that were proposed by [9]. A proportional flow shop problem was addressed by [12] who considered options of with and without a no-wait restriction, and proposed dynamic programming algorithms.
Given the difficulty of directly solving this class of problems, some authors preferred to convert them into other types of optimization problems, such as the partition problem [9] and the modeling of acyclic directed graphs [11]. A bi-criteria problem of maximizing the weighted number of just-in-time jobs and minimizing the total resource consumption cost in a two-machine flow shop was considered by [2].
Focusing on maximizing the number of just-in-time jobs, only one work [2] presented computational experiments. Gerstl et al. [12] only mentioned that a model is implemented. Unlike most studies in the shop scheduling area employing experimental research methodologies, all other papers examined used theoretical demonstrations and properties to attest to the validity of their proposed methods, as well as analyses of algorithmic complexity, but did not present computational results.
Yin et al. [13] considered the two-machine flow shop problem with two agents, each of them having its own job set to process. The agents need to maximize individually the weighted number of just-in-time jobs of their respective set. The authors provided two pseudo-polynomial-time algorithms and their conversion into two-dimensional fully polynomial-time approximation schemes (FPTAS) for the problem.
In general, the research studies about the maximization of the number of just-in-time jobs encountered in the literature are limited to a two-machine flow shop problem. No constructive heuristic was found for a m-machine flow shop or computational experiments, which are important to evaluate the effectiveness of the method in terms of solution quality and computational efficiency. One of the main contributions of this research is the presentation of efficient and effective solution methods for maximizing the number of just-in-time jobs which are demonstrated to be applicable to practical multiple-machine flow shop problems. Preliminary results of this research are presented in [14,15].
3. A Mixed Integer Linear Programming Model
The flow shop scheduling problem can be generically formulated as follows. Consider a set of n independent jobs (J = {J1, J2, ..., Jn}), all of which have the same weight or priority, cannot be interrupted, are released for processing at zero time, have to be executed in m machines (M = {M1, M2, ..., Mm}) and are physically arranged to follow identical unidirectional linear flows (i.e., all the jobs are processed through the machines at the same sequence). Each job (Jj) requires a processing time (pjk) in each machine (Mk) and have its due date represented by dj, both considered known and fixed. The solution consists of finding a schedule that maximizes the number of jobs finished at exactly their respective due dates.
To formulate a mathematical model to represent the problem, consider the following parameters, indices and variables.
Parameters and indices:
| n | number of jobs | |
| m | number of machines | |
| i, j | job index | i = 0, …, n, j = 0, …, n |
| k | machine index | k = 0, …, m |
| pjk | processing time of job Jj on machine Mk | j = 1, ..., n, k = 1, ..., m |
| dj | due date of job Jj | j = 1, ..., n |
| B | very large positive integer, the value considered in Section 5 is: | |
| J0 | dummy job—the first in the scheduling | |
| M0 | dummy machine—theoretically considered before the first (physical) machine | |
Decision variables:
| Cjk | completion time of job Jj on machine Mk | j = 0, ..., n, k = 0, ..., m |
| Uj | equals 1 if job Jj is just-in-time or 0 otherwise | j = 1, ..., n |
| xij | equals 1 if job Ji is assigned immediately before job Jj or 0, otherwise | |
| j = 0, ..., n, j = 1, ..., n, . | ||
The mixed integer programming model given by Expressions (1)–(12) is based on the approach proposed by Dhouib et al. [16].
Subject to:
The optimization criterion expressed in Equation (1) is to maximize the number of just-in-time jobs. Expressions in Equation (2) ensure the consistency of the completion times of jobs, that is, if job Ji immediately precedes job Jj (i.e., xij = 1), the difference between their completion times on each machine must be at least equal to the processing time of job Jj on the machine considered; otherwise (if xij = 0), if there is no relationship between the completion times of this pair of jobs, then the constraints in Equation (2) are redundant. Constraints in Equation (3) require that the kth operation of job Jj be completed after the (k − 1)th operation plus the processing time (pjk). Generally, the value of B is an upper bound to the makespan.
The expressions in Equations (4) and (5) jointly establish that the variable Uj equals 1 if job Jj finishes on time or 0 otherwise. When job Jj does not finish on time, i.e., Uj = 0, these two sets of constraints become redundant. The constraints in Equation (6) ensure that only one job is assigned to the first position in the sequence (not considering the dummy job J0). The expressions in Equation (7) establish that job Jj (j ≠ 0) either occupies the first position (after J0) or is necessarily preceded by another job. The constraints in Equation (8) ensure that one job, at most, immediately precedes another. The expressions in Equation (9) define that all the jobs are ready to be initiated on machine M1, that is the completion time for all jobs in the dummy machine (k = 0) is zero, and so ensure the consistency of the restrictions in Equation (3). The expressions in Equations (10)–(12) define the domain of the variables.
The model’s size in relation to its numbers of variables and constraints are presented in Table 1. For example, an instance with jobs and machines has 69 variables and 91 constraints and another one with jobs and machines has 236 variables and 268 constraints.

Table 1.
Model’s size in relation to numbers of variables and constraints.
4. Constructive Heuristics
To efficiently solve the problem described in Section 3, ten constructive heuristic methods are proposed based on an investigation of the problem structure and inspired by relevant classical algorithms, such as the NEH heuristic [17], Hodgson’s algorithm [18] and well-known priority rules, such as the EDD which is the ascending order of due dates, and the minimum slack time (MST) which sequences jobs according to the smallest amount of slack (). It is known that, in a single-machine problem, the EDD and MST rules minimize the maximum tardiness and earliness, respectively [19].
All the heuristics require a timing adjustment procedure that consists of checking the best instant to start the operations for a given sequence to complete a greater number of jobs on time. The simple shifting of an early job with a slack time to match its conclusion to its due date could result in an overall improvement in the solution. A pseudo-code of the timing adjustment procedure is given in Algorithm 1. Note that a shift is applied only in the last operation of a job (Step 3 in Algorithm 1) because keeping each previous operation starting at its earliest possible instant can be an advantage in this problem as it enables jobs that could be late because of their first operations to be anticipated. In addition, this shift is maintained when there is an improvement in the solution (or at least a tie); otherwise, the replacement is reversed to anticipate operations which contribute to eliminating possible tardiness in subsequent jobs.
Timing adjustment procedure
- Step 1.
- For the given sequence, considering starting each operation as early as possible, compute the number of just-in-time jobs (nJIT) and consider Jinitial = J[1], where J[j] is the job in position j of the sequence.
- Step 2.
- From Jinitial, identify the first early job in the sequence (JE) and go to Step 3. If there are no early jobs (from Jinitial), STOP.
- Step 3.
- Move the last operation of job JE to eliminate earliness and make its conclusion coincide with its due date. Properly reschedule the last operations of the jobs after JE.
- Step 4.
- Compute the new number of just-in-time jobs (nJIT’).If nJIT’ < nJIT (the new solution is worse than the previous one), return both the last operation of JE and the operations of the following jobs to their previous positions, set Jinitial = J[initial] + 1 and go to Step 2.Else (the new solution is better than or equal to the previous one), keep the new schedule, set Jinitial = J[E] + 1 and go to Step 2.
Algorithm 1. Pseudo-code of timing adjustment procedure.
The first four heuristics proposed are adaptations of the NEH algorithm’s insertion method and are given in Algorithms 2–5. H1 and H2 employ the EDD rule as the initial order while H3 and H4 consider the MST rule. Another feature is that H2 and H4 improve on H1 and H3, respectively, by using neighborhood search in the partial sequence.
Two types of neighborhood search are employed, insertion and permutation, in the same way as [20]. Given a sequence (or a partial sequence) of n jobs, its insertion neighborhood consists of all (n − 1)2 sequences obtained by removing a job from its place and relocating it to another position. The permutation neighborhood is composed by all n(n − 1)/2 sequences obtained by permuting the positions of two jobs (see Example 1).
Table 2 summarizes the main procedures used in each one of the constructive heuristics. Example 1. Consider the initial sequence with four jobs: {J3, J2, J1, J4}. The insertion neighborhood results in (n − 1)2 = 9 sequences:

Table 2.
Composition of heuristic’s structure.
- -
- Initially, inserting the first job J3: {J2, J3, J1, J4}, {J2, J1, J3, J4}, {J2, J1, J4, J3};
- -
- Then, inserting the second job J2 only in the positions not considered yet: {J3, J1, J2, J4}, {J3, J1, J4, J2}; for example, it is not necessary to insert J2 in the first position because the sequence resulting was already listed; and
- -
- Next, the third job J1 is inserted and, lastly, the fourth one J4: {J1, J3, J2, J4}, {J3, J2, J4, J1}, {J4, J3, J2, J1}, {J3, J4, J2, J1}.
Starting again from the initial sequence {J3, J2, J1, J4} of the same example, the permutation neighborhood results in n(n − 1)/2 = 6 sequences:
- -
- First, the first two jobs are permuted: {J2, J3, J1, J4}; then the first and third jobs: {J1, J2, J3, J4}; and the first and fourth jobs: {J4, J2, J1, J3};
- -
- Next, from the initial sequence, the second and third are permutated: {J3, J1, J2, J4}; and the second and fourth: {J3, J4, J1, J2}; and
- -
- Lastly, from the initial sequence, the third and fourth jobs are permutated: {J3, J2, J4, J1}.
Heuristic H1
- Step 1.
- Order jobs according to the EDD rule (in the case of a tie, use the lower ∑pjk).
- Step 2.
- For the first two jobs, apply the timing adjustment procedure to find the best partial sequence (between these two possibilities) with the lower nJIT.
- Step 3.
- For h = 3 to n, do:Keeping the relative positions of the jobs of the partial sequence, insert the hth job of the order defined in Step 1 in all possible positions and apply the timing adjustment procedure in each insertion; consider the new partial sequence with the best nJIT (in the case of a tie, use the upper position).
Algorithm 2. Pseudo-code of heuristic H1.
Heuristic H2
- Step 1.
- Order jobs by the EDD rule (in the case of a tie, use the lower ∑pjk).
- Step 2.
- For the first two jobs, apply the timing adjustment procedure to find the best partial sequence (between these two possibilities) with the lower nJIT.
- Step 3.
- For h = 3 to n, do:Add the hth job of order defined in Step 1 in the last position of the partial sequence;Considering the insertion neighborhood with (h − 1)2 partial sequences and applying the timing adjustment procedure, determine that with the best nJIT;From the best solution obtained so far, considering the permutation neighborhood with h(h − 1)/2 partial sequences and applying the timing adjustment procedure, determine that with the best nJIT.
Algorithm 3. Pseudo-code of heuristic H2.
Heuristic H3
- Step 1.
- Order jobs by the MST rule (in the case of a tie, use the lower ∑pjk).
- Steps 2 and 3.
- The same as in heuristic H1.
Algorithm 4. Pseudo-code of heuristic H3.
Heuristic H4
- Step 1.
- Order jobs by the MST rule (in the case of a tie, use the lower ∑pjk).
- Steps 2 and 3.
- The same as in heuristic H2.
Algorithm 5. Pseudo-code of heuristic H4.
The next four heuristics, H5, H6, H7 and H8, employ ideas from the classic Hodgson’s algorithm which provides the optimal solution for minimizing the number of tardy jobs in a single-machine problem. They are presented in Algorithms 6–9. Again, the first two consider the EDD rule and the last two the MST. In addition, H6 and H8 are improved versions of H5 and H7, respectively, which use neighborhood search methods at the end of execution.
Heuristic H5
- Step 1.
- Order jobs by the EDD rule (in the case of a tie, use the lower ∑pjk).
- Step 2.
- Apply the timing adjustment procedure.
- Step 3.
- Identify the first tardy job in the sequence (JT). If there are no tardy jobs, STOP.
- Step 4.
- Replace/Place job JT as the final in the sequence and go to Step 2.
Algorithm 6. Pseudo-code of heuristic H5.
Heuristic H6
- Step 1.
- Order jobs by the EDD rule (in the case of a tie, use the lower ∑pjk).
- Step 2.
- Apply the timing adjustment procedure.
- Step 3.
- Identify the first tardy job in the sequence (JT). If there are no tardy jobs, STOP.
- Step 4.
- Replace job JT as the final in the sequence.
- Step 5.
- Considering the insertion neighborhood with (h − 1)2 partial sequences and applying the timing adjustment procedure, determine that with the best nJIT; andFrom the best solution obtained so far, considering the permutation neighborhood with h(h − 1)/2 partial sequences and applying the timing adjustment procedure, determine that with the best nJIT.
Algorithm 7. Pseudo-code of heuristic H6.
Heuristic H7
- Step 1.
- Order jobs by the MST rule (in the case of a tie, use the lower ∑pjk).
- Steps 2–4.
- The same as in heuristic H5.
Algorithm 8. Pseudo-code of heuristic H7.
Heuristic H8
- Step 1.
- Order jobs by the MST rule (tie-break by the lower ∑pjk).
- Steps 2–5.
- The same as in heuristic H6.
Algorithm 9. Pseudo-code of heuristic H8.
For the last two heuristics, H9 (Algorithm 10) uses the EDD rule as the initial order and H10 (Algorithm 11) the MST rule, both adopting a different form of neighborhood search, the forward/backward procedure. The new procedure re-insert one job at a time in the last position in a sequence by considering the best solution found so far, and then iteratively re-insert the last job in all other positions retaining the one with the best nJIT. This corresponds to a diverse way to test neighbor solutions (see Example 2).
Example 2. Consider again the sequence: {J3, J2, J1, J4}. For position h = 1, the first job J3 is replaced in the last position; if the new solution is improved, the new sequence is kept (and also the value of h = 1), otherwise, the previous one is recovered (and the h is incremented). Thus, if the current sequence is {J2, J1, J4, J3}, then the new first job J2 is replaced in the last position and the test is repeated for {J1, J4, J3, J2}. Considering now that the new solution is not better than the previous one, the sequence is kept {J2, J1, J4, J3} and h = h + 1 = 2. In the next step, the second job (i.e., the one in the hth position) is replaced in the last position and the test is redone. This forward procedure is repeated until the (n − 1)th position. Then, a backward procedure is applied, reinserting the last job in all previous positions, and so on.
Heuristic H9
- Step 1.
- Order jobs by the EDD rule (in the case of a tie, use the lower ∑pjk).
- Step 2.
- Apply the timing adjustment procedure.
- Step 3.
- Set h = 1. While h < n, do (from position 1 to n − 1):Forward procedure: replace the hth job defined in Step 1 in the last position of the partial sequence and apply the timing adjustment procedure. If the new nJIT is better than the previous one, keep the new schedule (and the h value); otherwise, go back to the previous one and set h = h + 1.
- Step 4.
- Set h = n. While h > 1, do (from the last position to the second):Backward procedure: Replace the hth job in all the previous positions and apply the timing adjustment procedure considering the best solution found. If a new best solution is found, keep the new schedule (and the h value); otherwise, go back to the previous solution and set h = h − 1.
- Step 5.
- STOP.
Algorithm 10. Pseudo-code of heuristic H9.
Heuristic H10
- Step 1.
- Order jobs by the MST rule (in the case of a tie, use the lower ∑pjk).
- Steps 2–5.
- The same as in heuristic H9.
Algorithm 11. Pseudo-code of heuristic H10.
5. Computational Experiments and Results
In this section, we describe the computational experiments conducted to study the behavior of the mathematical model presented in Section 3 and the heuristics described in Section 4. The codes for the heuristics were implemented in the Delphi programming environment, the mathematical model was written in the syntax of the AMPL modeling language and the instances solved with the branch-and-cut algorithm included in the IBM-CPLEX 12.6.1.0. All tests were conducted on a Pentium Dual-Core with a 2.0 GHz processor, 3.0 GB RAM and Windows Operating System.
A total of 15,600 instances were generated. They are separated into Group 1 of small instances and Group 2 of medium and large ones as described in Section 5.1. The computational study was divided in two parts: Experiment 1 and Experiment 2. Section 5.2 presents the comparative results of the procedures described in Section 4 (Experiment 1). The quality of the heuristics solutions is reinforced when they are compared to the best solution obtained by solving the instances of the mathematical model with CPLEX, as described in Section 5.3 (Experiment 2). The computational efficiency of the solution’s strategies, computed in terms of CPU time, is discussed in Section 5.4.
5.1. Problem Instances
The instances were separated into two groups, with Group 1 consisting of small instances and Group 2 of medium and large ones. In each group, the instances are divided into classes defined by the number of jobs (n), number of machines (m) and scenarios of due dates, with 100 instances randomly generated for each class to reduce the sampling error.
The processing times were generated in the interval U[1,99], as in the most production scheduling scenarios found in the literature (e.g., [21,22]). In Group 1, the parameters were n ∈ {5, 6, 7, 8, 10} and m ∈ {2, 3, 5} and, in Group 2, n ∈ {15, 20, 30, 50, 80, 100} and m ∈ {5, 10, 15, 20}. These values were chosen to cover a significant range of instances of various sizes.
The generation of due dates followed the method used by [23], with a uniform distribution in the interval [P(1 − T − R/2), P(1 − T + R/2)], where T and R are the tardiness factor of jobs and dispersion range of due dates, respectively, and P the lower bound for the makespan which is defined as in Taillard [24]:
The following scenarios represent the configurations obtained by varying the values of T and R:
- Scenario 1: low tardiness factor (T = 0.2) and small due date range (R = 0.6);
- Scenario 2: low tardiness factor (T = 0.2) and large due date range (R = 1.2);
- Scenario 3: high tardiness factor (T = 0.4) and small due date range (R = 0.6); and
- Scenario 4: high tardiness factor (T = 0.4) and large due date range (R = 1.2).
Using these parameters, 6000 instances were generated in Group 1, divided in 60 classes. That is, five levels of number of jobs, three levels of number of machines, four scenarios and 100 instances per class (5 × 3 × 4 × 100 = 6000). For Group 2, 9600 instances were generated, divided in 96 classes, six levels of number of jobs, four levels of number of machines, four scenarios and 100 instances per class (6 × 4 × 4 × 100 = 9600). A total of 15,600 instances were generated and their parameters are summarized in Table 3.

Table 3.
Parameters for generation of the instances.
5.2. Experiment 1: Relative Comparison of the Proposed Heuristics
In this first part of the results evaluation, a relative comparison of the proposed heuristics was conducted. The most common measure used in the literature to compare the performances of solution methods is the relative percentage deviation (RPD) (e.g., [22,25]), which, adapted to the maximization problem addressed, is calculated as:
where is the best solution found and the heuristic solution evaluated. The lower is a method’s RPD, the better is its performance, with a RPD of zero indicating that the method provided the best solution found (or achieved a tie).
To compare the heuristics performances for Group 1’s instances, the solution of an enumeration method (EM), based on [25], was used as a reference (see the pseudo-code in Algorithm 12). It is important to note that the EM provides a reference solution to the problem and, although it listed n! possible permutations (sequences) of jobs, it does not warrant an optimal solution since the schedule is composed by sequencing and timing. That is, for the same sequence, it is possible to find several schedules with different starting times for each operation, thereby resulting in many possibilities for the same number of just-in-time jobs, as can be seen in Figure 1.
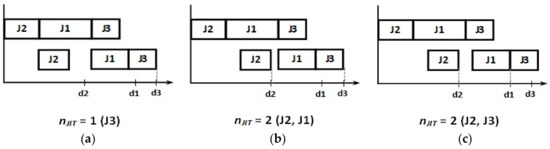
Figure 1.
Example of different schedules with the same sequence of jobs: (a) only J3 is just-in-time; (b) J2 and J1 are just-in-time; and (c) J2 and J3 are just-in-time.
Therefore, the EM enumerates all possible sequences, but it is impractical to probe all possible schedules, especially for medium and large scale instances. Given that, the EM was not applied for Group 2’s instances, and the best solution found by the heuristics H1–H10 was considered as reference for the instances in this group.
Enumeration Method
- Step 1.
- Enumerate the n! possible sequences and consider the one with the best nJIT.
- Step 2.
- Apply the timing adjustment procedure.
Algorithm 12. Pseudo-code of the enumeration method.
Figure 2 graphically presents the results, with 95% confidence intervals of the average RPD obtained by each heuristic method for both Groups 1 and 2. The 95% confidence interval means that the results (RPD) of 95 cases among 100 are within the displayed range.
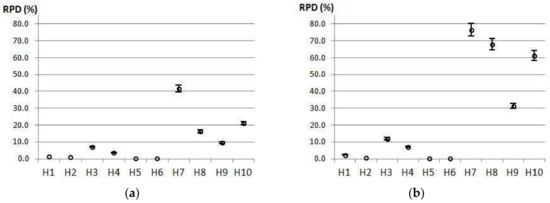
Figure 2.
Comparison of performances of heuristics by group with 95% confidence interval of average RPD: (a) related to EM for Group 1; and (b) related to the best H1–H10 solution for Group 2.
The global analysis of results revealed that H6 clearly outperformed the other heuristics, with a RPD of 0.2% for both Groups 1 and 2 (as can be seen in Table 4) which indicates that it provided the best or very close to the best solutions for many cases.

Table 4.
Overall performance rankings (RPD) of proposed heuristics in relation to EM for Group 1 and to the best found solution for Group 2.
The results from H6 were similar to those from H5 which ranked second for overall performance with RPDs of 0.4% in Group 1 and 0.3% in Group 2, as shown in Table 4. Both these heuristics considered the EDD rule as the initial order and iteratively placed the first tardy job at the end of the sequence. However, H6 also employed insertion and permutation neighborhood searches. Therefore, it can be seen that, although this improvement phase provided better performance, H6 had already produced very good results before the neighborhood searches (explained by the behavior of H5).
Following the rankings, H2 and H1 were third and fourth, respectively, and both exhibited similar behavior by considering the EDD rule as the initial order and then employing the insertion method to construct the sequence. The difference between them is that H2 employs neighborhood searches before attempting to insert the new job in the partial sequence.
In addition, it may be noted in Table 4 that the rankings for Groups 1 and 2 were almost the same, with the sole exception of the inversion between heuristics H8 and H10 in eighth and ninth places. Another observation is that, in the five worst methods, the deviations in Group 1 were much lower than those in Group 2 which indicated that there is a greater dispersion of solution quality for medium and large instances, as can be seen in Figure 2.
The worst method was H7 which considered the MST rule as the initial order and iteratively placed the first tardy job at the end of the sequence. Although it is very similar to H5, as the only difference between them was in their initial orders (the EDD rule was used in H5), the discrepancies in their results were quite significant. This demonstrated that, of the two options used for the initial rule, the EDD was always more advantageous than the MST, as was obvious for every pair of heuristics which were only differentiated by these rules, that is, H1 and H3, H2 and H4, H5 and H7, H6 and H8, and H9 and H10.
Table 5, Table 6, Table 7 and Table 8 provide detailed average results for the instances according to the group and size for each heuristic considering different numbers of jobs and machines.

Table 5.
Comparison of performances (RPD) of heuristics by number of jobs for Group 1.

Table 6.
Comparison of performances (RPD) of heuristics by number of jobs for Group 2.

Table 7.
Comparison of performances (RPD) of heuristics by number of machines for Group 1.

Table 8.
Comparison of performances (RPD) of heuristics by number of machines for Group 2.
As the number of jobs grows, the four best methods, H6, H5, H2 and H1, had relatively stable performances for Groups 1 (Table 5) and Group 2 (Table 6), with very low RPD values (below 1.5). The exception was H1 for Group 2 (Table 6), which had decreasing relative deviations ranging from 3.9% with 15 jobs to 0.6% with 100. The other heuristics had increasing RPD values with increasing numbers of jobs, except H7 and H8 for Group 2 which had decreasing values for instances with up to 100 jobs. Furthermore, H3 showed a slight decrease in instances with 15 to 50 jobs, and an increase in those with 80 and 100.
In terms of the numbers of machines, as can be seen in Table 7 and Table 8, the results indicate, in each group, high stability with relatively small variations in their RPD amplitudes. This may suggest that the number of machines was not a relevant factor in performances for the problem addressed.
Table 9 presents each group’s deviations for the four defined scenarios, varying the values of T and R due date factors. These results were consistent with those obtained from the previous analyses of ranking methods, with H6 presenting the best result followed by H5. The results of different scenarios suggest that variations in the tardiness factor and due date range did not exert any relevant influence. It is interesting to note the two top heuristics, H6 and H5, obtained identical results for both groups in Scenarios 2 and 4 characterized by their wide due date ranges. That is, when the interval between due dates was large, neighborhood searches did not provide improvements.

Table 9.
Performances (RPD) of heuristics by group and scenario in relation to EM for Group 1 and to the best found solution for Group 2.
5.3. Experiment 2: Quality of the Heuristic Solutions in Relation to the Optimal Solution
In the second part of the computational experimentation, the quality of each heuristic solution was measured by the RPD in relation to the optimal solution provided by solving the instances of mathematical model by CPLEX. The RPD is calculated by Expression (14), where is the optimal solution given by CPLEX.
The optimality of the CPLEX solution was proven for the 6000 instances of Group 1. The analysis of quality the heuristics’ results in relation to those optimal solutions, using 95% confidence intervals of the average RPDs, is depicted in Figure 3.
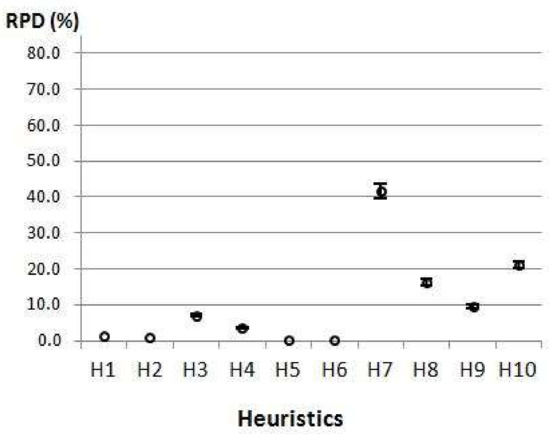
Figure 3.
Comparisons of performances of heuristics in relation to those of model (95% confidence intervals of average RPD).
It is remarkable that the values of graphs in Figure 2a (Group 1) and Figure 3 are very similar. Table 10 presents rankings of the solution quality of the heuristics, i.e., the values of the RPD of the optimal solutions.

Table 10.
Overall performance rankings (average RPD) of heuristics in relation to optimal solution for instances in Group 1.
Table 10 shows the same ranking and values very close to the ones presented in Table 4 for relative comparisons of Group 1, which validated and reinforced the results from the previous analyses. It is important to highlight the excellent performance of the best heuristic (H6) that had a deviation from the optimal solution of just 0.6% which meant that it provided a near-optimal solution.
Of the 6000 instances optimally solved, H6 reached the optimal solution in 5830 cases (97.2% of instances) and, in the other 170 instances, the difference between its result and the optimal solution was only one just-in-time job in 168 cases and two just-in-time jobs in two other cases. It is also relevant to emphasize that the average running times of H6 were 0.1 ms and 0.39 s for the instances in Groups 1 and 2, respectively.
According to the previous comparative analysis, the results for H5 and H6 were very close and H2 and H1 also achieved significant performances. This confirmed that the EDD was better than the MST rule for the instances considered and the procedure based on Hodgson’s approach (used in H6 and H5) outperformed the insertion method of NEH (applied in H2 and H1). Similarly, in all cases of each pair of heuristics, those which applied a neighborhood search produced improved results.
Another interesting observation is that the enumeration method, as explained in Section 5.3, did not guarantee the optimal solution in the case of a flow shop with just-in-time jobs. Of the instances optimally solved, the deviations from the enumeration method were on average 0.4%, as expected, with an average running time of 1.48 s. The average running time of CPLEX was 199.88 s (3.33 min).
Given the difficulties to prove optimality, for Group 2, only one instance per class was solved by CPLEX with the CPU time was limited to 3600 s. Thus, 96 medium and large instances were executed. For 22 instances, no integer solution was found or the model provided a solution with zero value. In most cases, the heuristic solutions were much better than the lower bound given by CPLEX, leading to very negative RPD, as can be observed in Table 11.

Table 11.
Overall performance (average RPD) of heuristics in relation to lower bound given by CPLEX by number of jobs for instances of Group 2.
The more negative is the RPD of a heuristic, the better is its result in relation to the lower bound. It could be noted that even the worst heuristic (H7) provided results that were better than the lower bound given by CPLEX. These results confirm all previous inferences. The coincidence of the results for H5 and H6 is remarkable, suggesting that neighborhood searches do not improve the solution of medium and large instances.
5.4. Computational Efficiency
The comparison of computational efficiency, i.e., the average consumption of CPU time measured in milliseconds (ms), of each heuristic for Groups 1 and 2, the enumeration method and CPLEX for Group 1 are shown in Table 12.

Table 12.
Computational efficiency (average CPU times in milliseconds).
As expected, the EM and CPLEX consumed much more CPU time than the heuristics. For the small instances (Group 1), the computational times of all the heuristics were almost zero and, for the medium and large ones (Group 2), H2 and H4 took the longest times, nearly 8 s on average, which were relatively high compared with those of other methods but does not preclude their use. All other heuristics required far less time than one second which demonstrated the viability of using them in practice. It is worth noting that H5, which ranked second with a solution quality very close to that of H6, consumed less than a half second on average for large instances, thereby indicating its high computational efficiency.
Finally, in an overall analysis of the results and the solution approaches proposed in this paper (exact and heuristic), the applicability of the developed heuristics were justified and demonstrated in terms of both solution quality (an average of 0.6% deviation from the optimum with the best heuristic H6) and computational efficiency (an average of 0.4 s for large instances also with H6). The mathematical model and the enumeration method were useful as quality certificate. Moreover, the mathematical model can be useful if other constraints or requirements are added to the problem.
6. Final Remarks
This research achieves its proposed goals of developing and implementing effective and efficient methods for solving a flow shop scheduling problem by maximizing the number of just-in-time jobs, as demonstrated in the computational experiments. A MIP model is proposed to represent the problem and, together with an enumeration algorithm, is useful as quality certificate for the solution values given by the constructive heuristics proposed.
The CPLEX system solves instances of the MIP model with up to 10 jobs and five machines in at most 47 min. It provides a lower bound for the optimal solution for instances with up to 100 jobs and 20 machines. The enumeration method does not guarantee optimality because the solution is formed by job sequencing and timing (the starting times of jobs). However, it shows relative applicability and considerable quality (0.2% deviations in small instances) with an average running time of 1.5 s.
The practicability and applicability of all proposed heuristic methods are demonstrated, in particular for large-scale instances, with very good quality results and non-prohibitive runtimes. The best heuristic, H6, demonstrates a near-optimal solution, with just a 0.5% average relative deviation from the exact solution and optimal solutions for more than 98% of instances, while the performance of the second best, H5, is very close. In total, 15,600 instances are solved, with the average relative deviation of H6 only 0.2% and that of H5 approximately 0.3%. The H6 and H5 heuristics consider the EDD rule as the initial solution and then iteratively place the first tardy job at the end of the sequence. Although their results are very close, H6 improves on H5 by using neighborhood searches.
In this study, the focus is on solving a flow shop scheduling problem by reducing the interval between the completion time of the last operation of a job and its due date. This enables an adjustment in the timing of jobs which results in the possibility of inserting idle time between operations. Therefore, there is no concern about the first operations of each job, i.e., their executions could be approximated. Rescheduling these operations could reduce the idle time between them and possibly also minimize the total time required to complete the schedule (makespan). Therefore, it is suggested that future work consider multiple-criteria functions, including flow measures (as a makespan and/or flow time), in scenarios with earliness and tardiness.
Acknowledgments
This work was supported by CNPq (502547/2014-6, 443464/2014-6, and 233654/2014-3), CAPES (BEX 2791/15-3), FAPESP (2013/07375-0 and 2016/01860-1) and FAPEG (201510267000983).
Author Contributions
Helio conceived, designed and performed the experiments; Helio, Ruhul and Socorro analyzed the data and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pinedo, M.L. Scheduling: Theory, Algorithms and Systems, 5th ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2016; ISBN 978-3319265780. [Google Scholar]
- Shabtay, D.; Bensoussan, Y.; Kaspi, M. A bicriteria approach to maximize the weighted number of just-in-time jobs and to minimize the total resource consumption cost in a two-machine flow-shop scheduling system. Int. J. Prod. Econ. 2012, 136, 67–74. [Google Scholar] [CrossRef]
- Lann, A.; Mosheiov, G. Single machine scheduling to minimize the number of early and tardy jobs. Comput. Oper. Res. 1996, 23, 769–781. [Google Scholar] [CrossRef]
- Kanet, J.J.; Sridharan, V. Scheduling with inserted idle time: Problem taxonomy and literature review. Oper. Res. 2000, 48, 99–110. [Google Scholar] [CrossRef]
- Baker, K.R.; Scudder, G.D. Sequencing with earliness and tardiness penalties: A review. Oper. Res. 1990, 38, 22–36. [Google Scholar] [CrossRef]
- Józefowska, J. Just-in-Time Scheduling: Models and Algorithms for Computer and Manufacturing Systems; Springer Science: New York, NY, USA, 2007; ISBN 978-387-71717-3. [Google Scholar]
- Ríos-Solís, Y.A.; Ríos-Mercado, R.Z. Just-In-Time Systems; Springer Sciences: New York, NY, USA, 2012; ISBN 978-1-4614-1122-2. [Google Scholar]
- Shabtay, D.; Steiner, G. Scheduling to maximize the number of just-in-time jobs: A survey. In Just-in-Time Systems; Ríos-Solís, Y.A., Ríos-Mercado, R.Z., Eds.; Springer Sciences: New York, NY, USA, 2012; ISBN 978-1-4614-1122-2. [Google Scholar]
- Choi, B.-C.; Yoon, S.-H. Maximizing the weighted number of just-in-time jobs in flow shop scheduling. J. Sched. 2007, 10, 237–243. [Google Scholar] [CrossRef]
- Shabtay, D.; Bensoussan, Y. Maximizing the weighted number of just-in-time jobs in several two-machine scheduling systems. J. Sched. 2012, 15, 39–47. [Google Scholar] [CrossRef]
- Shabtay, D. The just-in-time scheduling problem in a flow-shop scheduling system. Eur. J. Oper. Res. 2012, 216, 521–532. [Google Scholar] [CrossRef]
- Gerstl, E.; Mor, B.; Mosheiov, G. A note: Maximizing the weighted number of just-in-time jobs on a proportionate flowshop. Inf. Process. Lett. 2015, 115, 159–162. [Google Scholar] [CrossRef]
- Yin, Y.; Cheng, T.C.E.; Wang, D.-J.; Wu, C.-C. Two-agent flowshop scheduling to maximize the weighted number of just-in-time jobs. J. Sched. 2017, 20, 313–335. [Google Scholar] [CrossRef]
- Fuchigami, H.Y.; Rangel, S. Métodos heurísticos para maximização do número de tarefas just-in-time em flow shop permutacional. In Proceedings of the Simpósio Brasileiro de Pesquisa Operacional, Porto de Galinhas, Brazil, 25–28 August 2015. [Google Scholar]
- Fuchigami, H.Y.; Rangel, S. Um estudo computacional de um modelo matemático para flow shop permutacional com tarefas just-in-time. In Proceedings of the Simpósio Brasileiro de Pesquisa Operacional, Vitória, Brazil, 27–30 September 2016. [Google Scholar]
- Dhouib, E.; Teghem, J.; Loukil, T. Minimizing the number of tardy jobs in a permutation flowshop scheduling problem with setup times and time lags constraints. J. Math. Model. Algorithm 2013, 12, 85–99. [Google Scholar] [CrossRef]
- Nawaz, M.; Enscore, E.E., Jr.; Ham, I. A heuristic algorithm for the m-machine n-job flow-shop sequencing problem. OMEGA–Int. J. Manag. Sci. 1983, 11, 91–95. [Google Scholar] [CrossRef]
- Hodgson, T.J. A note on single machine sequencing with random processing times. Manag. Sci. 1977, 23, 1144–1146. [Google Scholar] [CrossRef][Green Version]
- Baker, K.R.; Trietsch, D. Principles of Sequencing and Scheduling; John Wiley & Sons: New York, NY, USA, 2009; ISBN 978-0-470-39165-5. [Google Scholar]
- Nagano, M.S.; Branco, F.J.C.B.; Moccellin, J.V. Soluções de alto desempenho para programação da produção flow shop. GEPROS 2009, 4, 11–23. [Google Scholar]
- Li, X.; Chen, L.; Xu, H.; Gupta, J.N.D. Trajectory scheduling methods for minimizing total tardiness in a flowshop. Oper. Res. Perspect. 2015, 2, 13–23. [Google Scholar] [CrossRef][Green Version]
- Vallada, E.; Ruiz, R.; Minella, G. Minimizing total tardiness in the m-machine flowshop problem: A review and evaluation of heuristics and metaheuristics. Comput. Oper. Res. 2008, 35, 1350–1373. [Google Scholar] [CrossRef]
- Ronconi, D.P.; Birgin, E.G. Mixed-integer programming models for flow shop scheduling problems minimizing the total earliness and tardiness. In Just-in-Time Systems; Ríos-Solís, Y.A., Ríos-Mercado, R.Z., Eds.; Springer Sciences: New York, NY, USA, 2012; ISBN 978-1-4614-1122-2. [Google Scholar]
- Taillard, E. Benchmarks for basic scheduling problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]
- Laha, D.; Sarin, S.C. A heuristic to minimize total flow time in permutation flow shop. OMEGA–Int. J. Manag. Sci. 2009, 37, 734–739. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).