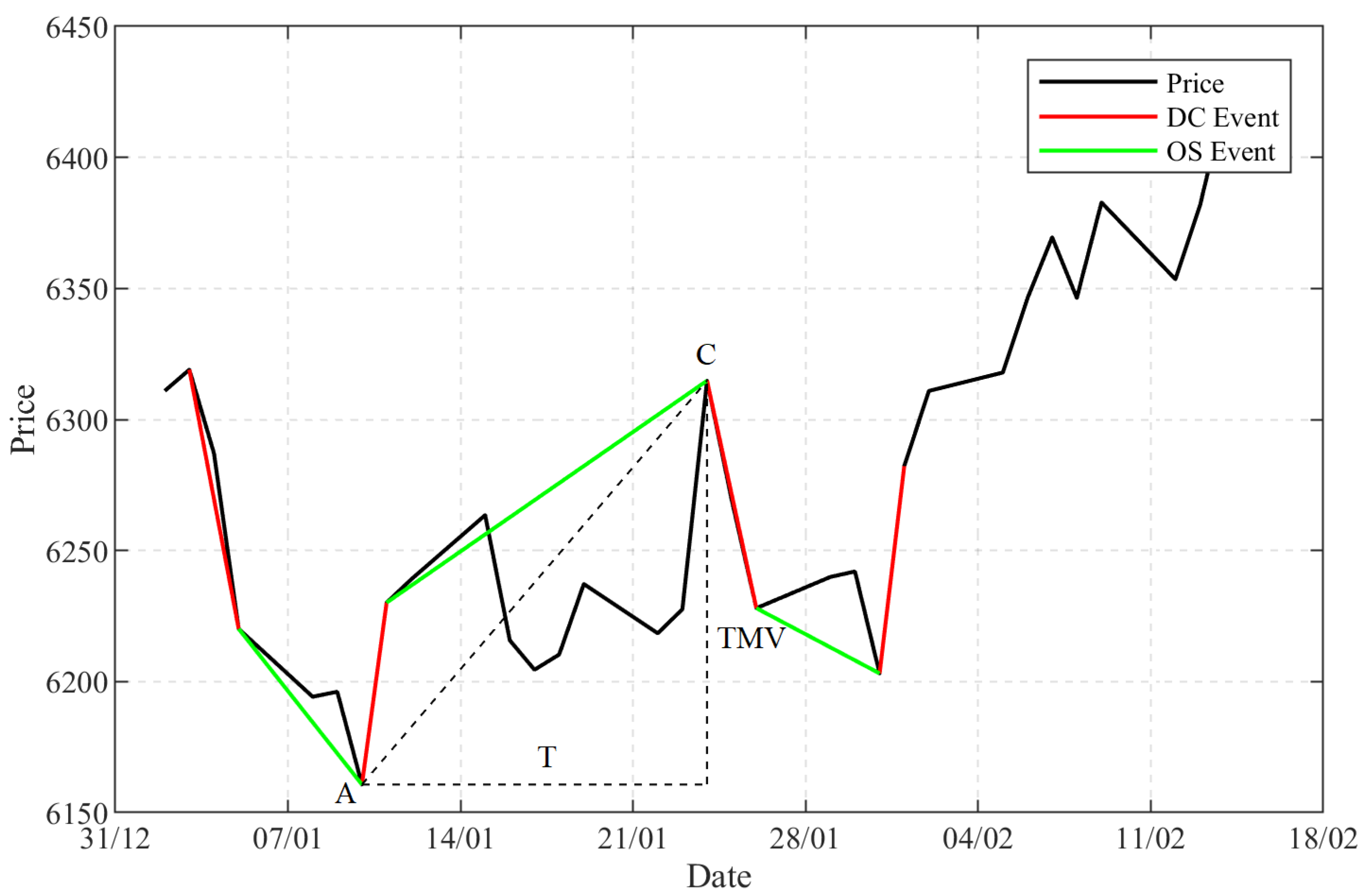
So far, we have explained that under a given threshold, DC summarised a dataset into trends. HMM classified these trends into regimes, with each regime comprising a sequence of trends. Each trend defines a TMV and a T value. We computed the average TMV and average T values for each regime in each data set. In this section, we compare the normalised TMV and T values of the two regimes from different markets and time periods.
For each dataset, we computed the average TMV and T values for all the trends of each regime. For example, we computed the average normalised TMV and T values of all trends in Regime 1 in the data of GBP–USD, which is summarised under the threshold 0.1%, and the same is done for Regime 2. Each market regime in each dataset will occupy a position within the two dimensional (T-TMV) indicator space. This will allow us to see whether Regimes 1 and 2 occupy different regions of the indicator space. If they do, then it is possible to define the region of normal regime and abnormal regime.
5.1. Market Regimes in the Indicator Space
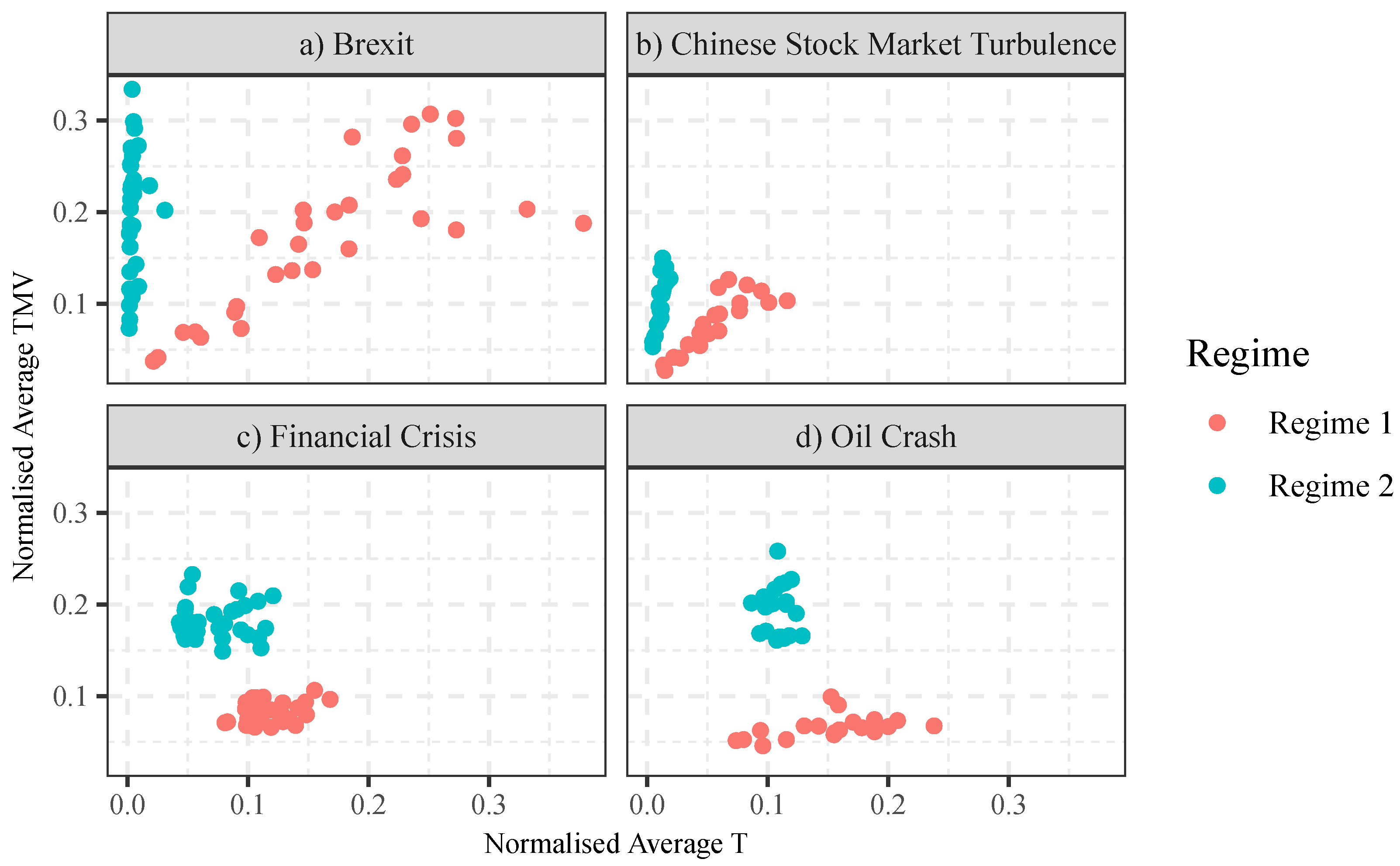
Figure 6 shows the positions of the regimes from all data sets on the T-TMV indicator space. They are grouped by their periods as shown in
Table 1. To recap, the
x-axis measures the normalised average value of the indicator T, and the
y-axis measures the normalised average value of the indicator TMV. Each point in the indicator space shows the position of one market regime of one data set. The red points showed the positions of Regime 1, and the blue points showed the positions of Regime 2. For example, one of the red points in
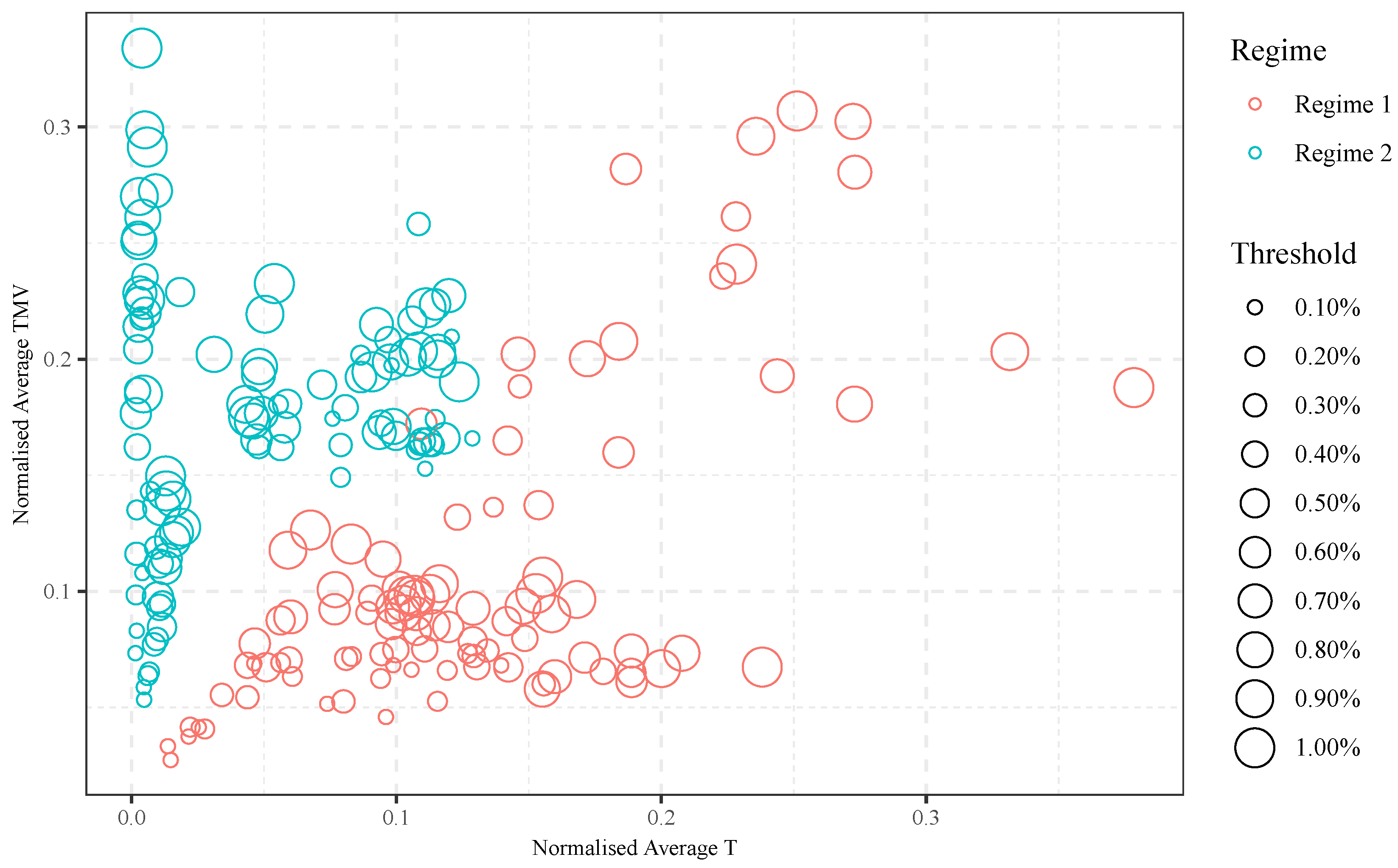
Figure 6a would show the average normalised TMV and T values of all trends in Regime 1 in GBP–USD summarised under the threshold 0.1%.
In
Figure 6, we shall study the market regimes found in the four market events separately: (a) market regimes from the data of Brexit; (b) market regimes from the data of Chinese stock market turbulence of 2015–2016; (c) market regimes from the (three) data sets of the financial crisis of 2007–2008; (d) market regimes from the (two) data sets of the oil crash of 2014–2016.
As we examined three foreign exchange pairs (EUR–USD, EUR–GBP and GBP–USD) and each data set is summarised with ten thresholds, there are 30 data points for each regime in
Figure 6a. As we used two Chinese indices (SSE and SZSE) and ten thresholds per data set, there are 20 data points for each regime in
Figure 6b. There are 30 and 20 data points per regime for
Figure 6c,d, respectively.
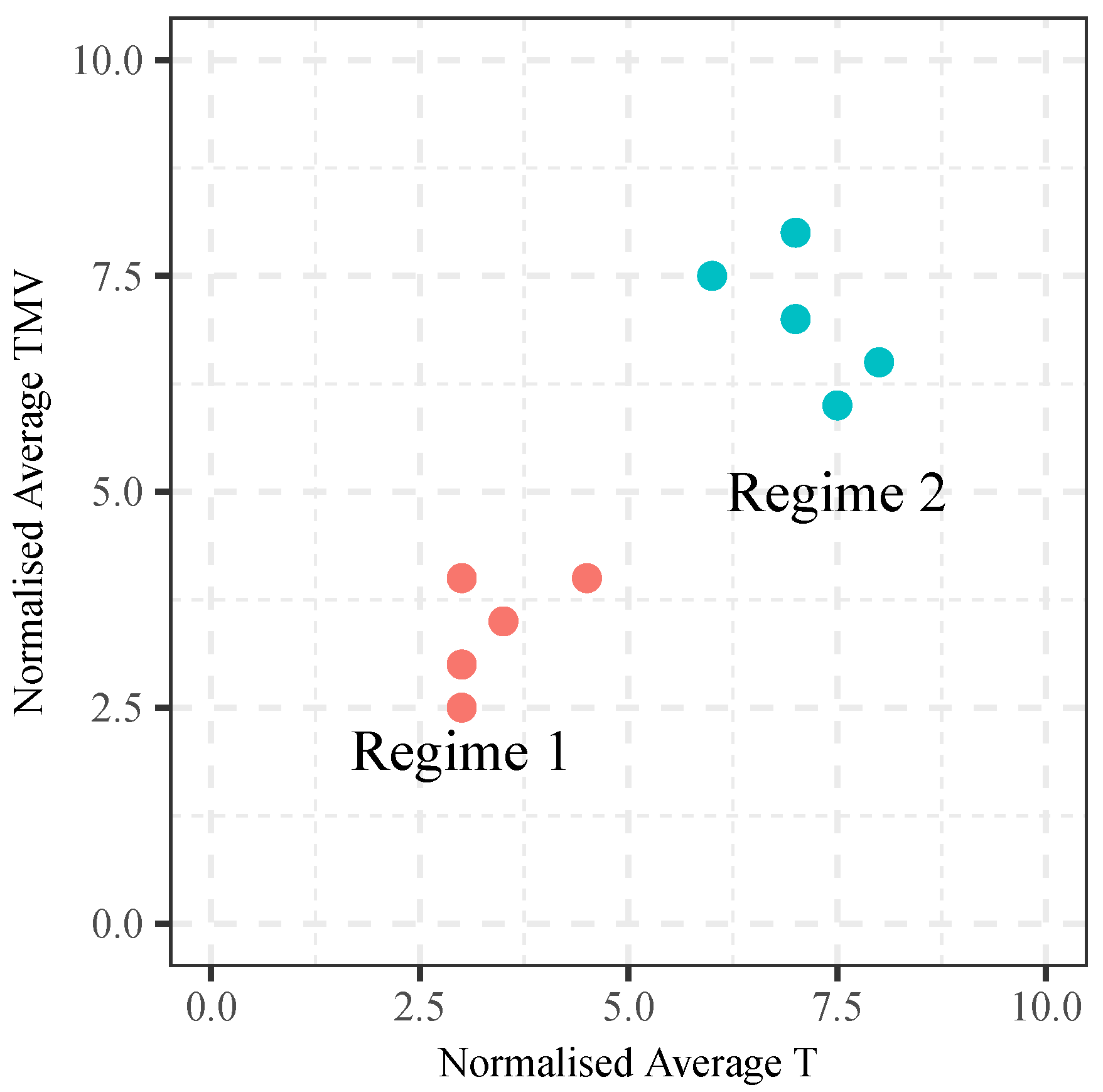
Figure 6 clearly shows that, within each group, Regime 1 and Regime 2 are clearly separable in the T-TMV indicator space. For example,
Figure 6a shows that, compared to Regime 1, Regime 2 takes a much shorter time than normal to complete (readers are reminded that the
x-axis represents normalised T, not absolute T).
Figure 6a shows that Regime 2 has a much higher (normalised) TMV to (normalised) T ratio. The same is observed in
Figure 6b–d.
Distribution of the regimes in the normalised T-TMV space is also significant: the market regimes that occurred from the data taken from the events of Brexit and that of the Chinese stock market turbulence were linearly distributed. But the market regimes from the data of the financial crisis and the oil crash formed clusters. The obvious difference between these data sets is that high frequency (minute-to-minute) data was used for the former, and low frequency (daily) data was used for the latter. Having said that, the exact reason for these differences in distributions demands further investigation; this will be left to future research.
In general, Regime 2 suggests a market with higher TMV to (normalised) T ratio. This means, given the same T, Regime 2 tends to have a larger TMV than Regime 1. Given the same TMV, Regime 2 tends to have a smaller T than Regime 1. As pointed out by Tsang et al. [
4], both larger TMV and smaller T are indicators of higher volatility. Therefore, one could roughly understand Regime 2 as a regime that represents periods of higher volatility.
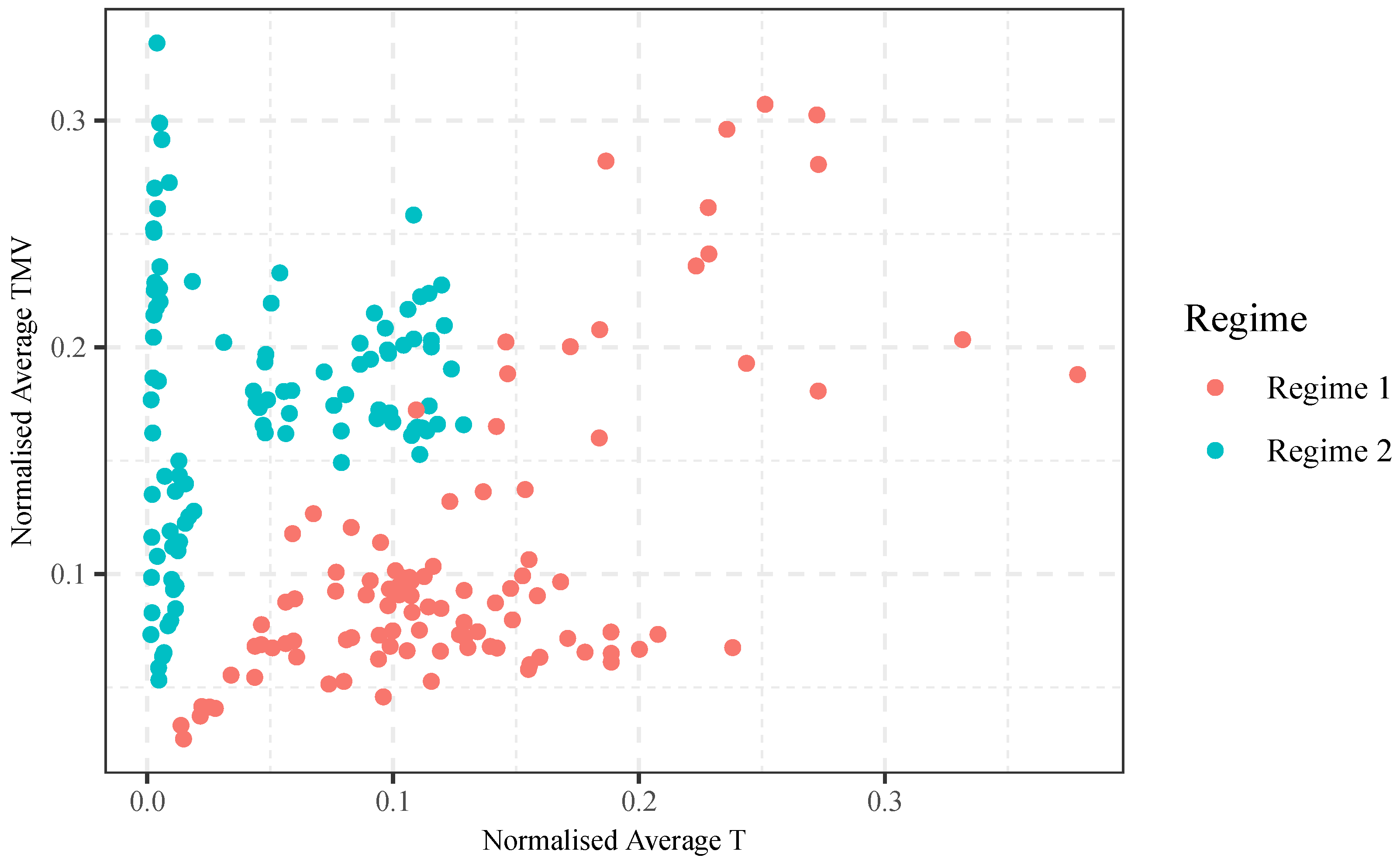
Figure 7 shows the market regimes of all the datasets together in one indicator space. We can see from
Figure 7 that the positions of Regime 1 and Regime 2 are largely separable, with some exceptions around (0.11, 0.16).
Figure 7 suggests that, across asset types, time and thresholds, Regimes 1 and 2 occupy different areas in the normalised T-TMV indicator space.
5.2. Market Regimes under Different Thresholds
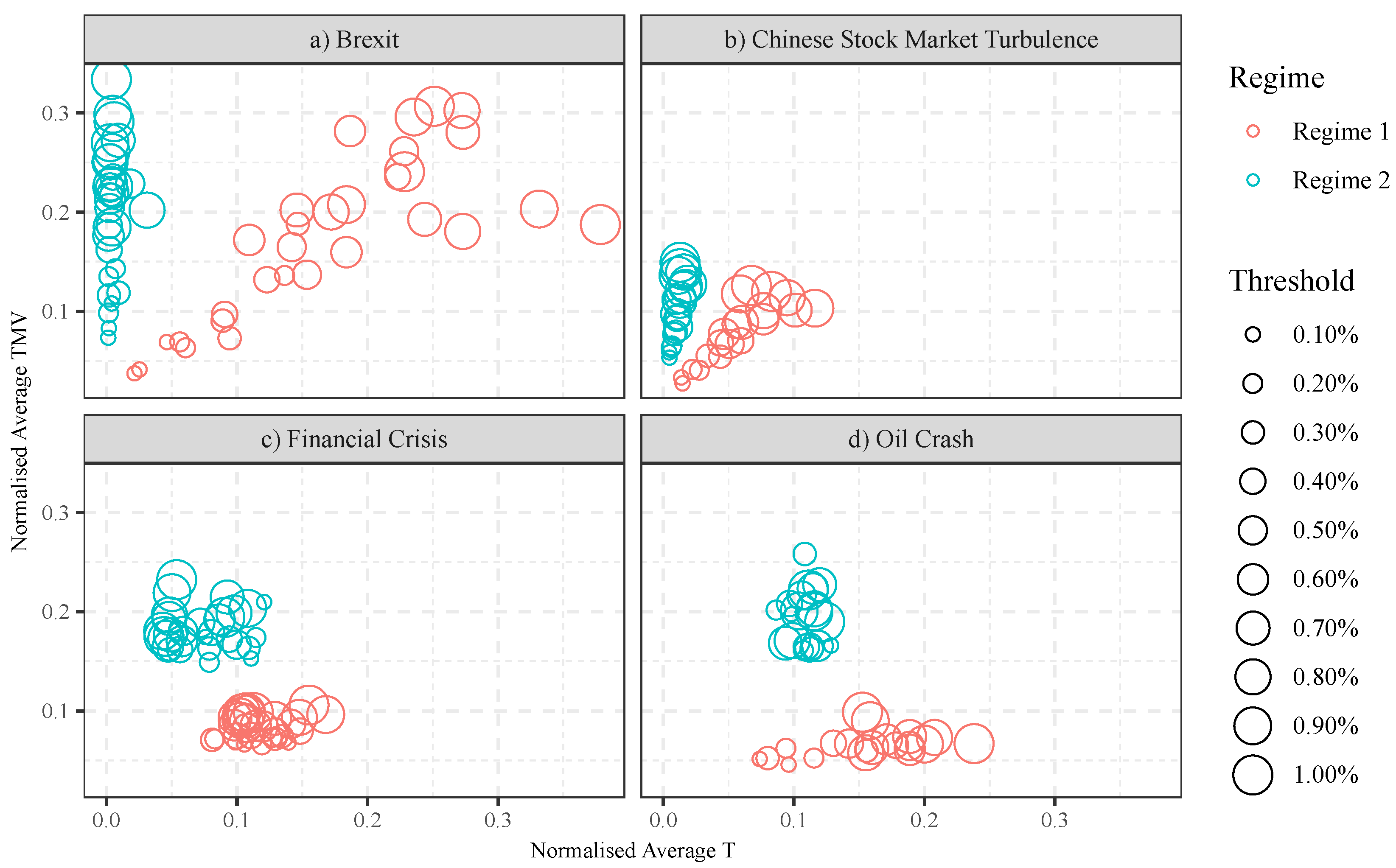
When summarising data with DC, different observers may use different thresholds. The question is: are the positions of the regimes sensitive to the thresholds used? To be able to answer that, we analyse the market regimes observed under different thresholds.
Figure 8 depicts the market regimes in the normalised T-TMV indicator space with regard to different value of thresholds. It shows that positions of the market regimes are changing along with the value of thresholds in some data-sets, but not all of them. For instance, in
Figure 8a,b, the market regimes with larger price movements (indicator TMV) are captured under larger thresholds, even after normalisation.
However,
Figure 8c,d shows a different picture. Data points collected from different thresholds mingled. This suggests that the size of threshold has little effect on the T-TMV positions of the market regimes in these two data-sets.
For reference,
Figure 9 shows the regimes from all data sets. Obviously, the positions of the regimes are the same as those shown in
Figure 7.
Figure 9 gives an idea of the thresholds which are generated from the different regimes.
5.3. Discussion
In this section, we shall highlight some of the major points made in this paper.
Firstly, we have demonstrated that the DC indicator space is useful for comparing different markets. By positioning the market regimes in the DC indicator space, the distance between different regimes can be measured. This allows us to quantitatively measure the distance between different regimes in different markets. We can determine whether regimes are different or similar to each other, in terms of their positions in the indicator space.
Secondly, the position of the market regimes allows us to classify different types of the market regimes. We have found that all the Regime 1’s are similar to each other across assets, markets and time. All of the Regime 2’s are similar to each other. But Regime 1’s and Regime 2’s occupy different positions in the DC indicator space. As shown in
Figure 8, the two regimes are clearly separable in each of the four markets studied. Even when we put the regimes found in different markets together, Regime 1s and Regime 2s are separable, with a little amount of overlap (see
Figure 9). The overlap is mainly due to regimes found in the Oil Crash market (2014–2016). This could suggest that the commodity market is slightly different from the stock and foreign exchange market; this is a much bigger topic which will be left for future research.
Thirdly, by observing the positions of the market regimes, it is possible to define the region of normal market and the abnormal market in the indicator space. We called them normal and abnormal because in all the periods that we chose, dramatic external events took place, for example the bank failures in the 2007–2008 global financial crisis or the shock result of the Brexit referendum in Britain in 2016, all of which affected financial markets. In all our observations, the market changed from Regime 1 (which experienced less volatility) to Regime 2 (higher volatility) around these events. It is reasonable to believe that the regime change was either an anticipation, or a reaction, to these unpredictable events. For convenience, we have described what has happened when the markets changed from a normal regime to an abnormal regime.
Let us elaborate our findings by looking more closely into the results. We say that the market experienced less volatility in Regime 1, the normal market. This can be seen in
Figure 6a,b, where less time (indicator T) is required to complete similar amount of price movements (indicator TMV) in Regime 2 than that of in Regime 1, and in
Figure 6c,d, less price movements are achieved within a similar amount of time when the market was in Regime 1, compared to the market periods in Regime 2. This indicated that Regime 1 represented a less volatile market period.
On the other hand, we say that the market experienced higher volatility in Regime 2, the abnormal market. This can be seen in
Figure 6a,b, where bigger price movements were observed within a shorter period of time in the region of Regime 2, than those in the region of Regime 1. In
Figure 6c,d, bigger price movements (TMV) were completed in Regime 2, than those completed in Regime 1, within a similar amount of time (T). These indicated that Regime 2 represented a higher level of market volatility.
We note that the choice of threshold affected the positions of the markets on the indicator space in some markets but not others. But overall, independent of the thresholds used, the two regimes occupy different areas of the DC indicator space. The relative positions of the normal and abnormal regimes are insensitive to the thresholds used, which indicated that our research is correct, that thresholds do not influence the outcome of regime positions.
Finally, it is worth clarifying that our aim is not about finding the “optimal” threshold for regimes clarification. The intention was to generalise DC characteristics of normal regimes. That is why various thresholds are used to find normal regimes, and their results are used together to characterise normal regimes.
Figure 8c,d shows that the same regimes found under different thresholds mingle with each other.