Modeling and Evaluation of Power-Aware Software Rejuvenation in Cloud Systems

Abstract

Long and continuous running of software can cause software aging-induced errors and failures. Cloud data centers suffer from these kinds of failures when Virtual Machine Monitors (VMMs), which control the execution of Virtual Machines (VMs), age. Software rejuvenation is a proactive fault management technique that can prevent the occurrence of future failures by terminating VMMs, cleaning up their internal states, and restarting them. However, the appropriate time and type of VMM rejuvenation can affect performance, availability, and power consumption of a system. In this paper, an analytical model is proposed based on Stochastic Activity Networks for performance evaluation of Infrastructure-as-a-Service cloud systems. Using the proposed model, a two-threshold power-aware software rejuvenation scheme is presented. Many details of real cloud systems, such as VM multiplexing, migration of VMs between VMMs, VM heterogeneity, failure of VMMs, failure of VM migration, and different probabilities for arrival of different VM request types are investigated using the proposed model. The performance of the proposed rejuvenation scheme is compared with two baselines based on diverse performance, availability, and power consumption measures defined on the system.

1. Introduction

Cloud computing is the practice of storing, managing, and processing data using a network of remote servers accessed via the Internet [1]. As such, cloud computing is a model for easy and ubiquitous access to a set of servers, storage devices, networks, applications, and services with minimal interaction with the service provider and minimal management cost [2]. Virtualization techniques are used in cloud systems to appropriately handle user requests. By applying virtualization, multiple Virtual Machines (VMs) are simultaneously run on a single Physical Machine (PM) controlled by software usually known as Hypervisor or Virtual Machine Monitor (VMM) [3,4,5]. In Infrastructure-as-a-Service (IaaS) clouds, each user request is in the form of one or more VM requests.

The tendency of software to fail or cause a system failure after running continuously for a specific time period is referred to as software aging [6,7]. Software aging is a phenomenon in long-run software systems that causes an increased failure rate and/or degraded performance due to accumulation of aging errors [8,9]. Since VM requests in IaaS clouds are usually different in terms of software and tools for which they are initiated, their corresponding VMs exhibit complex behaviors and sophisticated interactions throughout their lifetime that enable VMMs to manage a wide variety of VM behaviors. Consequently, after running for a long time or managing heavy workloads, VMMs, like any other software, age and slow due to a multitude of internal errors and diverse behaviors of VMs [7,10,11,12,13]. If these errors are not prevented or addressed properly, the performance of the system degrades and the cloud provider may fail to meet Quality of Service (QoS) requirements [14].

Software rejuvenation is an effective method used to cope with software aging and performance degradation [11,15,16]. In this method, software is restored to its original state before causing aging-induced crashes and system failures. In cloud systems, providers can also benefit from software rejuvenation by rejuvenating their VMMs before they fail. However, the main problem in this regard is how to choose the right VMM to be rejuvenated and the correct time to do so. In addition to the selection of the appropriate VMM and the proper time for rejuvenation, the selection of the right method amongst existing options is of utmost importance. The majority of models proposed in the literature use a series of side programs to measure the efficiency and performance of VMMs. A study showed that the majority of previous studies in the field of software rejuvenation adopted time-based or prediction-based strategies [17], both of them show low performance.

The rapid worldwide growth of the cloud computing paradigm has led to the emergence of massive data centers with high power consumption across the world [18]. In 2016, the total energy consumption of the world’s data centers was 416 terawatt hours (TWh), which is 38% higher than the 300 TWh of energy that the entire U.K. consumed in the same year [19]. As a result, the power consumption of cloud computing servers and the field of green computing are worthy of more attention [20]. Active PMs, i.e., switched-on PMs, consume a major portion of a cloud system’s power. Therefore, a cloud provider with many active but lightly loaded PMs/VMMs has high power waste, resulting in low energy efficiency. The technique proposed to increase the energy efficiency in this paper involves migration of VMs from lightly loaded VMMs, and then switching free PMs off, leading to a smaller number of active VMMs and PMs. In real-world cloud systems, requested VMs are heterogeneous and they differ in terms of processing speed, memory, and storage capacities. Therefore, in order to match real-world systems as much as possible, we consider two categories of VMs in this paper: (1) small VMs, which are VMs that need to be served for a short while and therefore utilize a small share of resources, and (2) big VMs, which are the VMs that need to be executed for a longer period of time and thus use a significant share of system resources. Over the course of their life, larger VMs have a greater impact on software aging of their host VMMs in contrast to the smaller VMs.

In this paper, we present a Stochastic Activity Networks (SAN) model for cloud data centers and provide a strategy for applying rejuvenation to candidate VMMs at the appropriate time. Model-based studies are amongst the most prevalent analyses that researches completed to study software aging and software rejuvenation [21]. Since one of the main causes of failures of VMMs is the continuous execution of VMs running on VMMs [17], the type and the total number of VMs executed by a VMM serve as the measure for determining the appropriate time of rejuvenation. Therefore, we define an upper bound for the maximum number of VMs that a VMM can run, starting from its last boot time, and force a rejuvenation whenever the age of a VMM reaches this limit. The age of a VMM can be expressed as the cumulative workload that the VMM has served since its last failure or rejuvenation. By analyzing the proposed model with the rejuvenation scheme, the benefits of applying the rejuvenation to VMMs of an IaaS cloud provider in reducing the number of VM failures and improving the performance and availability in the steady-state are observed. In addition, the proposed model enables power-awareness in the cloud management system by migrating active VMs from lightly loaded VMMs to more heavily loaded ones and switching off free PMs. Evaluation of the proposed scheme demonstrates that this power saving mechanism improves the system’s steady-state performance and availability. The formalism used in this paper to model the power-aware VMM rejuvenation scheme is SANs [22,23,24]. SANs are probabilistic extensions of activity networks that are equipped with a set of activity time distribution functions, reactivation predicates, and enabling rate functions. They were developed to facilitate performance and dependability evaluation and have features that permit the representation of parallelism, timeliness, fault tolerance, and degradable performance [25]. More detailed information about SANs can be found in the previous literature [26,27,28].

The main contributions of this paper are summarized as follows. (1) A SAN model is presented for performance evaluation of IaaS clouds that considers many details of real systems, including VM multiplexing, migration of VMs between VMMs, VM heterogeneity, failure of VMMs, failure of VM migration, and different probabilities for arrival of different VM request types. (2) Using the presented SAN, a two-threshold power-aware software rejuvenation scheme is proposed and compared with two baselines based on diverse performance, availability, and power consumption measures defined on the system.

The rest of this paper is organized as follows. Section 2 reviews the previous work in the field of software rejuvenation in cloud systems. Section 3 provides a brief introduction to the SAN formalism. In Section 4, the general structure of our system is explained. In Section 5, the proposed SAN model and the rejuvenation scheme presented for the SAN are introduced in detail. Section 6 presents the output measures of interest and the results of the performance evaluation, and finally, Section 7 concludes the paper and provides some directions for future work.

2. Related Work

Evaluation of performance, availability, and power consumption of rejuvenation techniques in cloud systems using analytical models is an emerging topic. Machida et al. studied different methods of rejuvenation and suggested three main methods for software rejuvenation in a server virtualized system: cold, warm, and migration rejuvenation [11]. In the cold rejuvenation method, active VMs on a VMM that want to be rejuvenated are switched off. After completion of the VMM rejuvenation, the switched-off VMs are restarted on the rejuvenated VMM. In the warm method, active VMs are suspended, and after completion of the VMM rejuvenation, the suspended VMs resume their running on the rejuvenated VMM. In the migration method, active VMs on the intended VMM are moved to another host VMM before rejuvenation of the intended VMM occurs. When rejuvenation is completed, they move back to their original PM. Therefore, the downtime caused by the migration method is shorter than that of other methods. Our model is also based on the migration rejuvenation method. In the model presented in Machida et al. [11], the rejuvenation is periodically performed without considering the system’s workload. In contrast, the rejuvenation in our model is performed according to the VMM’s age.

Bruneo et al. analyzed the best period for rejuvenation to achieve high availability considering the VMM’s workload [15]. They suggested a specific period of rejuvenation as the best one for each specified input workload. By changing the rate of input workload, the rejuvenation period also changes. More simply, the heavier the amount of workload, the longer the rejuvenation period; and the lighter the input workload, the shorter the rejuvenation period. Thus, rejuvenation time is adopted according to the VMM’s workload. In contrast to Bruneo et al. [15], in our proposed model, the rejuvenation time is determined based on the age of a VMM instead of using a constant period, which provides a flexible model and an accurate analysis.

Melo et al. presented a rejuvenation model for cloud data centers to evaluate the availability in the steady-state [10]. In their model, only one active VMM and one standby VMM were considered. Our proposed model is similar to the model presented in Melo et al. [10]. In both models, the age of a VMM increases when a new workload is admitted. However, in Melo et al. [10], rejuvenation is periodically performed, and the status of a VMM is checked at the end of each period to ensure that performance degradation is due to the age of the VMM and not the overload of the data center itself. If rejuvenation is required, all active VMs on the target VMM are moved to the standby VMM to continue their execution. Notably, the model with only one active VMM is not realistic for cloud data centers. In contrast to Melo et al. [10], we consider several active VMMs in our model.

Melo et al. studied cloud data centers in different scenarios and analyzed different periods for setting rejuvenation timer in each scenario [29]. The authors specified the best rejuvenation time for achieving high availability in the steady-state. Liu et al. studied rejuvenation from different aspects [16]. Amongst the presented ideas in Liu et al. [16], saving a system’s checkpoints periodically can also be used in case of failure to recover the state of the system. The authors applied warm rejuvenation, in which paused VMs are maintained on external memory. Compared to the approach presented in Liu et al. [16], both migration rejuvenation and power-awareness are simultaneously applied in our presented model.

Roohitavaf et al. represented a SAN model using the Mӧbius tool to evaluate the availability and power consumption of cloud data centers [22]. Based on their evaluation, by switching off low load VMMs, providers not only decrease the power consumption of a cloud data center but also reach higher availability if the migration time is short enough. Roohitavaf et al. [22] only considered the energy saving aspect of cloud data centers; in contrast, we studied the simultaneous effect of power saving and rejuvenation on cloud data centers.

There are also other related studies in the field of VMM rejuvenation that presented models and schemes using techniques other than analytical modeling. Kourai and Ooba proposed VMBeam, which enables lightweight software rejuvenation of virtualized systems using zero-copy migration [30]. The proposed VMBean has been implemented in Xen, an open source hypervisor. Sudhakar et al., proposed a neural network-based approach to approximate the non-linear relationship between resource usage statistics and the time to failure of VMMs caused by aging-related errors [31]. Araujo et al., investigated the software aging effects in the Eucalyptus framework, considering workloads composed of intensive requests for remote storage attachment and VM instantiations [32]. They also presented an approach that applies time series analysis to schedule rejuvenation to reduce the downtime by predicting the proper moment to perform the rejuvenation.

In summary, the approaches that analyze the performance, availability, and power consumption of VMM rejuvenation tasks in cloud systems using analytical models are rare. In contrast to existing work, our presented scheme allows power-aware rejuvenation of VMMs using a two-threshold mechanism. The proposed model supports PM heterogeneity, which has not been considered in previously presented models. Moreover, the model considers several other aspects of real cloud systems that have not usually been considered in previously published reports. In addition, the number of PMs/VMMs and the number of VMs that can simultaneously be serviced on a PM/VMM are larger than those modeled in other approaches.

3. Overview of SANs

SANs are stochastic generalizations of Petri Nets (PNs), defined for modeling and analysis of distributed real-time systems [27,28]. SANs, which are more powerful and flexible than other extensions of PNs, can be formally defined as a 7-tuple (P, IA, T A, IG, OG, IR, OR) [24], where:

• P is a finite set of places. Places are similar to places in PNs and are represented by circles.
• IA is a finite set of instantaneous activities that represent system activities that are completed almost instantly compared to the corresponding performance variables. Each instantaneous activity is assigned to a case probability function, which returns a value between zero and one, that allows us to express uncertainty. Instantaneous activities are represented by thin lines.
• TA is a finite set of timed activities that represent system activities whose running time affects the system’s functionality and evaluation results. A timed activity is exhibited with X inputs and Y outputs, where X + Y > 0. Each input can be a place or an input gate, and each output can be a place or an output gate. Each timed activity is assigned to an activity time distribution function and an enabling function. Timed activities are represented by thick lines.
• IG is a finite set of input gates. Each input gate has a finite number of inputs. Each G ∈ IG with m inputs is associated with a function $f_G:N^m\to N^m$, called the function of G; and a predicate $g_G:N^m\to \left\{true,false\right\}$, called the enabling predicate of G. Input gates provide more flexibility in defining activity enabling and completion rules. Input gates are represented by triangles.
• OG is a finite set of output gates. Each output gate has a finite number of outputs. Each G ∈ OG with m outputs is associated with a function $f_G:N^m\to N^m$, called the function of G. Like input gates, output gates are represented by triangles.
• IR⊆ P × {1, ..., |P|} × IG × (IA∪ TA) is the input relation. IR satisfies the following conditions:

  ○

  For any (P₁, i, G, a) ∈ IR such that G has m inputs, i ≤ m,

  ○

  For any G ∈ IG with m inputs and i ∈ N, i ≤ m, there exists a ∈ (IA ∪ T A) and P₁ ∈ P, such that (P₁, i, G, a) ∈ IR,

  ○

  For any (P₁, i, G₁, a), (P₁, j, G₂, a) ∈ IR, i = j and G₁ = G₂,

• OR⊆ (IA∪ TA) × OG × {1, ..., |P|} × P is the output relation. OR satisfies the following conditions:

  ○

  For any (a, G, i, P₁) ∈ OR, such that G has m outputs, i ≤ m,

  ○

  For any G ∈ OG with m outputs and i ∈ N, i ≤ m, there exists a ∈ (IA ∪ T A) and P₁ ∈ P. such that (a, G, i, P₁) ∈ OR,

  ○

  For any (a, G₁, i, P₁), (a, G₂, j, P₁) ∈ OR, i = j and G₁ = G₂.

Several tools have been developed, such as Mӧbius [33], UltraSAN [34], and METASAN [35], to provide support for SANs as a modeling formalism. All these software packages are intended for automatic evaluation of performance, dependability, and performability of systems. Among them, we chose Mӧbius as the modeling tool in this paper.

4. System Description

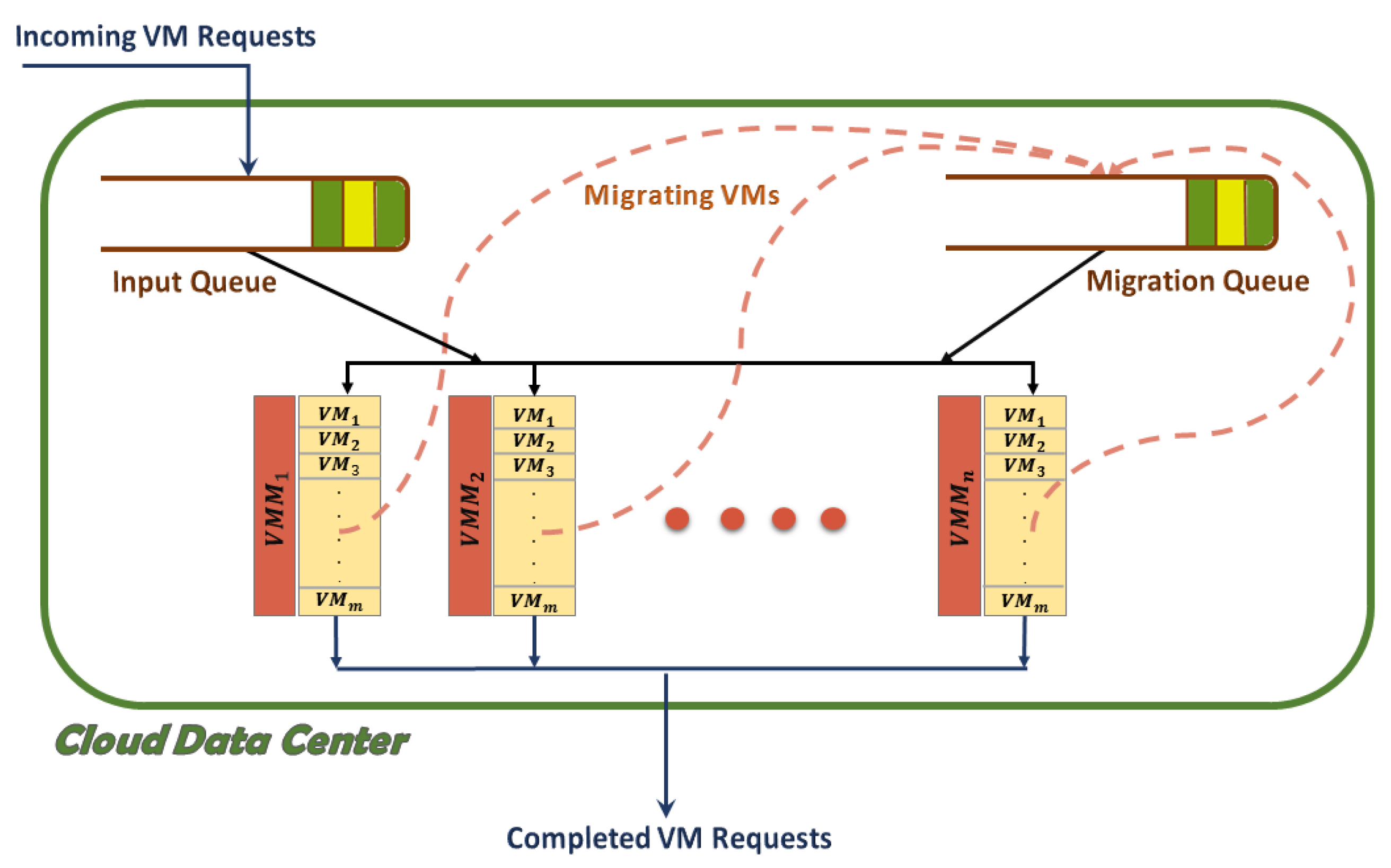
Figure 1 shows the structure of an IaaS cloud system where user requests are expressed as requests for VMs. This system contains N physical machines, each one with an active VMM. User requests are placed in the input queue upon arrival. The migration queue is used when VMs need to be migrated between VMMs.

Right after system startup, all PMs of the cloud data center are assumed to be switched-off and they are switched on only on demand after receiving requests for VMs. Since active PMs consume more power, as long as there is free capacity on active VMMs, no PM is switched on. In other words, a new PM is switched on only if none of the active VMMs have sufficient capacity to accept migrating or requested VMs. When there is a VM request in the input queue, one of the active VMMs with free capacity is randomly selected to service the request. Similarly, when there is a VM in the migration queue, one of the active VMMs with free capacity is randomly chosen to service the migrating VM. We supposed that a PM can host up to M VMs concurrently. After finishing the tasks defined for a VM, the resources assigned to that VM are returned to their corresponding VMM, thereby providing the VMM some capacity to accept another VM. In order to make the model more realistic, we assumed that the system is able to handle two different types of VMs: big and small VMs. Big VMs are VMs that have a greater impact on VMM aging due to having a longer runtime or equivalently, using a more significant share of system resources. Here, we assumed that a big VM has a runtime twice as large as the runtime of a small VM.

A VMM may fail due to different reasons. One of the notable causes of VMM failure is aging-related errors. If an aged VMM is not rejuvenated at in time, the VMM fails. Thus, the failure of all VMs running on top of that VMM is possible. In serving a VM, the age of its hosting VMM increases, but completion of that VM does not decrease the VMM’s age. This is because running a VM has some adverse effects on the corresponding VMM that are not removed once VM’s tasks are completed. Therefore, both the number and the type of VMs served by a VMM can be considered indicators of its age. By VMM age, we mean the cumulative workloads that are accepted and served by that VMM after its last reboot. In our considered system, once the age of a VMM reaches the maximum threshold F, regardless of there being free capacity on other VMMs, the active VMs of that VMM are put in the migration queue, and the VMM is then rejuvenated. In order to improve system reliability, when the age of a VMM reaches the threshold F′ (F′ < F), and if other VMMs have enough free capacity to accept the VMs running on that VMM, these VMs are put in the migration queue, and the aged VMM is rejuvenated before reaching the threshold F. With the aim of power saving, when a VMM is relatively idle and other VMMs can serve its active VMs, these VMs are put in the migration queue to be migrated to those VMMs, and the emptied PM is switched off.

5. The Proposed Model

The proposed model is composed of five sub-models shown in Figure 2. The insertion sub-model (Figure 2a) models the arrival of user requests to the system, the migration sub-model (Figure 2b) addresses the migration of VMs between VMMs, the service and green computing sub-model (Figure 2c) models serving VMs and termination of lightly loaded VMMs with the aim of green computing goals, the rejuvenation sub-model (Figure 2d) addresses rejuvenation of the aged VMMs, and the failure sub-model (Figure 2e) models the failure of VMMs. We assumed that the times assigned to all timed activities follow an exponential distribution [36,37,38,39]. In Figure 2a, the arrival of new requests to the system and selection of appropriate VMM to handle them are modeled. Timed activity $T{A}_{Arr}$ models the arrival of VM requests. Upon completion of $T{A}_{Arr}$, a token is inserted into place $P_{Ini}$. Place $P_{Ini}$ represents the input queue, and a token in this place serves as a request waiting in the queue. Once the number of tokens in place $P_{Ini}$ reaches the threshold $Q_{in}$, representing the capacity of the input queue, the input gate $I{G}_{Arr}$ prevents timed activity $T{A}_{Arr}$ from completion. The completion rate of activity $T{A}_{Arr}$ is ${\lambda }_{va}$. The timed activity $T{A}_{Ini}$ randomly selects one of the active VMMs to serve a requested VM. Whenever at least one token is in place $P_{Ini}$, representing a VM request, and there is enough capacity on one of the VMMs to accept a new VM, timed activity $T{A}_{Ini}$ is enabled and can complete the activity. Upon completion of this activity, one token is removed from place $P_{Ini}$ by input gate $I{G}_{Ini}$. If more than one VMM can accept an incoming request, $T{A}_{Ini}$ randomly chooses the destination VMM. When VMM_i is chosen by this activity, one of the output gates $O{G}_{In{i}_{S_i}}$ or $O{G}_{In{i}_{B_i}}$ is selected. If the requested VM is small, the output gate $O{G}_{In{i}_{S_i}}$ is enabled; otherwise, the output gate $O{G}_{In{i}_{B_i}}$ is enabled. Here, we assumed that the chance of arrival of a small VM is twice as large as that of a big VM. In the output gate $O{G}_{In{i}_{S_i}}$, the number of active VMs running on VMM_i and the age of that VMM are both increased by one. However, in the output gate $O{G}_{In{i}_{B_i}}$, the number of active VMs running on VMM_i increases by one and the related age increases by two. The completion rate of activity $T{A}_{Ini}$ depends on the number of VMs that can be assigned to all available VMMs and the number of VM requests waiting in place $P_{Ini}—$whichever is smaller—and the initiation rate of a VM is ${\lambda }_{vi}$. The rate of activity $T{A}_{Ini}$ is demonstrated in

Table 1. Rate of timed activities of the proposed Stochastic Activity Network (SAN) model.

Timed Activity	Rate
$\mathit{T}{\mathit{A}}_{\mathit{I}\mathit{n}\mathit{i}}$	possibleIni =$\sum _{i=1}^N(P\_tota{l}_i\to Mark()==T_2)$ &&$\left(P\_Faile{d}_i\to Mark()==1\right)?$ M: (M – $P_{CurrentVM{s}_i}$ $\to Mark$()); possibleIni ⎼ = $P_{Mig}\to Mark()$; minimum = (possibleIni <= $P_{Ini}\to Mark$())? possibleIni: $P_{Ini}\to Mark$(); return minimum * ${\lambda }_{vi}$;
$\mathit{T}{\mathit{A}}_{\mathit{M}\mathit{i}\mathit{g}}$	possibleIni =$\sum _{i=1}^N(P\_tota{l}_i\to Mark()==T_2)$ &&$\left(P\_Faile{d}_i\to Mark()==1\right)?$ M: (M – $P_{CurrentVM{s}_i}$ $\to Mark$()); possibleIni ⎼ = $P_{Mig}\to Mark()$; minimum = (possibleIni <= $P_{Mig}\to Mark$())? possibleIni: $P_{Mig}\to Mark$(); return minimum * ${\lambda }_{vmg}$;

. The predicates and functions corresponding to the input gates of the insertion sub-model are presented in rows 1 and 2 of

Table 2. Predicates and functions of input gates of the proposed SAN mod.

Gate	Predicate	Function
$\mathit{I}{\mathit{G}}_{\mathit{A}\mathit{r}\mathit{r}}$	systemLoad =$\sum _{i=1}^N{P}_{CurrentVM{s}_i}\to Mark()+P_{Ini}\to Mark()+P_{Mig}\to Mark()$; ($Q_{in}$> systemLoad)? return 1: 0;	;
$\mathit{I}{\mathit{G}}_{\mathit{I}\mathit{n}\mathit{i}}$	availCapacity = $\sum _{i=1}^N(P\_tota{l}_i\to Mark()==T_2)$ &&$\left(P\_Faile{d}_i\to Mark()==1\right)?$ M : (M – $P_{CurrentVM{s}_i}$ $\to Mark$()); availCapacity ⎼ = $P_{Mig}\to Mark()$; ($P_{Ini}\to Mark$() > 0) && (availCapacity > 0)? return 1: 0;	${\mathit{P}}_{\mathit{I}\mathit{n}\mathit{i}}$$\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}()--;$
$\mathit{I}{\mathit{G}}_{\mathit{M}\mathit{i}\mathit{g}}$	availCapacity = $\sum _{i=1}^N(P_{Tota{l}_i}\to Mark()==T_2)$ &&$\left(P_{Faile{d}_i}\to Mark()==1\right)?$ M : (M ⎼ $P_{CurrentVM{s}_i}$ $\to Mark$()); ($P_{Mig}\to Mark$() > 0) && (availCapacity > 0)? return 1 : 0;	${\mathit{P}}_{\mathit{M}\mathit{i}\mathit{g}}\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}()--;$
$\mathit{I}{\mathit{G}}_{\mathit{W}\mathit{a}\mathit{k}\mathit{e}\mathit{u}\mathit{p}}$	availCapacity = (N –$\sum _{i=1}^N{P}_{Failed}{}_i\to Mark()$) * M; systemLoad =$\sum _{i=1}^N{P}_{CurrentVM{s}_i}\to Mark()$; (availCapacity < systemLoad +$P_{Ini}\to Mark()+P_{Mig}\to Mark()$) && ($P_{Idle}$⟶Mark() > 0)? return 1: 0;	${\mathit{P}}_{\mathit{I}\mathit{d}\mathit{l}\mathit{e}}\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}()--;$
$\mathit{I}{\mathit{G}}_{\mathit{I}\mathit{d}\mathit{l}{\mathit{e}}_{\mathit{i}}}$	availCapacity = $\sum _{j=1.i\ne j}^N(P_{Tota{l}_j}\to Mark()==T_2)$ &&$\left(P_{Faile{d}_j}\to Mark()==1\right)?$ 0 : (M ⎼$P_{CurrentVM{s}_i}$ $\to Mark$ ()); ($P_{Faile{d}_i}\to Mark$() < 1) && (availCapacity > $P_{CurrentVM{s}_i}$ $\to Mark$() + $P_{Ini}\to Mark()+P_{Mig}\to Mark()$)? return 1: 0;	${\mathit{P}}_{\mathit{M}\mathit{i}\mathit{g}}\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}()+={\mathit{P}}_{\mathit{C}\mathit{u}\mathit{r}\mathit{r}\mathit{e}\mathit{n}\mathit{t}\mathit{V}\mathit{M}{\mathit{s}}_{\mathit{i}}}$$\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}();$ ${\mathit{P}}_{\mathit{C}\mathit{u}\mathit{r}\mathit{r}\mathit{e}\mathit{n}\mathit{t}\mathit{V}\mathit{M}{\mathit{s}}_{\mathit{i}}}$$\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}()=\mathbf{0};$ ${\mathit{P}}_{\mathit{T}\mathit{o}\mathit{t}\mathit{a}{\mathit{l}}_{\mathit{i}}}\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}()=\mathbf{0};$
$\mathit{I}{\mathit{G}}_{\mathit{T}\mathit{u}\mathit{r}\mathit{n}\mathit{O}\mathit{f}{\mathit{f}}_{\mathit{i}}}$	$P_{CurrentVM{s}_i}$$\to Mark$() > 0	${\mathit{P}}_{\mathit{C}\mathit{u}\mathit{r}\mathit{r}\mathit{e}\mathit{n}\mathit{t}\mathit{V}\mathit{M}{\mathit{s}}_{\mathit{i}}}$$\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}()--;$
$\mathit{I}{\mathit{G}}_{\mathit{R}\mathit{e}{\mathit{j}}_{\mathit{i}}}$	($P_{Tota{l}_i}\to Mark$() == $T_2$) && ($P_{Faile{d}_i}\to Mark$() < 1)	${\mathit{P}}_{\mathit{M}\mathit{i}\mathit{g}}\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}()+=$ ${\mathit{P}}_{\mathit{C}\mathit{u}\mathit{r}\mathit{r}\mathit{e}\mathit{n}\mathit{t}\mathit{V}\mathit{M}{\mathit{s}}_{\mathit{i}}}\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}();$ ${\mathit{P}}_{\mathit{C}\mathit{u}\mathit{r}\mathit{r}\mathit{e}\mathit{n}\mathit{t}\mathit{V}\mathit{M}{\mathit{s}}_{\mathit{i}}}\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}()=0;$
$\mathit{I}{\mathit{G}}_{\mathit{P}\mathit{r}\mathit{e}\mathit{R}\mathit{e}{\mathit{j}}_{\mathit{i}}}$	availCapacity = $\sum _{j=1.i\ne j}^N(P_{Tota{l}_j}\to Mark()==T_2)$ &&$\left(P_{Faile{d}_j}\to Mark()==1\right)?$ 0: (M – $P_{CurrentVM{s}_i}$ $\to Mark$ ()); (availCapacity > $P_{CurrentVM{s}_i}$ $\to Mark()$ + $P_{Ini}\to Mark()+P_{Mig}\to Mark()$) && ($P_{Faile{d}_i}\to Mark$() < 1) && ($P_{Tota{l}_i}\to Mark$() == $T_1$)? return 1: 0;	${\mathit{P}}_{\mathit{T}\mathit{o}\mathit{t}\mathit{a}{\mathit{l}}_{\mathit{i}}}\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}()=$${\mathit{T}}_{\mathbf{2}}$; ${\mathit{P}}_{\mathit{M}\mathit{i}\mathit{g}}\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}()+=$ ${\mathit{P}}_{\mathit{C}\mathit{u}\mathit{r}\mathit{r}\mathit{e}\mathit{n}\mathit{t}\mathit{V}\mathit{M}{\mathit{s}}_{\mathit{i}}}$$\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}();$ ${\mathit{P}}_{\mathit{C}\mathit{u}\mathit{r}\mathit{r}\mathit{e}\mathit{n}\mathit{t}\mathit{V}\mathit{M}{\mathit{s}}_{\mathit{i}}}\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}()=\mathbf{0}$
$\mathit{I}{\mathit{G}}_{\mathit{F}\mathit{a}\mathit{i}\mathit{l}\mathit{e}{\mathit{d}}_{\mathit{i}}}$	$VMM\_loa{d}_i$ = ($P_{Faile{d}_i}\to Mark$() < 1)? $P_{CurrentVM{s}_i}$ $\to Mark$(): M+1; (($P_{Faile{d}_i}\to Mark$() == 0) && ($VMM\_loa{d}_i$ < M + 1))? return 1: 0;	${\mathit{P}}_{\mathit{F}\mathit{a}\mathit{i}\mathit{l}\mathit{e}{\mathit{d}}_{\mathit{i}}}\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}()++;$ ${\mathit{P}}_{\mathit{C}\mathit{u}\mathit{r}\mathit{r}\mathit{e}\mathit{n}\mathit{t}\mathit{V}\mathit{M}{\mathit{s}}_{\mathit{i}}}\to \mathit{M}\mathit{a}\mathit{r}\mathit{k}()=\mathbf{0};$

, and the functions corresponding to the output gates of the insertion sub-model are presented in rows 1 and 2 of

Table 3. Functions of outputs gates of the proposed SAN model.

Gate	Function
$\mathit{O}{\mathit{G}}_{\mathit{I}\mathit{n}{\mathit{i}}_{{\mathit{S}}_{\mathit{i}}}}$	$VMM\_Loa{d}_i$= (($P_{Faile{d}_i}\to Mark()<1$) && ($P_{Tota{l}_i}\to Mark$() < $T_2$))? $P_{CurrentVM{s}_i}\to Mark()$: M; ($VMM\_Loa{d}_i<M$)? {$P_{currentVM{s}_i}\to Mark$() ++; $P_{Tota{l}_i}\to Mark$() ++;}: $P_{Ini}\to Mark$() ++;
$\mathit{O}{\mathit{G}}_{\mathit{I}\mathit{n}{\mathit{i}}_{{\mathit{B}}_{\mathit{i}}}}$	$VMM\_Loa{d}_i$= (($P_{Faile{d}_i}\to Mark()<1$) && ($P_{Tota{l}_i}\to Mark$() < $T_2$ – 2))? $P_{CurrentVM{s}_i}\to Mark()$ : M; ($VMM\_Loa{d}_i<M$)? {$P_{CurrentVM{s}_i}\to Mark$() ++; $P_{Tota{l}_i}\to Mark$ () += 2;}: $P_{Ini}\to Mark$() ++;
$\mathit{O}{\mathit{G}}_{\mathit{M}\mathit{i}{\mathit{g}}_{{\mathit{S}}_{\mathit{i}}}}$	$VMM\_Loa{d}_i$= (($P_{Faile{d}_i}\to Mark()<1$) && ($P_{Tota{l}_i}\to Mark$() < $T_2$)) ? $P_{CurrentVM{s}_i}\to Mark()$ : M; ($VMM\_Loa{d}_i<M$)? {$P_{CurrentVM{s}_i}\to Mark$() ++; $P_{Tota{l}_i}\to Mark$() ++;}: $P_{Mig}\to Mark$() ++;
$\mathit{O}{\mathit{G}}_{\mathit{M}\mathit{i}{\mathit{g}}_{{\mathit{B}}_{\mathit{i}}}}$	$VMM\_Loa{d}_i$= (($P_{Faile{d}_i}\to Mark()<1$) && ($P_{Tota{l}_i}\to Mark$() < $T_2$ - 2))? $P_{CurrentVM{s}_i}\to Mark()$ : M; ($VMM\_Loa{d}_i<M$)? {$P_{CurrentVM{s}_i}\to Mark$() ++; $P_{Tota{l}_i}\to Mark$() += 2;}: $P_{Mig}\to Mark$() ++;
$\mathit{O}{\mathit{G}}_{\mathit{M}\mathit{i}{\mathit{g}}_{\mathit{F}\mathit{a}\mathit{i}\mathit{l}\mathit{e}\mathit{d}}}$	$P_{Mig}\to Mark$() ++;
$\mathit{O}{\mathit{G}}_{\mathit{W}\mathit{a}\mathit{k}\mathit{u}{\mathit{p}}_{\mathit{i}}}$	$P_{CurrentVM{s}_i}\to Mark$() = 0;
$\mathit{O}{\mathit{G}}_{\mathit{R}\mathit{e}{\mathit{j}}_{\mathit{i}}}$	$P_{Tota{l}_i}\to Mark$() = 0;
$\mathit{O}{\mathit{G}}_{\mathit{P}\mathit{r}\mathit{e}\mathit{R}\mathit{e}{\mathit{j}}_{\mathit{i}}}$	$P_{Tota{l}_i}\to Mark$() = 0;
$\mathit{O}{\mathit{G}}_{\mathit{F}\mathit{a}\mathit{i}\mathit{l}\mathit{e}{\mathit{d}}_{\mathit{i}}}$	$P_{Tota{l}_i}\to Mark$() = 0; $P_{Repai{r}_i}\to Mark$() ++;
$\mathit{O}{\mathit{G}}_{\mathit{R}\mathit{e}\mathit{p}\mathit{a}\mathit{i}\mathit{r}}{}_{\mathit{i}}$	$P_{Faile{d}_i}\to Mark$ () ⎼ ⎼; $P_{CurrentVM{s}_i}\to Mark$() = 0;

. In these tables, the $P_i\to Mark()$ function returns the number of tokens inside place $P_i$. Notably, though places, activities, and gates of the proposed sub-models are not explicitly connected to each other, these sub-models are implicitly interconnected. The actual connections can be considered by reviewing the predicates and functions of the gates of these sub-models presented in Table 2 and Table 3. As an example, the predicate of $I{G}_{Arr}$ shown in Table 2 indicates that the activation of this input gate of insertion sub-model is dependent on the markings of places $P_{CurrentVM{s}_i}$ and $P_{Mig}$, which are elements of service and green computing sub-model and migration sub-model, respectively.

In Figure 2b, the migration of VMs between VMMs is modeled. When the rejuvenation mechanism or the power saving scheme requires a VM to migrate, a token is put into place $P_{Mig}$, representing the migration queue. Then, timed activity $T{A}_{Mig}$ randomly selects one of the active VMMs that have enough capacity to accept the migrating VM. When there is no VMM with free capacity to serve a migrating VM, input gate $I{G}_{Mig}$ prevents timed activity $T{A}_{Mig}$ from completion. Assuming that VMM_i is selected to serve the migrating VM, if the VM is small, output gate $O{G}_{Mi{g}_{S_i}}$ is enabled, and the number of active VMs and the age of that VMM increases by one. If the migrating VM is large, output gate $O{G}_{Mi{g}_{B_i}}$ is enabled, the number of active VMs running on VMM_i increases by one, and the age of the corresponding VMM increases by two. The completion rate of activity $T{A}_{Mig}$ depends on the number of VMs that can be assigned to all available VMMs and the number of VMs waiting for migration in place $P_{Mig}$, whichever is smaller, and the migration rate of a VM is called ${\lambda }_{vmg}$ [40]. The rate of activity $T{A}_{Mig}$ is demonstrated in Table 1. We also assumed a constant number for probability of failure of a VM migration task. Therefore, we assumed that output gate $O{G}_{Mig}{}_{Failed}$ is enabled with probability $p_{vmf}$. In this output gate, the removed token from place $P_{Mig}$ turns back to place $P_{Mig}$. Using this mechanism, the migration of a VM fails and should be retried. The predicate and function corresponding to the input gate of the migration sub-model are presented in row 3 of Table 2, and the output functions of the output gates of this sub-model are presented in rows 3–5 of Table 3.

In Figure 2c, timed activity $T{A}_{VMTurnOff}{}_i$ models the serving process of a VM on the VMM_i. Upon completion of activity $T{A}_{VMTurnOff}{}_i$, the number of tokens in place $P_{CurrentV{M}_{S_i}}$ decreases by one. The tokens in place $P_{CurrentV{M}_{S_i}}$ represent the number of active VMs on the VMM_i. When there is no token in place $P_{CurrentV{M}_{S_i}}$, input gate $I{G}_{TurnOff}{}_i$ disables time activity $T{A}_{VMTurnOff}{}_i$. Serving individual VMs occurs at rate ${\lambda }_{vt}$, so the actual service rate of all VMs running on a VMM during the execution of timed activity $T{A}_{VMTurnOff}{}_i$ is equal to ${\lambda }_{vt}\ast Mark\left(P_{CurrentV{M}_{S_i}}\right)$, where $Mark(P_{CurrentV{M}_{S_i}})$ indicates the number of tokens inside place $P_{CurrentV{M}_{S_i}}$. In other words, the actual service rate of VMs running on a VMM is the product of the ${\lambda }_{vt}$ and the number of active VMs running on that VMM.

Timed activity $T{A}_{WakeUp}$, with completion rate ${\lambda }_{pw}$, models the PM wakeup process. The tokens inside place $P_{Idle}$ represent the number of inactive or switched-off PMs in the system. Right after system start up, all PMs are assumed to be switched off, so place $P_{Idle}$ holds as many tokens as there are PMs in the cloud data center. Upon completion of activity $T{A}_{WakeUp}$, a token is removed from place $P_{Idle}$ by input gate $I{G}_{WakeUp}$. If there is no token in places $P_{Ini}$ or $P_{Mig}$, input gate $I{G}_{WakeUp}$ prevents the completion of activity $T{A}_{WakeUp}$. If more than one token exists in place $P_{Idle}$, representing several switched-off PMs in the system, one token is randomly chosen by timed activity $T{A}_{WakeUp}$. In this case, PM_i is activated by enabling output gate $O{G}_{WakeUp}{}_i$ and becomes ready for accepting VMs.

Instantaneous activity $I{A}_{Idle}{}_i$ models the shutdown process of the active VMM_i that is lightly loaded or has no workload. When other active VMMs have enough free capacity to accept all VMs running on top of VMM_i, the VMs are placed into the migration queue, and then VMM_i and its hosting PM are switched off. Upon completion of instantaneous activity $I{A}_{Idle}{}_i$, the number of tokens in place $P_{Idle}$ increases by one, and the number of tokens in place $P_{CurrentV{M}_{S_i}}$ is set to zero. If the tokens in place $P_{CurrentV{M}_{S_i}}$ cannot be moved to places $P_{CurrentV{M}_{S_j}}$ (i ≠ j), input gate $I{G}_{Idle}{}_i$ prevents instantaneous activity $I{A}_{Idle}{}_i$ from completion because other VMMs are unable to accept VMs running on VMM_i. The predicates and functions corresponding to the input gates of the service and green computing sub-model are presented in rows 4–6 of Table 2, and the function corresponding to the output gate of this sub-model is presented in row 6 of Table 3.

In Figure 2d, the number of tokens in place $P_{Total}{}_i$ represents the age of the VMM_i. Therefore, the number of tokens in place $P_{Total}{}_i$ is set to zero just after rejuvenation or reboot of VMM_i. When the number of tokens in place $P_{Total}{}_i$ reaches threshold $T_2$, the input gate $I{G}_{Rej}$ is enabled and moves tokens from place $P_{CurrentV{M}_{S_i}}$ to place $P_{Mig}$. By applying this mechanism, the migration of VMs from VMM_i to other VMMs of the data center is modeled when a VMM has to be rejuvenated. Timed activity $T{A}_{Re{j}_i}$ models the rejuvenation process of a VMM with rate ${\lambda }_{hrj}$. Upon completion of this activity, the number of tokens in place $P_{Total}{}_i$ is set to zero by output gate $O{G}_{Re{j}_i}$, which represents the age of the newly rejuvenated VMM_i. A rejuvenated VMM is active and can accept and serve VMs. However, if there is no VM to be hosted by the rejuvenated VMM, the VMM is switched off by input gate $I{G}_{Idle}{}_i$ modeled in the service and green computing sub-model.

The model also uses timed activity $T{A}_{PreRe{j}_i}$ for early rejuvenation of aged VMM_i. When the number of tokens in place $P_{Total}{}_i$ reaches the threshold $T_1$, where $T_1$ < $T_2$, and there are less tokens in place $P_{CurrentV{M}_{S_i}}$ than free capacity on other active VMMs, the input gate $I{G}_{PreRe{j}_i}$ is enabled. In this situation, input gate $I{G}_{PreRe{j}_i}$ moves all tokens of place $P_{CurrentV{M}_{S_i}}$ to place $P_{Mig}$. The completion rate of timed activity $T{A}_{PreRe{j}_i}$ is ${\lambda }_{hrj}$. The output gate $O{G}_{PreRe{j}_i}$ sets the number of tokens in place $P_{Total}{}_i$ to zero right after the rejuvenation process. The predicates and functions corresponding to the input gates of the rejuvenation sub-model are presented in rows 7 and 8 of Table 2, and the functions corresponding to the output gates of this sub-model are presented in rows 7 and 8 of Table 3.

In Figure 2e, the failure of active VMMs in the system is modeled. Whenever VMM_i fails, a token is put in place $P_{Failed}{}_i$. After failure detection and during the repair of VMM_i, a token is put into place $P_{Repair}{}_i$. Timed activity $T{A}_{Failed}{}_i$ models the failure event of VMM_i. If there is a token in place $P_{Failed}{}_i$ or there are as many tokens in place $P_{Total}{}_i$ as in $T_2$, the input gate $I{G}_{Faile{d}_i}$ disables activity $T{A}_{Failed}{}_i$. Upon completion of activity $T{A}_{Failed}{}_i$, the number of tokens in place $P_{Total}{}_i$ is set to zero by output gate $O{G}_{Failed}{}_i$, and the number of tokens in place $P_{Repair}{}_i$ increases by one. Once VMM_i is repaired, the numbers of tokens in places $P_{Repair}{}_i$ and $P_{Failed}{}_i$ become zero, and the VMM is reactivated. The completion rate of timed activity $T{A}_{Failed}{}_i$ is the product of the number of tokens in place $P_{Total}{}_i$ and the failure rate of an active VMM called ${\lambda }_{hf}$. The greater the age of a VMM, the greater the failure probability of that VMM.

Timed activity $T{A}_{Repair}{}_i$ represents the repair process of VMM_i. When there is a token in place $P_{Repair}{}_i$, timed activity $T{A}_{Repair}{}_i$ is enabled and can complete the activity. Then, the number of tokens in places $P_{Total}{}_i$ and $P_{Failed}{}_i$ is set to zero by the output gate $O{G}_{Repair}{}_i$. The completion rate of timed activity $T{A}_{Repair}{}_i$ is ${\lambda }_{hrp}$. The predicate and function corresponding to the input gate of failure sub-model are presented in row 9 of Table 2, and the functions corresponding to the output gates of this sub-model are presented in rows 9 and 10 of Table 3.

6. Performance Evaluation

In this section, the desired output measures that can be obtained using the proposed SAN model are defined, and then the proposed model is evaluated. The output measures are computed applying the Markov reward approach [41]. In this approach, appropriate reward rates are assigned to each feasible marking of a SAN model, and then the expected accumulated reward is computed in the steady state. To this end, the proposed analytical model is solved with the Mӧbius tool [33]. In the following formulas, $Mark\left(P_i\right)$ returns the number of tokens inside place $P_i$.

The ratio of serving VMs to accepted requests is defined as the ratio of the steady-state number of VMs that are being served to the steady-state number of accepted VM requests in the cloud system. This measure is computed using Equation (1):

$$RSA={\displaystyle \sum }_{i=1}^{N}E[Mark(P_{CurrentV{M}_{S_i}})]/(E[Mark(P_{Ini})]+\mathrm{E}[Mark(P_{Mig})]+{\displaystyle \sum }_{i=1}^{N}E[Mark(P_{CurrentV{M}_{S_i}})])$$

(1)

The other measure that is obtained by applying the proposed SAN model is the probability of VMM failure, which can be computed by the following equation:

$$P{R}_{VMMF}={\displaystyle \sum }_{i=1}^{N}E\left[Mark\left(P_{Failed}{}_i\right)\right]/N$$

(2)

One of the main goals of introducing rejuvenation in cloud systems is to reduce the mean number of failed VMs, which can be computed by the product of the mean number of VMs that are being served on each VMM and the probability of VMM failure in the steady state. The mean number of failed VMs can be calculated as follows:

$$NFV=({\displaystyle \sum }_{i=1}^{N}E\left[Mark\left(P_{CurrentV{M}_{S_i}}\right)\right]/N)\ast ({\displaystyle \sum }_{i=1}^{N}E\left[Mark\left(P_{Failed}{}_i\right)\right]/N)$$

(3)

The total power consumption of cloud servers is another measure which can be computed by the proposed model and is the mean value of power consumed by PMs, VMMs, and VMs of the data center. It can be computed by Equation (4).

$$TPC={\rho }_b\ast \left(N-E\left[Mark\left(P_{Idle}\right)\right]\right)+{\rho }_v\ast {\displaystyle \sum }_{i=1}^{N}E[Mark(P_{CurrentV{M}_{S_i}})]$$

(4)

where ${\rho }_b$ is the average power consumed by a switched-on PM running a VMM, ${\rho }_v$ is the average power consumed by a VM, and N denotes the number of PMs in the system.

In order to evaluate the proposed model, we assumed a system with 3 PMs and the maximum of 3 VMs per each VMM. In this setting, the input parameter $T_1$ is 8, which means a VMM of age 8 could be rejuvenated if other VMMs have enough capacity to accept its VMs. The parameter $T_2$ is set to 10, which means a VMM of age 10 has to be rejuvenated instantaneously. In other words, regardless of the capacity of other VMMs, the active VMs of a VMM aged 10 should be placed on the migration queue, and the VMM should be rejuvenated.

The other values set for the input parameters of the proposed model are presented in

Table 4. Configuration of the cloud system under study.

Parameter	Description	Value/Range	Unit
${\lambda }_{hf}$	VMM failure rate	0.00139	VMM/h
${\lambda }_{hrj}$	VMM rejuvenation rate	30	VMM/h
${\lambda }_{hrp}$	VMM repair rate	2	VMM/h
${\lambda }_{pw}$	PM wakeup rate	1440	PM/h
${\lambda }_{va}$	VM requests arrival rate	[5 … 20]	VM/h
${\lambda }_{vt}$	VM switch off rate	0.5	VM/h
${\lambda }_{vmg}$	VM migration rate	1200	VM/h
${\lambda }_{vi}$	VM initiation rate	120	VM/h
$p_{vmf}$	Probability of VM migration failure	0.01	-
$N$	Number of PMs	3	-
$M$	Number of VMs per PM	3	-
$Q_c$	Size of input queue	5	-
$Q_m$	Size of migration queue	6	-
${\rho }_b$	Power consumption of a PM running a VMM	100	W
${\rho }_v$	Power consumption of a VM	10	W

. Most of the values used herein as input parameters of the proposed SAN model are in the range of the values considered in other related work [10,11,15,22,29,36,37,39,42]. In order to compare different situations, the proposed model was evaluated in three modes: (1) pure power saving, (2) pure rejuvenation, and (3) with simultaneous application of rejuvenation and power saving, called power-aware rejuvenation. Modes 1 and 2 are the baselines for our main proposed scheme, which is mode 3. In mode 3, all five sub-models of Figure 2 are used. In mode 1, the rejuvenation sub-model shown in Figure 2d is omitted. In mode 2, the power saving sub-model represented in Figure 2c is removed, and the model is adjusted so that no token would be placed in place ${\mathrm{P}}_{\mathrm{Idle}}$. 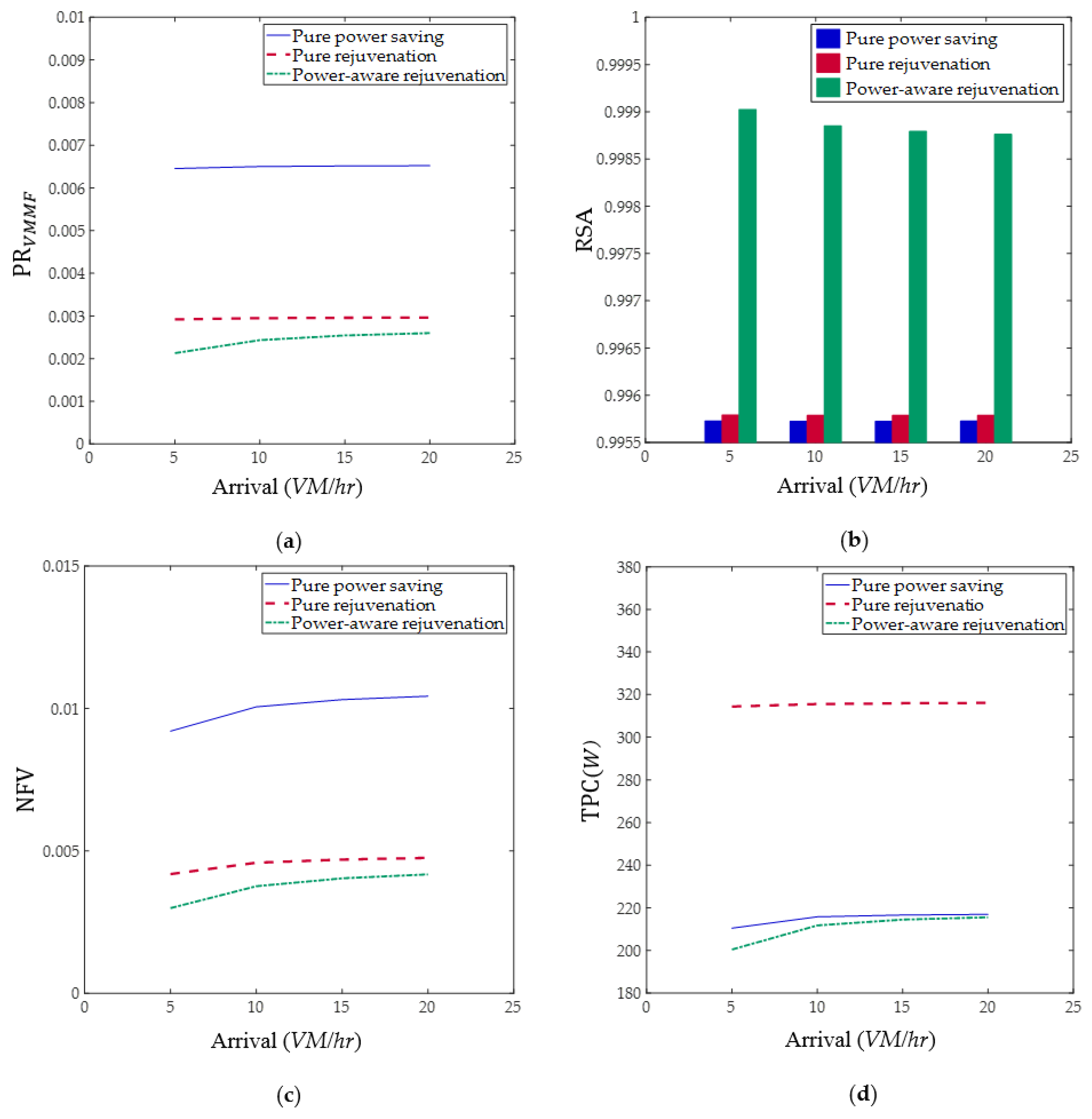The results obtained from solving the proposed model in the three modes are presented in Figure 3.

Figure 3a shows the average probability of VMM failure in the proposed model in the three evaluation modes. One of the main causes of VMM failure is the increasing number of served VMs and the errors introduced due to VMM aging. With the pure rejuvenation scheme, aged VMMs are identified and rejuvenated before age-induced failures occur. Thus, the forced rejuvenation of mode 2 decreases the probability of VMM failure compared to mode 1. The power saving scheme switches off idle VMMs, which in turn restarts the age of those VMMs, and result in even lower probability of VMM failure when combined with pure rejuvenation in mode 3.

As shown in Figure 3b, simultaneous modeling of power saving and rejuvenation schemes in mode 3 improves the availability-related measure RSA of the cloud system. Such implementation of power-aware rejuvenation involves the migration of VMs between VMMs, so the number of tokens in place $P_{Mig}$ increases and the denominator of the fraction in Equation (1) increases. However, as shown in Figure 3a, pure rejuvenation decreases the average probability of VMM failure, and thereby increases the mean number of active VMMs, increasing the average number of VMs that can be served at a given time. Since $P_{CurrentV{M}_{S_i}}$ increases more than $P_{Mig}$, power-aware rejuvenation causes a significant improvement in the ratio of serving VMs to accepted requests.

Figure 3c represents the effect of applying rejuvenation and power-awareness schemes to cloud systems on the mean number of failed VMs. The greater the average probability of VMM failure, the greater the number of failed VMs. Consequently, for the same VMM failure probability results shown in Figure 3a, mode 3 performed the best and mode 1 the worst.

In Figure 3d, the impact of software rejuvenation and power-awareness on power consumption of cloud system is considered. As indicated in Equation (4), the power consumption is directly related to the number of switched-on PMs and active VMs in a data center. In the pure rejuvenation mode, mode 2, all PMs are always on and therefore the power consumption in this mode is the greatest compared to the power consumed in modes 1 and 3, which are power-aware. In mode 3, newly rejuvenated VMMs are free of running VMs. Thus, they are more likely to be switched off by the power saving mode. Therefore, the total power consumption of mode 3 is less than that of mode 1. Figure 3d acknowledges the fact that by applying rejuvenation and power saving simultaneously, the number of active PMs decreases compared to the situation where rejuvenation is not applied.

7. Conclusions and Future Work

In this paper, a power-aware VMM rejuvenation scheme was presented for IaaS cloud systems based on a SAN model proposed for IaaS clouds. Several real aspects of cloud systems that were not considered in previous related work are encompassed in the proposed model, including failure/repair behavior of VMMs, VM heterogeneity, VM migration, VM multiplexing, and different PM power consumption states. The proposed scheme uses two different thresholds for optional and mandatory rejuvenation of aged VMMs, in which the age of a VMM is computed as the cumulative workload that is accepted and served by that VMM after its last reboot. Mӧbius software was used to solve the proposed SAN. Then, the performance, availability, and power consumption of the presented scheme were compared with two different baselines: a pure power saving scheme and a pure rejuvenation scheme. The results showed that the proposed scheme improves all output measures of interest including the ratio of serving VMs to accepted VM requests, the probability of VMM failure, the mean number of failed VMs, and the total power consumption of cloud servers.

Though the proposed scheme is more scalable than the models and schemes presented in the literature, scalability is still an issue that should be investigated in the future. This limitation can be addressed by applying approximation techniques to presented analytical model, such as folding and fixed-point methods. We plan to complete real-world experiments to validate the analytical results and to address the scalability limitation. Another interesting extension to the model proposed in this work could be to support heterogeneous PMs in addition to heterogeneous VMs. Colored extensions of PNs and SANs could be used for this extension. Considering cloud data center topologies and network architectures and considering availability and power consumption of network equipment are other interesting extensions of current work. Investigating the overhead of VM migration on the performance and availability of the cloud system under study is another possible future line of this research work.