SLoPCloud: An Efficient Solution for Locality Problem in Peer-to-Peer Cloud Systems

Abstract

Peer-to-Peer (P2P) cloud systems are becoming more popular due to the high computational capability, scalability, reliability, and efficient data sharing. However, sending and receiving a massive amount of data causes huge network traffic leading to significant communication delays. In P2P systems, a considerable amount of the mentioned traffic and delay is owing to the mismatch between the physical layer and the overlay layer, which is referred to as locality problem. To achieve higher performance and consequently resilience to failures, each peer has to make connections to geographically closer peers. To the best of our knowledge, locality problem is not considered in any well known P2P cloud system. However, considering this problem could enhance the overall network performance by shortening the response time and decreasing the overall network traffic. In this paper, we propose a novel, efficient, and general solution for locality problem in P2P cloud systems considering the round-trip-time (RTT). Furthermore, we suggest a flexible topology as the overlay graph to address the locality problem more effectively. Comprehensive simulation experiments are conducted to demonstrate the applicability of the proposed algorithm in most of the well-known P2P overlay networks while not introducing any serious overhead.

1. Introduction

Foster et al. [1] defined Cloud systems as “a large-scale distributed computing paradigm that is driven by economies of scale, in which a pool of abstracted, virtualized, dynamically scalable, managed computing power, storage, platforms, and services are delivered on demand to external costumers over the Internet”. Such systems can be implemented as peer to peer (P2P) networks to avoid bottlenecks and single point of failure in addition to meeting other advantages of P2P systems [2,3]. Cloud systems that are implemented as peer to peer networks are called P2P cloud systems. These systems have been become a very attractive area of research in recent years while P2P systems have become quite popular due to the ability of accessing shared resources, regardless of their location worldwide [4,5,6,7]. In P2P cloud systems, services are offered at the end user machines, which referred to as peers, rather than any central server. In contrast to traditional client–server systems, services are provided directly between peers in P2P cloud systems. These systems usually form a logical layer over other networks, such as TCP/IP, as underlay or physical infrastructure.

Despite the structure of P2P cloud systems, most of these systems consider no dependency between the real distance of the nodes and their position in the overlay network. Hence, if one of the nodes requests a service, it is not guaranteed to be assigned to the nearest available service provider in the physical network. Such mismatching may waste the network resources, such as bandwidth, and impose delay to the network services. The mismatching problem between the overlay and the physical or underlay layer is known as locality problem [8].

Locality problem is a challenging problem in P2P cloud systems as in the former P2P overlay networks such as Chord [9], Pastry [10], and Tapestry [11]. Unfortunately, locality is not considered in most of the current P2P designs. There are three main solutions to provide the locality in P2P Systems that suffer from some kind of deficiencies. The first one uses address prefixes to locate those nodes that are being geographically closer to each other, however, similar prefixes can be located at different geographic zones [12]. In addition, the prefixes could not be extracted from the hashed IP addresses. The second solution uses distributed reliable servers that are some kind of network hotspots, multiple single points of failure, and bottlenecks. The third category of locality solutions uses a method with the random initialization of node coordinates which leads to the high probability of instability of the network estimations and comparisons. Overall, these solutions are not suitable for most of the current P2P networks.

In this paper, we extend our previous specific-purpose locality solution [13,14] to become a general solution for locality problem in P2P cloud systems while increasing the performance of the network. Obviously, any solution for matching the position of joining nodes in overlay layer with their real physical position has some overhead. The overhead is typically control traffic overhead and imposed delay. Accordingly, we perform comprehensive simulations to represent the performance gain of our proposed solution. Moreover, simulation results show the applicability of this solution on most of the well-known overlay networks.

Hereupon, the main contribution of this paper is to propose an efficient solution for locality problem based on RTT in P2P cloud systems. More specifically:

(i)

This paper uses RTT as a metric to estimate the distance between nodes. Consequently, it proposes a locality solution referred to as SLoPCloud, to solve the mismatch problem between the overlay and physical layer. The proposed solution does not impose a serious overhead on network performance parameters, such as traffic and delay, while it could be applied to most of the well-known overlay networks.

(ii)

This paper suggests a flexible topology, i.e. Generalized Hypercube Connected Cycle (GHCC), to be used as an overlay layer in P2P cloud networks. GHCC is compatible with the proposed solution and could be easily converted into different well-known topologies with just a simple modification in its parameters. It is worth noting that choosing a proper graph has a considerable effect on the network performance metrics such as the bandwidth, congestion, and delay.

(iii)

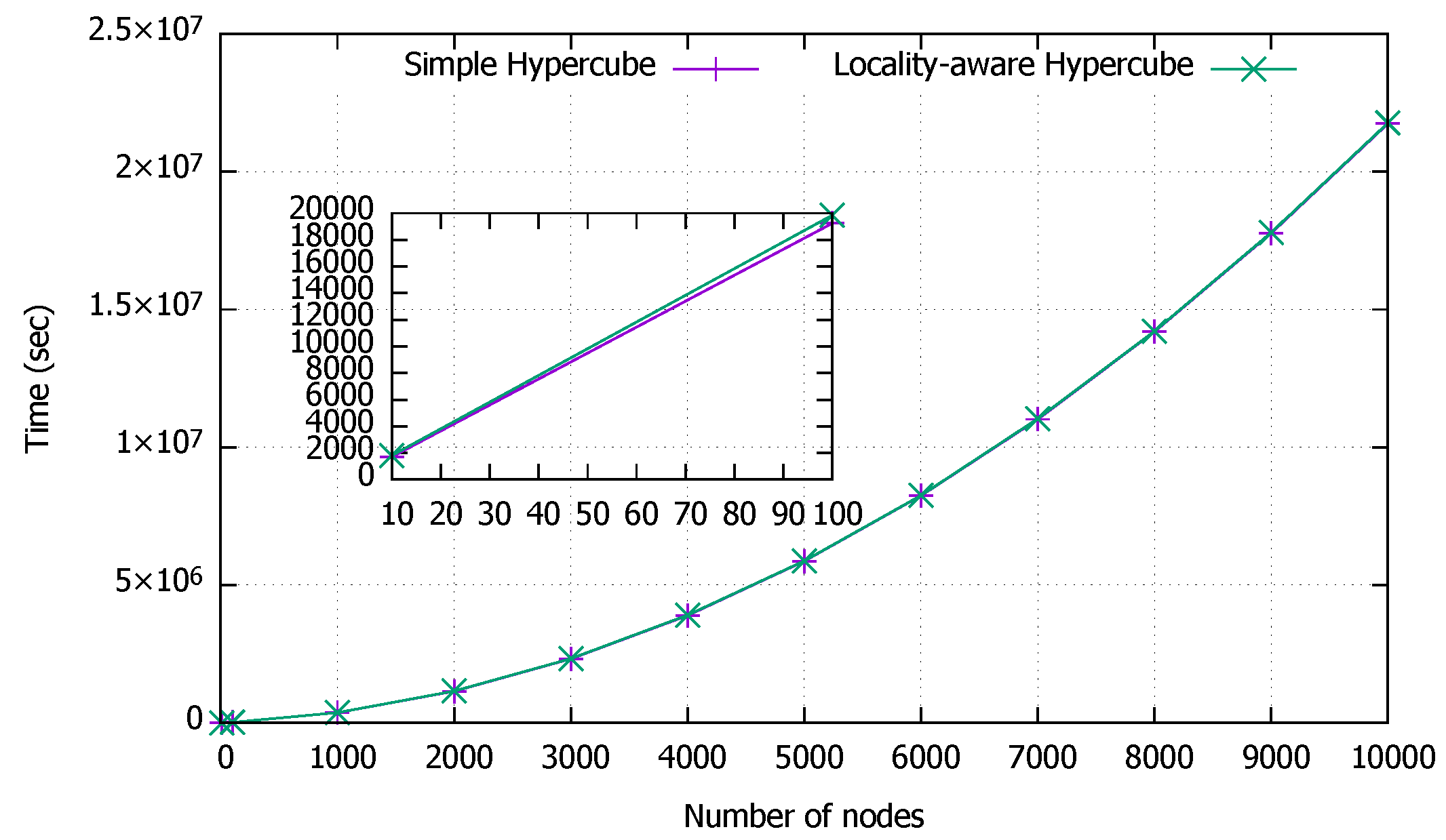
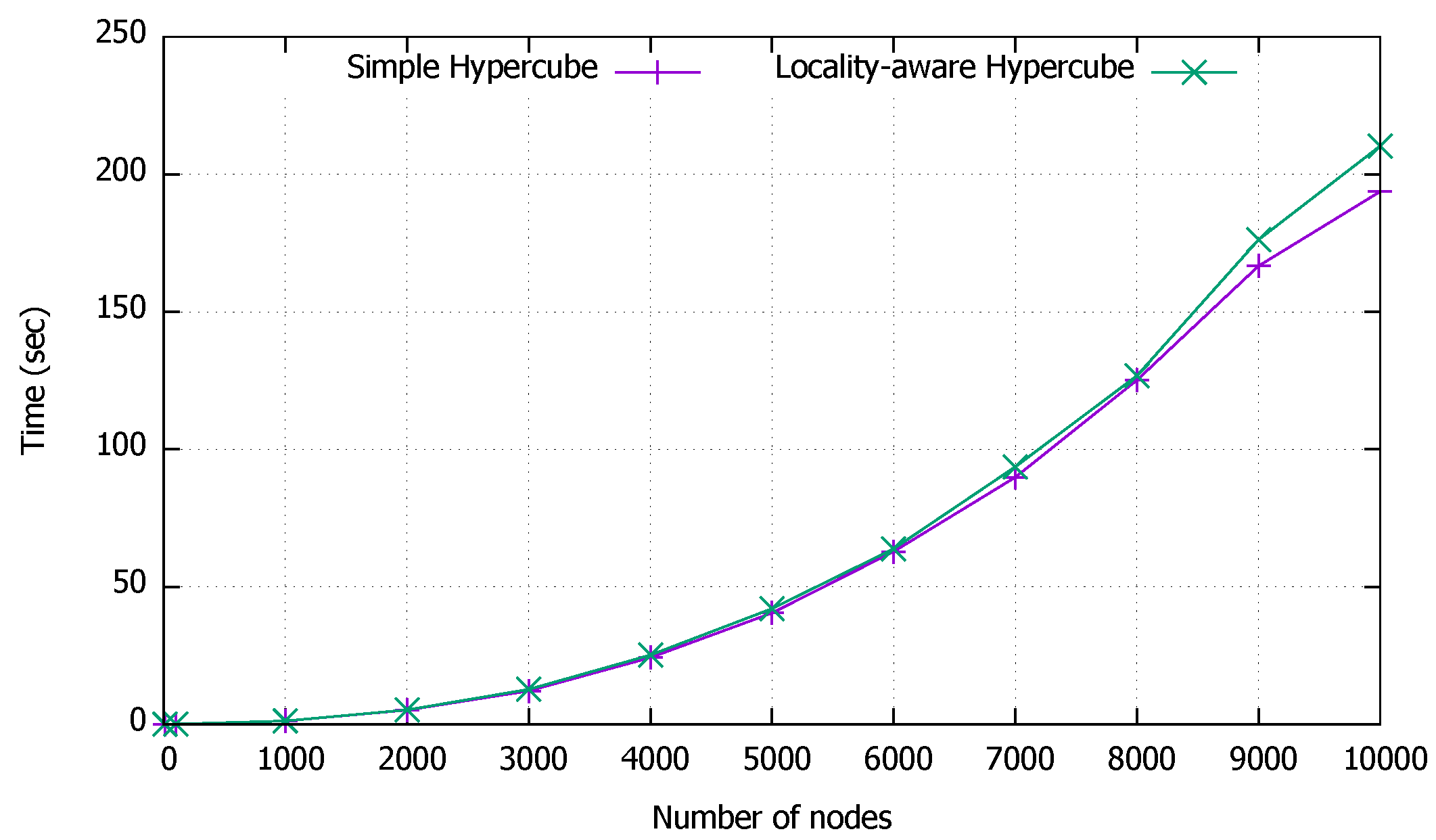
This paper proves the performance and the scalability of the proposed solution SLoPCloud, through comprehensive simulations. Here, SLoPCloud solution has been implemented while topologies Ring, Hypercube, CCC, and GHCC are considered as the overlay network. The focus of simulation study in this paper is on the network bootstrapping time and the control traffic caused by the locality solution.

The rest of the paper is as follows. The related works are represented in Section 2. Section 3 provides a preliminary background information on P2P network topologies. In Section 4, the proposed solution regarding a suggested topology for the overlay graph is presented in details. Simulation parameters and experimental results are illustrated in Section 5. Finally, the paper is concluded in Section 6.

2. Related Work

P2P cloud systems such as well-known P2P networks have two-layer architecture, overlay, and physical layer [15]. Locality problem, as mentioned in the previous section, is a mismatch problem between these two layers [8]. Since the locality problem is not considered in the most well known P2P cloud systems, in this section, first the history of P2P networks and solution for locality problem in P2P networks are stated. Then, a brief background on P2P Cloud Systems is provided.

2.1. P2P Networks and Locality Problem

The first generation of P2P systems uses central directory servers to locate files. When a new node wants to join the network, it sends a message to the central server for overlay address allocation. In this generation, every node knows its neighbors in the overlay network and exchanges file with them through the server. The first generation of P2P systems provides file-sharing and storage services. Napster [16] is an example of this generation. It is worth mentioning that there is a main difference between the first generation of P2P networks and the typical client–server systems, in the tasks of the central server. The central server of the first generation of P2P networks is responsible just for network management operations, while the shared files are located in peers. The second generation of P2P systems such as Gnutella [17], MojoNation [18], and Freenet [19], is working based on message broadcasting. Such systems are designed to provide a similar, but distributed, service using scoped broadcast queries. However, they suffer from the limitations in scalability, due to the frequentative broadcast operations.

The third and the last generation of P2P systems is structured overlay networks, including Chord [9], Pastry [10], Tapestry [11], and CAN [20]. One of the key features of these systems is to provide scalable routing performance. This feature is obtained by maintaining a scalable amount of routing state at each node which means that the expected number of forwarding hops between any two communication nodes is small, with respect to the total number of nodes in the system. The second key feature of these systems is that they are able to route the destination addresses which is not equal to the address of any existing node. This task is done by a special high-level interface called distributed hash table (DHT). Using this interface, each message is routed to the node whose address is the closest address to that specified in the destination field of the message. The overlay topology in this generation implements a basic key-based routing (KBR) interface which supports deterministic routing of messages to a live node that has responsibility for the destination key. They can also support decentralized object location and routing (DOLR) [21]. These systems guarantee that queries find existing objects under non-failure conditions.

In this generation, Pastry [10] and Tapestry [11] share similarities to the work of Plaxton [22] for a static network. Others [23,24] explore distributed object location schemes with provably low search overhead, but they require precomputation. Therefore, they are not suitable for dynamic networks. The third generation of the P2P networks contains some systems that highly attracted researchers’ attention. For example, Kademlia [25] uses XOR for overlay routing, Viceroy [26] provides logarithmic hops through nodes with constant degree routing tables and SkipNet [27] uses a multidimensional skip-list data structure to support overlay routing by maintaining both a DNS-based namespace for operational locality and a randomized namespace for network locality.

However, there are three main solutions for the locality problem, in general. The first one uses address prefixes to locate those nodes that are being geographically closer to each other, based on the regulations of BGP protocol [28]. The disadvantage of this solution is that sometimes similar prefixes are located at different geographic zones [12]. Furthermore, IP addresses are usually hashed before being stored in the distributed hash table, while the prefixes could not be extracted from the hashed IP addresses. In the second solution [20], there are a set of distributed reliable servers, referred to as landmarks. Every node measures its distance to each of these landmarks. Those nodes that are closer to a specific landmark are placed close to each other in overlay network. The main side effect of this category of locality solutions is that the landmarks are some kind of network hotspots, multiple single points of failure, and bottlenecks. The last category of locality solutions assigns a random non-trivial coordinate to each node, and, at the same time, estimates the real distance among nodes. This category compares the distance calculated based on a predefined function and the non-trivial coordinates with the real physical distance and then tries to modify the non-trivial coordinates toward the reality [29]. The high probability of instability of the network under such a method, due to the random initialization of node coordinates, is worth mentioning.

2.2. P2P Cloud Systems

Cloud computing has many different definitions [1,30,31,32] with a common property of introducing the cloud computing from the vantage point of the end users. This property obviously represents the ability of cloud systems to be implemented as P2P networks. Hereupon, many researchers have been attracted by the concept of P2P cloud systems. In what follows, a few of them are mentioned. Xiong et al. [33] proposed an efficient and memory-less search algorithm for P2P Cloud systems. Yoon et al. [34] analyzed the efficiency of key search algorithm by combining P2P and cloud computing. They showed that P2P computing based on cloud virtualization provides scalability and flexibility while it has performance efficiency. Li et al. [35] proposed a blockchain-based security architecture for distributed P2P cloud storage to address the problem of large communication overhead caused by encrypted files and to guarantee the data security.

P2P cloud solutions have been widely adopted by Live media streaming applications. Chang et al. [36] proposed a P2P cloud system for live video Streaming Platform and named it CloudPP. CloudPP architecture uses public cloud servers as peers, to construct a robust and scalable video streaming platform with scalable video coding (SVC) technology. Provensi et al. [37] presented a cloud-assisted P2P solution that is self-organizing, robust to user churn and leverages streaming trees to push data to users with low latency. Zhao et al. [38] proposed a replica distribution for P2P real-time streaming platforms while describe a mathematical model and design an optimal algorithm for distributing chunk replicas.

Video-on-demand (VoD) streaming based on P2P overlay has become one of the most popular applications over the Internet. Cloud computing infrastructure assists the P2P streaming overlay to guarantee the minimum level of users’ satisfaction. Liu et al. [39] proposed a VoD system capable of delivering cinematic-quality video streams to end users based on P2P cloud systems. Huang et al. [40] presented an analytical optimization model to tackle with the bandwidth allocation problem while proposing a greedy-based policy aiming to improve user satisfaction. Huang et al. [41] provided service differentiation to encourage the cooperative behavior of users in hybrid VoD system while Hybrid cloud assisted P2P VoD systems augment P2P VoD systems with cloud computing infrastructure, aiming at increasing the available bandwidth resource in the system to guarantee the video playback quality. Clearly, P2P cloud system is a novel concept that attracts researchers’ attention. It is worthy highlighting that a considerable number of challenges faced by P2P cloud systems are already existing in P2P network.

3. Background

Since the considered topology for overlay network has a huge impact on the performance of locality solution in P2P cloud systems, we discuss the topologies of overlay networks in this section.

In any P2P network, including P2P cloud systems, the overlay layer is formed by a specific topology, i.e., graph, while it is proven that choosing a proper graph has a considerable effect on the network performance [42]. The results in [13,14,43] confirm the importance of used topology as the overlay graph on the performance metrics such as the bandwidth, congestion, and delay. Henceforward, we present a general overview on the overlay topologies. Three major factors influence the selection of a specific graph for the topology of the overlay. These factors are degree $\left(\delta \right)$, diameter (D), and scalability of the network [13]. Degree is the maximum number of outgoing edges from each node, i.e. the number of neighbors. Diameter is the maximum distance between two nodes in the network. Scalability refers to the ability of increment or decrement in the number of nodes (N), without any serious effect on performance. Overall, a suitable topology should preferably be symmetric, regular with a low degree as well as low diameter and highly scalable. Regularity means that all nodes have the same degree while symmetricity means that the graph is homomorphic from the view point of all other network nodes.

There are two main categories of the graphs used as overlay topologies, basic graphs and composite graphs. Five popular and well known basic graphs are complete graph, mesh graph, Ring graph, torus graph, and Hypercube, while cube connected cycle (CCC) [44] is an instance of composite graphs. CCC is formed from the combination of Hypercube and Ring topologies. The main goal of combining two basic topologies together to form a new graph is to gain the advantages of both, while omitting their side effects. As an instance, CCC preserves the scalability and diameter from Hypercube while it fixes the degree of each node to three. Figure 1 shows the three dimensional CCC graph.

Figure 1. Three-dimensional Cube Connected Cycle topology.

As we mentioned above, this paper aims at extending our previous works [13,14], in which Hypercube and CCC are used as the overlay topology, to solve the locality problem in P2P cloud systems. In [13], we used Hypercube topology due to the noted properties of Hypercube graph to further its similarity with some other overlay topologies such as butterfly [28] and Torus. This fact leads to the proposed algorithm being able to be applied to other P2P overlays with almost all similar overlay topologies, e.g. Pastry, Tapestry, Viceroy, and CAN. In [14], we chose CCC as an overlay in the proposed locality solution, because of the similarity between CCC and Hypercube, whereas CCC topology have two other important properties, regularity and symmetricity. Gharib et al. [45] published a survey representing many overlay networks require two layer routing, with different overlay topologies. In this paper, we suggest another composite topology as an overlay network to solve the locality problem. This topology is GHCC [46] which is explained in Section 4.3.

4. Proposed Solutions for Locality Problem in P2P Cloud System

In this section, a novel solution for locality problem in P2P cloud systems is proposed, to solve the mismatch problem between the overlay and physical layer. Hereupon, choosing a metric to represent the distance between peers becomes crucially important. Since the bandwidth plays an essential role in the performance of the services provided by P2P cloud systems, the time distance seems to be more effective than the location-based distance. Accordingly, to estimate the distance between nodes, we chose to use RTT as a distance metric. The other significantly effective factor in locality problem is the topology of the overlay graph [42]. In this paper, we suggest the GHCC as a general composite topology for overlay P2P cloud networks. GHCC is a flexible graph capable of easily reshaping into many well-known graphs, with just a simple modification in its parameters. In this graph, any two of the three main graph characteristics, i.e., the number of nodes, graph degree, and graph diameter, could be easily changed while the third one becomes fix. It is worth mentioning that, in most of the known graphs, fixing just one of the mentioned parameters, leads to fix the others.

While we name the proposed algorithm SLoPCloud, our solution does not have a serious impact on network performance parameters such as traffic and delay. Furthermore, since the overlay graph of our algorithm is a flexible and reshapable graph, our solution could be applied to most of the well-known overlay networks. As mentioned above, the proposed solution is the extension of our previously published works [13,14]. Hereupon, since Hypercube is a well-studied topology and close to the architecture of the most well known overlay topologies, we first review SLoPCloud based on Hypercube [13]. Then, the proposed solution based on CCC is reviewed [14]. This topology is used to improve the performance of the network under our solution, due to its unique properties such as a fixed and small degree. Finally, SLoPCloud is proposed based on GHCC topology.

In any P2P system, there is an initialization phase for the network, in which the network is bootstrapping. In this phase, some initialization processes are conducted and then any new node can join or leave the network. Accordingly, to introduce any locality solution for P2P cloud systems, we have to propose the bootstrapping process, and then the process of joining new nodes. Finally, the routing process according to the locality solution has to be proposed. Although the problem of two layer routing is optimized recently [47,48], the routing in P2P systems is yet done by considering just the overlay layer. It is worth mentioning that the resource management processes are done according to the nodes’ connections in the overlay layer. Hence, the routing problem, in the context of this paper, is specifying the responder to the requested resources in the P2P cloud system. That is why the routing problem is of crucial importance in this field of research.

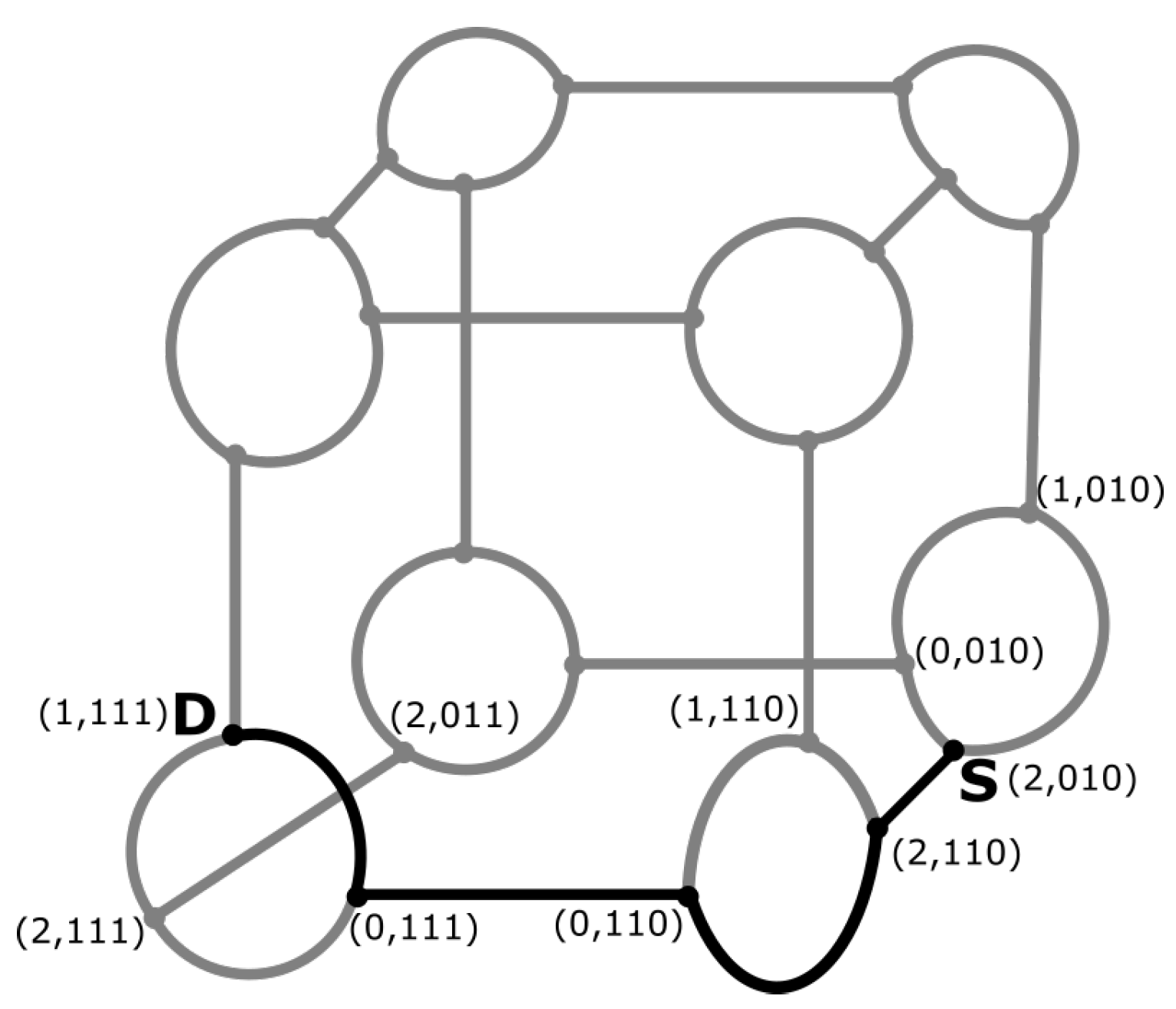
4.1. Hypercube Based Overlay Network

In this part, we propose our locality solution for Hypercube based overlay P2P cloud systems. The basic idea of this solution is represented in [13]. As mentioned above, the main graph factors that have the major effect on the network performance are the diameter, degree, and scalability, while Hypercube seems to be a good choice with the fairly acceptable values for all of the mentioned factors, simultaneously. In x-dimension Hypercube topology, as in most well-known topologies, the number of nodes is exponentially affected by the change in the number of dimensions. However, the number of nodes is just duplicated with the unity increment in the number of dimensions. The both diameter and the degree of the graph in Hypercube topology are as equal as the number of dimensions. Accordingly, greater degree leads to more neighbors, which makes the access to other nodes easier; however, it also leads to generating more messages for search and any other network operation. As the result, the traffic of the network increases while obviously there is a trade-off between the control traffic and the access space in the network. The other considerable Hypercube property is its optimal routing algorithm.

At the initialization phase of the network, network administrator sets the number of Hypercube dimensions and then arrange the position of the first set of nodes, i.e. network starting nodes, on the overlay layer. The position of each node is chosen according to the RTT between the starting nodes. The nodes with lower RTT in between are placed close to each other. While these simple steps are forming the initialization phase of the network, the new node joins the network as follows.

The new node broadcasts a message to notify all of its neighboring nodes, far away just one physical hop. Time to live (TTL) is used as a bound to limit the propagation. If the new node does not receive any response until a specific timeout, the TTL is increased by one and the operation is continued until the first response. It is worth mentioning that, since each P2P network uses a specific port to send its control messages, just the joined nodes are able to receive such a message. Hence, the responding node is probably the nearest physical node to the new node. Accordingly, we propose to place the new node beside the responder node in the overlay network. It means that the overlay addresses of the two nodes have to differ by just one bit. To assign addresses, the least significant bit is flipped and the new address is checked for whether it is assigned previously to a node. In the negative case, the address is assigned to the new node. Otherwise, the changed bit is reset and the next bit is flipped. This process continues until an address is assigned to the new node.

When the new node joins the network, it calculates the RTT among itself and all other nodes that are placed in one or two hops away in the overlay network. This operation is used to update the position of nodes. For two neighbor nodes, if RTT of one node is less than the other, these two nodes are swapped. For example, in the 3-D Hypercube that is illustrated in Figure 2, one message is sent by node A to neighbor nodes with one or two hops distances and calculates RTT for each node. RTT between node A and node B is $7ms$, and between node A and node C is $6ms$. Therefore, node B and node C are displaced with each other. RTT between node A and node E is less than RTT between node A and node B, however, they are not swapped because they are not in the same direction. Although node E is the second node but not the second one in the direction of node B. This process is further repeated for any node that gets new overlay address. To avoid possible falling in loop and infinite repetition of this procedure, each node has to hold its state. The pseudo-code of the solution is represented in Algorithm 1.

Figure 2. Instance of 3-D Hypercube and routing presentation [13].

As mentioned above, the routing algorithm in Hypercube is optimal. In this algorithm, the least significant bits of the source and destination addresses are compared. If the bits are different, the message is routed in the dimension of that bit. The same procedure is done for the all bits, one by one, until the all bits are checked and the message is delivered to the destination. It is further worthy to mention that, unlike most of the well-known P2P networks, there is not any cost for leaving the network in the proposed solution, due to the repetitive checks of nodes to their neighbors.

4.2. Cube Connected Cycle Based Overlay Network

A CCC graph is constructed from a x-dimension Hypercube graph in which each node is replaced by an x node Ring. In this topology, each node has a coordinate address represented with two numbers $(p,q)$, while $0<p<x-1$ and $0<q<2^x-1$. As stated above, CCC has also an optimal routing algorithm and benefits from a fixed and small degree, exactly equal to 3, for any number of nodes.

While the general locality solution for CCC is as the same as that of Hypercube, the optimal routing algorithm is as follows. At first, the second element of the source and destination addresses are compared. Each q element contains x bit binary digits. If q is the same in both nodes, then p elements are compared. A difference in p elements means a difference in the dimension of two nodes. Therefore, to reach the destination node, the path must be moved on the Ring to change the dimension. When the p elements become equal to each other, then the q elements have to be compared. If q values are not equal in both addresses, the corresponding dimension’s bit of q is compared between the source and destination addresses. If they are not equal, the source bit is flipped to become equal to that of the destination. Otherwise, the bit stays as it is. At the next step, the other bits of the parameter q for the next dimensions have to be compared. When the q elements of both addresses become equal, the destination is already reached.

Algorithm 1: SLoPCloud $(d,\aleph ,\theta )$

1: Start the initialization phase of the network by network admin. 2: Form the overlay topology by considering the number of Hypercube dimensions, i.e. d. 3: Arrange the position of the first set of nodes, i.e. ℵ, on the overlay layer as the nodes with lower RTT are placed close to each other. 4: Start the process of joining new nodes. 5: A new node joins the network. 6: repeat 7:  The new node broadcasts a message to notify all of its neighboring nodes, far away based on TTL. 8:  Wait for a specific timeout, $\theta$. 9:  if no response is received, then 10:   Increase TTL by one. 11:  end if 12: until The first response is received. 13: Start to assign addresses to the new node, beside the responder. 14: Consider the address of the responder. 15: repeat 16:  Flip the least significant bit 17:  if The new address is not assigned previously, then 18:   The address is assigned to the new node 19:  else 20:   The changed bit is reset and the next bit is flipped. 21:  end if 22: until An address is assigned to the new node. 23: for all nodes j that are placed in one or two hops away from the newly joined node, in the overlay network. do 24:  calculates the RTT among node j and the new node. 25: end for 26: while there are still two neighboring nodes in which the RTT of the far away node is less than the more closer one, do 27:  for all two neighbor nodes i and j do 28:   if RTT of one node is less than the other, swap these two nodes. 29:  end for 30: end while 31: return 0

Consider an example of the 3-dimension CCC as stated in Figure 3) while $p\in \{0,1,2\}$ and $q\in \{000,\dots ,111\}$. Consider nodes $S:(2,010)$ and $D:(1,111)$ as the source node and the destination node, respectively. First, by comparing the q elements we realized that the source node is at the second dimension, i.e., $(p=2)$, while the second bits are not as the same. Therefore, q element of S becomes 110 and p element does not change. Then, the dimension is increased by one and becomes zero in modulus of 3, i.e., $p=(2+1)\%3=0$. The least significant bits are different, therefore q element changes to 111 while p remains 0. At the next step, we have to change the value of the dimension, i.e., p, to 1. Now the source and destination are both at the same dimension and their q elements are equal. The overall flow of routing, starting from the source node S and terminating at the destination node D is as follows.

$$(2,010)\to (2,110)\to (0,110)\to (0,111)\to (1,111)$$

Figure 3. Routing presentation in Cube Connected Cycle.

The same as the solution for the Hypercube topology, the new node has to find at least a joining node through broadcast. The new node address becomes the neighborhood of the found node. Hence, the address of the new node has to have one unit difference in p or one bit flapping in the pth bit of q. For example, for node $A:(0,000)$, the neighbors are $(1,000),(2,000)$ and $(0,001)$. The update and leave operations are as the same as those of Hypercube topology.

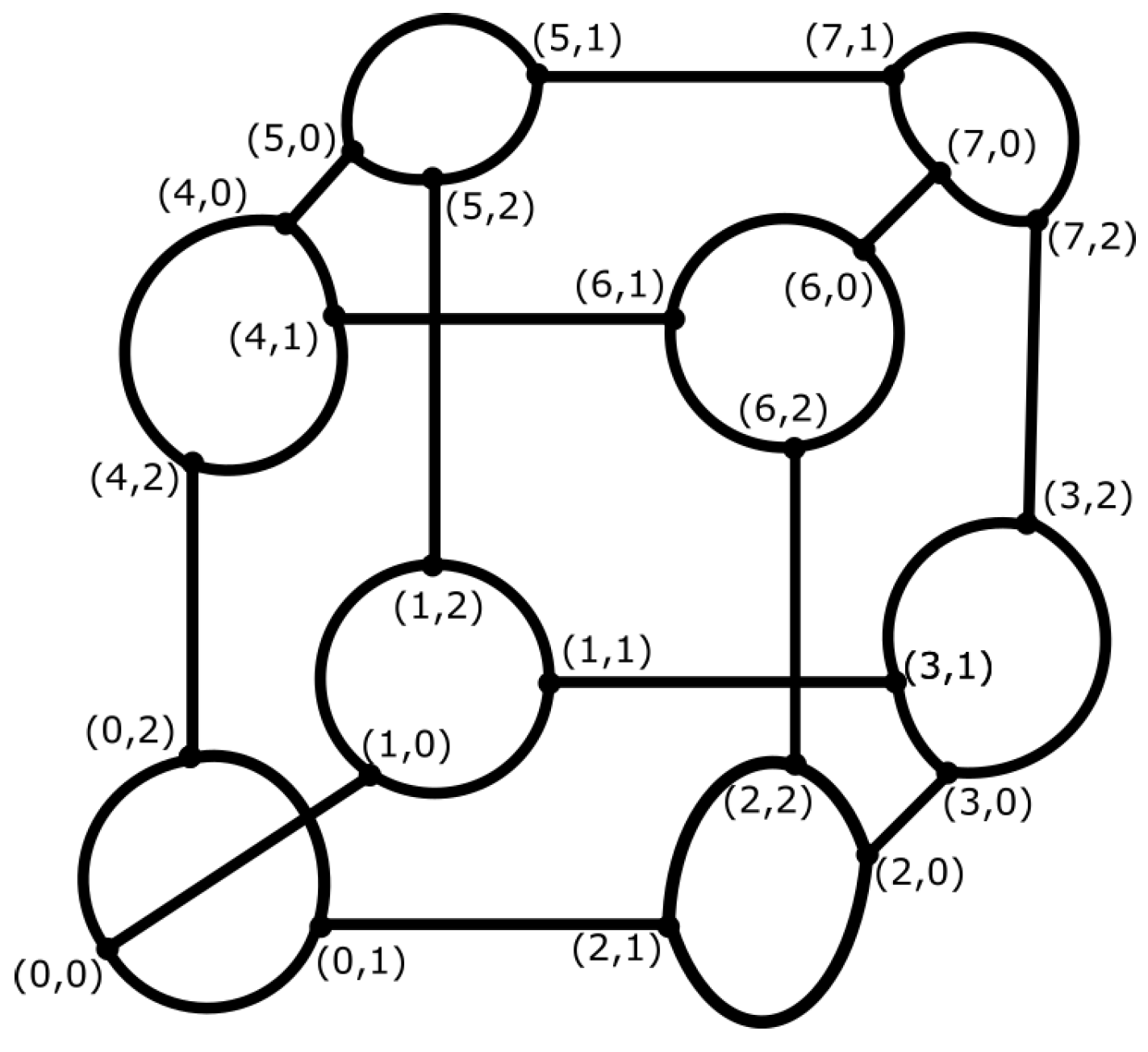
4.3. Generalized Hypercube Connected Cycle Overlay Network

Generalized Hypercube Connected Cycle (GHCC) is a composite graph, defined with a pair of parameters l and m and represented as $GHCC(l,m)$ [46]. This topology has suitable characteristics which attract our attention to consider it as an overlay graph. GHCC graph characteristics are listed in the following, while Table 1 represents the notations along with their brief description.

Table 1. Table of notations.

d	Number of Overlay Topology Dimensions
ℵ	The set of starting nodes
$\theta$	The timeout threshold
N	Number of network nodes
D	Diameter of the graph
$\delta$	Degree of the graph
l	GHCC parameter representing number of levels
m	GHCC parameter
$(p;u_{l-1}{u}_{l-2}···u_1{u}_0)$	Representation of a node in GHCC
p	Level number of the node in GHCC
$u_{l-1}{u}_{l-2}···u_1{u}_0$	String node index in level p
$(p,n)$	Another representation of a node in GHCC
n	Decimal node index in level p

(i)

Total number of nodes in the graph is represented by N.

(ii)

l and m are the parameters of the graph, where $N=l{m}^l$.

(iii)

The nodes of the graph are divided into l levels, which are numbered as $0,1,\dots ,l-1$, and each level consists of $m^l$ nodes.

(iv)

Specification of each node:

(a)

All nodes in one level are numbered by a variable in a range from 0 to $m^l-1$. This variable is called the index of a node in the specific level. The index is displayed by a string with l literals and each literal has a value from 0 to $m-1$.

(b)

Another literal is used to identify different levels of nodes. It is in the range of 0 to $l-1$.

Here is an example of representing a node in GHCC (l,m). The ordered set of literals $(p;u_{l-1}{u}_{l-2}···u_1{u}_0)$ is used where p indicates the number of levels, $0\le p\le l-1$, and the string $u_{l-1}{u}_{l-2}···u_1{u}_0$ represents the index of a node in level p. Thus, p is l-valued while $u_i$s are m-valued. There is also another way to display a node, which is a two-tuple $(p,n)$ form, where p is the number of level and n is the index such that $n={\sum }_{i=0}^{l-1}{u}_i\times m^i$.

(v)

There are two kinds of links in this topology, inter-level and intra-level links, which are defined as follows:

(a)

Inter-level links:l nodes with different levels and same indices are distributed in the network. These l nodes are connected in a way that forms a Ring. The links between these nodes are called inter-level links. For example, if we consider a node $(p;u_{l-1}{u}_{l-2}···u_1{u}_0)$, it is connected to two other nodes in adjacent levels, $((p\pm 1);u_{l-1}{u}_{l-2}···u_1{u}_0)$. Consider that all additions and subtractions are in the modulus l. There are $m^l$ cycles in the graph which are constructed by inter-level links. Each cycle consists of l nodes.

(b)

Intra-level links: There are some other links which connect nodes in the same level. Node $(p;u_{l-1}{u}_{l-2}···u_{p+1}{u}_p{u}_{p-1}···u_1{u}_0)$ is connected to $m-1$ other nodes $(p;u_{l-1}{u}_{l-2}···u_{p+1}{\overline{u}}_p{u}_{p-1}···u_1{u}_0)$ through clique edges, where ${\overline{u}}_p$ signifies all values of the corresponding literal which is in the range of 0 to $m-1$, excluding the value $u_p$. The intra-level links form $m^{l-1}$ number of disjoint cliques in each level, each clique is with the size of m.

(vi)

Since there are $m-1$ inter-level links and two intra-level links emerging from each node, the degree of the graph is $m+1$.

(vii)

As is obvious, the graph is symmetric.

GHCC is a composite topology, a combination of a Ring, a complete graph and a Hypercube. The nodes in one clique form a complete graph, while the nodes with the same node-index in different levels form a Ring. GHCC could be also formed as other topologies by choosing different values for l and m. For example, for $m=2$, the resulting topology will be a CCC graph with $l\times 2^l$ nodes. For $m=1$, the topology is reduced to a simple Ring while for $l=1$ the resulting topology is complete graph. Figure 4, shows a GHCC graph with parameters $m=3$ and $l=3$. In this figure, the nodes at different levels are in separate columns, and each dotted box is a cliques.

Figure 4. An instance of Generalized Hypercube Connected Cycle with parameters $l=3$ and $m=3$, i.e. GHCC (3,3) [46].

As mentioned earlier, using GHCC graph as overlay topology provides to choose any two out of three parameters N, $\delta$ and D, independently. For example, given the two design parameters D and $\delta$, it is easy to find the appropriate values for m and l to form a network with the size of $N=l\times m^l$. As an other instance, we can fix the values of N and $\delta$, and find appropriate values for l and m in such a way that $l\times m^l\ge N$ and the degree is $\delta$. The diameter of this graph is then calculable as the following [46].

$$D=\lfloor \frac{5l}{2}\rfloor -2,forl\ge 4,m\ne 1andD=\lfloor \frac{5l}{2}\rfloor -1,forl\le 3,m\ne 1$$

SLoPCloud algorithm on the GHCC topology is implemented the same way as on the Hypercube and CCC topologies. Network administrator chooses the appropriate values for parameters l and m. The starting nodes then placed close to each other according to the RTT in between. The network then starts to work. A new node to join the network should start to broadcast a join request message limited by the TTL. After receiving the first response, the new node tries to find an empty position in the neighborhood of the responder node, in the overlay network. Then, the new node calculates the RTT among itself and the neighbors to update the positions. Similar to Hypercube and CCC topologies, there also exists an optimal routing algorithm for GHCC topology. Describing the optimal routing of GHCC is out of the scope of this paper, hence we refer the interested researchers to read the detailed optimal routing algorithm of GHCC in [49].

5. Experimental Results

We conducted experiments to assess the performance of the proposed solution, i.e., SLoPCloud. The proposed solution was simulated using PlanetSim network simulator [50]. This simulator is an overlay network simulation framework written in Java, and provides an easy transition from simulation code to prototypes by providing wrapper scripts. It is worth noting that PlanetSim includes a trivial P2P simulation framework. It supports static visualizations with GML or Pajek outputs of network topologies. It is an event-based simulator, which uses a time-stepped method, i.e., there is a central clock that controls the events in a simulation.

We implemented SLoPCloud solution on GHCC, whereas we considered the Ring, Hypercube, and CCC as the overlay networks. While SLoPCloud can be applied to any overlay network, different overlays are considered by changing the GHCC parameters. The focus of our work was on the network bootstrapping time and control traffic. Network bootstrapping time is the time required for the initialization process and measured by second. The number of control messages was also measured to represent the traffic overhead of the proposed solution.

It is worth mentioning that different scenarios with different number of nodes ranging from 10 to ${10}^4$ nodes were conducted to show the scalability of the proposed solution. Each simulation scenario was run several times and the reported results are the average of the output values. We first simulated a simple Hypercube overlay without considering the locality problem, and then compared it with a Hypercube overlay in which our locality solution is implemented on. We refer to them as simple Hypercube and locality-aware Hypercube, respectively. Figure 5 illustrates the comparison between the control traffic of the both mentioned scenarios for different number of nodes. The control traffic imposed on the network by the SLoPCloud solution is negligible. This value for the network with ${10}^4$ nodes is less than $\frac{1}{{10}^4}$ of the control traffic generated without considering the locality problem.

Figure 5. A comparison between the control traffic of simple Hypercube and locality-aware Hypercube.

While Figure 5 shows that the imposed control traffic by the SLoPCloud solution is negligible, Figure 6 represents a comparison between different overlay topologies, implementing SLoPCloud solution. The control traffic represented in Figure 6 is measured by the number of sent control packets, for Ring, Hypercube, and CCC topologies. Clearly, the overlay topology does not have an eminent effect on the control traffic.

Figure 6. The comparison of control traffic for different overlay topologies, using SLoPCloud.

The next investigated parameter was the bootstrapping time, i.e. the time required for the network to start its functionality. Figure 7 represents this time measured in second, for different number of nodes. To investigate the effect of SLoPCloud on this parameter, this figure represents the results for a simple Hypercube and locality-aware Hypercube. Obviously, although the SLoPCloud increases the bootstrapping time, the delay imposed by SLoPCloud seems to be acceptable. For instance, this value for a network with ${10}^4$ nodes is about $0.5\%$ of the network bootstrapping time for a network that does not consider the locality problem.

Figure 7. A comparison between the network bootstrapping time for a network with simple Hypercube versus locality-aware Hypercube overlay.

The same parameter, i.e., network bootstrapping time, was calculated and compared between Hypercube, Ring, and CCC topologies, all with the presence of SLoPCloud. Figure 8 represents the results for different number of nodes. Clearly, CCC and Ring represent almost close results to each other, however, Hypercube shows an obvious better performance. The main reason is owing to the number of neighboring nodes in different overlay topologies. While the neighboring nodes for Ring and CCC are fixed and equal to two and three, respectively, it is equal to the number of dimensions in Hypercube overlay. More neighboring nodes leads to faster neighbor checking for the repositioning operation. It is worth mentioning that more neighboring nodes may lead to higher traffic in broadcast operation.

Figure 8. A comparison between the network bootstrapping time for different overlay topology, using SLoPCloud.

Table 2 represents a sample of a brief comparison for the results of the network with ${10}^4$ nodes. This table represents both network bootstrapping time and network bootstrapping control traffic for different overlays. Furthermore, to verify the efficiency of our solution, we fixed the incoming and outgoing queues of each node and run the simulation for a network with one million nodes. While the results are not represented here, there are no significant impacts on the pattern of reported results.

Table 2. Network bootstrapping time and traffic for different overlays, each overlay by ${10}^4$ nodes.

Overlay	Bootstrapping Time (Sec)	Bootstrapping Control Traffic (# of Packets)
Simple Hypercube	$193.74$	$21,739,304$
Locality Aware Hypercube	$210.35$	$21,760,842$
Locality Aware Cube connected cycle	$452.29$	$21,762,639$
Locality Aware Ring	$472.53$	$21,764,176$

6. Conclusions

P2P cloud systems have become an attractive area of research in recent years. Such systems, similar to any other P2P network, consist of two layers, overlay and physical layer. Locality problem, the mismatch between overlay and physical layer of P2P cloud systems, may lead to bandwidth waste and network delay. In this paper, a solution for locality problem is proposed to put the physically closer nodes beside each other, in overlay network. The proposed solution is an extension of our previously published works, extended to be a general solution applicable on P2P cloud systems. While the proposed solution considers RTT as the metric of distance, it is generally proposed to be able to be applied on the existing P2P systems. For this reason, GHCC is suggested to be the topology of the overlay. The proposed solution is then supported with comprehensive simulation to verify its applicability. The main concern about the proposed solution is the delay and control traffic caused by the proposed solution. Simulation results show that the imposed traffic is negligible, while the delay is very low. The wide range of simulated network sizes is a further validation of the scalability of the proposed solution. Since GHCC could be reshaped to many other well known topologies, the formal analysis of its parameters, such as traffic overhead and delay, could be considered as a general formal analysis of many topologies. We propose the mentioned interesting analysis as a future work of this paper. Furthermore, experimental analysis on the data of real existed P2P cloud systems could represent interesting results, which could be considered as another future work.