Total Coloring Conjecture for Certain Classes of Graphs

Abstract

A total coloring of a graph G is an assignment of colors to the elements of the graph G such that no two adjacent or incident elements receive the same color. The total chromatic number of a graph G, denoted by ${\chi }^{″}\left(G\right)$, is the minimum number of colors that suffice in a total coloring. Behzad and Vizing conjectured that for any graph G, $\Delta \left(G\right)+1\le {\chi }^{″}\left(G\right)\le \Delta \left(G\right)+2$, where $\Delta \left(G\right)$ is the maximum degree of G. In this paper, we prove the total coloring conjecture for certain classes of graphs of deleted lexicographic product, line graph and double graph.

1. Introduction

All the graphs in this paper are finite, simple and connected. The edge chromatic number of a graph G, denoted by ${\chi }^{\prime }\left(G\right)$, is the smallest number of colors needed to color the edges of G so that no two adjacent edges share the same color. For any graph G, it clear that from the Vizing’s theorem that the edge chromatic number ${\chi }^{\prime }\left(G\right)\le \Delta \left(G\right)+1$, where $\Delta \left(G\right)$ is the maximum degree of G. If ${\chi }^{\prime }\left(G\right)=\Delta \left(G\right)$ then G is called class-I graph and if ${\chi }^{\prime }\left(G\right)=\Delta \left(G\right)+1$ then G is called class-II graph. For example, $K_{2n}$ is class-I where as $K_{2n+1}$ is class-II. Also, any bipartite graph is class-I. In a proper total coloring, any two elements that are either adjacent or incident are assigned different colors. The minimum number of colors needed for a proper total coloring is the total chromatic number of G, denoted by ${\chi }^{″}\left(G\right)$. Behzad [1,2] and Vizing [3] conjectured [also called as the Total Coloring Conjecture (TCC)] that for any graph G the following inequality holds: $\Delta \left(G\right)+1\le {\chi }^{″}\left(G\right)\le \Delta \left(G\right)+2$. The lower bound is clearly the best possible. A graph G is said to total colorable if it satisfies TCC. If a graph G is total colorable with $\Delta \left(G\right)+1$ colors then the graph is called type-I, and if it is total colorable with $\Delta \left(G\right)+2$ colors, then it is type - II. McDiarmind and S$\acute{\mathrm{a}}$nchez-Arroyo [4] proved that determining the total chromatic number is NP-hard even for $\mu$-regular bipartite graphs, for each fixed $\mu \ge 3$.

Graph products were first defined by Sabidussi [5] and Vizing [6]. A lot of work was done on various topics related to graph products, but on the other hand there are still many open questions. The TCC was verified for graph products, such as Cartesian and Direct products, of certain classes of graphs. The TCC holds for Cartesian product graphs G and H, if the TCC holds for each of the graphs G and H. Seoud [7,8] proved that the Cartesian product graphs $P_m\square P_n$, $m,n\ge 2$, except $P_2\square P_2$ are of type I. Campos and de Mello [9] determined the total chromatic number of some bipartite graphs. The equitable total chromatic number of a graph G is the smallest integer $\mu$ for which G has a total $\mu$-coloring such that the number of elements of any two colors differs by at most one. Tong et al. [10] showed that equitable total chromatic number of $C_m\square C_n$ is $\Delta (C_m\square C_n)$ + 1. Pranaver and Zmazek [11] proved that ${\chi }^{″}(P_m\times P_n)$ and ${\chi }^{″}(C_m\times P_n)$ are 5. Geetha and Somasundaram [12] proved the TCC for generalized Sierpi$\acute{\mathrm{n}}$ski graphs. A survey on graph coloring for its types, methods and applications are given in [13]. Recently [14] it is proved that the graphs $K_n\times K_n$, $C_m\times C_n$ and $G⊠H$ are type-I graphs, where G is any bipartite graph. Mohan et al. [15] proved that certain classes of Corona product graphs are type-I. In [16], they also proved the TCC for certain classes of product graphs.

In this paper, we prove the TCC for certain classes of deleted lexicographic product. We obtain results on the total chromatic number for line graphs, which is a subclass of claw-free graphs. Also we obtain the total chromatic number for double graphs. The following theorems are due to Yap [17].

Theorem 1.

For any complete graph $K_n$, ${\chi }^{″}\left(K_n\right)=\left\{\begin{array}{cc}n,\hfill & ifnisodd\hfill \\ n+1,\hfill & ifniseven.\hfill \end{array}\right.$

Theorem 2.

For any cycle $C_n$, ${\chi }^{″}\left(C_n\right)=\left\{\begin{array}{cc}\Delta \left(G\right)+1,\hfill & ifn\equiv 0\left(mod3\right)\hfill \\ \Delta \left(G\right)+2,\hfill & otherwie.\hfill \end{array}\right.$

Theorem 3.

For any complete bipartite $K_{m,n}$, ${\chi }^{″}\left(G\right)=\left\{\begin{array}{cc}\Delta \left(G\right)+1,\hfill & ifn\ne m\hfill \\ \Delta \left(G\right)+2,\hfill & ifn=m.\hfill \end{array}\right.$

2. Deleted Lexicographic Product

Let G and H be two graphs. The lexicographic product [18,19] of graphs G and H is the graph $G\circ H$ whose vertex set is $V\left(G\right)\times V\left(H\right)$, and for which $((g,h),(g^{\prime },h^{\prime }))$ is an edge of $G\circ H$ precisely if $(g,g^{\prime })\in E\left(G\right)$, or $g=g^{\prime }$ and $(h,h^{\prime })\in E\left(H\right)$. The lexicographic product is also known as graph $substitution$, a name that bears witness to the fact that $G\circ H$ can be obtained from G by substituting a copy $H_g$ of H for every vertex g of G and then joining all vertices of $H_g$ with all vertices of $H_{g^{\prime }}$ if $(g,g^{\prime })\in E\left(G\right)$. The lexicographic product is associative but not commutative. The total coloring of some classes of lexicographic product graph were discussed in [14]. For example it is proved that $K_m\circ K_n\cong K_{mn}$ is type-I if m and n are odd other wise type-II.

The deleted lexicographic product [19] of two graphs G and H, denoted by $D_{lex}$ $(G,H)$, is a graph with the vertex set $V\left(G\right)\times V\left(H\right)$ and the edge set $\{((g,h),(g^{\prime },h^{\prime })):(g,g^{\prime })\in E\left(G\right)$ and $h\ne h^{\prime }$, or $(h,h^{\prime })\in E\left(H\right)$ and $g=g^{\prime }\}$. Similar to lexicographic product, $D_{lex}(G,H)$ and $D_{lex}(H,G)$ are not necessarily isomorphic. 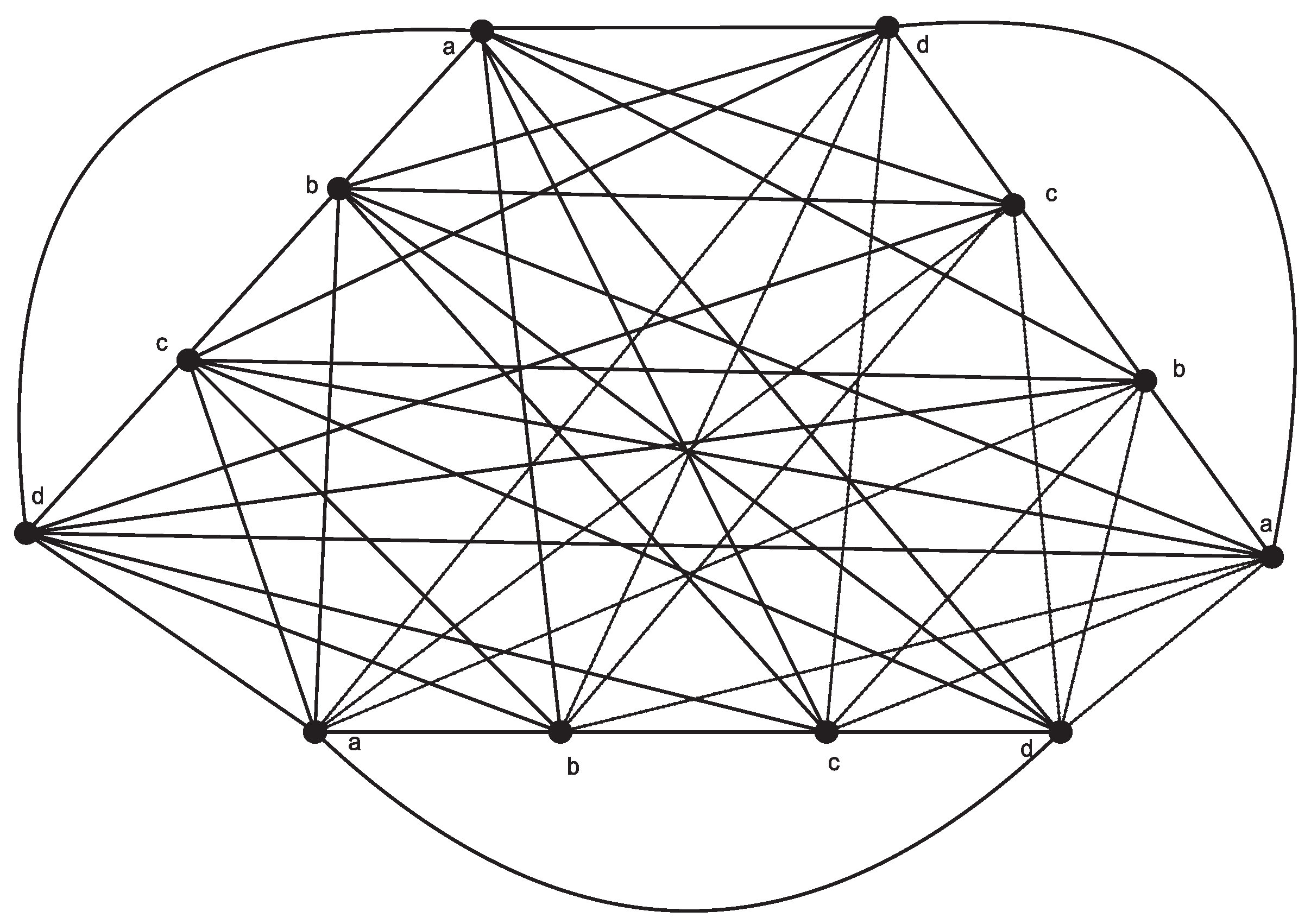Figure 1 shows the graph $D_{lex}(C_3,C_4)$. Please note that $D_{lex}(G,H)=G\circ H\backslash kG$, where $kG$ denotes the graph consisting of k vertex disjoint copies of G and $G\circ H\backslash kG$ denotes the deletion of $kG$ from $G\circ H$.

The join of two graphs G and H, denoted as $G\vee H$, is obtained by taking G and H, and adding edges between every vertex of G to every vertex of H. Let G and H be two graphs with m and n vertices respectively. $D_{lex}(G,H)$ can be obtained from G by substituting a copy $H_u$ of H for every vertex u of G and then joining all vertices h of $H_u$ with all vertices $h^{\prime }$ of $H_v$ if $h\ne h^{\prime }$ and $(u,v)\in E\left(G\right)$. The maximum degree (of this graph) is $\Delta \left(D_{lex}(G,H)\right)=\Delta \left(H\right)+(n-1)\Delta \left(G\right)$. It is easy to see that $D_{lex}(P_1,G)\cong G$.

Theorem 4.

For any total colorable graph G, $K_2\circ G$ is total colorable.

Proof. 

The graph $K_2\circ G\cong G\vee G$ [14]. Denote the two copies of G by $G_1$ and $G_2$. The maximum degree of $G\vee G$ is $\Delta (G\vee G)=\Delta \left(G\right)+n$, where n is the order of G. Color the elements (vertices and edges) of $G_1$ using colors $1,\dots \Delta \left(G\right)+2$. Assign n new colors to the vertices of $G_2$ and color the edges of $G_2$ as the edge coloring of $G_1$. Here, the corresponding vertices in $G_1$ and $G_2$ have common missing colors from $\{1,\dots ,\Delta (G)+2\}$. Now, assign a common missing color to the edges (all edges together give one 1-factor of $G\vee G$) between the corresponding vertices. At each vertex in $G_2$, there are $n-1$ available colors among the n vertex colors and using these available colors we color the remaining join edges between $G_1$ and $G_2$. □

The above theorem can be extended to any bipartite graph.

Corollary 1.

Let G be a bipartite graph and H be a total colorable graph then $G\circ H$ is total colorable.

Proof. 

Let us consider the graph $G\circ H$, where G is bipartite. Let X and Y be the two vertex partitions of G. Color all the elements of the layer $H_x$ for all $x\in X$ as $H_0$ and all the elements of $H_y$ for all $y\in Y$ as $H_1$. Please note that all the vertices of $G\circ H$ are properly colored.

Since G is bipartite, the edges of G can be colored with $\Delta \left(G\right)$ colors. Moreover, in any edge coloring of G with $\Delta \left(G\right)$ colors each major vertex (vertex with maximum degree) is incident with an edge of each color. Consider the set F of all edges of G of an arbitrary fixed color. For each edge $xy\in F$ color the edges between $H_x$ and $H_y$ in $G\circ H$ as in $K_2\circ H$.

So far, $\left|F\right|$ copies of $K_2\circ H$ and the remaining $\left|V\left(G\right)\right|-2\left|F\right|$ layers $H_y$ are colored in $G\circ H$ using at most $\Delta (K_2\circ H)+2$ colors. The uncolored edges induce a bipartite graph of maximum degree $\Delta (G\circ H)-\Delta (K_2\circ H)=n(\Delta \left(G\right)-1)$ which implies that they can be colored with this number of additional colors. Hence ${\chi }^{″}(G\circ H)\le \Delta (K_2\circ H)+2+n(\Delta \left(G\right)-1)=\Delta (G\circ H)+2$. Therefore TCC holds for $G\circ H$. □

The above theorem and corollary can be extended to deleted lexicographic product. In the following theorem, we prove the total coloring conjecture for deleted lexicographic product of two large classes of graphs.

Theorem 5.

For any class-I graph G and a graph H with at least 3 vertices, $D_{lex}(G,H)$ is total colorable. In particular, if H is class-I then $D_{lex}(G,H)$ is also type-I.

Proof. 

Let H be a graph with n vertices, $n\ge 3$. The maximum degree of $D_{lex}(G,H)$ is $\Delta \left(D_{lex}(G,H)\right)=\Delta \left(H\right)+(n-1)\Delta \left(G\right)$. Assign $\Delta \left(H\right)+1$ colors to the edges and n colors to all the vertices of all the copies of H. Now, each edge $(u,v)$ in G gives a set of join edges between the copies $H_u$ and $H_v$. Since G is class-I graph, the edges are partitioned into $\Delta \left(G\right)$ independent sets. Correspondingly, the join edges between the copies of H are partitioned into $\Delta \left(G\right)$ sets $P_1,P_2,\dots ,P_{\Delta \left(G\right)}$.

Since $n\ge 3$, there are $n-1$ available colors at each vertex in each copy of H. Using these available colors we color the join edges in $P_1$ and using the remaining $(n-1)(\Delta (G)-1)$ unused colors, we color the join edges in the remaining partitions. This is same as problem of finding a perfect rainbow matching in $K_{n,n}$ [20]. Therefore we used $\Delta \left(H\right)+1+n+(n-1)(\Delta \left(G\right)-1)=\Delta \left(D_{lex}(G,H)\right)+2$ colors for the total coloring of $D_{lex}(G,H)$. Hence $D_{lex}(G,H)$ satisfy the TCC.

If H is class-I then assign $\Delta \left(H\right)$ colors to the edges in all the copies of H and remaining elements are colored as in above. Therefore $D_{lex}(G,H)$ is type-I. □

We know that any bipartite graph is class-I and any regular graph with even order is also class-I. Based on these facts, we have the following two corollaries.

Corollary 2.

For any bipartite graph G and a graph H with at least 3 vertices, $D_{lex}(G,H)$ is total colorable. In particular, if H is class-I then $D_{lex}(G,H)$ is type-I.

Corollary 3.

If G is a regular graph with even order and H is any graph with at least 3 vertices then $D_{lex}(G,H)$ is total colorable. In particular, if H is class-I then $D_{lex}(G,H)$ is type-I.

In Theorem 5, we can obtain the tight bound for certain classes of G. For example, it is easy to see that $D_{lex}(P_2,P_n)$ is type-I graph. Also, in Theorem 5 either G or H must have at least three vertices. For example, we know that $P_2$ is class-I graph and $D_{lex}(P_2,P_2)\cong C_4$ and $C_4$ is type-II (see Theorem 2).

There are classes of graphs G and H such that $D_{lex}(G,H)$ may be type-II. For example, consider the graph $D_{lex}(P_2,C_{2n+1})$, $n\ge 3$, $D_{lex}(P_2,C_{2n+1})\cong C_{2n+1}\vee C_{2n+1}-F$, where F is the one factor $\left\{(u_i,u_i)\right|i=1,2,\dots ,2n+1\}$. Here the maximum degree is $2(n+1)$. Vertices in each cycles are colored with $2n+1$ colors and the join edges are colored with the same $2n+1$ colors with a proper permuation of colors. Also, the edge colorings of any odd cycle requires 3 colors. Therefore $2n+3$ colors are not sufficient to color the elements of $D_{lex}(P_2,C_{2n+1})$. Hence $D_{lex}(P_2,C_{2n+1})$ is type-II.

It is easy to prove that $D_{lex}(P_2,C_{2n})$ is type-I since the edge colorings of any even cycle requires only 2 colors. In the following theorem, we prove that $D_{lex}(P_m,H)$ is type-I for any graph H.

Theorem 6.

For any graph H, $D_{lex}(P_m,H),m\ge 3$, is type-I.

Proof. 

The assertion is obvious if H has at most 2 vertices. If $H\cong K_1$ then the graph is empty, if $H\cong 2K_1$ the graph is $2P_m$, and if $H\cong K_2$ then the graph is a ladder graph. Hence let H be a graph with n vertices, $n\ge 3$. Here, $\Delta \left(D_{lex}(P_m,H)\right)=\Delta \left(H\right)+2(n-1)$. We know that $P_m$ is class-I graph. Suppose H is class-I then from the Theorem 5 $D_{lex}(P_m,H)$ is type-I.

Suppose H is class-II then assign $\Delta \left(H\right)+1$ colors to all the edges of odd copies of H and assign n colors to all the vertices in all copies of H. Permute the edge colorings of the odd copies and assign to even copies of H. Now, we can find a one to one mapping between the vertices of odd and even copies such that the mapping vertices have a same missing color. We assign these missing colors to the mapping edges. Still there are $n-2$ unused colors. Using these unused colors and missing colors we color the edges between odd and even copies of H. Since the vertices are colored with n colors, $n\ge 3$, at each vertex there are $n-1$ colors available and using these available colors we color the join edges between even and odd copies of H. Hence we used $\Delta \left(H\right)+1+n+(n-2)=\Delta \left(D_{lex}(P_m,H)\right)+1$. □

Note: The above theorem is also holds good if we replace the path with any even cycles. Consider the two graphs G and H with m and n vertices respectively. If $D_{lex}(G,\overline{K_n})$ has a total coloring with $\Delta \left(G\right)+1$ colors such that the vertices of each $\overline{K_n}$ copy are colored pairwise distinctly and $D_{lex}(G,H)$ is total colorable. This can be proved very easily. $D_{lex}(G,\overline{K_n})=D_{lex}(G,H)\backslash mH$, where $mH$ denotes the edges in the m copies of H. Color all the edges in m copies of H with $\Delta \left(H\right)+1$ colors and color all the elements of $D_{lex}(G,\overline{K_n})$ with $(n-1)\Delta \left(G\right)+1$ colors. This will give a total coloring of $D_{lex}(G,H)$.

3. Line Graphs and Double Graphs

A graph G is said to be claw-free if it does not contain an induced subgraph that is isomorphic to $K_{1,3}$. There are several well-known and important families of graphs that are also claw-free [21]. We consider classes of claw-free graphs, Line graphs is classes of claw-free graphs. Many characterizations of claw-free graphs where given in [21]. There are several well-known and important families of graphs that are also claw-free. Complement of triangle-free graphs, Inflation of a graph, Comparability graphs, Generalized line graphs. In this section, we considered one classes of claw-free graphs.

Line Graphs

The line graph of G, denoted by $L\left(G\right)$, has the set $E\left(G\right)$ as its vertex set and two distinct vertices $e_1,e_2\in V\left(L\left(G\right)\right)$ are adjacent if and only if they share a common vertex in G. Characterization of line graphs are given in [22] including a forbidden subgraph characterization. Figure 2 shows the line graph of $K_4$ and a total coloring with 5 colors. The following are easy observations: (i). We know that the line graph of a path of length m is again a path of length $m-1$ and the line graph of a cycle is again a cycle of the same length. Therefore, it is easy to find the total chromatic number for $L\left(P_n\right)$ and $L\left(C_n\right)$ (see Theorem 2). (ii). A complete bipartite graph is not always type-I (see Theorem 3). We know that $L\left(K_{m,n}\right)\cong K_m\square K_n$ and $K_m\square K_n$ is type-I if n and m are even and $m\ge n\ge 4,m\equiv 0$ (mod 4) or $m>n\ge 4,m\equiv 2$ (mod 4) and $K_m\square K_n$ is type-II if m is even and n is odd and $m>{(n-1)}^2$ [23,24]. The TCC is open for other cases.

Theorem 7.

For $n\le 4$, ${\chi }^{″}\left(L\left(K_n\right)\right)=\Delta \left(L\left(K_n\right)\right)+1$.

Proof. 

For $n=2$, $L\left(K_2\right)=K_1$ and ${\chi }^{″}\left(K_1\right)=\Delta \left(K_1\right)+1$. And $n=3$, $L\left(K_3\right)\cong K_3$, ${\chi }^{″}\left(K_3\right)=\Delta \left(K_3\right)+1$.

Also, ${\chi }^{″}\left(L\left(K_4\right)\right)=\Delta \left(L\left(K_4\right)\right)+1$. The total coloring of $L\left(K_4\right)$ is given in Figure 2. □

From the Theorem 1, we know that $K_n$ is type-I if n is odd and it is type-II if n is even. We believe that $L\left(K_n\right)$ is always type-I. In this regard, we proposed the following conjecture.

Conjecture: For any complete graph $K_n$, ${\chi }^{″}\left(L\left(K_n\right)\right)=2n-3$.

The double graph $D\left(G\right)$ of a given graph G is constructed by making two copies of G (including the initial edge set of each) and adding edges $\left(\right(u,1),(v,2\left)\right)$ and $\left(\right(v,1),(u,2\left)\right)$ for every edge $uv$ of G. Munarini et al. [25] studied various properties of double graphs.

Theorem 8.

For any total colorable graph G,${\chi }^{″}\left(D\left(G\right)\right)\left\{\begin{array}{cc}=\Delta \left(D\right(G\left)\right)+1\hfill & ifGistypeI\hfill \\ \le \Delta \left(D\right(G\left)\right)+2\hfill & ifGistypeII.\hfill \end{array}\right.$

Proof. 

Here, $\Delta \left(D\right(G\left)\right)=2\Delta \left(G\right)$.

Suppose G is type I.

Color the elements of two copies of G using $\Delta \left(G\right)+1$ colors. The two vertices in $D\left(G\right)$ are adjacent only if the corresponding vertices are adjacent in G. The remaining uncolored edges in $D\left(G\right)$ will form $\Delta \left(G\right)$ matchings, these edges can be colored with additional $\Delta \left(G\right)$ colors since they induce a bipartite graph with partition sets corresponding to the vertex sets of the two copies of G.

Suppose G is type II.

Color the elements of two copies of G using $\Delta \left(G\right)+2$ colors. Again the remaining uncolored edges will form $\Delta \left(G\right)$ matchings. In this coloring assignment, two adjacent vertices in $D\left(G\right)$ will receive different vertex colors. We color the remaining edges using addtional $\Delta \left(G\right)$ colors.

Hence the proof. □