Abstract
Usually, a fabric weave pattern is recognized using methods which identify the warp floats and weft floats. Although these methods perform well for uniform or repetitive weave patterns, in the case of complex weave patterns, these methods become computationally complex and the classification error rates are comparatively higher. Furthermore, the fault-tolerance (invariance) and stability (selectivity) of the existing methods are still to be enhanced. We present a novel biologically-inspired method to invariantly recognize the fabric weave pattern (fabric texture) and yarn color from the color image input. We proposed a model in which the fabric weave pattern descriptor is based on the HMAX model for computer vision inspired by the hierarchy in the visual cortex, the color descriptor is based on the opponent color channel inspired by the classical opponent color theory of human vision, and the classification stage is composed of a multi-layer (deep) extreme learning machine. Since the weave pattern descriptor, yarn color descriptor, and the classification stage are all biologically inspired, we propose a method which is completely biologically plausible. The classification performance of the proposed algorithm indicates that the biologically-inspired computer-aided-vision models might provide accurate, fast, reliable and cost-effective solution to industrial automation.
1. Introduction
The woven fabric weave pattern is a distinguishable feature for fabric texture recognition, as the fabric weave pattern represents different textures. The fabric weave pattern can be defined statistically, such as using the average value, variance, co-occurrence matrix, and histogram [1]. Haralick used the gray-level features to propose a method for texture identification [1]. In some earlier studies, Fourier transformation technology was used to identify the fabric, and the identification accuracy was found to be 90%, but fabrics with similar weave patterns were not identified successfully [2,3]. In some recent studies, the identification of the warp floats and weft floats from the fabric image were used to determine the fabric texture [4,5,6,7]. Xin et al. used the active-grid-model (AGM) to recognize the weave pattern of fabrics, but the error rate was high [8]. In recent years, the co-occurrence matrix was utilized extensively [9,10]. Alvarenga et al. employed the gray-level co-occurrence matrix method for the identification of textures in images [11]. Hu et al. applied the gray level co-occurrence matrix method for the analysis of the fabric textures [12]. However, poor judgment of warp floats and weft floats leads to an inability to identify fabric texture or, in other words, it leads to high errors. Although, these methods perform well over uniform (simple) or repetitive weave pattern fabric images, in the case of complex weave patterns, the use of these methods for the fabric texture recognition involves more complex computations and also leads to higher classification error. The challenging difficulty of recognizing fabric textures in images is due to the changes in view-points, light intensity, shift and scale transforms, and occlusions. Meanwhile, the difficulty of pattern recognition lies in capturing the variance of shape and appearance of different fabric weave patterns that belongs to the same class label, while avoiding confusing weave patterns from different class labels. The trade-off between selectivity and invariance is a major challenge. Therefore, it is vital to develop a fabric texture recognition system with improved texture (complex patterns) recognition.
Color is also an important property, yet remained unutilized to recognize patterns in most of the approaches. Recently, the use of color images has become a hot research topic. A number of researchers have made different attempts to extract color features in different ways, and the combination of color features with the object shape or texture features (in gray scale) has significantly improved the recognition performance in many recent studies [13,14,15]. The extensive use of the color information in the primary visual cortex is well known [16]. Although the extraction and utilization of color features for pattern recognition has become a hot research topic, yet most of the developed algorithms for fabric weave pattern recognition are still based on black and white images or gray scale images. The prime focus of our study is to perform fabric color feature extraction inspired by the primate visual cortex [17]. Biologically-plausible algorithms may prove to be a good alternative method for the classification of the fabric texture and yarn color features. The main reason behind this motivation is that the human vision system is the most powerful, intelligent, and flexible system to date, which out-performs machine vision in terms of learning capability, as well as recognition and classification performance, in most cases. Therefore, it is quite obvious that human-like intelligence can only be achieved in machine vision by imitating the neurological findings which explain the mechanism of the processing of pattern and color features inside human brain. Furthermore, biologically-inspired algorithms can be further improved in the future by mimicking the newest neurological findings. Recent studies developed [18,19] several neural network algorithms to mimic the computation performed inside the human brain as described by the neurological findings [20].
The Extreme Learning Machine (ELM) is an emerging algorithm in machine learning [21,22,23,24,25], which is biologically-inspired and which performs with accuracy similar to Support Vector Machines (SVM) [26] and is also relatively fast to train as compared to iterative training methods. Although ELM is getting popular, ELM-based classifiers have not been used for fabric texture classifications. Numerous implementations of multi-layered extreme learning machines have been developed [27,28,29], and it was found that the multi-layer implementation of extreme learning machine performed better than the conventional ELM in term of the recognition and classification performance. Recent works that were intended to develop neuromorphic implementations of Extreme Learning Machines [30,31,32] motivated this current work. Further details of neuromorphic implementations are described elsewhere [33]. One of the potential limitations is the simultaneous activation of the several hidden layers. The main focus of our study is to develop a deep machine learning algorithm based on extreme learning machine architecture, which requires fewer hidden layers needed for simultaneous activation, offering good classification accuracy, and trains relatively faster.
In this paper, we have taken inspiration from the advances in the architectures of deep learning [34,35,36] and from neurological findings of deep learning architecture in the primate visual cortex. In order to improve the recognition accuracy of fabric weave pattern and yarn color recognition and classification, this paper bring together two biologically-inspired algorithms, namely, color HMAX and deep ELM (a multi-layer variant of the conventional Extreme Learning Machine), and insights to develop a novel biologically-inspired model for robust pattern recognition and classification. In the following section, first we describe the outline of the proposed method with a flowchart. Then we propose a novel approach to deep ELM (D-ELM) implementation as a weave pattern classifier, and describe the method briefly. In the later sub-sections we describe the weave pattern and yarn color feature descriptor in detail, followed by the brief description about the integration of the pattern feature descriptor with the weave pattern classifier.
2. Method
The overall flow of the proposed algorithm is summarized in Figure 1. A fabric texture image is fed to the proposed fabric weave pattern recognition and classification system in RGB (red-green-blue) color format. Three color filters are applied over each input image to separate each color channel from the input fabric image. These three color channels, namely, red, green, and blue, are then combined into three opponent color channels, namely, red-green (RG), yellow-blue (YB), and white-black (WB). These three opponent color channels are inspired by human vision as proposed by the classical opponent color channel theory [16]. These opponent color channel features are then fed to the feature descriptor, where they are processed further for the fabric weave pattern and yarn color feature extraction. The two main parts of our model are the feature descriptor and the weave pattern classifier, which will be described in detail in the following sub-sections of the method.
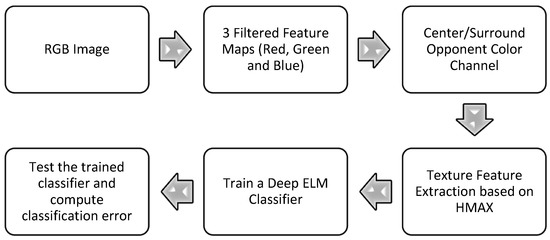
Figure 1.
Flowchart of the proposed algorithm.
We combined the two biologically inspired algorithms in cascade, feed-forward hierarchy. The input fabric pattern image (RGB color image) is fed to the feature descriptor for the weave pattern and color features extraction. The output matrix of the feature descriptor with feature values corresponding to different patterns in the color images, acts as an input to the featureclassifier (deep Extreme Learning Machine). The class label prediction for the pattern in an image under examination is then made by the classifier stage of our model (see Figure 1).
2.1. Biologically-Inspired Deep ELM-Based Pattern Recognition Network Design (D-ELM)
In most conventional multi-layer implementations of extreme learning machine, the computational complexity, memory capacity requirement, and the hidden layers that are required to be activated simultaneously are very high. To reduce the computational complexity, computation time, memory capacity requirement, and the simultaneously activated hidden layers, while maintaining good classification accuracy, we proposed a different approach. In conventional deep ELM structures, initially the ELM is trained with the training dataset as the desired target without the use of class labels. The input weights of the ELM are calculated by taking the transpose of the resultant trained output weights. Then the activation functions for the hidden layers are also trained in the similar way repeatedly, prior to finally training the large hidden layer as the classifier output [26]. The deep ELM network we propose in this paper significantly differs with a conventional one in the following three ways. Firstly, the input weights are untrained in multiple ELM modules which are combined to create a deep ELM network. Secondly, each module’s input layer is auto-encoded with the input, rather than auto-encoding the hidden-layer responses. Thirdly, each module’s output weights are trained using labeled data. We further describe the proposed method in detail below.
In our model, we create a multi-layered Deep ELM network by adding a cascade of standard ELM modules (three layer model, namely, the input layer, single hidden layer, and output layer), with each following ELM module receiving its input from the preceding module, as shown in Figure 2. Therefore, the output of each ELM module acts as an input of the following ELM module, and vice versa. Thus, a D-module deep ELM can be implemented by repeatedly adding identical ELM modules D times.

Figure 2.
D-module deep ELM network.
We describe the proposed network with the help of the functional flow of the N-dimensional vector input throughout the proposed network. As described earlier, the vector input to the deep ELM based classifier will be the feature representation output matrix of the training and testing images in the dataset from the color HMAX-based feature descriptor. Our deep ELM network is a multi-layer variant of the conventional ELM model, with multiple hidden layers. The training vector or test vector X ∊ ℝN⨯1 is fed as an input to the input layer. This input layer and the ELM module’s hidden layers (of size M) are connected with each other (as shown in Figure 3) by an n weight matrix Wp1X ∊ ℝM⨯1. The ith hidden layer’s output is obtained by the logical sigmoid function:
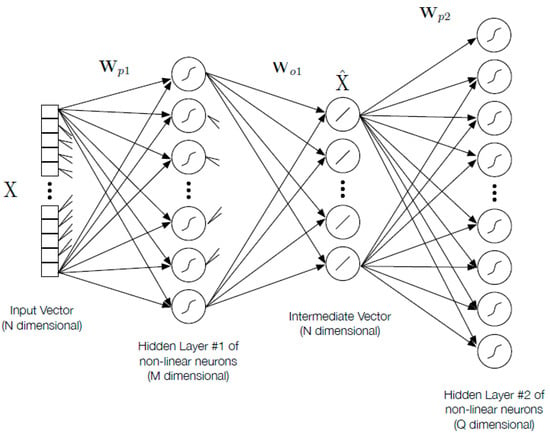
Figure 3.
Deep ELM network architecture.
The approximation of the input, X ∊ ℝN⨯1 is produced by the product (multiplication) of WO1, the output weight with the hidden-layer responses. The autoencoding is performed by the training the output weight vectors using the K training vector, a matrix is defined as A ∊ ℝM⨯K where each column holds the hidden layer output f[H1] at one training point. Then, in order to minimize the square mean error, we solve for WO1 ∊ ℝN⨯M using the training data Y ∊ ℝN⨯1 where each column holds training vectors:
Ypredicted: = WO1A
The original training set images, Y, like the supervised training of an extreme learning machine has been conducted elsewhere [23,28,37], we find the solution of the following set of NM linear equations in NM unknown variables comprised from the elements of WO1:
where c is the regularization parameter that can be optimized as a hyperparameter, and I is an identity matrix of order (M).
YAT = WO1(AAT + cI),
An input instance X is converted into a new vector using this trained weight matrix WO1 as follows:
which is the auto-encoded form of the input data.
The weight matrix Wp2 ∊ ℝQ⨯N is used to construct the next module of the proposed network, the second hidden layer input is with input H2 ∊ ℝQ⨯1 is connected to X, where Q may not be the same as the size of the first hidden layer, M. Then the fashion in which the output weight vectors of the first module were trained, is repeated again to train the output weights of the second module to produce a new auto-encoded response:
A D-module deep ELM network can be formed by repeating the process explained above, several times.
The sequential steps involved in the training procedure is explained above. After completing the training process, the two weight matrices WO1, WO2 are combined to form one single weight matrix Wh12 ∊ ℝQ⨯M, that connects the first two hidden layers:
Wh12 = WO2WO1,
Similarly the entire process explained above can be repeated for the subsequent modules because the input layers and the output layers of an ELM module are linear.
We used an approach for the classification of the dataset images by embedding the class labels as integers in the first column of the image vector for training, where each row represents the class label for that respective feature vectors (to which it belongs). The addition of label pixels is shown in Table 1, where each image contains “N” unique features are represented as attribute 1, attribute 2 through attribute N. Furthermore, the corresponding class category of the particular image can be represented as the “target” class in Table 1. The first column in the Table 1 represents the class to which the features of that row (particular input image) belong. Each row represents several features from an image, attribute1 through attributeN are the several features for an input image. The resulting training vector dataset is used as the target vector matrix, Y, to train every auto-encoding ELM module. The first module receives the image only as input. Hence, the labeled training image sets are contained in matrix Y, but the network’s first module’s input, X, are only the images. In the classification step, the elements of the prediction vector corresponds to the class labels.

Table 1.
Training labels embedded in the first column of the training vector.
The deep extreme learning machine (ELM) algorithm proposed in our study improves the training time of the network relative to a single ELM using a similar size of hidden layers and can also improve the classification accuracy relative to the other single-module ELM methods.
2.2. Parameter Selection of the Deep ELM Network
The input and output dimension (N) for the deep ELM network was 1000 features per image. We chose the number of non-linear neurons (M) in a hidden layer as 12,800 and the number of ELM modules in cascade (D) equal to 3 (see [17,20] for a detailed explanation for the selection of values for optimum results).
The input weights of the standard extreme learning machine network are initialized randomly. Although this performs well, but explicit computation of the input weights based on the use (supervised) of the training dataset was shown to be advantageous [38].
Moreover, the classification performance can be enhanced when using ELMs by the restriction of the input pixels or features that acts as an input to the ELM hidden layer [37]. In other words, it is advantageous to ensure the input weights vector is sparse. It is also found that keeping the non-zero weights to every hidden layer unit to a random size and locating as rectangular patches, as analogous to the RF (receptive fields) in the biological vision system, achieves improved performance than the random selection of the zero weights.
2.3. Brief Description of Color HMAX Based Feature Descriptor (Opponent Color Channels)
The biologically-inspired HMAX model [39] was extended to include color cues for recognition from color images and significantly improved performance was reported on different color datasets images [40,41,42]. We implemented the extension of HMAX model for pattern recognition to recognize and classify fabric weave patterns and yarn’s color [17]. The main difference in the extension was the incorporation of the pattern’s color information in the feature descriptor using opponent color channels. The two main parts of this model are the feature descriptor and the classifier. The feature descriptor was based on the fusion of opponent color channel and HMAX model, and the classifier is implemented using deep ELM. The descriptor performs the extraction of the object texture and object color information from the image. While the classifier in the later stage uses this information from the preceding descriptor stage to perform the regression and to perform the classification. To improve the recognition accurateness of the previously developed algorithm [17], we replaced the SVM classifier in the previously proposed algorithm with the ELM-based classifier in this paper.
Processing starts with an input RGB image (see Figure 1). The processing architecture comprises two stages, namely, the feature descriptor stage and the classification stage. In stage I, individual red, green, and blue color channels are combined in three pairs of opponent color channels, namely, red-green, yellow-blue, and white-black opponent color channels using a Gabor filter. The opponent color channels were integrated with the HMAX model, so that the pattern features and color features be processed simultaneously. The extracted features which correspond to the pattern and color are then fed to the deep neural network-based classification stage. In the classification stage (stage II), we first train the classifier over features of the training image set, and then test the trained classifier with the testing image set.
The process of filtering the RGB image into individual color channels and then combining individual color channels into opponent color channels and its integration with the HMAX model is explained in detail in [17], as the feature descriptor stage is the same as the implementation in [17]. We further improved the earlier proposed model by replacing the classifier stage with a neural network based classifier. Next, we describe the method used to construct our proposed deep extreme learning network briefly as a weave pattern and yarn color classifier.
The architecture and hierarchy of the layers of HMAX model and their functionality is discussed in detail elsewhere [39,43,44,45,46,47]. The color HMAX implementation for the fabric texture recognition and classification was also achieved in our earlier study [17].
3. Experiments
Three groups of experiments were performed on the entire datasets, to show the novelty and advantage of our proposed model over existing algorithms. The dataset images used for all our experiments were customly built according to the experimental design; in other words, there is no standard benchmark dataset for our problem. The first experiment is to test the algorithm for recognizing changes in fabric texture type, we used four classes of texture types in our experiment, namely, plain, horizontal stripes, vertical stripes, and check textures. We gathered images for different texture types and arranged them in different class categories, with each class category representing a unique texture type (shown in Figure 4 as Experiment 1). As a second test, we performed a test to determine the recognition accuracy of the algorithm for recognizing different yarn colors. We arranged the fabric images in different class categories, with each class category representing a unique yarn color (shown in Figure 4 as Experiment 2). As a final test, we evaluated the recognition accuracy of the proposed algorithm for a change in fabric texture type and yarn color simultaneously. Therefore, for this test, we created different class categories such that each class represents a unique fabric texture type and yarn color (shown in Figure 4 as Experiment 3). It is very important to understand the arrangement of the different classes in the dataset for the three experiments (see Figure 4 for details).

Figure 4.
Illustration example of the custom-built dataset images with four classes for each test.
The images in our dataset with several color and texture features of different fabrics were re-organized to form classes in different arrangements to perform different experiments, as explained earlier, with the help of Figure 4. Moreover, the images in every class category consist of several fabric images with similar features belonging to the same class to capture “feature invariance”. This can be seen in Figure 5, where four class categories are shown for an experiment (see Experiment 3 shown in Figure 4) to test the algorithm for fabric recognition. In this image, class I represents fabric images with horizontal stripes and different colors, class II represents fabric images with check patterns, whereas class III represents plain fabric images with different colors. A set of images similar to those shown in Figure 5 are used to create a collection of images arranged in different classes to capture feature invariance and to perform a recognition test of the algorithm for different weave patterns and different yarn colors.

Figure 5.
Sample of the images in the dataset to capture feature invariance for a test.
The method is applied to 400 images, divided into four class categories. In each class category, there were a total of 100 images. The training images and the testing images were selected from the dataset images using k-fold cross-validation method (for k = 10, 20, and 25), in order to train and test the developed algorithm over the entire image set. The entire dataset is divided into N/k segments, where N is the number of images in the dataset. Each segment is used for testing turn by turn, and the remaining segments are used for training in each turn. Finally the results are averaged together to calculate the average performance of the proposed method over entire dataset. The results obtained by the experiments performed are summarized in Table 2, Table 3 and Table 4.

Table 2.
A comparison of recognition & classification accuracy for different types of textures between our model (deep ELM based classifier) and the HMAX model with an SVM-based classifier (shirt fabric; different texture type), with standard deviation in parenthesis.

Table 3.
A comparison of recognition and classification accuracy for different yarn colors between our model and the HMAX model with and SVM-based classifier (shirt fabric; color type), with standard deviation in parenthesis.

Table 4.
A comparison of recognition and classification accuracy for different fabric textures and yarn colors between our model (deep ELM-based classifier) and the HMAX model with an SVM-based classifier (shirt fabric; inter-texture changes), with standard deviation in parenthesis.
The software package used for the implementation of the feature extraction and classification modules was MATLAB 2014a developed by Mathworks (Natick, MA, USA) used on Microsoft Windows 7 operating system. The images used for all the experiments, were of a moderate resolution of up to 500 × 500 px, in JPEG format.
The recognition performance of the algorithm was evaluated according to the statistical criteria as follows:
4. Results and Discussion
The fabric’s texture and yarn color features are extracted using the biologically-inspired proposed algorithm and then recognized successfully and classified automatically to the respective class category using deep (multiple hidden layers) ELM. The automatic recognition and classification accuracy of the proposed improved model is calculated and compared with the earlier proposed model [17] for all three experiments stated in the previous section (see Table 2, Table 3 and Table 4).
Cumulatively, there are a total of four classes in the dataset, but in order to analyze the impact of the usage of the increase in number of classes on the recognition performance of the proposed algorithm, we have repeated our experiment for two, three, and four classes turn by turn. For example, in order to test the proposed algorithm for two classes, we used two out of four classes of the dataset by creating six subsets where each subset contains two classes, such as subset 1 with Class I and Class II, subset 2 with Class I and Class III, subset 3 with Class I and Class IV, subset 4 with Class II and Class III, subset 5 with Class II and Class IV, and subset 6 with Class III and Class IV. Finally, the resulting accuracy was obtained by taking the average of all six subsets. Similarly, three subsets were created for three classes, such as subset1 with Class I, Class II and Class III, subset 2 with Class I, Class II and Class IV, and subset3 with Class II, Class III, and Class IV. Finally, the resulting accuracy for three classes was obtained by taking the average over all three subsets. Likewise, the accuracy was evaluated for four classes using only one subset. The recognition accuracy of the proposed algorithm was evaluated over the entire dataset (several subsets incase of recognition performance between two and three classes, as described above) using k-folds cross-validation over each subset (with k = 10, 20, and 25) to validate and assess the performance of our model.
It is evident from Table 2, Table 3 and Table 4 that use of the deep ELM as a classifier achieved better recognition accuracy. Although the dataset images contain illumination variance and wrinkles (see Figure 4), the developed algorithm is capable of providing successful recognition and accurate classification. Hence, we conclude that the developed algorithm performs fabric weave pattern and yarn color recognition and classification invariantly and efficiently.
As we claimed that our algorithm may provide a fast alternative to pattern or color recognition and classification, the results in Table 5 present a comparison of the computation speed of the proposed algorithm as compared to the SVM counterpart and standard ELM classifier. It is evident that the standard ELM and deep ELM classifiers are faster as compared to the SVM-based classifier; furthermore, it is important to note that deep ELM classifier networks achieve better accuracy as compared to the standard ELM at the cost of speed. Apart from the computation speed, there are several other benefits of using ELM classifiers as well. The SVM classifiers need to be trained and are computationally more extensive, whereas ELM classifiers use random weight initialization followed by fine tuning and is computationally less extensive. Additionally, the ELM-based classifiers have strong generalizing capability, hence, improving specificity.

Table 5.
Speed comparison of the proposed method with others. (Recognition accuracy is taken from quoted references [17]).
Earlier, we proposed a model for fabric weave pattern and yarns color recognition from color images using a support vector machine as a classifier [17]. We have shown a comparison of the proposed algorithm with our previous implementation [17] in Table 5. A confusion matrix is also presented as Table 6, for all four fabric patterns used in the experiment. Unlike existing computer vision models for fabric texture recognition and classification, our study not only analyzes the texture of the fabric, but the yarn color (fabric color) is also recognized and classified. It can be seen clearly that the biologically-plausible fabric texture analysis method is much efficient and accurate than other existing computer vision models in woven fabric pattern and color recognition and classification. It is evident from Table 5 that the ELM is a good alternative to the Support Vector Machine classifier, and is biologically plausible as well. Furthermore, we noticed that a multi-hidden layer variant of ELM further improves the recognition and classification performance. Hence, we believe that use of the extreme learning machine as a classifier to construct a biologically-inspired network to imitate human vision and human intelligence is a great leap forward to achieve human-like efficient intelligence.

Table 6.
Confusion matrix for the four fabric patterns used in the experiment.
5. Conclusions
We have proposed a biologically-inspired model of joint processing for the extraction of fabric texture and yarn color information based on known properties of the primate visual cortex, which is capable of recognizing and classifying woven fabric textures (weave pattern) invariantly from the color image. Once the algorithm is trained for all the fabric weave patterns (textures) and yarn colors manufactured by a fabric manufacturer, the algorithm will provide an automated recognition and classification of the texture to facilitate the process of sorting the fabric with respect to color and pattern.
We have tested the algorithm to recognize three different types of changes in the fabric texture, and have shown that the proposed descriptor performs on par, or better than the existing algorithms. We found that the recognition accuracy is significant with an average accuracy rate of 97.5%. It should be noted that although we used shirt fabrics to test our algorithm, the algorithm can also be used on other apparel or clothes, like towels or bed sheets.
We further found that the algorithm can also be used to recognize a particular texture woven over a fabric. The developed algorithm may also be trained to recognize and correctly classifying complex textures efficiently. The proposed model was shown to yield higher accuracy for automated classification of woven fabric texture and yarn color, the recognition accuracy is also improved. Unlike other existing models, the proposed model is also capable of automatically recognizing the fabric and yarn color and classifying it to the respective color and texture class category. Overall, the relative success of the proposed biologically-inspired approach suggests that neuroscience may contribute new ideas and superior algorithms for automatic recognition and classification applications using color images.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Nos. 11572084, 11472061, 71371046, 61603088), the Fundamental Research Funds for the Central Universities and DHU Distinguished Young Professor Program (No. 17D210402), and Babar Khan was supported by a grant from China Scholarship Council (CSC).
Author Contributions
Babar Khan and Ather Iqbal designed the experiments; Babar Khan performed the experiments; Rana J. Masood analyzed the data; Babar Khan wrote the paper; and Zhijie Wang and Fang Han supervised the study and verified the findings of the study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haralick, R.M.; Shaunmmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–620. [Google Scholar] [CrossRef]
- Xu, B. Identifying Fabric Structures with Fast Fourier Transform Techniques. Text. Res. J. 1996, 66, 496–506. [Google Scholar]
- Ravandi, S.A.H.; Toriumi, K. Fourier Transform Analysis of Plain Weave Fabric Appearance. Text. Res. J. 1995, 65, 676–683. [Google Scholar] [CrossRef]
- Huang, C.C.; Liu, S.C.; Yu, W.H. Woven Fabric Analysis by Image Processing Part I: Identification of Weave Patterns. Text. Res. J. 2000, 70, 481–485. [Google Scholar] [CrossRef]
- Kang, T.J.; Choi, S.H.; Kin, S.M. Automatic Recognition of Fabric Weave Patterns by Digital Image Analysis. Text. Res. J. 1999, 69, 77–83. [Google Scholar] [CrossRef]
- Kuo, C.F.J.; Shih, C.Y.; Kao, C.Y.; Lee, J.Y. Automatic Recognition of Fabric Weave Patterns by Fuzzy C-Means Clustering Method. Text. Res. J. 2004, 74, 107–111. [Google Scholar] [CrossRef]
- Wang, L.; He, D.C. A New Statistical Approach for Texture Analysis. Photogramm. Eng. Remote Sens. 1990, 56, 61–66. [Google Scholar]
- Xin, B.; Hu, J.; Baciu, G.; Yu, X. Investigation on the Classification of Weave Pattern based on an Active Grid Model. Text. Res. J. 2009, 79, 1123–1134. [Google Scholar]
- Guo, Z.; Zhang, D.; Zhang, L.; Zuo, W. Palmprint Verification Using Binary Orientation Co-Occurrence Vector. Pattern Recognit. Lett. 2009, 30, 1219–1227. [Google Scholar] [CrossRef]
- Potiyaraj, P.; Subhakalin, C.; Sawangharsub, B.; Udomkichdecha, W. Recognition and Revisualization of Woven Fabric Structures. Int. J. Cloth. Sci. Tech. 2010, 22, 79–87. [Google Scholar] [CrossRef]
- Alvarenga, A.V.; Teixeira, C.A.; Ruano, M.G.; Pereira, W.C.A. Influence of Temperature Variations on the Entropy and Correlation of the Grey-Level Co-Occurrence Matrix from B-Mode Images. Ultrasonics 2010, 50, 290–293. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Zhao, C.X.; Wang, H.N. Directional Analysis of Texture Images Using Gray Level Co-Occurrence Matrix. In Proceedings of the IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application, Wuhan, China, 19–20 December 2008. [Google Scholar]
- Zhang, J.; Xie, Z.; Gao, J.; Wu, K. Beyond Shape: Incorporating Color Invariance into a Biologically Inspired Feed-Forward Model of Category Recognition. In Proceedings of the 7th Indian Conference on Computer Vision, Graphics and Image Processing, Chennai, India, 12–15 December 2010; pp. 85–92. [Google Scholar]
- Jalali, S.; Tan, C.; Lim, J.; Tham, J.; Ong, S.; Seekings, P.; Taylor, E. Visual Recognition Using a Combination of Shape and Color Features. In Proceedings of the Annual Conference of the Cognitive Science Society, Berlin, Germany, 29 July–3 August 2013; pp. 2638–2643. [Google Scholar]
- Zhao, H.; Zhou, B.; Liu, P.; Zhao, T. Modulating a Local Shape Descriptor through Biologically Inspired Color Feature. J. Bionic Eng. 2014, 2, 311–321. [Google Scholar] [CrossRef]
- Conway, B.R.; Chatterjee, S.; Field, G.D.; Horwitz, G.D.; Johnson, E.N.; Koida, K.; Mancuso, K. Advances in color science: From retina to behavior. J. Neurosci. 2010, 30, 14955–14963. [Google Scholar] [CrossRef] [PubMed]
- Khan, B.; Han, F.; Wang, Z.J.; Masood, R. Bio-Inspired Approach to Invariant Recognition and Classification of Fabric Weave Patterns and Yarn Color. Assem. Autom. 2016, 36, 152–158. [Google Scholar] [CrossRef]
- Furber, S.B.; Galluppi, F.; Temple, S.; Plana, L.A. The SpiNNaker Project. Proc. IEEE 2014, 102, 652–665. [Google Scholar] [CrossRef]
- Benjamin, B.V.; Gao, P.; McQuinn, E.; Choudhary, S.; Chandrasekaran, A.R.; Bussat, J.M.; Alvarez-Icaza, R.; Arthur, J.V.; Merolla, P.A.; Boahen, K. Neurogrid: A mixed Analog–Digital Multichip System for Large-Scale Neural Simulations. Proc. IEEE 2014, 102, 699–716. [Google Scholar] [CrossRef]
- Tissera, M.D.; McDonnell, M.D. Deep extreme learning machines: Supervised autoencoding architecture for classification. J. Neurocomput. 2016, 174, 42–49. [Google Scholar] [CrossRef]
- Eliasmith, C.; Anderson, C.H. Neural Engineering: Computation, Representation, and Dynamics in Neurobiological Systems; The MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.B.; Wang, D.H.; Lan, Y. Extreme learning machines: A survey. Int. J. Mach. Learn. Cybern. 2011, 2, 107–122. [Google Scholar] [CrossRef]
- Cambria, E.; Huang, G.B. Extreme learning machines. IEEE Intell. Syst. 2013, 28, 30–31. [Google Scholar] [CrossRef]
- Penrose, R. A generalized inverse for matrices. Math. Proc. Camb. Philos. Soc. 1955, 51, 406–413. [Google Scholar] [CrossRef]
- Huang, G.B. An insight into extreme learning machines: random neurons, random features and kernels. Cognit. Comput. 2014, 6, 376–390. [Google Scholar] [CrossRef]
- Kasun, L.L.C.; Zhou, H.; Huang, G.B. Representational learning with ELMs for big data. IEEE Intell. Syst. 2013, 28, 31–34. [Google Scholar]
- Yu, W.; Zhuang, F.; He, Q.; Shi, Z. Learning deep representations via extreme learning machines. Neurocomputing 2015, 149, 308–315. [Google Scholar] [CrossRef]
- Han, H.G.; Wang, L.D.; Qiao, J.F. Hierarchical extreme learning machine for feedforward neural network. Neurocomputing 2014, 128, 128–135. [Google Scholar]
- Basu, A.; Shuo, S.; Zhou, H.; Lim, M.H.; Huang, G.B. Silicon spiking neurons for hardware implementation of extreme learning machines. Neurocomputing 2013, 102, 125–134. [Google Scholar] [CrossRef]
- Galluppi, F.; Davies, S.; Furber, S.; Stewart, T.; Eliasmith, C. Real time on-chip implementation of dynamical systems with spiking neurons. In Proceedings of the International Joint Conference on Neural Networks IJCNN, Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Choudhary, S.; Sloan, S.; Fok, S.; Neckar, A.; Trautmann, E.; Gao, P.; Stewart, T.; Eliasmith, C.; Boahen, K. Silicon neurons that compute. In Proceedings of the International Conference on Artificial Neural Networks and Machine Learning (ICANN 2012), Lausanne, Switzerland, 11–14 September 2012; pp. 121–128. [Google Scholar]
- Tapson, J.; van Schaik, A. Learning the pseudo inverse solution to network weights. Neural Netw. 2013, 45, 94–100. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y. Learning deep architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- McDonnell, M.D.; Tissera, M.D.; Ladusich, T.V.; van Schaik, A.; Tapson, J. Fast, simple and accurate handwritten digit classification by training shallow neural network classifiers with the extreme learning machine algorithm. PLOS ONE 2015, 10, e0134254. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Miao, J.; Qing, L. Constrained extreme learning machine: A novel highly discriminative random feedforward neural network. In Proceedings of the International Joint Conference on Neural Networks (IJCNN 2014), Beijing, China, 6–11 July 2014; pp. 800–807. [Google Scholar]
- Serre, T.; Wolf, L.; Bileschi, S.M.; Reisenhuber, M.; Poggio, T. Robust object recognition with cortex-like mechanism. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 411–426. [Google Scholar] [CrossRef] [PubMed]
- Van de Weijer, J.; Schmid, C. Coloring local feature extraction. In Proceedings of the 9th European Conference on Computer Vision–Volume Part II (ECCV’06), Graz, Austria, 7–13 May 2006. [Google Scholar]
- Nilsback, M.E.; Zisserman, A. A visual vocabulary for flower classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2006), New York, NY, USA, 17–22 June 2006; pp. 1447–1454. [Google Scholar]
- Everingham, M.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. The Pascal Visual Object Classification Challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef]
- Riesenhuber, M.; Poggio, T. Hierarchical models of object recognition in cortex. Nat. Neurosci. 1999, 2, 1019–1025. [Google Scholar] [PubMed]
- Serre, T.; Wolf, L.; Poggio, T. Object recognition with features inspired by visual cortex. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2005), San Diego, CA, USA, 20–25 June 2005; pp. 994–1000. [Google Scholar]
- Mutch, J.; Lowe, D.G. Object class recognition and localization using sparse features with limited receptive fields. Int. J. Comput. Vis. 2008, 80, 45–57. [Google Scholar] [CrossRef]
- Huang, Y.; Huang, K.; Tao, D.; Tan, T.; Li, X. Enhanced biologically inspired model for object recognition. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2011, 41, 1668–1680. [Google Scholar] [CrossRef] [PubMed]
- Theriault, C.; Thome, N.; Cord, M. Extended coding and pooling in the HMAX model. IEEE Trans. Image Process. 2013, 22, 764–777. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).