Comparative Analysis of Classifiers for Classification of Emergency Braking of Road Motor Vehicles

Abstract

We investigate the feasibility of classifying (inferring) the emergency braking situations in road vehicles from the motion pattern of the accelerator pedal. We trained and compared several classifiers and employed genetic algorithms to tune their associated hyperparameters. Using offline time series data of the dynamics of the accelerator pedal as the test set, the experimental results suggest that the evolved classifiers detect the emergency braking situation with at least 93% accuracy. The best performing classifier could be integrated into the agent that perceives the dynamics of the accelerator pedal in real time and—if emergency braking is detected—acts by applying full brakes well before the driver would have been able to apply them.

1. Introduction

In recent years, there has been noticeable progress in technologies devoted to driving aids in road motor vehicles [1]. The interest in this field is driven by the continuous desire to increase road safety. There are two main types of driving aids: passive and active. Passive driving aids simply notify the driver about the detected improper condition of the car (e.g., low tire pressure, low hydraulic brake pressure, elevated temperature of the coolant of the engine, etc.), driver (sleepiness, fatigue, distraction), road (possibility of ice, wet conditions), or even dangerous traffic situations (unintended lane crossing, presence of objects in the blind spots of the driver’s vision, etc.). On the other hand, active driving braking aids are even able to revoke the inputs of the human driver and delegate control to itself if an imminent traffic accident has been anticipated or if the driver loses the control of the car. Examples of active driving aids include anti-locking brake systems, traction control, an electronic stability program, and automated brake assistance. The latter can be implemented either as a fully automated braking system [2,3] or as an assistant to the human driver [4,5]. Automated braking aids are meant to be rather helpful; however, the current realization of these systems faces many engineering and psychological challenges. Among them is the recognition that fully automated driving aids seldom result in safer driving due to the inflated sense of safety of human drivers (according to the risk homeostasis theory [6]). With the intention of building a reliable and easily applicable helpful system, we decided to leave fully automated braking aids out of the scope of our current research and focus on brake assistance instead.

The modern research on brake-assisting typically considers the brain and the myoelectric activities measured by electroencephalography (EEG) and electromyography (EMG), respectively [7,8,9]. These approaches demonstrate the high feasibility of predicting the emergency situation on the road. However, while EMG measurements are reliable, the brain waves that are recorded by EEG cannot be considered as a credible signal because it is usually affected by the variety of circumstances that dynamically (and, usually, unpredictably) arise while driving. For example, an eventual unsteady directional motion of the vehicle or even simple movements of the head or body of the driver could significantly alter the obtained signals. Moreover, as the researcher investigating these approaches acknowledges, the interference of simple actions such as chewing, raising eyebrows, or eye blinking will be prevalent in real driving. Also, we would like to emphasize both the inconvenience and questionable practical applicability of these approaches: the contemporary implementations of mobile EEG and EMG do not allow for convenient, easy, or quick setup.

In another study [10], the authors built a framework that allows for the assessment of both the degree of criticality of the current road traffic situation and the need for intervention by an intelligent driving system. The proposed framework is based on the processing of several parameters obtained from the sensors of the vehicle via the controller area network (CAN). These parameters include the displacement time of the driver’s foot (e.g., the time needed to move the foot from the accelerator pedal to the brake pedal), and head and facial movements. An alternative approach [11] takes into account the speed of releasing the accelerator pedal, foot displacement, and the speed of the brake pedal in order to detect emergency braking situations. The current industrial systems, however, from the whole set of parameters that could, in principle, characterize the behavior of the driver during emergency braking situations, consider only the motion pattern of the pressed brake pedal [12]. These systems are intended to support drivers who apply the brake pedal quickly but not strongly enough by applying the maximum force to the brakes in emergency situations. The behavior of the driver in such emergency braking situations was extensively explored in [13]. In the latter studies, the authors also proposed both a brake-force-based and a speech-based approach for identifying hazardous situations on the roads.

Without any doubt, in cases of emergency braking, the aforementioned approaches are able to reduce the driver’s response time and, as a consequence, the braking distance of the car. In none of these studies, however, was the motion pattern of the (lifting) accelerator pedal considered as the sole information needed for the reliable detection of the emergency braking situations.

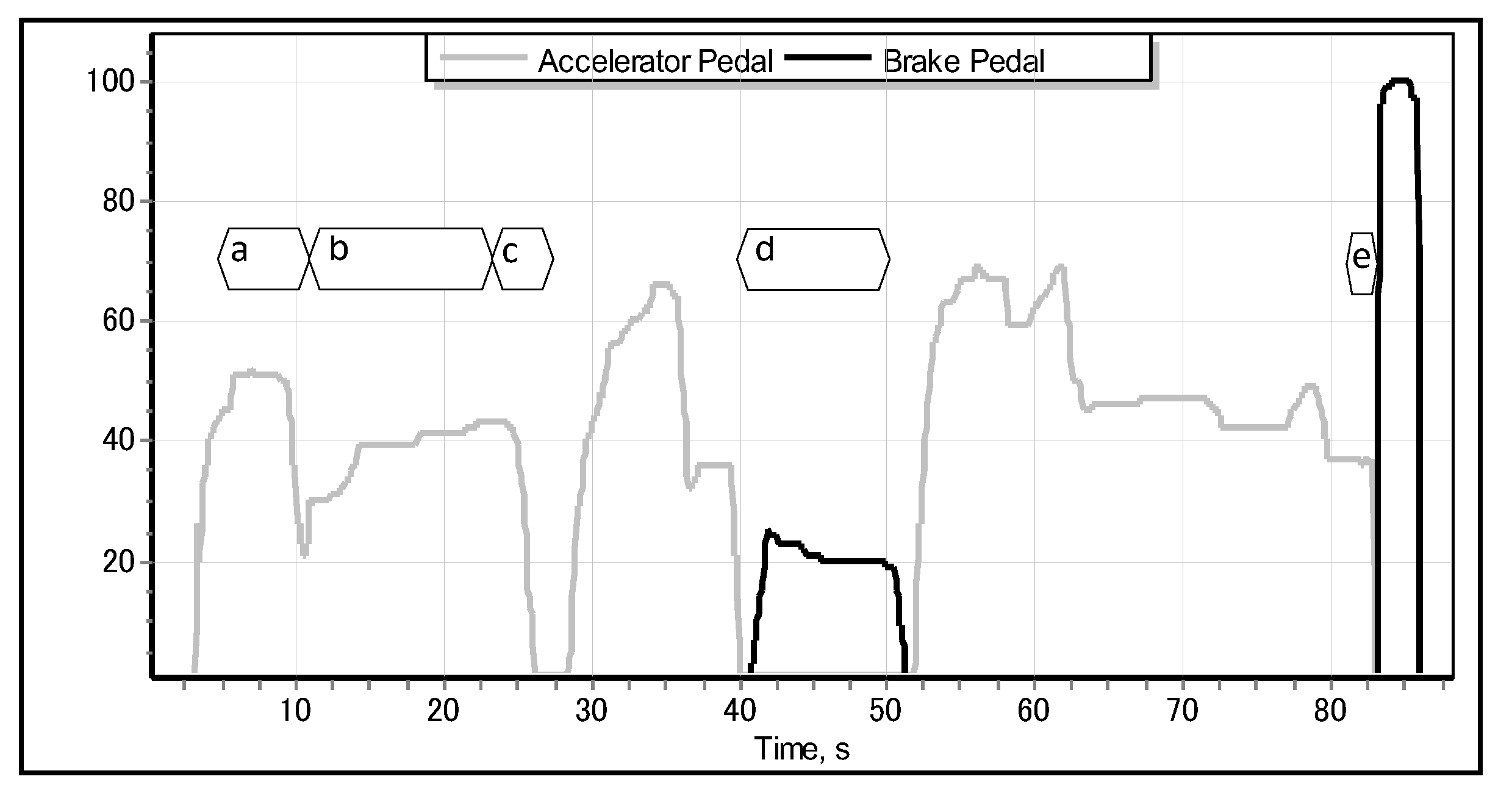
These facts motivated us to investigate the feasibility of predicting the emergency braking situation even before the driver presses the brake pedal (as implemented by most of the current industrial brake assistant systems)—namely, from the pattern of lifting the accelerator pedal [14]. In the case of detecting the special pattern—pertinent to the emergency braking situation—of the motion of accelerator pedal, the proposed system should be able to automatically activate the brakes well before the driver would have been able to apply them. As shown in Figure 1, different driving situations—such as accelerating, cruising, slowing down, normal braking, and emergency braking—exhibit different, specific motion of the accelerator pedal. We obtained the data illustrated in Figure 1 from the modelled parametric data recorder of a car driven by a sample human driver in a full-scale Forum-8 drive simulator [15], as shown in Figure 2. The simulator realistically models a real-world car featuring an automatic transmission, which implies that the driver lifts the accelerator pedal (Figure 1c–e) only when they really intend to reduce the speed of the car (or, ultimately, to stop it). 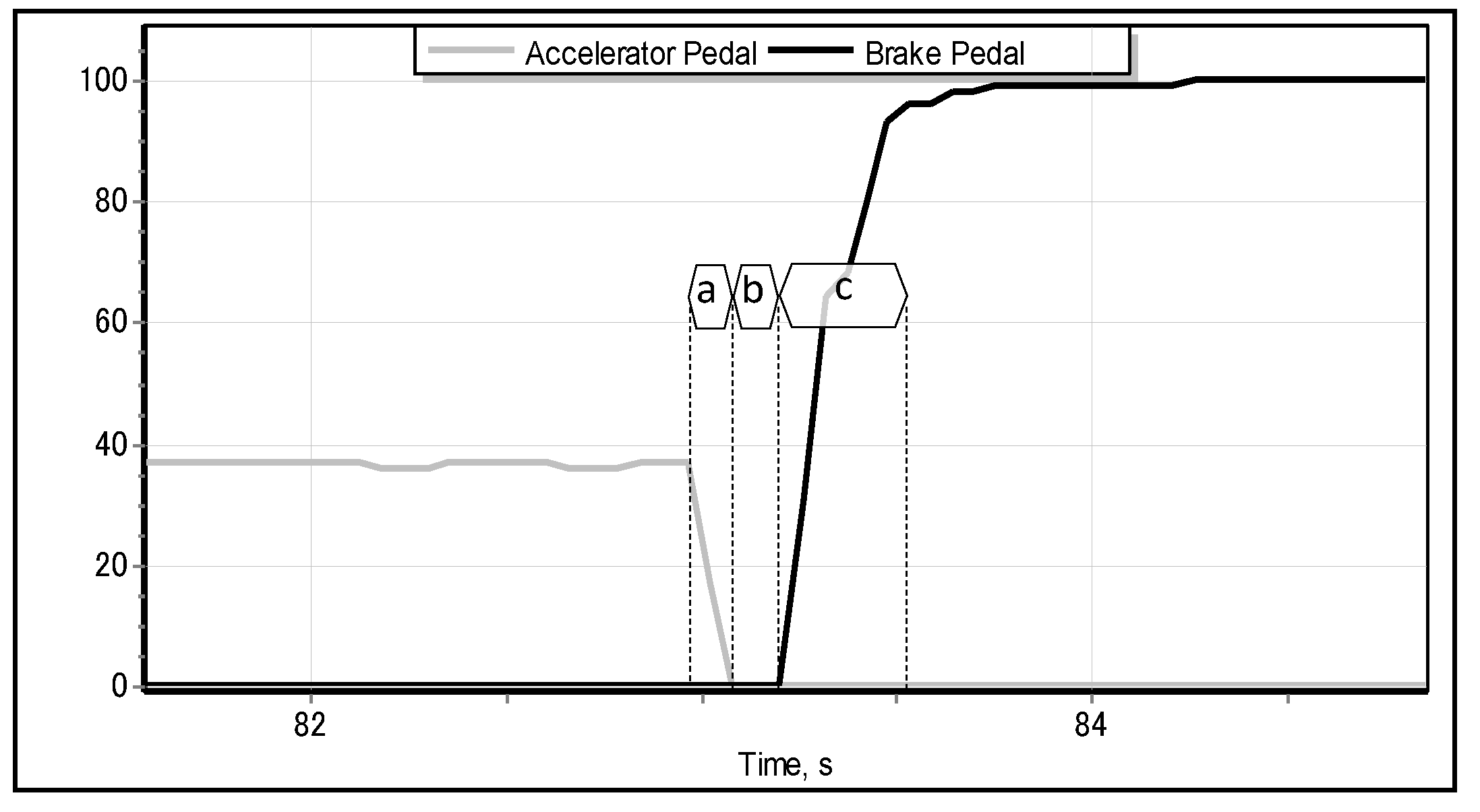Apparently, just before the driver applies the emergency brake, they abruptly lift the accelerator, and the latter quickly returns to its original position [11,16], as illustrated in detail in Figure 3.

In principle, it might be possible to predict the emergency braking situation solely by considering the dynamics of the accelerator pedal. By saying “to predict” we actually mean to classify the current driver’s intention: whether they are going to apply emergency brakes or just normally decelerate the car. A straightforward approach for classification of driver’s intention could be based on a comparison of the rate of change of the position of accelerator with a predefined threshold. Exceeding the threshold would be associated with an urgency of the driving situation, and, consequently, with the intention of the driver to apply emergency braking soon. This assumption is based on the fact that the driver lifts their foot faster than the speed at which the pedal returns to its neutral position. In such a situation, the latter will, indeed, return to its initial position without being hindered by the moving foot of the driver. The motion pattern of the unhindered accelerator pedal could be established analytically from its (known) mechanical characteristics—mass, moment of inertia, friction, displacement of the return spring, and its constant. However, the results of preliminary experiments suggest that such a threshold criterion could not be applied straightforwardly to every driver due to the natural variations in the patterns of the drivers lifting their foot from the accelerator.

The main objective of our research is to resolve the problem of emergency braking classification (EBC) solely from the motion pattern of the accelerator pedal by building an intelligent classifier. We also intend to verify the robustness and generality of the proposed solution to the EBC problem on the data of drivers who have not participated in the process of training the classifiers. In addition, we shall integrate and test the classifier as a brake assisting aid in the full-scale driving simulator that we initially used to collect the training data. The key motivation of our research is in the opportunity of reducing the time lag between two instants: when the driver moves their foot from the accelerator pedal (Figure 3a) and the moment when they press the brake pedal to its maximum position (Figure 3c). In properly classified cases, the proposed brake assisting system would be able to activate the brakes automatically and, as a consequence, to reduce the above-mentioned time lag.

2. Methods

Apart from building the real-time braking assistance, in our research we also intend to compare the alternative classification approaches and to optimize the values of their respective parameters.

2.1. Quality Metrics

In order to evaluate the performance and quality of the trained classifier, applied to the particular EBC problem, we consider using metrics which are not commonly considered. The straightforward approach would have been to use the percentage of correct answers—accuracy. However, this metric if not feasible for the considered EBC problem because if the classifier detects all normal driving cases and ¼ of emergency braking cases, then the accuracy will be equal to 0.7. However, we will miss almost all emergency braking events, suggesting that the metric is not adequate for the evaluation of quality of the classifiers. Therefore, in our approach we apply more informative metrics like precision, recall, and F-score [17] to evaluate the performance of the classifier. For illustration of these metrics, we shall consider the confusion matrix as shown in

Table 1. Confusion matrix.

		True Condition
		Positive	Negative
Predicted condition	Positive	TP	FP
	Negative	FN	TN

. The table illustrates four categories and provides information about how many times the classifier has given the correct answer and how many times the wrong decision has been adopted.

The true positive category (TP) is equal to the number of samples which are classified as class “1” (emergency braking) and are actually in the class “1”. False positive (FP) corresponds to the samples for which the correct class is “0” (normal driving) but the classifier returns “1”; vice versa, if the classifier recognizes the sample as “0” but the real answer is “1”, then the sample is considered as a false negative (FN). Finally, true negative (TN) corresponds to the cases when the sample belongs to the class “0” and the classifier indeed returns “0”. In this way, recall and precision can be expressed as follows:

$$Precision=\frac{TP}{TP+FP} ,$$

$$Recall=\frac{TP}{TP+FN} .$$

Both of these metrics describe different aspects of the classifier: the higher the precision, the lower the FP; and the higher the recall, the lower the FN. Obviously, FP (resulting in emergency braking during normal driving conditions) cases are not preferable due to the resulting uncomfortable driving (and, in some cases, unsafe). However, FP should not necessarily be considered dangerous; we shall elaborate as to why later, in the discussions section of this article. Therefore, for the sake of the comfort of the driver (and passengers) we are interested in maximizing the precision metric. On the other hand, it is necessary to detect as many cases of emergency braking as possible and, as a consequence, to outperform the straightforward threshold classifier which apparently features relatively low values of recall. Thereby, we should pay attention to both of these metrics, and the F-score allows us to do this objective:

$$F=2*\frac{Precision\times Recall}{Precision+Recall} .$$

The F-score can be seen as the harmonic mean of both precision and recall. The scaling coefficient 2 is used in order to normalize the value of the F-score to 1 when both recall and precision are equal to 1.

2.2. Cross-Validation

Cross-validation (CV) [18] is a method of evaluating the model (in the considered case: the classifier of emergency braking situations) and its behavior on independent data. When evaluating the classifier, the available dataset is divided into k subsets (folds). Then, the model is trained on k − 1 folds and the rest of data is used for validation. The procedure is repeated k times. As a result, each of the k folds is used for testing. By averaging the validation quality as illustrated in Figure 4, we obtain the value of the final quality—CV score—of the chosen model with the most even use of the available data. Calculating the CV score is computationally expensive. However, at the same time, it is rather parsimonious in terms of the required amount of data. In addition, it is proven to be able to prevent overfitting of classifiers to a particular set of training data [19].

2.3. Threshold Classifier

The threshold classifier is a one-dimensional classifier which determines the class affiliation of the sample by comparing its value to the predetermined threshold. In our work, we use the threshold classifier as a benchmark. In the Methodology section, we describe the building process of this classifier.

2.4. K-Nearest Neighbors

K-nearest-neighbors-based (k-NN) [20] classification is a type of non-generalizing learning; this means that the method doesn’t build a general model with an eye to classify the sample, but simply stores the whole dataset. The classifier makes a decision by the majority voting of the k nearest neighbors of each sample. A testing sample is assigned the class which has the most significant number of representatives within the nearest neighbors of the sample. For the example, shown in Figure 5, the white sample will be assigned the red class when k is equal to 3.

2.5. Support Vector Machine

Another classification method which is being used in the considered classification problem is the support vector machine (SVM) [21]. This method performs well in many linear and non-linear problems; it is also able to process high-dimensional and large data sets.

The basic idea of SVM is building a hyperplane which splits the training set into the necessary number of classes (in our case, two). When the hyperplane is built, a testing sample is placed on the plane. Depending on its position relative to the hyperplane, we infer the class affiliation of the testing sample.

Formally, the problem can be formulated as follows: begin with a training set of N points (x_i, y_i), where x_i ∈ ${ℝ}^n$ and y_i ∈ $ℝ$ are the i-th input and output samples, respectively. SVM constructs a classifier, which can be represented by a function:

$$f\left(x\right)=sign\left[{\displaystyle \sum }_{i=1}^N{\alpha }_i{y}_{i}K\left(x,x_k\right)+b\right]$$

where x_k are support vectors, α_i are positive real numbers, while b (bias) is a real number. The kernel K can be used in various forms: $x_k^{T}x$ (linear kernel), ${(\gamma x_k^{T}x+r)}^n$ (polynomial kernel of degree n), $e^{-\gamma {\Vert x-x^{\prime }\Vert }^2}\left(\mathrm{radial}\mathrm{basis}\mathrm{function}\mathrm{kernel}\right)$, or $\tanh \left[\gamma x_k^{T}x+r\right]$ (sigmoid kernel), where kernel parameters $\gamma =\frac{1}{2{\sigma }^2}$ and $r$ are real constants.

The learning of SVM lies in finding f(x), which minimizes the following objective:

$$Obj=C{\displaystyle \sum }_i^{N}l\left(f\left(x_i\right), y_i\right)+\mathsf{\Omega }\left({\alpha }_i,b\right)$$

where the first term l is a loss function, $l\left(\widehat{y},y\right)=0$ if $\widehat{y}=y$, and the second term Ω is a penalty function of our model parameters. The parameter C specifies the desire of avoiding the misclassification of each training sample. For example, a large value of C will reduce the width of the hyperplane margin, which will potentially cause fewer errors on the training set. At the same time, a low C will widen the hyperplane margin, as shown in Figure 6.

2.6. Extreme Gradient Boosting

The last method which is considered in our work is Extreme gradient boosting (XGBoost) [22]. XGBoost is a scalable machine learning approach which has proved to be successful in many machine learning and data mining challenges [23,24]. Essentially, XGBoost is an ensemble of K classification and regression trees (CART) [25]. Unlike decision trees, CART assign a real score to each leaf (outcome or target). The final score of y (output) is a sum of K additive functions as follows:

$$\widehat{y}={\displaystyle \sum }_{k=1}^K{f}_k\left(x_i\right), f_k\in F$$

where f_k corresponds to independent tree structure and leaf weights, while x_i is a testing object. F represents a testing space of all CART. For learning the set of functions, the following objective is used:

$$ℒ\left(\phi \right)={\displaystyle \sum }_{i}l(\widehat{y_i},y_i)+{\displaystyle \sum }_k\mathsf{\Omega }\left(f_k\right), \mathsf{\Omega }\left(f\right)=\gamma T+\frac{1}{2}\lambda {\Vert w\Vert }^2.$$

The first term $l$ is a differentiable loss function, l, which calculates the difference between the target $y_i$ and the predicted $\widehat{y_i}$. Ω is a regularization term which prevents over-fitting by penalizing the complexity of the model. Parameters T and w correspond to the number of leaf nodes and the weight of each of them, respectively. Parameters γ and λ are constants which control the degree of regularization.

The ensemble tree model includes functions as parameters and cannot be optimized within traditional methods in Euclidian space; therefore, we employed the following additive approach for its training: assuming that at the tth iteration we have a prediction $\widehat{y_i}$ of the ith instance, we add f_t(x_i) to our objective function.

$${ℒ}^{\left(t\right)}={\displaystyle \sum }_i^{n}l(y_i,{\widehat{y}}_i^{\left(t-1\right)}+f_t\left(x_i\right))+\mathsf{\Omega }\left(f_t\right)$$

In order to quickly optimize the general setting of this objective, the second-order approximation is used:

$${ℒ}^{\left(t\right)}\approx {\displaystyle \sum }_i^n[l(y_i,{\widehat{y}}_i^{\left(t-1\right)})+g_i{f}_t\left(x_i\right)+\frac{1}{2}{h}_i{f}_t^2\left(x_i\right)]+\mathsf{\Omega }\left(f_t\right),$$

$$g_i={\partial }_{{\widehat{y}}^{\left(t-1\right)}}l\left(y_i,{\widehat{y}}_i^{\left(t-1\right)}\right), h_i={\partial }_{{\widehat{y}}^{\left(t-1\right)}}^{2}l\left(y_i,{\widehat{y}}_i^{\left(t-1\right)}\right).$$

Because the loss function is calculated at the current time step t, we can easily remove it:

$${\widehat{ℒ}}^{\left(t\right)}={\displaystyle \sum }_i^n[g_i{f}_t\left(x_i\right)+\frac{1}{2}{h}_i{f}_t^2\left(x_i\right)]+\mathsf{\Omega }\left(f_t\right).$$

By defining I_j = {i|q(x_i) = j} as an instance set of leaf j for a given tree structure q(x), the objective function can be rewritten as follows:

$${\widehat{ℒ}}^{\left(t\right)}={\displaystyle \sum }_i^n[g_i{f}_t\left(x_i\right)+\frac{1}{2}{h}_i{f}_t^2\left(x_i\right)]+\mathsf{\Omega }\left(f_t\right)={\displaystyle \sum }_{j=1}^T[({\displaystyle \sum }_{i\in I_j}{g}_i)w_j+\frac{1}{2}({\displaystyle \sum }_{i\in I_j}{h}_i+\lambda )w_j^2]+\gamma T.$$

For a fixed structure q(x), the optimal weight w_j of leaf j will be

$$w_j^{*}=-\frac{{{\displaystyle \sum }}_{i\in I_j}{g}_i}{{{\displaystyle \sum }}_{i\in I_j}{h}_i+\lambda }$$

while the corresponding optimal value will be

$${\widehat{ℒ}}^{\left(t\right)}\left(q\right)=-\frac{1}{2}{\displaystyle \sum }_{j=1}^T\frac{{\left({{\displaystyle \sum }}_{i\in I_j}{g}_i\right)}^2}{{{\displaystyle \sum }}_{i\in I_j}{h}_i+\lambda }+\gamma T.$$

Finally, in order to score a leaf node during splitting, we use the following expression:

$${ℒ}_{split}=\frac{1}{2}\left[{\displaystyle \sum }_{j=1}^T\frac{{\left({{\displaystyle \sum }}_{i\in I_j}{g}_i\right)}^2}{{{\displaystyle \sum }}_{i\in I_L}{h}_i+\lambda }+\frac{{\left({{\displaystyle \sum }}_{i\in I_j}{g}_i\right)}^2}{{{\displaystyle \sum }}_{i\in I_R}{h}_i+\lambda }+\frac{{\left({{\displaystyle \sum }}_{i\in I_j}{g}_i\right)}^2}{{{\displaystyle \sum }}_{i\in I}{h}_i+\lambda }\right]-\gamma .$$

Here I_L and I_R are the instance sets of the left and right nodes after the split, I = I_L ∪ I_R, and $\gamma$ is the regularization on the additional leaves. It is important to note that—besides the regularization technique—shrinkage and feature subsampling are also used in XGBoost [22].

2.7. Genetic Algorithms

GA are nature-inspired searching algorithms initially proposed by Holland [26]. GA are widely used in various design, control, and optimization problems when exact analytical approaches either do not exist or are too time-consuming to be applied. Moreover, GA [27,28] can be used for solving problems that feature an unknown, non-uniform, discontinuous, or intractably large search space. The representation of the candidate solution in GA is in the form of a population of linear strings (i.e., chromosome) of evolving values of parameters (genetic alleles). Mathematically, the chromosome could be represented as an n-dimensional vector (x₁, x₂, …, x_n) where each coordinate x_i of the vector—the value of a parameter to be optimized—represents a genetic allele. The objective of applying GA is to find such a chromosome that results in an optimal value of a given target—fitness function F. It is important to note that the design of fitness function F is domain-specific, and depends on the nature of the problem being solved. In GA, the quest for the best chromosome (solution), i.e., the chromosome that yields an optimal value of F, consists of the following main steps:

Step 0

Creating the initial population of randomly generated chromosomes;

Step 1

Evaluating the fitness of chromosomes in the population;

Step 2

Checking the termination criteria: good enough fitness value (of the best chromosome in the population), too long runtime, or too many generations. GA terminates if one of the criteria is satisfied;

Step 3

Selection: selecting the mating pool of chromosomes. The size of the mating pool is a fraction (i.e., 10%) of the overall size of the population, and the selection of the chromosomes in the mating pool is fitness-proportional (roulette-wheel, tournament, elitism, etc.);

Step 4

Reproduction: implementing crossover by swapping random fragments of randomly selected pairs (parents) of chromosomes from the mating pool. Crossover produces pairs of offspring chromosomes that are inserted into the newly growing population; and

Step 5

Mutation: random gene(s) of newly generated offspring chromosomes are randomly modified with a given probability.

The implementation of GA could be illustrated by the following pseudo-code:

  Generate initial population;
  Evaluate population;
  While not (Termination Criteria) do
  Selection; // Creating the mating pool of surviving chromosomes
  Reproduction; // Crossing over a randomly selected pair of survived
  chromosomes
  Mutation; // Mutating the newly produced (by crossover) offspring
  Evaluate population;
       

3. Proposals

Achieving our objective of building a learned EBC implies that our research should be implemented in the following five consecutive stages: (i) acquiring and analyzing the data on the dynamics of the accelerator and brake pedals of a car simulated in a full-scale drive simulator; (ii) exploring the straightforward techniques for EBC; (iii) adopting machine learning methods for EBC; (iv) evaluating the proposed classifier on unforeseen data; and, finally, (v) integrating EBC in the full-scale drive simulator in order to verify its performance in a real-time setting and to evaluate the feedback from the drivers.

4. Methodology

4.1. Acquiring Data

In order to acquire the time series data of the dynamics of the accelerator pedal, we asked 12 drivers (men and women, aged 22–52) to drive a simulated car in a full-scale Forum-8 driving simulator [15] in various traffic situations and road conditions. The main requirement for drivers was the possession of a driving license. The details of experimental tracks are shown in

Table 2. Details of the tracks used in experiments on Forum 8 full-scale drive simulator.

Track	Length	Road Conditions	Traffic Conditions
Highway	1 km	Dry	Moderate (high-speed) traffic
Countryside road	3 km	Both dry and wet	Empty road (no traffic)
City road	5 km	Both dry and wet	Dense (low-speed) traffic

.

For the sake of separating the data samples into two categories—normal driving and emergency braking, respectively—we conducted two series of experiments, as elaborated in

Table 3. Details of the two series of experiments.

Experiment	Range of the Position of Accelerator Pedal	Sampling Frequency, Hz	Requirements	Number of Data Samples
Normal driving	[0 … 100]	25	Emergency braking is not allowed	529
Emergency braking	[0 … 100]	25	Audible signal prompts the drivers to apply emergency braking	775

.

During the experiment on normal driving, the drivers were asked to drive a car in a normal way which actually implies that they were not allowed to apply emergency braking. In the emergency braking experiments, each of the drivers was audibly signaled to stop the car suddenly, even though there was no real danger on the simulated road. When the driver heard the specific signal, they were supposed to apply the brake pedal to its maximum as soon as possible. With the intention of maintaining complete separation of the data samples belonging to the two classes (normal driving and emergency braking, respectively), the drivers were asked not to use normal brakes during the second series of experiments. However, they were allowed to decelerate the car by means of lifting the accelerator pedal only. The modeled parametric data recorder logged all the relevant time series for future offline analysis. The acquired raw time series were a sequence of positioning of both pedals (within the range 0–100) sampled with a frequency of 25 Hz. This is the maximum sampling frequency allowed by the adopted drive simulator. During the processing of the mentioned time series, we could extract 1304 events in total, including both normal driving (class “0”) and emergency braking (class “1”) events.

4.2. Data Analysis and Feature Extraction

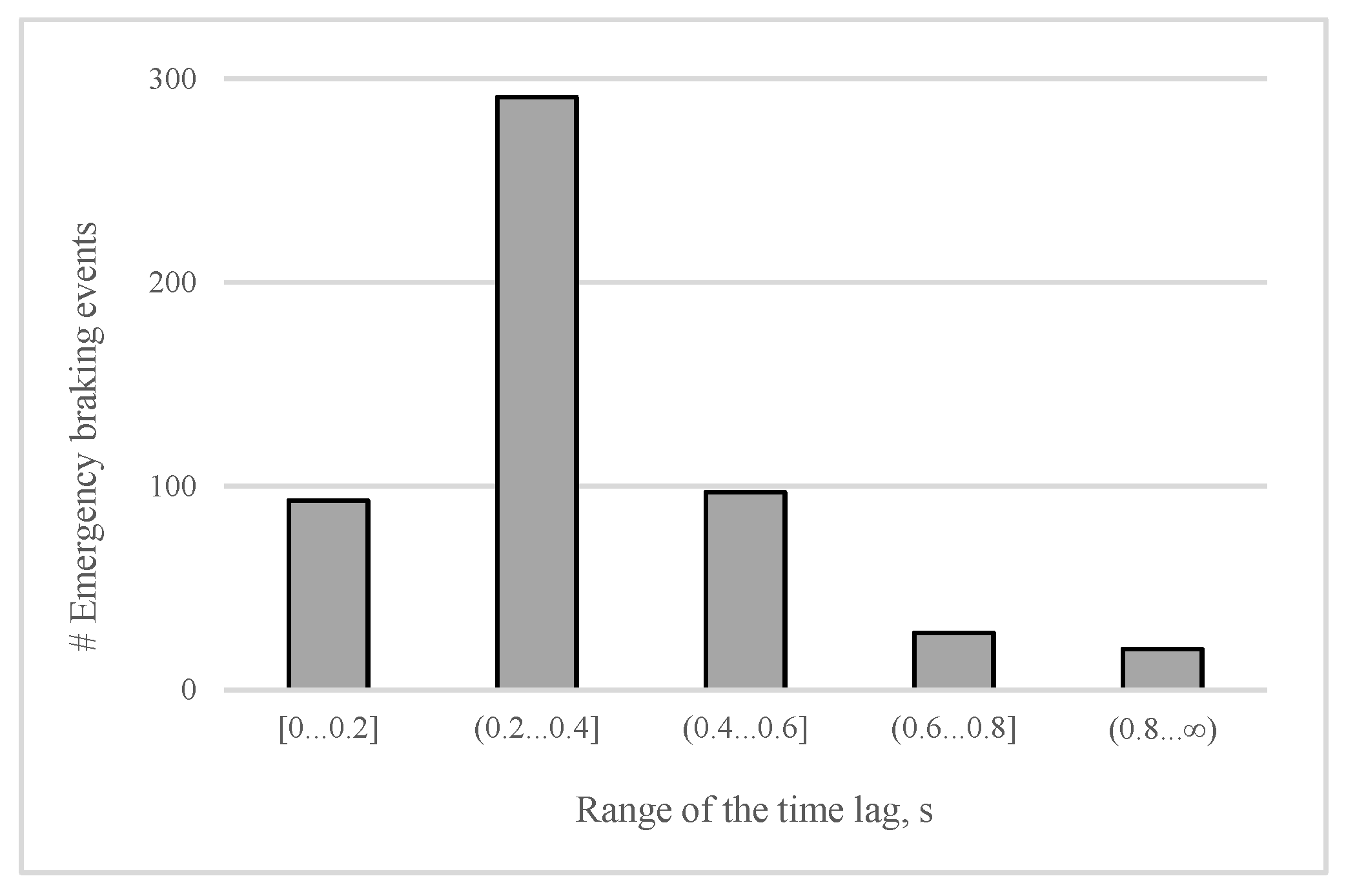
First, we shall analyze the distribution of the time lag between lifting the accelerator and pressing the brake pedal completely (emergency cases) among all testers. The importance of the distribution is that it allows us to estimate the average time that the proposed brake assisting system could save. As illustrated in Figure 7, in most (55%) of the emergency braking events, the time lag covers the interval (0.2 s, 0.4 s]. For the car moving at a speed of 50 km/h, this time lag matches to a traveled distance of between 2.8 m and 5.6 m. Furthermore, a time lag of 0.4 s or higher is registered in about 27% of the emergency braking cases, suggesting that, in more than half of cases at the speed of 50 km/h, the corresponding traveled distance can be even longer than 5.6 m. Consequently, in more than half of the cases of emergency braking, an eventual automated application of brakes would be able to reduce the overall stopping distance, remarkably, by at least 5.6 m (when the driving speed is 50 km/h). As well as measuring the time lag for all drivers, we also extracted several key features of both pedals. Among them are the highest position of the accelerator pedal before starting the deceleration (mP), the maximum and average rate of lifting the accelerator (mR and aR respectively), the maximum and the average rate of pressing the brake pedal, and the maximum position of the pressed brake pedal. The average rate is the pedal speed on the interval where the pedal position is decreasing or increasing (in the case of applying brakes). The maximum rate value is the maximum pedal speed among 0.04 s periods of the mentioned interval.

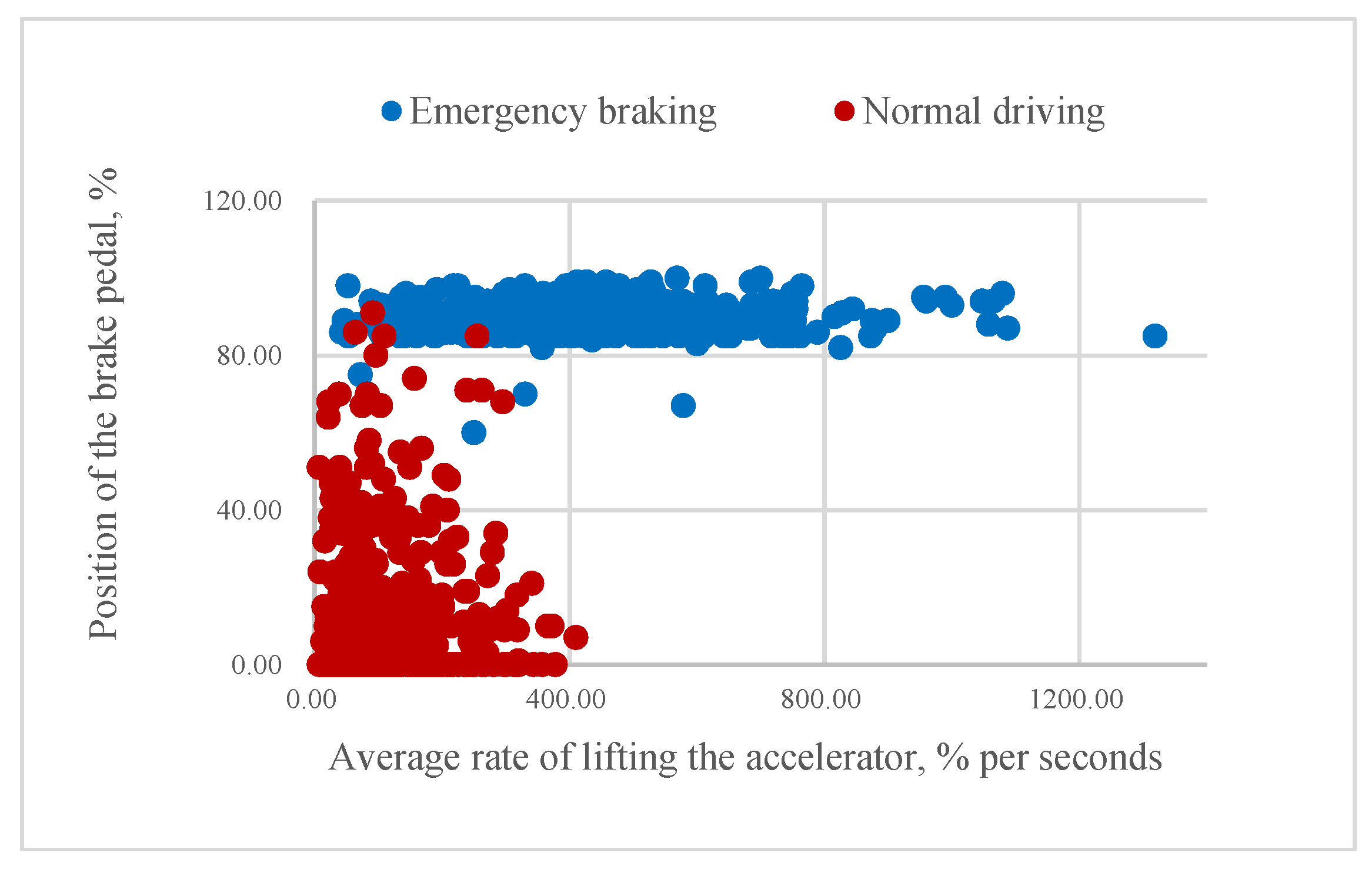
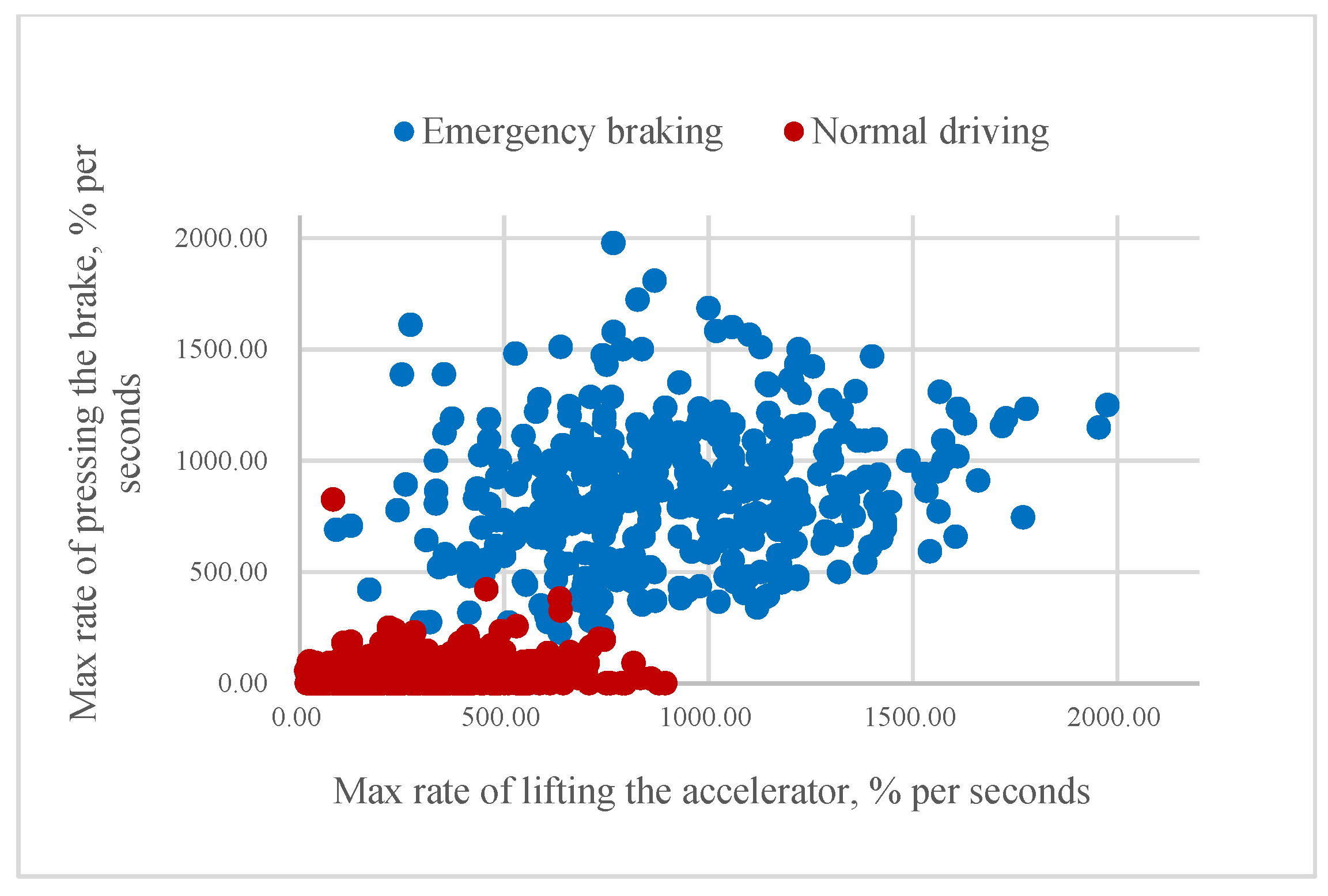
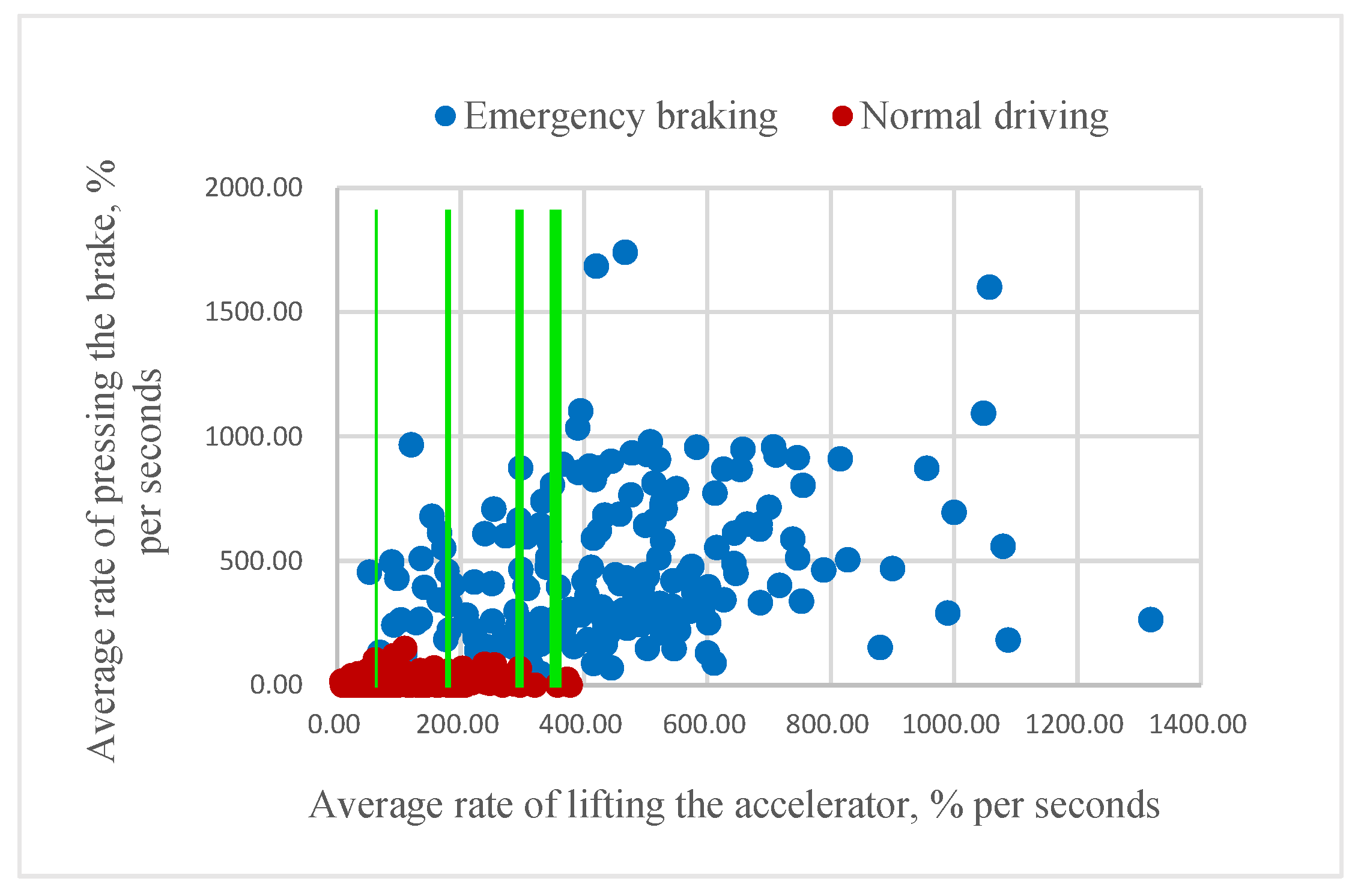
According to our assumption, it could be possible to classify the driver’s intention to apply emergency braking if the value of mR or aR is higher than a certain threshold. As Figure 8 and Figure 9 illustrate, higher rates of pressing the brake pedal correspond to emergency braking situations and often come before the swift release of the accelerator pedal. Consequently, some of the samples belonging to the same class are very close to each other.

4.3. Building Classifiers

Before proceeding with the training of classifiers, we assigned the time series data obtained from 10 sample drivers to the training set and the data of 4 other drivers to the testing set. This approach of separating the data allows good generalization for the classifier. Eventually, the number of samples in the training and testing sets are 1044 and 260 respectively: for the training set there are 447 samples of class “1” and 597 of class “0”, while in the testing set, these numbers are 82 and 178, respectively.

In order to build an eventual threshold classifier, we gradually “move” the threshold for both mR and aR until the classifier ceases to misclassify the samples from class “1” in the training set. In this way, the threshold for mR was found to be 894, and that for aR was found to be 411, as shown in Figure 10.

Despite its simplicity, the threshold classifier is able, indeed, to detect some of the emergency braking cases from the testing set (see Results). However, we presume that a combination of features (rather than single ones) pertinent to the dynamics of the accelerator pedal would be needed for successful classification of emergency braking. Therefore, we investigate the feasibility of solving the EBC problem by applying more intelligent approaches based on machine learning.

In order to employ SVM and k-NN for the emergency brake classification, we use a powerful machine learning library for the Python programming language: scikit-learn [29]. Besides providing an enormous amount of various machine learning methods with its friendly APIs [30], scikit-learn allows us to visualize the dataset in a very representative way. To employ gradient-boosted trees in our work, we used an open source package of XGBoost [31] which supports multiple programming languages including C++, Python, R, Java, Scala, and Julia.

It is important to note that, for using k-NN and SVM, we applied a standardization procedure to the dataset since this is a common requirement for these methods. This procedure standardizes features by removing the mean and scaling to unit variance. However, this procedure was not applied to the XGBoost classifier since the base learners of XGBoost are trees, and any monotonic function of any feature variable will have no effect on how the trees are formed. All three classifiers were trained with respect to all 3 features: mP, mR, and aR.

4.4. Quality Estimation and Applying of GA

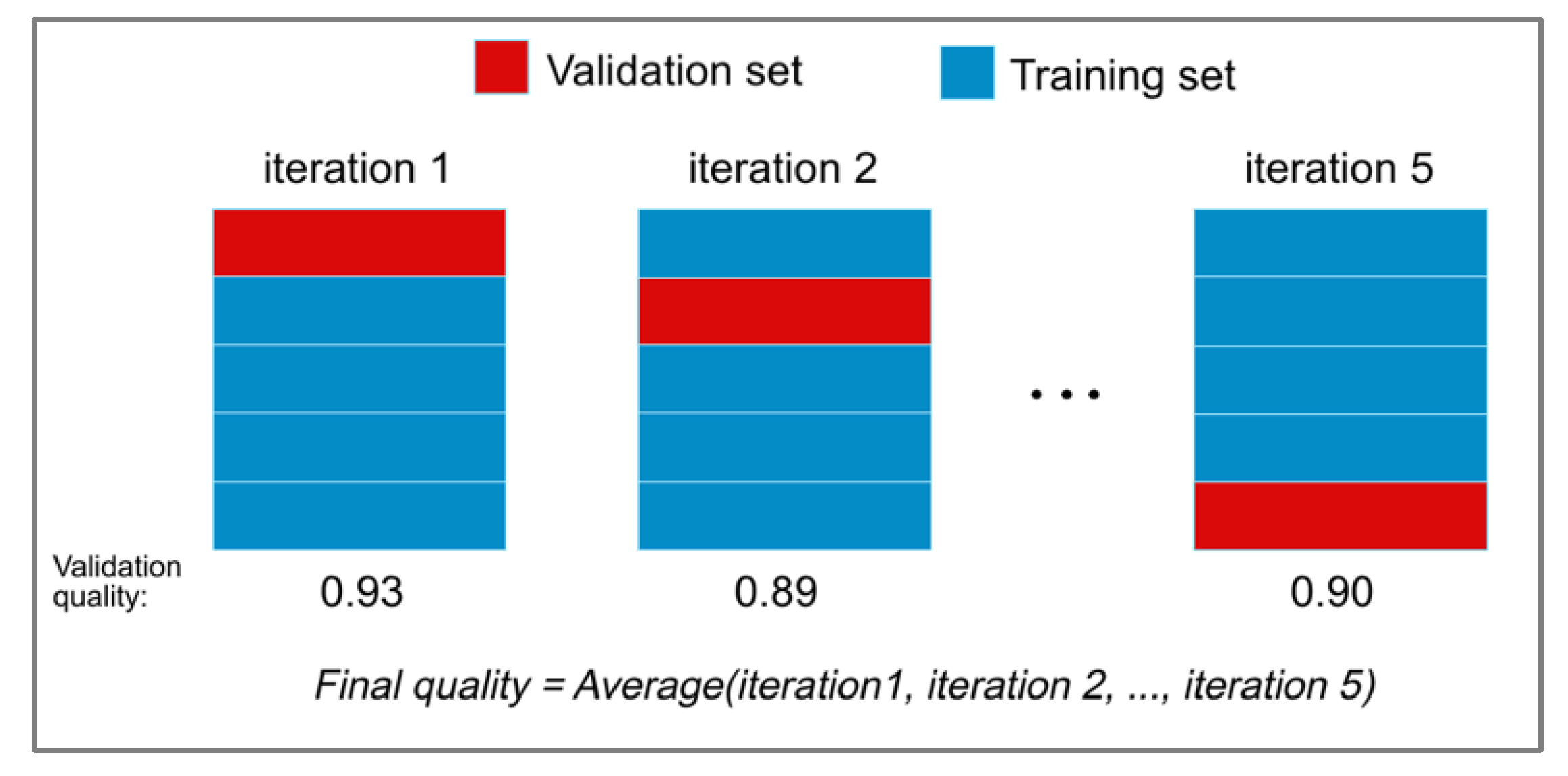
For estimating the quality of classifying the emergency braking situations and to verify the degree of optimality of the values of hyperparameters, we used the cross-validation (CV) score. We split the training subset into 5 folds (smaller subsets), and implemented the following two procedures for each of the two folds: first, we trained all classifiers using four (of the five) folds, then we tested the resulting classifier on the remaining (fifth) fold.

Taking into account the computational overhead of CV, an eventual application of a brute-force approach for finding the best combinations of values of hyperparameters for the proposed classifiers would be unfeasible. Instead, in our approach, we propose an evolutionary search based on GA.

The objective of applying GA is to search for a solution (represented as a chromosome) that results in an optimal value of a given target (fitness) function F. This function usually evaluates the quality with which the given candidate-solution tackles the problem. In our work, we employed the F-score as a fitness function.

In addition to the fitness function, we shall define the second domain-specific feature of the GA—the genetic representation of chromosomes. XGBoost and SVM classifiers will have their own representation of chromosomes which contain the discretized values of classifiers’ hyperparameters. However, since the considered k-NN method has only one significant parameter k (number of nearest neighbors), we omit the chromosome representation for this method and employ an exhaustive search to determine the significant features and k in the range [1, …, n − 1], where n is the number of samples in the training set. The ranges and discretized values of the hyperparameters of XGBoost and SVM, representing the corresponding alleles in chromosomes of GA, are illustrated in

Table 4. Content of chromosome of GA applied for optimizing the values of hyperparameters of SVM.

Allele (Hyperparameter)	Interval of Discretization	Range	Meaning
C	0.002	[0, 100]	Penalty parameter C of the error term
kernel	–	{linear, poly, rbf, sigmoid}	Specifies the kernel type to be used in SVM
degree	1	[1, 5]	Degree of the polynomial kernel function. Ignored by all other kernels
gamma	0.1	[0.01, 100]	Kernel coefficient for rbf, poly, and sigmoid
coef0	0.1	[0.01, 100]	Independent term in kernel function. Significant in poly and sigmoid
shrinking	–	{True, False}	Whether to use shrinking heuristic

and

Table 5. Content of chromosome of GA applied for optimizing the values of hyperparameters of XGBoost.

Allele (Hyperparameter)	Interval of Discretization	Range	Meaning
eta	0.002	[0, 1]	Step size shrinkage. Controls the learning rate in update and prevents overfitting
gamma	0.1	[0, 100]	Minimum loss reduction required to make a node split. Split happens when the resulting split gives a positive reduction in the loss function.
max_depth	1	[1, 20]	The maximum depth of a tree
min_child_weight	1	[1, 100]	Minimum sum of weights of all observations required in a child
subsample	0.002	(0.001, 1)	Subsample ratio of the training instance
colsample_bytree	0.001	(0.5, 1)	Subsample ratio of columns when constructing each tree
n_estimators	1	[100, 500]	The number of boosting stages to perform

.

With regard to the SVM chromosome, as described in Table 4, several hyperparameters become meaningless when a specific kernel is applied. In this case, GA ignores the pointless chromosome and, consequently, the CV score is not calculated. Besides the tuning of these hyperparameters, we also select the features pertinent to the dynamics of the accelerator pedal that should participate in the training of the classifier: mP, mR, and aR. Moreover, instead of selecting just two or three of these single features, we also consider additional (compound) features that are obtained by multiplication of these three single features.

The parameters of the GA framework are presented in

Table 6. Main parameters of GA.

Parameter	Value
Genotype	Each classifier has its own set of parameters (as shown in Table 4 and Table 5) encoded in the genotype. In addition, a fixed combination of features (pertinent to the dynamics of the accelerator pedal) is also incorporated into the genotype: {mP, aR}, {mP, mR}, {mR, aR}, {mP, aR, mR}, {mP, aR, mR, mP*aR}, {mP, aR, mR, mP*mR}, {mP, aR, mR, mR*aR}
Population size	40 individuals
Selection	Binary Tournament
Selection ratio	10%
Elite	Best 2 individuals
Crossover	Single-point
Mutation	Single-point
Mutation ratio	5%
Fitness value	F-score
Termination criteria	(#Generations > 100) or (Fitness Value = 100%)

. The genotype (chromosome) of GA comprises alleles, corresponding to the evolved values (as real numbers) of the hyperparameters of the considered classifiers. The considered size of the evolved population of chromosomes is 40 (parameter Population size in Table 6). The mating pool of each following generation consists of four chromosomes (10% of the population of 40 chromosomes, as indicated by the parameter Selection ratio in Table 6) selected via a binary selection mechanism (parameter Selection in Table 6) plus the best (elite) two chromosomes (parameter Elite in Table 6). The number of elite chromosomes is selected empirically to provide the best tradeoff between the convergence of evolution (yet preventing the premature convergence to suboptimal solutions) and diversity of population. The remaining 34 (of 40) chromosomes are produced by single-point crossover operations (parameter Crossover in Table 6) on pairs of chromosomes, randomly selected from the chromosomes in the mating pool. The chromosomes newly produced by crossover are mutated via single-point mutation (parameter Mutation in Table 6) with a probability of 5% (parameter Mutation ratio in Table 6). The details of the implementation of the binary selection, single-point crossover, and mutation operations are provided in [26].

5. Experimental Results

For the purpose of obtaining benchmark results for the considered EMC problem, we obtained the results of the simple threshold classifier on both the training set and testing set, and used these results as a benchmark. Later, we will compare the performance of the simple threshold classifier with the proposed learned classifiers on the same EMC problem. The performance of the simple threshold classifier is illustrated in

Table 7. Performance of simple threshold classifiers on training and testing set.

Metric	Classifier Based on mR Feature		Classifier Based on aR Feature
	Training Set	Testing Set	Training Set	Testing Set
Accuracy	0.769	0.791	0.888	0.873
Precision	1.000	1.000	0.964	0.980
Recall	0.461	0.513	0.671	0.610
F-score	0.631	0.677	0.791	0.752

.

In spite of the high precision, the threshold classifier has a very low recall and, as a consequence, a very low F-score. The reason for such a poor performance is that the classifier fails to classify many of the samples (events) of class “1” (emergency braking). By employing a single feature, the classifier fails on many samples of class “1” due to the existence of overlapping (“gray”) zones in the landscape of the classified cases. It is important to note that the threshold classifiers built on aR and mR miss different emergency braking samples. Moreover, the samples which were correctly classified by the mR-based threshold classifier were not classified correctly by the aR-based classifier, and vice versa. These facts illustrate that a simple thresholding of the rates of lifting the accelerator pedal would not result in a good quality of classification of emergency braking situations.

Unlike the one-dimensional classifier, k-NN performed much better with respect to the metrics under consideration. As can be seen from

Table 8. Performance of k-NN classifier on training and testing set.

Metric	5-NN Method		23-NN Method
	Training Set	Testing Set	Training Set	Testing Set
Accuracy	0.944	0.938	0.926	0.95
Precision	0.937	0.867	0.918	0.896
Recall	0.933	0.951	0.908	0.951
F-score	0.935	0.907	0.913	0.923

, k-NN with k = 23 and the best feature combination of {mP, aR, mR} (obtained through exhaustive search) performs slightly better than that with the default value of the parameter (k = 5). We notice that the accuracy, F-score, and recall of 23-NN on the testing set are higher than the same metrics on the training set. We speculate that the reason for this result is that either the training set has many “difficult” cases to learn or the testing set has “easier” cases to predict (or, the combination of both).

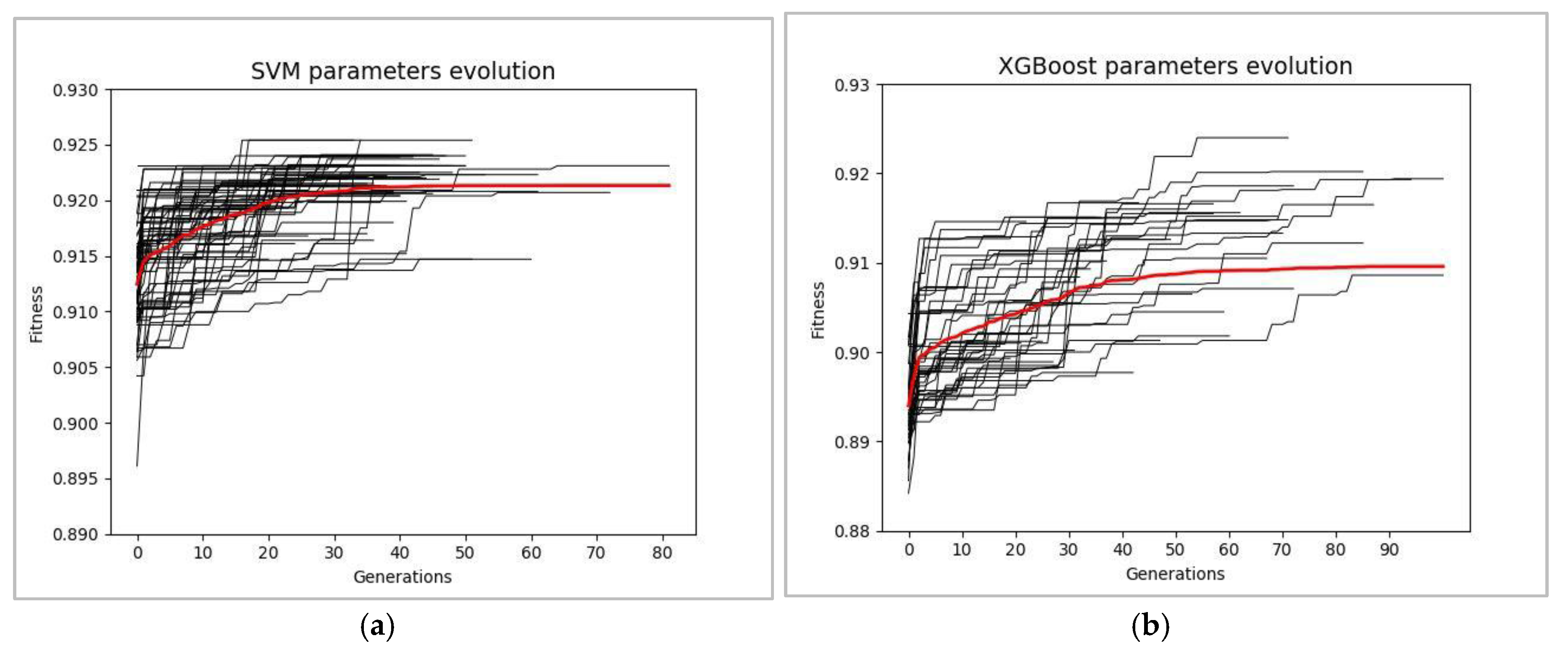
As a result of applying GA both (i) for tuning the hyperparameters of XGBoost and SVM classifiers and (ii) for configuring the combinations of features pertinent to the dynamics of the accelerator, in the best of multiple independent runs of GA, the value of the F-score for the XGBoost and SVM classifiers reached 0.924 and 0.925, respectively. The convergence of the fitness value (CV F-score) during 100 independent runs of GA for XGBoost and SVM classifiers is shown in Figure 11.

The sample best-evolved chromosomes containing the optimal values of hyperparameters of SVM and XGBoost are shown in

Table 9. Best-evolved values of hyperparameters of SVM.

Allele (Hyperparameter)	Value Obtained via GA
C	0.802
kernel	rbf
gamma	0.8
coef0	9.0
shrinkage	True
features	{mP, aR, mR}

and

Table 10. Best-evolved values of hyperparameters of XGBoost.

Allele (Hyperparameter)	Optimal Value Obtained via GA
eta	0.374
gamma	6.6
max_depth	3
min_child_weight	2
subsample	0.454546
colsample_bytree	0.624
n_estimators	96
features	{mP, aR, mR, mP*aR}

, respectively.

Similar to the results obtained via other nature-inspired optimization approaches (genetic programming, evolutionary strategies, neural networks, etc.), the exact values evolved via GA are hard to interpret, due to both (i) the enormous complexity of the computational structures they define and (ii) the lack of any human-understandable logic—e.g., similar to that of the “canonical” top-down problem-solving approaches—applied in the process of obtaining these solutions. However, some of the SVM evolved parameters are similar to the default parameters of the scikit-learn SVM [29] which will cause almost identical results for these classifiers. With regard to XGBoost, the max_depth parameter which was obtained via GA is similar to the one that was obtained empirically by the author of XGBoost [22]. Despite this, the usual mechanisms of adjustment of the parameters are more like an art than a science, and each problem requires its own unique combinations of the values of hyperparameters of the learning method. In this sense, as both a holistic and heuristic approach, GA contributed to the relatively fast, automated optimization of the hyperparameters of XGBoost.

As show in

Table 11. Performance of SVM classifiers on training and testing sets.

Metric	Default SVM Classifier		Evolved SVM Classifier
	Training Set	Testing Set	Training Set	Testing Set
Accuracy	0.9348	0.95	0.9396	0.95
Precision	0.9479	0.9058	0.9465	0.9058
Recall	0.8971	0.939	0.9105	0.939
F-score	0.9218	0.9221	0.9281	0.9221

, the evolved SVM classifier performed in the same way as the default SVM classifier on the testing set and showed very close results on the training set.

The comparison between the evolved XGBoost and out-of-the-box XGBoost classifiers is shown in

Table 12. Performance of evolved XGBoost classifier on training and testing sets.

Metric	Default XGBoost		Evolved XGBoost
	Training Set	Testing Set	Training Set	Testing Set
Accuracy	0.9502	0.9461	0.953	0.9538
Precision	0.954	0.8953	0.9461	0.917
Recall	0.9284	0.939	0.944	0.939
F-score	0.941	0.917	0.9451	0.9277

; XGBoost with evolved values of hyperparameters demonstrated better results on the testing set than XGBoost with the default values of these parameters [32].

With respect to each metric under consideration, the evolved XGBoost demonstrated the best results on both the training and testing sets (

Table 13. Comparison of best classifiers.

Metric	23-NN Method	Default (and Evolved) SVM	Evolved XGBoost
Accuracy	0.95	0.95	0.9538
Precision	0.896	0.9058	0.917
Recall	0.951	0.939	0.939
F-score	0.923	0.9221	0.9277

). This classifier also featured a higher generalization ability manifested by a superior fitness value (CV F-score).

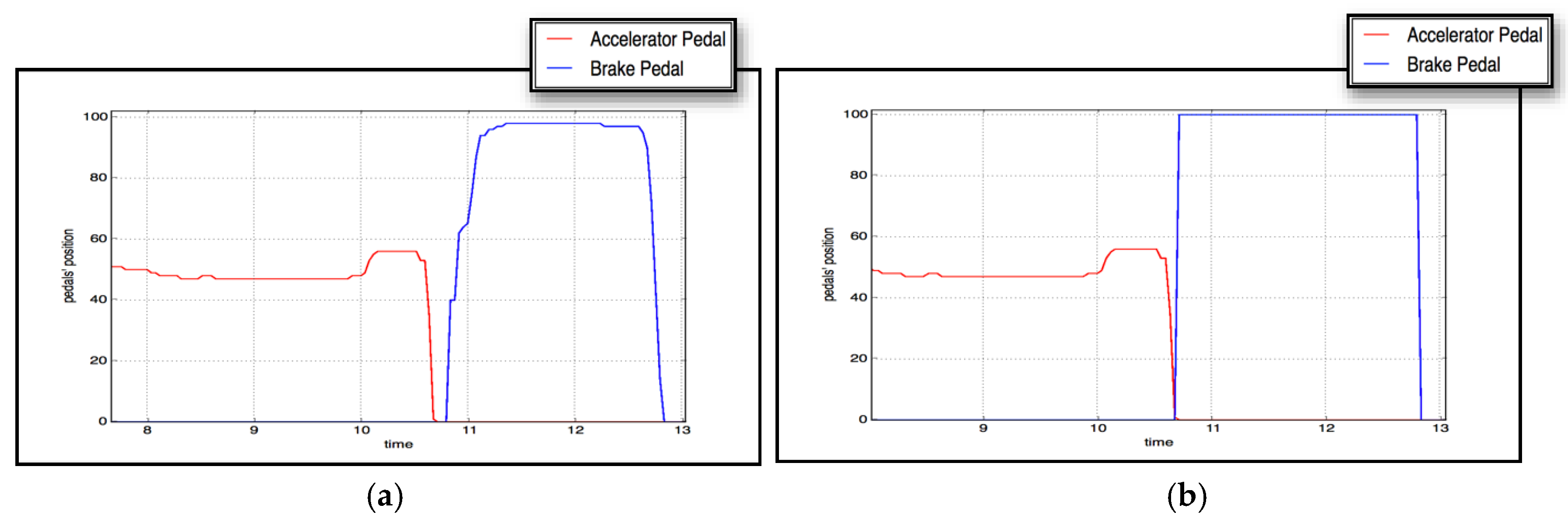
Due to the superiority of the evolved XGBoost classifier over the others, we integrated it into the braking assistant in the full-scale Forum-8 driving simulator. The sample dynamics of the accelerator and brake pedals in two cases of emergency braking—with and without automated braking activated by the driver-supporting agent—are shown in Figure 12.

6. Discussion

In a real-world driving situation, the most critical error might be in false positive cases, i.e., when automated braking is activated in an incorrectly classified emergency braking situation. It may seem that this error is a potentially dangerous one, as it may increase the likelihood of rear-end collision with the vehicle(s) traveling behind. However, our system is supposed to activate the emergency braking for a very brief period of time that is equivalent to the average delay of the driver’s response. We assume that the driver behind respects the common 3 s rule, which claims that each driver should always keep a safe distance in order to have enough time to respond to problems in front of his/her car.

As can be seen from

Table 14. The effect of FP on the reduction of distances to the following car.

Speed of the Car		Distance between Two Cars, m		Reduction of the Distance to the Following Car as a Result of Eventual False Positive Emergency Braking of 200 ms, m
km/h	m/s	For 3 s Interval between Cars (Marginal)	For 6 s Interval between Cars (Good)
36	10	30	60	2
54	15	45	90	3
72	20	60	180	4
90	25	75	150	5
108	30	90	180	6
126	35	105	210	7

, in the case of a wrongly classified situation the amount of braking would be insignificant, and would never cause a dangerous situation on the road. In cases of actual emergency braking situations, however, the driver would press the brake pedal just before the disengagement of the (brief) automated braking. This will ensure both early (due to the automated braking) and continuous (due to the driver’s input) braking of the car in actual emergency braking situations.

Nevertheless, our best classifier made several mistakes: 5 FN, 7 FP. Obviously, FN will not cause inconvenience to the driver; however, FP may lead to uncomfortable driving. It is probable that the incorrect classification is a result of either wrong sample marking by the expert in the testing set or wrong sample marking in the training set which caused the XGBoost classifier to learn on noisy samples. Another possible reason for the mistakenly classified samples might be the prevalence of similar driving style samples in the training dataset. For instance, if one driver prefers a fast driving style, the way he or she releases the accelerator pedal will definitely differ from the quiet driving style. This can result in “uncertain” output of the XGBoost classifier. For example, several instances from the training and testing sets have the output value close to 0.5, which indicates that XGBoost “doubts”. A way of improving this possible drawback will be investigated in further research.

7. Conclusions

We examined the feasibility of classifying the emergency braking situations in road vehicles solely from the motion pattern of the accelerator pedal. We compared the classifiers and employed genetic algorithms to tune the hyperparameters associated with them. With regard to the performance of all classifiers under consideration, XGBoost showed the best results for the EBC problem. The experimental results suggest that the evolved classifier detects the emergency braking situations with an accuracy of about 95% on the test set of offline time series data of the dynamics of the accelerator pedal.

In our future work, we are planning to investigate ways to further improve the quality of the classifier. We are considering alternative approaches for the training of the latter. Also, we intend to increase the data set and to get rid of noise (both for training and testing) in order to obtain more general and more robust classifier(s).

Our ultimate objective would be an implementation of a brake assistant that would be the best fit to the driving style of a particular driver. Thus, we contemplate an incremental approach of training the classifier: first, to train a general classifier offline on a wide set of training data and, then, to adapt the general classifier online to the driving style of a particular driver.