Iterative Parameter Estimation Algorithms for Dual-Frequency Signal Models
Abstract
:1. Introduction
2. The Gradient-Based Iterative Parameter Estimation Algorithm
- Let , give a small number and set the initial value , is generally taken to be a large positive number, e.g., .
- Collect the observed data , , where L is the data length, form by Equation (10).
- Form by Equation (13) and by Equation (11).
- Form by Equation (14) and by Equation (12).
- Choose a larger satisfying Equation (16), and update the estimate by Equation (15).
- Compare with , if , then terminate this procedure and obtain the iteration time k and the estimate ; otherwise, increase k by 1 and go to Step 3.
3. The Newton Iterative Parameter Estimation Algorithm
- Let , give the parameter estimation accuracy , set the initial value .
- Collect the observed data , , form by Equation (19).
- Form by Equation (22), form by Equation (20).
- Form by Equation (23), form by Equation (21).
- Compute by Equations (25)–(34), , , and form by Equation (24).
- Update the estimate by Equation (35).
- Compare with , if , then terminate this procedure and obtain the estimate ; otherwise, increase k by 1 and go to Step 3.
4. The Moving Data Window Gradient-Based Iterative Algorithm
- Pre-set the length of p, let , give the parameter estimation accuracy and the iterative length .
- To initialize, let , , .
- Collect the observed data , form by Equation (43).
- Form by Equation (45), form by Equation (42).
- Form by Equation (46), form by Equation (44).
- Select a larger satisfying Equation (48), update the estimate by Equation (47).
- If , increase k by 1 and go to Step 4; otherwise, go to the next step.
- Compare with , if , then let , , go to Step 2; otherwise, obtain the parameter estimate , terminate this procedure.
5. Examples
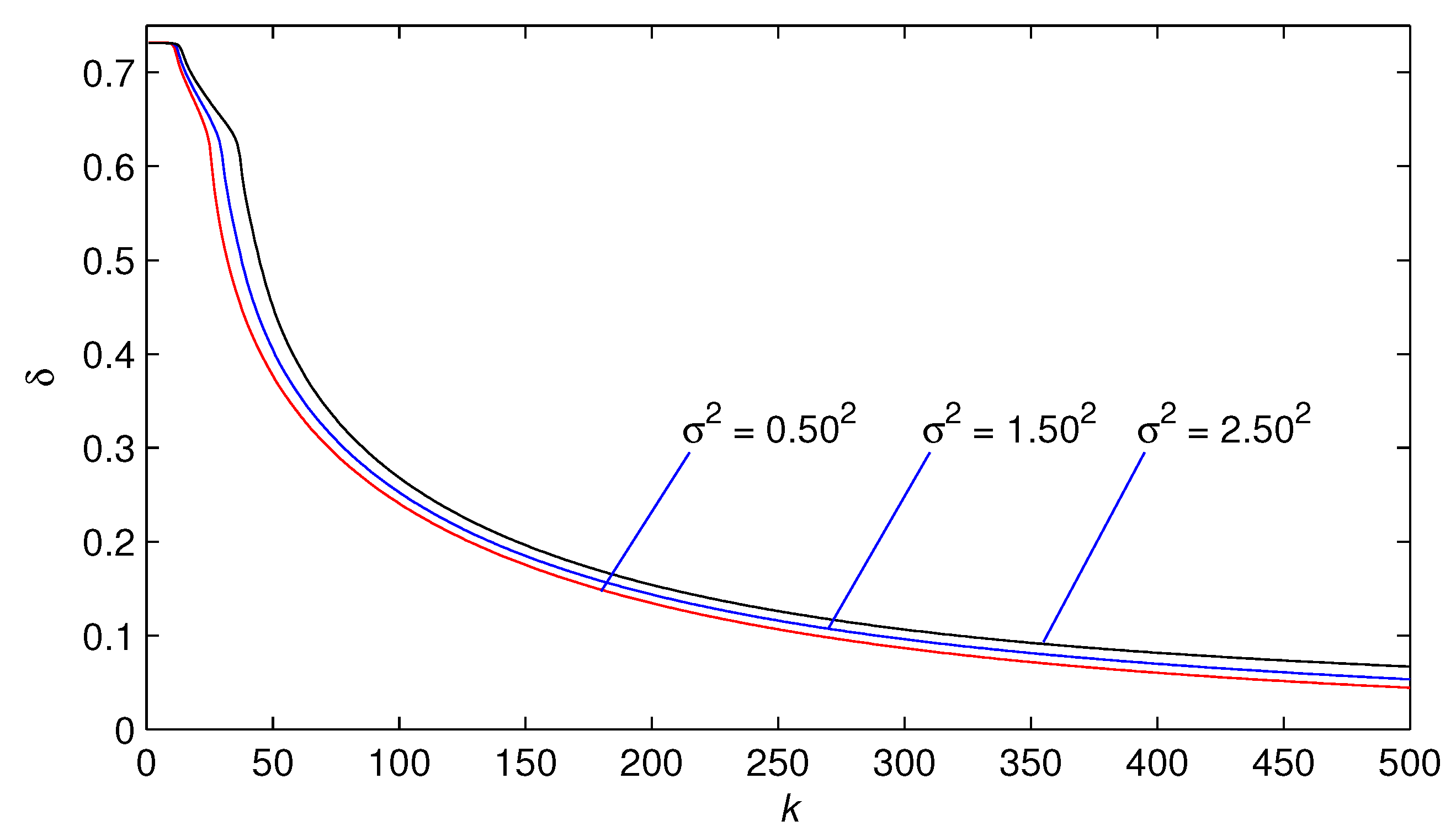
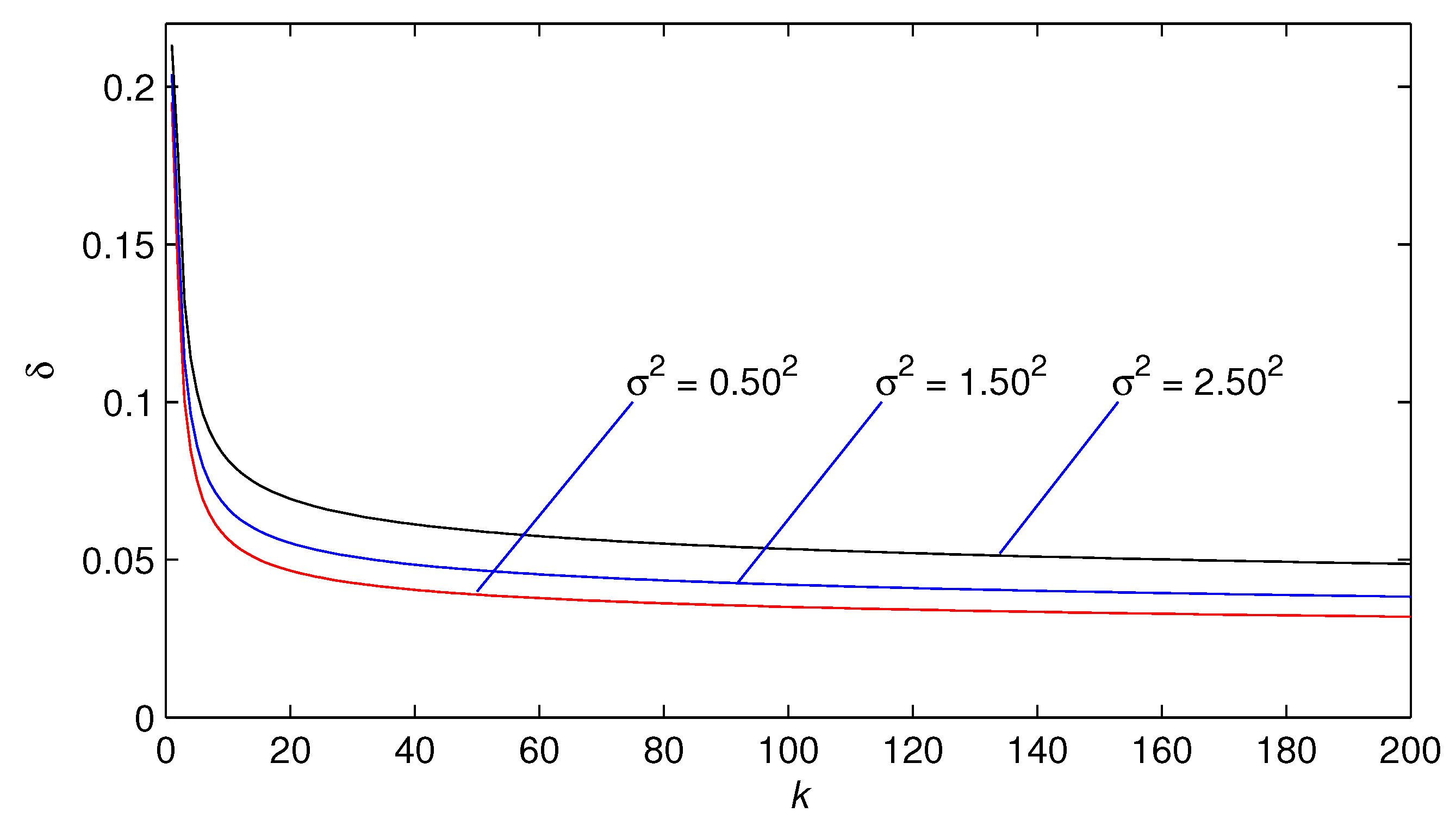
- The parameter estimation errors obtained by the presented three algorithms gradually decreasing trend as the iterative variable k increases.
- The parameter estimation errors given by three algorithms become smaller with the noise variance decreasing.
- In the simulation, these three algorithms are fulfilled in the same conditions (), and the estimated models obtained by the MDW-GI and NI algorithms have higher accuracy than the GI algorithm.
- The outputs of estimated signal are very close to the actual signal model . In other words, the estimated model can capture the dynamics of the signal.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ding, F. Complexity, convergence and computational efficiency for system identification algorithms. Control Decis. 2016, 31, 1729–1741. [Google Scholar]
- Ding, F.; Wang, F.F. Recursive least squares identification algorithms for linear-in-parameter systems with missing data. Control Decis. 2016, 31, 2261–2266. [Google Scholar]
- Xu, L. Moving data window based multi-innovation stochastic gradient identification method for transfer functions. Control Decis. 2017, 32, 1091–1096. [Google Scholar]
- Xu, L.; Ding, F. Recursive least squares and multi-innovation stochastic gradient parameter estimation methods for signal modeling. Syst. Signal Process. 2017, 36, 1735–1753. [Google Scholar] [CrossRef]
- Xu, L. The parameter estimation algorithms based on the dynamical response measurement data. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef]
- Zhang, Q.G. The Rife frequency estimation algorithm based on real-time FFT. Signal Process. 2009, 25, 1002–1004. [Google Scholar]
- Yang, C.; Wei, G. A noniterative frequency estimator with rational combination of three spectrum lines. IEEE Trans. Signal Process. 2011, 59, 5065–5070. [Google Scholar] [CrossRef]
- Jacobsen, E.; Kootsookos, P. Fast accurate frequency estimators. IEEE Signal Process. Mag. 2007, 24, 123–125. [Google Scholar] [CrossRef]
- Deng, Z.M.; Liu, H.; Wang, Z.Z. Modified Rife algorithm for frequency estimation of sinusoid wave. J. Data Acquis. Process. 2006, 21, 473–477. [Google Scholar]
- Elasmi-Ksibi, R.; Besbes, H.; López-Valcarce, R.; Cherif, S. Frequency estimation of real-valued single-tone in colored noise using multiple autocorrelation lags. Signal Process. 2010, 90, 2303–2307. [Google Scholar] [CrossRef]
- So, H.C.; Chan, K.W. Reformulation of Pisarenko harmonic decomposition method for single-tone frequency estimation. IEEE Trans. Signal Process. 2004, 52, 1128–1135. [Google Scholar] [CrossRef]
- Cao, Y.; Wei, G.; Chen, F.J. An exact analysis of modified covariance frequency estimation algorithm based on correlation of single-tone. Signal Process. 2012, 92, 2785–2790. [Google Scholar] [CrossRef]
- Boashash, B.; Khan, N.A.; Ben-Jabeur, T. Time-frequency features for pattern recognition using high-resolution TFDs: A tutorial review. Digit. Signal Process. 2015, 40, 1–30. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. A new music-empirical wavelet transform methodology for time-frequency analysis of noisy nonlinear and non-stationary signals. Digit. Signal Process. 2015, 45, 56–68. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.F.; Wu, H.T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Ding, F.; Xu, L.; Liu, X.M. Signal modeling—Part A: Single-frequency signals. J. Qingdao Univ. Sci. Technol. (Nat. Sci. Ed.) 2017, 38, 1–13. (In Chinese) [Google Scholar]
- Ding, F.; Xu, L.; Liu, X.M. Signal modeling—Part B: Dual-frequency signals. J. Qingdao Univ. Sci. Technol. (Nat. Sci. Ed.) 2017, 38, 1–17. (In Chinese) [Google Scholar]
- Ding, F.; Xu, L.; Liu, X.M. Signal modeling—Part C: Recursive parameter estimation for multi-frequency signal models. J. Qingdao Univ. Sci. Technol. (Nat. Sci. Ed.) 2017, 38, 1–12. (In Chinese) [Google Scholar]
- Ding, F.; Xu, L.; Liu, X.M. Signal modeling—Part D: Iterative parameter estimation for multi-frequency signal models. J. Qingdao Univ. Sci. Technol. (Nat. Sci. Ed.) 2017, 38, 1–11. (In Chinese) [Google Scholar]
- Ding, F.; Xu, L.; Liu, X.M. Signal modeling—Part E: Hierarchical parameter estimation for multi-frequency signal models. J. Qingdao Univ. Sci. Technol. (Nat. Sci. Ed.) 2017, 38, 1–15. (In Chinese) [Google Scholar]
- Ding, F.; Xu, L.; Liu, X.M. Signal modeling—Part F: Hierarchical iterative parameter estimation for multi-frequency signal models. J. Qingdao Univ. Sci. Technol. (Nat. Sci. Ed.) 2017, 38, 1–12. (In Chinese) [Google Scholar]
- Ding, J.L. Data filtering based recursive and iterative least squares algorithms for parameter estimation of multi-input output systems. Algorithms 2016, 9. [Google Scholar] [CrossRef]
- Yun, B.I. Iterative methods for solving nonlinear equations with finitely many roots in an interval. J. Comput. Appl. Math. 2013, 236, 3308–3318. [Google Scholar] [CrossRef]
- Dehghan, M.; Hajarian, M. Analysis of an iterative algorithm to solve the generalized coupled Sylvester matrix equations. Appl. Math. Model. 2011, 35, 3285–3300. [Google Scholar] [CrossRef]
- Wang, T.; Zheng, Q.Q.; Lu, L.Z. A new iteration method for a class of complex symmetric linear systems. J. Comput. Appl. Math. 2017, 325, 188–197. [Google Scholar] [CrossRef]
- Xu, L. Application of the Newton iteration algorithm to the parameter estimation for dynamical systems. J. Comput. Appl. Math. 2015, 288, 33–43. [Google Scholar] [CrossRef]
- Pei, K.; Wang, G.T.; Sun, Y.Y. Successive iterations and positive extremal solutions for a Hadamard type fractional integro-differential equations on infinite domain. Appl. Math. Comput. 2017, 312, 158–168. [Google Scholar] [CrossRef]
- Dehghan, M.; Hajarian, M. Fourth-order variants of Newtons method without second derivatives for solving nonlinear equations. Eng. Comput. 2012, 29, 356–365. [Google Scholar] [CrossRef]
- Gutiérrez, J.M. Numerical properties of different root-finding algorithms obtained for approximating continuous Newton’s method. Algorithms 2015, 8, 1210–1216. [Google Scholar] [CrossRef]
- Wang, X.F.; Qin, Y.P.; Qian, W.Y.; Zhang, S.; Fan, X.D. A family of Newton type iterative methods for solving nonlinear equations. Algorithms 2015, 8, 786–798. [Google Scholar] [CrossRef]
- Simpson, T. The Nature and Laws of Chance; University of Michigan Library: Ann Arbor, MI, USA, 1740. [Google Scholar]
- Dennis, J.E.; Schnable, R.B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1983. [Google Scholar]
- Jürgen, G. Accelerated convergence in Newton’s method. Soc. Ind. Appl. Math. 1994, 36, 272–276. [Google Scholar]
- Djoudi, M.S.; Kennedy, D.; Williams, F.W. Exact substructuring in recursive Newton’s method for solving transcendental eigenproblems. J. Sound Vib. 2005, 280, 883–902. [Google Scholar] [CrossRef]
- Benner, P.; Li, J.R.; Penzl, T. Numerical solution of large-scale Lyapunov equations, Riccati equations, and linear-quadratic optimal control problems. Numer. Linear Algebra Appl. 2008, 15, 755–777. [Google Scholar] [CrossRef]
- Seinfeld, D.R.; Haddad, W.M.; Bernstein, D.S.; Nett, C.N. H2/H∞ controller synthesis: Illustrative numerical results via quasi-newton methods. Numer. Linear Algebra Appl. 2008, 15, 755–777. [Google Scholar]
- Liu, M.M.; Xiao, Y.S.; Ding, R.F. Iterative identification algorithm for Wiener nonlinear systems using the Newton method. Appl. Math. Model. 2013, 37, 6584–6591. [Google Scholar] [CrossRef]
- Curry, H.B. The method of steepest descent for non-linear minimization problems. Q. Appl. Math. 1944, 2, 258–261. [Google Scholar] [CrossRef]
- Vrahatis, M.N.; Androulakis, G.S.; Lambrinos, J.N.; Magoulas, G.D. A class of gradient unconstrained minimization algorithms with adaptive stepsize. J. Comput. Appl. Math. 2000, 114, 367–386. [Google Scholar] [CrossRef]
- Hajarian, M. Solving the general Sylvester discrete-time periodic matrix equations via the gradient based iterative method. Appl. Math. Lett. 2016, 52, 87–95. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J.Y.; Zhang, T.S. Operational modal analysis for slow linear time-varying structures based on moving window second order blind identification. Signal Process. 2017, 133, 169–186. [Google Scholar] [CrossRef]
- Al-Matouq, A.A.; Vincent, T.L. Multiple window moving horizon estimation. Automatica 2015, 53, 264–274. [Google Scholar] [CrossRef]
- Boashash, B. Estimating and interpreting the instantaneous frequency of a signal—Part 1: Fundamentals. Proc. IEEE 1992, 80, 520–538. [Google Scholar] [CrossRef]


| k | a | b | ||||
|---|---|---|---|---|---|---|
| 10 | 0.55350 | 0.55350 | 0.00064 | 0.00148 | 73.11514 | |
| 20 | 0.61211 | 0.61528 | 0.03325 | 0.14768 | 68.89718 | |
| 50 | 1.06694 | 1.08276 | 0.00000 | 0.58116 | 45.10172 | |
| 100 | 1.20074 | 1.56991 | 0.00002 | 0.56483 | 26.83480 | |
| 200 | 1.28232 | 1.88059 | 0.00018 | 0.56030 | 15.39800 | |
| 500 | 1.34925 | 2.12940 | 0.01473 | 0.55767 | 6.68183 | |
| 10 | 0.55290 | 0.55290 | 0.00212 | 0.00487 | 73.10844 | |
| 20 | 0.63483 | 0.63629 | 0.02549 | 0.17931 | 67.62638 | |
| 50 | 1.10299 | 1.20478 | 0.00002 | 0.56478 | 40.47663 | |
| 100 | 1.21921 | 1.60904 | 0.00014 | 0.55812 | 25.26461 | |
| 200 | 1.29994 | 1.90343 | 0.00137 | 0.55428 | 14.36541 | |
| 500 | 1.37665 | 2.14898 | 0.03582 | 0.55443 | 5.33204 | |
| 10 | 0.55237 | 0.55240 | 0.00604 | 0.01387 | 73.04062 | |
| 20 | 0.65958 | 0.65653 | 0.01624 | 0.21377 | 66.34478 | |
| 50 | 1.09460 | 1.28918 | 0.00009 | 0.55852 | 37.71802 | |
| 100 | 1.22332 | 1.64271 | 0.00026 | 0.55228 | 24.07888 | |
| 200 | 1.31323 | 1.92538 | 0.00158 | 0.54864 | 13.44312 | |
| 500 | 1.39090 | 2.17489 | 0.02450 | 0.54741 | 4.43172 | |
| True values | 1.48000 | 2.25000 | 0.06000 | 0.55000 | ||
| k | a | b | ||||
|---|---|---|---|---|---|---|
| 1 | 1.83060 | 1.78268 | 0.09923 | 0.52087 | 21.32333 | |
| 2 | 1.84736 | 1.93621 | 0.13360 | 0.55852 | 17.77782 | |
| 10 | 1.68078 | 2.16420 | 0.11020 | 0.56216 | 8.16074 | |
| 20 | 1.65675 | 2.19656 | 0.10597 | 0.56159 | 6.93411 | |
| 100 | 1.62036 | 2.23024 | 0.09748 | 0.55889 | 5.34256 | |
| 200 | 1.60860 | 2.23778 | 0.09416 | 0.55763 | 4.86795 | |
| 1 | 1.80786 | 1.79728 | 0.09883 | 0.52380 | 20.40210 | |
| 2 | 1.78233 | 1.95654 | 0.12241 | 0.55564 | 15.49323 | |
| 10 | 1.63563 | 2.16656 | 0.10287 | 0.56022 | 6.61985 | |
| 20 | 1.61619 | 2.19588 | 0.09943 | 0.56005 | 5.53200 | |
| 100 | 1.58796 | 2.22530 | 0.09256 | 0.55823 | 4.20939 | |
| 200 | 1.57898 | 2.23150 | 0.08988 | 0.55730 | 3.82961 | |
| 1 | 1.78529 | 1.81118 | 0.09845 | 0.52670 | 19.51195 | |
| 2 | 1.73467 | 1.97038 | 0.11519 | 0.55453 | 13.90292 | |
| 10 | 1.60314 | 2.16384 | 0.09847 | 0.55978 | 5.65377 | |
| 20 | 1.58703 | 2.19039 | 0.09570 | 0.55991 | 4.65522 | |
| 100 | 1.56461 | 2.21617 | 0.09023 | 0.55871 | 3.50636 | |
| 200 | 1.55766 | 2.22129 | 0.08812 | 0.55803 | 3.19386 | |
| True values | 1.48000 | 2.25000 | 0.06000 | 0.55000 | ||
| p | k | a | b | |||
|---|---|---|---|---|---|---|
| 100 | 1 | 1.58254 | 1.64339 | 0.07785 | 0.57750 | 22.40827 |
| 2 | 1.87594 | 1.97597 | 0.11125 | 0.57907 | 17.64461 | |
| 5 | 1.83227 | 2.00369 | 0.11020 | 0.57801 | 15.77345 | |
| 10 | 1.77887 | 2.05136 | 0.10879 | 0.57605 | 13.20660 | |
| 20 | 1.69892 | 2.12339 | 0.10526 | 0.57220 | 9.37923 | |
| 50 | 1.57751 | 2.23398 | 0.09153 | 0.56174 | 3.79684 | |
| 200 | 1 | 1.78604 | 1.85970 | 0.10256 | 0.57011 | 18.12068 |
| 2 | 1.81880 | 1.95055 | 0.10931 | 0.57243 | 16.56384 | |
| 5 | 1.73791 | 2.01245 | 0.10997 | 0.57420 | 12.91251 | |
| 10 | 1.64148 | 2.08926 | 0.10871 | 0.57449 | 8.52118 | |
| 20 | 1.53916 | 2.17165 | 0.09906 | 0.56944 | 3.90746 | |
| 50 | 1.47938 | 2.22055 | 0.08073 | 0.56051 | 1.36478 | |
| 300 | 1 | 1.74606 | 1.85586 | 0.10881 | 0.56979 | 17.40188 |
| 2 | 1.78854 | 1.97309 | 0.11616 | 0.57303 | 15.23989 | |
| 5 | 1.69704 | 2.05038 | 0.11528 | 0.57458 | 10.94891 | |
| 10 | 1.59705 | 2.12840 | 0.10877 | 0.57251 | 6.44220 | |
| 20 | 1.50943 | 2.19678 | 0.09034 | 0.56412 | 2.52463 | |
| 50 | 1.46715 | 2.23197 | 0.07030 | 0.55621 | 0.91639 | |
| True values | 1.48000 | 2.25000 | 0.06000 | 0.55000 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Xu, L.; Ding, F. Iterative Parameter Estimation Algorithms for Dual-Frequency Signal Models. Algorithms 2017, 10, 118. https://doi.org/10.3390/a10040118
Liu S, Xu L, Ding F. Iterative Parameter Estimation Algorithms for Dual-Frequency Signal Models. Algorithms. 2017; 10(4):118. https://doi.org/10.3390/a10040118
Chicago/Turabian StyleLiu, Siyu, Ling Xu, and Feng Ding. 2017. "Iterative Parameter Estimation Algorithms for Dual-Frequency Signal Models" Algorithms 10, no. 4: 118. https://doi.org/10.3390/a10040118
APA StyleLiu, S., Xu, L., & Ding, F. (2017). Iterative Parameter Estimation Algorithms for Dual-Frequency Signal Models. Algorithms, 10(4), 118. https://doi.org/10.3390/a10040118




