Water Uptake Behavior and Young Modulus Prediction of Composites Based on Treated Sisal Fibers and Poly(Lactic Acid)
Abstract
:1. Introduction
2. Experimental
2.1. Materials
2.2. Fiber Surface Treatments
2.3. Compounding and Processing of Composites
2.4. Contact Angle Measurements
2.5. Water Uptake
2.5.1. Mechanical Properties of Composites
2.5.2. Scanning Electron Microscopy
2.6. Analysis of Young Modulus
2.6.1. Hill Equation
2.6.2. Halpin–Tsai Equation
2.6.3. Shear-Lag Analysis
3. Results and Discussion
3.1. Contact Angle and Water Drop Absorption
3.2. Water Uptake of Composites
Effect of Water Uptake on Mechanical Properties
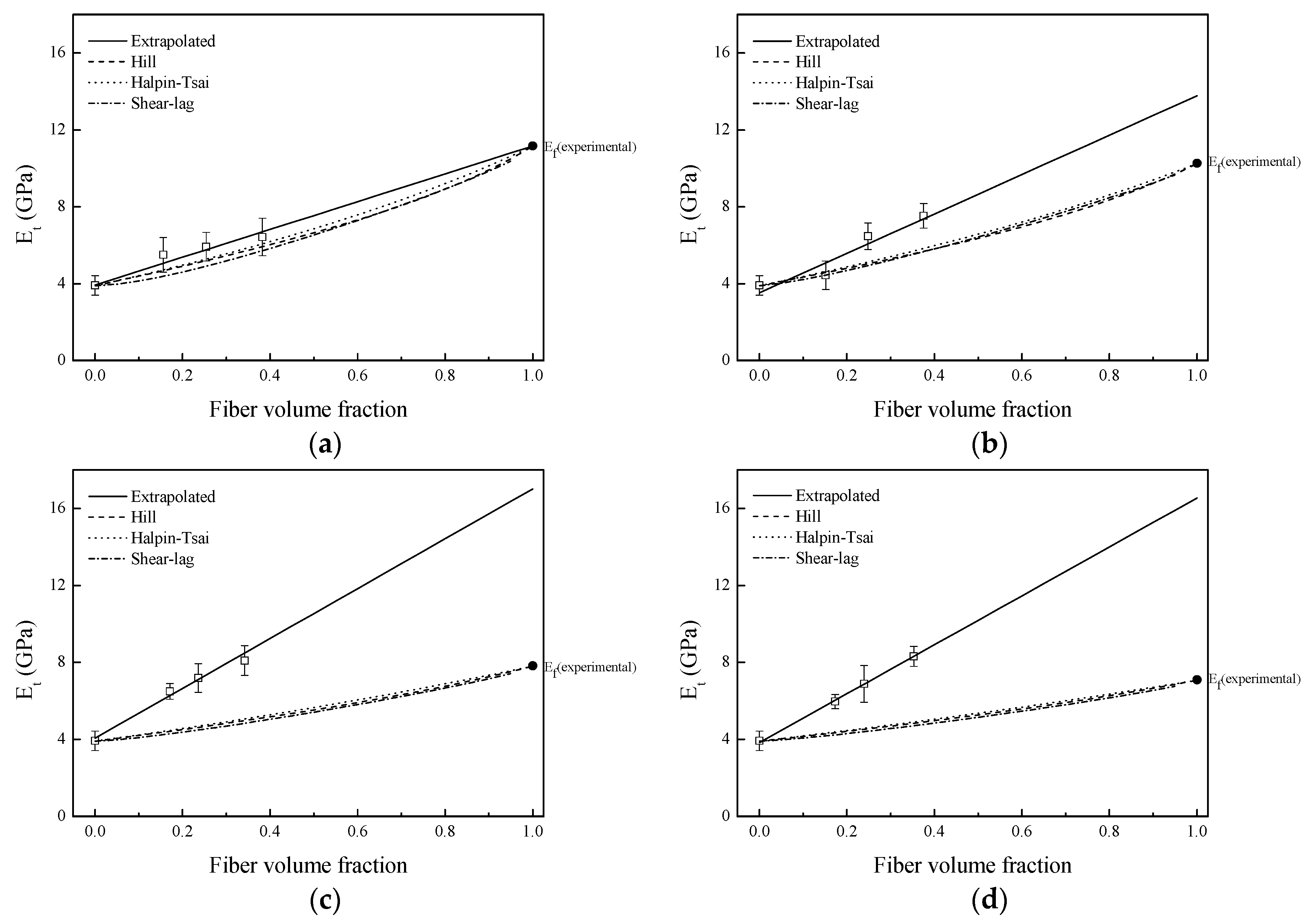
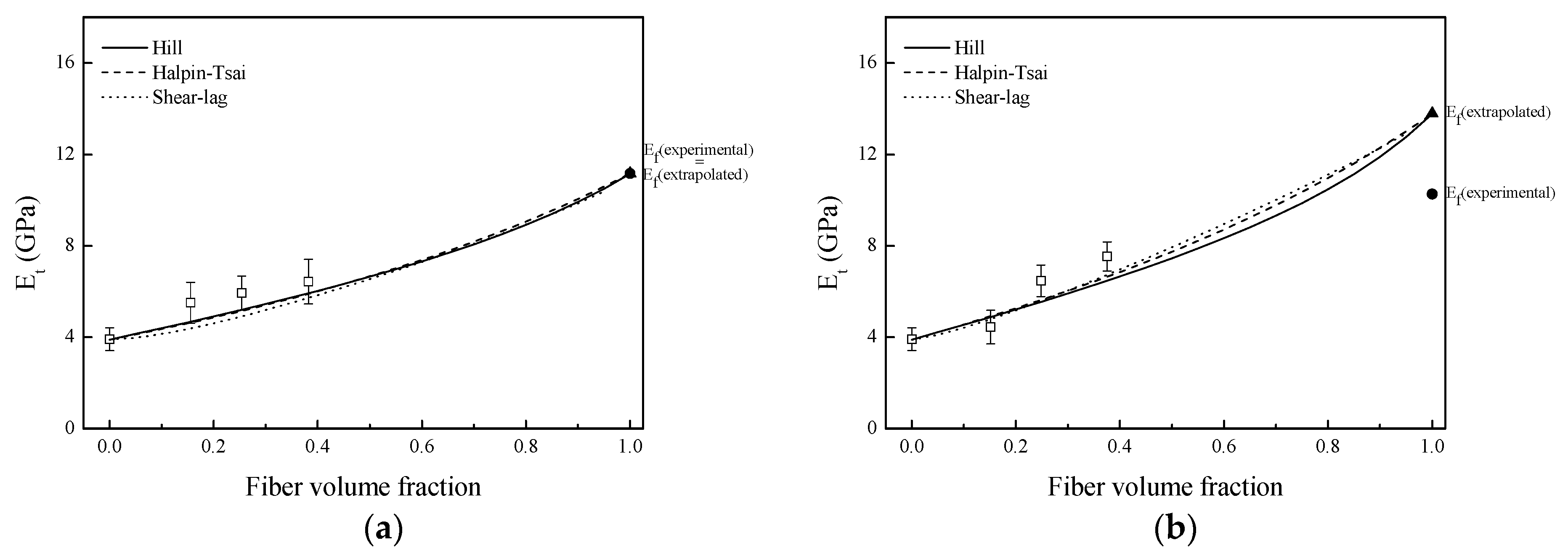
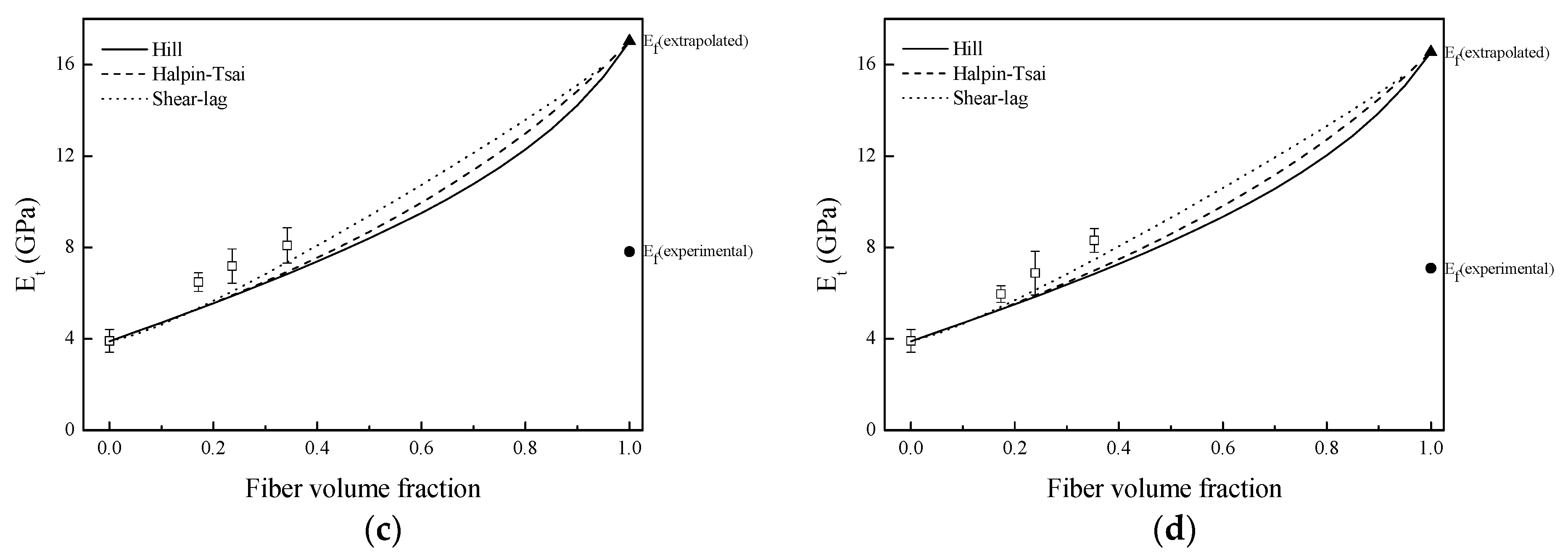
3.3. Young Modulus Prediction
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Arbelaiz, A.B.; Fernández, B.; Ramos, J.A.; Retegi, A.; Llano-Ponte, R.; Mondragon, I. Mechanical properties of short flax fibre bundle/polypropylene composites: Influence of matrix/fibre modification, fibre content, water uptake and recycling. Compos. Sci. Technol. 2006, 65, 1582–1592. [Google Scholar] [CrossRef]
- Cantero, G.; Arbelaiz, A.; Mugika, F.; Valea, A.; Mondragon, I. Mechanical behaviour of wood/polypropylene composites: Effects of fibre treatments and ageing processes. J. Reinf. Plast. Comp. 2003, 22, 37–50. [Google Scholar] [CrossRef]
- Orue, A.; Jauregi, A.; Peña-Rodriguez, C.; Labidi, J.; Eceiza, A.; Arbelaiz, A. The effect of surface modifications on sisal fiber properties and sisal/poly (lactic acid) interface adhesion. Compos. Part B Eng. 2015, 73, 132–138. [Google Scholar] [CrossRef]
- Raj, G.; Balnois, E.; Baley, C.; Grohens, Y. Role of Polysaccharides on Mechanical and Adhesion Properties of Flax Fibres in Flax/PLA Biocomposite. Int. J. Polym. Sci. 2011, 2011, 1–11. [Google Scholar] [CrossRef]
- Orue, A.; Jauregi, A.; Unsuain, U.; Labidi, J.; Eceiza, A.; Arbelaiz, A. The effect of alkaline and silane treatments on mechanical properties and breakage of sisal fibers and poly(lactic acid)/sisal fiber composites. Compos. Part A Appl. Sci. Manuf. 2016, 84, 186–195. [Google Scholar] [CrossRef]
- Arbelaiz, A.; Cantero, G.; Fernández, B.; Mondragon, I.; Gañán, P.; Kenny, J.M. Flax fiber surface modifications: Effects on fiber physico mechanical and flax/polypropylene interface properties. Polym. Compos. 2005, 26, 324–332. [Google Scholar] [CrossRef]
- Fernandes, E.M.; Mano, J.F.; Reis, R.L. Hybrid cork-polymer composites containing sisal fibre: Morphology, effect of the fibre treatment on the mechanical properties and tensile failure prediction. Compos. Struct. 2013, 105, 153–162. [Google Scholar] [CrossRef]
- Zou, H.; Wang, L.; Gan, H.; Yi, C. Effect of fiber surface treatments on the properties of short sisal fiber/poly(lactic acid) biocomposites. Polym. Compos. 2012, 33, 1659–1666. [Google Scholar] [CrossRef]
- Aziz, S.H.; Ansell, M.P. The effect of alkalization and fibre alignment on the mechanical and thermal properties of kenaf and hemp bast fibre composites: Part 1-polyester resin matrix. Compos. Sci. Technol. 2004, 64, 1219–1230. [Google Scholar] [CrossRef]
- Demir, H.; Atikler, U.; Balköse, D.; Tıhmınlıoğlu, F. The effect of fiber surface treatments on the tensile and water sorption properties of polypropylene–luffa fiber composites. Compos. Part A Appl. Sci. Manuf. 2006, 37, 447–456. [Google Scholar] [CrossRef]
- Abdelmouleh, M.; Boufi, S.; Belgacem, M.N.; Dufresne, A. Short natural-fibre reinforced polyethylene and natural rubber composites: Effect of silane coupling agents and fibres loading. Compos. Sci. Technol. 2007, 67, 1627–1639. [Google Scholar] [CrossRef]
- Rong, M.Z.; Zhang, M.Q.; Liu, Y.; Yang, G.C.; Zeng, H.M. The effect of fiber treatment on the mechanical properties ofunidirectional sisal-reinforced epoxy composites. Compos. Sci. Technol. 2001, 61, 1437–1447. [Google Scholar] [CrossRef]
- Huda, M.S.; Drzal, L.T.; Mohanty, A.K.; Misra, M. Effect of fiber surface-treatments on the properties of laminated biocomposites from poly(lactic acid) (PLA) and kenaf fibers. Compos. Sci. Technol. 2004, 68, 424–432. [Google Scholar] [CrossRef]
- Rajesh, G.; Ratna Prasad, A.V.; Gupta, A.V.S. Mechanical and degradation properties of successive alkali treated completely biodegradable sisal fiber reinforced poly lactic acid composites. J. Reinf. Plast. Compos. 2015, 34, 951–961. [Google Scholar] [CrossRef]
- Jiang, A.; Xi, J.; Wu, H. Effect of surface treatment on the morphology of sisal fibers in sisal/polylactic acid composites. J. Reinf. Plast. Compos. 2012, 31, 621–630. [Google Scholar] [CrossRef]
- Joseph, P.V.; Rabello, M.S.; Mattoso, L.H.C.; Joseph, K.; Thomas, S. Environmental effects on the degradation behaviour of sisal fibre reinforced polypropylene composites. Compos. Sci. Technol. 2002, 62, 1357–1372. [Google Scholar] [CrossRef]
- Karad, S.K.; Jones, F.R.; Attwood, D. Moisture absorption by cyanate ester modified epoxy resin matrices. Part I. Effect of spiking parameters. Polymer 2002, 43, 5209–5218. [Google Scholar] [CrossRef]
- Facca, A.G.; Kortschot, M.T.; Yan, N. Predicting the elastic modulus of natural fibre reinforced thermoplastics. Compos. Part A Appl. Sci. Manuf. 2006, 37, 1660–1671. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Halpin, J.C.; Tsai, S.W. Environmental Factors in Composite Materials Design. In U.S. Air Force Technical Report; Air Force Materials Laboratory: Wright-Patterson Air Force Base, OH, USA, 1967; pp. 67–423. [Google Scholar]
- Cox, H.L. The elasticity and strength of paper and other fibrous materials. Br. J. Appl. Phys. 1952, 3, 72–79. [Google Scholar] [CrossRef]
- Nairn, J.A. On the use of shear-lag methods for analysis of stress transfer in unidirectional composites. Mech. Mater. 1997, 26, 63–80. [Google Scholar] [CrossRef]
- Sun, Z.; Zhao, X.; Wang, X.; Ma, J. Predicting the elastic properties of sisal fiber reinforced polypropylene composites by a new method based on generalized method of cells and laminate analogy approach. Compos. Sci. Technol. 2014, 91, 45–49. [Google Scholar] [CrossRef]
- Jamshidian, M.; Tehrany, E.A.; Imran, M.; Jacquot, M.; Desobry, S. Poly-Lactic Acid: Production, applications, nanocomposites, and release studies. Compr. Rev. Food Sci. Food Saf. 2010, 9, 552–571. [Google Scholar] [CrossRef]
- Pothan, L.A.; Thomas, S. Effect of hybridization and chemical modification on the water-absorption behavior of banana fiber-reinforced polyester composites. J. Appl. Polym. Sci. 2004, 91, 3856–3865. [Google Scholar] [CrossRef]
- Bourmaud, A.; Riviere, J.; Le Duigou, A.; Raj, G.; Baley, C. Investigations of the use a mussel-inspired compatibilizer to improve the matrix-fiber adhesion of a biocomposite. Poly. Test. 2009, 28, 668–672. [Google Scholar] [CrossRef]
- George, J.; Bhagawan, S.S.; Thomas, S. Effects of environment on the properties of low-density polyethylene composites reinforced with pineapple-leaf fibre. Compos. Sci. Technol. 1998, 58, 1471–1485. [Google Scholar] [CrossRef]
- Yew, G.H.; Yusof, A.M.M.; Ishak, Z.A.M.; Ishiaku, U.S. Water absorption and enzymatic degradation of poly (lactic acid)/rice starch composites. Polym. Degrad. Stab. 2005, 90, 488–500. [Google Scholar] [CrossRef]
- Deroiné, M.; Le Duigou, A.; Corre, Y.; Le Gac, P.; Davies, P.; César, G.; Bruzaud, S. Accelerated ageing of polylactide in aqueous environments : Comparative study between distilled water and seawater. Polym. Degrad. Stab. 2014, 108, 319–329. [Google Scholar] [CrossRef]
- Le Duigou, A.; Bourmaud, A.; Davies, P.; Baley, C. Long term immersion in natural seawater of Flax/PLA biocomposite. Ocean. Eng. 2014, 90, 140–148. [Google Scholar] [CrossRef]
- Espert, A.; Vilaplana, F.; Karlsson, S. Comparison of water absorption in natural cellulosic fibres from wood and one-year crops in polypropylene composites and its influence on their mechanical properties. Compos. Part A Appl. Sci. Manuf. 2004, 35, 1267–1276. [Google Scholar] [CrossRef]
- Hammiche, D.; Boukerrou, A.; Djidjelli, H.; Corre, Y.M.; Grohens, Y.; Pillin, I. Hydrothermal ageing of alfa fiber reinforced polyvinylchloride composites. Constr. Build. Mater. 2013, 47, 293–300. [Google Scholar] [CrossRef]
- Islam, M.S.; Pickering, K.L.; Foreman, N.J. Influence of hygrothermal ageing on the physico-mechanical properties of alkali treated industrial hemp fibre reinforced polylactic acid composites. J. Polym. Environ. 2010, 18, 696–704. [Google Scholar] [CrossRef]


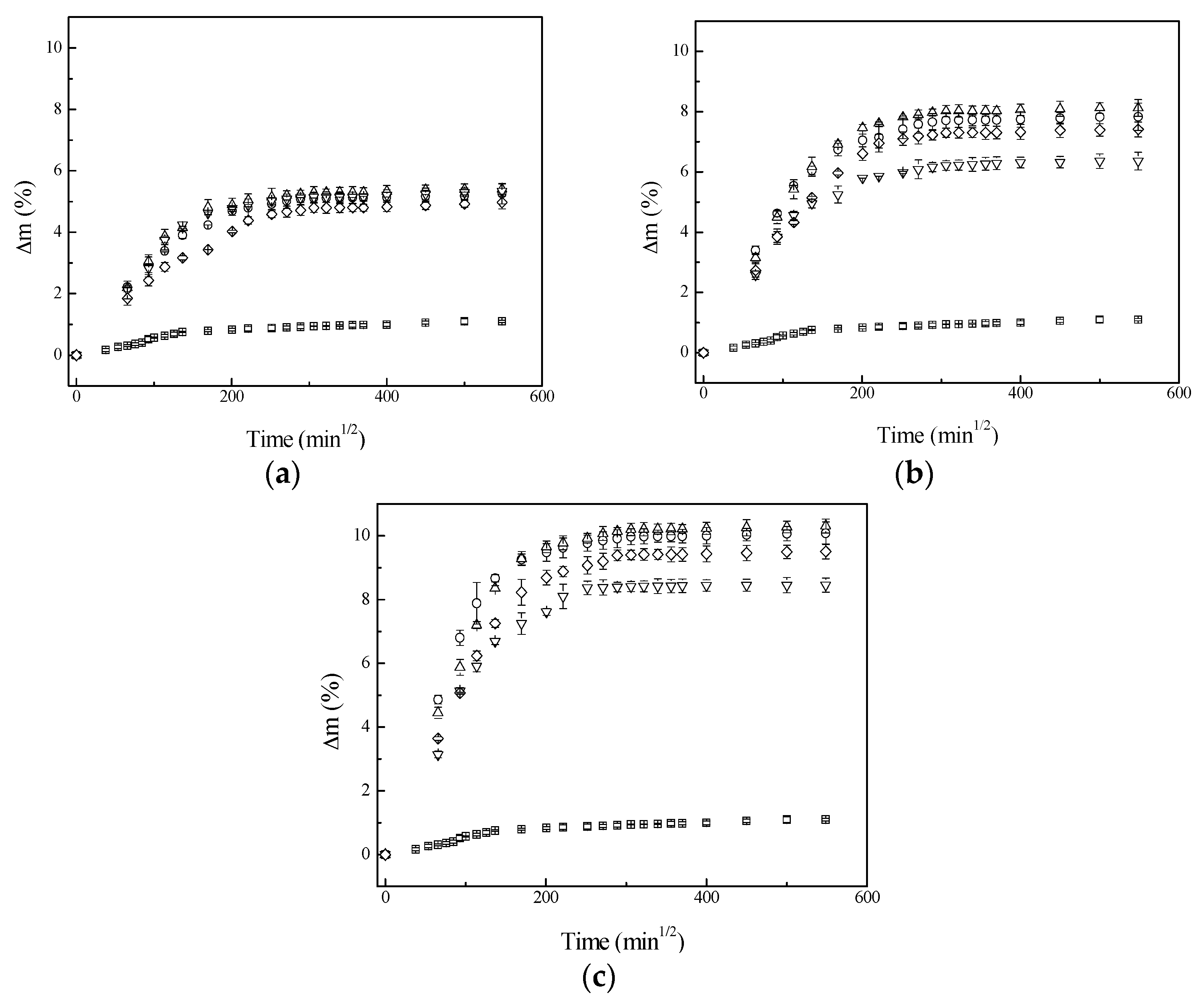

| Sample | θ (%/min1/2) | D × 10−9 (cm2/s) | Dc × 10−9 (cm2/s) | ||
|---|---|---|---|---|---|
| PLA | 0 | 0.00479 | 1.10 | 6.7 | 3.4 |
| Untreated | 0.156 | 0.02869 | 5.26 | 10.5 | 5.4 |
| 0.254 | 0.04547 | 7.83 | 11.9 | 6.1 | |
| 0.382 | 0.06518 | 10.08 | 14.8 | 7.6 | |
| Silane | 0.152 | 0.03150 | 5.41 | 12.0 | 6.2 |
| 0.248 | 0.04595 | 8.12 | 11.3 | 5.8 | |
| 0.375 | 0.06135 | 10.31 | 12.5 | 6.4 | |
| NaOH | 0.171 | 0.03143 | 5.33 | 12.3 | 6.3 |
| 0.236 | 0.03761 | 6.26 | 12.4 | 6.4 | |
| 0.341 | 0.05057 | 8.87 | 12.7 | 6.5 | |
| NaOH + silane | 0.174 | 0.02364 | 4.97 | 8.0 | 4.1 |
| 0.239 | 0.03768 | 7.41 | 9.2 | 4.7 | |
| 0.345 | 0.05352 | 9.51 | 11.2 | 5.7 |
| Sample | Before Water Uptake Period | After Water Uptake Period | |||||
|---|---|---|---|---|---|---|---|
| σt (MPa) | Et (GPa) | εb (%) | σt (MPa) | Et (GPa) | εb (%) | ||
| PLA | 0 | 66.1 ± 1.7 | 3.9 ± 0.5 | 2.4 ± 0.3 | 62.9 ± 1.5 | 3.5 ± 0.3 | 2.8 ± 0.1 |
| Untreated | 0.156 | 53.8 ± 0.9 | 5.5 ± 0.9 | 1.8 ± 0.4 | 48.1 ± 1.6 | 3.2 ± 0.4 | 3.1 ± 0.1 |
| 0.254 | 47.3 ± 1.7 | 5.9 ± 0.7 | 1.1 ± 0.3 | 40.4 ± 1.8 | 4.0 ± 0.1 | 2.2 ± 0.1 | |
| 0.382 | 39.3 ± 3.4 | 6.4 ± 1.0 | 0.8 ± 0.1 | 35.6 ± 1.4 | 1.5 ± 0.2 | 2.2 ± 0.1 | |
| Silane | 0.152 | 57.6 ± 2.9 | 4.4 ± 0.7 | 1.9 ± 0.3 | 33.8 ± 2.2 | 2.8 ± 0.3 | 2.5 ± 0.1 |
| 0.248 | 59.9 ± 1.5 | 6.4 ± 0.7 | 1,5 ± 0.3 | 34.5 ± 2.0 | 2.7 ± 0.1 | 1.9 ± 0.1 | |
| 0.375 | 61.8 ± 3.1 | 7.5 ± 0.6 | 1.0 ± 0.2 | 32.0 ± 1.9 | 1.6 ± 0.2 | 1.6 ± 0.2 | |
| NaOH | 0.171 | 66.1 ± 3.2 | 6.5 ± 0.4 | 1.6 ± 0.3 | 45.4 ± 1.0 | 3.3 ± 0.2 | 2.4 ± 0.3 |
| 0.236 | 74.8 ± 3.5 | 7.2 ± 0.7 | 1.5 ± 0.1 | 35.1 ± 0.4 | 3.0 ± 0.2 | 2.3 ± 0.3 | |
| 0.341 | 81.5 ± 1.4 | 8.1 ± 0.8 | 1.4 ± 0.1 | 31.9 ± 1.3 | 2.1 ± 0.5 | 2.4 ± 0.1 | |
| NaOH + silane | 0.174 | 66.9 ± 1.0 | 5.9 ± 0.4 | 1.8 ± 0.2 | 42.3 ± 0.9 | 3.5 ± 0.1 | 3.2 ± 0.3 |
| 0.239 | 74.7 ± 1.4 | 6.9 ± 0.9 | 1.5 ± 0.1 | 38.0 ± 1.3 | 2.9 ± 0.2 | 2.0 ± 0.2 | |
| 0.345 | 78.6 ± 3.5 | 8.3 ± 0.5 | 1.4 ± 0.2 | 34.9 ± 2.0 | 2.7 ± 0.3 | 1.9 ± 0.2 | |
| Sample | Δσt (MPa) | Δ Et (GPa) | Δεb (%) | |
|---|---|---|---|---|
| PLA | 0 | −5 | −10 | +17 |
| Untreated | 0.156 | −11 | −42 | +72 |
| 0.254 | −15 | −32 | +100 | |
| 0.382 | −9 | −77 | +175 | |
| Silane | 0.152 | −41 | −36 | +32 |
| 0.248 | −42 | −58 | +27 | |
| 0.375 | −48 | −79 | +60 | |
| NaOH | 0.171 | −31 | −49 | +50 |
| 0.236 | −53 | −58 | +53 | |
| 0.341 | −61 | −74 | +71 | |
| NaOH + silane | 0.174 | −37 | −41 | +78 |
| 0.239 | −49 | −58 | +33 | |
| 0.345 | −59 | −67 | +36 |
| Fiber | Length (μm) | Diameter (μm) | l/d | Ef (Experimental) (GPa) | Ef (Extrapolated) (GPa) |
|---|---|---|---|---|---|
| Untreated | 513 | 130 | 3.9 | 11.1 | 11.2 |
| Silane | 571 | 104 | 5.5 | 10.3 | 13.8 |
| NaOH | 543 | 94 | 5.8 | 7.8 | 17.0 |
| NaOH + silane | 555 | 84 | 6.6 | 7.1 | 16.5 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orue, A.; Eceiza, A.; Peña-Rodriguez, C.; Arbelaiz, A. Water Uptake Behavior and Young Modulus Prediction of Composites Based on Treated Sisal Fibers and Poly(Lactic Acid). Materials 2016, 9, 400. https://doi.org/10.3390/ma9050400
Orue A, Eceiza A, Peña-Rodriguez C, Arbelaiz A. Water Uptake Behavior and Young Modulus Prediction of Composites Based on Treated Sisal Fibers and Poly(Lactic Acid). Materials. 2016; 9(5):400. https://doi.org/10.3390/ma9050400
Chicago/Turabian StyleOrue, Ander, Arantxa Eceiza, Cristina Peña-Rodriguez, and Aitor Arbelaiz. 2016. "Water Uptake Behavior and Young Modulus Prediction of Composites Based on Treated Sisal Fibers and Poly(Lactic Acid)" Materials 9, no. 5: 400. https://doi.org/10.3390/ma9050400
APA StyleOrue, A., Eceiza, A., Peña-Rodriguez, C., & Arbelaiz, A. (2016). Water Uptake Behavior and Young Modulus Prediction of Composites Based on Treated Sisal Fibers and Poly(Lactic Acid). Materials, 9(5), 400. https://doi.org/10.3390/ma9050400







