A Phase-Shifting Method for Improving the Heating Uniformity of Microwave Processing Materials
Abstract
:1. Introduction
2. Methodology
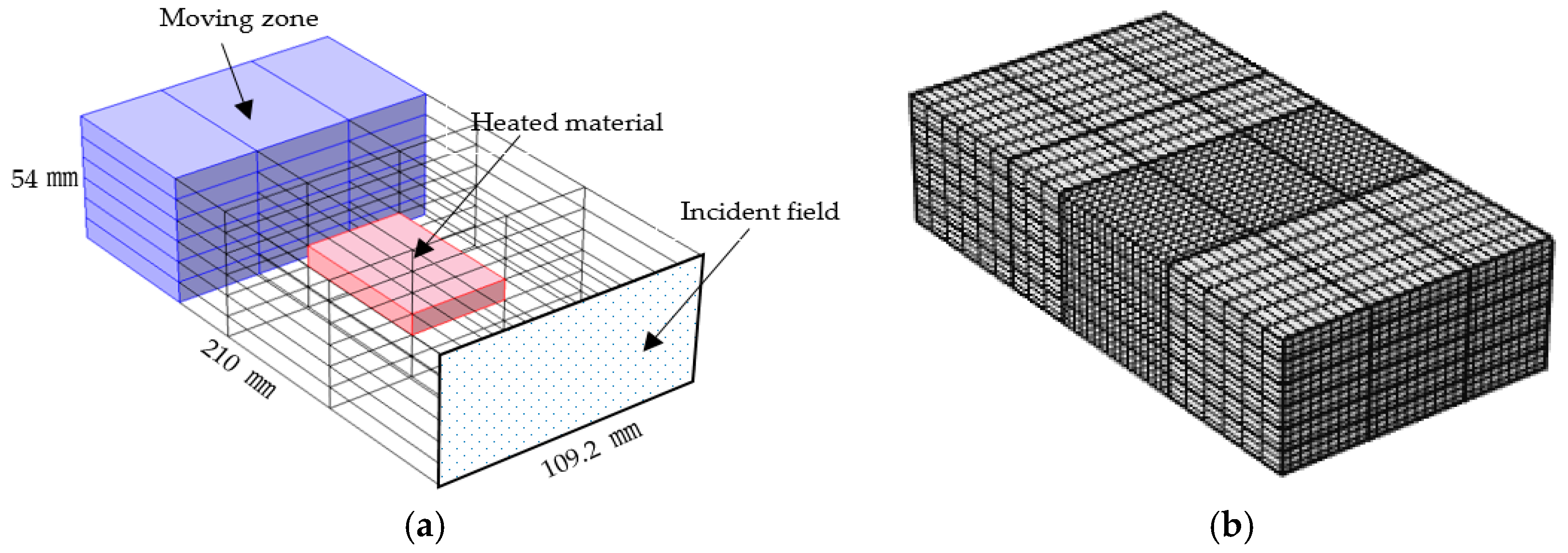
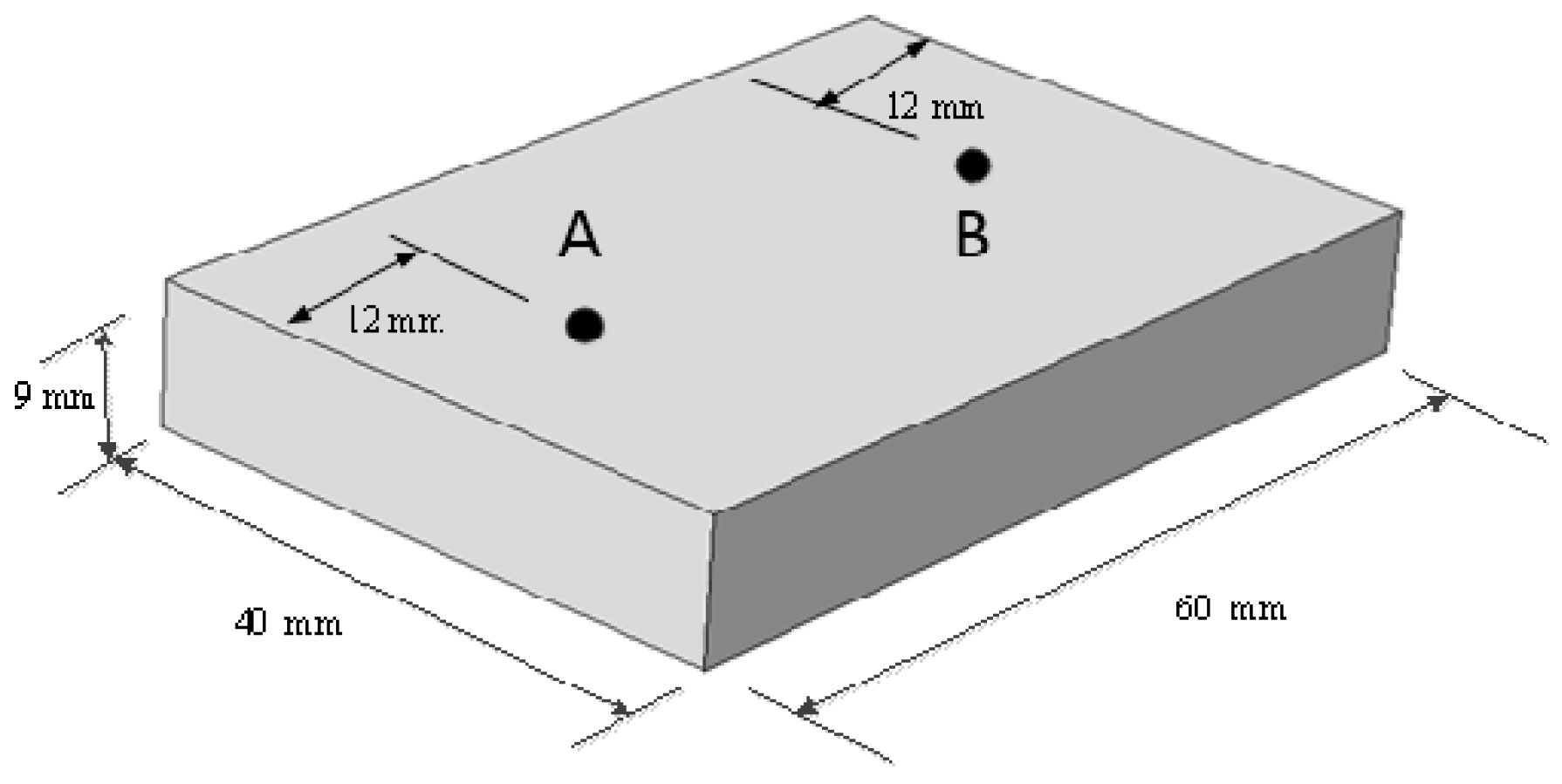
2.1. Model Description
2.2. Multi-Physics Calculation
2.2.1. Governing Equation
2.2.2. Boundary Condition
- Electromagnetic boundary condition
- Heat transfer boundary condition
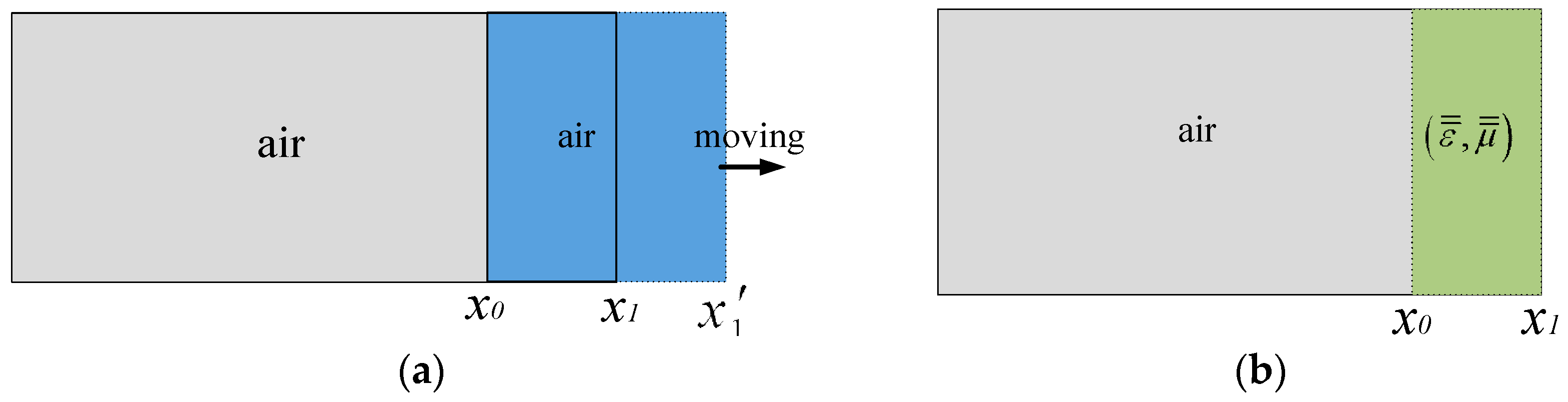
2.3. The Transformation Optics Algorithms for Sliding Short
2.4. Phase-Shifting Method and Experiment Setup
2.4.1. Phase-Shifting Method
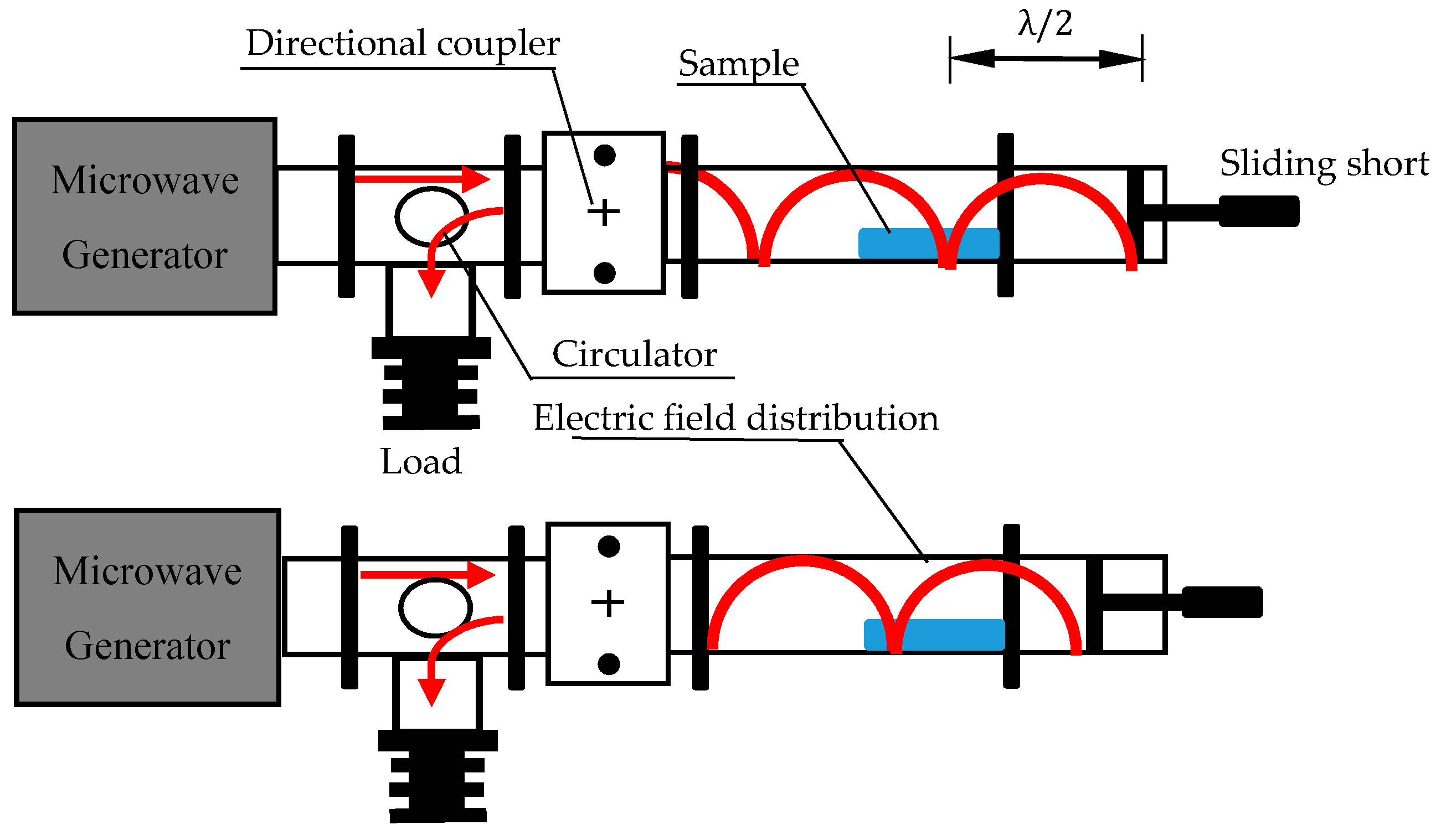
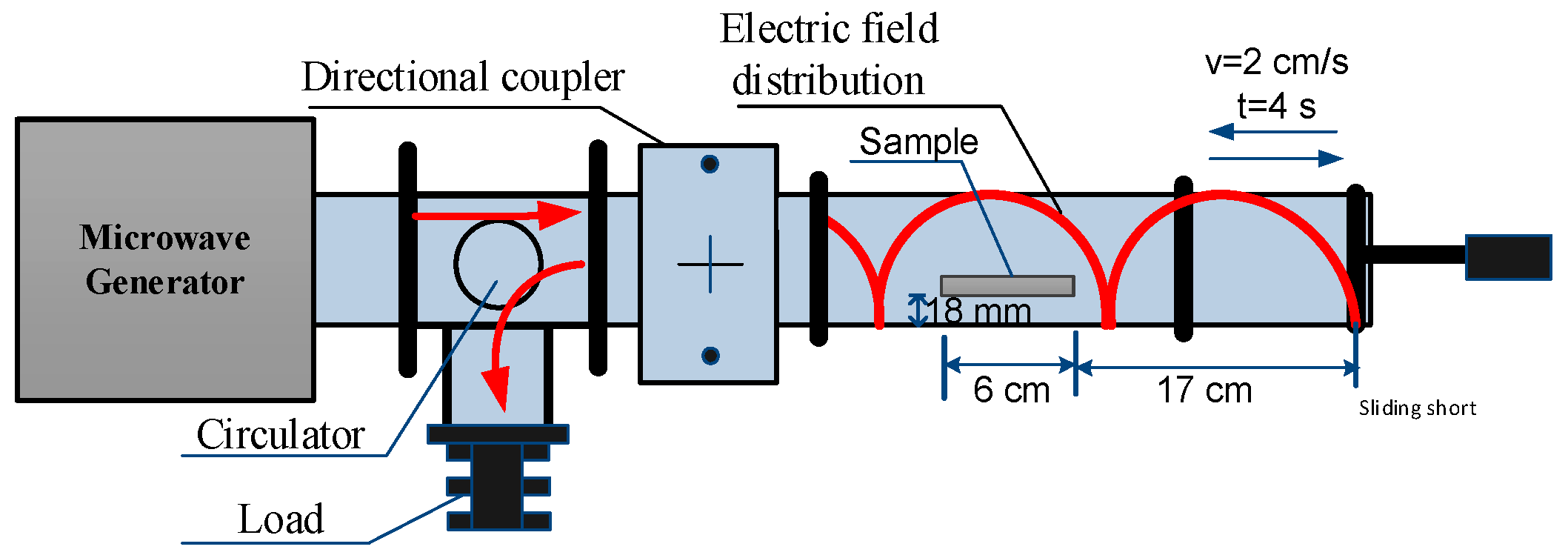
2.4.2. Experiment Setup
3. Results and Discussion
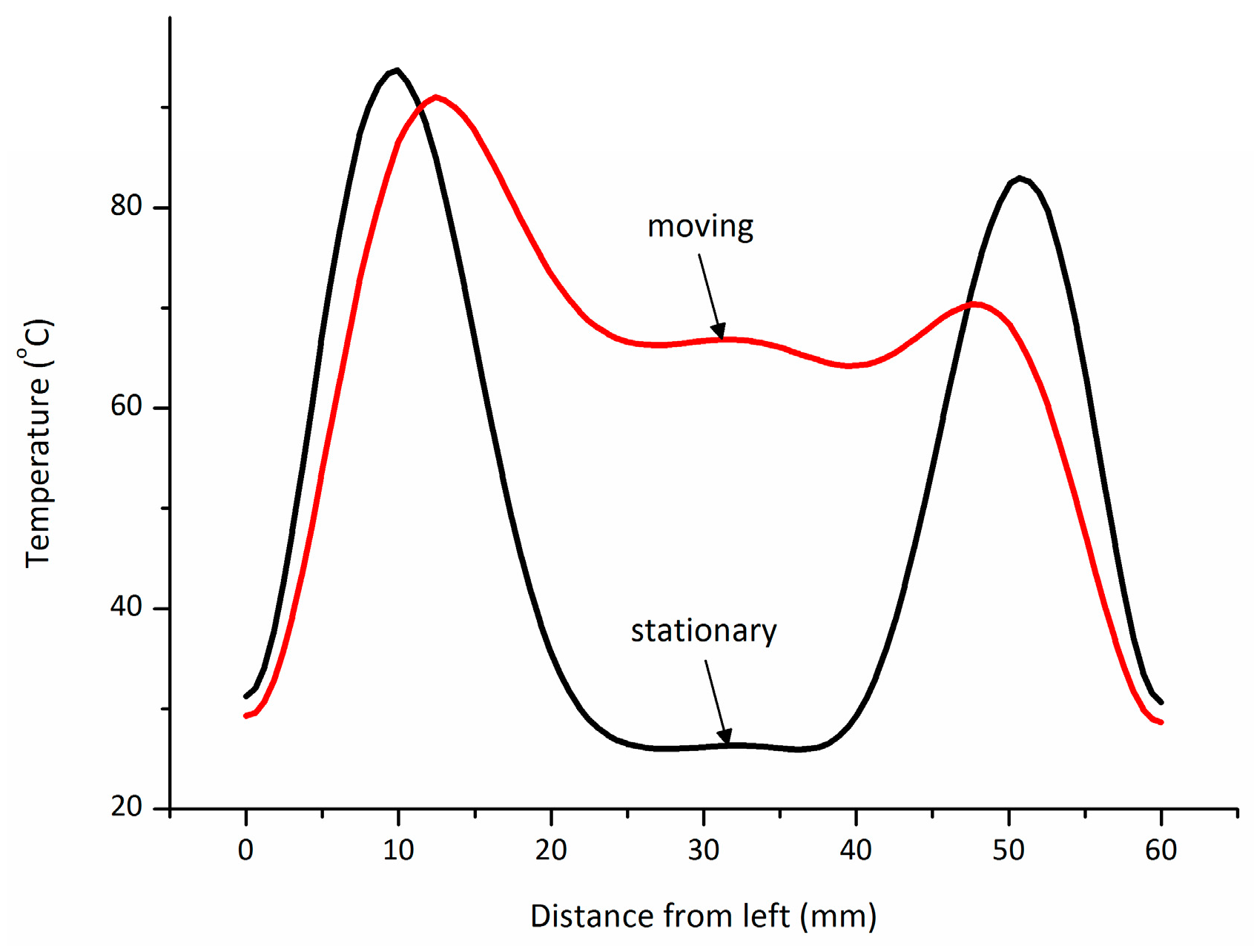
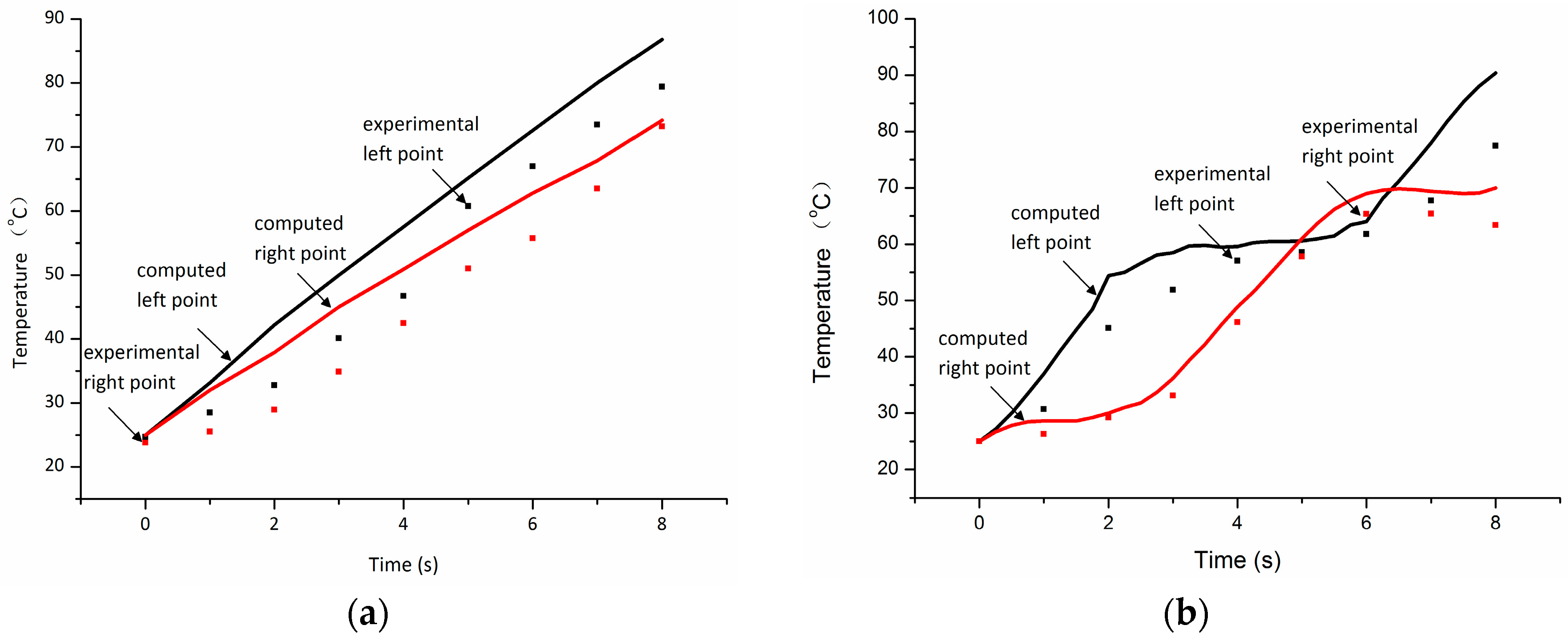
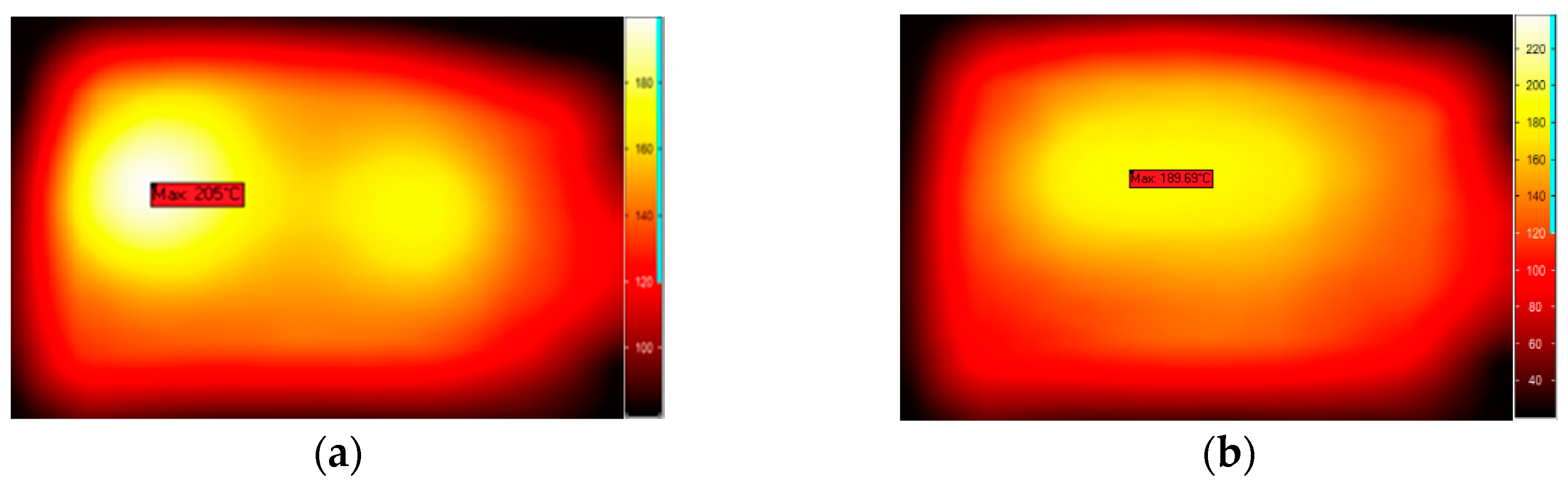
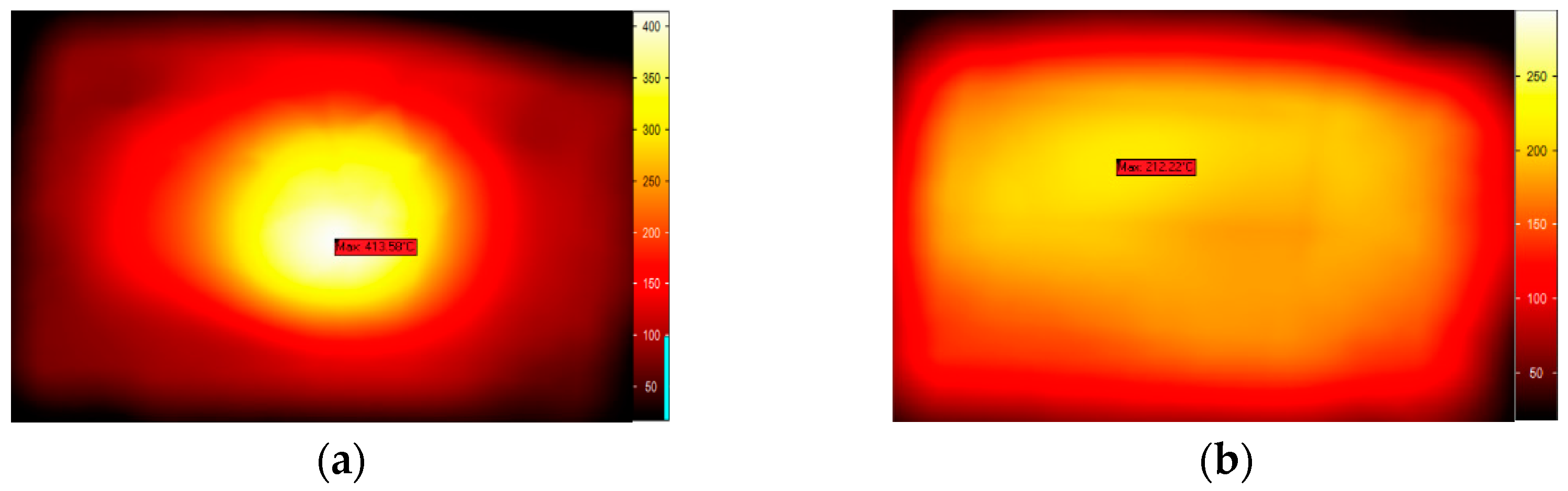
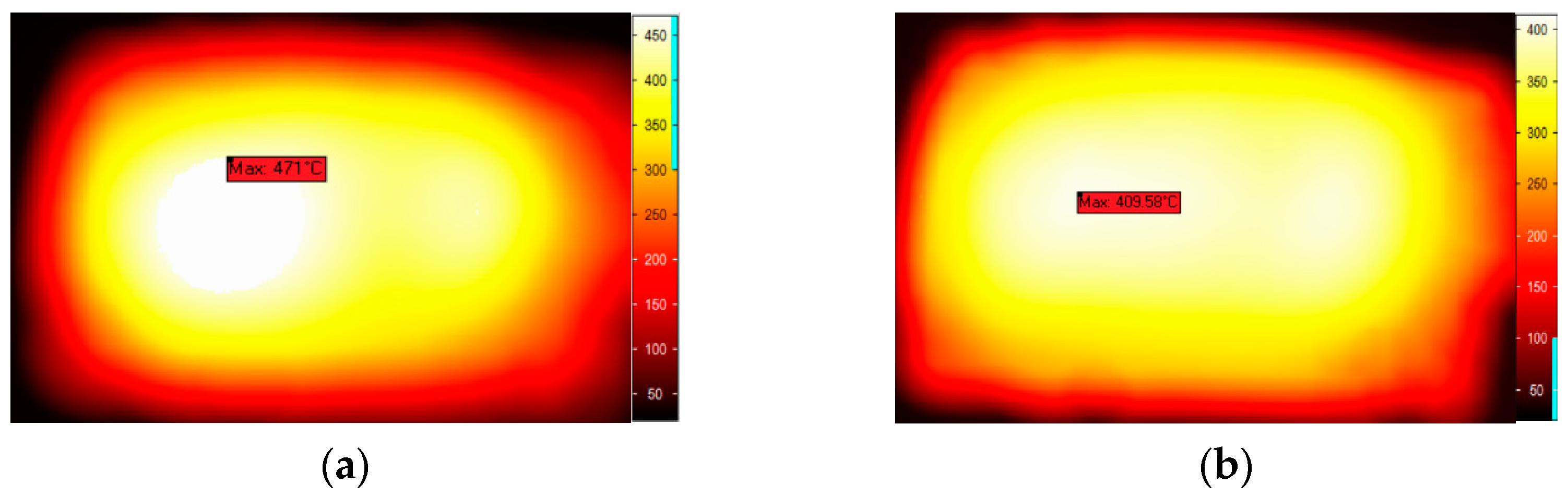
3.1. Experimental Validation
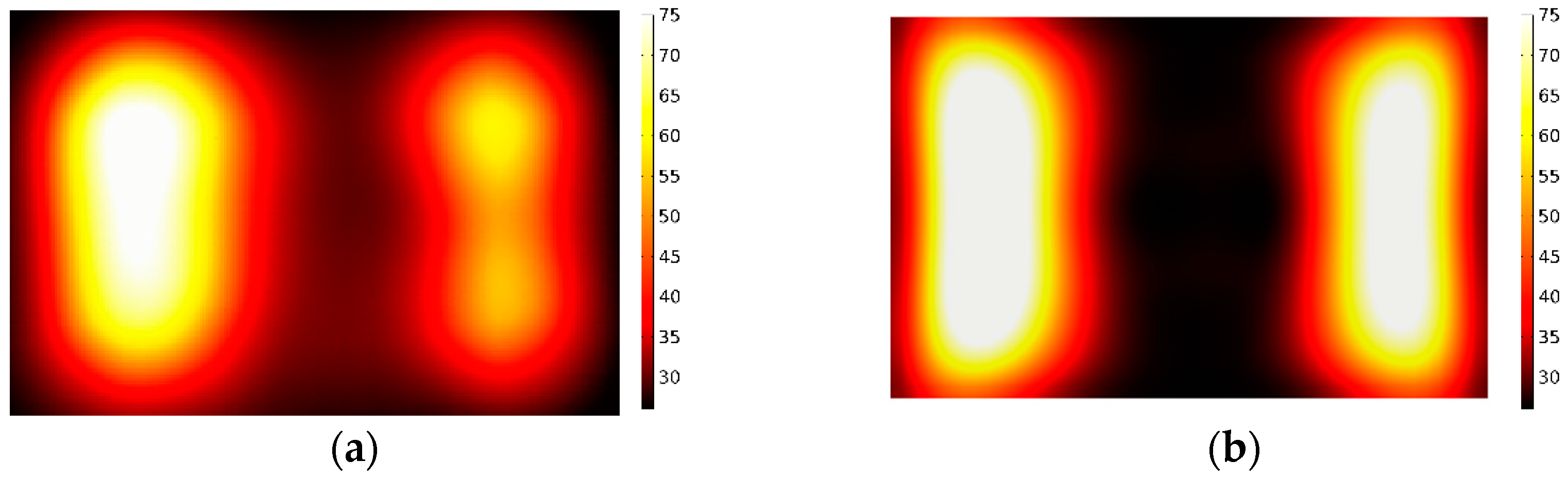
3.2. Results Discussion
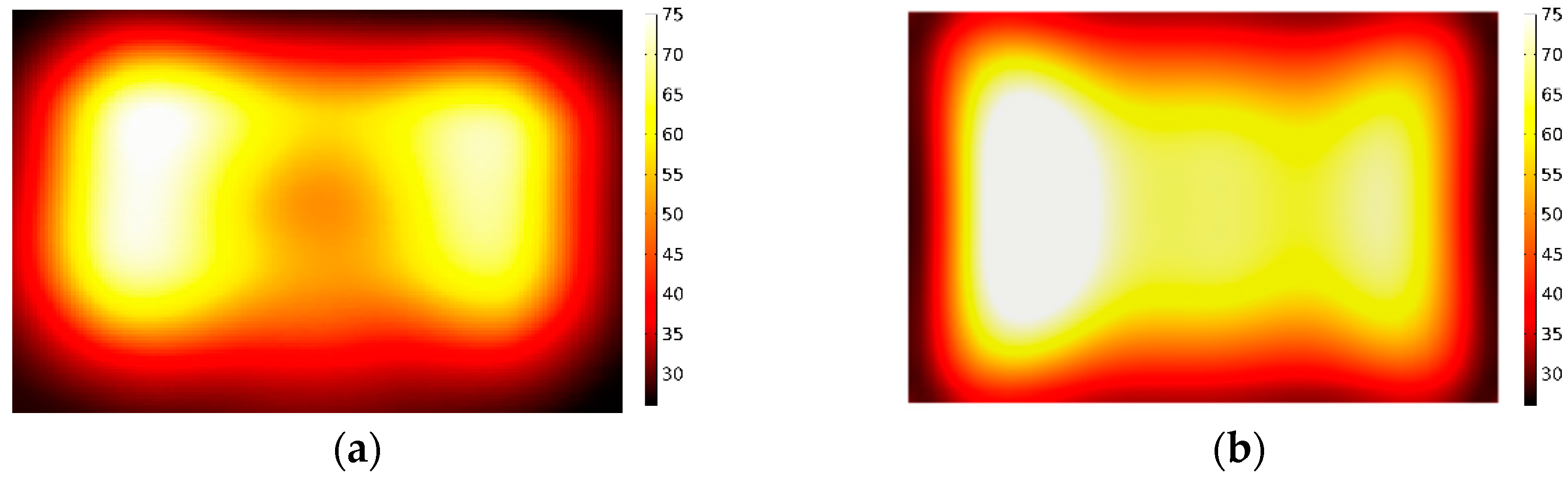
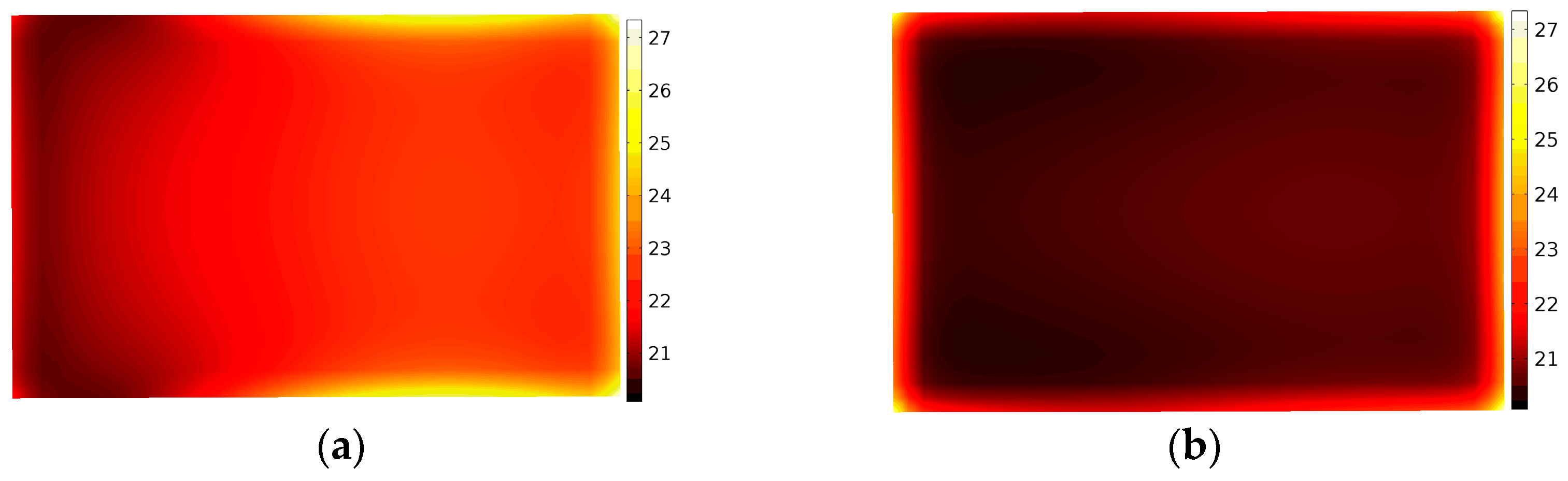
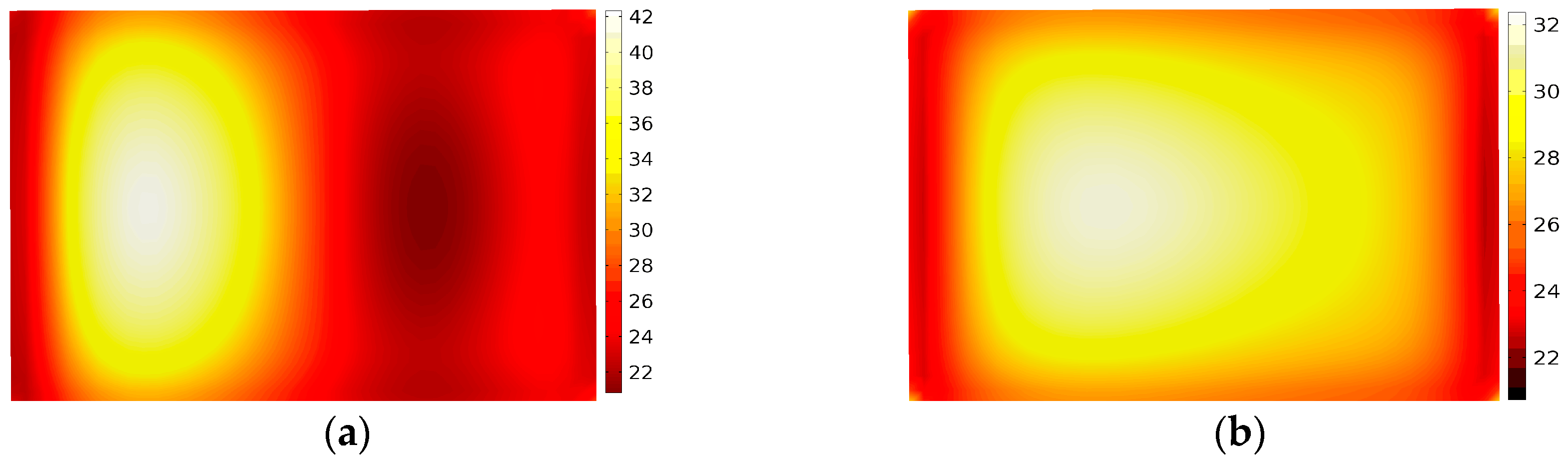
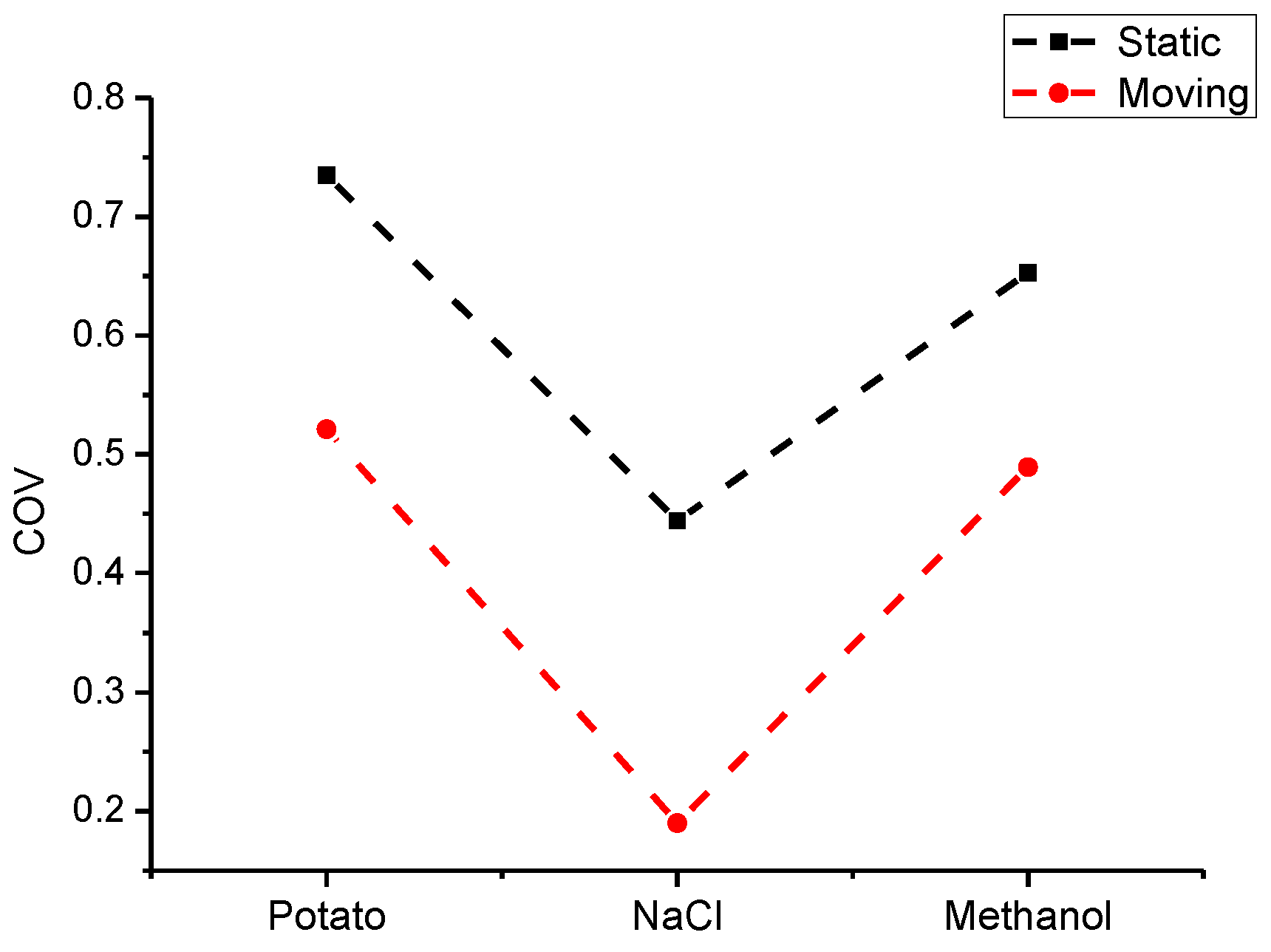
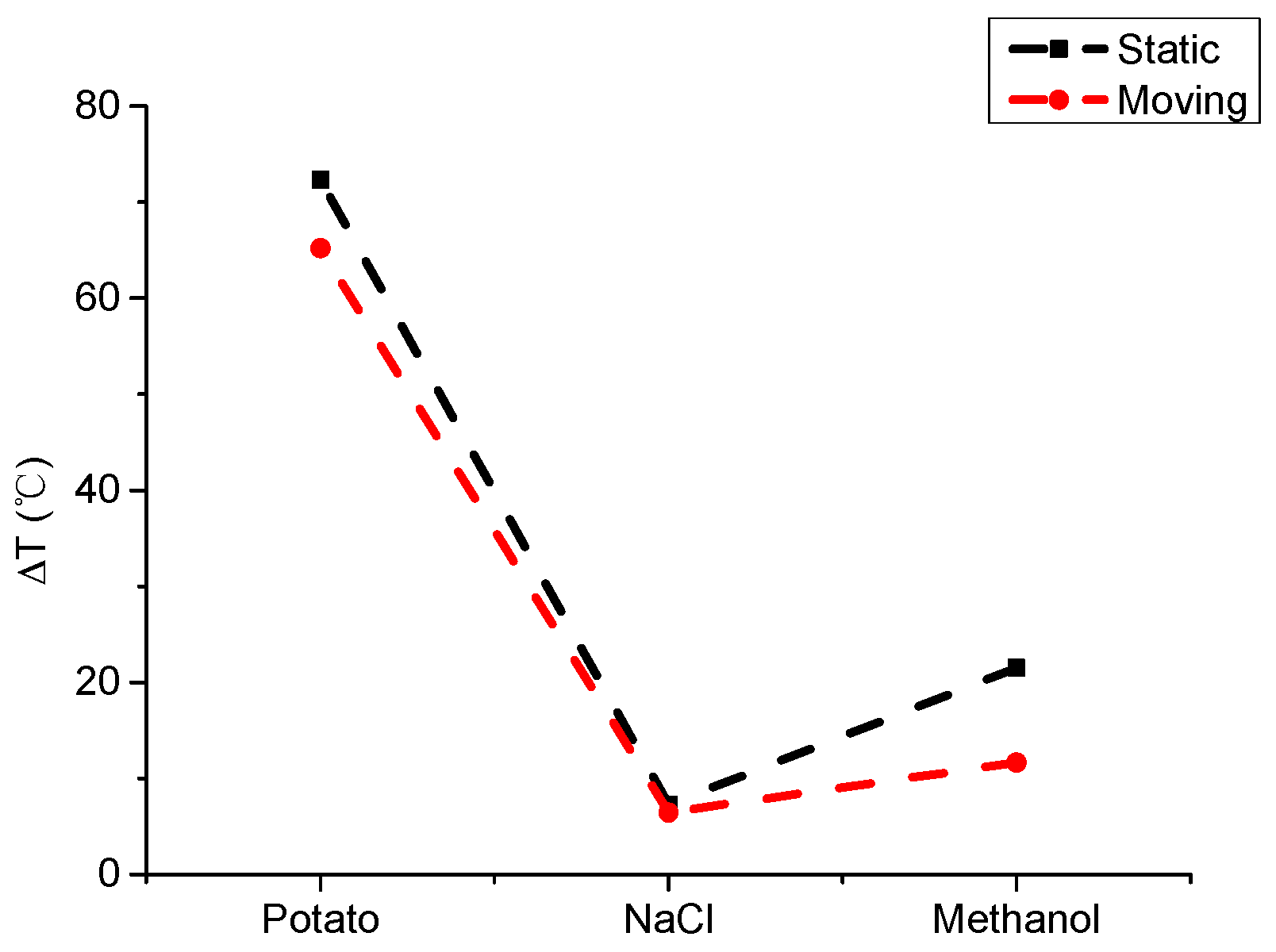
- Different kinds of materials
- The application of phase shifting for material processing
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Singh, S.; Gupta, D.; Jain, V.; Sharma, A.K. Microwave processing of materials and applications in manufacturing industries: A review. Mater. Manuf. Process. 2015, 30, 1–29. [Google Scholar] [CrossRef]
- Veronesi, P.; Rosa, R.; Colombini, E.; Leonelli, C. Microwave-Assisted Preparation of High Entropy Alloys. Technologies 2015, 3, 182–197. [Google Scholar] [CrossRef]
- Tang, J. Unlocking Potentials of Microwaves for Food Safety and Quality. J. Food Sci. 2015, 80, E1776–E1793. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Xu, F.; Hu, X.; Li, Y.; Liu, W.; Dong, B. In situ Investigation of Titanium Powder Microwave Sintering by Synchrotron Radiation Computed Tomography. Metals 2016, 6. [Google Scholar] [CrossRef]
- Roy, R.; Agrawal, D.; Cheng, J.; Gedevanishvili, S. Full sintering of powdered-metal bodies in a microwave field. Nature 1990, 399, 668–670. [Google Scholar]
- Janney, M.A.; Kimrey, H.D.; Allen, W.R.; Kiggans, J.O. Enhanced diffusion in sapphire during microwave heating. J. Mater. Sci. 1997, 32, 1347–1355. [Google Scholar] [CrossRef]
- Subrata, S.; Ram Mohan, V.C.; Delregno, G.E. Method of Microwave Processing Ceramics and Microwave Hybrid Heating System for Same. U.S. Patent 2007/0023971 A1, 1 February 2007. [Google Scholar]
- Upadhya, P.N.; Srinivasan, K.; Adhikari, A.; Satapathy, L. Evaluation of Calcium Fluoroaluminosilicate Based Glass Ionomer Luting Cements Processed Both by Conventional and Microwave Assisted Methods. Technologies 2015, 3, 58–73. [Google Scholar]
- Funawatashi, Y.; Suzuki, T. Numerical analysis of microwave heating of a dielectric. Heat Transf. Asian Res. 2003, 32, 227–236. [Google Scholar] [CrossRef]
- Pedreño-Molina, J.L.; Monzó-Cabrera, J.; Catalá-Civera, J.M. Sample movement optimization for uniform heating in microwave heating ovens. Int. J. RF Microw. Comput. Aided Eng. 2007, 17, 142–152. [Google Scholar] [CrossRef]
- Chen, H.; Tang, J.; Liu, F. Simulation model for moving food packages in microwave heating processes using conformal FDTD method. J. Food Eng. 2008, 88, 294–305. [Google Scholar] [CrossRef]
- Hill, D.A. Electronic mode stirring for reverberation chambers. IEEE Trans. Electromagn. Compat. 1994, 36, 294–299. [Google Scholar] [CrossRef]
- Guo, Q.-G.; Yang, X.-Q.; Yang, L.-J. Influences of Stir and Viscosity Coefficient on the Formation of Hotspots during Microwave Heating. Asian J. Chem. 2010, 22, 4450–4454. [Google Scholar]
- Plaza-González, P.; Monzó-Cabrera, J.; Catalá-Civera, J.M.; Sánchez-Hernández, D. Effect of mode-stirrer configurations on dielectric heating performance in multimode microwave applicators. IEEE Trans. Microw. Theory Tech. 2005, 53, 1699–1706. [Google Scholar] [CrossRef]
- Bows, J.R.; Patrick, M.L.; Janes, R.; Dibben, D.C. Microwave phase control heating. Int. J. Food Sci. Technol. 1999, 34, 295–304. [Google Scholar] [CrossRef]
- Gulati, T.; Zhu, H.; Datta, A.K.; Huang, K. Microwave drying of spheres: Coupled electromagnetics-multiphase transport modeling with experimentation. Part II: Model validation and simulation results. Food Bioprod. Process. 2015, 96, 326–337. [Google Scholar] [CrossRef]
- Chen, Q.; Huang, K.; Yang, X.; Luo, M. A bp neural network realization in the measurement of material permittivity. J. Softw. 2011, 116, 1089–1095. [Google Scholar] [CrossRef]
- Chen, Q.; Huang, K.M.; Yang, X.; Luo, M.; Zhu, H. An artificial nerve network realization in the measurement of material permittivity. Prog. Electromagn. Res. 2011, 116, 347–361. [Google Scholar] [CrossRef]
- Ozgun, O.; Kuzuoglu, M. Form invariance of Maxwell’s equations: The pathway to novel metamaterial specifications for electromagnetic reshaping. Antennas Propag. Mag. IEEE 2010, 52, 51–65. [Google Scholar] [CrossRef]
- Dollin, L. On the possibility of comparison of three-dimensional electromagnetic systems with nonuniform anisotropic filling. Izv. Vuzov Radiofiz. 1961, 4, 964–967. [Google Scholar]
- Zhang, H.; Datta, A. Microwave power absorption in single-and multiple-item foods. Food Bioprod. Process. 2003, 81, 257–265. [Google Scholar] [CrossRef]
| Parameter | Value | Source |
|---|---|---|
| Cavity interior dimensions (mm) | 109.2 × 210 × 54 | This study |
| Sample dimension (mm) | 40 × 60 × 9 | This study |
| Placement of material position (mm) (center) | 54.6 (x) 90 (y) 22.5 (z) | This study |
| Microwave frequency (MHz) | 2450 | This study |
| Heating time (s) | 8 | This study |
| Dielectric constant and loss of potato | 70-j18 (15 °C) | Gulati, T. [16] |
| Dielectric constant and loss of NaCl | 5.20-j10.61 (15 °C) | Chen, Q [17] |
| Dielectric constant and loss of methanol | 25.910-j14.523 (15 °C) | Chen, Q [18] |
| Microwave frequency (GHz) | 2.45 | This study |
| Microwave power (W) | 700 | This study |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Y.; Lan, J.; Zhang, C.; Hong, T.; Yang, Y.; Huang, K.; Zhu, H. A Phase-Shifting Method for Improving the Heating Uniformity of Microwave Processing Materials. Materials 2016, 9, 309. https://doi.org/10.3390/ma9050309
Liao Y, Lan J, Zhang C, Hong T, Yang Y, Huang K, Zhu H. A Phase-Shifting Method for Improving the Heating Uniformity of Microwave Processing Materials. Materials. 2016; 9(5):309. https://doi.org/10.3390/ma9050309
Chicago/Turabian StyleLiao, Yinhong, Junqing Lan, Chun Zhang, Tao Hong, Yang Yang, Kama Huang, and Huacheng Zhu. 2016. "A Phase-Shifting Method for Improving the Heating Uniformity of Microwave Processing Materials" Materials 9, no. 5: 309. https://doi.org/10.3390/ma9050309
APA StyleLiao, Y., Lan, J., Zhang, C., Hong, T., Yang, Y., Huang, K., & Zhu, H. (2016). A Phase-Shifting Method for Improving the Heating Uniformity of Microwave Processing Materials. Materials, 9(5), 309. https://doi.org/10.3390/ma9050309







