Investigation on the Regional Loss Factor and Its Anisotropy for Aortic Aneurysms
Abstract
:1. Introduction
2. Materials and Methods
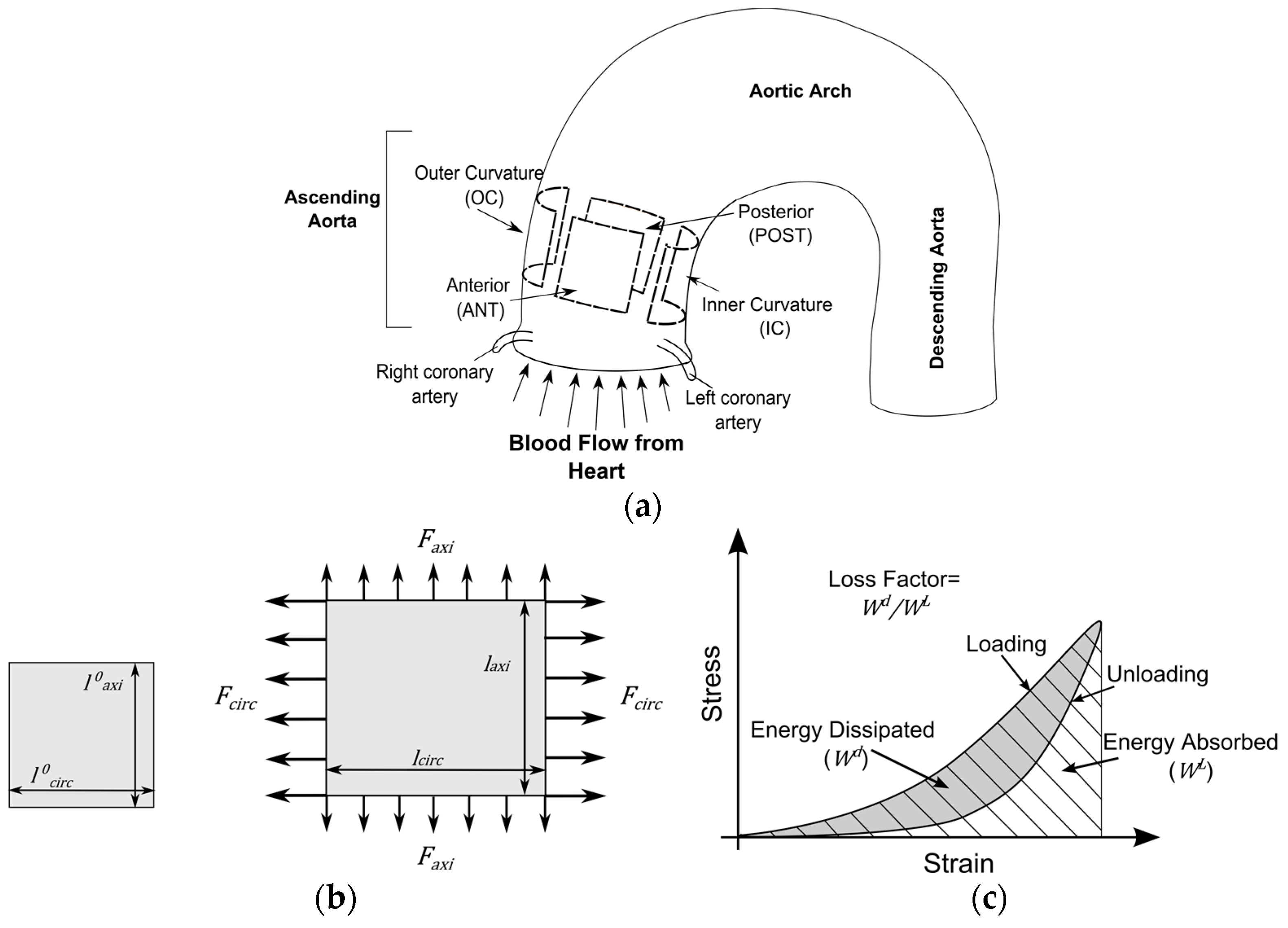
2.1. Tissue Collection and Preparation
2.2. Biaxial Tensile Tests
2.2.1. Method of Experiments
2.2.2. Method of Analysis
2.3. Statistical Analyses
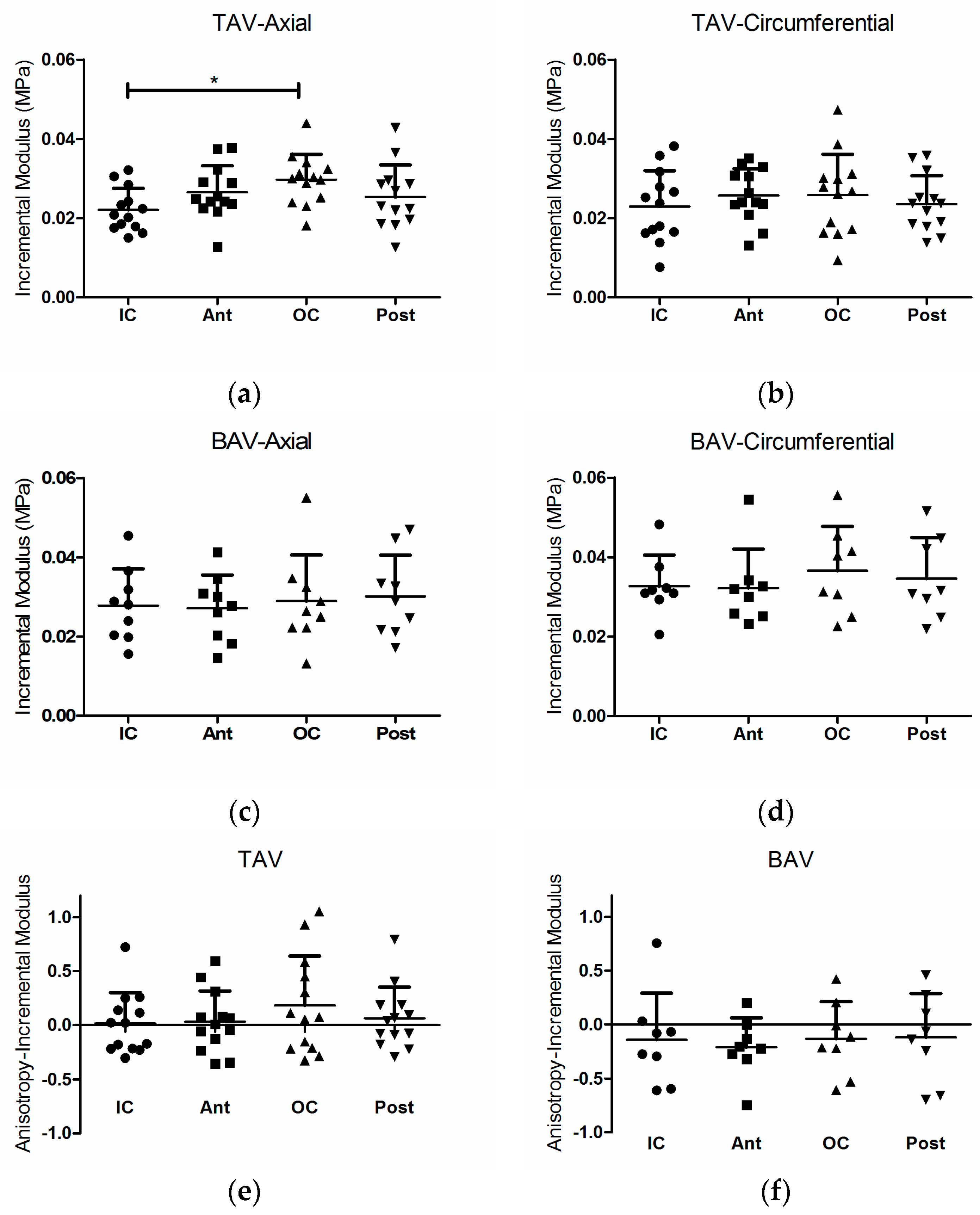
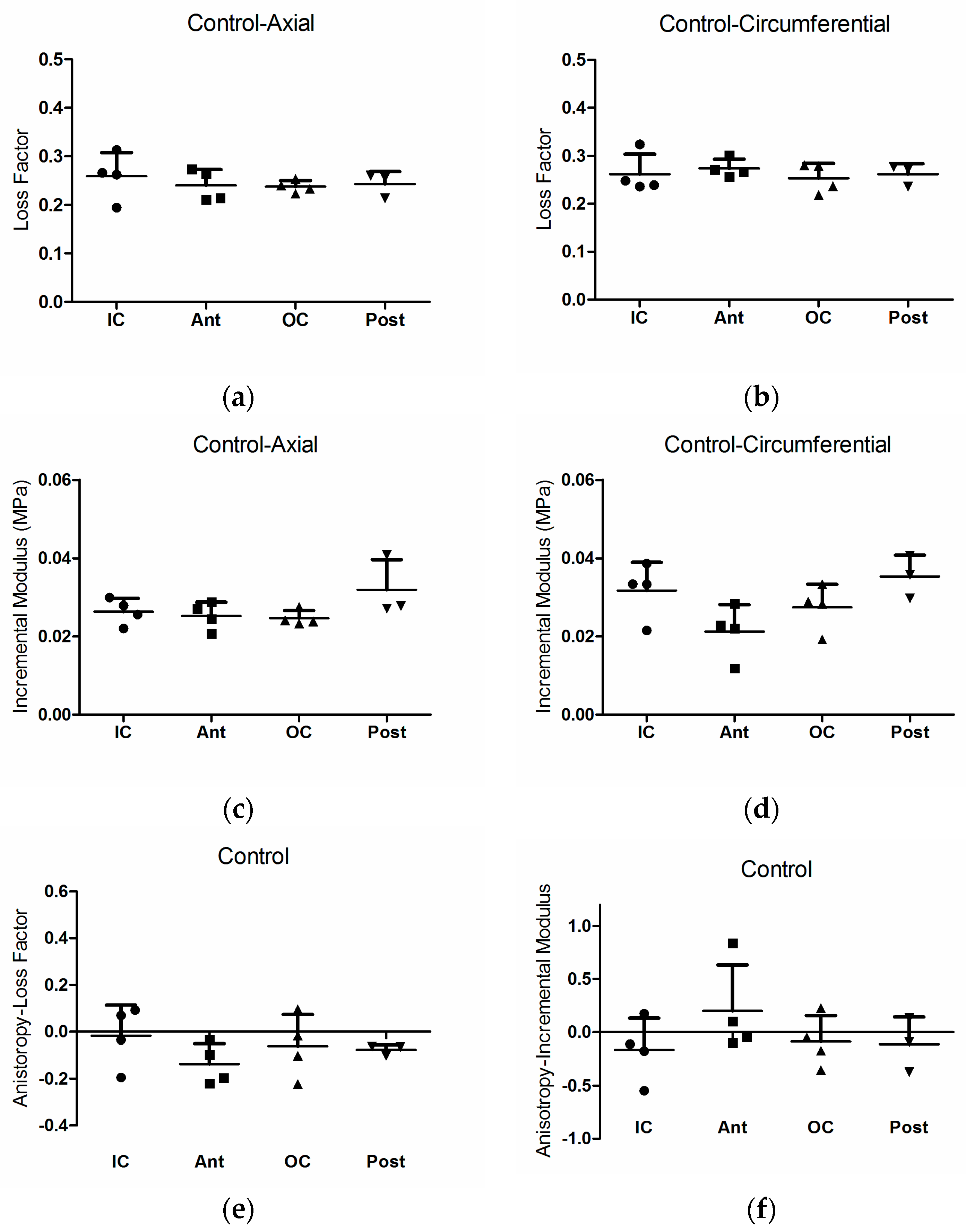
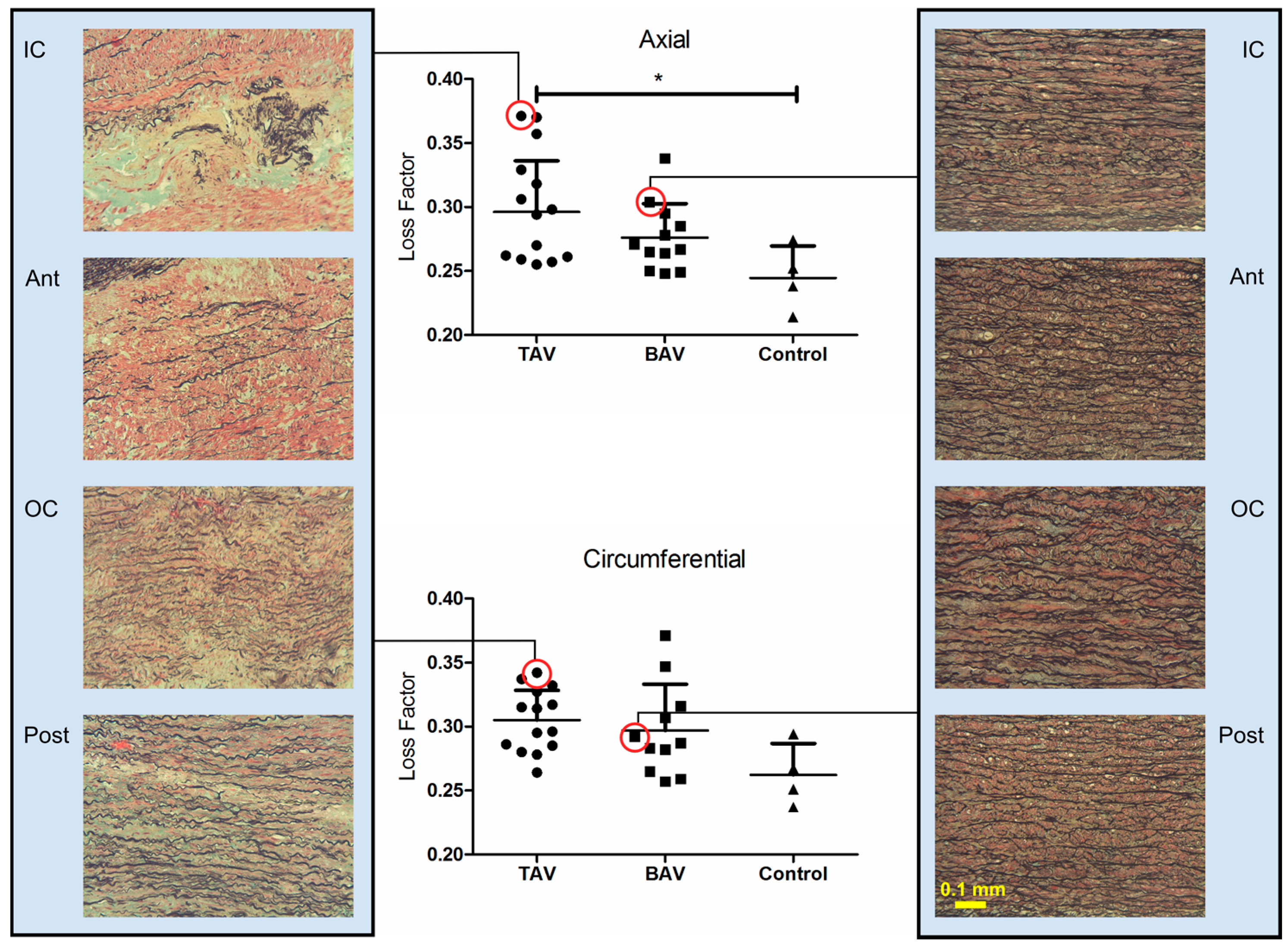
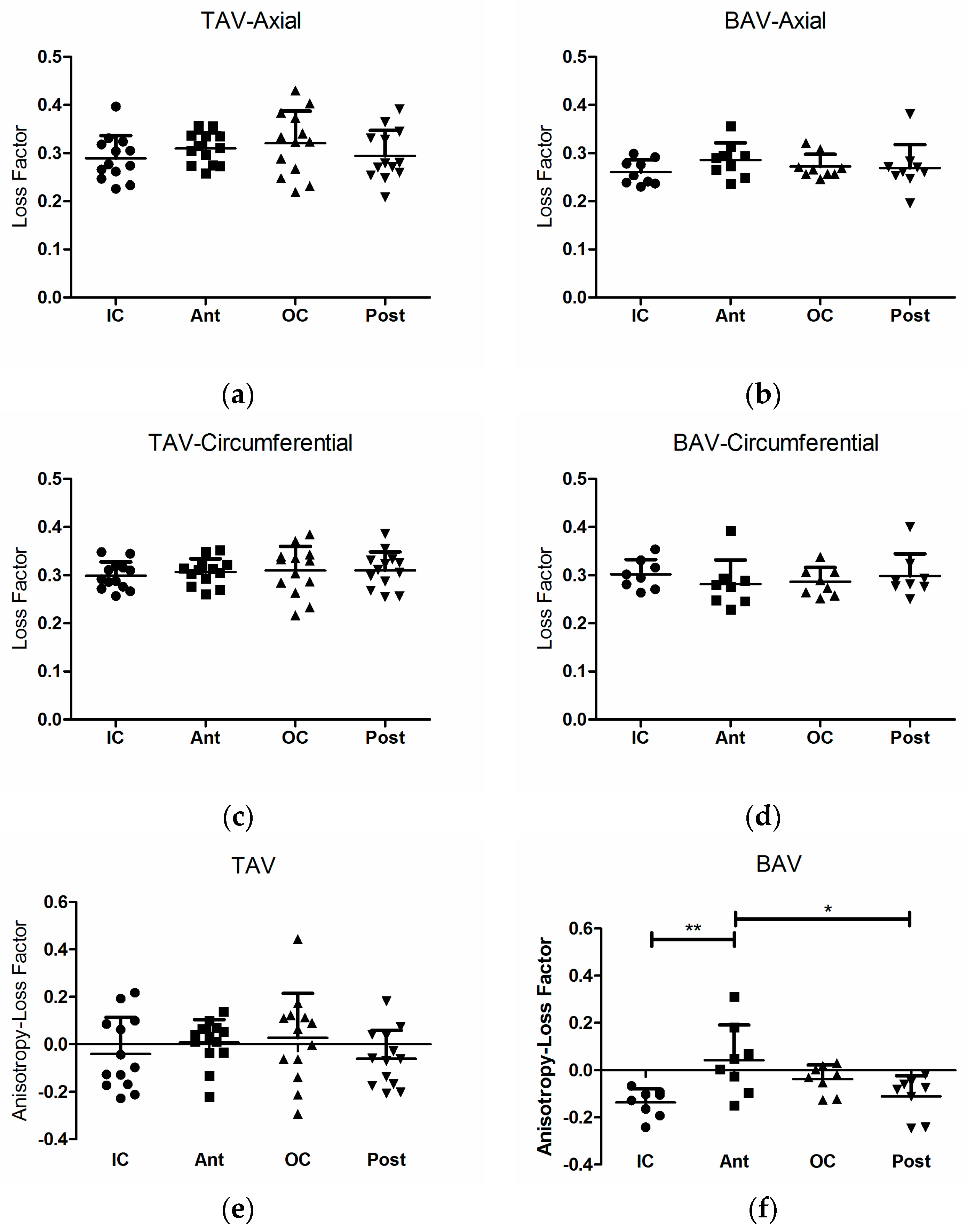
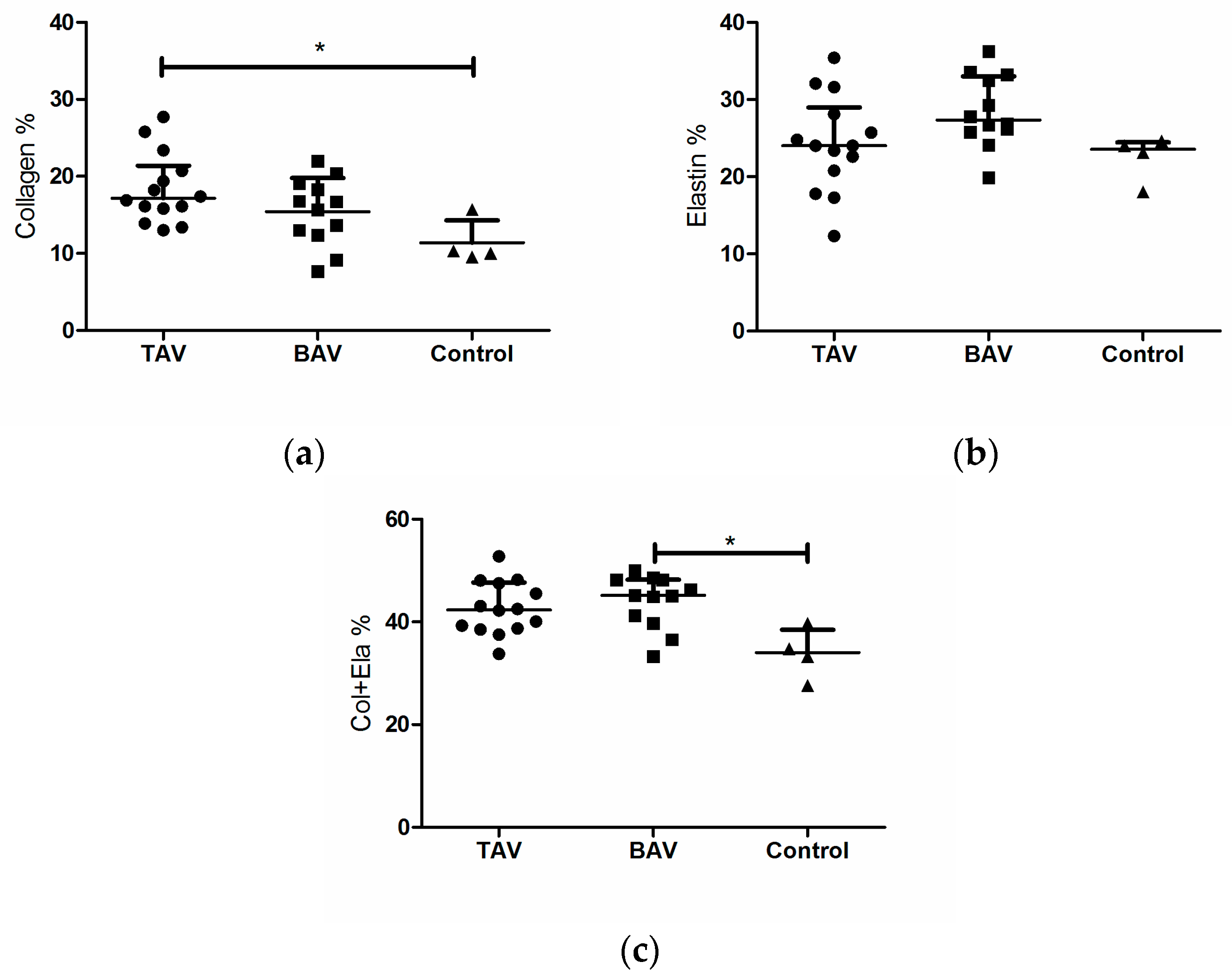
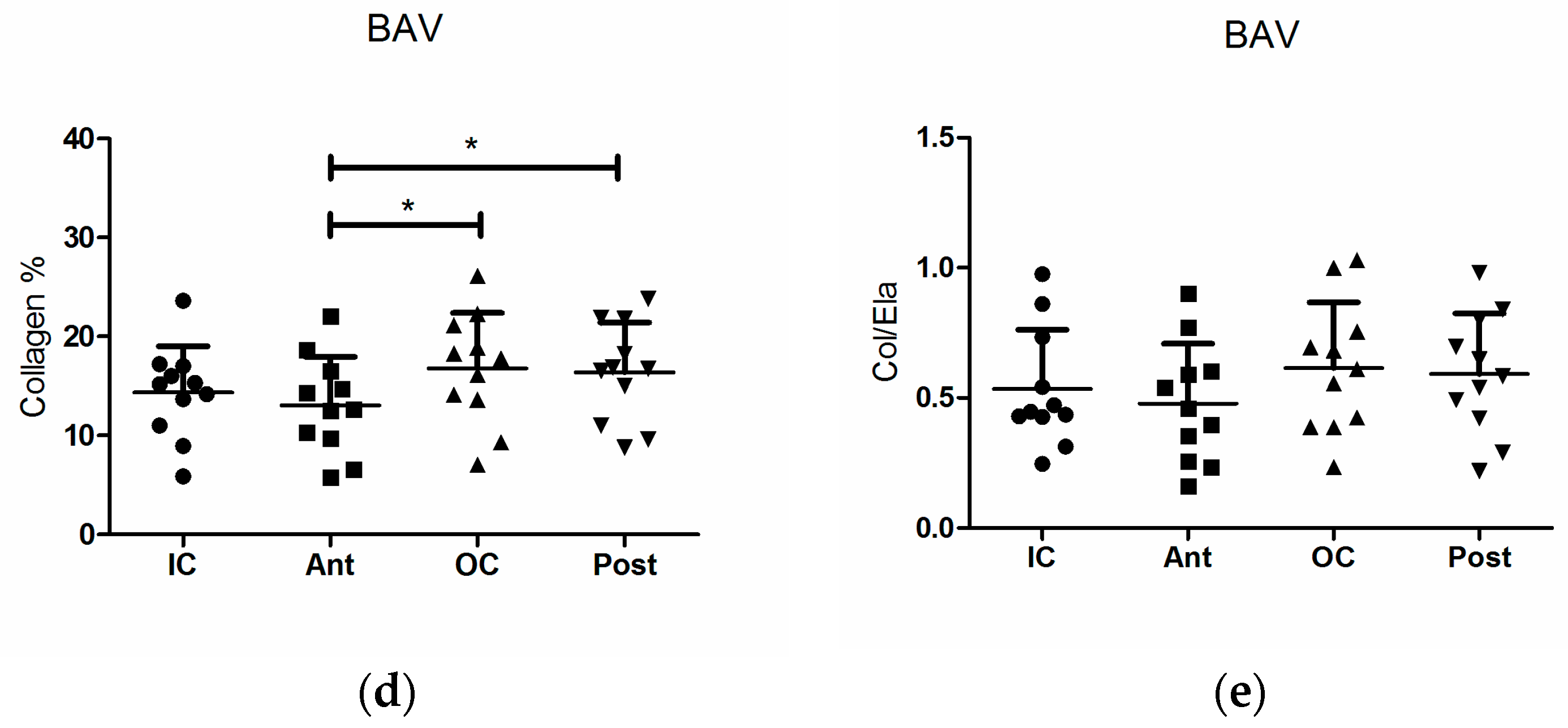
3. Results
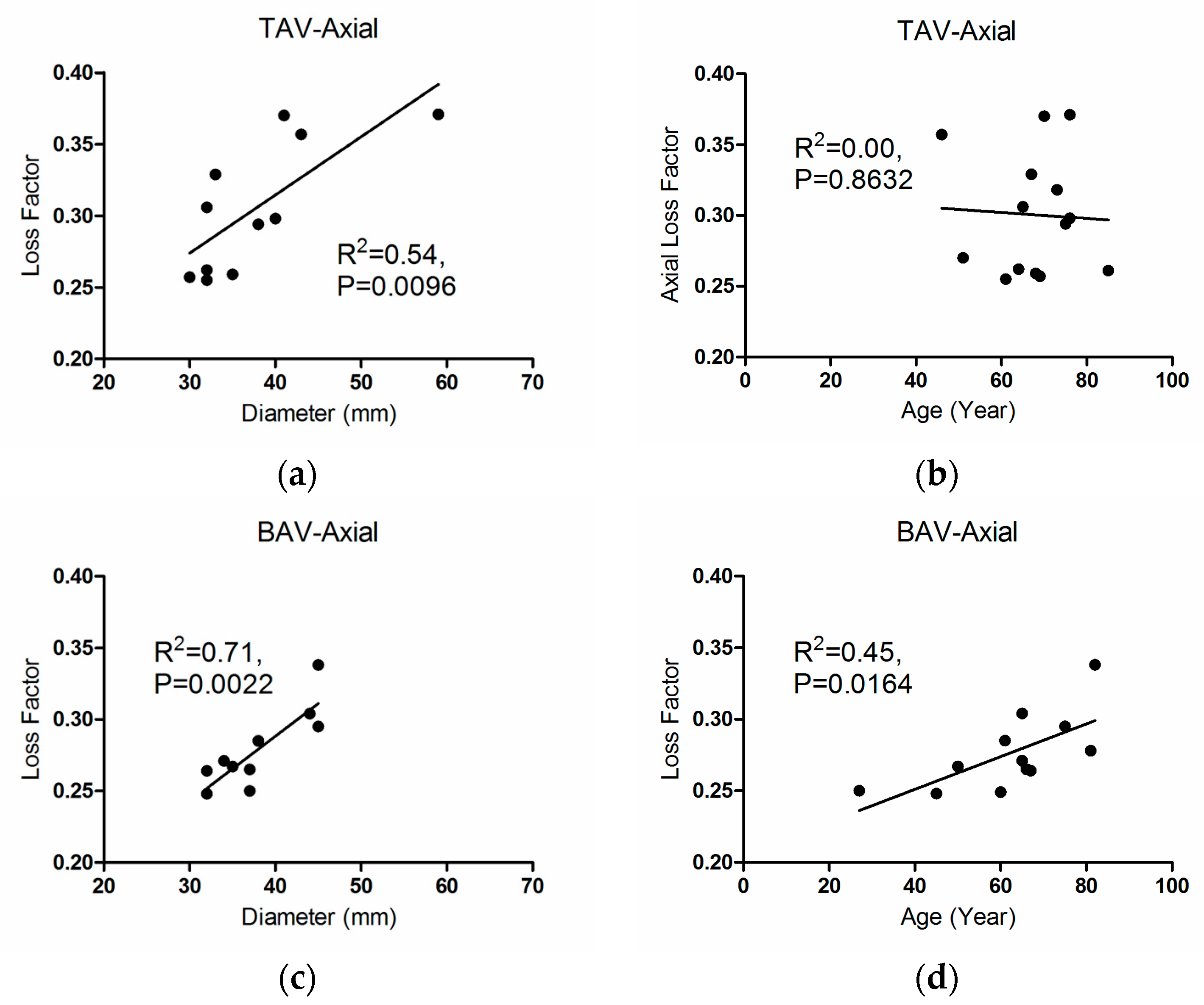
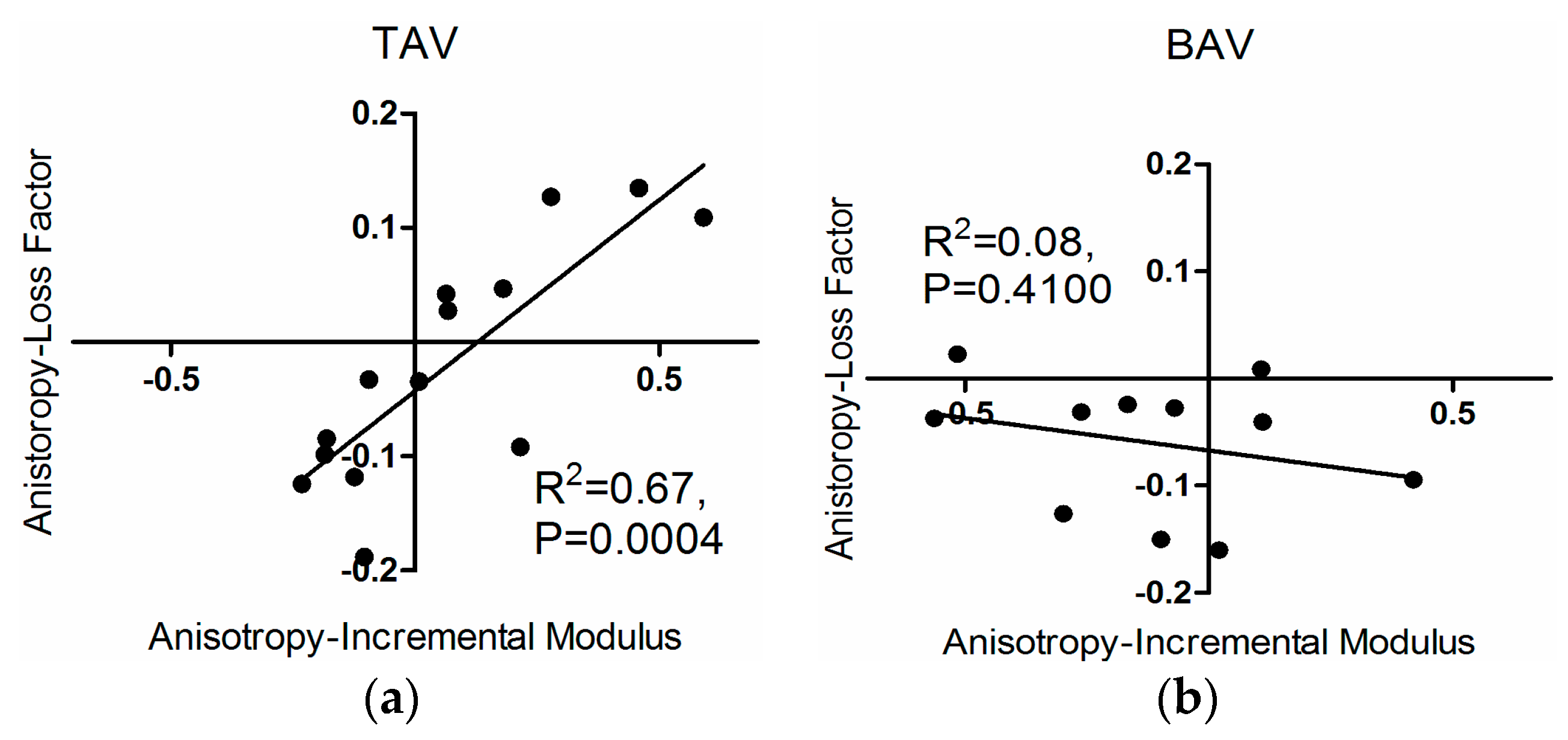
3.1. Loss Factor and Loss Factor Anisotropy
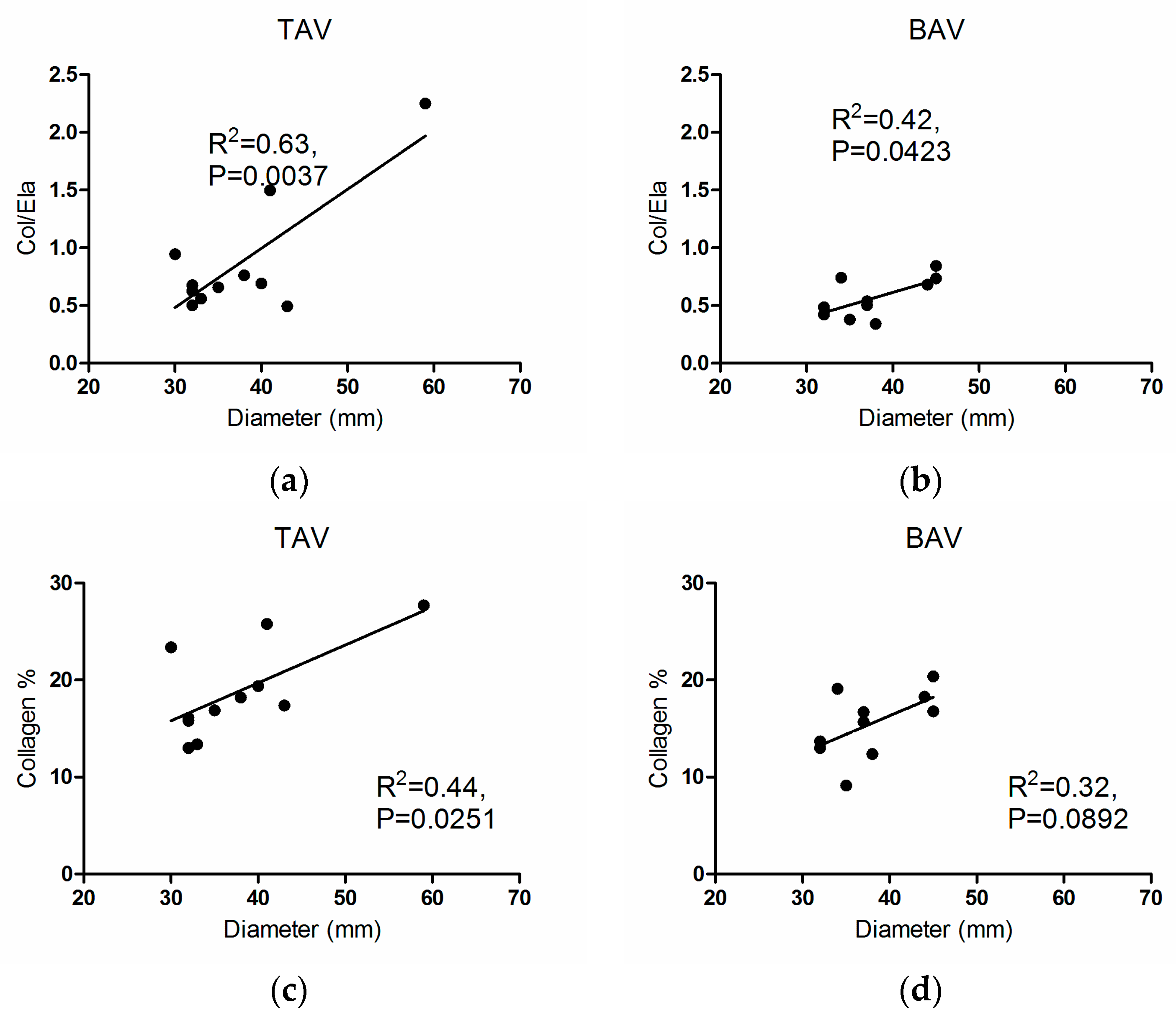
3.2. Structural Fiber Contents
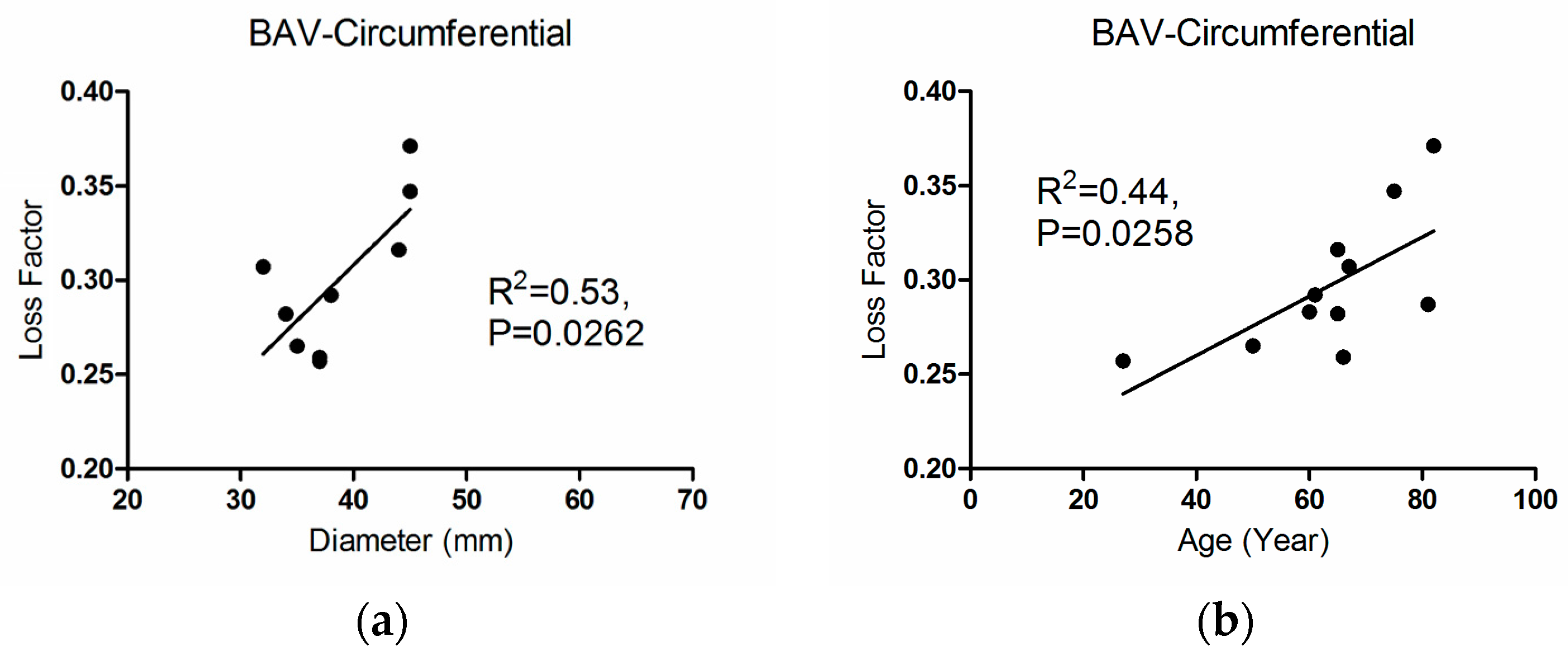
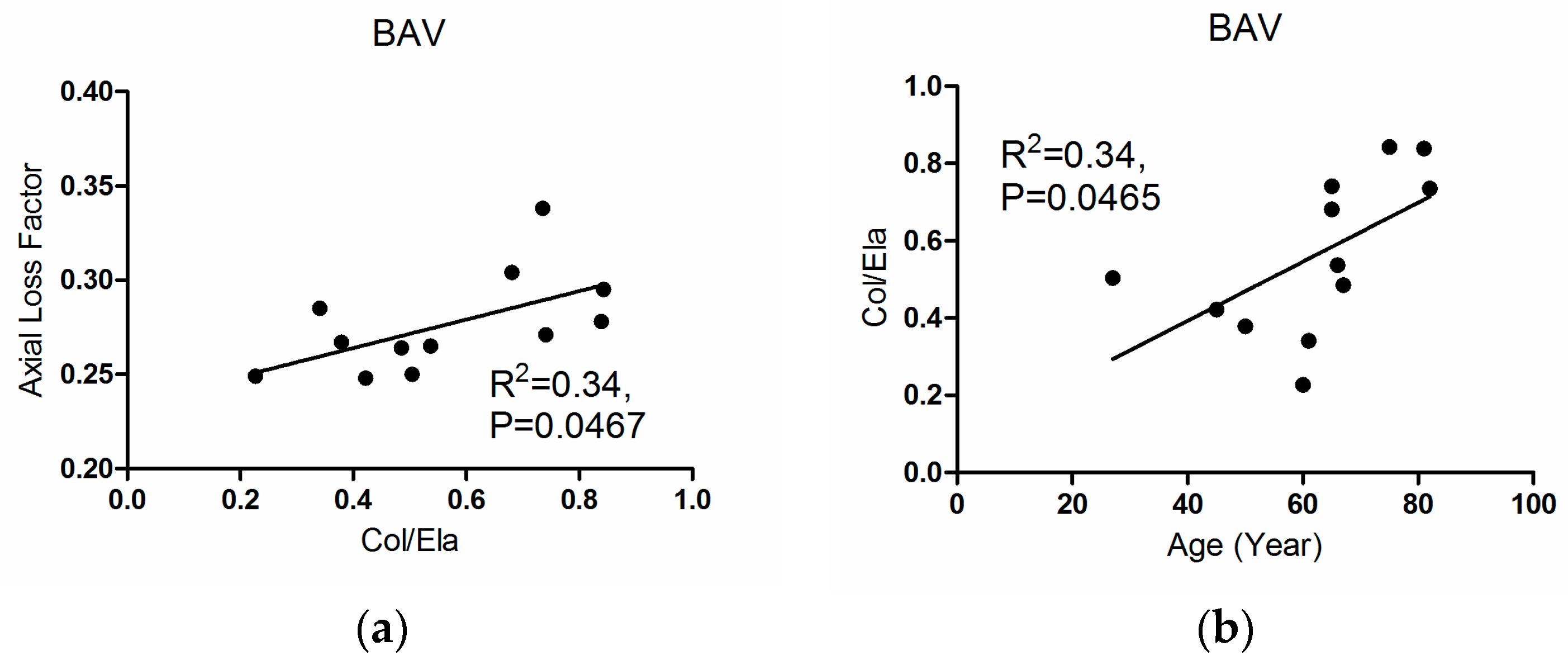
3.3. Correlations
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Elefteriades, J.A.; Farkas, E.A. Thoracic Aortic Aneurysm: Clinically Pertinent Controversies and Uncertainties. J. Am. Coll. Cardiol. 2010, 55, 841–857. [Google Scholar] [CrossRef] [PubMed]
- Hiratzka, L.F.; Bakris, G.L.; Beckman, J.A.; Bersin, R.M.; Carr, V.F.; Casey, D.E., Jr.; Eagle, K.A.; Hermann, L.K.; Isselbacher, E.M.; Kazerooni, E.A.; et al. 2010 ACCF/AHA/AATS/ACR/ASA/SCA/SCAI/SIR/STS/SVM Guidelines for the Diagnosis and Management of Patients With Thoracic Aortic Disease: A Report of the American College of Cardiology Foundation/American Heart Association Task Force on Practice Guidelines, American Association for Thoracic Surgery, American College of Radiology, American Stroke Association, Society of Cardiovascular Anesthesiologists, Society for Cardiovascular Angiography and Interventions, Society of Interventional Radiology, Society of Thoracic Surgeons, and Society for Vascular Medicine. Circulation 2010, 121, e266–e369. [Google Scholar] [PubMed]
- Verma, S.; Yanagawa, B.; Kalra, S.; Ruel, M.; Peterson, M.D.; Yamashita, M.H.; Fagan, A.; Currie, M.E.; White, C.W.; Wai Sang, S.L.; et al. Knowledge, attitudes, and practice patterns in surgical management of bicuspid aortopathy: A survey of 100 cardiac surgeons. J. Thorac. Cardiovasc. Surg. 2013, 146, 1033–1040. [Google Scholar] [CrossRef] [PubMed]
- Emmott, A.; Garcia, J.; Chung, J.; Lachapelle, K.; El-Hamamsy, I.; Mongrain, R.; Cartier, R.; Leask, R.L. Biomechanics of the Ascending Thoracic Aorta: A Clinical Perspective on Engineering Data. Can. J. Cardiol. 2016, 32, 35–47. [Google Scholar] [CrossRef] [PubMed]
- Khanafer, K.; Duprey, A.; Zainal, M.; Schlicht, M.; Williams, D.; Berguer, R. Determination of the elastic modulus of ascending thoracic aortic aneurysm at different ranges of pressure using uniaxial tensile testing. J. Thorac. Cardiovasc. Surg. 2011, 142, 682–686. [Google Scholar] [CrossRef] [PubMed]
- Pichamuthu, J.E.; Phillippi, J.A.; Cleary, D.A.; Chew, D.W.; Hempel, J.; Vorp, D.A.; Gleason, T.G. Differential Tensile Strength and Collagen Composition in Ascending Aortic Aneurysms by Aortic Valve Phenotype. Ann. Thorac. Surg. 2013, 96, 2147–2154. [Google Scholar] [CrossRef] [PubMed]
- Vorp, D.A.; Schiro, B.J.; Ehrlich, M.P.; Juvonen, T.S.; Ergin, M.A.; Griffith, B.P. Effect of aneurysm on the tensile strength and biomechanical behavior of the ascending thoracic aorta. Ann. Thorac. Surg. 2003, 75, 1210–1214. [Google Scholar] [CrossRef]
- Iliopoulos, D.C.; Kritharis, E.P.; Giagini, A.T.; Papadodima, S.A.; Sokolis, D.P. Ascending thoracic aortic aneurysms are associated with compositional remodeling and vessel stiffening but not weakening in age-matched subjects. J. Thorac. Cardiovasc. Surg. 2009, 137, 101–109. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, R.J.; Wagenseil, J.E.; Delong, W.R.; Peterson, S.J.; Kouchoukos, N.T.; Sundt, T.M., III. Mechanical properties of dilated human ascending aorta. Ann. Biomed. Eng. 2002, 30, 624–635. [Google Scholar] [CrossRef] [PubMed]
- Oishi, Y.; Miyoshi, H.; Mizuguchi, Y.; Iuchi, A.; Nagase, N.; Oki, T. Aortic stiffness is strikingly increased with age ≥50 years in clinically normal individuals and preclinical patients with cardiovascular risk factors: Assessment by the new technique of 2D strain echocardiography. J. Cardiol. 2011, 57, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Martin, C.; Sun, W.; Pham, T.; Elefteriades, J. Predictive biomechanical analysis of ascending aortic aneurysm rupture potential. Acta Biomater. 2013, 9, 9392–9400. [Google Scholar] [CrossRef] [PubMed]
- Davis, F.; Luo, Y.; Avril, S.; Duprey, A.; Lu, J. Pointwise characterization of the elastic properties of planar soft tissues: Application to ascending thoracic aneurysms. Biomech. Model. Mechanobiol. 2015, 14, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Davis, F.M.; Luo, Y.; Avril, S.; Duprey, A.; Lu, J. Local mechanical properties of human ascending thoracic aneurysms. J. Mech. Behav. Biomed. Mater. 2016, 61, 235–249. [Google Scholar] [CrossRef] [PubMed]
- Sassani, S.G.; Tsangaris, S.; Sokolis, D.P. Layer- and region-specific material characterization of ascending thoracic aortic aneurysms by microstructure-based models. J. Biomech. 2015, 48, 3757–3765. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.; Lachapelle, K.; Wener, E.; Cartier, R.; De Varennes, B.; Fraser, R.; Leask, R.L. Energy loss, a novel biomechanical parameter, correlates with aortic aneurysm size and histopathologic findings. J. Thorac. Cardiovasc. Surg. 2014, 148, 1082–1089. [Google Scholar] [CrossRef] [PubMed]
- Belz, G.G. Elastic properties and Windkessel function of the human aorta. Cardiovasc. Drugs. Ther. 1995, 9, 73–83. [Google Scholar] [CrossRef] [PubMed]
- Choudhury, N.; Bouchot, O.; Rouleau, L.; Tremblay, D.; Cartier, R.; Butany, J.; Mongrain, R.; Leask, R.L. Local mechanical and structural properties of healthy and diseased human ascending aorta tissue. Cardiovasc. Pathol. 2009, 18, 83–91. [Google Scholar] [CrossRef] [PubMed]
- Tremblay, D.; Zigras, T.; Cartier, R.; Leduc, L.; Butany, J.; Mongrain, R.; Leask, R.L. A Comparison of Mechanical Properties of Materials Used in Aortic Arch Reconstruction. Ann. Thorac. Surg. 2009, 88, 1484–1491. [Google Scholar] [CrossRef] [PubMed]
- Ferrara, A.; Morganti, S.; Totaro, P.; Mazzola, A.; Auricchio, F. Human dilated ascending aorta: Mechanical characterization via uniaxial tensile tests. J. Mech. Behav. Biomed. Mater. 2016, 53, 257–271. [Google Scholar] [CrossRef] [PubMed]
- Duprey, A.; Trabelsi, O.; Vola, M.; Favre, J.-P.; Avril, S. Biaxial rupture properties of ascending thoracic aortic aneurysms. Acta Biomater. 2016, 42, 273–285. [Google Scholar] [CrossRef] [PubMed]
- Sokolis, D.P.; Kritharis, E.P.; Iliopoulos, D.C. Effect of layer heterogeneity on the biomechanical properties of ascending thoracic aortic aneurysms. Med. Biol. Eng. Comput. 2012, 50, 1227–1237. [Google Scholar] [CrossRef] [PubMed]
- Sokolis, D.P. Effects of aneurysm on the directional, regional, and layer distribution of residual strains in ascending thoracic aorta. J. Mech. Behav. Biomed. Mater. 2015, 46, 229–243. [Google Scholar] [CrossRef] [PubMed]
- Sokolis, D.P.; Kritharis, E.P.; Giagini, A.T.; Lampropoulos, K.M.; Papadodima, S.A.; Iliopoulos, D.C. Biomechanical response of ascending thoracic aortic aneurysms: Association with structural remodelling. Comput. Methods Biomech. Biomed. 2012, 15, 231–248. [Google Scholar] [CrossRef] [PubMed]
- El-Hamamsy, I.; Yacoub, M.H. Cellular and molecular mechanisms of thoracic aortic aneurysms. Nat. Rev. Cardiol. 2009, 6, 771–786. [Google Scholar] [CrossRef] [PubMed]
- Hirst, A.E., Jr.; Varner, J.J.; Kime, S.W., Jr. Dissecting aneurysm of the aorta: A review of 505 cases. Medicine 1958, 37, 217. [Google Scholar] [CrossRef] [PubMed]
- Shahmansouri, N.; Alreshidan, M.; Emmott, A.; Lachapelle, K.; Cartier, R.; Leask, R.L.; Mongrain, R. Evaluating ascending aortic aneurysm tissue toughness: Dependence on collagen and elastin contents. J. Mech. Behav. Biomed. Mater. 2016, 64, 262–271. [Google Scholar] [CrossRef] [PubMed]
- Roberts, W.C. Aortic dissection: Anatomy, consequences, and causes. Am. Heart J. 1981, 101, 195–214. [Google Scholar] [CrossRef]
- Collins, M.J.; Dev, V.; Strauss, B.H.; Fedak, P.W.M.; Butany, J. Variation in the histopathological features of patients with ascending aortic aneurysms: A study of 111 surgically excised cases. J. Clin. Pathol. 2008, 61, 519–523. [Google Scholar] [CrossRef] [PubMed]
- Phillippi, J.A.; Green, B.R.; Eskay, M.A.; Kotlarczyk, M.P.; Hill, M.R.; Robertson, A.M.; Watkins, S.C.; Vorp, D.A.; Gleason, T.G. Mechanism of aortic medial matrix remodeling is distinct in patients with bicuspid aortic valve. J. Thorac. Cardiovasc. Surg. 2014, 147, 1056–1064. [Google Scholar] [CrossRef] [PubMed]
- O’leary, S.A.; Healey, D.A.; Kavanagh, E.G.; Walsh, M.T.; Mcgloughlin, T.M.; Doyle, B.J. The biaxial biomechanical behavior of abdominal aortic aneurysm tissue. Ann. Biomed. Eng. 2014, 42, 2440–2450. [Google Scholar] [CrossRef] [PubMed]
- Vitarelli, A.; Giordano, M.; Germanò, G.; Pergolini, M.; Cicconetti, P.; Tomei, F.; Sancini, A.; Battaglia, D.; Dettori, O.; Capotosto, L. Assessment of ascending aorta wall stiffness in hypertensive patients by tissue Doppler imaging and strain Doppler echocardiography. Heart 2010, 96, 1469–1474. [Google Scholar] [CrossRef] [PubMed]
- Pasta, S.; Rinaudo, A.; Luca, A.; Pilato, M.; Scardulla, C.; Gleason, T.G.; Vorp, D.A. Difference in hemodynamic and wall stress of ascending thoracic aortic aneurysms with bicuspid and tricuspid aortic valve. J. Biomech. 2013, 46, 1729–1738. [Google Scholar] [CrossRef] [PubMed]
| Sample Number | Gender | Age (Year) | Aortic Diameter (mm) | Valve Type |
|---|---|---|---|---|
| 1 | M | 65 | 44 | BAV |
| 2 | F | 82 | 45 | BAV |
| 3 | M | 61 | 38 | BAV |
| 4 | F | 66 | 37 | BAV |
| 5 | F | 27 | 37 | BAV |
| 6 | M | 50 | 35 | BAV |
| 7 | M | 67 | 32 | BAV |
| 8 | M | 75 | 45 | BAV |
| 9 | M | 65 | 34 | BAV |
| 10 | M | 45 | 32 | BAV |
| 11 | M | 81 | 48 * | BAV |
| 12 | M | 60 | 50 * | BAV |
| 13 | M | 51 | 58 * | TAV |
| 14 | F | 70 | 41 | TAV |
| 15 | M | 61 | 32 | TAV |
| 16 | M | 64 | 32 | TAV |
| 17 | M | 76 | 59 | TAV |
| 18 | M | 65 | 32 | TAV |
| 19 | M | 75 | 38 | TAV |
| 20 | M | 73 | 38 * | TAV |
| 21 | M | 67 | 33 | TAV |
| 22 | M | 69 | 30 | TAV |
| 23 | M | 76 | 40 | TAV |
| 24 | M | 68 | 35 | TAV |
| 25 | M | 46 | 43 | TAV |
| 26 | F | 85 | 50 * | TAV |
| 27 | M | 49 | 37 | Control |
| 28 | M | 81 | 37 | Control |
| 29 | M | 52 | 24 | Control |
| 30 | M | 48 | 24 | Control |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahmansouri, N.; Alreshidan, M.; Emmott, A.; Lachapelle, K.; El-Hamamsy, I.; Cartier, R.; Leask, R.L.; Mongrain, R. Investigation on the Regional Loss Factor and Its Anisotropy for Aortic Aneurysms. Materials 2016, 9, 867. https://doi.org/10.3390/ma9110867
Shahmansouri N, Alreshidan M, Emmott A, Lachapelle K, El-Hamamsy I, Cartier R, Leask RL, Mongrain R. Investigation on the Regional Loss Factor and Its Anisotropy for Aortic Aneurysms. Materials. 2016; 9(11):867. https://doi.org/10.3390/ma9110867
Chicago/Turabian StyleShahmansouri, Nastaran, Mohammed Alreshidan, Alexander Emmott, Kevin Lachapelle, Ismaïl El-Hamamsy, Raymond Cartier, Richard L. Leask, and Rosaire Mongrain. 2016. "Investigation on the Regional Loss Factor and Its Anisotropy for Aortic Aneurysms" Materials 9, no. 11: 867. https://doi.org/10.3390/ma9110867
APA StyleShahmansouri, N., Alreshidan, M., Emmott, A., Lachapelle, K., El-Hamamsy, I., Cartier, R., Leask, R. L., & Mongrain, R. (2016). Investigation on the Regional Loss Factor and Its Anisotropy for Aortic Aneurysms. Materials, 9(11), 867. https://doi.org/10.3390/ma9110867





