Experimental Study and Numerical Modeling of Inter-Pass Forging in Wire-Arc Additive Manufacturing of Inconel 718
Abstract
1. Introduction
2. Materials and Methods
- By comparing the dynamic (implicit) and quasi-static solutions to the problem of a high-speed collision of a massive sphere with an elastic–plastic cylinder, where the insignificance of the influence of inertial terms is demonstrated.
- By comparing the solutions to the specimen forging problem in a dynamic (explicit, DYNA) formulation, performed by other authors and by us in a quasi-static formulation (ANSYS).
3. Results and Discussion
3.1. Effect of Inter-Pass Forging on the Structure of the Material
- Without inter-pass forging (specimen 1);
- With single-stage forging in three passes (specimen 2);
- With two-stage forging in six passes (specimen 3).
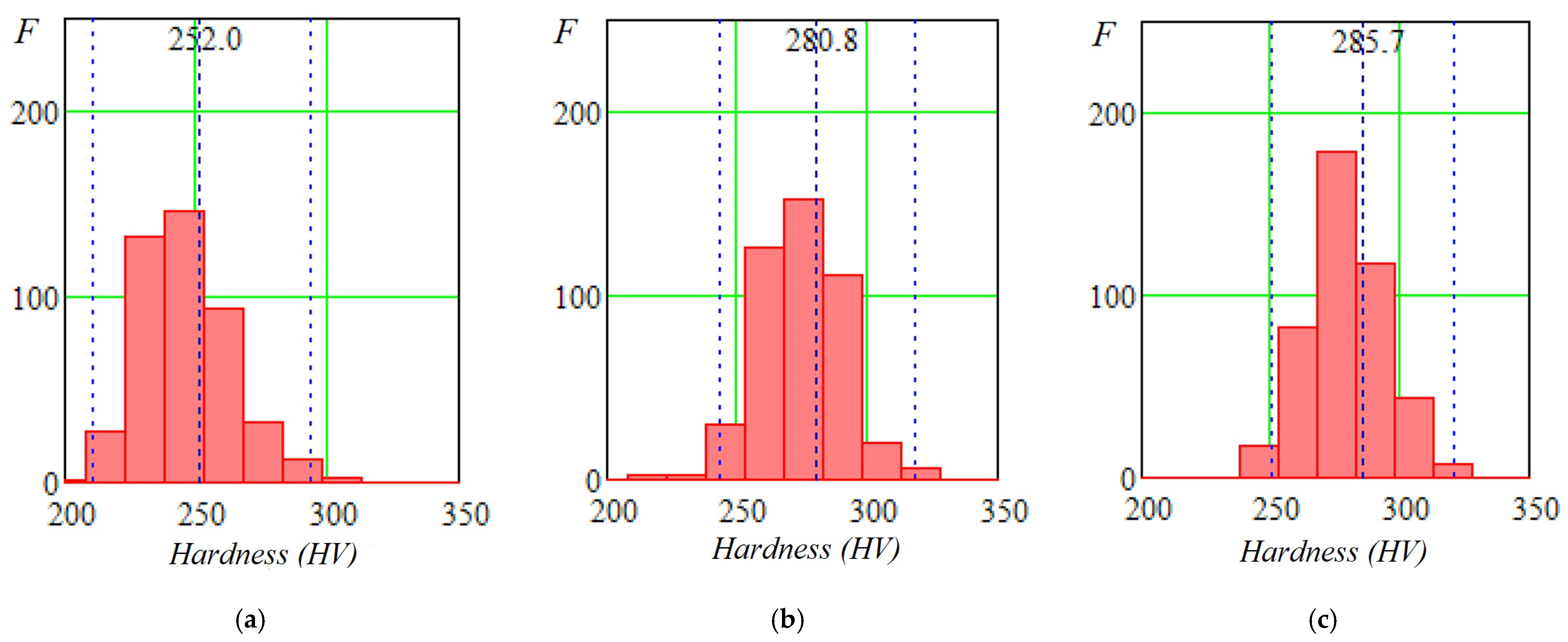
3.2. Effect on Mechanical Properties and Johnson–Cook Parameters
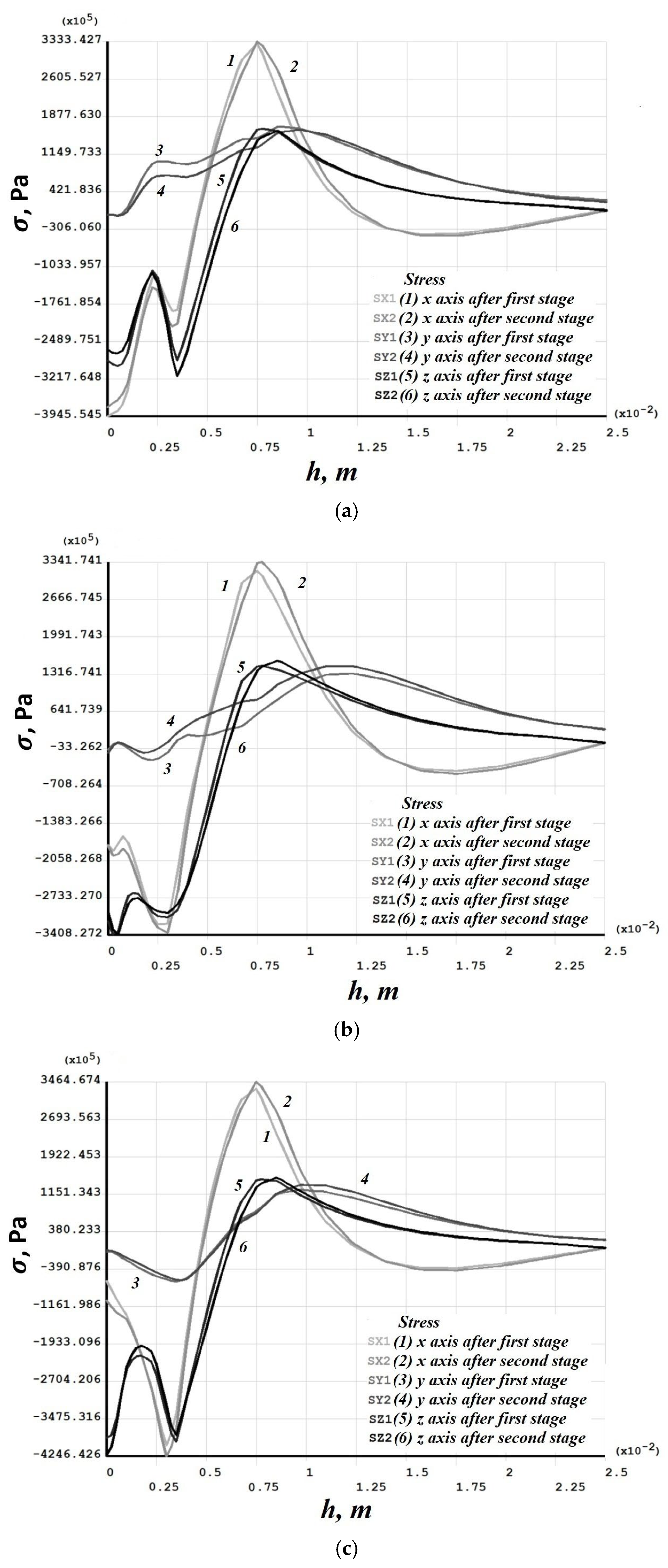
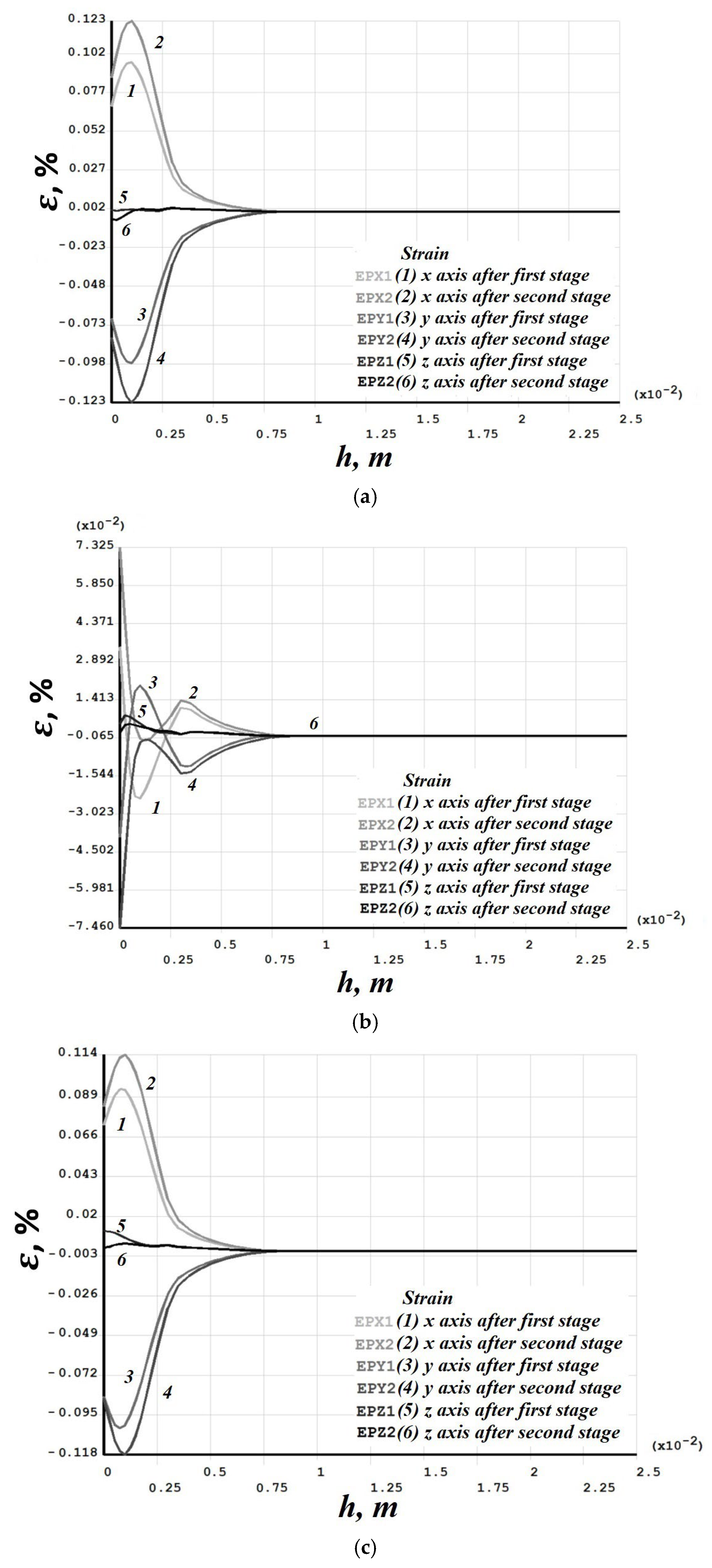
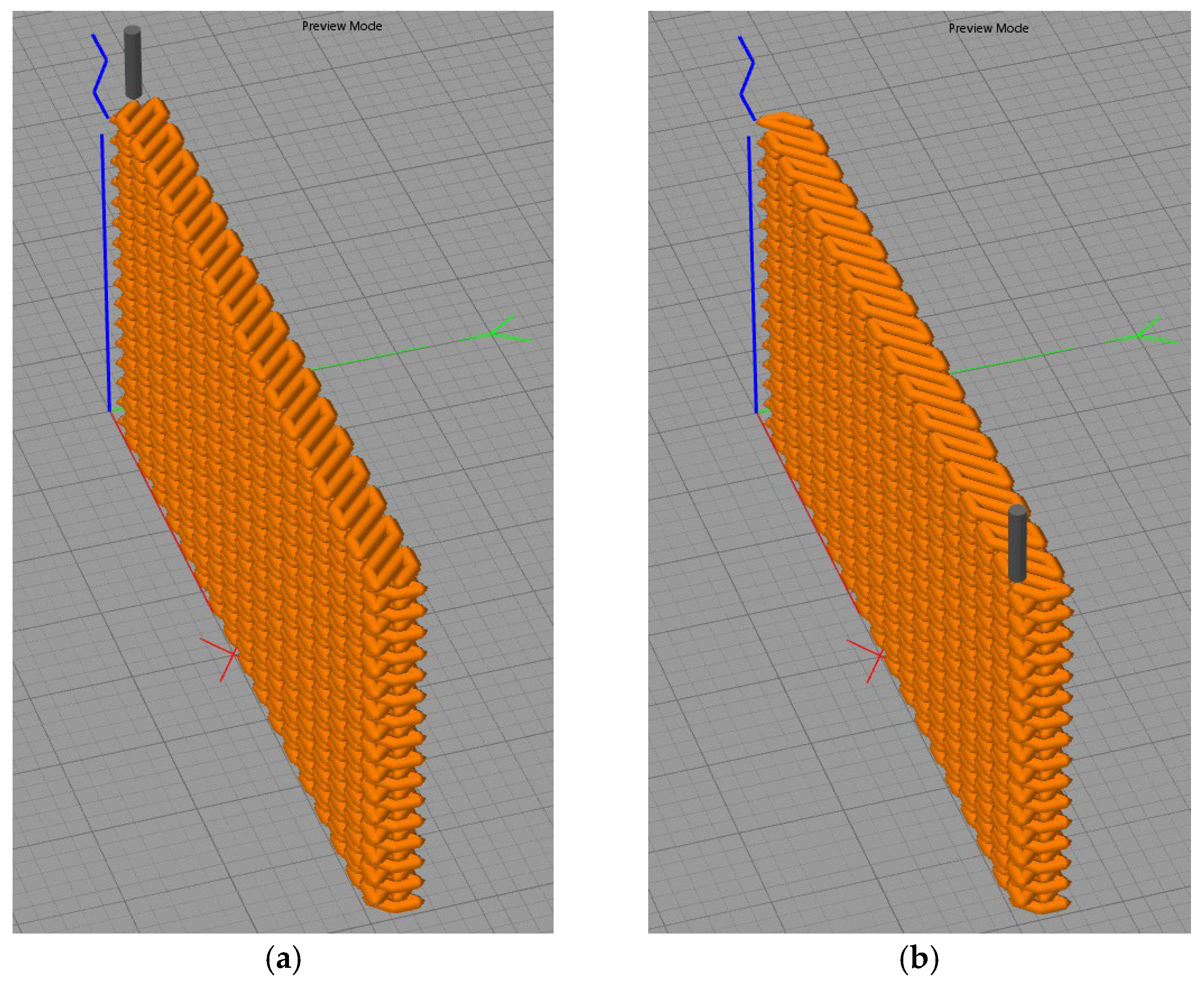
3.3. Finite Element Modeling of Inter-Pass Forging
- Case 1 (PC1): Left ↑, central ↓, right ↑; left ↓, central ↑, right ↓.
- Case 2 (PC2): Central ↑, left ↓, right ↑; central ↓, left ↑, right ↓.


- → Case 1 (PC1) Results




- → Case 2 (PC2) Results



4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Elefterie, C.F.; Guragata, C.; Bran, D.; Ghiban, B. Aeronautical Requirements for Inconel 718 Alloy. IOP Conf. Ser. Mater. Sci. Eng. 2017, 209, 012060. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Tsongas, K.; Tzetzis, D. Finite Element Analysis of Orthopedic Hip Implant with Functionally Graded Bioinspired Lattice Structures. Biomimetics 2020, 5, 44. [Google Scholar] [CrossRef] [PubMed]
- Achitei, D.C.; Baltatu, M.S.; Vizureanu, P.; Sandu, A.V.; Benchea, M.; Istrate, B. Ni-Cr Alloys Assessment for Dental Implants Suitability. Appl. Sci. 2022, 12, 12814. [Google Scholar] [CrossRef]
- Ghiban, B.; Elefterie, C.F.; Guragata, C.; Bran, D. Requirements of Inconel 718 Alloy for Aeronautical Applications. AIP Conf. Proc. 2018, 1932, 030016. [Google Scholar] [CrossRef]
- Debarbadillo, J.J.; Mannan, S.K. Alloy 718 for Oilfield Applications. JOM 2012, 64, 265–270. [Google Scholar] [CrossRef]
- Taylor, P. Machinability of Nickel-Based High Temperature Alloys. Mach. Sci. Technol. 2014, 4, 37–41. [Google Scholar]
- Sonar, T.; Balasubramanian, V.; Malarvizhi, S.; Venkateswaran, T.; Sivakumar, D. An Overview on Welding of Inconel 718 Alloy-Effect of Welding Processes on Microstructural Evolution and Mechanical Properties of Joints. Mater. Charact. 2021, 174, 110997. [Google Scholar] [CrossRef]
- Cao, X.; Rivaux, B.; Jahazi, M.; Cuddy, J.; Birur, A. Effect of Pre- and Post-Weld Heat Treatment on Metallurgical and Tensile Properties of Inconel 718 Alloy Butt Joints Welded Using 4 kW Nd:YAG Laser. J. Mater. Sci. 2009, 44, 4557–4571. [Google Scholar] [CrossRef]
- Bai, Y.; Lu, Q.; Ren, X.; Yan, H.; Zhang, P. Inconel 718 Welded by Bead-on-Plate Laser Welding under High-Frequency Micro-Vibration. Metals 2019, 9, 1335. [Google Scholar] [CrossRef]
- Thavamani, R.; Balusamy, V.; Nampoothiri, J.; Subramanian, R.; Ravi, K.R. Mitigation of Hot Cracking in Inconel 718 by Ultrasonic Vibration during GTAW. J. Alloys Compd. 2018, 740, 870–878. [Google Scholar] [CrossRef]
- Chlebus, E.; Gruber, K.; Kuźnicka, B.; Kurzac, J.; Kurzynowski, T. Effect of Heat Treatment on Microstructure and Mechanical Properties of Inconel 718 Processed by SLM. Mater. Sci. Eng. A 2015, 639, 647–655. [Google Scholar] [CrossRef]
- Ni, M.; Liu, S.; Chen, C.; Li, R.; Zhang, X.; Zhou, K. Effect of Heat Treatment on the Microstructural Evolution of a Precipitation-Hardened Superalloy Produced by SLM. Mater. Sci. Eng. A 2019, 748, 275–285. [Google Scholar] [CrossRef]
- Ghorbanpour, S.; Deshmukh, K.; Sahu, S.; Riemslag, T.; Reinton, E.; Borisov, E.; Popovich, A.; Bertolo, V.; Jiang, Q.; Sanchez, M.T.; et al. Additive Manufacturing of Functionally Graded Inconel 718: Effect of Heat Treatment and Building Orientation on Microstructure and Fatigue Behaviour. J. Mater. Process. Technol. 2022, 306, 117573. [Google Scholar] [CrossRef]
- Sun, S.H.; Koizumi, Y.; Saito, T.; Yamanaka, K.; Li, Y.-P.; Cui, Y.; Chiba, A. Electron Beam Additive Manufacturing of Inconel 718 Rods: Impact of Build Direction on Microstructure and High-Temperature Tensile Properties. Addit. Manuf. 2018, 23, 457–470. [Google Scholar] [CrossRef]
- Anush Raj, B.; Jappes, J.W.; Khan, M.A.; Dillibabu, V.; Brintha, N.C. Direct Metal Laser Sintered (DMLS) Inconel 718 for Turbine Engine Components. Optik 2020, 202, 163735. [Google Scholar] [CrossRef]
- Kindermann, R.M.; Roy, M.J.; Morana, R.; Francis, J.A. Effects of Microstructural Heterogeneity and Defects on Mechanical Behaviour of WAAM Inconel 718. Mater. Sci. Eng. A 2022, 839, 142826. [Google Scholar] [CrossRef]
- Seow, C.E.; Coules, H.E.; Wu, G.; Khan, R.H.; Xu, X.; Williams, S. WAAM Inconel 718: Effect of Post-Deposition Heat Treatments on Microstructure and Tensile Properties. Mater. Des. 2019, 183, 108157. [Google Scholar] [CrossRef]
- Xu, X.; Ding, J.; Ganguly, S.; Williams, S. Process Factors Affecting Mechanical Properties of Inconel 718 in WAAM. J. Mater. Process. Technol. 2019, 265, 201–209. [Google Scholar] [CrossRef]
- Hönnige, J.; Seow, C.E.; Ganguly, S.; Xu, X.; Cabeza, S.; Coules, H.; Williams, S. Residual Stress and Microstructural Evolution in As-Deposited and Inter-Pass Rolled WAAM Inconel 718 after Ageing. Mater. Sci. Eng. A 2021, 801, 140368. [Google Scholar] [CrossRef]
- Xu, X.; Ganguly, S.; Ding, J.; Seow, C.E.; Williams, S. Enhancing Mechanical Properties of WAAM Inconel 718 via In-Process Thermo-Mechanical Processing. Mater. Des. 2018, 160, 1042–1051. [Google Scholar] [CrossRef]
- Singh, S.; Andersson, J. Hot Cracking in Cast Alloy 718. Sci. Technol. Weld. Join. 2018, 23, 568–574. [Google Scholar] [CrossRef]
- Calandri, M.; Yin, S.; Aldwell, B.; Calignano, F.; Lupoi, R.; Ugues, D. Texture and Microstructural Features at Different Length Scales in SLM Inconel 718. Materials 2019, 12, 1293. [Google Scholar] [CrossRef] [PubMed]
- Mostafa, A.; Picazo Rubio, I.; Brailovski, V.; Jahazi, M.; Medraj, M. Structure, Texture and Phases in 3D-Printed IN718 Subjected to Homogenization and HIP. Metals 2017, 7, 196. [Google Scholar] [CrossRef]
- Xi, N.; Tang, K.; Fang, X.; Li, Y.; Duan, Y.; Huang, K. Enhanced Comprehensive Properties of DED Inconel 718 by an Integrated Deposition Strategy. J. Mater. Sci. Technol. 2023, 141, 42–55. [Google Scholar] [CrossRef]
- Zhang, T.; Li, H.; Gong, H.; Wu, Y.; Ahmad, A.S.; Chen, X. Effect of Rolling Force on Tensile Properties of AM Inconel 718 at Ambient and Elevated Temperatures. J. Alloys Compd. 2021, 884, 161050. [Google Scholar] [CrossRef]
- Colegrove, P.; Williams, S. High Deposition Rate High Quality Metal Additive Manufacture Using Wire+ Arc Technology. Ph.D. Thesis, Cranfield University, Bedford, UK, 2013. [Google Scholar]
- Martina, F.; Williams, S.W.; Colegrove, P.A. Improved microstructure and increased mechanical properties of additive manufacture produced Ti-6Al-4V by interpass cold rolling. In Proceedings of the 24th International Solid Freeform Fabrication Symposium, Austin, TX, USA, 12–14 August 2014. [Google Scholar]
- Colegrove, P.A.; Coules, H.E.; Fairman, J.; Martina, F.; Kashoob, T.; Mamash, H.; Cozzolino, L.D. Microstructure and residual stress improvement in wire and arc additively manufactured parts through high-pressure rolling. J. Mater. Process. Technol. 2013, 213, 1782–1791. [Google Scholar] [CrossRef]
- Karunakaran, K.P. Hybrid manufacturing. In Springer Handbook of Additive Manufacturing; Springer International Publishing: Cham, Switzerland, 2023; pp. 425–441. [Google Scholar]
- Hönnige, J.R.; Colegrove, P.; Williams, S. Improvement of microstructure and mechanical properties in wire+ arc additively manufactured Ti-6Al-4V with machine hammer peening. Procedia Eng. 2017, 216, 8–17. [Google Scholar] [CrossRef]
- Hönnige, J.R.; Davis, A.E.; Ho, A.; Kennedy, J.R.; Neto, L.; Prangnell, P.; Williams, S. The effectiveness of grain refinement by machine hammer peening in high deposition rate wire-arc AM Ti-6Al-4V. Metall. Mater. Trans. A 2020, 51, 3692–3703. [Google Scholar] [CrossRef]
- Kirichek, A.V. Possibilities of additive-subtractive-strengthening technology. Vestn. Bryanskogo Gos. Tekhnicheskogo Univ. 2016, 4, 151–160. [Google Scholar] [CrossRef]
- Kirichek, A.V.; Fedonin, O.; Coлoвьев, Д.; Solov’EV, D.; Zhirkov, A.; Хандoжкo, А.; Khandozhko, A.; Cмoленцев, Е.; Smolentsev, E. Additive-subtractive technologies-effective transition to innovative production. Vestn. Bryanskogo Gos. Tekhnicheskogo Univ. 2019, 8, 4–10. [Google Scholar]
- Byun, J.G.; Yi, H.; Cho, S.M. The effect of interpass peening on mechanical properties in additive manufacturing of Ti-6Al-4V. J. Weld. Join. 2017, 35, 6–12. [Google Scholar] [CrossRef]
- Shchitsyn, Y.; Kartashev, M.; Krivonosova, E.; Olshanskaya, T.; Trushnikov, D. Formation of Structure and Properties of Two-Phase Ti-6Al-4V Alloy during Cold Metal Transfer Additive Deposition with Inter-pass Forging. Materials 2021, 14, 4415. [Google Scholar] [CrossRef] [PubMed]
- Abbaszadeh, M.; Hönnige, J.; Martina, F.; Kashaev, N.; Williams, S.W.; Klusemann, B. Numerical study of rolling process on the plastic strain distribution in wire+ arc additive manufactured Ti-6Al-4V. AIP Conf. Proc. 2019, 2113, 150019. [Google Scholar]
- Abbaszadeh, M.; Hönnige, J.R.; Martina, F.; Neto, L.; Kashaev, N.; Colegrove, P.; Williams, S.; Klusemann, B. Numerical investigation of the effect of rolling on the localized stress and strain induction for wire+ arc additive manufactured structures. J. Mater. Eng. Perform. 2019, 28, 4931–4942. [Google Scholar] [CrossRef]
- Keller, I.E.; Kazantsev, A.V.; Dudin, D.S.; Permyakov, G.L. Shape Distortion, Plastic Strain Localization and Residual Stresses during One-Side Forging/Rolling of a Bar: Application to Additive Manufacturing of a Stringer with Layer-Wise Pressure Processing. Comput. Contin. Mech. 2021, 17, 51–60. (In Russian) [Google Scholar]
- Panov, D.; Permyakov, G.; Naumov, S.; Mirontsov, V.; Kudryavtsev, E.; Sun, L.; Aksenov, A.; Stepanov, N.; Trushnikov, D.; Salishchev, G. The Effect of Post-Deposition Heat Treatment on the Microstructure, Texture, and Mechanical Properties of Inconel 718 Produced by Hybrid Wire-Arc Additive Manufacturing with Inter-Pass Forging. Metals 2025, 15, 78. [Google Scholar] [CrossRef]
- Khan, A.S.; Huang, S. Continuum Theory of Plasticity; Wiley: Hoboken, NJ, USA, 1995. [Google Scholar]
- Maiz, D. Theory and Problems of Continuum Mechanics; Mir Publishers: Moscow, Russia, 1974. [Google Scholar]
- Johnson, G.R.; Cook, W.H. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates and High Temperatures. In Proceedings of the 7th International Symposium on Ballistics, Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture Characteristics of Three Metals Subjected to Various Strains, Strain Rates, Temperatures, and Pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Smetannikov, O.Y.; Trushnikov, D.N.; Anisimov, A.A. Simulation Of Interim Forging Of Deposited Products in Ansys Mechanical Apdl (Implicit Analysis). PNRPU Mech. Bull. 2022, 4, 148–162. (In Russian) [Google Scholar] [CrossRef]
- Smetannikov, O.Y.; Zhila, V.V. Adapting the Johnson–Cook Model for Inter-pass Forging of Deposited Parts in ANSYS Mechanical APDL. Master’s J. 2023, 2, 1–18. (In Russian) [Google Scholar]
- DeMange, J.J.; Prakash, V.; Pereira, J.M. Effects of Material Microstructure on Blunt Projectile Penetration of a Nickel-Based Superalloy. Int. J. Impact Eng. 2009, 36, 1027–1043. [Google Scholar] [CrossRef]




| C | Si | Mn | P | S | Cr | Mo | Ni | Cu | Ti | Al | Nb | B | Fe | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Welding wire | 0.06 | 0.05 | 0.02 | 0.0032 | 0.0014 | 19.19 | 2.96 | 52.29 | 0.02 | 0.93 | 0.48 | 5.25 | 0.002 | 18.65 |
| Deposited material | 0.06 | 0.05 | 0.02 | 0.0029 | 0.0008 | 19.14 | 2.98 | 51.98 | 0.01 | 0.93 | 0.47 | 5.28 | 0.002 | 18.96 |
| Layer Height | Single-Stage Forging (Specimen 2) | Two-Stage Forging (Specimen 3) |
|---|---|---|
| Equiaxed grain layers, mm | 0.90–1.25 | 1.42–1.56 |
| Columnar grain layers, mm | 0.80–1.00 | 0.64–0.77 |
| Parameter of Microhardness (HV0.1) | Without Forging (Specimen 1) | Single-Stage Forging (Specimen 2) | Two-Stage Forging (Specimen 3) |
|---|---|---|---|
| Mean value | 252.06 | 280.87 | 285.69 |
| Minimum value | 214.00 | 225.00 | 249.00 |
| Maximum value | 312.00 | 328.00 | 328.00 |
| Standard deviation | 17.586 | 16.021 | 15.259 |
| Confidence interval | 41.05 | 37.4 | 35.6 |
| Range of values | 211.0–293.1 | 243.5–318.3 | 250.1–321.3 |
| Material Categories | E, GPa | , MPa | , MPa | , MPa | , % | ψ, % |
|---|---|---|---|---|---|---|
| Without forging | 170 ± 10 | 816 | 350 ± 20 | 462 | 38 | 29 |
| Single-stage | 180 ± 15 | 916 | 450 ± 20 | 591 | 26 | 23 |
| Two-stage | 180 ± 15 | 949 | 460 ± 30 | 624 | 28 | 26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Smetannikov, O.Y.; Permyakov, G.L.; Neulybin, S.D.; Ovchinnikov, I.P.; Oskolkov, A.A.; Trushnikov, D.N. Experimental Study and Numerical Modeling of Inter-Pass Forging in Wire-Arc Additive Manufacturing of Inconel 718. Materials 2026, 19, 182. https://doi.org/10.3390/ma19010182
Smetannikov OY, Permyakov GL, Neulybin SD, Ovchinnikov IP, Oskolkov AA, Trushnikov DN. Experimental Study and Numerical Modeling of Inter-Pass Forging in Wire-Arc Additive Manufacturing of Inconel 718. Materials. 2026; 19(1):182. https://doi.org/10.3390/ma19010182
Chicago/Turabian StyleSmetannikov, Oleg Yu., Gleb L. Permyakov, Sergey D. Neulybin, Ivan P. Ovchinnikov, Alexander A. Oskolkov, and Dmitriy N. Trushnikov. 2026. "Experimental Study and Numerical Modeling of Inter-Pass Forging in Wire-Arc Additive Manufacturing of Inconel 718" Materials 19, no. 1: 182. https://doi.org/10.3390/ma19010182
APA StyleSmetannikov, O. Y., Permyakov, G. L., Neulybin, S. D., Ovchinnikov, I. P., Oskolkov, A. A., & Trushnikov, D. N. (2026). Experimental Study and Numerical Modeling of Inter-Pass Forging in Wire-Arc Additive Manufacturing of Inconel 718. Materials, 19(1), 182. https://doi.org/10.3390/ma19010182






