Influence of Alloying Elements on the Phase Structure, Stress–Strain Behavior, and Fracture Toughness of Ni3Sn: A First-Principles Study
Abstract
1. Introduction
2. Calculation Method and Structural Modeling
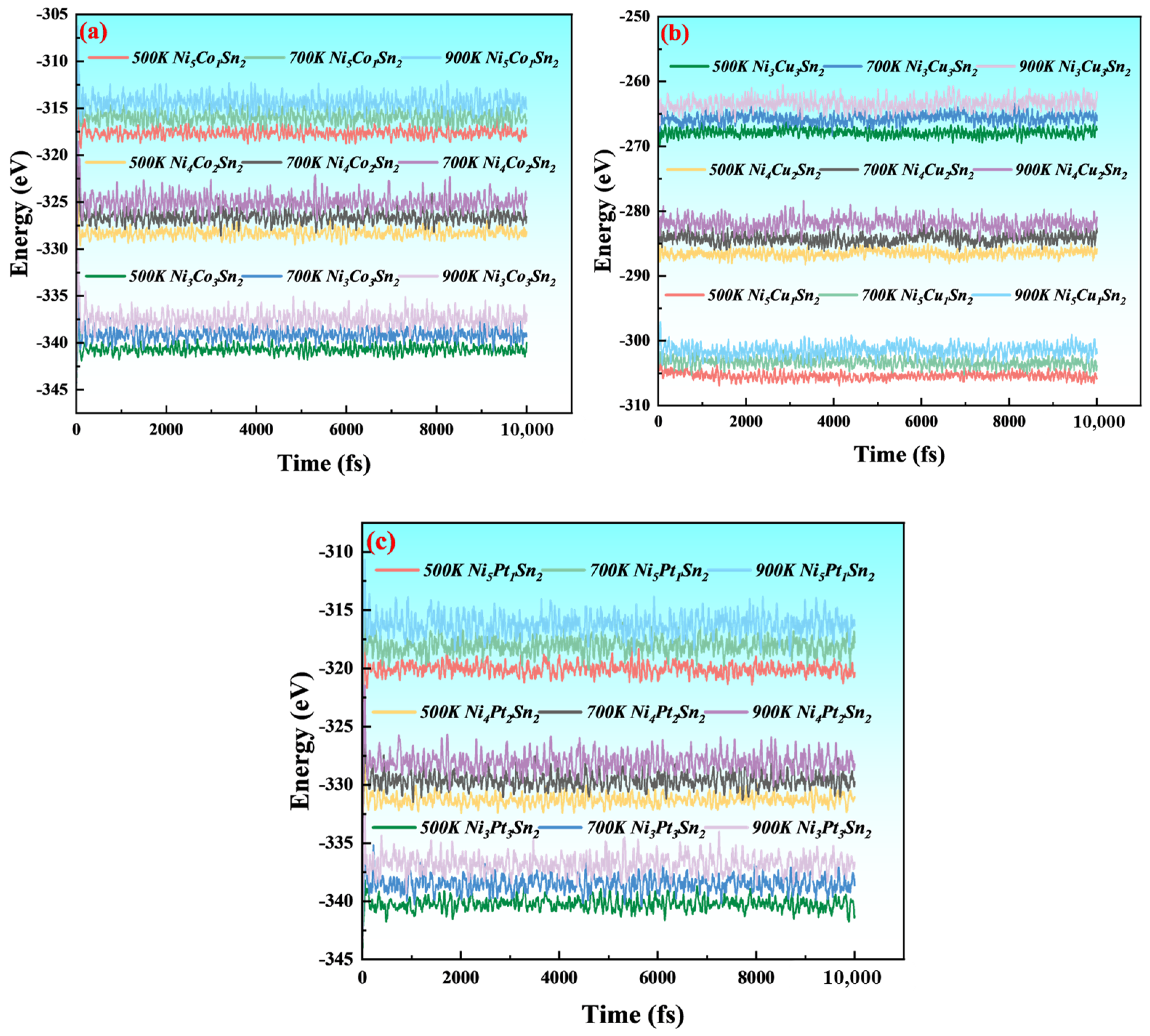
2.1. Calculation Methods
2.2. Structural Modeling
3. Results and Discussion
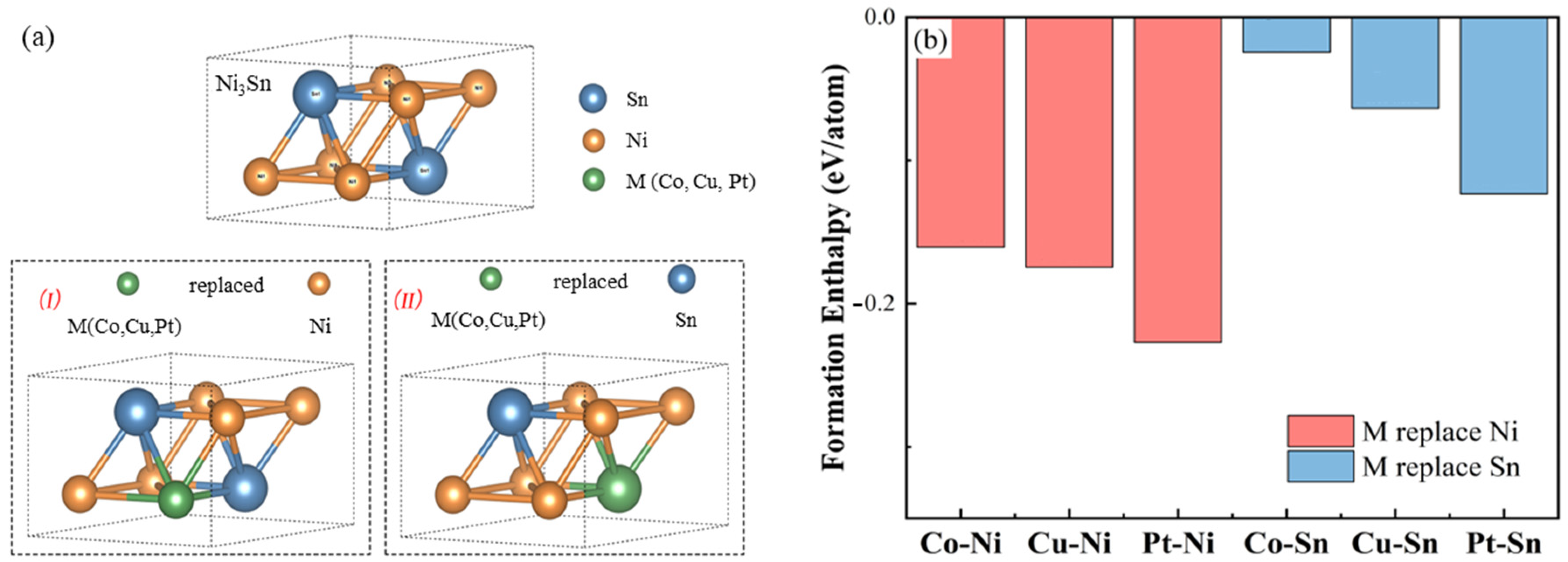
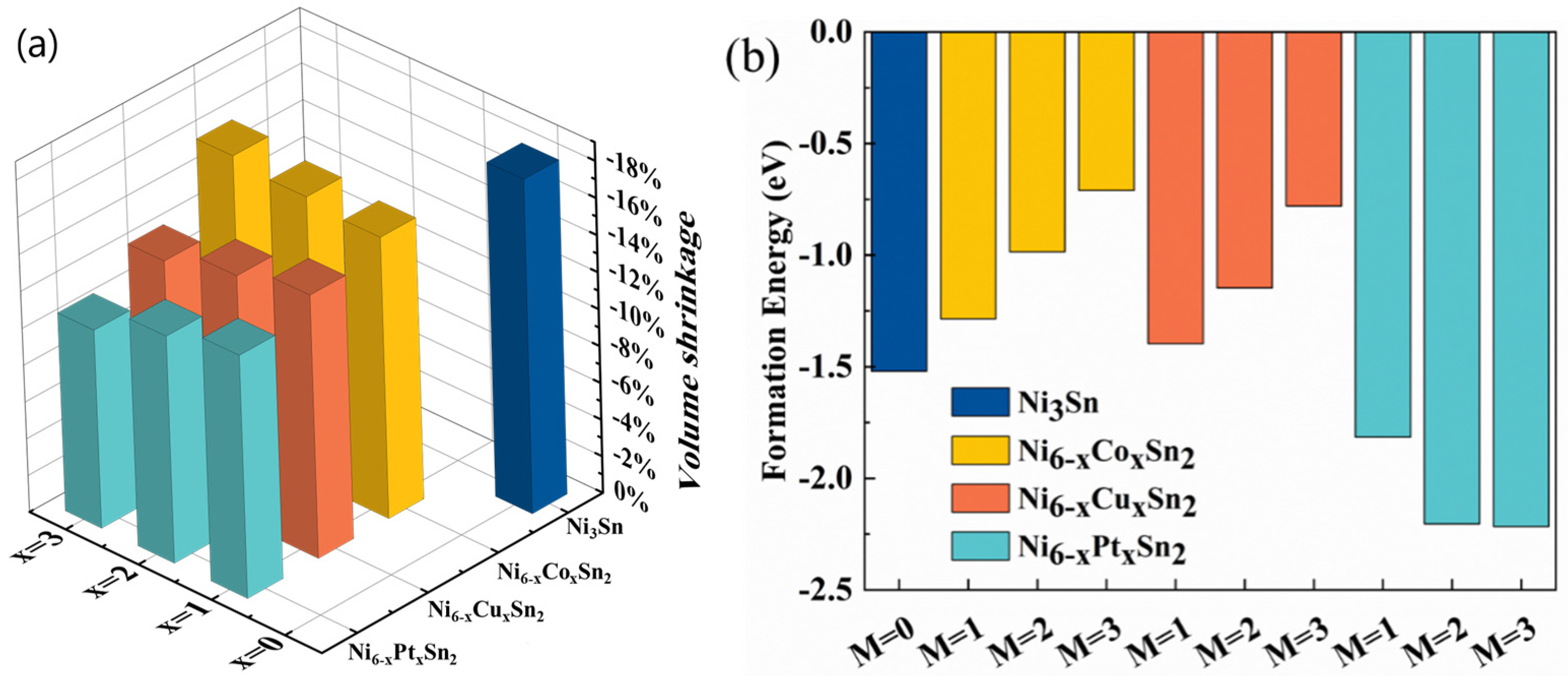
3.1. Crystal Structure and Stability
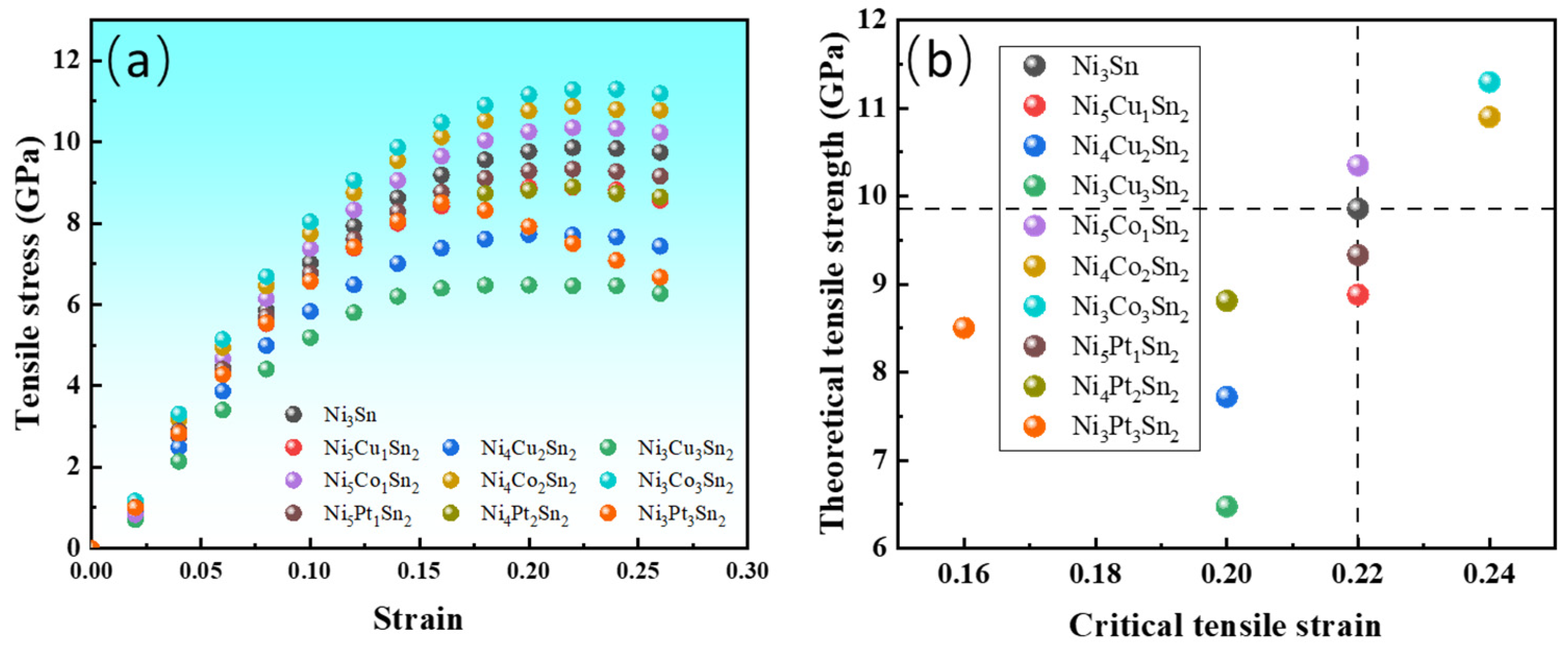
3.2. Effect of Alloying Elements on Mechanical Properties of Ni3Sn
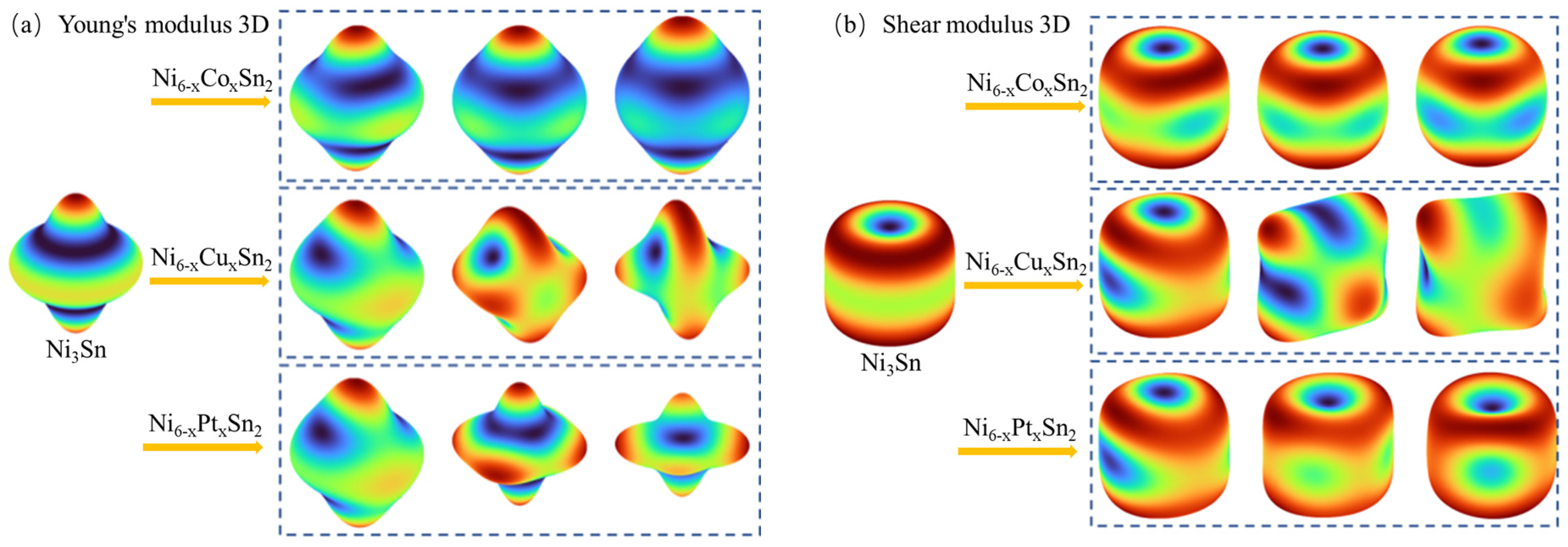
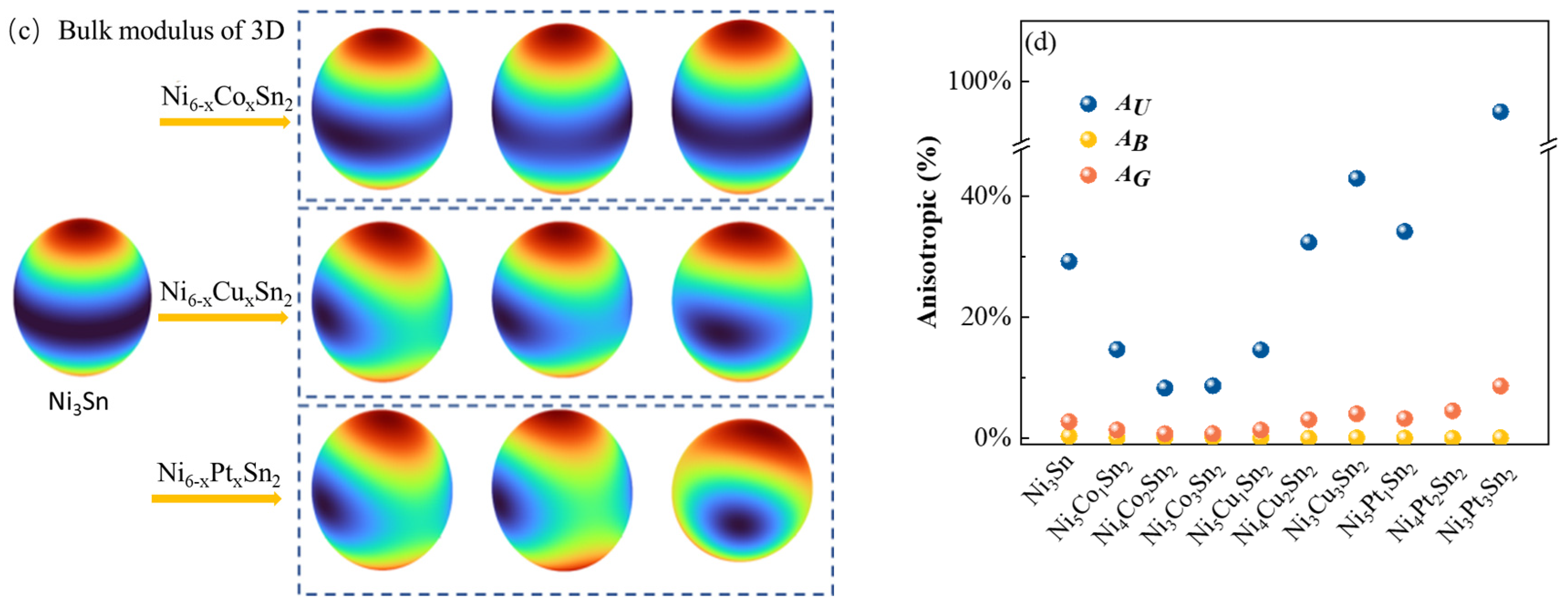
3.3. Effect of Alloying Elements on Ni3Sn Anisotropy
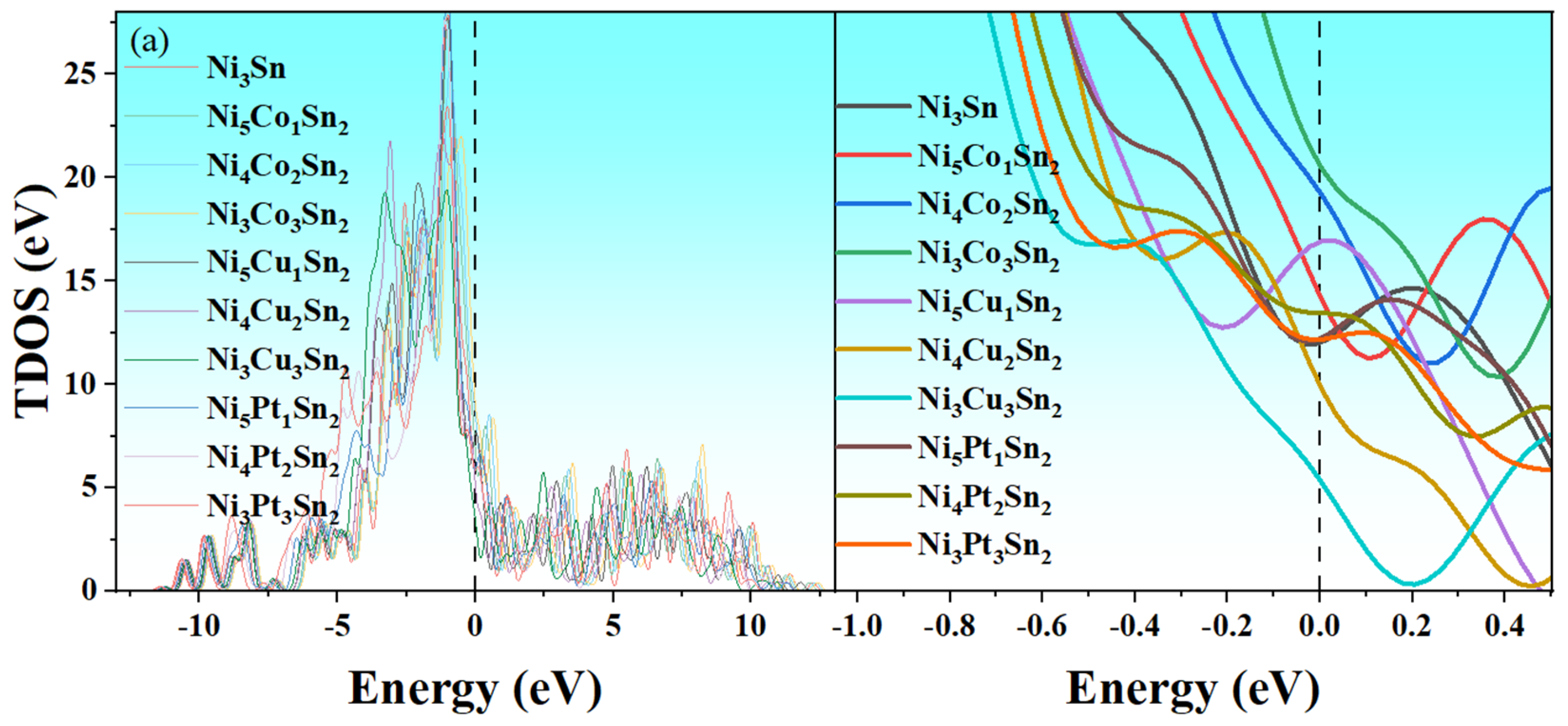
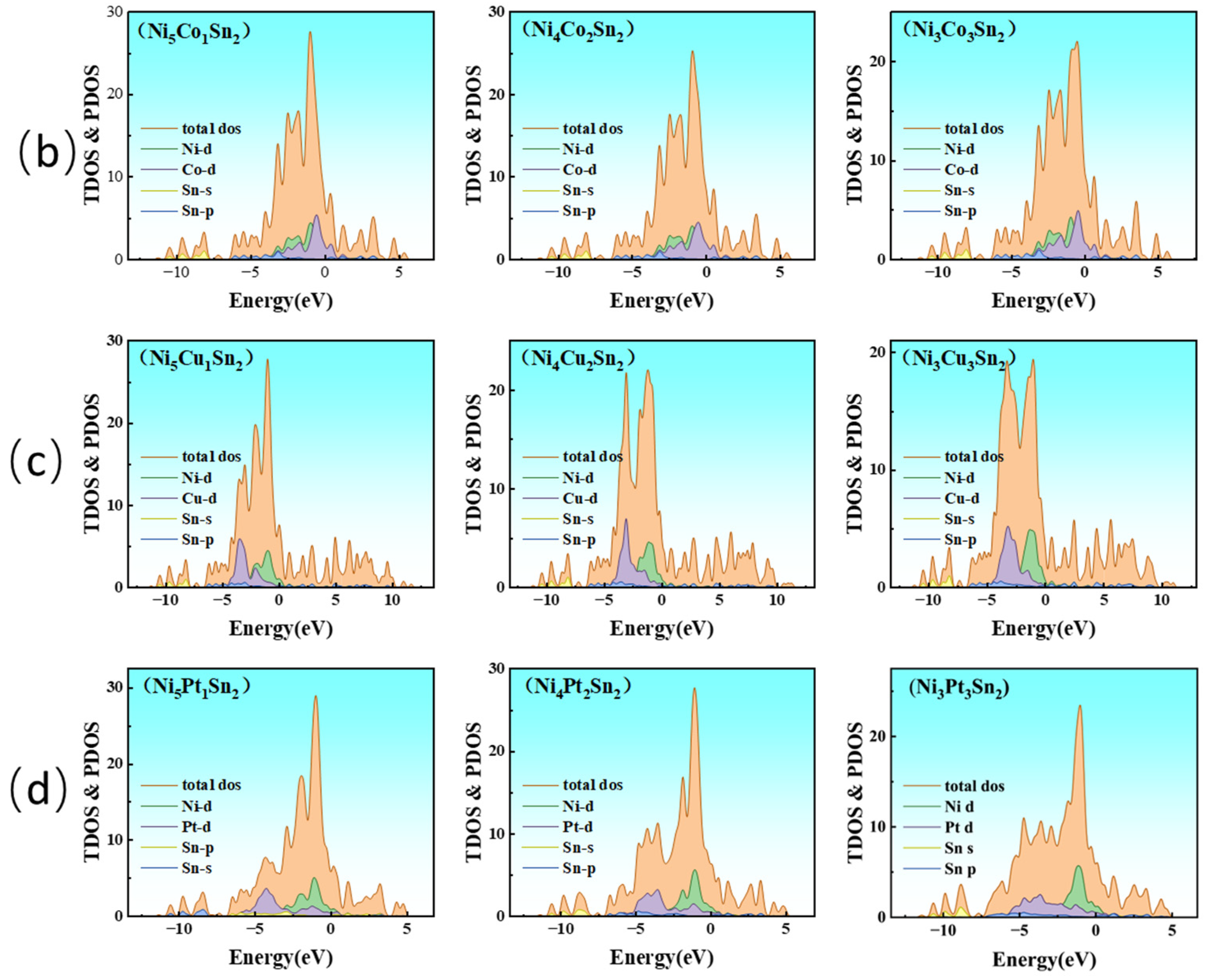
3.4. Effect of Alloying Elements on the Electronic Structure of Ni3Sn
4. Discussion
5. Conclusions
- (1)
- The formation energy calculation and electronic structure analysis show that the Ni6−XMXSn2 phase structure with Co, Cu, and Pt additions has good thermal stability.
- (2)
- Co, Cu, and Pt can reduce the theoretical volume shrinkage of the Ni + Sn → Ni3Sn reaction, and Pt can reduce the volume shrinkage by about 7%.
- (3)
- With the increase in alloy element content, Cu and Pt will increase the anisotropy of the Ni3Sn phase, and the addition of Cu and Pt will easily lead to an uneven stress field and induce the cracking of intermetallic compound solder joints during service.
- (4)
- The first-principles tensile and fracture toughness analysis results show that the toughness of Ni3Sn can be improved by adding the Co. Since the formation of Ni6−xCoxSn2 increases with the increase in Co content, the toughness of the Ni3Sn phase can be improved by adding a low Co content.
- (5)
- The B/G criterion is not suitable for evaluating the toughness and brittleness of Ni–Sn–M alloy systems with complex bonding types after Co, Cu, and Pt are added.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TLPB | transient liquid-phase bonding |
| IMCs | Intermetallic compounds |
| DFT | density functional theory |
| VASP | Vienna ab initio Simulation Package |
| PAW | Projector Augmented Wave Potentials |
| PBE | Perdew–Burke–Eruzerhof |
| GGA | Generalized Gradient Approximation |
| AIMD | ab initio molecular dynamics |
| DFPT | density functional perturbation theory |
| VRH | Voigt–Reuss–Hill |
| TDOS | total density of states |
| PDOS | partial density of states |
| APB | antiphase boundaries |
References
- Holaday, J.R.; Handwerker, C.A. Transient Liquid Phase Bonding. In Die-Attach Materials for High-Temperature Applications in Microelectronics Packaging: Materials, Processes, Equipment, and Reliability; Siow, K.S., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 197–249. [Google Scholar]
- Cook, G.O.; Sorensen, C.D. Overview of transient liquid phase and partial transient liquid phase bonding. J. Mater. Sci. 2011, 46, 5305–5323. [Google Scholar] [CrossRef]
- Jung, D.H.; Sharma, A.; Mayer, M.; Jung, J.P. A Review on Recent Advances in Transient Liquid Phase (TLP) Bonding for Thermoelectric Power Module. Rev. Adv. Mater. Sci. 2018, 53, 147–160. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, P.; Ren, J.; Huang, M. Full Ni3Sn4 IMC interconnects prepared by current driven bonding (CDB) method. In Proceedings of the 2023 24th International Conference on Electronic Packaging Technology (ICEPT), Shihezi City, China, 8–11 August 2023; pp. 1–6. [Google Scholar]
- Murayama, K.; Higashi, M.; Sakai, T.; Imaizumi, N. Electro-migration behavior in low temperature flip chip bonding. In Proceedings of the 2012 IEEE 62nd Electronic Components and Technology Conference, San Diego, CA, USA, 29 May–1 June 2012; pp. 608–614. [Google Scholar]
- Sun, F.; Pan, Z.; Liu, Y. The fracture mechanism of Cu3Sn-microporous copper composite joint by thermal compression bonding process. Mater. Lett. 2021, 291, 129536. [Google Scholar] [CrossRef]
- Yu, L.J.; Yen, H.W.; Wu, J.Y.; Yu, J.J.; Kao, C.R. Micromechanical behavior of single crystalline Ni3Sn4 in micro joints for chip-stacking applications. Mater. Sci. Eng. A 2017, 685, 123–130. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Z.; Liu, C.; Wu, Y.; An, B. Micro-mechanical and fracture characteristics of Cu6Sn5 and Cu3Sn intermetallic compounds under micro-cantilever bending. Intermetallics 2016, 76, 10–17. [Google Scholar] [CrossRef]
- Zhang, H.; Dai, J.; Cao, Y.; Zhang, Y.; Bao, M.; Yin, Y. A first-principles study of the mechanical and physical properties of Ni3Snx intermetallic compounds for high-temperature power device packaging. Intermetallics 2024, 164, 108112. [Google Scholar] [CrossRef]
- Yang, M.; Chen, J.; Yang, J.; Zhang, P.; Yu, Z.; Zeng, Z.; Lu, H. Interfacial transfer and phase evolution between Cu and Sn solder doped with minor Cu, Ag and Ni: Experimental and theoretical investigations. Appl. Phys. A 2020, 126, 652. [Google Scholar] [CrossRef]
- Emadi, F.; Vuorinen, V.; Mertin, S.; Widell, K.; Paulasto-Kröckel, M. Microstructural and mechanical characterization of Cu/Sn SLID bonding utilizing Co as contact metallization layer. J. Alloys Compd. 2022, 929, 167228. [Google Scholar] [CrossRef]
- Han, Y.; Chen, J.; Lin, M.; Zhang, K.; Lu, H. Synergistic effects of alloy elements on the structural stability, mechanical properties and electronic structure of Ni3Sn4: Using first principles. Vacuum 2023, 214, 112239. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Zhu, Y.; Epstein, A.; Mo, Y. Statistical variances of diffusional properties from ab initio molecular dynamics simulations. npj Comput. Mater. 2018, 4, 18. [Google Scholar] [CrossRef]
- Gonze, X.; Lee, C. Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B Condens. Matter Mater. Phys. 1997, 55, 10355–10368. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Huang, H.-L.; Li, G.; Xiao, X.; Lu, S.-Q.; Peng, P. Micromechanism in fracture toughness of NbCr2 laves phase improved by nickel alloying: First-principles calculation. J. Alloys Compd. 2020, 857, 158040. [Google Scholar] [CrossRef]
- Pan, Y.; Pu, D.; Liu, G.; Wang, P. Influence of alloying elements on the structural stability, elastic, hardness and thermodynamic properties of Mo5SiB2 from first-principles calculations. Ceram. Int. 2020, 46 Pt B, 16605–16611. [Google Scholar] [CrossRef]
- Feng, H.-L.; Huang, J.-H.; Yang, J.; Zhou, S.-K.; Zhang, R.; Wang, Y.; Chen, S.-H. Investigation of microstructural evolution and electrical properties for Ni-Sn transient liquid-phase sintering bonding. Electron. Mater. Lett. 2017, 13, 489–496. [Google Scholar] [CrossRef]
- Li, L.; Weidner, D.J.; Brodholt, J.; Alfè, D.; Price, G.D.; Caracas, R.; Wentzcovitch, R. Phase stability of CaSiO3 perovskite at high pressure and temperature: Insights from ab initio molecular dynamics. Phys. Earth Planet. Inter. 2006, 155, 260–268. [Google Scholar] [CrossRef]
- Skripnyak, N.V.; Ponomareva, A.V.; Belov, M.P.; Syutkin, E.A.; Khvan, A.V.; Dinsdale, A.T.; Abrikosov, I.A. Mixing enthalpies of alloys with dynamical instability: bcc Ti-V system. Acta Mater. 2020, 188, 145–154. [Google Scholar] [CrossRef]
- Yang, J.-W.; An, L.; Zheng, J.-J. Structure, mechanical and phonon stability of the Th-Sn system from ab initio. J. Nucl. Mater. 2021, 556, 153187. [Google Scholar] [CrossRef]
- Dai, X.; Savrasov, S.Y.; Kotliar, G.; Migliori, A.; Ledbetter, H.; Abrahams, E. Calculated Phonon Spectra of Plutonium at High Temperatures. Science 2003, 300, 953–955. [Google Scholar] [CrossRef]
- Voigt, W. Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Ann. Der Phys. 1889, 274, 573–587. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. ZAMM J. Appl. Math. Mech./Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Li, C.M.; Zeng, S.M.; Chen, Z.Q.; Cheng, N.P.; Chen, T.X. First-principles calculations of elastic and thermodynamic properties of the four main intermetallic phases in Al–Zn–Mg–Cu alloys. Comput. Mater. Sci. 2014, 93, 210–220. [Google Scholar] [CrossRef]
- Ganeshan, S.; Shang, S.L.; Wang, Y.; Liu, Z.K. Effect of alloying elements on the elastic properties of Mg from first-principles calculations. Acta Mater. 2009, 57, 3876–3884. [Google Scholar] [CrossRef]
- Zhang, H.; Shang, S.L.; Wang, Y.; Saengdeejing, A.; Chen, L.Q.; Liu, Z.K. First-principles calculations of the elastic, phonon and thermodynamic properties of Al12Mg17. Acta Mater. 2010, 58, 4012–4018. [Google Scholar] [CrossRef]
- Nielsen, O.H.; Martin, R.M. Quantum-mechanical theory of stress and force. Phys. Rev. B Condens. Matter 1985, 32, 3780–3791. [Google Scholar] [CrossRef] [PubMed]
- Niu, H.; Niu, S.; Oganov, A.R. Simple and accurate model of fracture toughness of solids. J. Appl. Phys. 2019, 125, 065105. [Google Scholar] [CrossRef]
- Li, L.H.; Wang, W.L.; Wei, B. First-principle and molecular dynamics calculations for physical properties of Ni–Sn alloy system. Comput. Mater. Sci. 2015, 99, 274–284. [Google Scholar] [CrossRef]
- Marmier, A.; Lethbridge, Z.A.D.; Walton, R.I.; Smith, C.W.; Parker, S.C.; Evans, K.E. ElAM: A computer program for the analysis and representation of anisotropic elastic properties. Comput. Phys. Commun. 2010, 181, 2102–2115. [Google Scholar] [CrossRef]
- Yang, C.; Hu, C.; Xiang, C.; Nie, H.; Gu, X.; Xie, L.; He, J.; Zhang, W.; Yu, Z.; Luo, J. Interfacial superstructures and chemical bonding transitions at metal-ceramic interfaces. Sci. Adv. 2021, 7, eabf6667. [Google Scholar] [CrossRef] [PubMed]
- Xing, H.; Dong, A.; Huang, J.; Zhang, J.; Sun, B. Revisiting intrinsic brittleness and deformation behavior of B2 NiAl intermetallic compound: A first-principles study. J. Mater. Sci. Technol. 2018, 34, 620–626. [Google Scholar] [CrossRef]
- Long, Q.; Nie, X.; Shang, S.-L.; Wang, J.; Du, Y.; Jin, Z.; Liu, Z.-K. C15 NbCr2 Laves phase with mechanical properties beyond Pugh’s criterion. Comput. Mater. Sci. 2016, 121, 167–173. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, M.; Zhu, Q.; Zhang, L.; Fan, G.; Qin, H.; Tian, Q. Micro Defects Evolution of Nickel-Based Single Crystal Superalloys during Shear Deformation: A Molecular Dynamics Study. Acta Metall. Sin. (Engl. Lett.) 2023, 36, 2089–2099. [Google Scholar] [CrossRef]
- Kakehi, K.; Latief, F.H.; Sato, T. Influence of primary and secondary orientations on creep rupture behavior of aluminized single crystal Ni-based superalloy. Mater. Sci. Eng. A 2014, 604, 148–155. [Google Scholar] [CrossRef]



| IMCs | Lattice | |||||
|---|---|---|---|---|---|---|
| Ni3Sn | 5.31 | 5.31 | 4.26 | 104.2 | 9.76 | −1.52 |
| Ni5Cu1Sn2 | 5.36 | 5.33 | 4.29 | 105.8 | 9.32 | −1.40 |
| Ni4Cu2Sn2 | 5.43 | 5.33 | 4.32 | 107.6 | 9.24 | −1.15 |
| Ni3Cu3Sn2 | 5.46 | 5.40 | 4.34 | 109.7 | 9.14 | −0.78 |
| Ni5Co1Sn2 | 5.29 | 5.33 | 4.24 | 103.9 | 9.42 | −1.29 |
| Ni4Co2Sn2 | 5.31 | 5.31 | 4.22 | 103.5 | 9.46 | −0.98 |
| Ni3Co3Sn2 | 5.32 | 5.32 | 4.20 | 103.1 | 9.50 | −0.71 |
| Ni5Pt1Sn2 | 5.31 | 5.32 | 4.26 | 110.1 | 10.95 | −1.82 |
| Ni4Pt2Sn2 | 5.56 | 5.45 | 4.10 | 114.7 | 12.47 | −2.20 |
| Ni3Pt3Sn2 | 5.62 | 5.57 | 4.47 | 120.5 | 13.76 | −2.21 |
| IMCs | C11 | C22 | C33 | C44 | C55 | C66 | C12 | C13 | C23 |
|---|---|---|---|---|---|---|---|---|---|
| Ni3Sn | 263.9 | 263.9 | 289.5 | 48.4 | 47.9 | 73.6 | 111.7 | 109.7 | 110.6 |
| Ni5Co1Sn2 | 262.9 | 260.9 | 298.1 | 57.4 | 55.2 | 72.7 | 121.3 | 114.7 | 114.7 |
| Ni4Co2Sn2 | 263.3 | 264.8 | 301.0 | 60.1 | 61.0 | 69.7 | 120.4 | 120.5 | 120.5 |
| Ni3Co3Sn2 | 268.1 | 270.2 | 315.8 | 64.3 | 64.9 | 70.5 | 122.9 | 121.4 | 119.4 |
| Ni5Cu1Sn2 | 245.1 | 239.1 | 272.2 | 50.7 | 57.8 | 64.6 | 114.8 | 105.4 | 107.1 |
| Ni4Cu2Sn2 | 228.4 | 233.1 | 247.8 | 43.7 | 57.8 | 58.5 | 102.2 | 106.6 | 98.6 |
| Ni3Cu3Sn2 | 194.6 | 184.0 | 219.9 | 37.6 | 40.4 | 45.7 | 111.6 | 99.6 | 105.6 |
| Ni5Pt1Sn2 | 259.0 | 260.5 | 280.2 | 41.6 | 42.7 | 66.0 | 119.0 | 125.1 | 120.4 |
| Ni4Pt2Sn2 | 262.7 | 265.6 | 278.7 | 37.5 | 36.9 | 62.3 | 125.9 | 132.1 | 126.2 |
| Ni3Pt3Sn2 | 266.1 | 248.5 | 277.3 | 27.7 | 33.9 | 66.2 | 137.3 | 133.5 | 137.9 |
| IMCs | B | G | E | ν | B/G | KIC |
|---|---|---|---|---|---|---|
| Ni3Sn | 165.00 | 67.00 | 172.00 | 0.32 | 2.46 | 1.61 |
| Ni5Co1Sn2 | 169.07 | 67.49 | 178.70 | 0.32 | 2.50 | 1.64 |
| Ni4Co2Sn2 | 172.12 | 68.80 | 182.13 | 0.32 | 2.50 | 1.67 |
| Ni3Co3Sn2 | 175.35 | 72.04 | 190.08 | 0.32 | 2.43 | 1.72 |
| Ni5Cu1Sn2 | 156.65 | 62.36 | 165.17 | 0.32 | 2.51 | 1.52 |
| Ni4Cu2Sn2 | 147.03 | 57.02 | 151.47 | 0.33 | 2.58 | 1.41 |
| Ni3Cu3Sn2 | 136.72 | 41.83 | 113.87 | 0.36 | 3.27 | 1.17 |
| Ni5Pt1Sn2 | 169.70 | 57.19 | 154.23 | 0.35 | 2.97 | 1.52 |
| Ni4Pt2Sn2 | 174.96 | 53.09 | 144.64 | 0.36 | 3.30 | 1.50 |
| Ni3Pt3Sn2 | 178.59 | 47.02 | 129.68 | 0.38 | 3.80 | 1.44 |
| Net Charge (Average) | |||
|---|---|---|---|
| Alloy System | Ni | Sn | Alloying Element (Co/Cu/Pt) |
| Pure Ni3Sn | −0.15 | 0.46 | - |
| Ni5Co1Sn2 | −0.16 | 0.45 | Co: −0.10 |
| Ni4Co2Sn2 | −0.16 | 0.43 | Co: −0.11 |
| Ni3Co3Sn2 | −0.16 | 0.42 | Co: −0.12 |
| Ni5Cu1Sn2 | −0.17 | 0.42 | Cu: −0.01 |
| Ni4Cu2Sn2 | −0.18 | 0.38 | Cu: −0.02 |
| Ni3Cu3Sn2 | −0.19 | 0.34 | Cu: −0.03 |
| Ni5Pt1Sn2 | −0.06 | 0.56 | Pt: −0.79 |
| Ni4Pt2Sn2 | 0.03 | 0.7 | Pt: −0.76 |
| Ni3Pt3Sn2 | 0.08 | 0.81 | Pt: −0.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Dai, J.; Cao, Y.; Zhang, Y.; Bao, M.; Yin, Y. Influence of Alloying Elements on the Phase Structure, Stress–Strain Behavior, and Fracture Toughness of Ni3Sn: A First-Principles Study. Materials 2025, 18, 1792. https://doi.org/10.3390/ma18081792
Zhang H, Dai J, Cao Y, Zhang Y, Bao M, Yin Y. Influence of Alloying Elements on the Phase Structure, Stress–Strain Behavior, and Fracture Toughness of Ni3Sn: A First-Principles Study. Materials. 2025; 18(8):1792. https://doi.org/10.3390/ma18081792
Chicago/Turabian StyleZhang, Haotian, Jiaoyan Dai, Yinwen Cao, Yanjie Zhang, Mingdong Bao, and Yanping Yin. 2025. "Influence of Alloying Elements on the Phase Structure, Stress–Strain Behavior, and Fracture Toughness of Ni3Sn: A First-Principles Study" Materials 18, no. 8: 1792. https://doi.org/10.3390/ma18081792
APA StyleZhang, H., Dai, J., Cao, Y., Zhang, Y., Bao, M., & Yin, Y. (2025). Influence of Alloying Elements on the Phase Structure, Stress–Strain Behavior, and Fracture Toughness of Ni3Sn: A First-Principles Study. Materials, 18(8), 1792. https://doi.org/10.3390/ma18081792





