Effect of Sn Content on Wettability and Interfacial Structure of Cu–Sn–Cr/Graphite Systems: Experimental and First-Principles Investigations

Abstract

The co-addition of chromium (Cr) and tin (Sn) is known to enhance the wettability between copper (Cu) and graphite (C_gr), but the effect of Sn content remains poorly understood. This study aims to systematically investigate the influence of Sn content a (a = 0, 10, 20, 30, 40, 50, 80, 99 at. %) on the wettability, interfacial structure, surface/interface energy (σ_lv/σ_sl), and adhesion behavior of the Cu–aSn–1Cr/C_gr system at 1100 °C. The experimental results show that as the Sn content increases, the equilibrium contact angle (θ_e) of the metal droplet shows a non-monotonic trend; the thickness of the reaction product layer (RPL, consisting of Cr carbides (Cr_mC_n)) gradually increases, accompanied by a decrease in the calculated adhesion work ($W_{\mathrm{ad}}^{\mathrm{cal}}$). A “sandwich” interface structure is observed, consisting of two interfaces: metal||Cr_mC_n and Cr_mC_n||C_gr. Sn content mainly affects the former. At metal||Cr_mC_n, Sn exists in various forms (e.g., Cu–Sn solid solution, Cu_xSn_y compounds) in contact with Cr_mC_n. To elucidate the wetting and bonding mechanisms of metal||Cr_mC_n, simplified interfacial models are constructed and analyzed based on first-principles calculations of density functional theory (DFT). The trend of theoretically calculated results (σ_metal and W_ad) agrees with the experimental results (σ_lv and $W_{\mathrm{ad}}^{\mathrm{cal}}$). Further analysis of the partial density of state (PDOS) and charge density difference (CDD) reveals that charge distribution and bonding characteristics vary with Sn content, providing the microscopic insight into the nature of wettability and interfacial bonding strength.

1. Introduction

Graphite (C_gr) has low density, high thermal conductivity, low thermal expansion coefficient, high-temperature resistance, and self-lubricating properties [1]. Copper (Cu) is commonly used to prepare composites with C_gr due to its economic feasibility, easy availability of resources, and excellent alloy solubility. With the continuous development of Cu/C_gr composites, their mechanical and functional properties have attracted increasing attention [2,3,4]. However, the applications of Cu matrices are limited by their inherent low hardness and strength, as well as poor creep and corrosion resistance. Recently, alloying copper matrix to prepare Cu/C composites has become a promising research hotspot. The addition of Sn to the Cu matrix significantly enhances its strength, wear resistance, and corrosion resistance through solid solution strengthening. Moreover, Sn improves the functional properties of both Cu/C_gr composites and brazed joints, such as electrical and thermal conductivity. These performance improvements are closely dependent on the Sn content [5,6,7,8,9]. Therefore, optimizing the Sn content is critical for enhancing the performance of Cu–Sn/C_gr composites and solder joints. It is expected to demonstrate significant potential in a wide range of advanced applications, including construction machinery, electronic packaging, sliding conductive components, and high-efficiency thermal management systems.

Good wettability and strong interfacial bonding are essential for brazed joints and Cu/C composites. However, the intrinsic wettability of Cu–Sn/C_gr is poor [10], and the bonding is weak due to van der Waals forces, making reliable connections difficult. Two approaches are commonly used to improve wettability: surface modification of carbon materials and copper-based alloying. The latter is more practical, as surface modification often struggles with coating uniformity and reliability. Copper-based alloying involves adding carbide-forming elements such as Ti, Cr, V, Mn, Nb, W, Mo, or Zr [11] to enhance interfacial reactivity. Among them, Cr is particularly effective. Most studies focus on Cu–Cr/C systems, with limited attention to the role of Sn. References [12,13] showed that adding a small amount of Cr significantly improves Cu/C interfacial wettability. However, Cr’s high reactivity causes rapid formation of dense carbides (Cr_mC_n), which hinders infiltration. Lin et al. [14] found that adding Sn to Cu–Cr alloys enhances wettability on porous C_gr by modifying Cr reactivity and reducing droplet surface energy, resulting in deeper infiltration. Thus, Sn content can effectively regulate wetting behavior. Moreover, Sn facilitates low-temperature joining, expanding the processing window for Cu/C composite preparation via melt infiltration.

Hsieh et al. [15] showed that Sn addition in Cu–Ti alloys lower the melting point and affects alloy microstructure and properties. As alloy complexity increases, interfacial structures become more intricate, affecting the interfacial bonding properties (IBPs) (abbreviations in this paper can be found in Supplementary Materials). Optimizing wettability and IBPs typically requires extensive trial-and-error experiments, which are time-consuming and inefficient. Thermodynamic calculations offer qualitative insights, but the underlying mechanisms remain unclear. Moreover, key parameters related to IBPs are environment-sensitive and difficult to measure directly. First-principles calculations based on density functional theory (DFT) have been widely used to study wettability and bonding behavior without empirical inputs [16]. A commonly used approach is the solid/solid slab model, which approximates the liquid/solid interface by neglecting atomic thermal vibrations at high temperatures [17]. When the trends from theoretical and experimental results are consistent, correction methods can be applied to improve accuracy [18]. Despite its advantages, this method is limited by computational cost, as only small-scale systems (typically 100–200 atoms) can be modeled. DFT studies are typically limited to simple interfaces involving pure metals or compounds and cannot easily handle large supercell models or multicomponent alloys. Meanwhile, extensive research exists on non-reactive metal/carbide interfaces (e.g., Al/TiC [19], Co/WC [20], Ag/Ti (C, N) [21], etc.).

This study investigates the wettability and interfacial behavior of Cu–aSn–1Cr alloys on C_gr using a modified sessile drop method, which minimizes pre-reaction and oxidation during heating. The interfacial structure and elemental composition of the samples are characterized using a scanning electron microscope (SEM) equipped with energy-dispersive spectroscopy (EDS). Typical interfacial configurations observed experimentally are then selected for simplified DFT modeling, aiming to uncover the mechanisms by which alloying elements and their concentrations influence wettability and IBPs. The results offer both experimental and theoretical guidance for designing Cu–Sn/C composites and solder alloys, and provide a reference for incorporating other non-reactive, low-melting-point elements (e.g., gallium, germanium, silver, indium, lead) into the Cu matrix.

2. Experimental and Calculation

2.1. Experimental Materials and Methods

The C_gr substrate has a purity of >99.9%, a size of 20 mm × 20 mm × 5 mm, an ash content of <40 ppm, a density of ~1.85 g/cm³, a porosity of 13%, and a surface roughness (Ra) of approximately 30–50 nm. The metallic materials used include Cu and Sn foils with a purity of 99.99% and Cr powder with a particle size of 400 μm. The Cu–aSn–1Cr alloys (a = 0, 10, 20, 30, 40, 50, 80, 99 at. %) are prepared based on atomic ratios. High-purity Ar gas (99.999%) is repeatedly introduced into the KDH-300B mini vacuum arc furnace, equipped with Ti getters, to purify the furnace chamber. To ensure the uniformity of alloy melting, the wrapped metal is first melted into spheres in an Ar atmosphere before using a robotic arm to flip the alloy and continue the melting process. This procedure is repeated 3–5 times. After the melting, the sample is cooled to room temperature under flowing Ar at a rate of ~15 °C/min. Based on the modified sessile drop method, the metal is first stored in a stainless-steel tube outside the furnace. The furnace is evacuated to ~6–7 × 10⁻⁴ Pa, and the chamber temperature is then heated to the preset experimental temperature of 1100 °C at a rate of 20 °C/min. After the dynamic vacuum is maintained at a stable level (~3–4 × 10⁻⁴ Pa), the metal is dropped onto the C_gr surface through an open alumina tube. Simultaneously, a high-resolution charge-coupled device (CCD) camera is used to record the dynamic spreading and wetting process of the molten metal, with a holding time of 30 min. The specific experimental setup and procedure are referenced in Ref. [22]. The contact angle (CA) in the photographs is measured using the Surface Meter software (SM, version 1.1.0.1, developed by NB Scientific Instruments Co., Ltd., Ningbo, China), and the variation curve of CA with time is obtained. The modified sessile drop method, compared to the traditional sessile drop method, effectively avoids the pre-reaction between the melt and the substrate during the experimental heating process. To prevent oxidation of the metal droplets, the droplets are first cooled to 600 °C under high vacuum, followed by a cooling process at a rate of 15 °C/min with flowing Ar until room temperature. The interface structure, microstructure, morphology of reaction products, and microregional elemental composition of the samples’ cross-section are analyzed and characterized using a Scanning Electron Microscopy (SEM, FEG 450, Thermo Fisher Scientific, Waltham, MA, USA) equipped with an Energy Dispersive Spectrometer (EDS, Oxford Instruments, Abingdon, UK) with a spot size of approximately 2 μm. The samples for high-resolution transmission electron microscope (HRTEM, JEOL, JEM–F200, Tokyo, Japan) are prepared using a focused ion beam (FIB; Helios G4 PFIB, Thermo Fisher Scientific, Waltham, MA, USA).

2.2. Calculation Methods

The calculations in this paper are performed using the Cambridge Sequential Total Energy Package (CASTEP, version 22.11, BIOVIA, San Diego, CA, USA) software, which is based on first-principles density functional theory [23]. The Perdew–Burke–Ernzerhof (PBE) function within the Generalized Gradient Approximation (GGA) is used to describe the exchange-correlation energy of Cu ([Ar] 3d¹⁰4s¹), Sn ([Kr] 4d¹⁰5s²5p²), Cr ([Ne] 3s²3p⁶3d⁵4s¹), and C ([He] 2s²2p²), respectively. The OTFG ultrasoft pseudopotentials are employed to model the interaction between atomic nuclei and valence electrons [24], and the energy cutoff is set as 500 eV. The energy fluctuation threshold for static self-consistent calculations is set to 2 × 10⁻⁵ eV/atom. The Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm is used for structure optimization, and the iterative self-consistent convergence criterion is that the energy fluctuation per atom is less than 1 × 10⁻⁵ eV. The interatomic force is less than 0.05 eV/Å. The maximum stress is below 0.05 GPa, and the atomic displacement fluctuation is less than 1.0 × 10⁻³ Å [25]. Using the density of 0.04 Å⁻¹ Monkhorst-Pack k-point for Brillouin zone sampling for the bulk, surface, and interface. The bulk models are presented in Figure S1 in Supplementary Materials. In the interface calculations, the interactions among surface layer atoms play a crucial role, while fixing the topmost and bottom layers of atoms ensures the convergence of energy.

3. Results

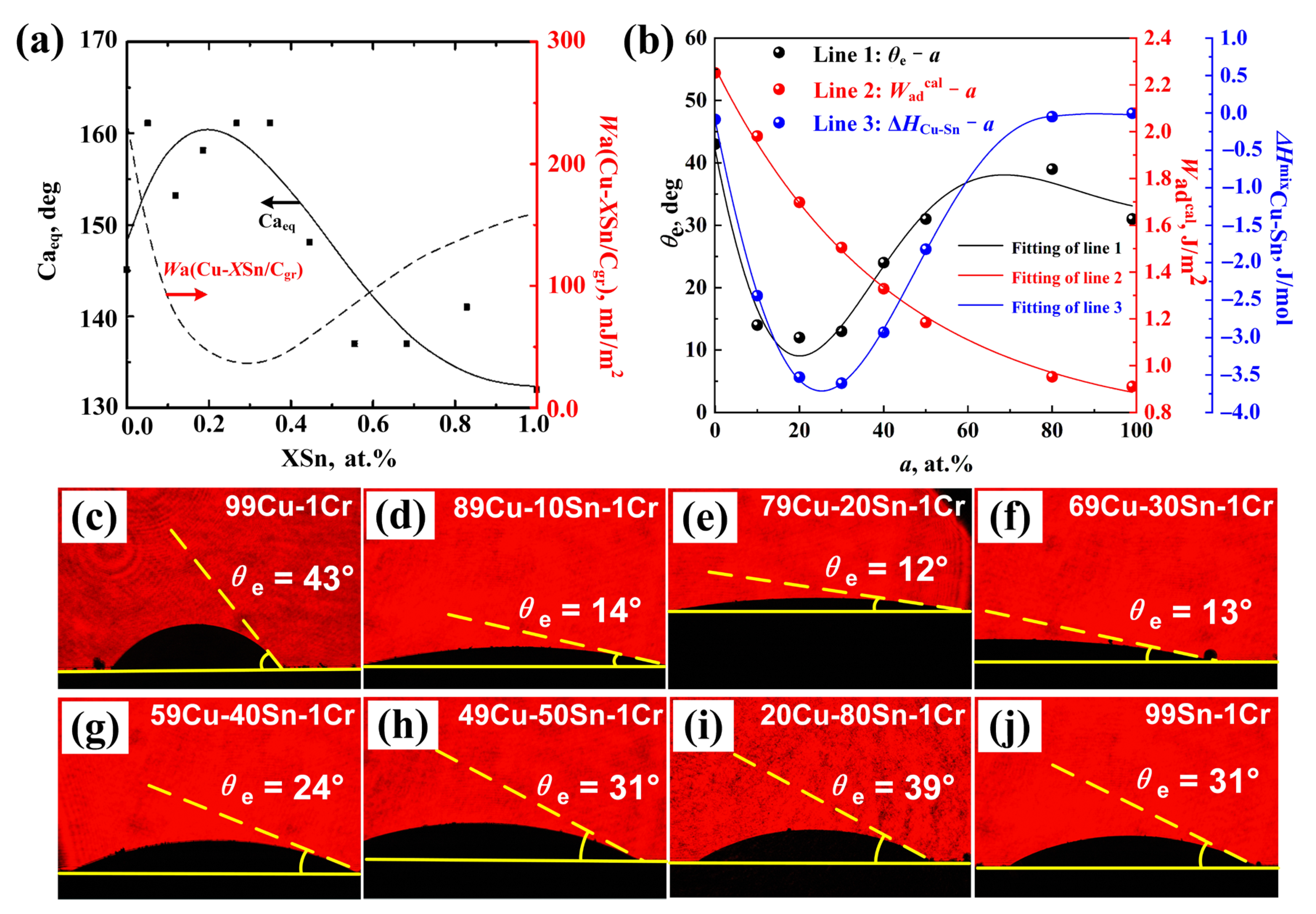
3.1. Wetting Experiment

Eustathopoulos et al. [26] have systematically analyzed the equilibrium contact angle (CA_eq) and adhesion work (W_{a(Cu–XSn/Cv)}) of Cu–XSn alloys on the vitreous carbon (Cv) surface as a function of Sn content, as shown in Figure 1a. The results show that CA_eq increases first and then decreases with increasing Sn, while W_{a(Cu–XSn/CV)} exhibits an inverse trend. In this study, after adding 1 at. % Cr, the measured θ_e (Figure 1b) follows a different trend—decreasing first, then increasing, and finally decreasing again. When Sn reaches 20 at. %, θ_e drops to 12°. According to Dupre’s definition of the adhesion work $W_{\mathrm{ad}}^{\mathrm{cal}}$ at solid/liquid interfaces, as shown in Equation (1) [27]:

$$W_{\mathrm{ad}}^{\mathrm{cal}} ={\sigma }_{\mathrm{lv}} + {\sigma }_{\mathrm{sv}} - {\sigma }_{\mathrm{sl}}$$

(1)

where σ_lv represents the surface energy of the liquid, σ_sv represents the surface energy of the solid, and σ_sl represents the solid/liquid interface energy. However, the value of $W_{\mathrm{ad}}^{\mathrm{cal}}$, σ_sv, and σ_sl cannot yet be accurately measured through experiments. Therefore, we used experimentally measured wetting parameters to estimate the adhesion work $W_{\mathrm{ad}}^{\mathrm{cal}}$ based on the well-known Young–Dupre Equation (2) [28]:

$$W_{\mathrm{ad}}^{\mathrm{cal}} ={\sigma }_{\mathrm{lv}} (1 + \cos {\theta }_{\mathrm{e}})$$

(2)

where σ_lv represents the surface energy of the Cu–Sn metallic melt, and its values under different Sn contents are listed in

Table 1. Experimental measurements and calculated values.

a (at. %)	0	10	20	30	40	50	79	99
θe (°)	43 43 [33]	14	12	13	24	31	39	31
σlv (J/m2) [29]	1.3	1.0	0.86	0.76	0.69	0.64	0.54	0.49
σsl (J/m2)	3.05	3.02	3.16	3.26	3.36	3.46	3.59	3.58
$W_{\mathrm{ad}}^{\mathrm{cal}}$ (J/m2)	2.25 2.16 [33]	1.98	1.70	1.50	1.33	1.18	0.95	0.91

, based on data reported in Ref. [29]. θ_e is expressed in radians. The measured values of θ_e are shown in Figure 1c–j. Substituting σ_lv and θ_e into Equation (1) yields the $W_{\mathrm{ad}}^{\mathrm{cal}}$, and the variation of $W_{\mathrm{ad}}^{\mathrm{cal}}$ with Sn content is shown as the blue curve in Figure 1b. Compared with the Cu–XSn/Cv system, θ_e is generally smaller and W_a (0.8–2.4 J/mol) is significantly larger than that of the Cr-free case (0.1–0.3 J/mol). This suggests that Cr addition enhances wettability and interfacial bonding. Lin et al. [14] attributed this wetting behavior to the decrease surface energy (σ_lv) of the alloy melt with increasing Sn content and a shift in reaction products from Cr₇C₃ (major) + Cr₃C₂ (minor) to Cr₇C₃ (minor) + Cr₃C₂ (major). This indicates that Sn affects both melt properties and solid/liquid interface energy (σ_sl). Unfortunately, they did not provide an in-depth explanation for this. Beyond σ_lv, Sn content also influences the alloy’s density, viscosity, and mixing enthalpy (ΔH^mix_Cu–Sn). According to References [30,31], both the density and viscosity of the Cu–Sn melt decrease with increasing Sn content, but do not explain the trend in θ_e. Interestingly, the variation of ΔH^mix_Cu–Sn [32] aligns well with θ_e (blue curve, Figure 1b). There may be a relationship between ΔH^mix_Cu–Sn and θ_e, as ΔH^mix_Cu–Sn influences the σ_lv and σ_sl of the melt droplet. However, no relevant studies to date have demonstrated a relationship between the two. This may be related to the fact that the complex mechanisms of action within the alloy and at the interface between the alloy and the reaction products have not yet been solved. Therefore, this study will attempt to explain the relationship between alloying elements and their content variations with wettability and IBPs, and their potential mechanisms in Section 4.

Figure 1. Variation of wetting parameters: (a) the variation of CA_eq and W_{ad(Cu–XSn/Cv)} with Sn content (X at. %) of Cu–Sn alloy on the C_V at 1150 °C [26]; (b) variation of θ_e, $W_{\mathrm{ad}}^{\mathrm{cal}}$, and ΔH^mix_Cu–Sn [32] with Sn content; (c–j) measured results of θ_e with Sn content.

Figure 1. Variation of wetting parameters: (a) the variation of CA_eq and W_{ad(Cu–XSn/Cv)} with Sn content (X at. %) of Cu–Sn alloy on the C_V at 1150 °C [26]; (b) variation of θ_e, $W_{\mathrm{ad}}^{\mathrm{cal}}$, and ΔH^mix_Cu–Sn [32] with Sn content; (c–j) measured results of θ_e with Sn content.

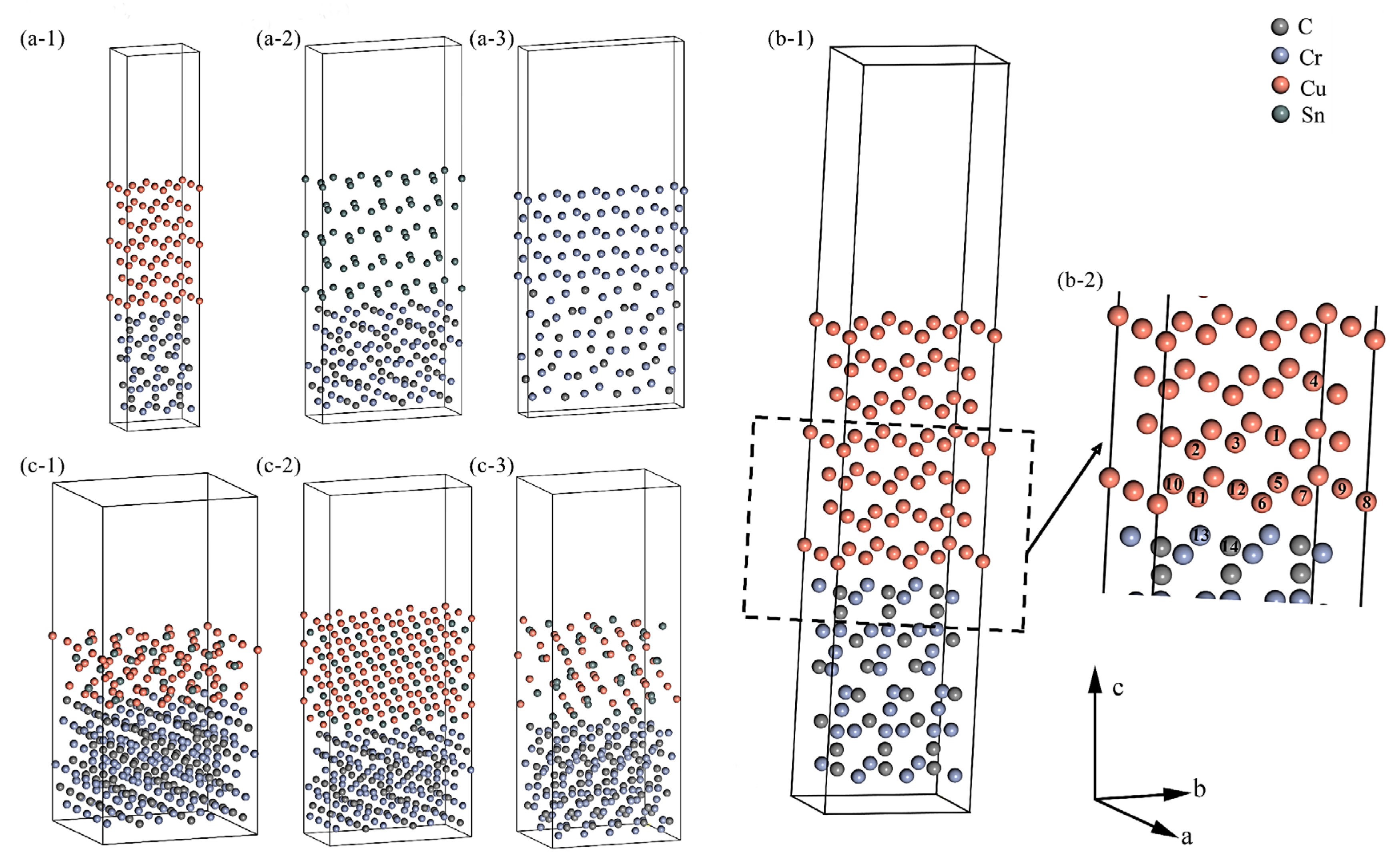
3.2. Interfacial Structure

The solidified cross-section of the Cu–aSn–1Cr/C_gr system after wetting is examined using SEM (backscattered mode) and EDS. As shown in Figure 2(a-1–d-1), the interfacial transition zone exhibits a typical “sandwich” structure, composed of two sub-interfaces: metal||reaction product layer (RPL) and RPL||C_gr. EDS analysis near the interface (Figure 2(a-4–c-4)) confirms that the RPL mainly consists of Cr₇C₃ and Cr₃C₂. With increasing Sn content, the dominant phase in the RPL gradually shifts from Cr₇C₃ (metallic) to Cr₃C₂ (covalent). At 10 at. % Sn (Figure 2(a-1)), Cr precipitates are observed on the RPL (point 3, Figure 2(d-4)), due to Cr’s limited solubility (0.98 at. %) in Cu–10Sn alloy at 1100 °C, which is lower than the nominal 1 at.%. As a result, a portion of Cr becomes supersaturated dissolution and precipitates out. For detailed calculations, please refer to the References [34,35,36]. When Sn reaches 20 at. %, the solubility increases to 1.96 at. %, and the Cr precipitates disappear, indicating complete dissolution into the melt (Figure 2(b-1)). The RPL becomes thicker and more continuous, increasing from ~1.4 μm (Figure 2(a-3)) to ~3 μm (Figure 2(d-3)). The alloy side exhibits various phases in contact with the RPL, including Cu–Sn solid solutions, Cu_xSn_y intermetallic (e.g., Cu₁₀Sn₃, Cu₃Sn, Cu₆Sn₅), and Sn/Cr segregation regions. EDS analyses in Figure 2(a-2,d-2) and points 1, 2, and 4–9 confirm that the Cu and Sn concentrations dominate, while Cr is nearly undetectable inside the alloy, justifying subsequent model simplifications. When the Sn content increases to 20 at. %, the alloy side transforms into a network structure (Figure 2(b-1)). Figure 2(b-2) shows an enlarged view near the interface of Figure 2(b-1), where the RPL thickness increases to 2.66 μm, and at the dark gray (point 4) and light gray (point 5) locations on the alloy side, Cu–Sn = 3.3:1, which may correspond to the Cu₁₀Sn₃ phase. To determine the alloy phase, FIB sampling is conducted at the location marked by the red rectangle in Figure 2(b-1). The HRTEM characterization confirms that the alloy phase is indeed Cu₁₀Sn₃, as shown in Figure 2(b-3). From Figure 2(c-1,c-2,d-1,d-3), it can be seen that Cu₃Sn and Cu₆Sn₅ are the key intermetallic compounds precipitated. In addition, regions of Sn segregation may appear near the interface, as shown in Figure 2(c-3). These observations suggest multiple interfacial contact forms—Cu–Sn solid solution, Cu_xSn_y (Cu₁₀Sn₃, Cu₃Sn, and Cu₆Sn₅) intermetallic, Cr precipitates, and Sn segregated zones—between the alloy and RPL (Figure 2(a-1–c-3)), corresponding to areas 1–6 in Figure 2(a-1,b-1,c-1–c-3), which likely influence the IBPs, as discussed in Section 4.

Figure 3 shows the top view SEM morphology (secondary electron mode) and EDS results of the interface RPL after etching the alloy droplets using FeCl₃ solution (mass ratio of FeCl₃–H₂O = 3:1). At 10 at. % Sn, dendritic Cr-rich precipitates appear in the RPL (Figure 3(a-1,a-2)), confirmed by EDS (point 1, Figure 3(d-4)) as mainly Cr with traces of C, O, Fe, and Cl—the latter likely from residual etchant. Figure 3(a-3–d-3) show the morphology near the triple line (TL). EDS analysis in Figure 3(a-4,b-4) indicates that the RPL is primarily composed of Cr, with small amounts of Cu, Sn, and C. The precipitates on the RPL are mainly concentrated at the center of the interface, with fewer near the TL. As the Sn content increases to 20 at. %, the dendritic Cr-rich phases disappear, replaced by numerous polygonal Cr_mC_n phases (Figure 3(b-1)). EDS analysis of point 3 suggests that the particles (point 3) in Figure 3(b-2) have a composition similar to that of the point 2 and may be the Cr₇C₃ phase. A precursor film enriched in Cr and C elements ahead of the RPL (Figure 3(b-3,b-4)), possibly due to Sn-induced Cr migration toward the TL. With 50 at. % Sn, no precipitates are seen on the RPL (Figure 3(c-1)). The RPL consists of nanoparticles in orthorhombic Cr₃C₂ (point 4) and hexagonal Cr₇C₃ (point 5) phases, as shown in Figure 3(c-1,c-2). At 80 at. % Sn, there are some cracks distributed in the continuous and dense Cr_mC_n layer (Figure 3(d-2)), possibly caused by stress concentration during cooling. EDS of point 6 suggests central RPL regions are Cr₇C₃, while river-like structures at the TL front (point 7) show Cr/C atomic ratios close to Cr₃C₂. These results indicate that Sn content not only alters the RPL morphology but also affects Cr diffusion and interfacial phase distribution. Further phase confirmation can be found in the X-ray diffraction results in Ref. [14].

4. Discussion

From the above, the interface structure analysis indicates that the Cu–aSn–1Cr/C_gr reactive wetting system exhibits a “sandwich” structure, composed of two interfaces: metal||Cr_mC_n and Cr_mC_n||C_gr. For the latter, although this study does not directly investigate the bonding mechanism at the Cr_mC_n||C_gr interface, previous work (Ref. [37]) has reported that bonding at the Cr₃C₂||diamond interface primarily arises from hybridization between C–2p states of diamond (001) and C–2p or Cr–3d states of Cr₃C₂ (001). Given the structural and electronic similarity between diamond and C_gr, it is reasonable to expect a similar bonding mechanism at the Cr_mC_n||C_gr interface in our system. Therefore, detailed discussion of this interface is omitted here. In this work, we focus on the metal||Cr_mC_n interface, as it plays a more dominant role in determining the overall wettability behavior observed in our experiments. As illustrated in Figure 4, Sn and Cr may interact with the RPL surface in multiple forms, including Cu–Sn solid solutions, Cu_xSn_y compounds, and Sn/Cr segregation.

From Section 3.2, it can be seen that when the Sn content is low, Cr undergoes supersaturation and precipitates out, and when the Sn content is high, according to the Cu–Sn binary phase diagram [38], Sn segregation occurs, and Cu_xSn_y varies with the Sn content. The contact phenomenon with the RPL surface may be caused by the strong interactions among Sn/Cr and Cu_xSn_y with Cr_mC_n. The EDS analysis in Figure 2 of Section 3.2 shows that the main precipitate phases in contact with RPL are Cu₁₀Sn₃, Cu₃Sn, and Cu₆Sn₅, which may result from reaction formulas Equations (3)–(10) occurring during the cooling process:

10Cu + 3Sn → Cu₁₀Sn₃

(3)

3Cu + Sn → Cu₃Sn

(4)

Cu + 5Sn → Cu₆Sn₅

(5)

Cu₁₀Sn₃→ Cu + 3Cu₃Sn

(6)

Cu₆Sn₅ + 9Cu → 5Cu₃Sn

(7)

5Cu₃Sn → 9Cu + Cu₆Sn₅

(8)

2Cu₃Sn + 3Sn → Cu₆Sn₅

(9)

L + Cu₃Sn → Cu₆Sn₅

(10)

Li et al. [39] reported that adding 1~2 wt. % Cr does not significantly affect the growth of Cu_xSn_y. In the initial reaction stage, Cu₁₀Sn₃, Cu₃Sn, and Cu₆Sn₅ are formed (Equations (3)–(5)), where Cu₁₀Sn₃ is a metastable phase that readily transforms into Cu₃Sn (Equation (6)). When there is less Sn, Cu₆Sn₅ may convert to Cu₃Sn (Equation (7)). Conversely, when there is more Sn, Cu₃Sn will transform into Cu₆Sn₅, and Cu₃Sn will decompose to form Cu₆Sn₅ (Equation (8)). Sn atoms continuously diffuse into Cu₃Sn and also react with Sn to produce Cu₆Sn₅ (Equation (9)). Furthermore, the outer layer of Cu₃Sn can also transform into Cu₆Sn₅ through a peritectic reaction (Equation (10)) [40]. To investigate the effect of the aforementioned forms of metal presence on the interfacial properties and to illustrate the specific mechanism of alloying elements, this paper focuses on the metal||Cr_mC_n interface. The electronic structure calculations of Cr₇C₃ and Cr₃C₂ indicate that the chemical bonds in these two compounds exhibit complex characteristics with a mixture of metallic, covalent, and ionic properties [41,42]. The difference between the two was primarily reflected in the stronger metallic of Cr₇C₃ than that of Cr₃C₂. Naidich [11] reported that the metallic properties of ceramics enhance the metal/ceramic adhesion. However, Cr₃C₂ is more stable than Cr₇C₃. Considering the computational cost (Cr₇C₃ requires more atoms for modeling than Cr₃C₂), the most stable Cr₃C₂ is chosen for this study. Based on the interface structure obtained from the experiments, this study approximates several typical configurations at the metal||Cr₃C₂ interface as follows: the effects of Cu–Cr and Cu–Sn solid solutions are simplified to the issue of Cr/Sn mono-/multi-atomic doping in the Cu matrix. The precipitation of Cr/Sn on the interface is simplified to the issue of contact between pure Cr/Sn and Cr₃C₂. The case with high Sn content is simplified to the influence of Cu_xSn_y (the effect of Cu_xSn_y on the interface also needs to be explored). Simplified interface models are established for pure metals (Cu/Sn/Cr), Cu-doped Cr/Sn single/multi-atom systems, and Cu_xSn_y (Cu₁₀Sn₃, Cu₃Sn, Cu₆Sn₅) with Cr₃C₂.

4.1. DFT Calculations

4.1.1. Surface Properties

The lattice parameters of Cu, β–Sn, Cr, Cu_xSn_y (Cu₁₀Sn₃, Cu₃Sn, Cu₆Sn₅), and Cr₃C₂ are shown in Table S1 in the Supplementary Materials. The optimized lattice constant values are compared with the calculated values from References [37,43,44,45,46], and there is a slight deviation of ± 2% in the obtained lattice parameters. The close-packed surfaces of Cu (111), β–Sn (100), Cr (110), and Cr₃C₂ (001) have stable atomic structures and the lowest surface energies [37,47,48,49], and the surface models are shown in Figure S2a–d. Here, the reason for selecting the surface with the lowest surface energy and high adhesion work for the calculation is explained below. The atomic radius difference between Cu and Sn atoms is large, and the lattice distortion is small when the doping quantity is low. Conversely, at higher doping quantities, the lattice distortion is larger. Therefore, to investigate the effect of high Sn content, this paper uses the Cu_xSn_y compounds shown in Figure 2(b-2,c-1,c-2) of Section 3.2 for comparison. The surface energy of Cu_xSn_y is investigated and found to be rarely reported in the literature, so the surface energy of Cu_xSn_y is calculated before building the interface model. According to Ref. [50], it is reported that the maximum Miller indices are 2 and 3 for noncubic and cubic crystals, respectively, when calculating the surface energy. Due to the limitation of the calculation conditions, in this paper, we only investigate the surface properties of (100), (010), and (001) of Cu₁₀Sn₃, Cu₃Sn, and Cu₆Sn₅. Based on the symmetry and periodicity of the structures, surfaces with the same structure but different indices are combined for analysis, and the constructed surface structure models are presented in Supplementary Materials Figure S2e–j. σ_metal is commonly defined as the energy required per unit area to form a new surface, which can be used to describe the stability of the surface, and is given by Equation (11) [51]:

$${\sigma }_{\mathrm{metal}}={\displaystyle \frac{E_{\mathrm{surface}}-{nE}_{\mathrm{bulk}}-{n_i\mu }_i+n_j{\mu }_j}{2A_{\mathrm{surface}}}}$$

(11)

σ_metal is the surface energy of the metal (J/m²); E_surface, n, E_bulk, and A_surface are the total energy of the metal surface, the number of unit cells, the energy of the unit cell, and the area of the surface, respectively. The doped surface model also needs to consider the number of dopant atoms and their chemical potential, where n_i and n_j are the number of dopant atoms and doped atoms, respectively. The μ_i and μ_j are the chemical potential of the dopant atoms and doped atoms, respectively. The σ_metal values for Cu (111), Sn (100), Cr (110), Cu₆Sn₅ (100), and Cr₃C₂ (001) are close to the reported results in the References [37,45,52,53,54], as presented in Table S2 in Supplementary Materials. The doping cases are as follows: single Cr atom doped Cu (111) and Sn (100) surfaces, named Cu₅₅Cr₁ and Sn₄₉Cr₁, respectively. Multiple Sn atoms doped Cu (111) surface with up to four dopant atoms, named Cu_56-kSn_k (k = 1, 2, 3, 4), the doping position is shown in Figure 5(b-2). As shown in Table S2, the doping of a small number of Cr atoms increases the σ_metal of Cu (111) but has little effect on the σ_metal of Sn (100). When multiple Sn atoms are doped, the σ (Cu_56-kSn_k) decreases slightly with increasing Sn atoms, while the σ_metal of Cu_xSn_y decreases significantly with the increase in Sn content. This trend is consistent with the changes in σ_lv of Cu–Sn alloys reported in Ref. [29]. Cu₁₀Sn₃ (100), Cu₃Sn (001) type2, and Cu₆Sn₅ (001) type2 with lower σ_metal values are selected for the study in the case of higher Sn content.

4.1.2. Interfacial Details

Before establishing the interface models of pure metals (Cu/Sn/Cr), Cu-doped single/multiple Cr/Sn atoms, and Cu_xSn_y with Cr₃C₂, the mismatch degree δ of the interfaces is calculated. Ref. [55] shows that when δ < 8%, the two surfaces can be considered well-matched, which allows the interface model to achieve good convergence. The formula for calculating δ is shown in Equation (12) [56]:

$$\begin{array}{c}\delta ={\displaystyle \frac{\left|a_1 - a_2\right|}{0.5{(a}_1+a_2)}}\times 100\%\end{array}$$

(12)

where a₁ and a₂ (Å) represent the lengths of the supercells that need to be matched in the same direction. $\left|a_1-a_2\right|$ is the difference between the matched lattice parameters, and $0.5{ (a}_1+a_2)$ is their average. The δ–values for the supercell interface models are all below 8%, which satisfies the matching criteria. The calculated δ–values are summarized in Table S3.

Based on this, interface models are constructed for Cu (111)||Cr₃C₂ (001), Sn (100)||Cr₃C₂ (001), Cr (110)||Cr₃C₂ (001), and the three compound interfaces Cu₁₀Sn₃ (100), Cu₃Sn (001), and Cu₆Sn₅ (001) with Cr₃C₂ (001). These are denoted as Cu||Cr₃C₂, Sn||Cr₃C₂, Cr||Cr₃C₂, and Cu_xSn_y||Cr₃C₂ (Cu_xSn_y = Cu₁₀Sn₃, Cu₃Sn, and Cu₆Sn₅), respectively, and are shown in Figure 5(a-1–a-3,c-1–c-3). A vacuum layer of 15 Å is added along the c-axis in all interface models to eliminate the effect of periodic boundary conditions.

To study the effect of atomic doping, 14 and 12 possible substitution positions are considered for single Cr or Sn atoms in Cu||Cr₃C₂ and Sn||Cr₃C₂ models, respectively, as shown in Figure 5(b-2). The doping difficulty at each site is evaluated by calculating the formation energy E_sub [57] (details in Supplementary Materials). The configurations with the lowest E_sub are selected and denoted as Cu₅₅Cr₁||Cr₃C₂ and Sn₄₉Cr₁||Cr₃C₂. For multiple Sn atom doping, four low E_sub positions are selected, labeled as Cu_56-kSn_k||Cr₃C₂ (k = 1, 2, 3, 4).

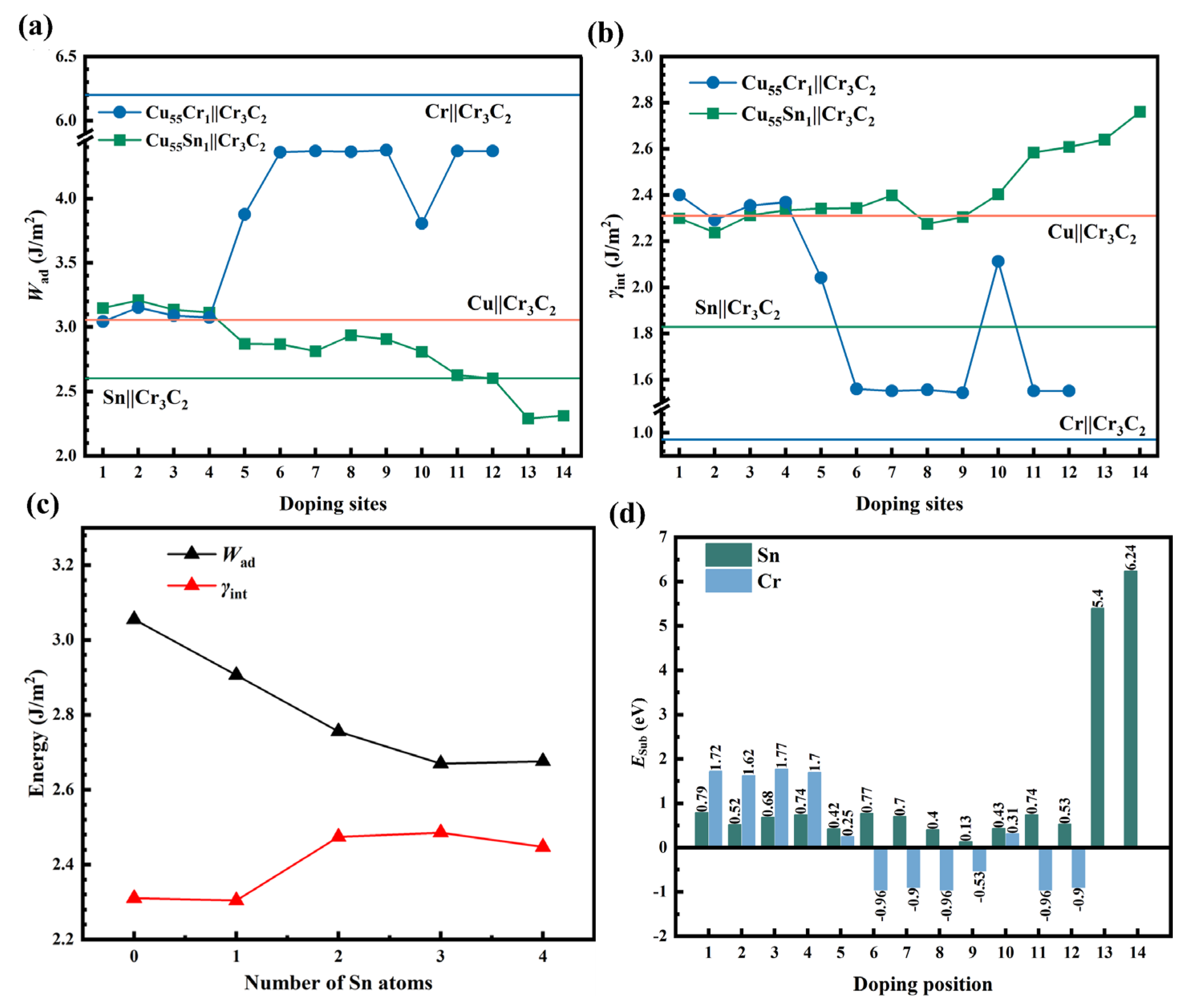
4.1.3. Interface Properties

The adhesion, stability, and wettability in the interfacial properties are related to the adhesion work and the surface/interfacial energy of the metal and Cr₃C₂. Therefore, this section primarily analyzes the effects of typical interface structures on interfacial properties at the atomic level by calculating the theoretical adhesion work W_ad and the interfacial energy γ_int. W_ad is obtained by Equation (13) [55]:

$$W_{\mathrm{ad}}={\displaystyle \frac{E_{\mathrm{metal}}+E_{C{r}_3{C}_2}-E_{\mathrm{int}}}{A_{\mathrm{int}}}}$$

(13)

where $E_{\mathrm{metal}}$ is the energy of the metal part, $E_{C{r}_3{C}_2}$ is the energy of Cr₃C₂, E_int is the total energy of the interface model, and A_int is the area of the interface. When W_ad is larger, the interface is more stable and the interfacial bond strength is higher. The interfacial equilibrium distance of the interface is determined based on the maximum value of the W_ad, as detailed in Figure S3 in Supplementary Materials. The γ_int is calculated as shown in Equation (14) [55]:

$${\gamma }_{\mathrm{int}}={\sigma }_{\mathrm{metal}}+{\sigma }_{{\mathrm{Cr}}_3{C}_2}-W_{\mathrm{ad}}$$

(14)

where σ_Cr3C2 is the surface energy of the Cr₃C₂. A lower γ_int indicates a more stable interface, as wetting is preferred to be carried out at interfaces with lower values of γ_int, which is often used as a basis for determining model parameters. The minimum value of σ_Cr3C2 (001) is 3.99 J/m². σ_metal and W_ad vary with the composition of the metal. For a stable interface to form between σ_metal and σ_Cr3C2, γ_int must be positive. If γ_int is negative, the interface is unstable. The lower the γ_int value (closer to zero), the more stable the interface. To ensure the value of γ_int is the minimum, the surface/interface models with the smallest difference of (σ_metal − W_ad) are chosen for calculation as much as possible. However, selecting a surface/interface model with a minimum (σ_metal − W_ad), γ_int > 0, and low δ requires extensive calculations. Therefore, the calculations in this paper utilize a maximum W_ad and a relatively low σ_metal.

(1)

Single Sn/Cr atom and multiple Sn atoms doped Cu||Cr₃C₂ interface

Figure 6 shows the variation of W_ad (Figure 6a) and γ_int (Figure 6b) for a single Sn/Cr atom doping at different positions of Cu||Cr₃C₂. From Figure 6a, it can be seen that the magnitude of W_ad is in the order of Sn||Cr₃C₂ (2.60 J/m²) < Cu||Cr₃C₂ (3.05 J/m²) < Cr||Cr₃C₂ (6.20 J/m²). This suggests that the precipitation of Cr on RPL, as shown in Figure 3(a-2) of Section 3.2, plays a role in enhancing the interface bonding. The W_ad of Cu||Cr₃C₂ is slightly higher than the value of W_ad (2.16 J/m²) in Ref [33]. Comparing the W_ad of Cu₅₅Cr₁||Cr₃C₂ and Cu₅₅Sn₁||Cr₃C₂, it is clear that the influence of Sn/Cr on the W_ad at positions 5–12 of the Cu||Cr₃C₂ is much greater than that at positions 1–4. Thus, the further the doping site is from the Cr₃C₂ surface, the smaller the effect. As shown in Figure 6a, except for positions 1–4, Sn doping at other sites decreases the W_ad of the interface. From Figure 6b, it can be seen that the Cr||Cr₃C₂ is more stable and possesses the lower γ_int (0.97 J/m²) compared to Cu||Cr₃C₂(2.31 J/m²) and Sn||Cr₃C₂(1.83 J/m²). Different Sn doping sites have less effect on the γ_int of Cu||Cr₃C₂, whereas Cr doping significantly reduces the γ_int of Cu||Cr₃C₂ and enhances the stability of the interface. The W_ad and γ_int at sites 13 and 14 in Figure 6 correspond to Sn atoms occupying the Cr and C sites in Cr₃C₂. It can be seen that the doping at these two sites significantly decreases the W_ad of the Cu||Cr₃C₂ and increases the γ_int, resulting in the interface being unstable. Therefore, the possibility of Sn occupying sites in Cr₃C₂ is relatively low. In addition, the W_ad of Sn₄₉Cr₁||Cr₃C₂ (3.99 J/m²) is higher than that of Sn||Cr₃C₂ (2.60 J/m²), and the γ_int of Sn₄₉Cr₁||Cr₃C₂ (0.84 J/m²) is lower than that of Sn||Cr₃C₂ (1.83 J/m²), indicating a significant improvement in interface stability.

(2)

Cu_xSn_y||Cr₃C₂ interface

After being compared to Cu||Cr₃C₂, Sn||Cr₃C₂, Cr||Cr₃C₂, and Cu_56-kSn_k||Cr₃C₂, the Cu₁₀Sn₃||Cr₃C₂ (W_ad = 1.28 J/m², γ_int = 3.58 J/m²), Cu₃Sn||Cr₃C₂ (W_ad = 1.09 J/m², γ_int = 3.93 J/m²), and Cu₆Sn₅||Cr₃C₂ (W_ad = 0.96 J/m², γ_int = 3.79 J/m²) interface possesses lower W_ad and higher γ_int. The W_ad gradually decreases, with increasing Sn content in Cu_xSn_y increases. Although the γ_int fluctuates, they are overall relatively high, which indicates that the interface between Cu_xSn_y and Cr₃C₂ is unstable. However, once Cu_xSn_y interacts with Cr₃C₂ to form a Cu_xSn_y||Cr₃C₂ interface structure, it will be unfavorable for interfacial bonding. Yu et al. [10] studied the interfacial properties of Cu_xSn_y with diamond and the results indicated that Cu₆Sn₅ (100) with diamond (111) had a stronger hybridization, lower γ_int, and better wettability compared to Cu (100) and Cu₃Sn (100). Cu_xSn_y had different effects on the Cu_xSn_y||diamond and Cu_xSn_y||Cr₃C₂ interfaces. Therefore, when considering the adjustment of Sn content to improve the wettability of Cu–aSn–1Cr/C_gr or enhance the mechanical and functional properties of the Cu matrix, the effects of Cu_xSn_y on W_ad and γ_int should also be taken into account. This provides theoretical guidance for the design and property optimization of compositions in Cu–aSn–1Cr/C_gr and similar systems.

(3)

Comparison of theoretical and calculated values

Table 1 has the $W_{\mathrm{ad}}^{\mathrm{cal}}$ obtained in Section 3.1 from experimental values of θ_e, σ_lv [29] and solid–liquid interfacial energy σ_sl; σ_sl can be obtained from Equation (15) [58,59]:

$$\cos {\theta }_{\mathrm{e}}={\displaystyle \frac{{\sigma }_{\mathrm{sv}}-{\sigma }_{\mathrm{sl}}}{{\sigma }_{\mathrm{lv}}}}$$

(15)

The value of σ_sv of Cr₃C₂ is 4.13 J/m² [37]. The a (at. %) values are obtained by converting the Sn content in the metal surface model according to the atomic ratio. Similarly, the σ_metal, W_ad, and γ_int obtained from the theoretical calculations are displayed in

Table 2. Theoretical calculated values.

a (at. %)	0	1.79	3.57	5.36	7.14	23.10	25	45.45	100
σmetal (J/m2)	1.32	1.22	1.24	1.16	1.13	0.87	0.85	0.76	0.43
γint (J/m2)	2.31	2.30	2.86	3.06	3.20	3.58	3.93	3.79	1.83
Wad (J/m2)	3.05	2.91	2.76	2.67	2.68	1.28	1.09	0.96	2.6

. Comparing Table 1 and Table 2, although there is a certain deviation between the theoretically calculated values and the experimentally calculated values, there is a trend of decreasing σ_metal and σ_lv, as well as W_ad and $W_{\mathrm{ad}}^{\mathrm{cal}}$ with the increase in a. The values of σ_metal and σ_lv are close to each other. However, some theoretically calculated values (W_ad and γ_int) are larger than the experimentally calculated values ($W_{\mathrm{ad}}^{\mathrm{cal}}$ and σ_sl), such as the Cu||Cr₃C₂ and Sn||Cr₃C₂ interfaces, which results in an inability to back extrapolate θ_e and thus hinders wettability predictions. The reason may be that W_ad and γ_int are based on first-principles calculations at 0 K, where the atoms are in equilibrium positions, whereas the experimentally calculated values are obtained from measurement and calculation after heating to 1100 °C. The theoretically calculated values of W_ad are smaller than $W_{\mathrm{ad}}^{\mathrm{cal}}$, and γ_int is larger than σ_sl for Cu_56-kSn_k||Cr₃C₂ and Cu_xSn_y||Cr₃C₂, probably because the composition of the RPL in the experiment includes not only Cr₃C₂ but also Cr₇C₃, which affects the experimental values and hence the larger values.

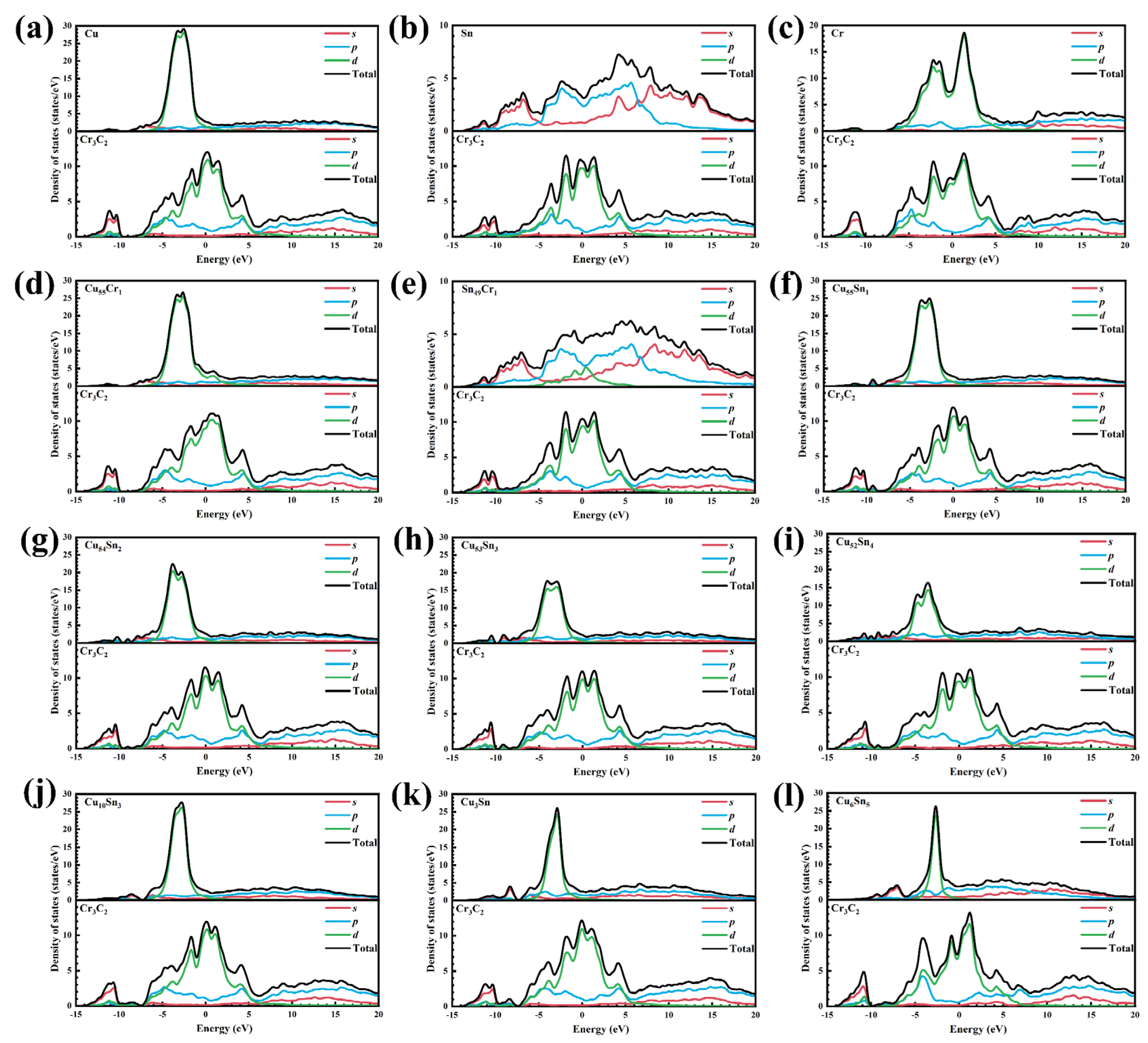
4.1.4. Interfacial Electronic Structure

The bonding of interface atoms depends on the configuration of the metal||Cr_mC_n interface. To better explore the interactions between atoms at the metal||Cr_mC_n interface, this section calculates the changes in the partial density of states (PDOS), charge density difference (CDD), and Mulliken population of the interface after relaxation and reveals the variation mechanism of the IBPs from an electronic perspective (charge transfer and distribution).

(1)

Partial density of states

Figure 7 shows the PDOS of the above interfacial structures near the Fermi energy level (E_F). The PDOS of the electronic orbitals of the relaxation state system can be used to determine the origin of the electronic orbitals that contribute to interatomic interactions in each system. In Figure 7, the upper and lower parts of each subplot represent the PDOS of the metal and the Cr₃C₂, respectively. The PDOS is divided into s, p, and d orbitals based on the orbitals in which the valence electrons are located, and the total is the sum of all orbitals of the metal||Cr₃C₂ part. Figure 7a–c correspond to the PDOS for the interfaces Cu||Cr₃C₂, Sn||Cr₃C₂, and Cr||Cr₃C₂, respectively. In the Cu||Cr₃C₂ interface (Figure 7a), the main contributions stem from the electronic interactions of the Cr–d and Cu–d orbitals. The density of states (DOS) of the d orbital electrons of Cu and Cr₃C₂ are mainly located in the range of −6eV~−0.9eV and −7.5eV~5.5eV. The range of DOS distribution of the d orbital electrons of Cr₃C₂ is generally consistent with that reported in Ref. [37]. Similarly, for the Cr||Cr₃C₂ interface, the d orbital contributes to the main electronic state (Figure 7c), where the Cr–d orbital of Cr hybridizes with the Cr–d orbital of Cr₃C₂. The metallic bonds formed at the interface of Cu||Cr₃C₂ and Cr||Cr₃C₂ provide the main role for adhesion at the interface. The DOS of Sn is mainly contributed by the Sn–p orbital electrons (Figure 7b), which are mainly distributed in the range of −5eV~9eV, with a small contribution from the d orbital electrons. The Sn||Cr₃C₂ interface is mainly contributed by metallic bonds formed by Sn–p orbital and Cr–d orbital electrons. The bonding strength Cr||Cr₃C₂ > Cu||Cr₃C₂ > Sn||Cr₃C₂ is due to the metallic bonds formed by p–d orbital hybridization being weaker than those formed by d–d orbital hybridization, and thus Sn||Cr₃C₂ is lower. Comparing Figure 7a,c, the DOS peak for Cr||Cr₃C₂ shows d–d orbital hybridization over a wider energy range, which has more homomorphic electrons compared to Cu||Cr₃C₂, and thus Cr||Cr₃C₂ is higher. Comparing Figure 7a,d, it is observed that the DOS near the E_F for the Cu₅₅Cr₁||Cr₃C₂ interface is higher than that of Cu||Cr₃C₂. This is because Cr doping effectively increases the d orbital electronics near the E_F at the Cu||Cr₃C₂ interface, thereby enhancing the bonding strength between the interface atoms. Comparing Figure 7a,d, it is observed that the DOS of d orbital electronics below the E_F for Cu₅₅Cr₁ is higher than for Cu. Similarly, Figure 7b,e show that Sn₄₉Cr₁ increases the DOS of d orbital electronics below the E_F for Sn. Therefore, Cr doping can effectively enhance the interface bonding strength. Figure 7f–i show the effect of doping with different numbers of Sn atoms on the PDOS near the E_F at the interface. Comparing Figure 7a,f, it is evident that Sn doping causes the peak value of the DOS for the d orbital electrons of Cu to decrease from 28 eV/states to 25 eV/states. With the increase in Sn doping number k (k = 1, 2, 3, 4), the DOS peak of the d orbital electrons below the E_F in the Cu_56-kSn_k decreases gradually, which indicates that Sn doping weakens the interfacial bonding strength. Figure 7j–l shows the effect of Cu_xSn_y on PDOS near the E_F at the interface. With the increase in Sn content, the DOS peak widths of the d orbital electrons below the E_F of Cu_xSn_y are in the order of Cu₁₀Sn₃ > Cu₃Sn > Cu₆Sn₅. Compared with Figure 7f–i, the DOS peak widths of the d orbital electrons below the E_F of Cu_xSn_y are narrower than those of Cu_56-kSn_k, which indicates that higher Sn content results in the number of d orbital electrons of Cu_xSn_y being less than that of Cu_56-kSn_k, so the bonding strength of the interface is gradually weakened.

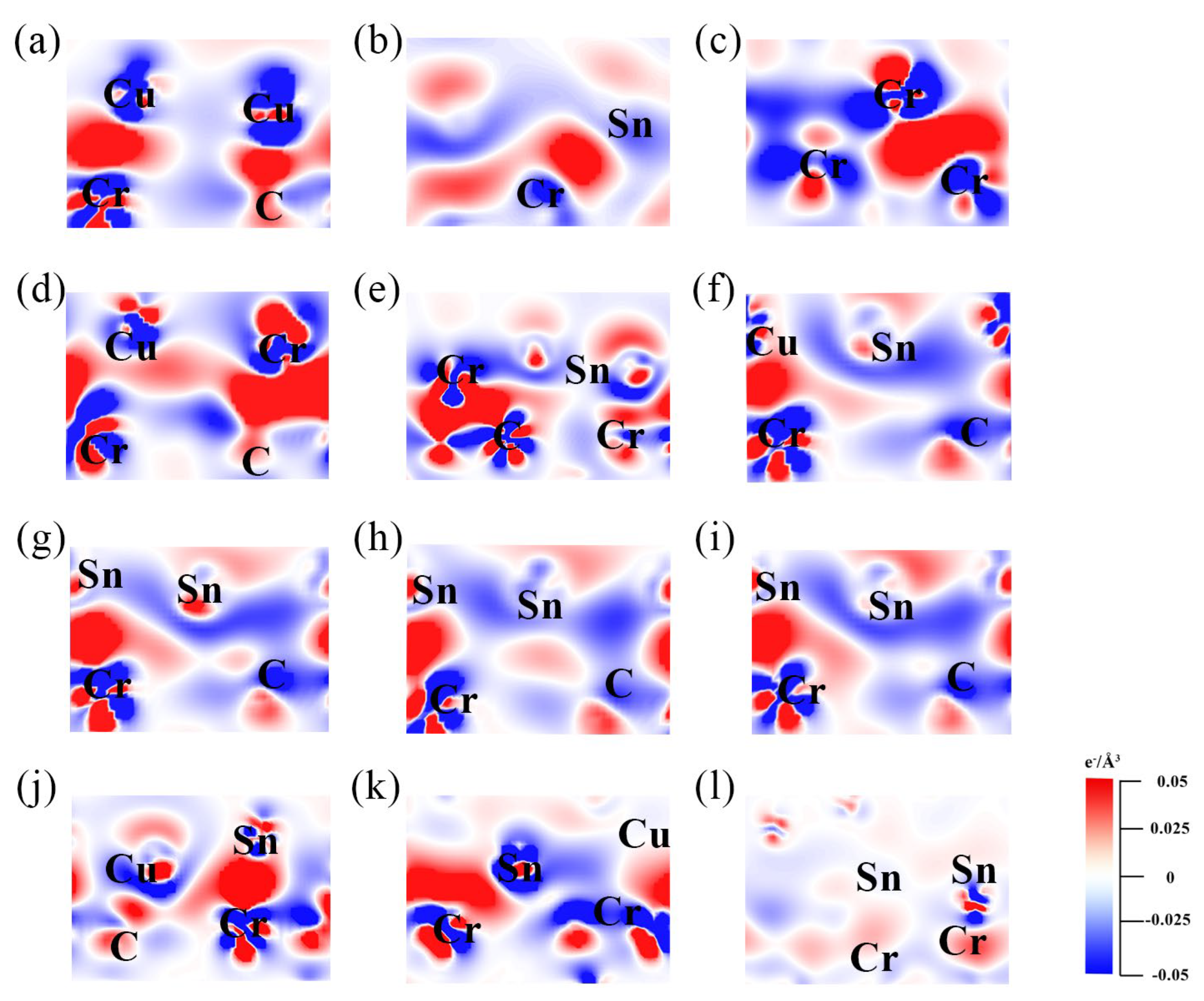
(2)

Charge density difference analysis

To further explore the interfacial bonding mechanisms at the atomic scale, charge density difference (CDD) analyses are performed for typical metal||Cr₃C₂ interfaces with different alloying configurations. The CDD (Δρ) is used to indicate the charge density redistribution and the degree of electron transfer at the interface. The Δρ can be expressed as Equation (16) [52]:

$$\Delta \rho ={ \rho }_{\mathrm{int}}-{\rho }_{\mathrm{metal}}-{ \rho }_{{\mathrm{Cr}}_3{C}_2}$$

(16)

where ρ_int is the total charge density of the metal||Cr₃C₂ interface, ρ_metal, and ρ_Cr3C2 are the charge densities of isolated metal slab and Cr₃C₂ slab, respectively. The red regions represent charge accumulation (electron gain), while the blue regions indicate charge dissipation (electron loss). The intensity of the color corresponds to the degree of charge accumulation or dissipation. The CDD results (Figure 8) show significant charge accumulation and dissipation at the Cr||Cr₃C₂ interface compared to Cu||Cr₃C₂ and Sn||Cr₃C₂, indicating strong interfacial charge transfer and bond formation, which is consistent with its high adhesion work (W_ad). In addition, the Cr-doped interfaces (Cu₅₅Cr₁||Cr₃C₂ and Sn₄₉Cr₁||Cr₃C₂) exhibit enhanced charge redistribution, confirming that Cr doping strengthens interfacial bonding. As the Sn doping content increases (Cu₅₆−_kSn_k||Cr₃C₂, k = 1–4), the charge accumulation near the interface gradually weakens, and dissipation becomes more prominent, as shown in Figure 8f–i. This trend continues in the Cu_xSn_y||Cr₃C₂ interfaces, as shown in Figure 8j–l, particularly at Cu₆Sn₅||Cr₃C₂, where charge dissipation is strongest, corresponding to the lowest W_ad observed.

5. Conclusions

In the reactive wetting experiments of the Cu–aSn–1Cr/C_gr system, variations in the Sn content can affect the physical and chemical properties of the alloy, the dissolution/precipitation of Cr elements, the microstructure of the alloy, and the phase composition and morphology of the RPL. These changes further impact the interface configurations and characteristics. Based on the first-principles study, several typical interfacial structures are selected, and simplified interfacial models are constructed. By calculating the W_ad, σ_metal, and γ_int of these models at the atomic level, the effects of these factors on the interface characteristics are elucidated. Additionally, from the electronic level, the nature of the effects of interatomic charge distribution on interfacial properties is explored using the PDOS and CDD. The conclusions from the experiments and calculations are as follows:

(1)

With the increase in Sn content, the σ_lv and $W_{\mathrm{ad}}^{\mathrm{cal}}$ of the alloy show a decreasing trend, and the RPL thickness increases. The overall interface presents a “sandwich” structure, consisting of the metal||Cr_mC_n (Cr₃C₂ and Cr₇C₃) and Cr_mC_n||C_gr interfaces. The influence of varying Sn content is primarily reflected in the metal||Cr_mC_n interface. The phase composition and morphology of Cr_mC_n change with the Sn content.

(2)

The various forms (Cu–Sn solid solutions, Cu_xSn_y compounds, and Sn/Cr element segregation) exist on the alloy side in contact with the Cr_mC_n surface. The doping and segregation of Cr can significantly increase the W_ad and stability of the metal||Cr₃C₂ interface. The effect of Sn is opposite to that of Cr and becomes more significant with the increase in Sn content. This is primarily because the metallic bond formed by Sn–p and Cr–d is weaker than the d–d metallic bonds (Cu–d and Cr–d, Cr–d and Cr–d). Sn increases the dissipation (or accumulation) of the interface’s CDD. The increase in Sn content reduces the number of d orbital electrons in the metal portion, leading to a decrease in the PDOS of electronics below the E_F.

(3)

The σ_metal of the Cu–Sn alloy obtained from theoretical calculations is in good agreement with the σ_lv reported in the literature. The trend in the theoretical calculation of W_ad agrees with that of $W_{\mathrm{ad}}^{\mathrm{cal}}$ calculated in the experiment.

(4)

The systematic experiments and simplified interfacial models based on the first-principles DFT calculations help elucidate the interaction among alloying elements and the effects of Sn content changes; reveal how typical interfacial configurations affect wettability, adhesion, and stability; and reduce the need for extensive experimental screening to avoid the influence of complex experimental conditions. This combined approach provides useful insights for designing interfaces in metal/carbon composites. In future work, advanced characterization techniques coupled with multiscale and dynamic interface simulations can be employed to refine the understanding of atomic-scale wetting behavior.