Quantitative Characterization of Bubble Defects in Ultra-Low Expansion Quartz Glass via Ultrasonic Interaction
Abstract
1. Introduction
2. Materials and Methods
2.1. Establishment of Simulation Model
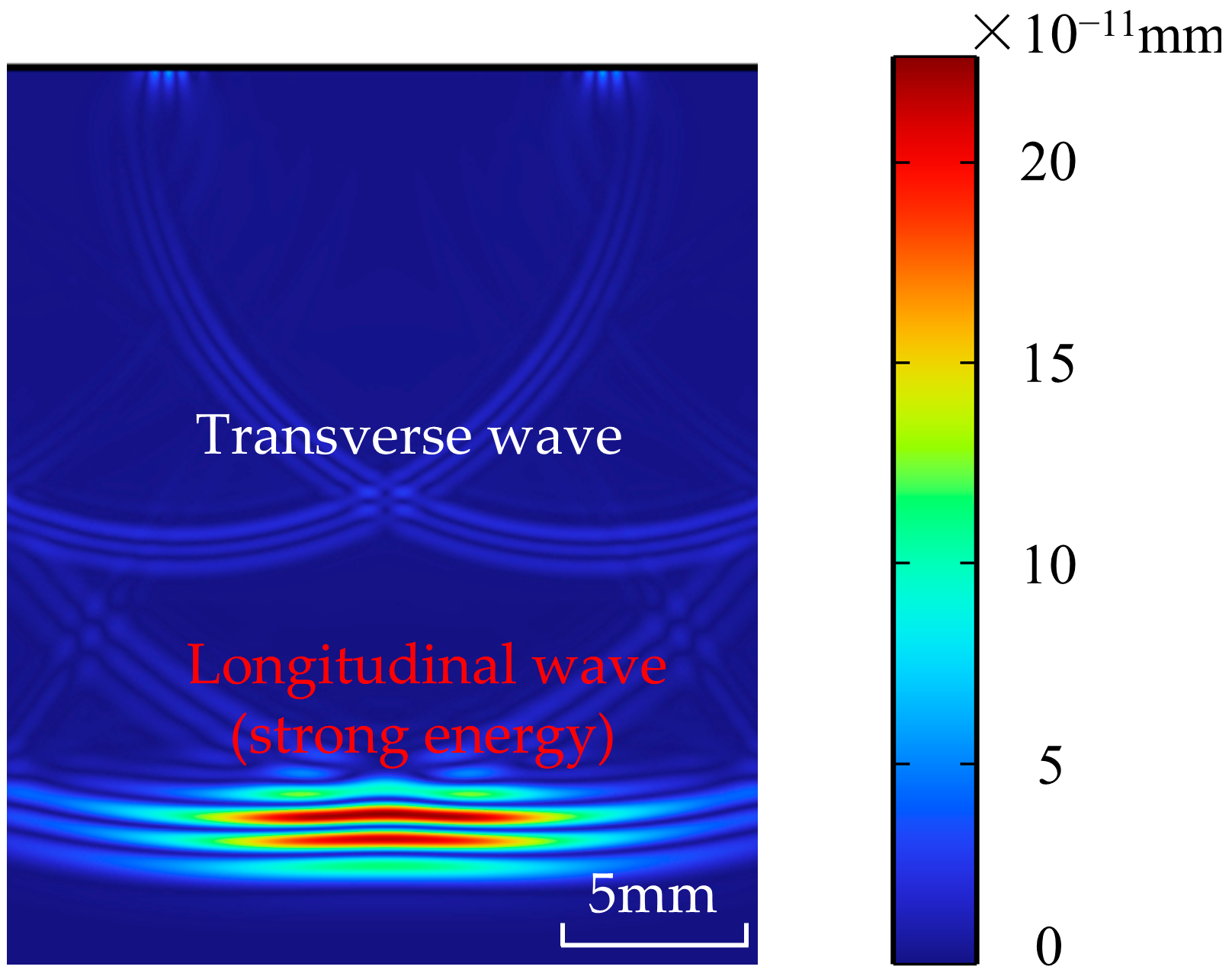
2.2. Analysis of Ultrasonic Propagation Characteristics and Interaction with Defects
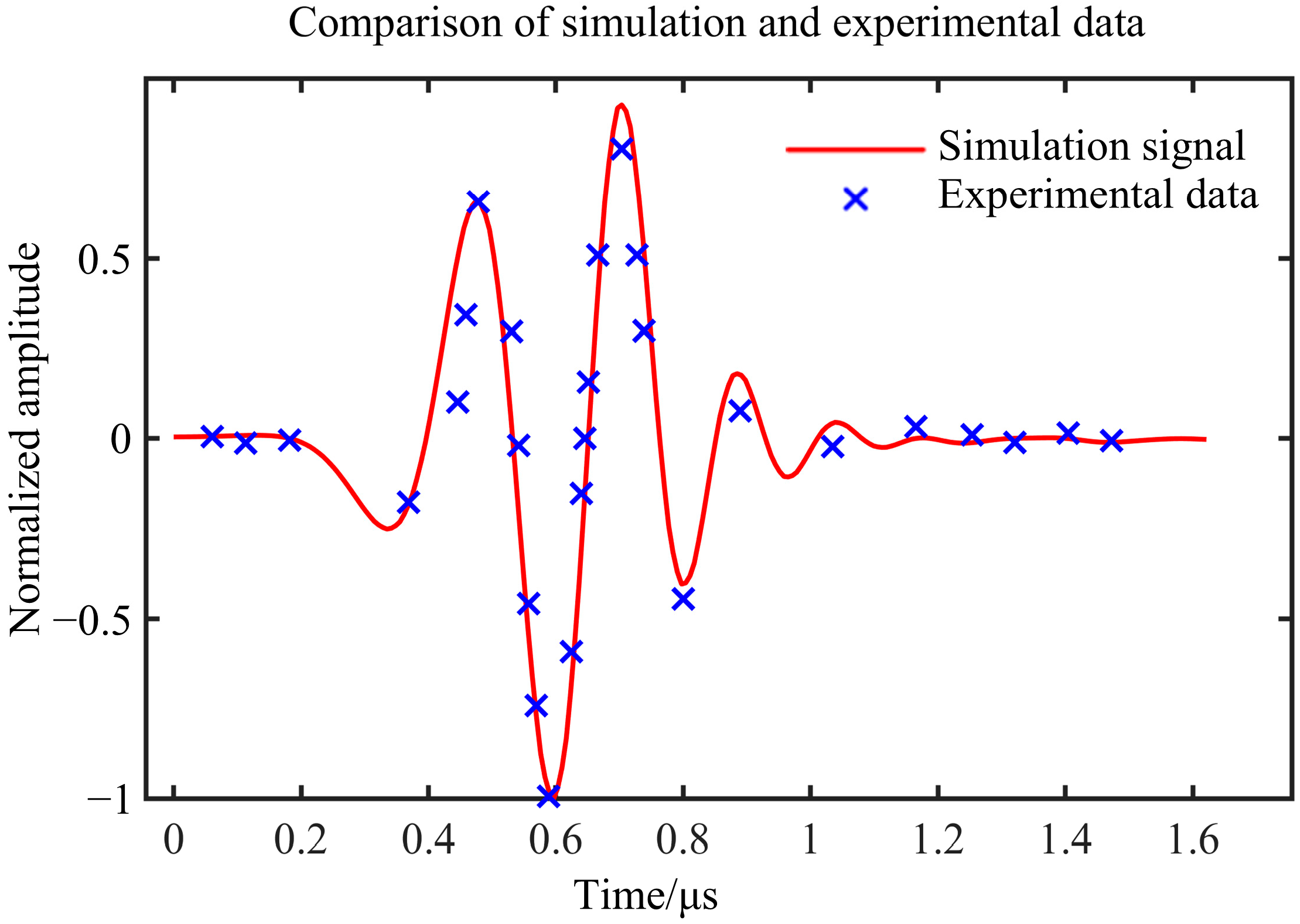
3. Results
4. Discussion
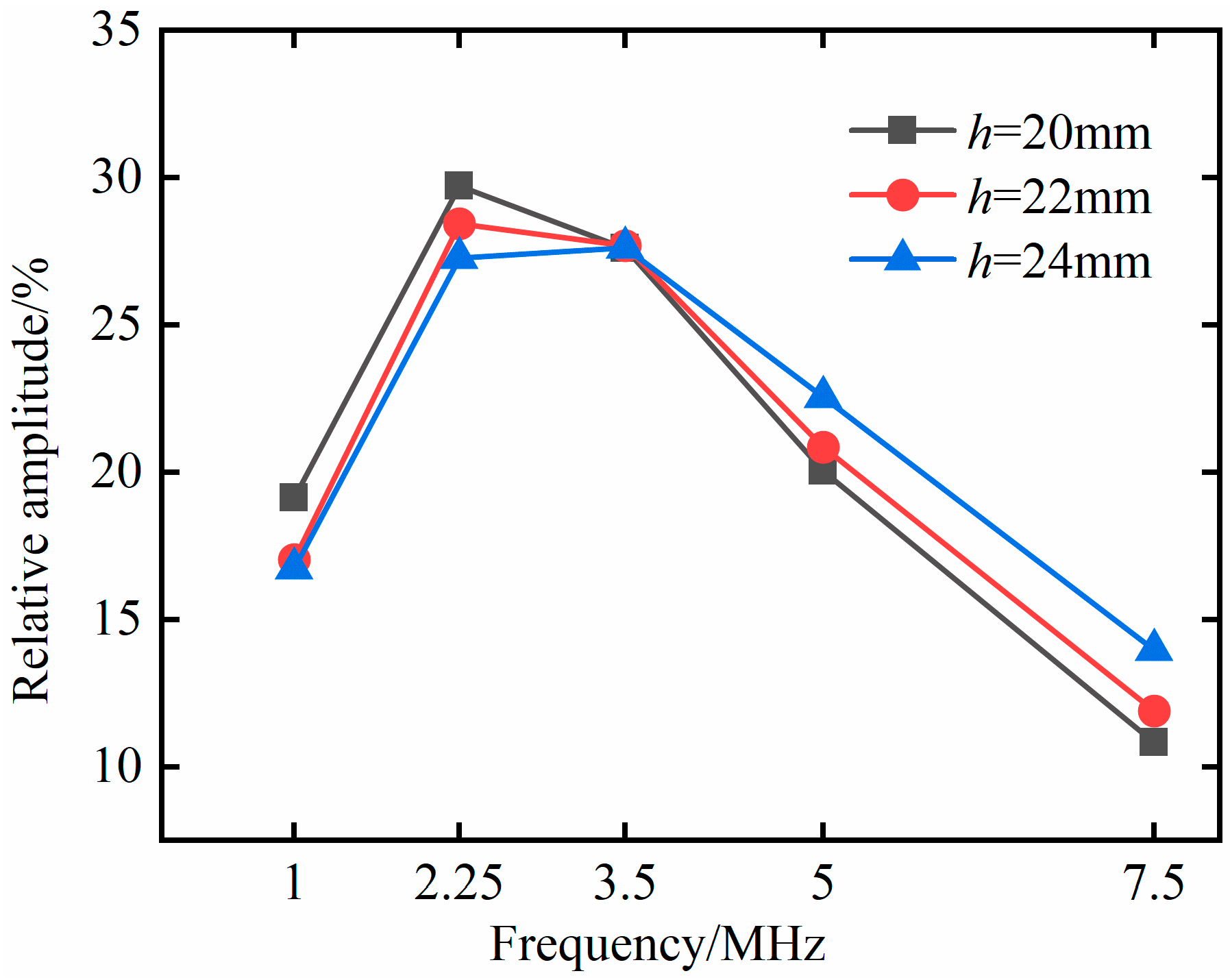
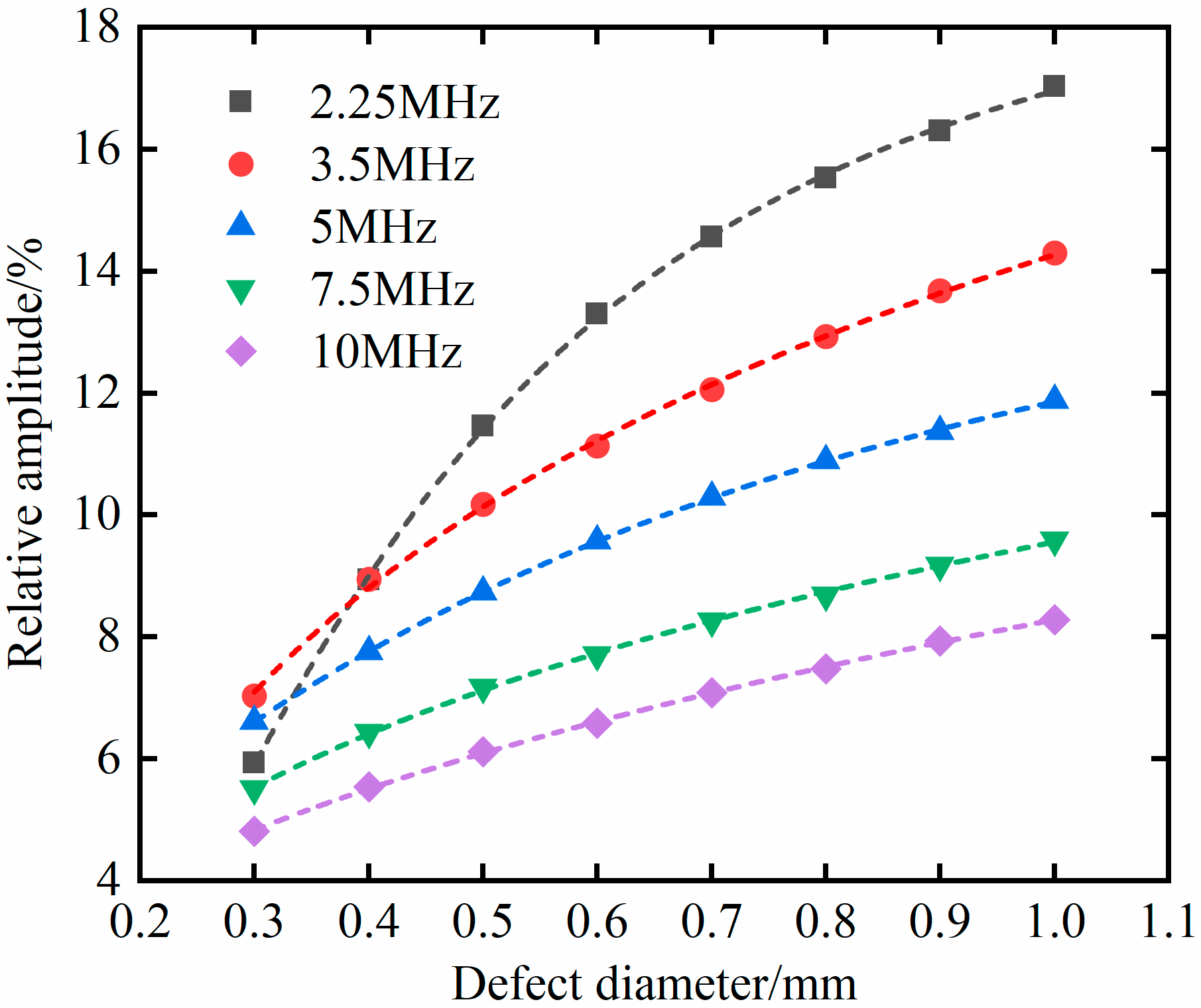
4.1. Effect of Probe Frequency
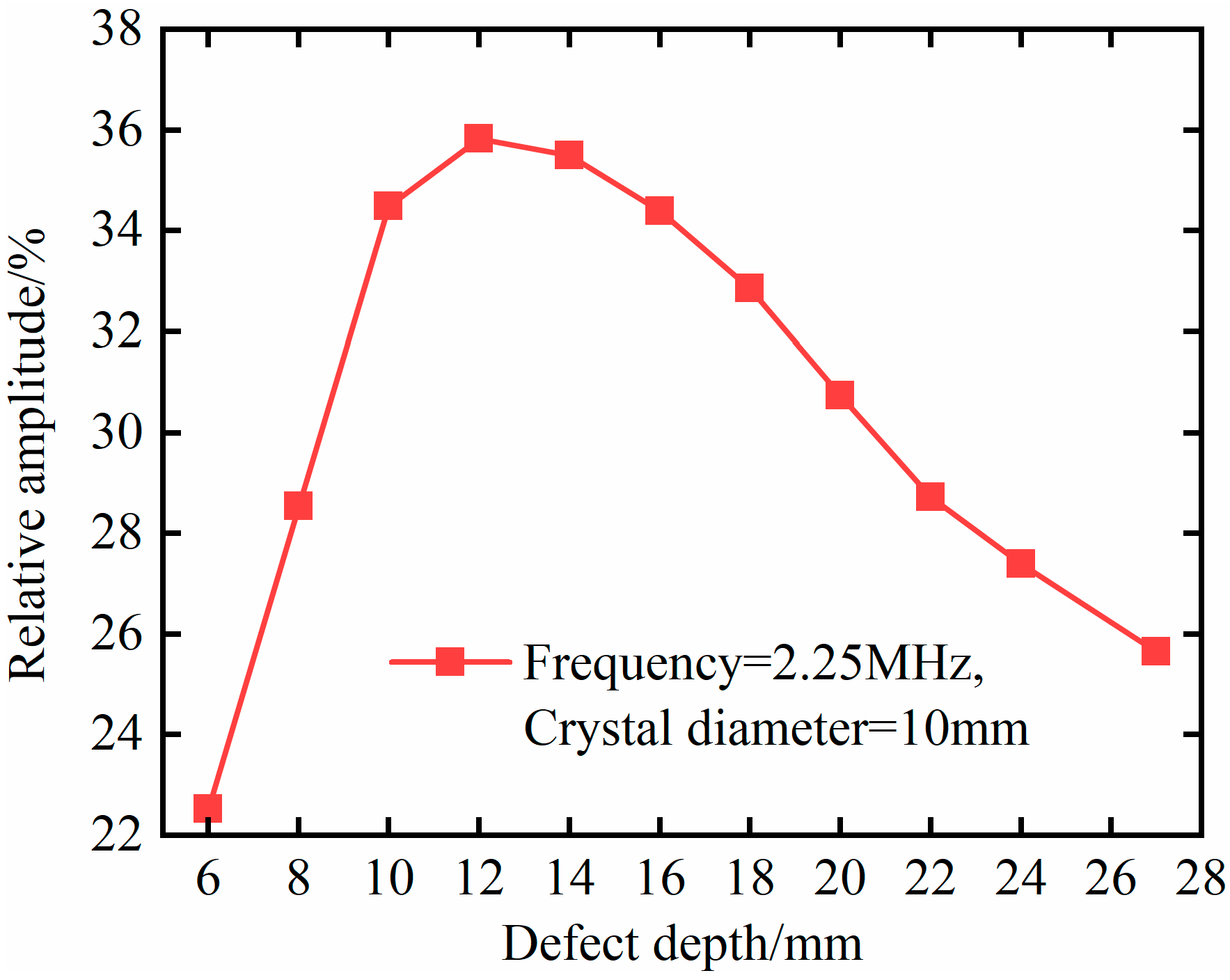
4.2. Effect of Probe Diameter
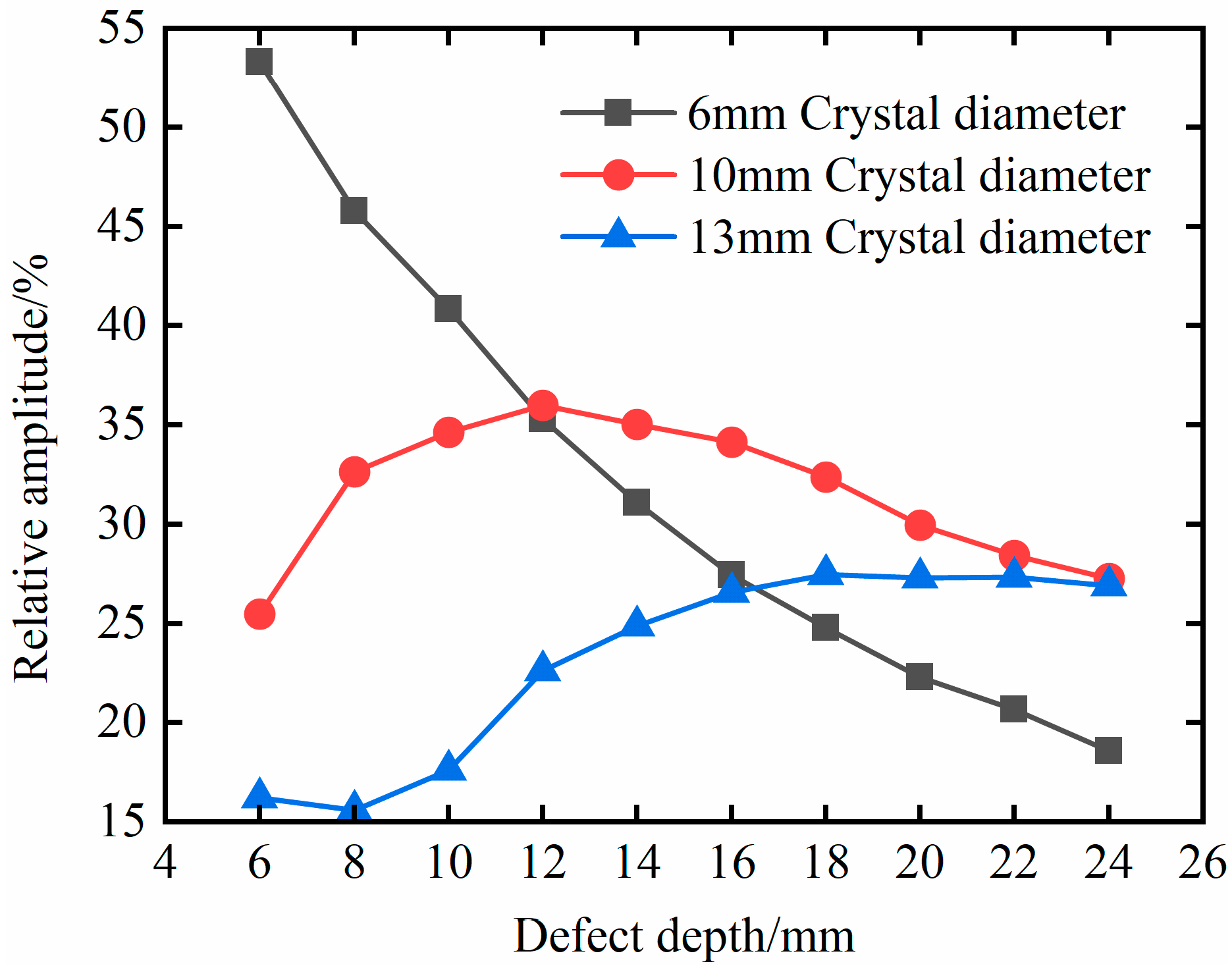
4.3. Effect of Defect Depth
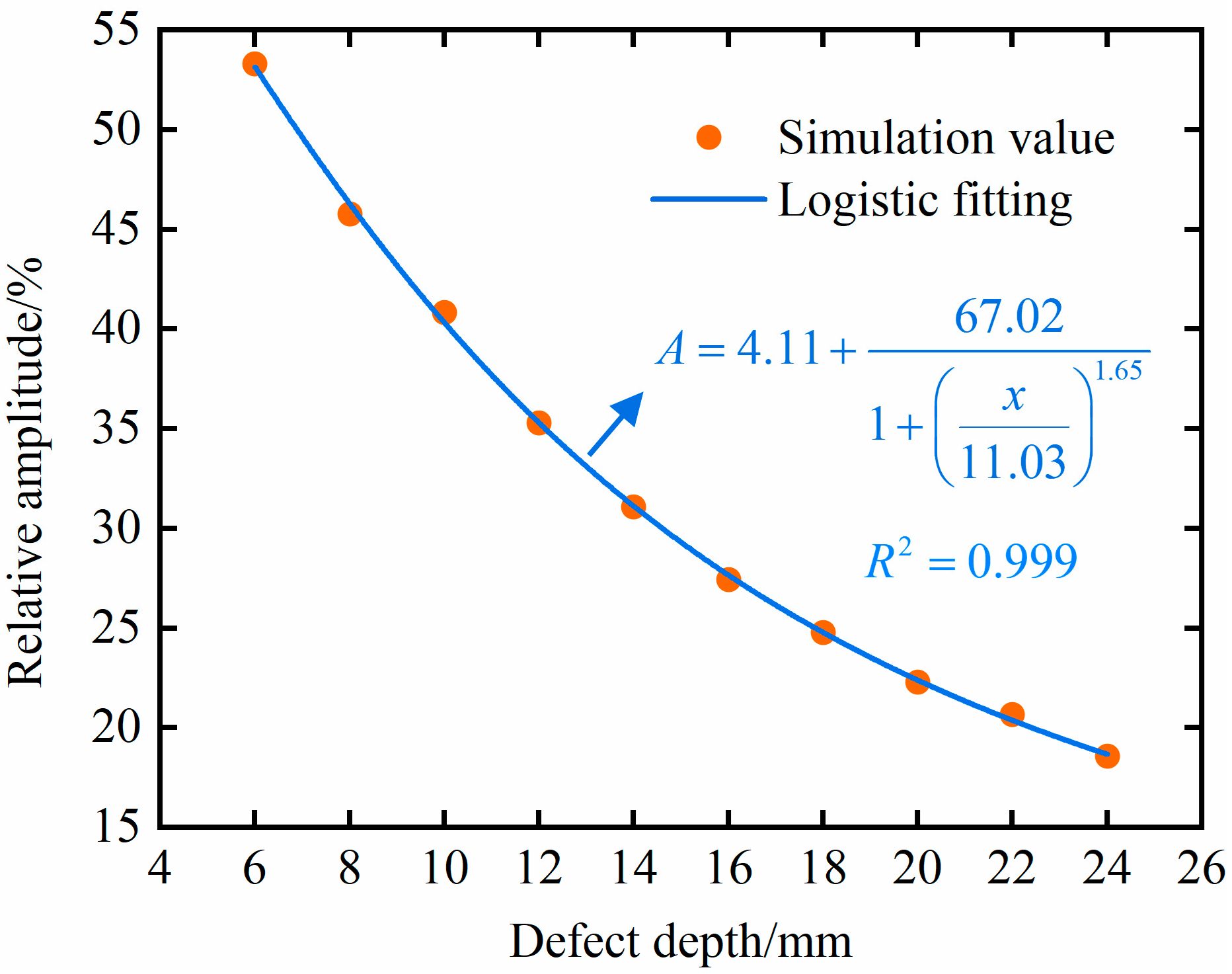
4.4. Quantitative Characterization Analysis of Defects
5. Conclusions
- (1)
- By analyzing the interaction between circular and elliptical bubble defects and the ultrasonic waves, it is found that the shape of the reflected wave is similar to that of the corresponding defect. When the ultrasonic wave is incident on the bubble defect interface with the positive radius of curvature, it will produce scattering characteristics, but due to different radii of curvature, the scattering of the reflected wave is different. When the ultrasonic wave is incident on the circular bubble defect interface, the radius of curvature of each point on the circle is the same, which is equal to the radius of the circular defect 0.75, and the ultrasonic scattering characteristics are obvious and the sound beam energy is dispersed, resulting in the defect echo energy being obviously weak. The radius of curvature of each point on the elliptical defect is different, which is located between the short half axis of 0.3 and the long half axis of 0.75. The reflecting interface is relatively flat. The ultrasonic scattering is not obvious, and the echo energy of the defect is strong;
- (2)
- By analyzing the interaction between a bubble defect and an ultrasonic wave at different depths, it is found that the relative amplitude of a defect echo corresponding to a 6 mm probe diameter shows a monotonic decreasing relationship with the defect depth, so the relative amplitude of the defect echo can be used to characterize the defect depth. However, there is no monotonic correspondence between a 10 mm probe diameter and a 13 mm probe diameter, and the relative amplitude of the defect echo cannot be used to characterize the defect depth. By analyzing the interaction between bubble defects with different sizes and the ultrasonic waves, it is found that there is also a monotonic correspondence between the relative amplitude of the defect echo and the size of the bubble defects, so the relative amplitude of the defect echo can be used to characterize the size of the bubble defects. The goodness of fit of the nonlinear fitting curve of the data is greater than 0.99, and it has a high prediction accuracy. In this paper, the interaction between bubble defect and ultrasonic wave is analyzed and verified, and the results show that the bubble defect can be quantitatively characterized by the relative amplitude of the defect echo.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gulati, S.T.; Edwards, M.J. ULE-Zero expansion, low density, and dimensionally stable material for lightweight optical systems. Adv. Mater. Opt. Precis. Struct. A Crit. Rev. 1997, 10289, 104–133. [Google Scholar]
- Lutpi, H.A.; Mohamad, H.; Abdullah, T.K.; Ismail, H. Effect of isothermal treatment on the structural, microstructure, and physio-mechanical properties of Li2O-Al2O3-SiO2 glass–ceramic. J. Aust. Ceram. Soc. 2022, 58, 9–20. [Google Scholar]
- Shayler, D.J.; Harland, D.M. The Hubble Space Telescope: From Concept to Success; Springer-Verlag: New York, NY, USA, 2016. [Google Scholar]
- VanBrocklin, R.R.; Edwards, M.J.; Wells, B. Review of Corning’s capabilities for ULE mirror blank manufacturing for an extremely large telescope. Optomech. Technol. Astron. 2006, 6273, 27301. [Google Scholar]
- Hrdina, K.E.; Duran, C.A. ULE® Glass with Improved Thermal Properties for EUVL Masks and Projection Optics Substrates. Int. J. Appl. Glass Sci. 2014, 5, 82–88. [Google Scholar] [CrossRef]
- Ma, Q.; Li, C.; Zhang, G.; Fang, H. A novel method for accelerating bubble rising in highly viscous molten quartz. Int. J. Heat Mass Transf. 2019, 138, 359–1367. [Google Scholar]
- Hrdina, K.E.; Hanson, B.Z.; Fenn, P.M.; Sabia, R. Characterization and characteristics of a ULE glass tailored for EUVL needs. In Emerging Lithographic Technologies VI; SPIE: Santa Clara, CA, USA, 2002; Volume 4688, pp. 454–461. [Google Scholar]
- Frank, S.; Seiler, M.; Bliedtner, J. Three-dimensional evaluation of subsurface damage in optical glasses with ground and polished surfaces using FF-OCT. Appl. Opt. 2021, 60, 2118–2126. [Google Scholar]
- Cao, H.; Peng, X.; Shi, F.; Tian, Y.; Kong, L.; Chen, M.; Hao, Q. Advances in Subsurface Defect Detection Techniques for Fused Silica Optical Components: A Literature Review. J. Mater. Res. Technol. 2025, 35, 809–835. [Google Scholar] [CrossRef]
- Stockman, T.; Knapp, C.; Henderson, K.; Carpenter, J.; Schneider, J. Stainless steel 304L LENS AM process monitoring using in-situ pyrometer data. JOM 2018, 70, 1835–1843. [Google Scholar]
- Vollmer, M.; Möllmann, K.P. Infrared Thermal Imaging: Fundamentals, Research and Applications; John Wiley & Sons: Bristol, UK, 2018. [Google Scholar]
- Ciampa, F.; Mahmoodi, P.; Pinto, F.; Meo, M. Recent advances in active infrared thermography for non-destructive testing of aerospace components. Sensors 2018, 18, 609. [Google Scholar] [CrossRef]
- Zarei, A.; Pilla, S. Laser ultrasonics for nondestructive testing of composite materials and structures: A review. Ultrasonics 2024, 136, 107163. [Google Scholar] [CrossRef]
- Cheeke, J.D.N. Fundamentals and Applications of Ultrasonic Waves; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Ginzel, E. Phased Array Ultrasonic Technology; Eclipse Scientific Products Incorporated: Waterloo, ON, Canada, 2013. [Google Scholar]
- Schnars, U.; Henrich, R. Applications of NDT methods on composite structures in aerospace industry. In Proceedings of the Conference on Damage in Composite Materials, Stuttgart, Germany, 18–19 September 2006; pp. 18–19. [Google Scholar]
- D’orazio, T.; Leo, M.; Distante, A.; Guaragnella, C.; Pianese, V.; Cavaccini, G. Automatic ultrasonic inspection for internal defect detection in composite materials. NDT E Int. 2008, 41, 145–154. [Google Scholar] [CrossRef]
- Tanaka, T.; Izawa, Y. Nondestructive detection of small internal defects in carbon steel by laser ultrasonics. Jpn. J. Appl. Phys. 2001, 40, 1477. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, L.; Behnamian, Y.; Song, S.; Wang, R.; Gao, Z.; Hu, W.; Xia, D.-H. Metal pitting corrosion characterized by scanning acoustic microscopy and binary image processing. Corros. Sci. 2020, 170, 108685. [Google Scholar] [CrossRef]
- Qin, F.; Li, B.; Chen, L.; Shang, Z.; Zhang, Z.; Huang, Y.; Wang, W.; Zheng, Y. Interaction analysis of different defects with laser ultrasonic sound waves and defect characterization. Opt. Laser Technol. 2023, 157, 108630. [Google Scholar] [CrossRef]
- Kim, J.; Cho, Y.; Lee, J.; Kim, Y.H. Defect detection and characterization in concrete based on FEM and ultrasonic techniques. Materials 2022, 15, 8160. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Deng, D.; Li, L.; Li, L.X. Ultrasonic phased array inspection for gas pressure welds joint of high speed railway. Prz. Elektrotechniczn 2012, 88, 173–176. [Google Scholar]
- Namboodiri, G.N.; Balasubramaniam, K.; Balasubramanian, T.; Jothinathan, G. Studies on feasibility of ultrasonic phased array in rail inspection. In Proceedings of the National Seminar & Exhibition on Non-Destructive Evaluation NDE 2011, Indian Society for Non-Destructive Testing, Chennai India, 8–10 December 2011; pp. 245–248. [Google Scholar]
- Rana, R. Wear and residual stress analysis of waste sea shell and b4c particles reinforced green hybrid aluminium metal composite. J. Eng. Res. 2021, 9, 215–224. [Google Scholar]
- Honarvar, F.; Varvani-Farahani, A. A review of ultrasonic testing applications in additive manufacturing: Defect evaluation, material characterization, and process control. Ultrasonics 2020, 108, 106227. [Google Scholar] [CrossRef] [PubMed]
- Jodhani, J.; Handa, A.; Gautam, A.; Ashwni; Rana, R. Ultrasonic non-destructive evaluation of composites: A review. Mater. Today Proc. 2023, 78, 627–632. [Google Scholar] [CrossRef]
- Cui, B.; Cui, J.; Barnard, D.J.; Bond, L.J. Internal defect detection and characterization of samarium-cobalt sintered magnets by ultrasonic testing technique. J. Magn. Magn. Mater. 2023, 570, 170524. [Google Scholar] [CrossRef]
- Guo, H.; Zheng, B.; Liu, H. Numerical simulation and experimental research on interaction of micro-defects and laser ultra-sonic signal. Opt. Laser Technol. 2017, 96, 8–64. [Google Scholar] [CrossRef]
- Zeng, Y.; Wang, X.K.; Qin, X.P.; Hua, L.; Liu, G.; Guan, S. Laser ultrasonic inspection of defects in wire arc additive manufactured samples with different surface profiles. Measurement 2022, 188, 110597. [Google Scholar] [CrossRef]
- Yang, X.W. Metal material is small defects ultrasonic reflection signal modeling and identification. World Nonferrous Met. 2016, 448, 1–72. [Google Scholar]
- Corning Incorporated. Available online: https://www.corning.com/worldwide/en.html (accessed on 14 February 2025).
- Chen, H.; Sun, K.; Ke, C.; Shang, Y. Simulation of ultrasonic testing technique by finite element method. In Proceedings of the IEEE 2012 Prognostics and System Health Management Conference (PHM-2012 Beijing), Beijing, China, 23–25 May 2012; IEEE: New York, NY, USA, 2012; pp. 1–5. [Google Scholar]
- Alleyne, D.; Cawley, P. A two-dimensional Fourier transform method for measurement of propagating multi mode signals. J. Acoust. Soc. Am. 1991, 89, 1159–1168. [Google Scholar] [CrossRef]
- Xu, C.; Li, W. Fundamentals of Ultrasonic Testing; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar]
- Hurtado-Aviles, E.A.; Torres, J.A.; Trejo-Valdez, M.; Torres-SanMiguel, C.R.; Villalpando, I.; Torres-Torres, C. Ultrasonic influence on plasmonic effects exhibited by photoactive bimetallic Au-Pt nanoparticles suspended in ethanol. Materials 2019, 12, 1791. [Google Scholar] [CrossRef] [PubMed]
- Hagy, H.E. High precision photoelastic and ultrasonic techniques for determining absolute and differential thermal expansion of titania–silica glasses. Appl. Opt. 1973, 12, 1440–1446. [Google Scholar] [CrossRef] [PubMed]
- Hagy, H.E.; Shirkey, W.D. Determining absolute thermal expansion of titania–silica glasses: A refined ultrasonic method. Appl. Opt. 1975, 14, 2099–2103. [Google Scholar] [CrossRef]
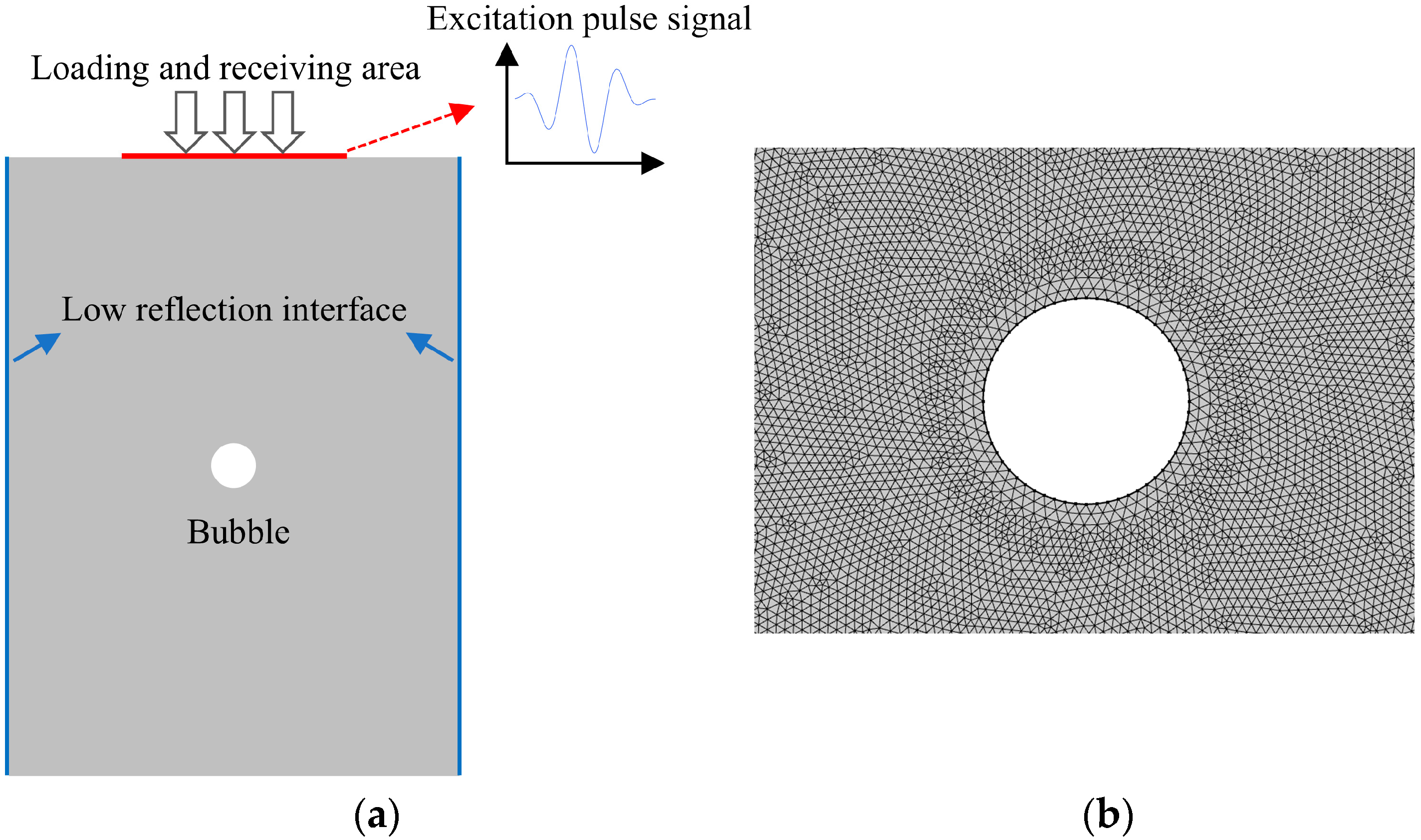


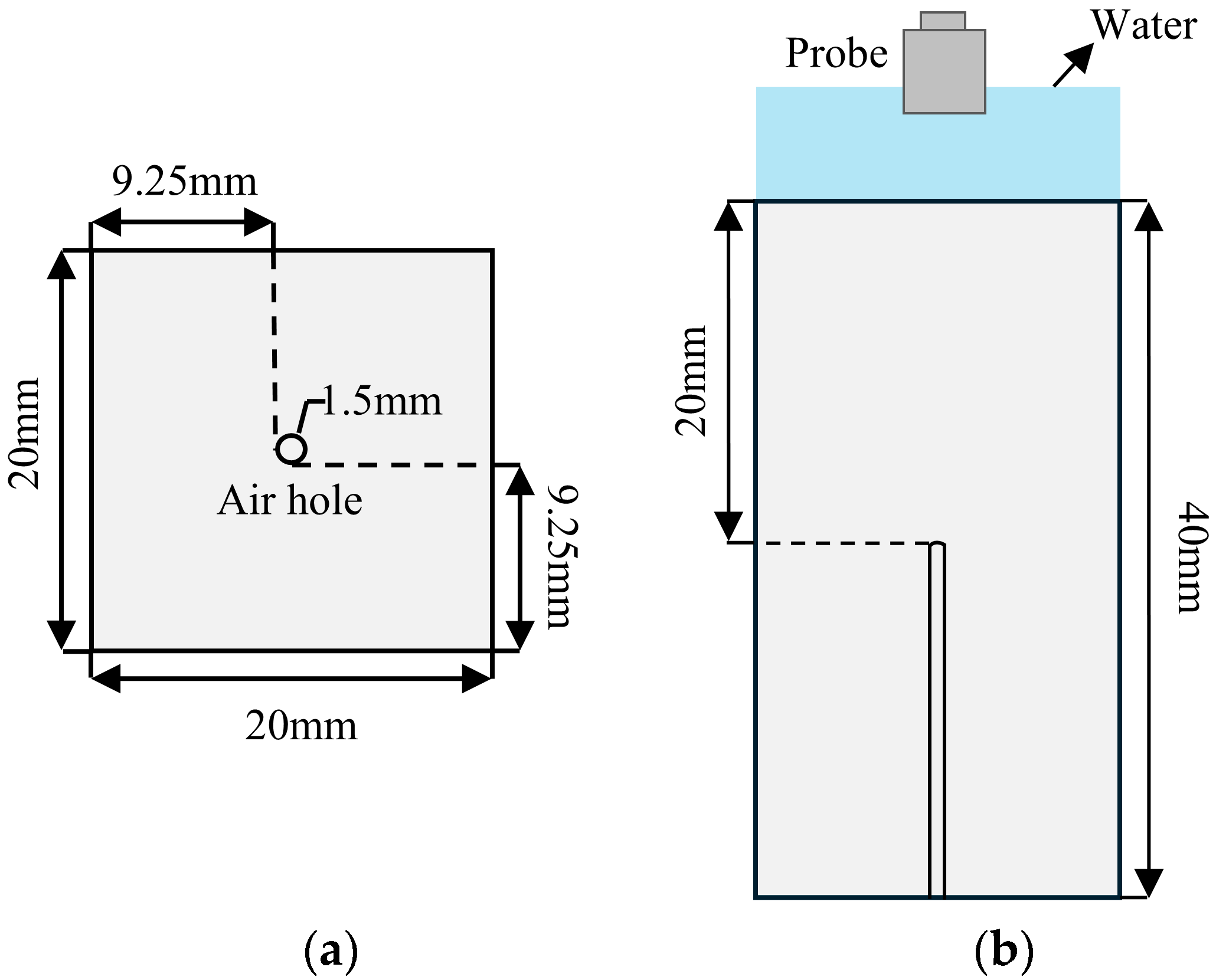

| Material | Density/(g/cm3) | Poisson’s Ratio | Young’s Modulus/(GPa) |
|---|---|---|---|
| ULE | 2.21 | 0.17 | 67.6 |
| Air | 1.29 | / | / |
| Probe Diameter/(mm) | Defect Echo Relative Amplitude/(%) |
|---|---|
| 6 | 22.29 |
| 10 | 29.98 |
| 13 | 27.34 |
| Geometric Dimensions/mm | Defect Diameter/mm | Simulation Value/% | Estimate/% | Prediction Value Difference/% |
|---|---|---|---|---|
| 0.45 | 14.81 | 15.40 | 0.59 | |
| 0.55 | 17.79 | 18.00 | 0.21 | |
| 0.65 | 19.71 | 20.25 | 0.54 | |
| 0.75 | 21.10 | 22.22 | 1.12 | |
| 0.85 | 22.15 | 23.99 | 1.84 | |
| 0.95 | 23.40 | 25.59 | 2.19 | |
| 0.45 | 10.27 | 10.21 | 0.06 | |
| 0.55 | 12.46 | 12.31 | 0.15 | |
| 0.65 | 13.97 | 13.89 | 0.08 | |
| 0.75 | 15.10 | 15.07 | 0.03 | |
| 0.85 | 15.86 | 15.96 | 0.10 | |
| 0.95 | 16.78 | 16.64 | 0.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Wei, W.; Tang, Z.; Qi, X.; Wu, Z.; Deng, H. Quantitative Characterization of Bubble Defects in Ultra-Low Expansion Quartz Glass via Ultrasonic Interaction. Materials 2025, 18, 1639. https://doi.org/10.3390/ma18071639
Zhou L, Wei W, Tang Z, Qi X, Wu Z, Deng H. Quantitative Characterization of Bubble Defects in Ultra-Low Expansion Quartz Glass via Ultrasonic Interaction. Materials. 2025; 18(7):1639. https://doi.org/10.3390/ma18071639
Chicago/Turabian StyleZhou, Lingxia, Wenqing Wei, Zisheng Tang, Xue Qi, Zhixiang Wu, and Hu Deng. 2025. "Quantitative Characterization of Bubble Defects in Ultra-Low Expansion Quartz Glass via Ultrasonic Interaction" Materials 18, no. 7: 1639. https://doi.org/10.3390/ma18071639
APA StyleZhou, L., Wei, W., Tang, Z., Qi, X., Wu, Z., & Deng, H. (2025). Quantitative Characterization of Bubble Defects in Ultra-Low Expansion Quartz Glass via Ultrasonic Interaction. Materials, 18(7), 1639. https://doi.org/10.3390/ma18071639






