The Bearing Characteristics of a Grillage Root Foundation Based on a Transparent Soil Material: Enhancing the Bearing Capacity
Abstract
1. Introduction
2. Model Experiments
2.1. Model Test Equipment
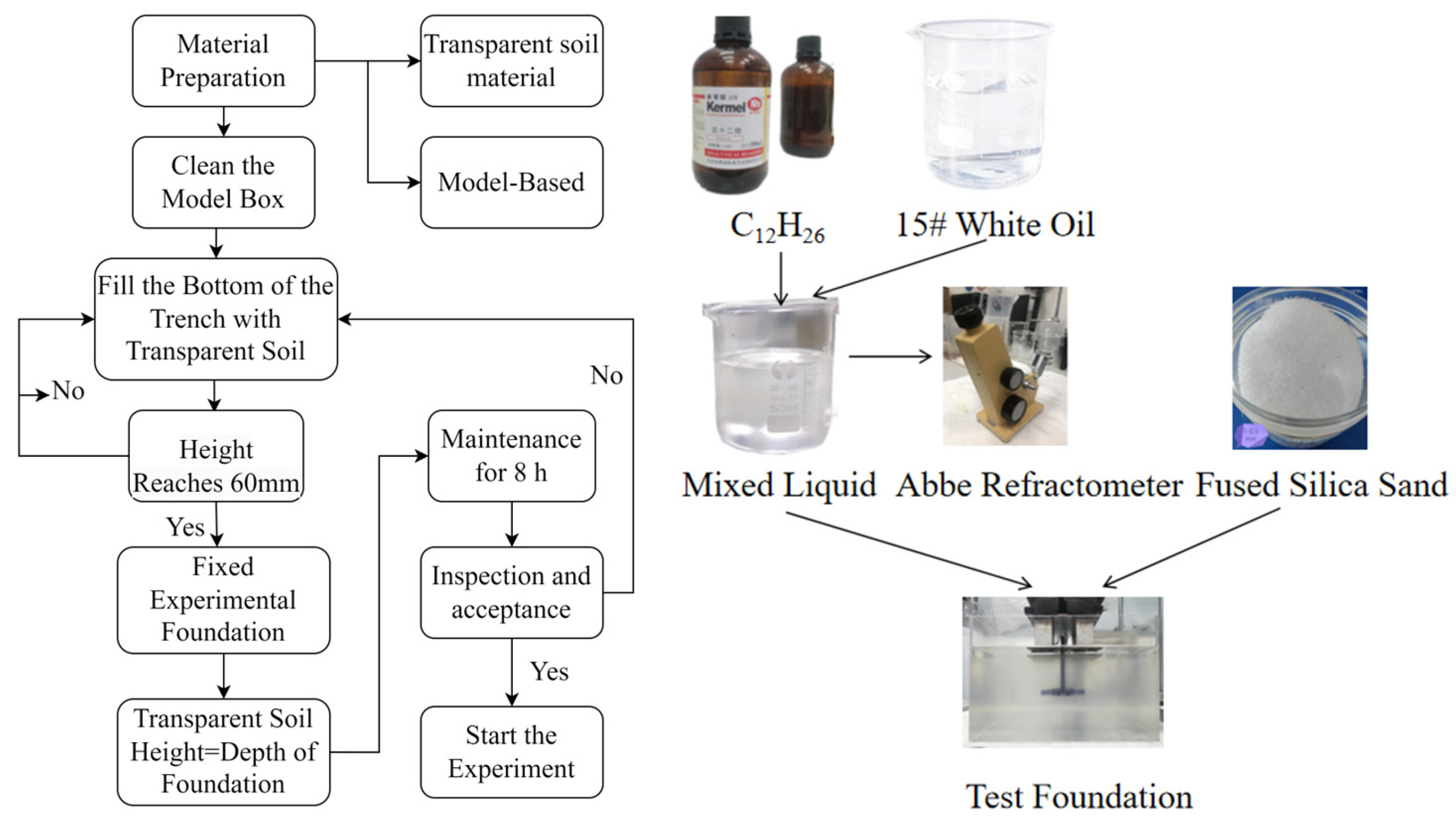
2.2. Preparation and Principle of Transparent Soil
- (1)
- The mixed liquid, primarily consisting of white oil and C12H26, must have a refractive index that matches that of the fused silica sand.
- (2)
- Pour the mixed liquid into the container, then slowly add the pre-prepared mixed solute while continuously stirring to ensure that the fused silica sand is fully immersed in the mixed liquid, thereby minimizing the formation of bubbles in the transparent soil.
- (3)
- Place the prepared transparent sand in a vacuum chamber and subject it to vacuum treatment at −0.1 MPa for 1 h. Maintain the vacuum environment to allow the transparent sand to settle within the chamber, ensuring the complete elimination of bubbles.
- (4)
- Transfer the vacuum-treated transparent sand into the experimental system and allow it to stand until the soil is fully consolidated.
2.3. Production of Model Boxes and Model Piles
2.4. Model Test Procedure
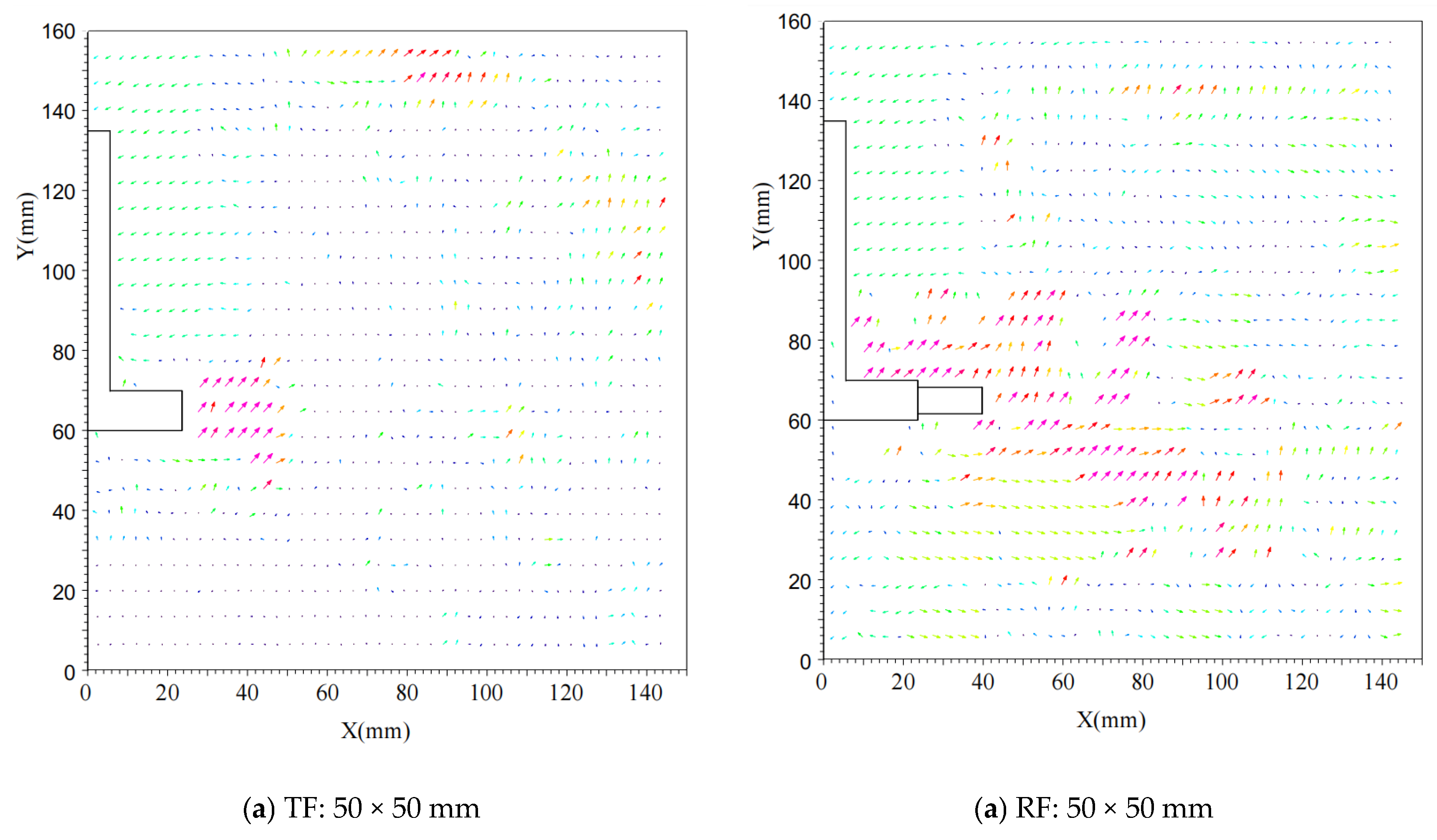
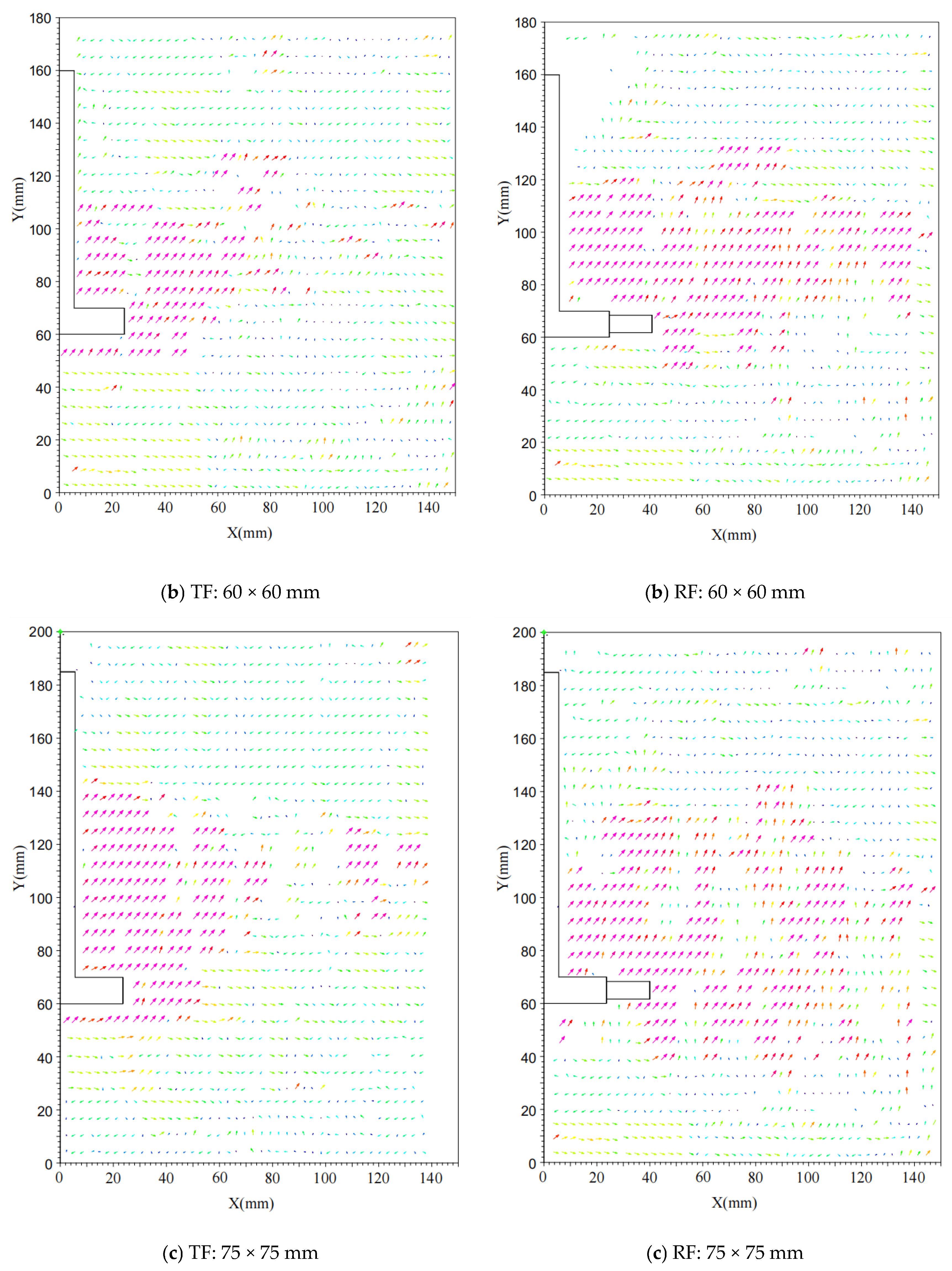
3. Analysis of Experimental Results
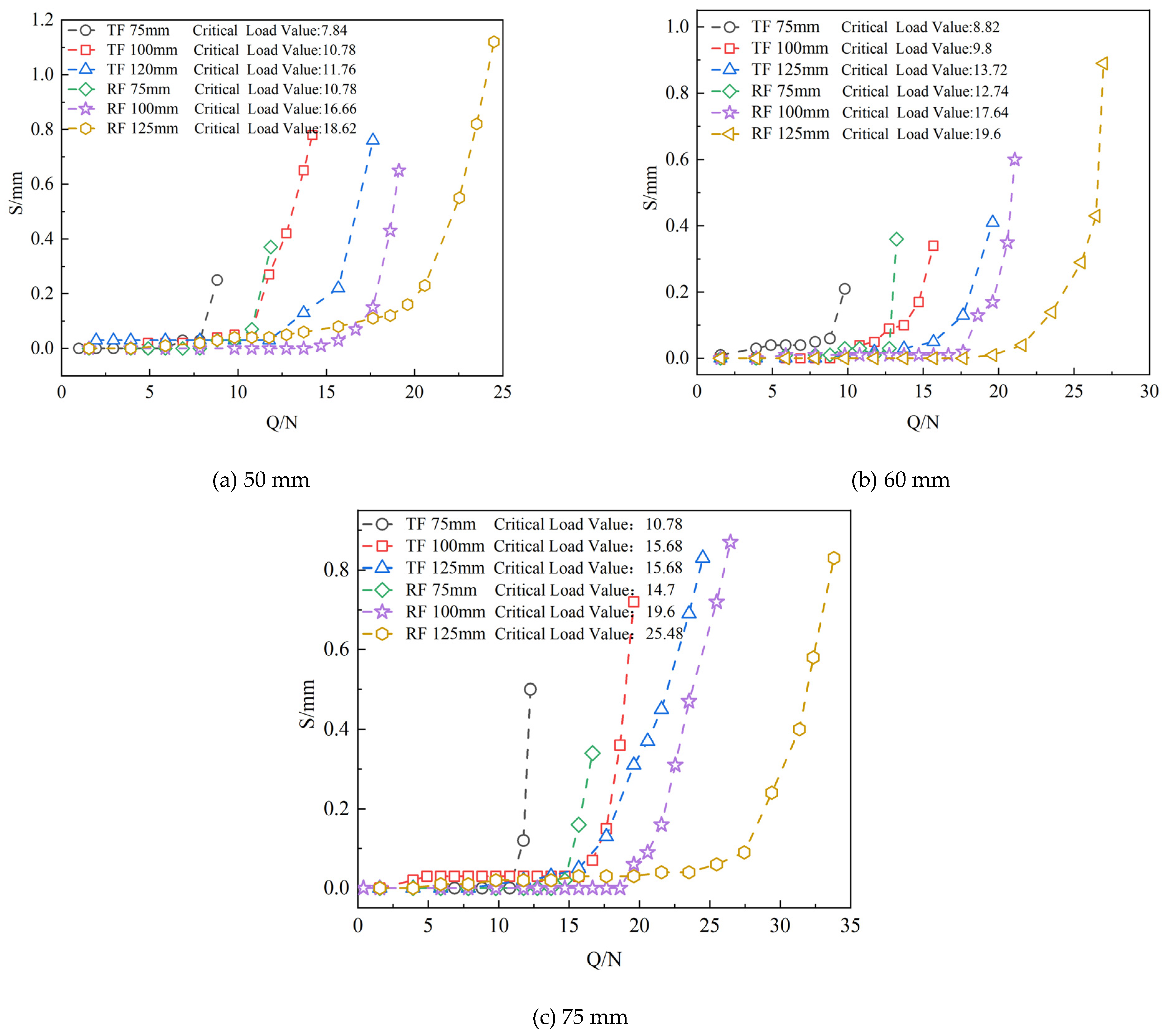
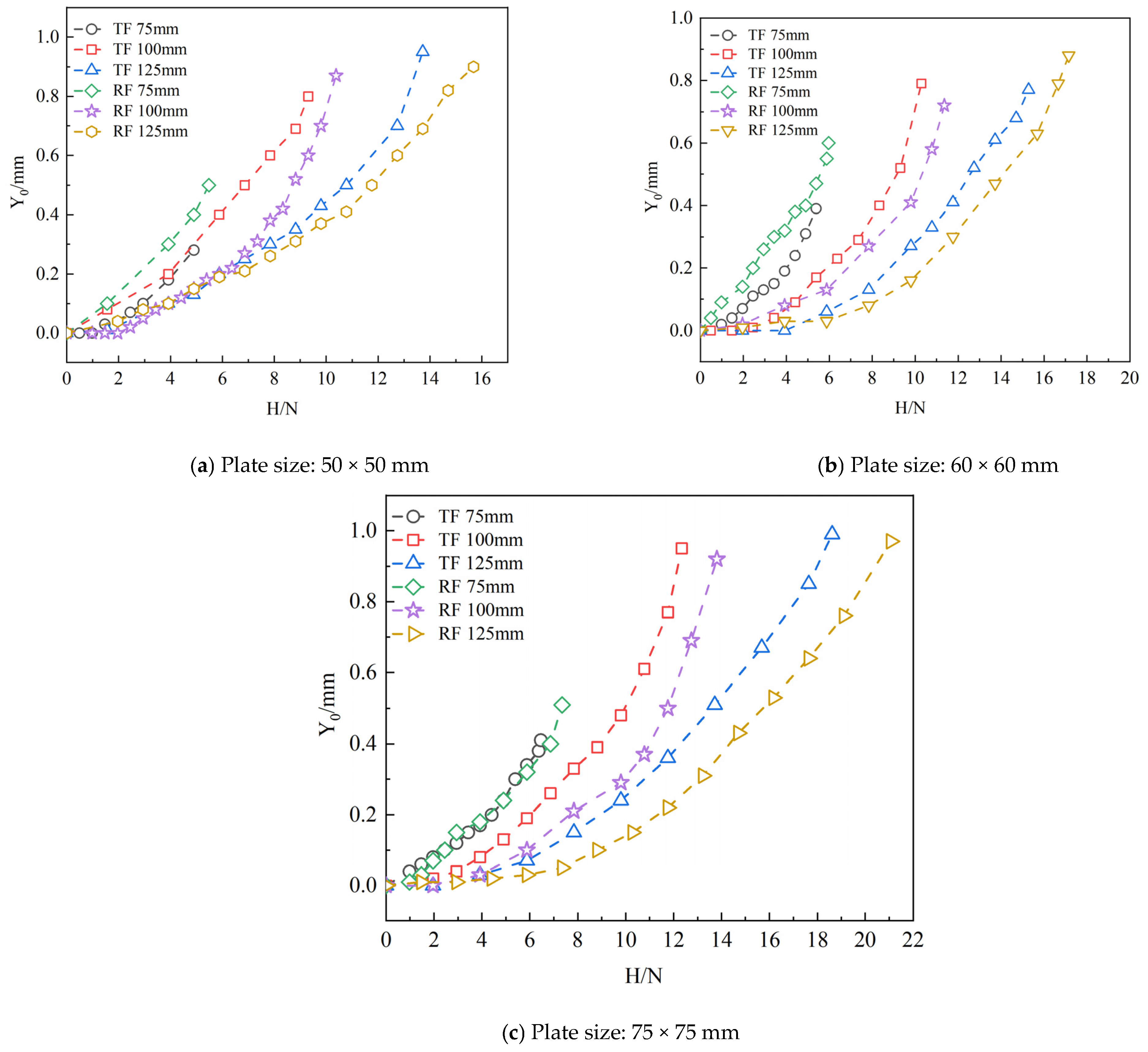
3.1. Pull-Up Test Results
3.2. Horizontal Test Results
4. Machine Learning
4.1. Elman Model
4.2. Elman Model Optimization Algorithm
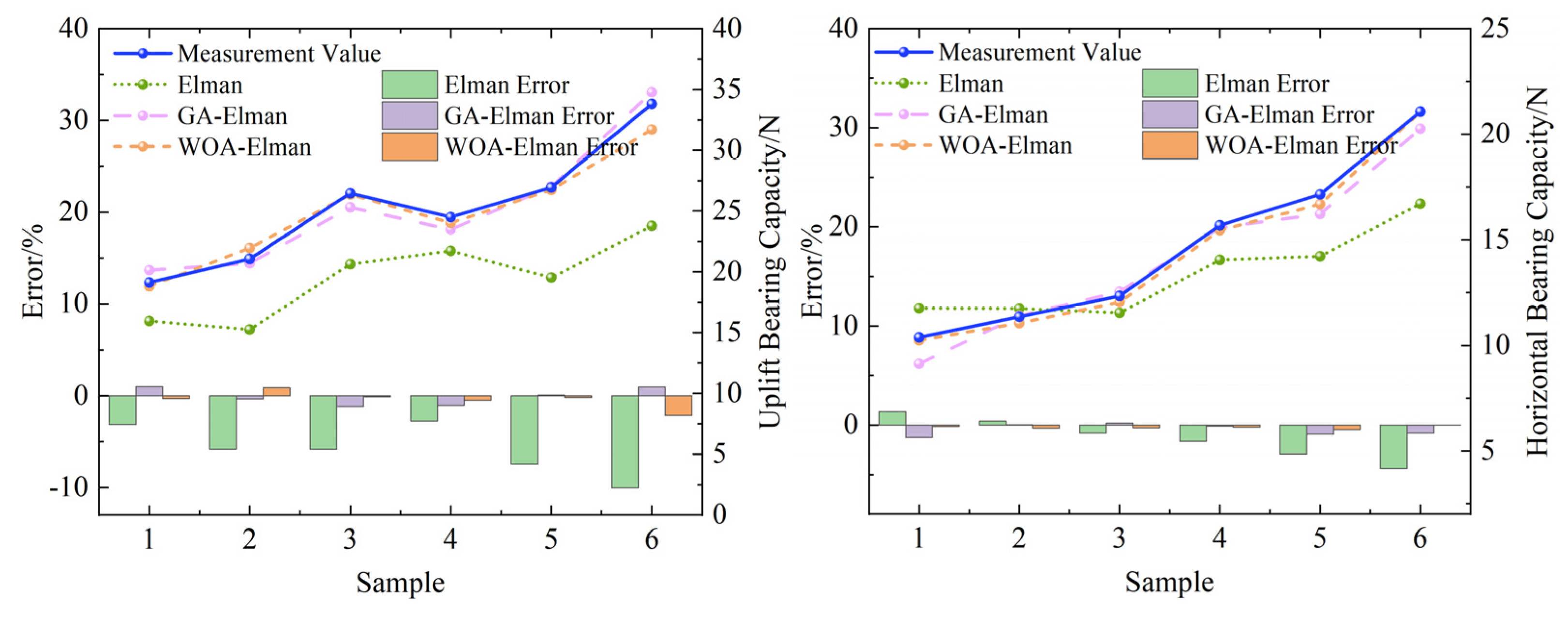
4.3. Result Analysis
5. Conclusions
- (1)
- The root structure significantly enhances the bearing capacity of the foundation, and the grillage root foundation effectively transfers and disperses loads through the interaction between the root and the soil. Experiments have shown that, compared to traditional foundations, the pull-out bearing capacity of the root foundation increases by 34.35% to 38.89%, while the horizontal bearing capacity improves by 10.76% to 14.29%.
- (2)
- The basic size and burial depth significantly impact the mechanical properties, and increasing either the size or burial depth of the bottom plate greatly enhances the foundation’s resistance to uplift and horizontal bearing capacity. For example, the ultimate uplift bearing capacity of a 75 mm base-plate foundation (33.81 N) is 38% higher than that of a 50 mm foundation (24.5 N). When the burial depth increases from 75 mm to 125 mm, the uplift bearing capacity rises by as much as 41.5%.
- (3)
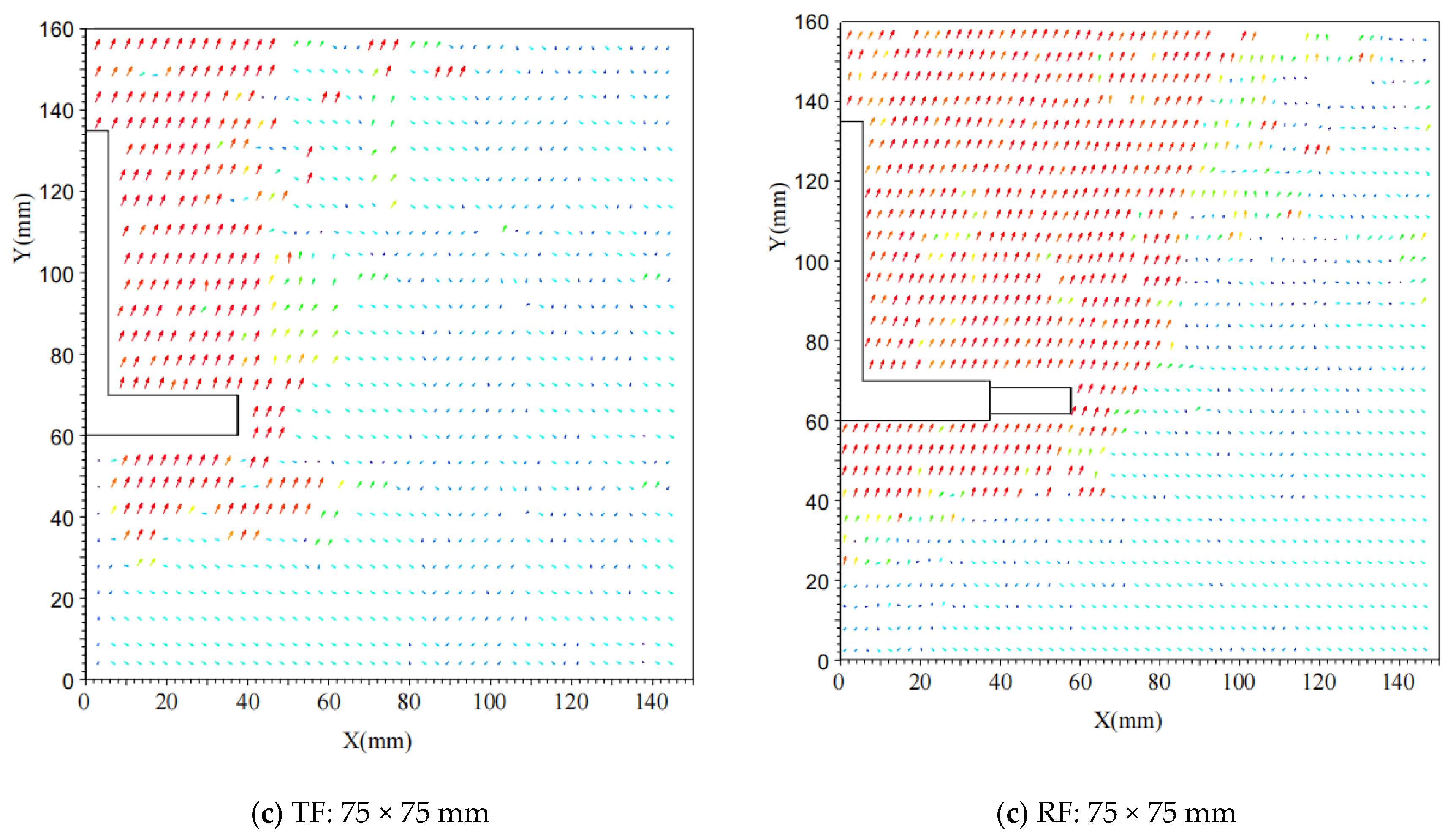
- Under external loads, the root increases the contact area and friction between the foundation and the soil, utilizing the surrounding undisturbed soil to effectively transmit and disperse external loads, thereby enhancing the foundation’s bearing capacity. Through transparent soil material model experiments and particle image velocimetry (PIV) technology, visualization of the internal displacement field of the soil was achieved, verifying the optimization effect of the root structure on the soil displacement field.
- (4)
- The Elman neural network was optimized using the genetic algorithm (GA) and the whale optimization algorithm (WOA), effectively addressing the issue of the model becoming stuck in local optima. The WOA Elman model has a prediction error controlled within 3%, which is superior to the traditional Elman model (with an error of up to 10%), providing a new method for high-precision prediction of complex soil-structure interactions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, C.; Wang, M.; Bai, Y.; Gong, Y.; Liang, Y.J.S. Stability and ultimate load bearing capacity of reinforced transmission tower members based on experiment and numerical simulation. Structures 2025, 71, 108154. [Google Scholar]
- Guo, L.; Zhang, Z.; Wang, X.; Yu, Q.; You, Y.; Yuan, C.; Xie, Y.; Gou, T. Stability analysis of transmission tower foundations in permafrost equipped with thermosiphons and vegetation cover on the Qinghai-Tibet Plateau. Int. J. Heat Mass Transf. 2018, 121, 367–376. [Google Scholar]
- Zhou, Y.; Sheng, Q.; Chen, J.; Li, N.; Fu, X.; Zhou, Y. The failure mode of transmission tower foundation on the landslide under heavy rainfall: A case study on a 500-kV transmission tower foundation on the Yanzi landslide in Badong, China. Bull. Eng. Geol. Environ. 2022, 81, 125. [Google Scholar]
- Wang, T.; Zhou, G.; Wang, J.; Yin, L. Stochastic Thermal-Mechanical Characteristics of Frozen Soil Foundation for a Transmission Line Tower in Permafrost Regions. Int. J. Geomech. 2018, 18, 06017025. [Google Scholar]
- Dong, X.; Wen, G.; Zhao, M.; Yang, Y.; Li, M.; Zhao, L. Study of the Prevention Method of ±800 kV Transmission Tower Foundation Deviation. Energies 2023, 16, 2557. [Google Scholar] [CrossRef]
- Wang, Q.; Ma, J.; Wang, M.; Ji, Y. Field test on uplift bearing characteristics of transmission tower foundation in mountainous areas of western China. Environ. Earth Sci. 2021, 80, 745. [Google Scholar]
- Zhao, H.; Kong, G.-Q.; Sui, W. Application of Transparent Soil Modeling Technique to Investigate Pile Foundation. In Transparent Soil Modelling Technique and Its Application; Springer Nature: Singapore, 2022; pp. 199–299. [Google Scholar]
- Yang, X.; Jin, G.; Huang, M.; Tang, K. Material preparation and mechanical properties of transparent soil and soft rock for model tests. Arab. J. Geosci. 2020, 13, 344. [Google Scholar]
- Trancone, G.; Policastro, G.; Spasiano, D.; Race, M.; Parrino, F.; Fratino, U.; Fabbricino, M.; Pirozzi, F. Treatment of concrete waste from construction and demolition activities: Application of organic acids from continuous dark fermentation in moving bed biofilm reactors. Chem. Eng. J. 2025, 505, 159536. [Google Scholar]
- Xiao, Y.; Sun, Y.; Yin, F.; Liu, H.; Xiang, J. Constitutive Modeling for Transparent Granular Soils. Int. J. Geomech. 2016, 17, 04016150. [Google Scholar]
- Bathurst, R. A Transparent Sand for Geotechnical Laboratory Modeling. Geotech. Test. J. 2011, 34, 590–601. [Google Scholar]
- Wang, Z.; Li, C.; Ding, X.-m. Application of transparent soil model tests to study the soil-rock interfacial sliding mechanism. J. Mt. Sci. 2019, 16, 935–943. [Google Scholar]
- Zhang, W.; Gu, X.; Zhong, W.; Ma, Z.; Ding, X. Review of transparent soil model testing technique for underground construction: Ground visualization and result digitalization. Undergr. Space 2022, 7, 702–723. [Google Scholar]
- Zhang, W.; Zhong, H.; Xiang, Y.; Wu, D.; Zeng, Z.; Zhang, Y. Visualization and digitization of model tunnel deformation via transparent soil testing technique. Undergr. Space 2022, 7, 564–576. [Google Scholar]
- Bathurst, R.J.; Ezzein, F.M. Geogrid and Soil Displacement Observations During Pullout Using a Transparent Granular Soil. Geotech. Test. J. 2015, 38, 673–685. [Google Scholar]
- Carvalho, T.; Suescun-Florez, E.; Omidvar, M.; Iskander, M. A Nonviscous Water-Based Pore Fluid for Modeling with Transparent Soils. Geotech. Test. J. 2015, 38, 805–811. [Google Scholar]
- Xiao, Y.; Yin, F.; Liu, H.; Chu, J.; Zhang, W. Model Tests on Soil Movement during the Installation of Piles in Transparent Granular Soil. Int. J. Geomech. 2016, 17, 06016027. [Google Scholar]
- Ding, X.; Wu, Q.; Huang, Y.; Zhang, Y. Model Test on the Soil Arching Effect of Pile-Supported Embankments Using Transparent Soil. Geotech. Test. J. 2021, 44, 20190347. [Google Scholar]
- Sang, Y.; Wang, Z.; Yu, S.; Zhao, H. The Loading Test on the Singe Pile with Pile Cap in Transparent Soil Model. Geotech. Test. J. 2019, 42, 20170153. [Google Scholar]
- Liu, C.; Tang, X.; Wei, H.; Wang, P.; Zhao, H. Model Tests of Jacked-Pile Penetration into Sand Using Transparent Soil and Incremental Particle Image Velocimetry. Ksce J. Civ. Eng. 2020, 24, 1128–1145. [Google Scholar]
- Wang, Z.; Fang, X.; Yao, Z.; Zhou, G.; Lin, X.; Shen, C. Investigating the influence of root layer quantity on the pullout bearing characteristics of root piles in coral sand foundations. Ocean. Eng. 2024, 293, 116616. [Google Scholar]
- Cui, M.-Z.; Ren, W.-X.; Yin, Y.-G. Numerical analysis and field load testing of a suspension bridge with a root pile anchorage. Structures 2021, 34, 1373–1382. [Google Scholar] [CrossRef]
- Luo, X.; Ren, W.; Yin, Y.-g.; Yu, Y.J.C. Geotechnics, An extended BNWF model for root piles incorporating soil–root interactions under lateral loading. Comput. Geotech. 2022, 152, 105039. [Google Scholar] [CrossRef]
- Fang, X.; Zhang, Y.; Wang, Z.; Xiong, P.; Hu, F.; Zhou, G.; Wang, C. Study on the pullout bearing characteristics of bio-inspired root piles in coral sand foundation under different root buried depths. Biogeotechnics 2024, 100145. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, X.; Yuan, J.; Zhang, J.; Wang, X. Comparative Study on the Influence of Pile Length and Diameter on Bearing Capacity and Efficiency of Root Piles, Straight-Shaft Piles and Pedestal Piles. Arab. J. Sci. Eng. 2021, 46, 10439–10456. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, G.; Tian, S.; Cai, M. Passive Soil Arching Effect in Aeolian Sand Backfills for Grillage Foundation. Sensors 2023, 23, 8098. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, J.; Huang, X.; Sun, K.; Yang, S.; Yuan, J. Mechanical Characteristics of Grillage Root Foundation for High-Voltage Tower Under Horizontal Conditions. Buildings 2024, 14, 3633. [Google Scholar] [CrossRef]
- Pham, T.A.; Nguyen, D.H.; Duong, H.-A.T. Development of Deep Learning Neural Network for Estimating Pile Bearing Capacity. In Proceedings of the CIGOS 2021, Emerging Technologies and Applications for Green Infrastructure, Singapore, 28–29 October 2021; Ha-Minh, C., Tang, A.M., Bui, T.Q., Vu, X.H., Huynh, D.V.K., Eds.; Springer Nature: Singapore, 2022; pp. 1815–1823. [Google Scholar]
- Jebur, A.A.; Atherton, W.; Al Khaddar, R.M.; Aljanabi, K.R. Performance analysis of an evolutionary LM algorithm to model the load-settlement response of steel piles embedded in sandy soil. Measurement 2019, 140, 622–635. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, Y.; Bai, L.; Guo, W.; Meng, Q. Landslide Displacement Prediction Method Based on GA-Elman Model. Appl. Sci. 2021, 11, 11030. [Google Scholar] [CrossRef]
- Jia, W.; Zhao, D.; Zheng, Y.; Hou, S. A novel optimized GA–Elman neural network algorithm. Neural Comput. Appl. 2019, 31, 449–459. [Google Scholar] [CrossRef]
- Lan, T.; Shen, S.; Yuan, H.; Jiang, Y.; Tong, H.; Ye, Y. A Rapid Prediction Method of Moisture Content for Green Tea Fixation Based on WOA-Elman. Foods 2022, 11, 2928. [Google Scholar] [CrossRef]



| Base Plate Size/mm | Bracket/mm | Depth/mm | Root Length/mm | Total Number of Roots |
|---|---|---|---|---|
| 50 × 50 | 130 | 75 100 125 | — | — |
| 50 × 50 | 130 | 15 | 8 | |
| 60 × 60 | 130 | — | — | |
| 60 × 60 | 130 | 20 | 12 | |
| 75 × 75 | 130 | — | — | |
| 75 × 75 | 130 | 20 | 12 |
| Base Plate Size/mm | Foundation Type | Depth/mm | Uplift Bearing Capacity/N | Increase Compared to TF/% |
|---|---|---|---|---|
| 50 × 50 | TF | 75 | 8.82 | — |
| 100 | 14.21 | |||
| 125 | 17.64 | |||
| RF | 75 | 11.85 | 34.35 | |
| 100 | 19.11 | 34.48 | ||
| 125 | 24.5 | 38.89 | ||
| 60 × 60 | TF | 75 | 9.8 | — |
| 100 | 15.68 | |||
| 125 | 19.6 | |||
| RF | 75 | 13.23 | 35.00 | |
| 100 | 21.07 | 34.38 | ||
| 125 | 26.95 | 37.50 | ||
| 75 × 75 | TF | 75 | 12.25 | — |
| 100 | 19.6 | |||
| 125 | 24.5 | |||
| RF | 75 | 16.66 | 36.00 | |
| 100 | 26.46 | 35.00 | ||
| 125 | 33.81 | 38.00 |
| Base Plate Size/mm | Foundation Type | Depth/mm | Horizontal Bearing Capacity/N | Increase Compared to TF/% |
|---|---|---|---|---|
| 50 × 50 | TF | 75 | 4.9 | — |
| 100 | 9.31 | |||
| 125 | 13.72 | |||
| RF | 75 | 5.48 | 11.84 | |
| 100 | 10.38 | 11.49 | ||
| 125 | 15.68 | 14.29 | ||
| 60 × 60 | TF | 75 | 5.39 | — |
| 100 | 10.29 | |||
| 125 | 15.28 | |||
| RF | 75 | 5.97 | 10.76 | |
| 100 | 11.36 | 10.40 | ||
| 125 | 17.15 | 12.24 | ||
| 75 × 75 | TF | 75 | 6.46 | — |
| 100 | 12.34 | |||
| 125 | 18.62 | |||
| RF | 75 | 7.35 | 13.78 | |
| 100 | 13.81 | 11.91 | ||
| 125 | 21.07 | 13.16 |
| Measurement Value/N | Elman Predicted Value | Elman Error | GA–Elman Predicted Value | GA– Elman Error | WOA–Elman Predicted Value | WOA– Elman Error | ||
|---|---|---|---|---|---|---|---|---|
| 1 | Uplift | 19.11 | 15.9561 | −3.1539 | 20.1364 | 1.0264 | 18.8093 | −0.3007 |
| 2 | 21.07 | 15.2503 | −5.8197 | 20.7206 | −0.3494 | 21.9598 | 0.8898 | |
| 3 | 26.46 | 20.6359 | −5.8241 | 25.3014 | −1.1586 | 26.3609 | −0.0991 | |
| 4 | 24.5 | 21.7289 | −2.7711 | 23.4788 | −1.0212 | 24.0187 | −0.4813 | |
| 5 | 26.95 | 19.5145 | −7.4355 | 27.0102 | 0.0602 | 26.7418 | −0.2082 | |
| 6 | 33.81 | 23.7747 | −10.0353 | 34.7861 | 0.9761 | 31.6929 | −2.1171 | |
| 1 | Horizontal | 10.38 | 11.7576 | 1.3776 | 9.124 | −1.256 | 10.2445 | −0.1355 |
| 2 | 11.36 | 11.7474 | 0.3874 | 11.3977 | 0.0377 | 11.0531 | −0.3069 | |
| 3 | 12.34 | 11.5387 | −0.8013 | 12.5326 | 0.1926 | 12.0495 | −0.2905 | |
| 4 | 15.68 | 14.0527 | −1.6273 | 15.5703 | −0.1097 | 15.4478 | −0.2322 | |
| 5 | 17.15 | 14.2167 | −2.9333 | 16.2236 | −0.9264 | 16.6813 | −0.4687 | |
| 6 | 21.07 | 16.7017 | −4.3683 | 20.2525 | −0.8175 | 21.0691 | −0.0009 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.; Wang, J.; Huang, X.; Ren, Z.; Wang, H. The Bearing Characteristics of a Grillage Root Foundation Based on a Transparent Soil Material: Enhancing the Bearing Capacity. Materials 2025, 18, 1470. https://doi.org/10.3390/ma18071470
Ma Z, Wang J, Huang X, Ren Z, Wang H. The Bearing Characteristics of a Grillage Root Foundation Based on a Transparent Soil Material: Enhancing the Bearing Capacity. Materials. 2025; 18(7):1470. https://doi.org/10.3390/ma18071470
Chicago/Turabian StyleMa, Zehui, Junjie Wang, Xuefeng Huang, Zhifeng Ren, and Hao Wang. 2025. "The Bearing Characteristics of a Grillage Root Foundation Based on a Transparent Soil Material: Enhancing the Bearing Capacity" Materials 18, no. 7: 1470. https://doi.org/10.3390/ma18071470
APA StyleMa, Z., Wang, J., Huang, X., Ren, Z., & Wang, H. (2025). The Bearing Characteristics of a Grillage Root Foundation Based on a Transparent Soil Material: Enhancing the Bearing Capacity. Materials, 18(7), 1470. https://doi.org/10.3390/ma18071470





