On the Mechanical Performance of an L-PBF 316l Part Using the Performance-Line Instrumented Indentation Test (PL-IIT)
Abstract
1. Introduction
2. Materials and Methods
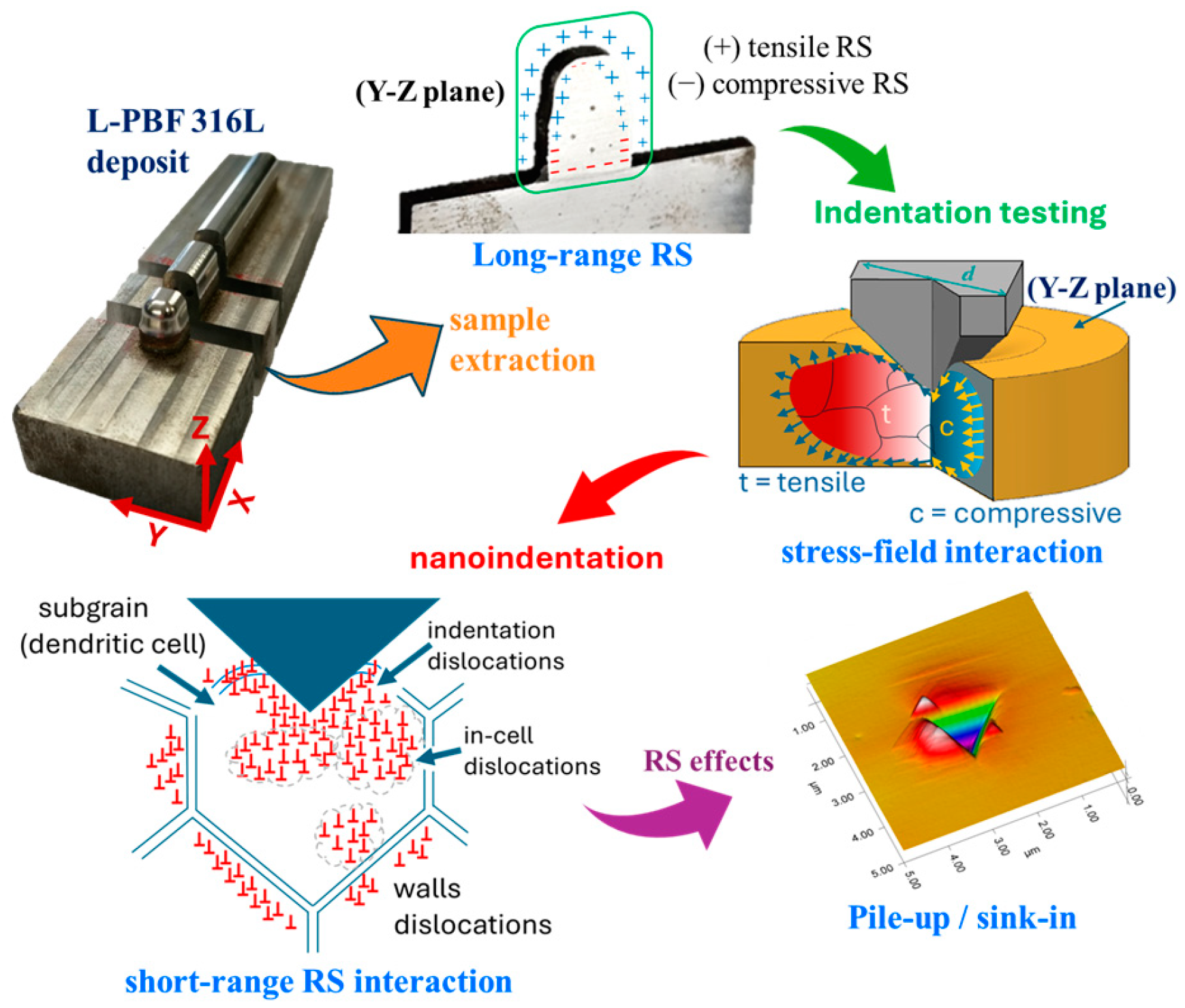
2.1. The L-PBF of 316L Build
2.2. Mechanical Performance of AM Products
2.3. Microstructure
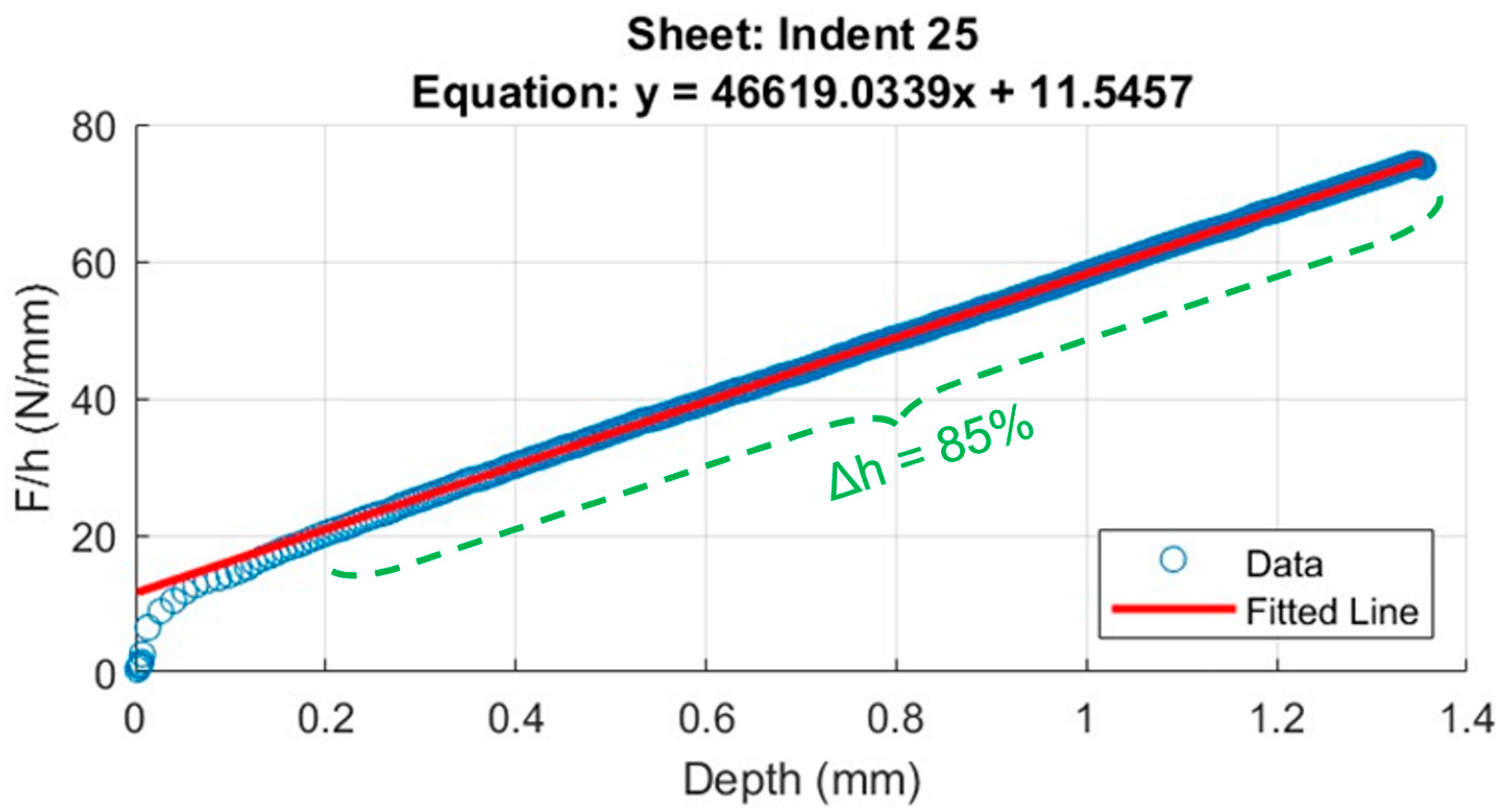
2.4. Loading Stiffness Rate (LSR)
2.5. Performance Line Nanoindentation (PL-nIIT)
2.6. Indentation Test Conditions
3. Results
3.1. Microstructure of the Deposit
3.2. Crystallographic Texture
3.3. Indentation Properties
4. Discussion
4.1. The 5PL-nIIT Scheme in the AM Components
4.2. Microstructure/Anisotropy in L-PBF 316L
4.3. RS During IIT
4.4. PZ with Critical Mechanical Performances: E1(H2) and D
4.5. PZ with an Outstanding Mechanical Performance: Deposit Root
4.6. PZ with an Indefinite Mechanical Response: CZ
4.7. PZ with an Outstanding Mechanical Response: S1
4.8. Gradient of Indentation Properties
4.9. The Role of LSR (a85) as a Mechanical Performance
4.10. Ranking of the Mechanical Performance of an L-PBF 316L Deposit
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hamidi, M.; Leuven, N.K.; Nasab, M.H.; Loge, R.; Casati, R. A Study on the Surface Features of the SLM Processed Parts and Their Journey to Become Bulk Defects. In Proceedings of the Euro PM 2019 Congress & Exhibition, European Powder Metallurgy Association (EPMA), Maastricht, The Netherlands, 13–16 October 2019; Available online: https://www.researchgate.net/publication/336084911 (accessed on 19 October 2023).
- Ramirez-Cedillo, E.; Uddin, M.J.; Sandoval-Robles, J.A.; Mirshams, R.A.; Ruiz-Huerta, L.; Rodriguez, C.A.; Siller, H.R. Process planning of L-PBF of AISI 316L for improving surface quality and relating part integrity with microstructural characteristics. Surf. Coat. Technol. 2020, 396, 125956. [Google Scholar] [CrossRef]
- Wang, X.; Muñiz-Lerma, J.A.; Sanchez-Mata, O.; Atabay, S.E.; Shandiz, M.A.; Brochu, M. Single-crystalline-like stainless steel 316L with different geometries fabricated by laser powder bed fusion. Prog. Addit. Manuf. 2020, 5, 41–49. [Google Scholar] [CrossRef]
- Im, Y.D.; Kim, K.H.; Jung, K.H.; Lee, Y.K.; Song, K.H. Anisotropic Mechanical Behavior of Additive Manufactured AISI 316L Steel. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2019, 50, 2014–2021. [Google Scholar] [CrossRef]
- Charmi, A.; Falkenberg, R.; Ávila, L.; Mohr, G.; Sommer, K.; Ulbricht, A.; Sprengel, M.; Neumann, R.S.; Skrotzki, B.; Evans, A. Mechanical anisotropy of additively manufactured stainless steel 316L: An experimental and numerical study. Mater. Sci. Eng. A 2021, 799, 140154. [Google Scholar] [CrossRef]
- Ni, X.; Kong, D.; Wen, Y.; Zhang, L.; Wu, W.; He, B.; Lu, L.; Zhu, D. Anisotropy in mechanical properties and corrosion resistance of 316L stainless steel fabricated by selective laser melting. Int. J. Miner. Metall. Mater. 2019, 26, 319–328. [Google Scholar] [CrossRef]
- Kong, D.; Ni, X.; Dong, C.; Zhang, L.; Man, C.; Cheng, X.; Li, X. Anisotropy in the microstructure and mechanical property for the bulk and porous 316L stainless steel fabricated via selective laser melting. Mater. Lett. 2019, 235, 1–5. [Google Scholar] [CrossRef]
- Maizza, G.; Hafeez, F.; Varone, A.; Montanari, R. Nanoscale and Tensile-Like Properties by an Instrumented Indentation Test on PBF-LB SS 316L Steel. Materials 2024, 17, 255. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Tan, X.; Tor, S.B.; Chua, C.K. Simultaneously enhanced strength and ductility for 3D-printed stainless steel 316L by selective laser melting. NPG Asia Mater. 2018, 104, 127–136. [Google Scholar] [CrossRef]
- Suwas, S.; Ray, R.K. Texture and Properties; Springer: London, UK, 2014; pp. 207–223. [Google Scholar] [CrossRef]
- Sun, Z.; Tsai, S.P.; Konijnenberg, P.; Wang, J.Y.; Zaefferer, S. A large-volume 3D EBSD study on additively manufactured 316L stainless steel. Scr. Mater. 2024, 238, 115723. [Google Scholar] [CrossRef]
- Uddin, M.J.; Ramirez-Cedillo, E.; Mirshams, R.A.; Siller, H.R. Nanoindentation and electron backscatter diffraction mapping in laser powder bed fusion of stainless steel 316L. Mater. Charact. 2021, 174, 111047. [Google Scholar] [CrossRef]
- Kurdi, A.; Tabbakh, T.; Basak, A.K.; Au, A.K.B. Microstructural and Nanoindentation Investigation on the Laser Powder Bed Fusion Stainless Steel 316L. Materials 2023, 16, 5933. [Google Scholar] [CrossRef] [PubMed]
- Andreau, O.; Koutiri, I.; Peyre, P.; Penot, J.-D.; Saintier, N.; Pessard, E.; De Terris, T.; Dupuy, C.; Baudin, T. Texture control of 316L parts by modulation of the melt pool morphology in selective laser melting. J. Mater. Process. Technol. 2019, 264, 21–31. [Google Scholar] [CrossRef]
- Terner, M.; Lee, J.; Marchese, G.; Biamino, S.; Hong, H.U. Electron Backscattered Diffraction to Estimate Residual Stress Levels of a Superalloy Produced by Laser Powder Bed Fusion and Subsequent Heat Treatments. Materials 2020, 13, 4643. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, J.L.; Li, X. An overview of residual stresses in metal powder bed fusion. Addit. Manuf. 2019, 27, 131–149. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Almasri, A.H. Variable Material Length Scale Associated with Nanoindentation Experiments. J. Eng. Mech. 2009, 135, 139–148. [Google Scholar] [CrossRef]
- Birnbaum, A.J.; Ryou, H.; Steuben, J.C.; Iliopoulos, A.P.; Wahl, K.J.; Michopoulos, J.G. Nested size effects in the nanoindentation response of additively manufactured 316L stainless steel. Mater. Lett. 2020, 280, 128570. [Google Scholar] [CrossRef]
- Pöhl, F.; Hardes, C.; Scholz, F.; Frenzel, J. Orientation-Dependent Deformation Behavior of 316L Steel Manufactured by Laser Metal Deposition and Casting under Local Scratch and Indentation Load. Materials 2020, 13, 1765. [Google Scholar] [CrossRef]
- Čech, J.; Haušild, P.; Kovářík, O.; Materna, A. Examination of Berkovich indenter tip bluntness. Mater. Des. 2016, 109, 347–353. [Google Scholar] [CrossRef]
- Fröhlich, F.; Grau, P.; Grellmann, W. Performance and analysis of recording microhardness tests. Phys. Status Solidi 1977, 42, 79–89. [Google Scholar] [CrossRef]
- Attaf, M.T. Connection between the loading curve models in elastoplastic indentation. Mater. Lett. 2004, 58, 3491–3498. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- ISO 14577-1:2015; Metallic Material—Instrumented Indentation Test for Hardness and Materials Parameters—Part 1: Test Method. International Organization for Standardization: Geneva, Switzerland, 2015. Available online: https://www.iso.org/standard/56626.html (accessed on 30 June 2023).
- ISO 4577-2:2015; Metallic Materials—Instrumented Indentation Test for Hardness and Materials Parameters—Part 2: Verification and Calibration of Testing Machines. International Organization for Standardization: Geneva, Switzerland, 2015. Available online: https://www.iso.org/standard/56628.html (accessed on 28 August 2023).
- Sabzi, H.E.; Rivera-Díaz-del-Castillo, P.E.J. Composition and process parameter dependence of yield strength in laser powder bed fusion alloys. Mater. Des. 2020, 195, 109024. [Google Scholar] [CrossRef]
- Kick, F. Das Gesetz der Proportionalen Widerstände und Seine Anwendungen: Nebst Versuchen über das Verhalten Verschiedener Materialien Bei Gleichen; A. Felix: New Orleans, LA, USA, 1885. [Google Scholar]
- Suresh, S.; Nieh, T.G.; Choi, B.W. Nano-indentation of copper thin films on silicon substrates. Scr. Mater. 1999, 41, 951–957. [Google Scholar] [CrossRef]
- Bernhardt, E.O. Über die Mikrohärte der Feststoffe im Grenzbereich des Kick’schen Ähnlichkeitssatzes. Int. J. Mater. Res. 1941, 33, 135–144. [Google Scholar] [CrossRef]
- Marciniak, Z.; Duncan, J.L.; Hu, J. Mechanics of Sheet Metal Forming; Butterworth-Heinemann: Oxford, UK, 2002. [Google Scholar]
- Wheeler, J.M.; Michler, J. Elevated temperature, nano-mechanical testing in situ in the scanning electron microscope. Rev. Sci. Instrum. 2013, 84, 045103. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. Springer Top. Signal Process. 2009, 2, 1–4. [Google Scholar] [CrossRef]
- Pitrmuc, Z.; Šimota, J.; Beránek, L.; Mikeš, P.; Andronov, V.; Sommer, J.; Holešovský, F. Mechanical and Microstructural Anisotropy of Laser Powder Bed Fusion 316L Stainless Steel. Materials 2022, 15, 551. [Google Scholar] [CrossRef]
- Shamsujjoha, M.; Agnew, S.R.; Fitz-Gerald, J.M.; Moore, W.R.; Newman, T.A. High Strength and Ductility of Additively Manufactured 316L Stainless Steel Explained. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2018, 49, 3011–3027. [Google Scholar] [CrossRef]
- Birnbaum, A.J.; Steuben, J.C.; Barrick, E.J.; Iliopoulos, A.P.; Michopoulos, J.G. Intrinsic strain aging, Σ3 boundaries, and origins of cellular substructure in additively manufactured 316L. Addit. Manuf. 2019, 29, 100784. [Google Scholar] [CrossRef]
- Bertoli, U.S.; MacDonald, B.E.; Schoenung, J.M. Stability of cellular microstructure in laser powder bed fusion of 316L stainless steel. Mater. Sci. Eng. A 2019, 739, 109–117. [Google Scholar] [CrossRef]
- Barkia, B.; Aubry, P.; Haghi-Ashtiani, P.; Auger, T.; Gosmain, L.; Schuster, F.; Maskrot, H. On the origin of the high tensile strength and ductility of additively manufactured 316L stainless steel: Multiscale investigation. J. Mater. Sci. Technol. 2020, 41, 209–218. [Google Scholar] [CrossRef]
- Li, C.; Liu, Z.Y.; Fang, X.Y.; Guo, Y.B. Residual Stress in Metal Additive Manufacturing. Procedia CIRP 2018, 71, 348–353. [Google Scholar] [CrossRef]
- Casati, R.; Lemke, J.; Vedani, M. Microstructure and Fracture Behavior of 316L Austenitic Stainless Steel Produced by Selective Laser Melting. J. Mater. Sci. Technol. 2016, 32, 738–744. [Google Scholar] [CrossRef]
- Kok, Y.; Tan, X.; Wang, P.; Nai, M.; Loh, N.; Liu, E.; Tor, S. Anisotropy and heterogeneity of microstructure and mechanical properties in metal additive manufacturing: A critical review. Mater. Des. 2018, 139, 565–586. [Google Scholar] [CrossRef]
- Hitzler, L.; Hirsch, J.; Heine, B.; Merkel, M.; Hall, W.; Öchsner, A. On the Anisotropic Mechanical Properties of Selective Laser-Melted Stainless Steel. Materials 2017, 10, 1136. [Google Scholar] [CrossRef]
- Zeng, Q.; Gan, K.; Wang, Y. Effect of Heat Treatment on Microstructures and Mechanical Behaviors of 316L Stainless Steels Synthesized by Selective Laser Melting. J. Mater. Eng. Perform. 2021, 30, 409–422. [Google Scholar] [CrossRef]
- Mukherjee, T.; Zhang, W.; DebRoy, T. An improved prediction of residual stresses and distortion in additive manufacturing. Comput. Mater. Sci. 2017, 126, 360–372. [Google Scholar] [CrossRef]
- Jang, J. Estimation of residual stress by instrumented indentation: A review. J. Ceram. Process. Res. 2009, 10, 391–400. [Google Scholar]
- Ulbricht, A.; Altenburg, S.J.; Sprengel, M.; Sommer, K.; Mohr, G.; Fritsch, T.; Mishurova, T.; Serrano-Munoz, I.; Evans, A.; Hofmann, M.; et al. Separation of the Formation Mechanisms of Residual Stresses in LPBF 316L. Metals 2020, 10, 1234. [Google Scholar] [CrossRef]
- Lavery, N.P.; Cherry, J.; Mehmood, S.; Davies, H.; Girling, B.; Sackett, E.; Brown, S.; Sienz, J. Effects of hot isostatic pressing on the elastic modulus and tensile properties of 316L parts made by powder bed laser fusion. Mater. Sci. Eng. A 2017, 693, 186–213. [Google Scholar] [CrossRef]
- Motibane, L.P.; Tshabalala, L.C.; Mathe, N.R.; Hoosain, S.; Knutsen, R.D. Effect of powder bed preheating on distortion and mechanical properties in high speed selective laser melting. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 655, p. 012026. [Google Scholar] [CrossRef]
- Wang, L.; Felicelli, S.; Gooroochurn, Y.; Wang, P.T.; Horstemeyer, M.F. Optimization of the LENS® process for steady molten pool size. Mater. Sci. Eng. A 2008, 474, 148–156. [Google Scholar] [CrossRef]
- Qiu, C.; Al Kindi, M.; Aladawi, A.S.; Al Hatmi, I. A comprehensive study on microstructure and tensile behaviour of a selectively laser melted stainless steel. Sci. Rep. 2018, 81, 7785. [Google Scholar] [CrossRef]
- Kurzynowski, T.; Gruber, K.; Stopyra, W.; Kuźnicka, B.; Chlebus, E. Correlation between process parameters, microstructure and properties of 316 L stainless steel processed by selective laser melting. Mater. Sci. Eng. A 2018, 718, 64–73. [Google Scholar] [CrossRef]
- Wang, X.; Muñiz-Lerma, J.A.; Shandiz, M.A.; Sanchez-Mata, O.; Brochu, M. Crystallographic-orientation-dependent tensile behaviours of stainless steel 316L fabricated by laser powder bed fusion. Mater. Sci. Eng. A 2019, 766, 138395. [Google Scholar] [CrossRef]
- Raghavan, N.; Simunovic, S.; Dehoff, R.; Plotkowski, A.; Turner, J.; Kirka, M.; Babu, S. Localized melt-scan strategy for site specific control of grain size and primary dendrite arm spacing in electron beam additive manufacturing. Acta Mater. 2017, 140, 375–387. [Google Scholar] [CrossRef]
- Evangelou, A.; Stylianou, R.; Loizou, A.; Kim, D.; Liang, A.; Reed, P.; Constantinides, G.; Kyratsi, T. Effects of process parameters and scan strategy on the microstructure and density of stainless steel 316 L produced via laser powder bed fusion. J. Alloys Metall. Syst. 2023, 3, 100027. [Google Scholar] [CrossRef]
- Song, Y.; Sun, Q.; Guo, K.; Wang, X.; Liu, J.; Sun, J. Effect of scanning strategies on the microstructure and mechanical behavior of 316L stainless steel fabricated by selective laser melting. Mater. Sci. Eng. A 2020, 793, 139879. [Google Scholar] [CrossRef]
- Hall, E.O. The Deformation and Ageing of Mild Steel: III Discussion of Results. Proc. Phys. Soc. Sect. B 1951, 64, 747. [Google Scholar] [CrossRef]
- Petch, N. The Cleavage Strength of Polycrystals. 1953. Available online: https://cir.nii.ac.jp/crid/1573387450368072704 (accessed on 23 January 2025).
- Mukherjee, M. Effect of build geometry and orientation on microstructure and properties of additively manufactured 316L stainless steel by laser metal deposition. Materialia 2019, 7, 100359. [Google Scholar] [CrossRef]
- Bertsch, K.M.; de Bellefon, G.M.; Kuehl, B.; Thoma, D.J. Origin of dislocation structures in an additively manufactured austenitic stainless steel 316L. Acta Mater. 2020, 199, 19–33. [Google Scholar] [CrossRef]
- Jiang, W.C.; Gong, J.M.; Tu, S.D.; Chen, H. Three-dimensional numerical simulation of brazed residual stress and its high-temperature redistribution for stainless steel plate-fin structure. Mater. Sci. Eng. A 2009, 499, 293–298. [Google Scholar] [CrossRef]
- Song, Y.; Yang, J.; Song, K.; Zhou, Y.; Huang, T.; Zhang, C.; Li, T.; Fan, W. Effect of tensile stress annealing on residual stress and strength of C19400 alloy. J. Mater. Res. Technol. 2023, 25, 786–798. [Google Scholar] [CrossRef]
- Zhao, C.; Bai, Y.; Zhang, Y.; Wang, X.; Xue, J.M.; Wang, H. Influence of scanning strategy and building direction on microstructure and corrosion behaviour of selective laser melted 316L stainless steel. Mater. Des. 2021, 209, 109999. [Google Scholar] [CrossRef]
- Khodabakhshi, F.; Farshidianfar, M.; Gerlich, A.; Khajepour, A.; Trembošová, V.N.; Mohammadi, M.; Shakil, S.; Haghshenas, M. Nanoindentation plasticity and loading rate sensitivity of laser additive manufactured functionally graded 316L and 410L stainless steels. Mater. Sci. Eng. A 2023, 862, 144437. [Google Scholar] [CrossRef]
- Sames, W.J.; List, F.A.; Pannala, S.; Dehoff, R.R.; Babu, S.S. The metallurgy and processing science of metal additive manufacturing. Int. Mater. Rev. 2016, 61, 315–360. [Google Scholar] [CrossRef]
- Zhang, Y.; Allahkarami, M.; Hanan, J.C. Measuring residual stress in ceramic zirconia–porcelain dental crowns by nanoindentation. J. Mech. Behav. Biomed. Mater. 2012, 6, 120–127. [Google Scholar] [CrossRef] [PubMed]
- Serda, M. Evaluation of Stacking Fault Energy in Anisotropic FCC Metal by Nanoindentation. Master’s Thesis, College of Engineering/Engineering Practice School, Seoul, Republic of Korea, 2016. Available online: https://s-space.snu.ac.kr/handle/10371/123370 (accessed on 24 July 2024).
- Mercelis, P.; Kruth, J.P. Residual stresses in selective laser sintering and selective laser melting. Rapid Prototyp. J. 2006, 12, 254–265. [Google Scholar] [CrossRef]
- Marattukalam, J.J.; Karlsson, D.; Pacheco, V.; Beran, P.; Wiklund, U.; Jansson, U.; Hjörvarsson, B.; Sahlberg, M. The effect of laser scanning strategies on texture, mechanical properties, and site-specific grain orientation in selective laser melted 316L SS. Mater. Des. 2020, 193, 108852. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Lu, Y.; Wu, S.; Gan, Y.; Huang, T.; Yang, C.; Junjie, L.; Lin, J. Study on the microstructure, mechanical property and residual stress of SLM Inconel-718 alloy manufactured by differing island scanning strategy. Opt. Laser Technol. 2015, 75, 197–206. [Google Scholar] [CrossRef]
- Fedorenko, A.; Fedulov, B.; Kuzminova, Y.; Evlashin, S.; Staroverov, O.; Tretyakov, M.; Lomakin, E.; Akhatov, I. Anisotropy of Mechanical Properties and Residual Stress in Additively Manufactured 316L Specimens. Materials 2021, 14, 7176. [Google Scholar] [CrossRef] [PubMed]
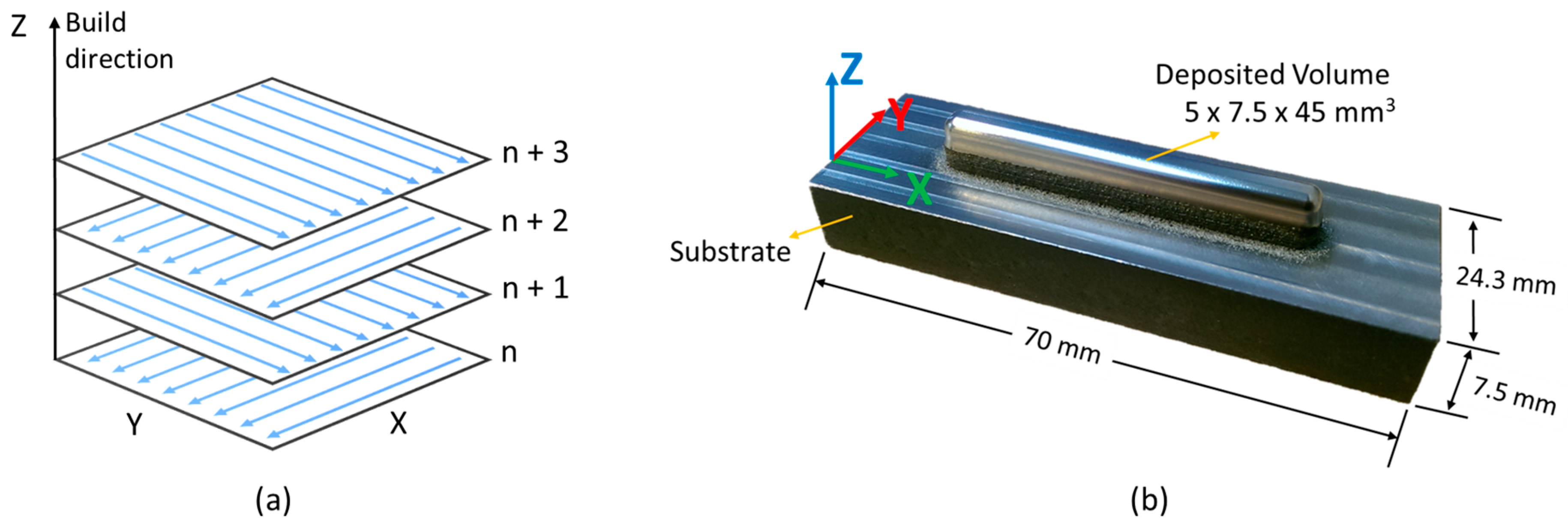
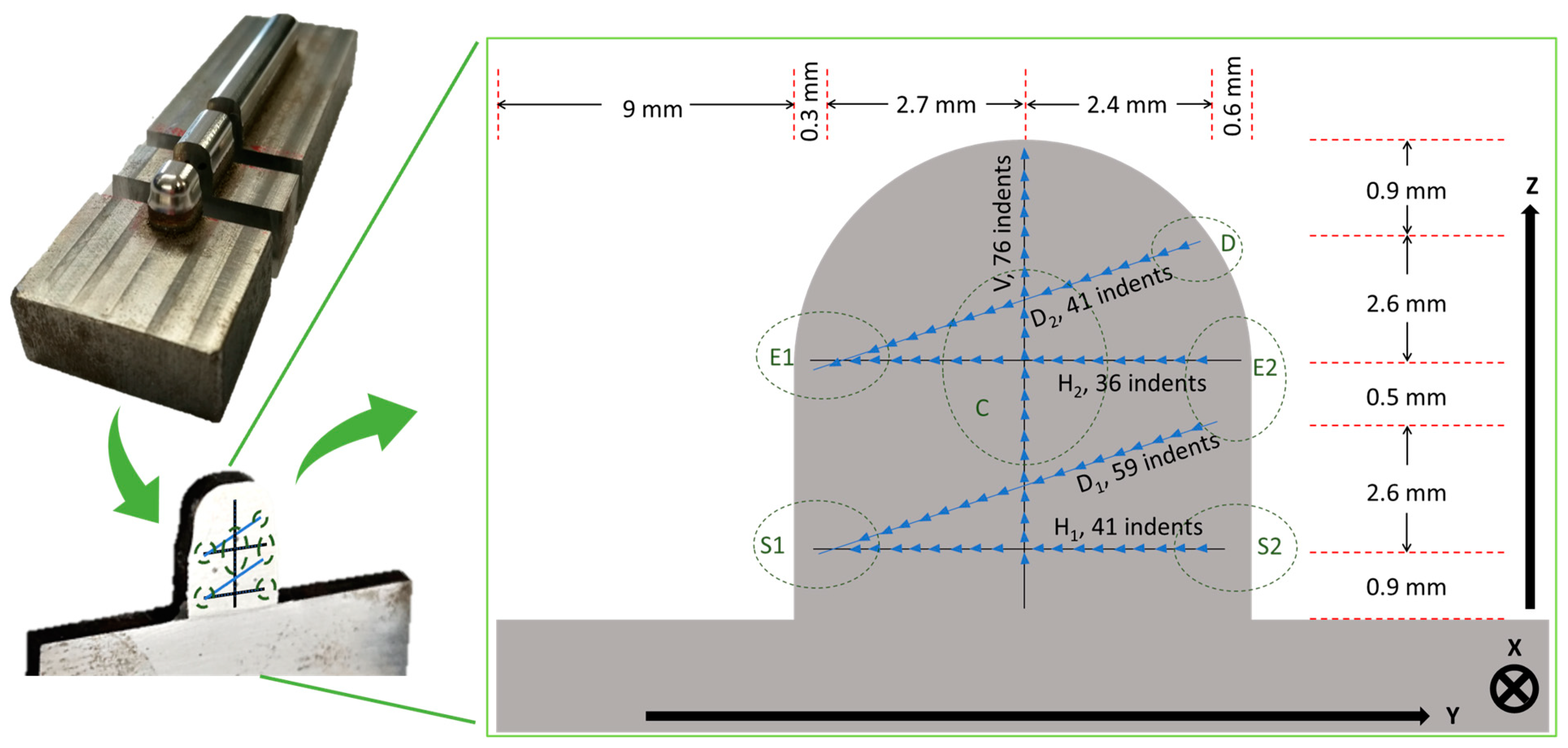

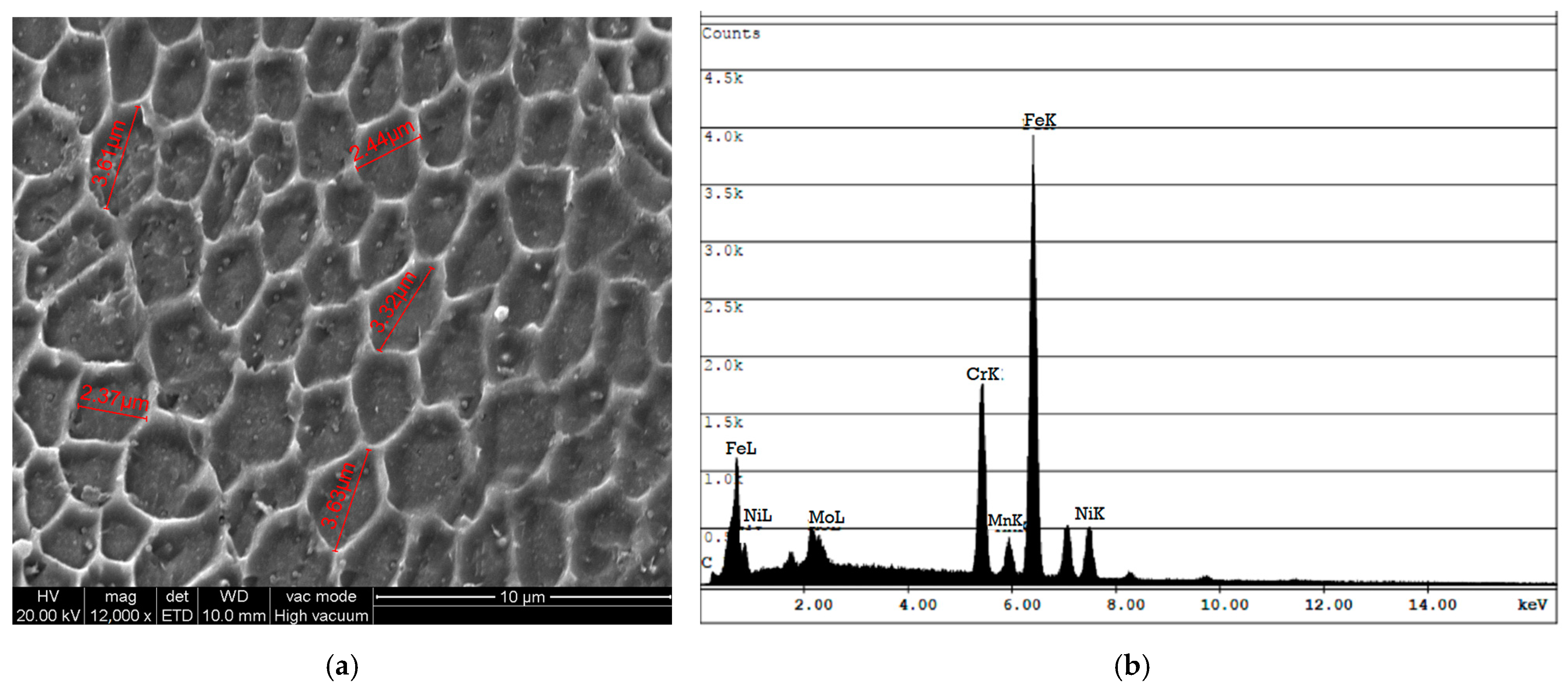
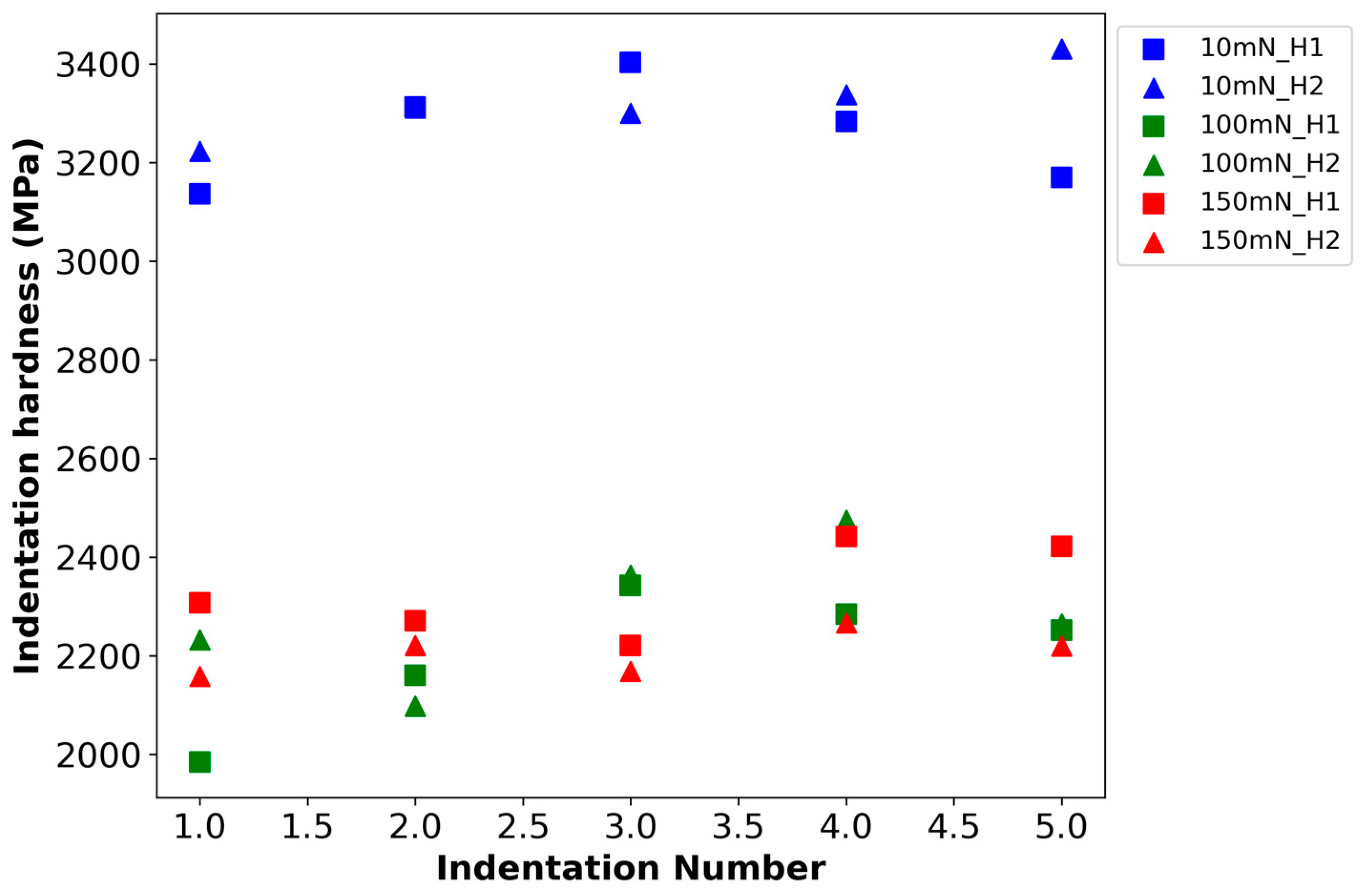
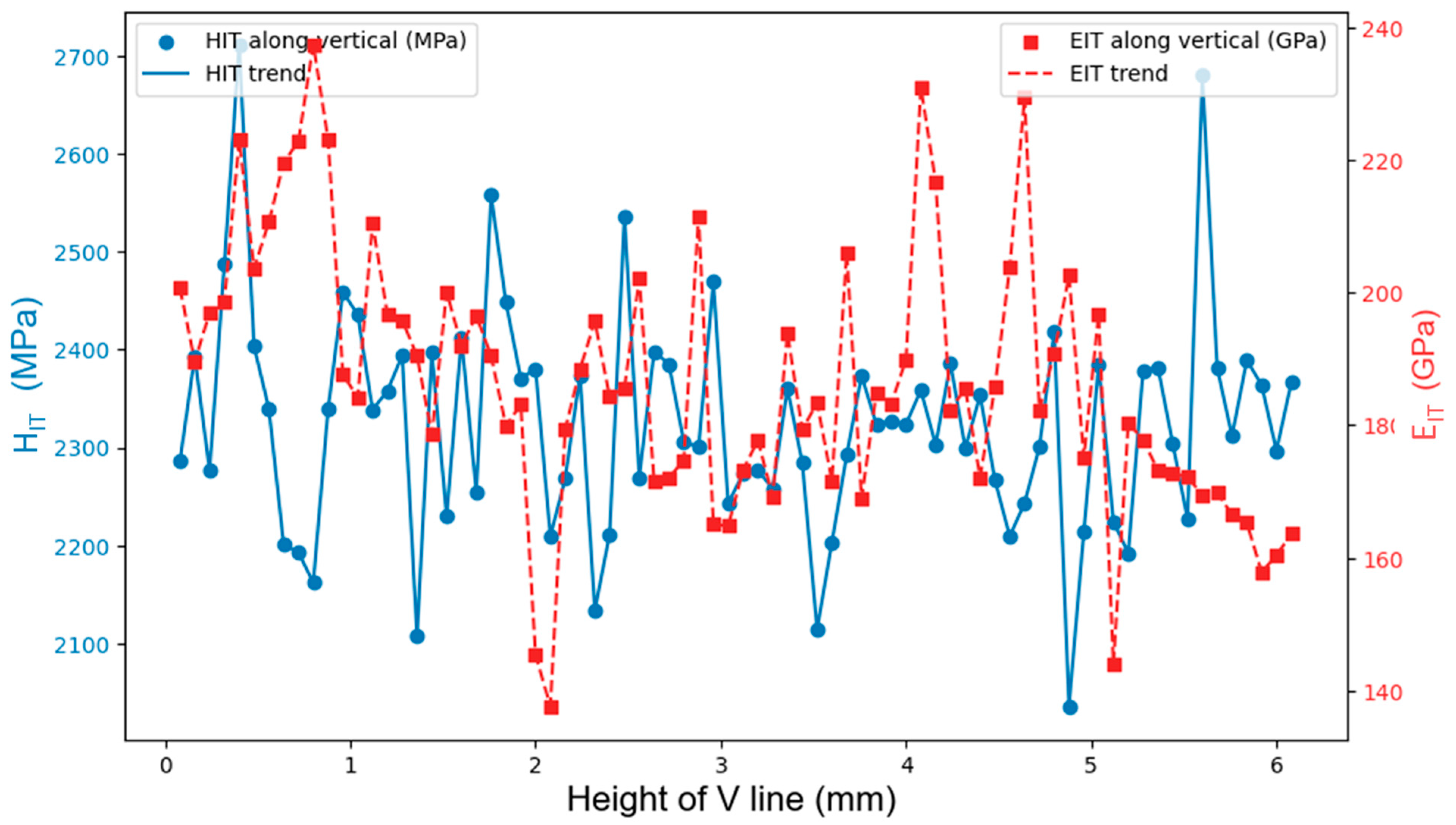
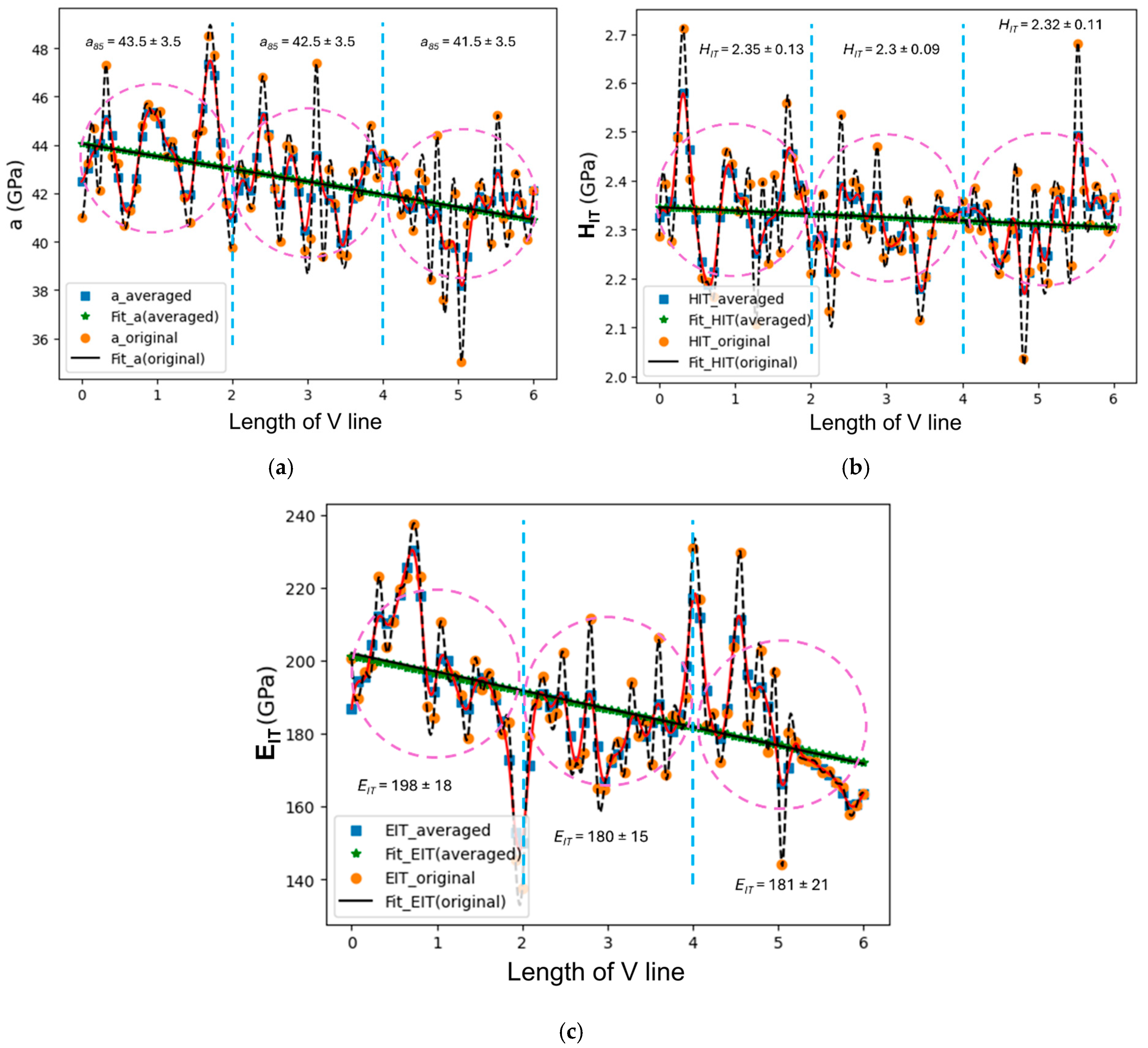
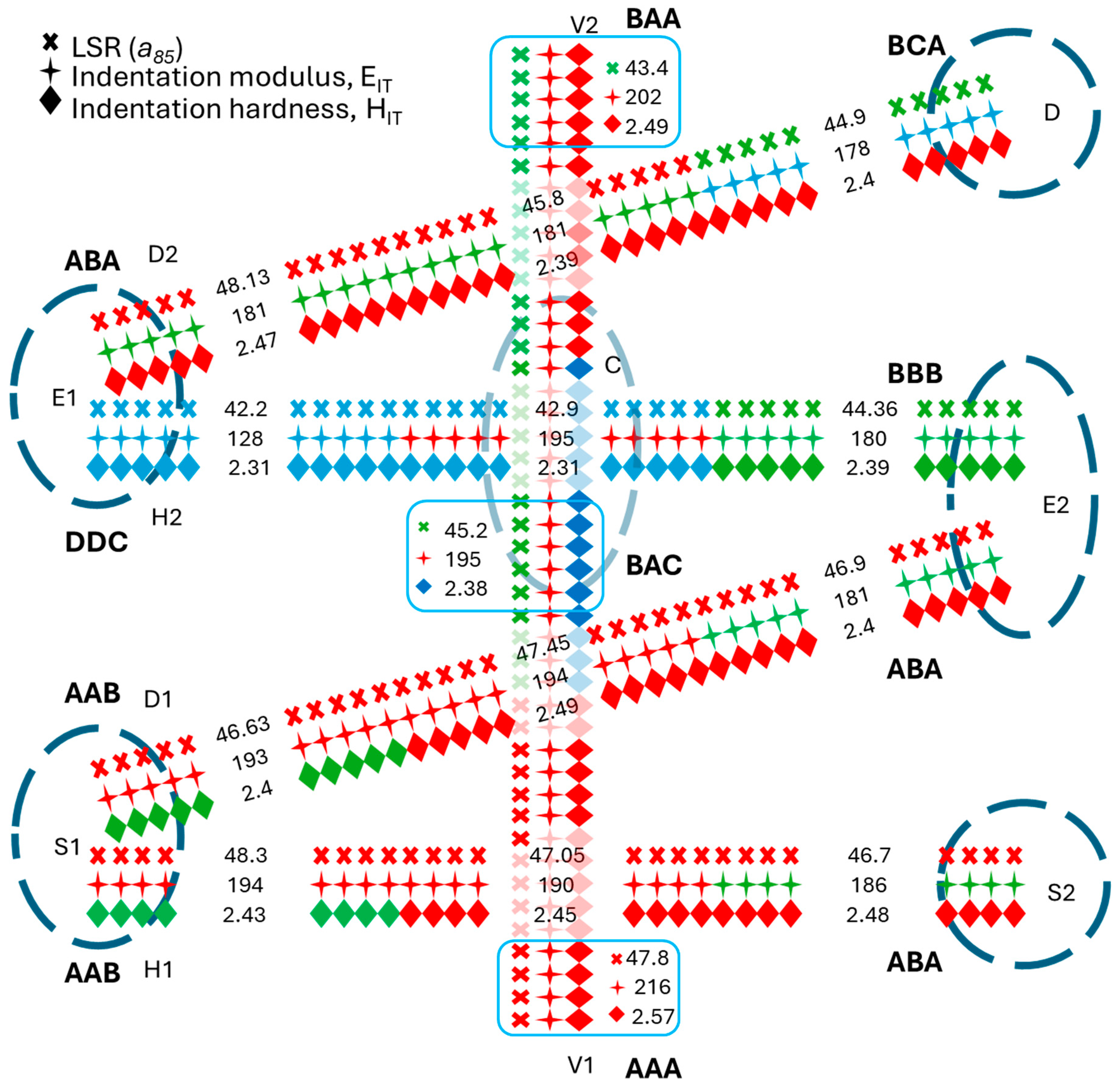
| Elements | Si | Mo | Cr | Mn | C | Ni | Fe |
|---|---|---|---|---|---|---|---|
| % wt | 0.91 | 2.34 | 18.05 | 1.57 | 0.03 | 12.3 | Balance |
| Near the Substrate | Near the Dome | Depositing Height | |||
|---|---|---|---|---|---|
| Direction of the Lines | H1 | D1 | H2 | D2 | V |
| HIT (GPa) | 2.32 ± 0.12 | 2.30 ± 0.12 | 2.26 ± 0.11 | 2.30 ± 0.11 | 2.32 ± 0.11 |
| (%RSD) | (5.1) | (5.2) | (4.9) | (4.8) | (4.7) |
| EIT (GPa) | 180.3 ± 11.0 | 178.8 ± 11.8 | 152.2 ± 28.3 | 171.1 ± 10.0 | 186.8 ± 20.1 |
| (%RSD) | (6.1) | (6.6) | (18.6) | (5.8) | (10.7) |
| hmax (nm) | 1372.4 ± 35.9 | 1377.9 ± 32.9 | 1398.6 ± 35.1 | 1381.4 ± 32.4 | 1367.9 ± 30.9 |
| %RSD | (2.6) | (2.4) | (2.5) | (2.3) | (2.2) |
| KL | 526.6 ± 172.6 | 580.6 ± 147.9 | 510.9 ± 262.0 | 492.7 ± 110.5 | 639.8 ± 210.9 |
| (%RSD) | (32.7) | (25.4) | (51.2) | (22.4) | (32.9) |
| nL | 1.7 ± 0.04 | 1.67 ± 0.036 | 1.7 ± 0.04 | 1.7 ± 0.03 | 1.66 ± 0.04 |
| (%RSD) | (2.6) | (2.2) | (2.4) | (1.7) | (2.7) |
| a85 (GPa) | 44.5 ± 2.9 | 44.36 ± 2.2 | 42.0 ± 2.2 | 44.3 ± 2.2 | 42.5 ± 2.3 |
| b85 (N/m) | 14.8 ± 2.4 | 14.33 ± 2.4 | 15.6 ± 2.2 | 14.4 ± 1.7 | 17.2 ± 2.5 |
| PLs | Wu | Wp | Wt | hmax | a85 | |
|---|---|---|---|---|---|---|
| H1 | HIT | 0.041 | −0.87 | −0.87 | −0.99 | 0.77 |
| H2 | −0.1 | −0.75 | −0.81 | −0.95 | 0.68 | |
| D1 | −0.07 | −0.83 | −0.84 | −0.99 | 0.68 | |
| D2 | −0.21 | −0.86 | −0.87 | −0.99 | 0.86 | |
| V | 0.26 | −0.81 | −0.77 | −0.97 | 0.6 | |
| H1 | EIT | −0.73 | −0.45 | −0.54 | −0.58 | 0.42 |
| H2 | −0.9 | 0.08 | −0.42 | −0.44 | 0.46 | |
| D1 | −0.83 | −0.31 | −0.45 | −0.5 | 0.4 | |
| D2 | −0.81 | −0.42 | −0.5 | −0.61 | 0.50 | |
| V | −0.83 | −0.05 | −0.23 | −0.14 | 0.35 | |
| H1 | hmax | 0.04 | 0.87 | 0.87 | 1 | −0.77 |
| H2 | 0.35 | 0.66 | 0.86 | 1 | −0.75 | |
| D1 | 0.15 | 0.83 | 0.84 | 1 | −0.68 | |
| D2 | 0.29 | 0.85 | 0.88 | 1 | −0.85 | |
| V | −0.12 | 0.84 | 0.83 | 1 | −0.65 |
| H1 | H2 | D1 | D2 | V | |
|---|---|---|---|---|---|
| ∇a85 | 0.08 | −0.06 | −0.02 | 0.09 | −0.04 |
| ∇HIT | 3.1 × 10−3 | −1 × 10−3 | −5 × 10−4 | 2.6 × 10−3 | −5 × 10−4 |
| ∇EIT | 0.34 | −1.62 | 0.31 | 0.14 | −0.4 |
| A | B | C | D | |
|---|---|---|---|---|
| a85 (GPa) | ≥46.5 | [44.5–46.5] | [44–43] | <43 |
| EIT (GPa) | >191 | [180.5–190.5] | [175–180] | <175 |
| HIT (GPa) | >2.40 | [2.35–2.39] | [2.2–2.34] | <2.2 |
| Base-Centerline | S1(H1, D1) | E1(D2) S2(H1) E2(D1) | Top-Centerline | CZ(H2, V) | E2(H2) | D(D2) | E1(H2) |
|---|---|---|---|---|---|---|---|
| AAA | AAB | ABA | BAA | BAC | BBB | BCA | DDC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maizza, G.; Hafeez, F.; Varone, A.; Montanari, R. On the Mechanical Performance of an L-PBF 316l Part Using the Performance-Line Instrumented Indentation Test (PL-IIT). Materials 2025, 18, 1462. https://doi.org/10.3390/ma18071462
Maizza G, Hafeez F, Varone A, Montanari R. On the Mechanical Performance of an L-PBF 316l Part Using the Performance-Line Instrumented Indentation Test (PL-IIT). Materials. 2025; 18(7):1462. https://doi.org/10.3390/ma18071462
Chicago/Turabian StyleMaizza, Giovanni, Faisal Hafeez, Alessandra Varone, and Roberto Montanari. 2025. "On the Mechanical Performance of an L-PBF 316l Part Using the Performance-Line Instrumented Indentation Test (PL-IIT)" Materials 18, no. 7: 1462. https://doi.org/10.3390/ma18071462
APA StyleMaizza, G., Hafeez, F., Varone, A., & Montanari, R. (2025). On the Mechanical Performance of an L-PBF 316l Part Using the Performance-Line Instrumented Indentation Test (PL-IIT). Materials, 18(7), 1462. https://doi.org/10.3390/ma18071462









