Electric Field-Induced Settling and Flotation of Flocs in Mixed Aqueous Suspensions of Poly(methyl methacrylate) and Aluminosilicate Hollow Particles
Abstract
1. Introduction
2. Experimental
2.1. Sample Preparation
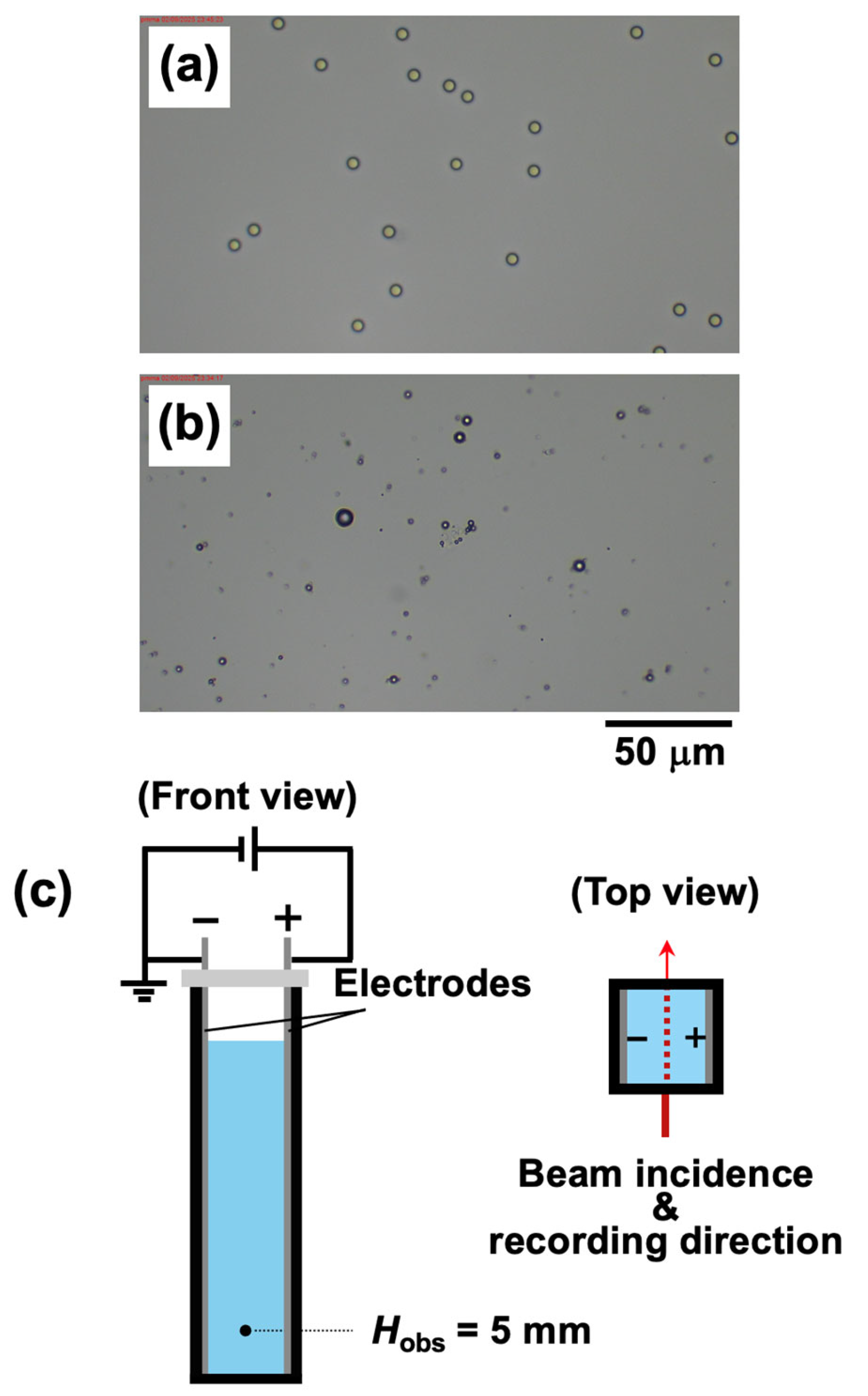
2.2. Measurement Method
3. Results and Discussion
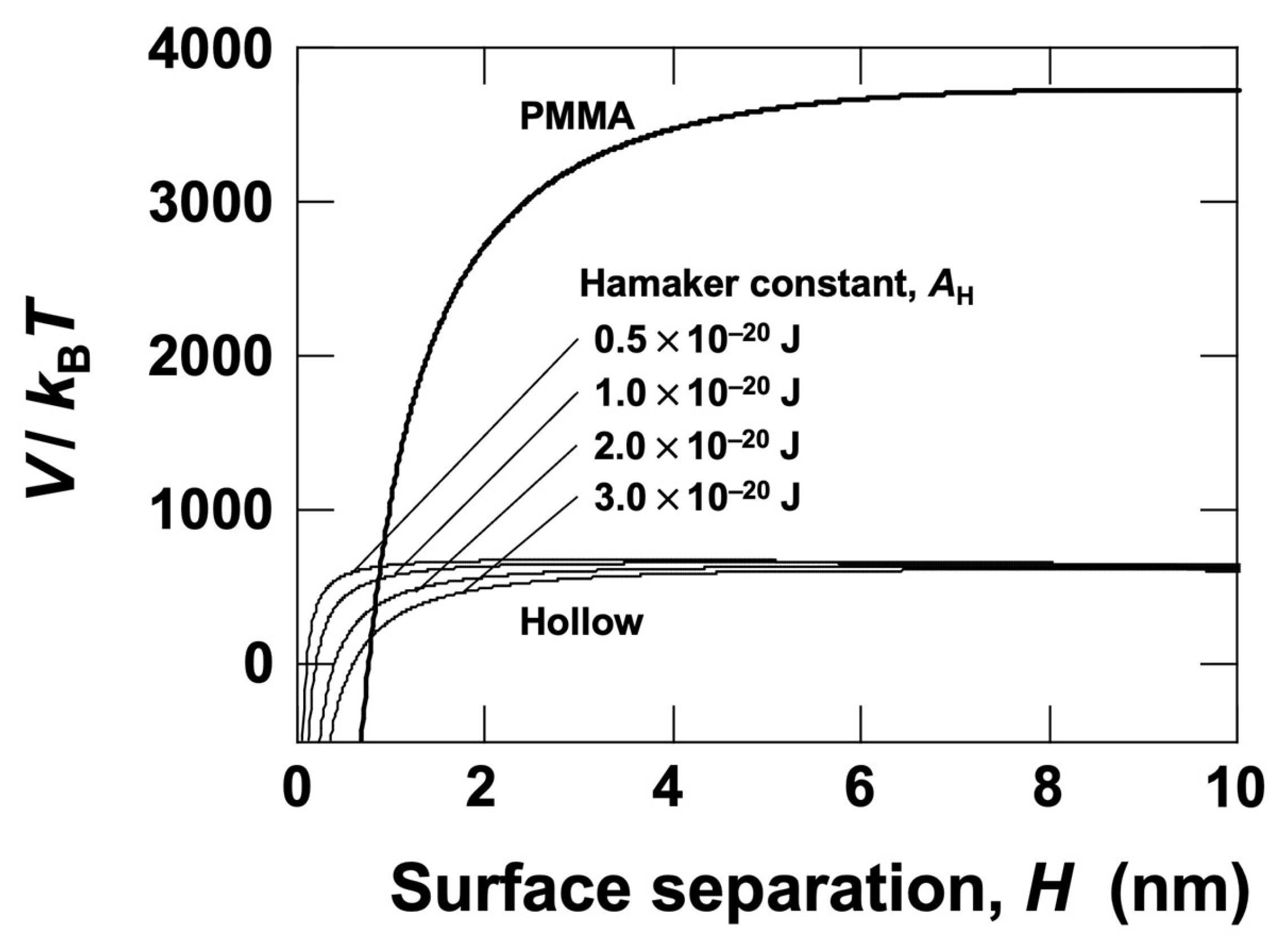
3.1. Potential Energy Curves from DLVO (Derjaguin–Landau–Verwey–Overbeek) Theory
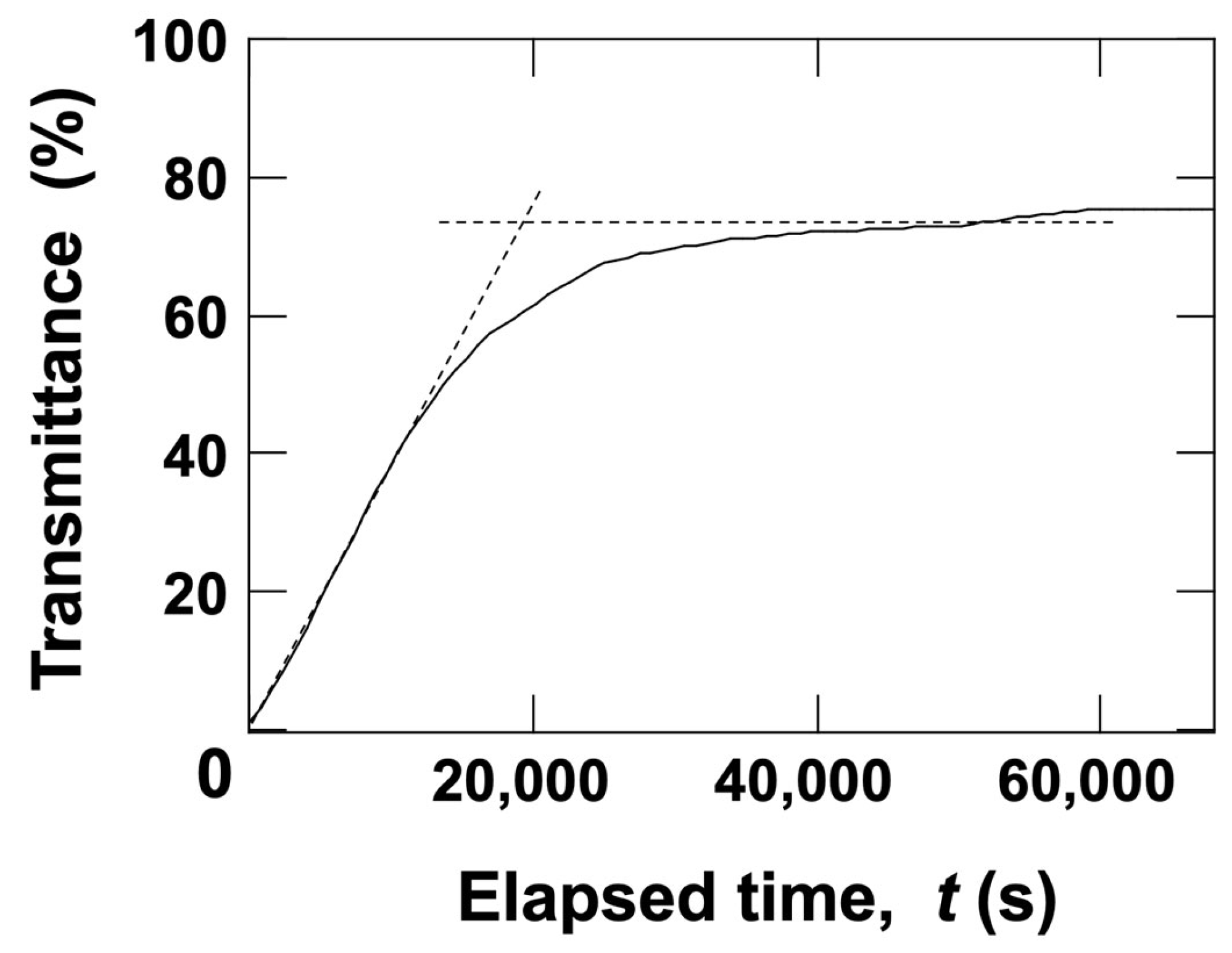
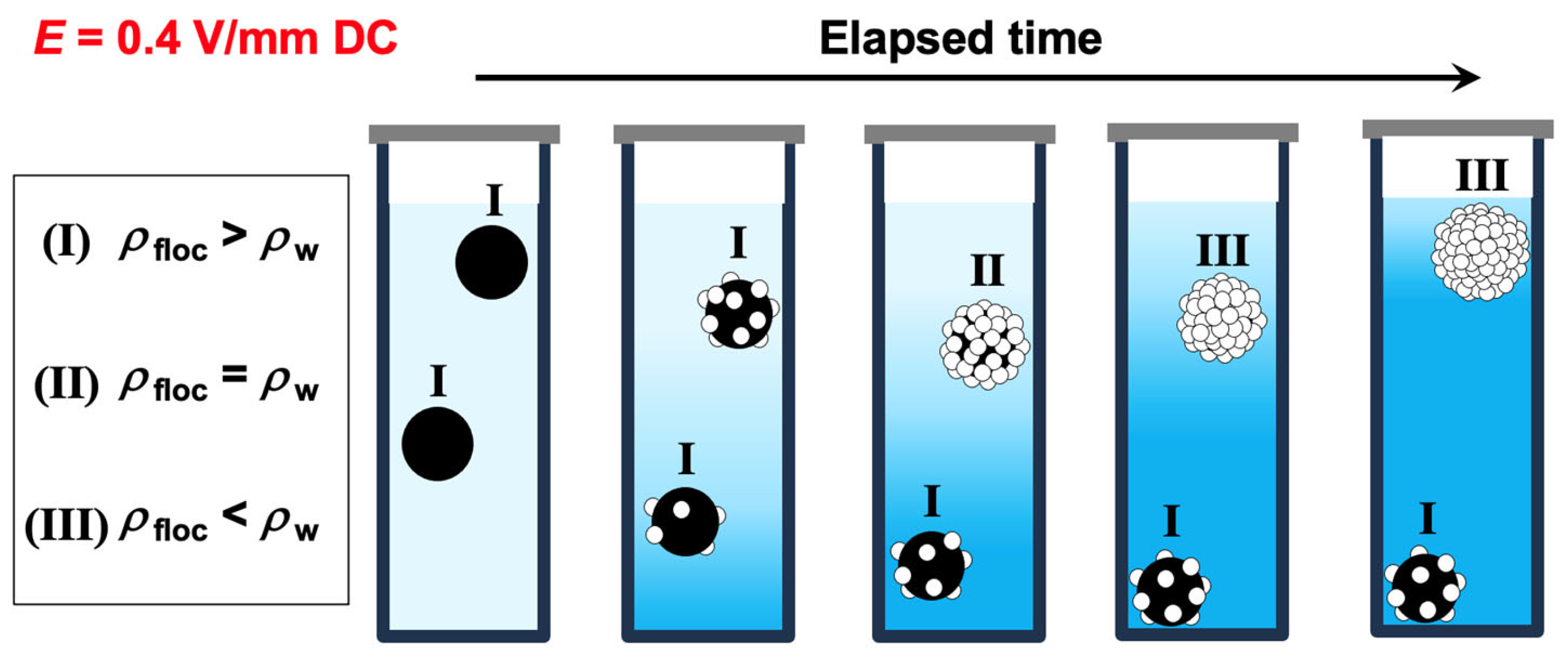
3.2. Time Evolution of Dispersion State Under Field-Free and Electric Field Conditions
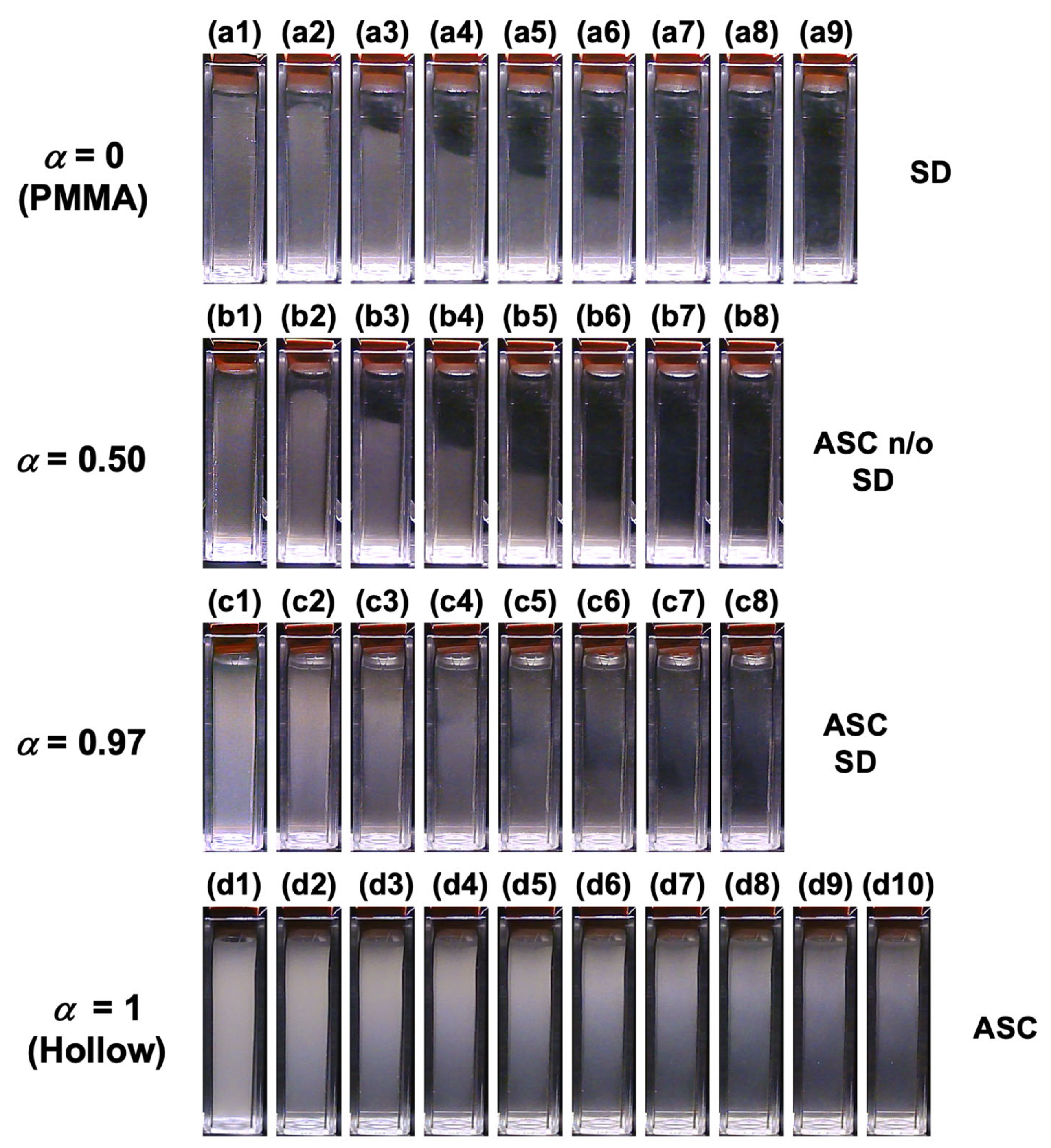
3.3. Influence of Hollow Particle Mixing Ratio on the ERS Effect
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kimura, H.; Takahashi, S.; Tsuchida, A. Rapid sedimentation of poly(methyl methacrylate) spheres and montmorillonite particles in water upon application of a DC electric field of the order of a few V/mm. Appl. Clay Sci. 2014, 101, 623–625. [Google Scholar] [CrossRef]
- Kimura, H.; Tsuchida, A. Sedimentation behavior of poly(methyl methacrylate) spheres in water upon application of a DC vertical electric field of the order of a few V/mm. Powder Technol. 2017, 320, 362–367. [Google Scholar] [CrossRef]
- Mori, T.; Nagashima, H.; Ito, Y.; Era, Y.; Tsubaki, J. Agglomeration of fine particles in water upon application of DC electric field. Miner. Eng. 2019, 133, 119–126. [Google Scholar] [CrossRef]
- Kimura, H. Co-flocculation of mixed-sized colloidal particles in aqueous dispersions under a DC electric field. Materials 2025, 18, 98. [Google Scholar] [CrossRef]
- Guelcher, S.A.; Solomentsev, Y.; Anderson, J.L. Aggregation of pairs of particles on electrodes during electrophoretic deposition. Powder Technol. 2000, 110, 90–97. [Google Scholar] [CrossRef]
- Kim, J.; Guelcher, S.A.; Garoff, S.; Anderson, J.L. Two-particle dynamics on an electrode in AC electric fields. Adv. Colloid Interface Sci. 2002, 96, 131–142. [Google Scholar] [CrossRef]
- Wei, Q.-H.; Liu, X.-H.; Zhou, C.-H.; Ming, N.-B. In situ studies of colloidal aggregation induced by alternating electrical fields. Phys. Rev. E 1993, 48, 2786–2791. [Google Scholar] [CrossRef]
- Fraden, S.; Hurd, A.J.; Meyer, R.B. Electric-field-induced association of colloidal particles. Phys. Rev. Lett. 1989, 63, 2373–2376. [Google Scholar] [CrossRef]
- Tang, F.; Uchikoshi, T.; Ozawa, K.; Sakka, Y. Electrophoretic deposition of aqueous nano-γ-Al2O3 suspensions. Mater. Res. Bull. 2002, 37, 653–660. [Google Scholar] [CrossRef]
- Mohd Sharif, S.; Abu Bakar, N.F.; Naim, M.N. Deposition of fine iron oxide particles in tap water using electrophoretic deposition (EPD) technique. J. Water Process Eng. 2015, 7, 123–130. [Google Scholar] [CrossRef]
- Trau, M.; Saville, D.A.; Aksay, I.A. Field-induced layering of colloidal crystals. Science 1996, 272, 706–709. [Google Scholar] [CrossRef] [PubMed]
- Gong, T.; Wu, D.T.; Marr, D.W.M. Electric field-reversible three-dimensional colloidal crystals. Langmuir 2003, 19, 5967–5970. [Google Scholar] [CrossRef]
- Lumsdon, S.O.; Kaler, E.W.; Velev, O.D. Two-dimensional crystallization of microspheres by a coplanar AC electric field. Langmuir 2004, 20, 2108–2116. [Google Scholar] [CrossRef] [PubMed]
- Yakovlev, E.V.; Komarov, K.A.; Zaytsev, K.I.; Kryuchkov, N.P.; Koshelev, K.I.; Zotov, A.K.; Shelestov, D.A.; Tolstoguzov, V.L.; Kurlov, V.N.; Ivlev, A.V.; et al. Tunable two-dimensional assembly of colloidal particles in rotating electric fields. Sci. Rep. 2017, 7, 13727. [Google Scholar] [CrossRef]
- Kim, K.; Nakayama, Y.; Yamamoto, R. Direct numerical simulations of electrophoresis of charged colloids. Phys. Rev. Lett. 2006, 96, 208302. [Google Scholar] [CrossRef]
- Kimura, H. Rapid ascent of hollow particles in water induced by an electric field. Powders 2023, 2, 737–748. [Google Scholar] [CrossRef]
- Derjaguin, B.; Landau, L.D. Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solution of electrolytes. Acta Physicochim. USSR 1941, 14, 633–662. [Google Scholar]
- Verwey, E.J.W.; Overbeek, J.T.G. Theory of the Stability of Lyophobic Colloids; Elsevier: Amsterdam, The Netherlands, 1948. [Google Scholar]
- Hunter, R.J. Foundations of Colloid Science, 2nd ed.; Oxford University Press Inc.: Oxford, UK, 2001. [Google Scholar]
- Tsai, C.-J.; Pui, D.Y.H.; Liu, B.Y.H. Elastic flattening and particle adhesion. Aerosol Sci. Technol. 1991, 15, 239–255. [Google Scholar] [CrossRef]
- Bergström, L. Hamaker constants of inorganic materials. Adv. Colloid Interface Sci. 1997, 70, 125–169. [Google Scholar] [CrossRef]
- Atkins, P.; de Paula, J. Physical Chemistry, 8th ed.; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Kimura, H. Influence of alternating electric field on electrorheological effect of aqueous dispersions of stevensite. Appl. Clay Sci. 2024, 254, 107393. [Google Scholar] [CrossRef]
- Tadros, T. General principles of colloid stability and the role of surface forces. In Colloid Stability: The Role of Surface Forces; Wiley-VCH: Weinheim, Germany, 2011; pp. 1–45. [Google Scholar]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles. J. Fluid Mech. 1979, 94, 795–796. [Google Scholar]




| α | ϕPMMA | ϕhollow | ϕtotal | NPMMA | Nhollow | Ntotal |
|---|---|---|---|---|---|---|
| 0 | 7.1 × 10−5 | 0 | 7.1 × 10−5 | 3.2 × 106 | 0 | 3.2 × 106 |
| 0.10 | 7.1 × 10−5 | 1.5 × 10−7 | 7.2 × 10−5 | 3.2 × 106 | 3.6 × 105 | 3.6 × 106 |
| 0.50 | 7.1 × 10−5 | 1.3 × 10−6 | 7.3 × 10−5 | 3.2 × 106 | 3.2 × 106 | 6.4 × 106 |
| 0.90 | 7.1 × 10−5 | 1.2 × 10−5 | 8.3 × 10−5 | 3.2 × 106 | 2.9 × 107 | 3.2 × 107 |
| 0.92 | 7.1 × 10−5 | 1.5 × 10−5 | 8.7 × 10−5 | 3.2 × 106 | 3.7 × 107 | 4.0 × 107 |
| 0.93 | 7.1 × 10−5 | 1.7 × 10−5 | 8.9 × 10−5 | 3.2 × 106 | 4.3 × 107 | 4.6 × 107 |
| 0.95 | 7.1 × 10−5 | 2.5 × 10−5 | 9.6 × 10−5 | 3.2 × 106 | 6.1 × 107 | 6.4 × 107 |
| 0.97 | 7.1 × 10−5 | 4.3 × 10−5 | 1.1 × 10−4 | 3.2 × 106 | 1.0 × 108 | 1.1 × 108 |
| 1 | 0 | 5.0 × 10−4 | 5.0 × 10−4 | 0 | 1.2 × 109 | 1.2 × 109 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kimura, H.; Sakakibara, M. Electric Field-Induced Settling and Flotation of Flocs in Mixed Aqueous Suspensions of Poly(methyl methacrylate) and Aluminosilicate Hollow Particles. Materials 2025, 18, 1289. https://doi.org/10.3390/ma18061289
Kimura H, Sakakibara M. Electric Field-Induced Settling and Flotation of Flocs in Mixed Aqueous Suspensions of Poly(methyl methacrylate) and Aluminosilicate Hollow Particles. Materials. 2025; 18(6):1289. https://doi.org/10.3390/ma18061289
Chicago/Turabian StyleKimura, Hiroshi, and Mirei Sakakibara. 2025. "Electric Field-Induced Settling and Flotation of Flocs in Mixed Aqueous Suspensions of Poly(methyl methacrylate) and Aluminosilicate Hollow Particles" Materials 18, no. 6: 1289. https://doi.org/10.3390/ma18061289
APA StyleKimura, H., & Sakakibara, M. (2025). Electric Field-Induced Settling and Flotation of Flocs in Mixed Aqueous Suspensions of Poly(methyl methacrylate) and Aluminosilicate Hollow Particles. Materials, 18(6), 1289. https://doi.org/10.3390/ma18061289






