Application of Polyurethane Foam as a Material for Reducing Vibration of Wheelchair User
Highlights
Abstract
1. Introduction
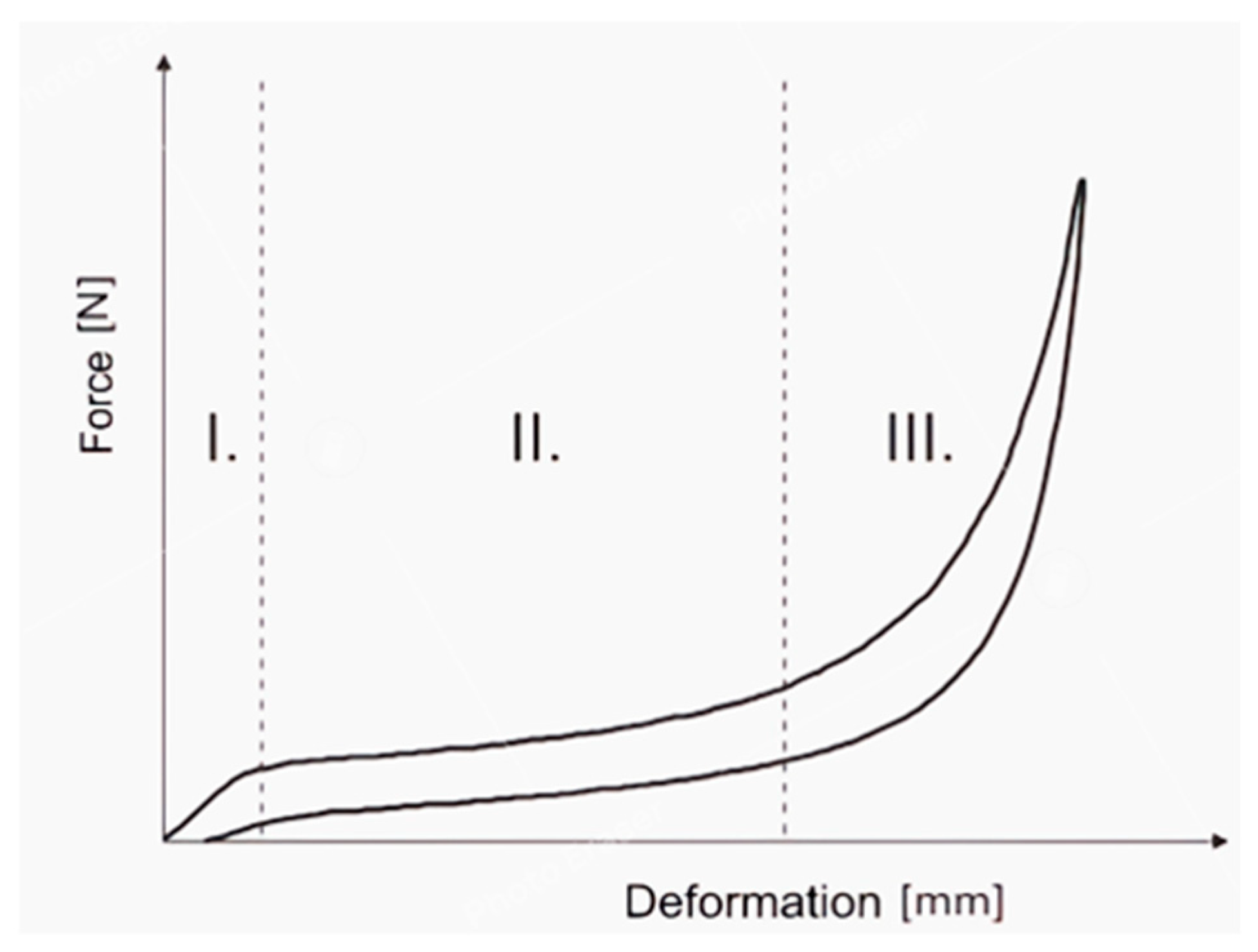
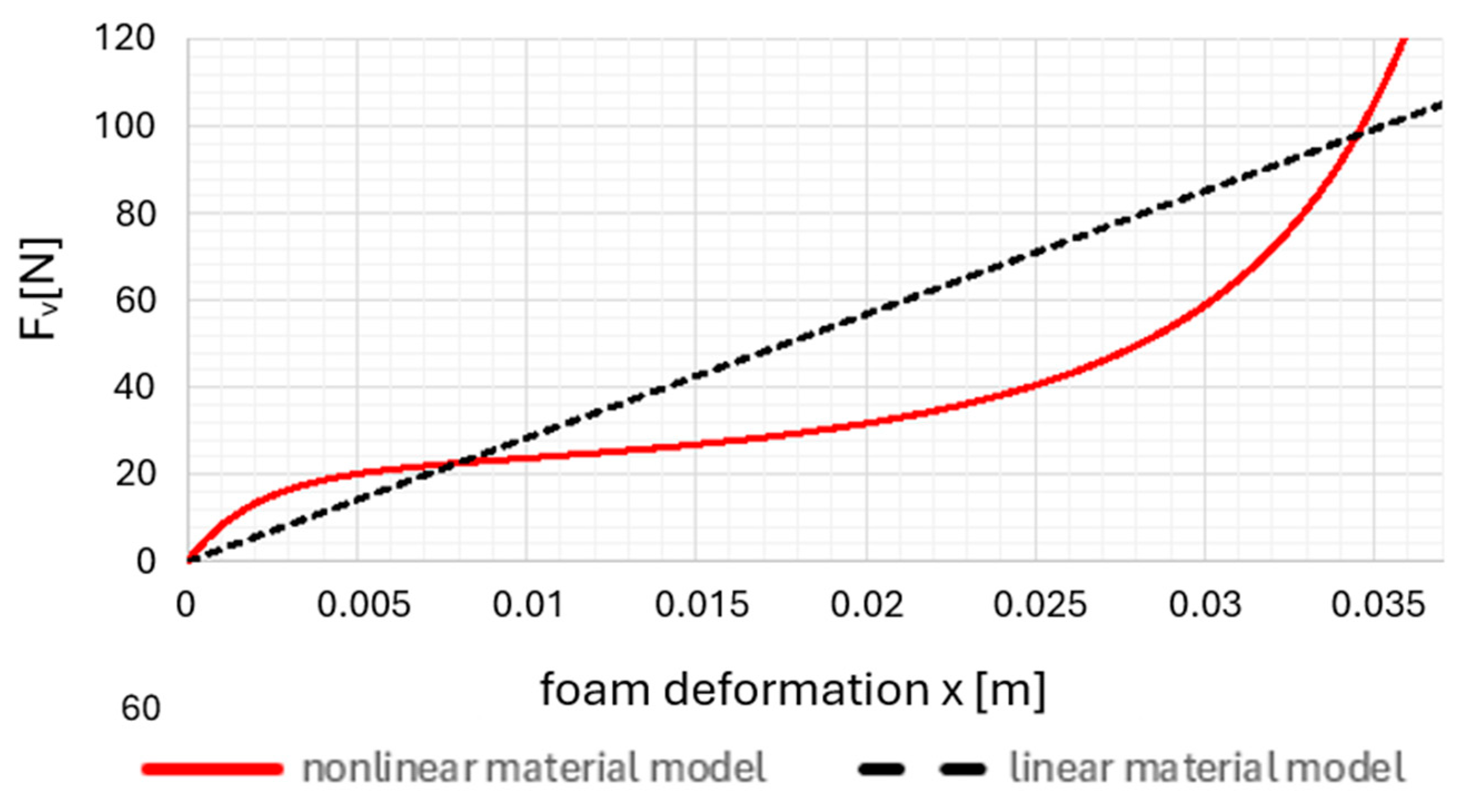
2. Polyurethane Foam and Its Material Properties
3. Wan–Schimmels Model
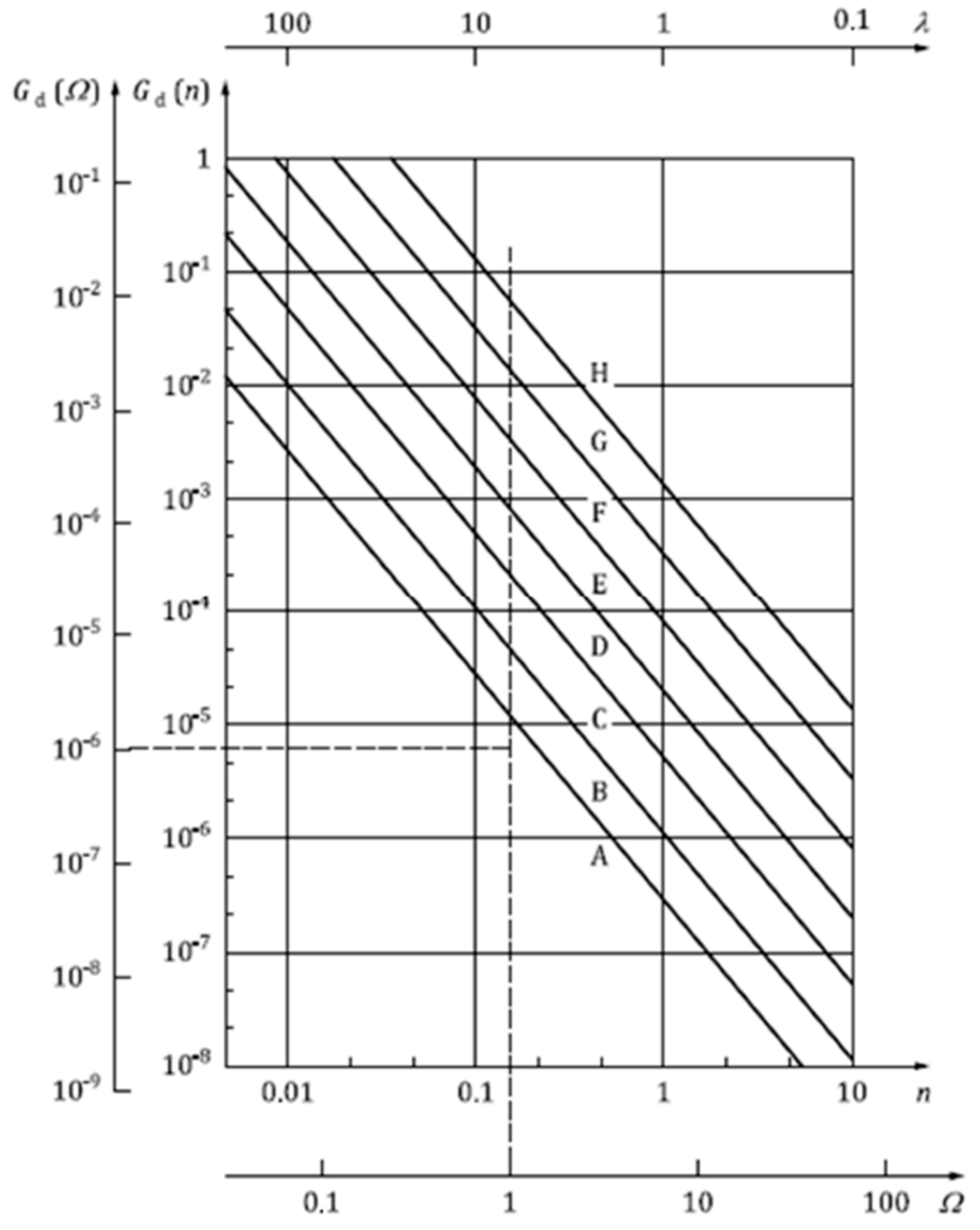
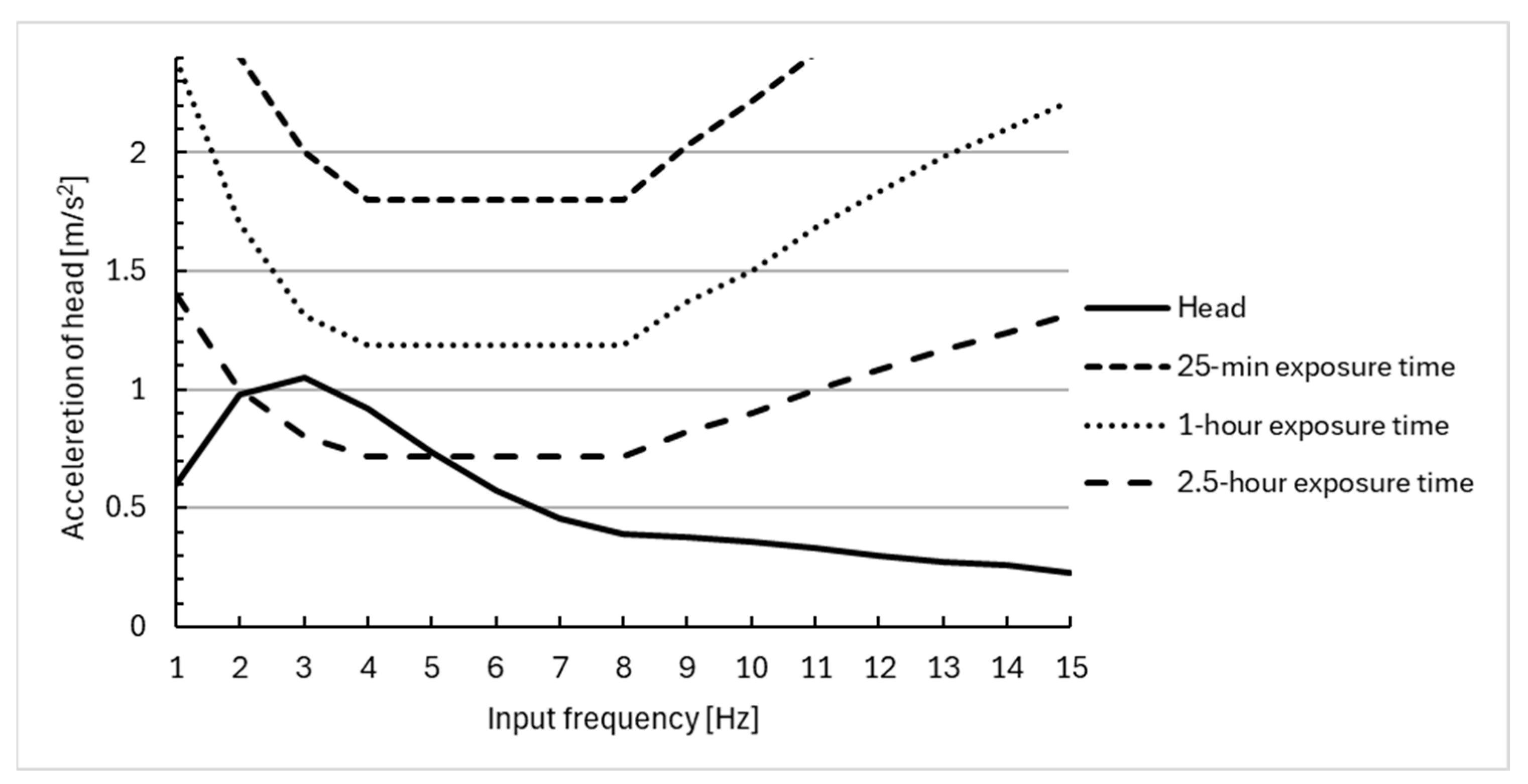
4. Simulation of Human Body Response
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- DiGiovine, C.P.; Cooper, R.A.; Wolf, E.J.; Hosfield, J.; Corfman, T.A. Analysis of Vibration and Comparison of Four Wheelchair Cushions during Manual Wheelchair Propulsion. In Proceedings of the Annual RESNA Conference, Orlando, FL, USA, 28 June–2 July 2000; pp. 242–244. [Google Scholar]
- Amiri, S.; Naserkhaki, S.; Parnianpour, M. Effect of whole-body vibration and sitting configurations on lumbar spinal loads of vehicle occupants. Comput. Biol. Med. 2019, 107, 292–301. [Google Scholar] [CrossRef] [PubMed]
- Brown, K.; Flashner, H.; McNitt-Gray, J.; Requejo, P. Modeling Wheelchair-Users Undergoing Vibrations. J. Biomech. Eng. 2017, 139, 094501. [Google Scholar] [CrossRef] [PubMed]
- Neti, A.; Brunswick, A.; Marsalko, L.; Shearer, C.; Koontz, A. Effects of In-Wheel Suspension on Whole-Body Vibration and Comfort in Manual Wheelchair Users. Vibration 2024, 7, 432–452. [Google Scholar] [CrossRef]
- Garcia-Mendez, Y.; Pearlman, J.L.; Cooper, R.A.; Boninger, M.L. Dynamic Stiffness and Transmissibility of Commercially Available Wheelchair Cushions Using a Laboratory Test Method. J. Rehabil. Res. Dev. 2012, 49, 7–22. [Google Scholar] [CrossRef]
- Lariviere, O.; Chadefaux, D.; Sauret, C.; Thoreux, P. Vibration Transmission during Manual Wheelchair Propulsion: A Systematic Review. Vibration 2021, 4, 444–481. [Google Scholar] [CrossRef]
- Wolf, E.J.; Cooper, M.S.R.A.; DiGiovine, C.P.; Boninger, M.L.; Guo, S. Using the Absorbed Power Method to Evaluate Effectiveness of Vibration Absorption of Selected Seat Cushions during Manual Wheelchair Propulsion. Med. Eng. Phys. 2004, 26, 799–806. [Google Scholar] [CrossRef]
- Boninger, M.L.; Cooper, R.A.; Fitzgerald, S.G.; Lin, J.; Cooper, R.; Dicianno, B.; Liu, B. Investigating Neck Pain in Wheelchair Users. Am. J. Phys. Med. Rehabil. 2003, 82, 197–202. [Google Scholar] [CrossRef]
- Chadefau, D.; Lariviere, O.; Sauret, C.; Bosio, C.; Thoreux, P. Understanding vibration exposure in wheelchair users: Experimental insights. Med. Eng. Phys. 2024, 113, 104253. [Google Scholar] [CrossRef]
- Hulshof, C.; Veldhuijzen van Zanten, B. Whole-body vibration and low-back pain. Int. Arch. Occup. Environ. Health 1987, 59, 205–220. [Google Scholar] [CrossRef]
- Burström, L.; Nilsson, T.; Wahlström, J. Whole-body vibration and the risk of low back pain and sciatica: A systematic review and meta-analysis. Int. Arch. Occup. Environ. Health 2015, 88, 403–418. [Google Scholar] [CrossRef]
- Chwalik-Pilszyk, G.; Dziechciowski, Z.; Kromka-Szydek, M.; Kozień, M.S. Experimental study of the influence of using polyurethane cushion to reduce vibration received by a wheelchair user. Acta Bioeng. Biomech. 2023, 25, 137–149. [Google Scholar] [CrossRef] [PubMed]
- Festa, M.; Durm, T.; Lünebach, M.; Gauterin, F. Difference Thresholds for the Perception of Sinusoidal Vertical Stimuli of Whole-Body Vibrations in Ranges of Amplitude and Frequency Relevant to Ride Comfort. Vibration 2020, 3, 116–131. [Google Scholar] [CrossRef]
- Rivin, E.I. Passive Vibration Isolation; ASME Press: New York, NY, USA, 2003. [Google Scholar]
- White, S.W.; Kim, S.K.; Davies, P.; Bajaj, A.K.; Liedtke, P.E.; Showers, D.K. Modeling and measurement of occupied car seats. SAE Trans. 1999, 108, 2602–2612. [Google Scholar]
- Meirovitch, L. Elements of Vibration Analysis; Mc-Graw Hill: New York, NY, USA, 1986. [Google Scholar]
- Dunaj, P.; Berczyński, S.; Miądlicki, K.; Irska, I.; Niesterowicz, B. Increasing Damping of Thin-Walled Structures Using Additively Manufactured Vibration Eliminators. Materials 2020, 13, 2125. [Google Scholar] [CrossRef]
- Zheng, W.; He, S.; Tang, R.; He, S. Damping Enhancement Using Axially Functionally Graded Porous Structure Based on Acoustic Black Hole Effect. Materials 2019, 12, 2480. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, X.; Wu, N.; Chu, F.; Luo, J. A Finite Element Model for the Vibration Analysis of Sandwich Beam with Frequency-Dependent Viscoelastic Material Core. Materials 2019, 12, 3390. [Google Scholar] [CrossRef]
- Piszczek, K.; Nizioł, J. Random Vibration of Mechanical Systems; PWN-Ellis Horwood Ltd.: Warszawa, Poland; Chichester, UK, 1986. [Google Scholar]
- Kozień, M.S. Using the Fourier Methods for Cycle Counting of Bimodal Stress Histories with Variable in Time Amplitudes of Components. Materials 2023, 16, 254. [Google Scholar] [CrossRef]
- Ippili, R.K.; Davies, P.; Bajaj, A.K.; Hagenmeyer, L. Nonlinear multi-body dynamic modeling of seat-occupant system with polyurethane seat and h-point prediction. Int. J. Ind. Ergon. 2008, 38, 368–383. [Google Scholar] [CrossRef]
- Joshi, G.; Bajaj, A.K.; Davies, P. Whole-body Vibratory Response Study Using a Nonlinear Multi-body Model of Seat-occupant System with Viscoelastic Flexible Polyurethane Foam. Ind. Health 2010, 48, 663–674. [Google Scholar] [CrossRef]
- Singh, R.; Davies, P.; Bajaj, K. Identification of nonlinear and viscoelastic properties of flexible polyurethane foam. Nonlinear Dyn. 2003, 34, 319–346. [Google Scholar] [CrossRef]
- Saint-Michel, F.; Chazeau, L.; Cavaillé, J.-Y.; Chabert, E. Mechanical Properties of High Density Polyurethane Foams: I. Effect of the Density. Compos. Sci. Technol. 2006, 66, 2700–2708. [Google Scholar] [CrossRef]
- Cirkl, D. Modelling of damping of polyurethane foam in dependence on its density. Shock Vib. 2010, 17, 371–383. [Google Scholar]
- Cirkl, D.; Hruš, T. Simulation model of polyurethane foam for uniaxial dynamical compression. Vibroeng. Proc. 2013, 1, 53–58. [Google Scholar]
- Qiu, D.; He, Y.; Yu, Z. Investigation on compression mechanical properties of rigid polyurethane foam trated under random vibration condition: An experimental and numerical simulation study. Materials 2019, 12, 3385. [Google Scholar] [CrossRef]
- Bai, X.X.; Xu, S.X.; Cheng, W.; Qian, L.J. On 4-degree-of-freedom biodynamic models of seated occupants: Lumped-parameter modeling. J. Sound Vib. 2017, 402, 122–141. [Google Scholar] [CrossRef]
- Jalali, P.; Ettefagh, M.M.; Hassannejad, R. Recognizing the viscoelastic safe area of work shoe sole in the sitting posture with vibration transmissibility in the vertical direction. Int. J. Ind. Ergon. 2021, 81, 103053. [Google Scholar] [CrossRef]
- Wan, Y.; Schimmels, J.M. A Simple Model That Captures the Essential Dynamics of a Seated Human Exposed to Whole Body Vibration. Adv. Bioeng. 1995, 31, 333–334. [Google Scholar]
- Múčka, P. Simulated Road Profiles According to ISO 8608 in Vibration Analysis. J. Test. Eval. 2018, 46, 405–418. [Google Scholar] [CrossRef]
- Weerapong, P.; Hashikura, K.; Kamal, A.S.; Yamada, K. A Numerical Study of Model Output for Whole-Body Vibration on Varying Wheelchair Cushions. In Proceedings of the 7th International Conference on Business and Industrial Research, Bangkok, Thailand, 19–20 May 2022; pp. 259–263. [Google Scholar]
- Weerapong, P.; Katahira, M.; Hashikura, K.; Kamal, M.; Murakami, I.; Yamada, K. Modal analysis for evaluating the transmission of vertical vibrations in a wheelchair-occupant model with foam-based seat cushion. Int. J. Innov. Comput. Inf. Control. 2023, 19, 1933–1952. [Google Scholar]
- Weerapong, P.; Katahira, M.; Kaewkongtham, K.; Sudsomboon, W.; Kaewdee, C.; Pansrinual, W.; Thi Mai, N.; Hashikura, K.; Kamal, M.; Murakami, I.; et al. A State-space approach to analyzing vertical vibration behavior in wheelchair-occupant systems with a composite model. Int. J. Innov. Comput. 2024, 20, 437–460. [Google Scholar]
- Boileau, P.E.; Rakheja, S. Whole-body vertical biodynamic response characteristics of the seated vehicle driver: Measurement and model development. Int. J. Ind. Ergon. 1998, 22, 449–472. [Google Scholar] [CrossRef]
- Gan, Z.; Hillis, A.J.; Darling, J. Biodynamic modelling of seated human subjects exposed to uncouples vertical and fore-and-aft whole-body vibration. J. Vib. Eng. Technol. 2015, 3, 301–314. [Google Scholar]
- Zhang, W.; Ma, Z.; Jin, A.; Yang, J.; Zhang, Y. An improved human biodynamic model considering the interaction between feet and ground. SAE Int. J. Commer. Veh. 2015, 8, 13–19. [Google Scholar] [CrossRef]
- Abbas, W.; Abouelatta, O.B.; El-Azab, M.; Elsaidy, M.; Megahed, A.A. Optimization of Biodynamic Seated Human Models Using Genetic Algorithms. Engineering 2010, 2, 710–719. [Google Scholar] [CrossRef]
- Elliot, J.A.; Windle, H.; Hobdell, J.R.; Eeckhaut, G.; Oldman, R.J.; Ludwig, W.; Boller, E.; Cloetens, P.; Baruchel, J. In-situ deformation of open-cell flexible polyurethane foam characterized by 3D computed microphotography. J. Mater. Sci. 2002, 37, 1547–1555. [Google Scholar] [CrossRef]
- Wang, Y.; Cuitino, A.M. Full-field measurements of heterogeneous deformation patterns of polymeric foam using digital image correlation. Int. J. Solid Struct. 2002, 39, 3777–3796. [Google Scholar] [CrossRef]
- Cirkl, D. Measurement of mechanical properties of polyurethane foam in vacuum. In Proceedings of the Colloquium Dynamics of Machines, Prague, Czech Republic, 6–7 February 2007; Institute of Thermomechanics, Czech Academy of Science: Prague, Czech Republic, 2007; pp. 29–34. [Google Scholar]
- Tamer, A.; Muscarello, V.; Quaranta, G.; Masarati, P. Cabin Layout Optimization for Vibration Hazard Reduction in Helicopter Emergency Medical Service. Aerospace 2020, 7, 59. [Google Scholar] [CrossRef]
- Zhao, L.; Yu, Y.; Zhou, C. Dynamic modeling, simulation and experimental investigation on cycling-trainers equipped with suspensions considering human biomechanical characteristics. J. Vibroengineering 2020, 22, 1228–1239. [Google Scholar] [CrossRef]
- Chwalik-Pilszyk, G.; Ziemianski, D.; Kozien, M.S. Experimental investigations on transmission of whole body vibration to the wheelchair user’s body. Open Eng. 2022, 12, 431–438. [Google Scholar] [CrossRef]
- ISO 8608:2016; Mechanical Vibration—Road Surface Profiles—Reporting of Measured Data. ISO: Geneva, Switzerland, 2016.
- Duvall, J.; Cooper, R.; Sinagra, E.; Stuckey, D.; Brown, J.; Pearlman, J. Development of Surface Roughness Standards for Pathways Used by Wheelchairs. Transp. Res. Rec. 2013, 2387, 149–156. [Google Scholar] [CrossRef]
- Hashizume, T.; Kitagawa, H.; Yoneda, I.; Takami, M.; Fujisawa, S.; Sueda, O.; Kamata, M. Study on the Wheelchair User’s Body Vibration and Wheelchair Driving Torque When Wheelchair Is Ascending/Descending the Boundary Curb between Pavement and Roadway. In Proceedings of the SICE Annual Conference, Chofu, Japan, 20–22 August 2008; pp. 1273–1276. [Google Scholar]
- Hischke, M.; Reiser, R.F. Effect of Rear Wheel Suspension on Tilt-in-Space Wheelchair Shock and Vibration Attenuation. PM&R 2018, 10, 1040–1050. [Google Scholar]
- Weerapong, P.; Hashikura, K.; Kamal, M.A.S.; Yamada, K. A model for the response of an occupant and wheelchair system subjected to vertical vibrations. Int. J. Innov. Comput. Inf. Control. 2021, 17, 1823–1841. [Google Scholar]
- ISO 2631:1978; Guide for the Evaluation of Human Exposure to Whole-Body Vibration, Part 1: General Requirements. International Organization for Standardization: Geneva, Switzerland, 1978.

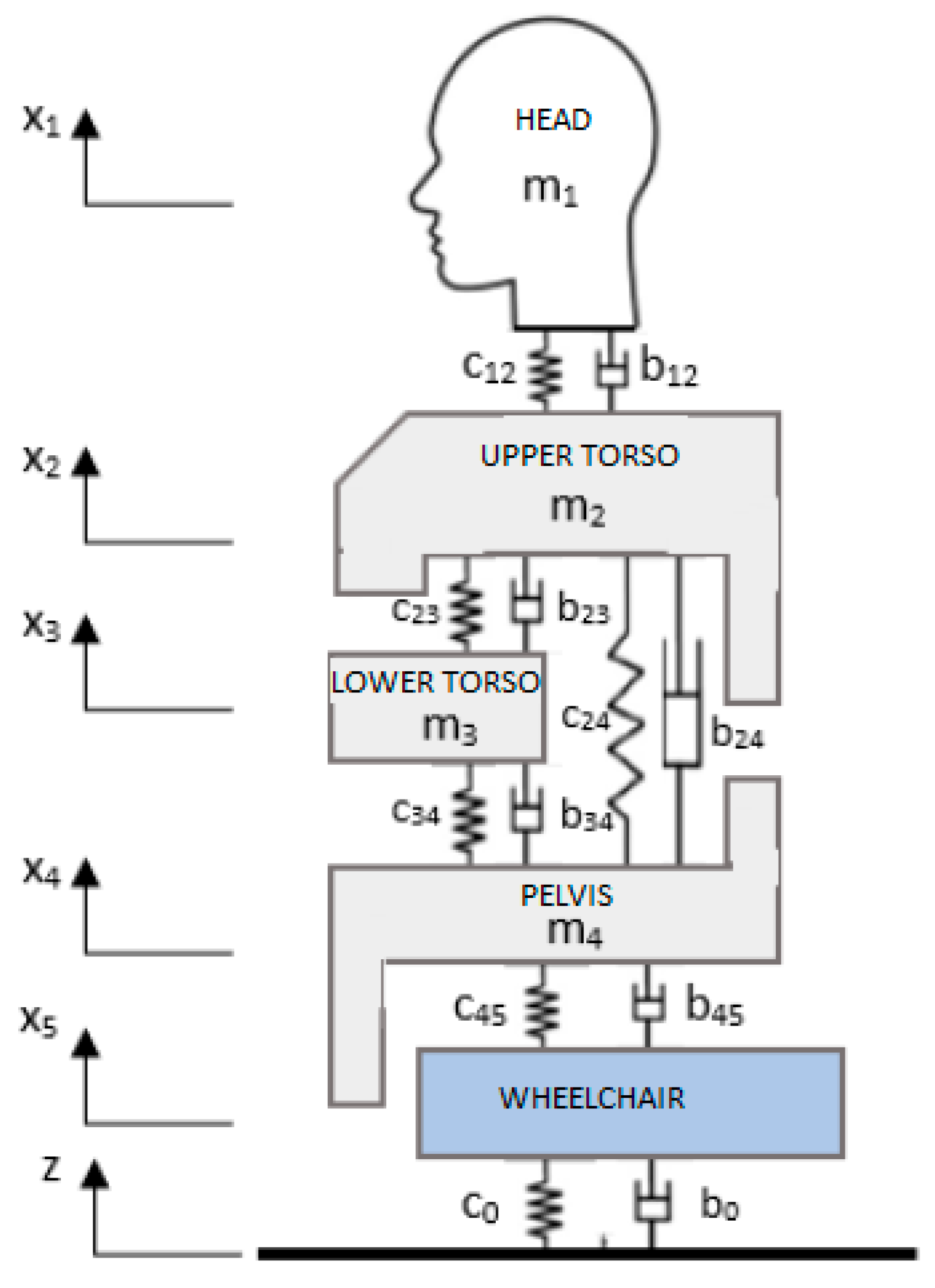


| Mass (mi) [kg] | Spring Constant (cij) [Nm−1] | Damping Constant (bij) [Nsm−1] |
|---|---|---|
| m1 = 4.17 | c12 = 134,400 | b12 = 250 |
| m2 = 15 | c23 = 10,000 | b23 = 200 |
| m3 = 5.5 | c24 = 192,000 | b24 = 909.1 |
| m4 = 36 | c34 = 20,000 | b34 = 330 |
| m5 = 18 | C45 = 49,341.6 1 | b45 = 2475 1 |
| f [Hz] | 1 | 2 | 4 |
|---|---|---|---|
| Ga [m2s−4Hz−1] | 4.0 × 10−9 | 5.0 × 10−8 | 5.0 × 10−6 |
| [m2s−4Hz−1] | 3.4 × 10−9 | 2.4 × 10−8 | 5.6 × 10−7 |
| Gz [m2Hz−1] | 2.2 × 10−12 | 9.6 × 10−13 | 1.4 × 10−12 |
| Number | Element | Displacement Dispersion σxi [mm] | |
|---|---|---|---|
| Category B/C | Category E/F | ||
| 1 | Head | 1.30 | 7.47 |
| 2 | Upper torso | 1.29 | 7.40 |
| 3 | Lower torso | 1.33 | 7.67 |
| 4 | Pelvis | 1.24 | 7.14 |
| 5 | Wheelchair | 0.74 | 4.22 |
| Number | Element | Acceleration Dispersion σxi [m/s2] | |
|---|---|---|---|
| Category B/C | Category E/F | ||
| 1 | Head | 0.57 | 3.68 |
| 2 | Upper torso | 0.57 | 3.63 |
| 3 | Lower torso | 0.57 | 3.58 |
| 4 | Pelvis | 0.55 | 3.49 |
| 5 | Wheelchair | 0.31 | 1.97 |
| Number | Element | Dispersion | |
|---|---|---|---|
| Displacements σxi [mm] | Accelerations σxi [m/s2] | ||
| 1 | Head | 1.59 | 0.613 |
| 2 | Upper torso | 1.57 | 0.607 |
| 3 | Lower torso | 1.55 | 0.630 |
| 4 | Pelvis | 1.51 | 0.590 |
| 5 | Wheelchair | 0.89 | 0.340 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chwalik-Pilszyk, G.; Cirkl, D.; Kozien, M.S. Application of Polyurethane Foam as a Material for Reducing Vibration of Wheelchair User. Materials 2025, 18, 1280. https://doi.org/10.3390/ma18061280
Chwalik-Pilszyk G, Cirkl D, Kozien MS. Application of Polyurethane Foam as a Material for Reducing Vibration of Wheelchair User. Materials. 2025; 18(6):1280. https://doi.org/10.3390/ma18061280
Chicago/Turabian StyleChwalik-Pilszyk, Gabriela, David Cirkl, and Marek S. Kozien. 2025. "Application of Polyurethane Foam as a Material for Reducing Vibration of Wheelchair User" Materials 18, no. 6: 1280. https://doi.org/10.3390/ma18061280
APA StyleChwalik-Pilszyk, G., Cirkl, D., & Kozien, M. S. (2025). Application of Polyurethane Foam as a Material for Reducing Vibration of Wheelchair User. Materials, 18(6), 1280. https://doi.org/10.3390/ma18061280






