Production and Mechanical Characterization by Compression Tests of Al Alloys with Weaire–Phelan Cells Manufactured by the Lost-PLA Technique
Abstract
1. Introduction
2. Materials and Methods
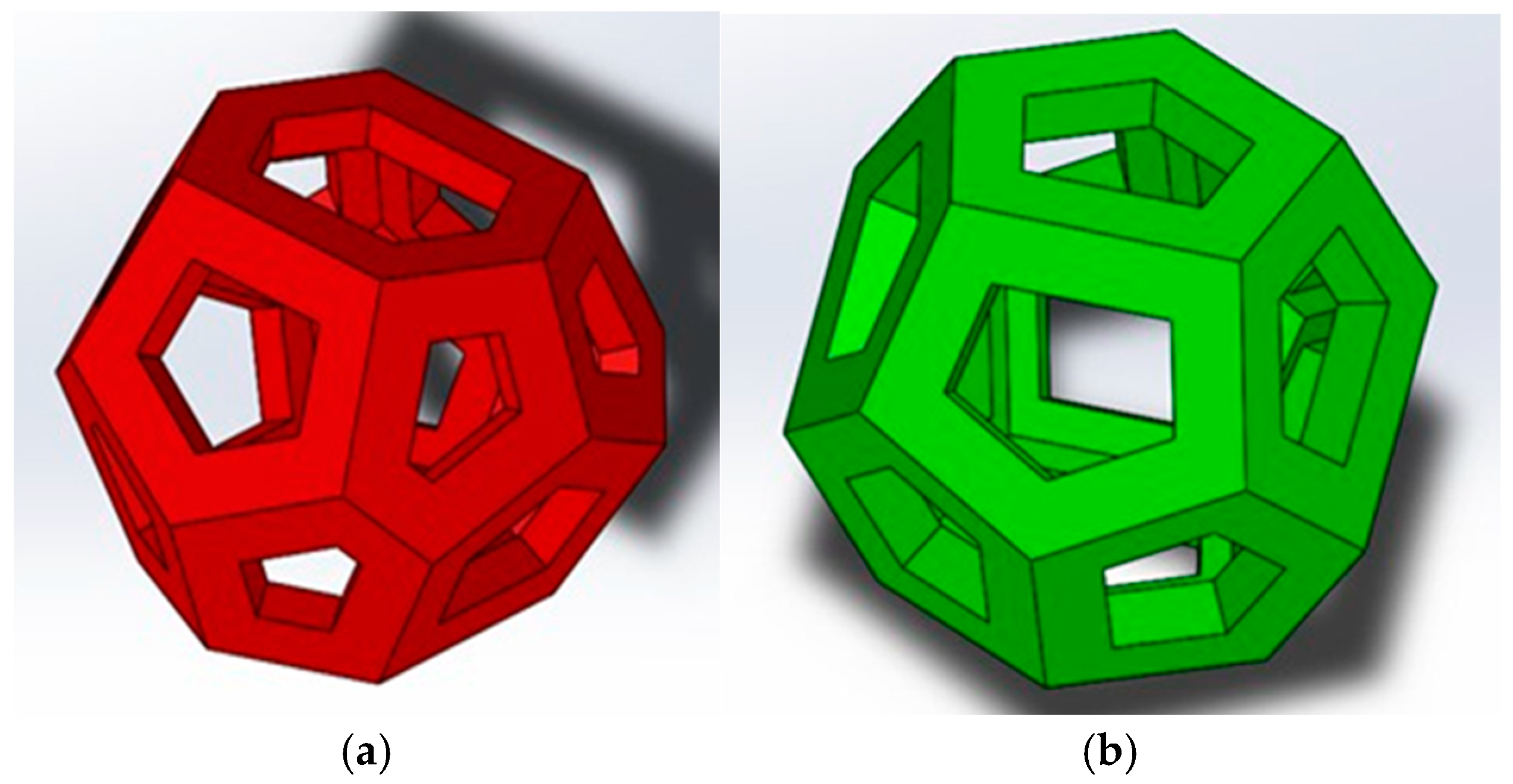
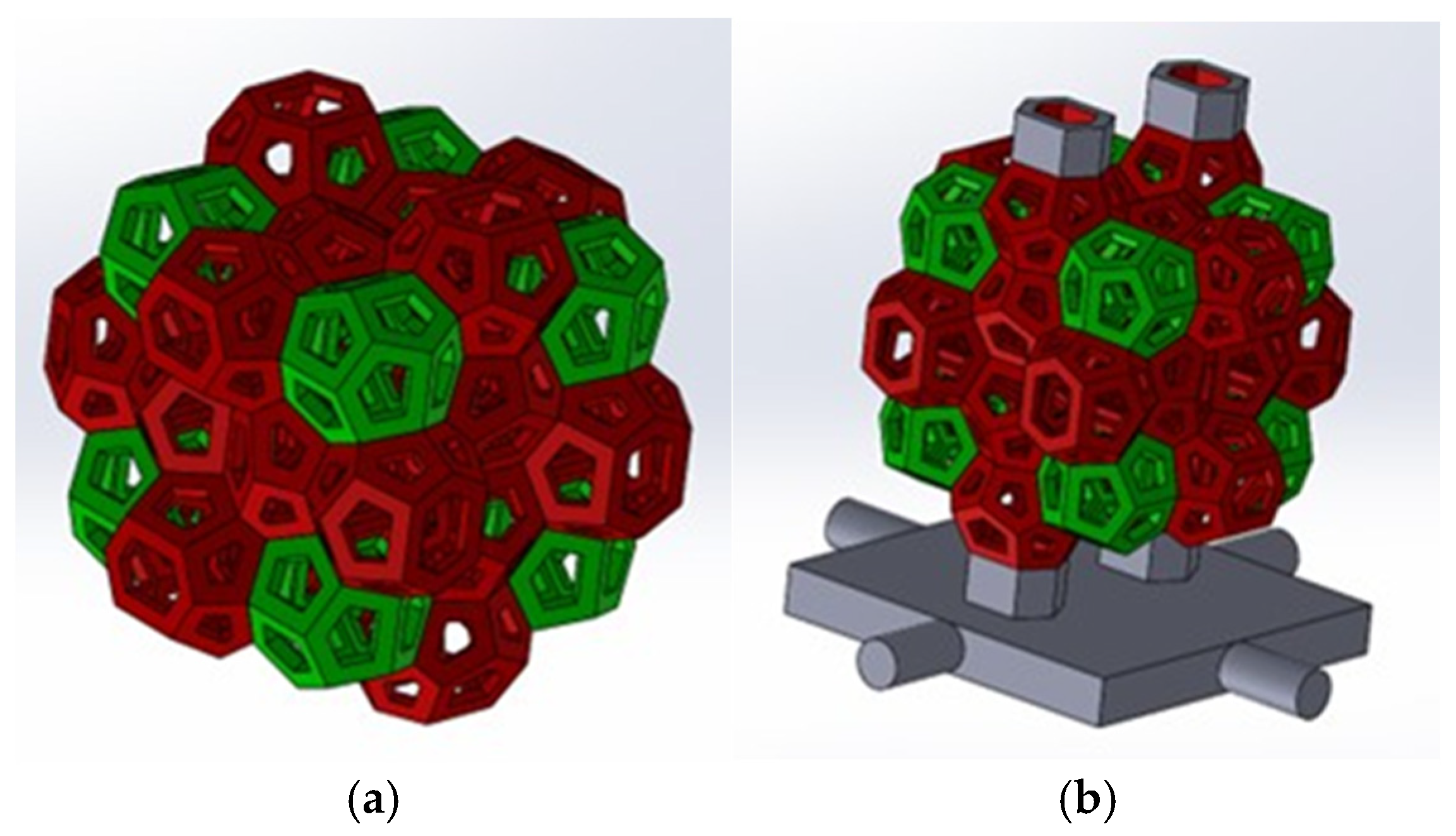
Weaire–Phelan Cell Selection
- Speed: 40 mm/s (PLA) and 60 mm/s (PVA).
- Temperature: 200 °C (extruders) and 60 °C (printing plate).
- Layer thickness: 0.25 mm.
- Fill density (relative to bulk PLA): 20%.
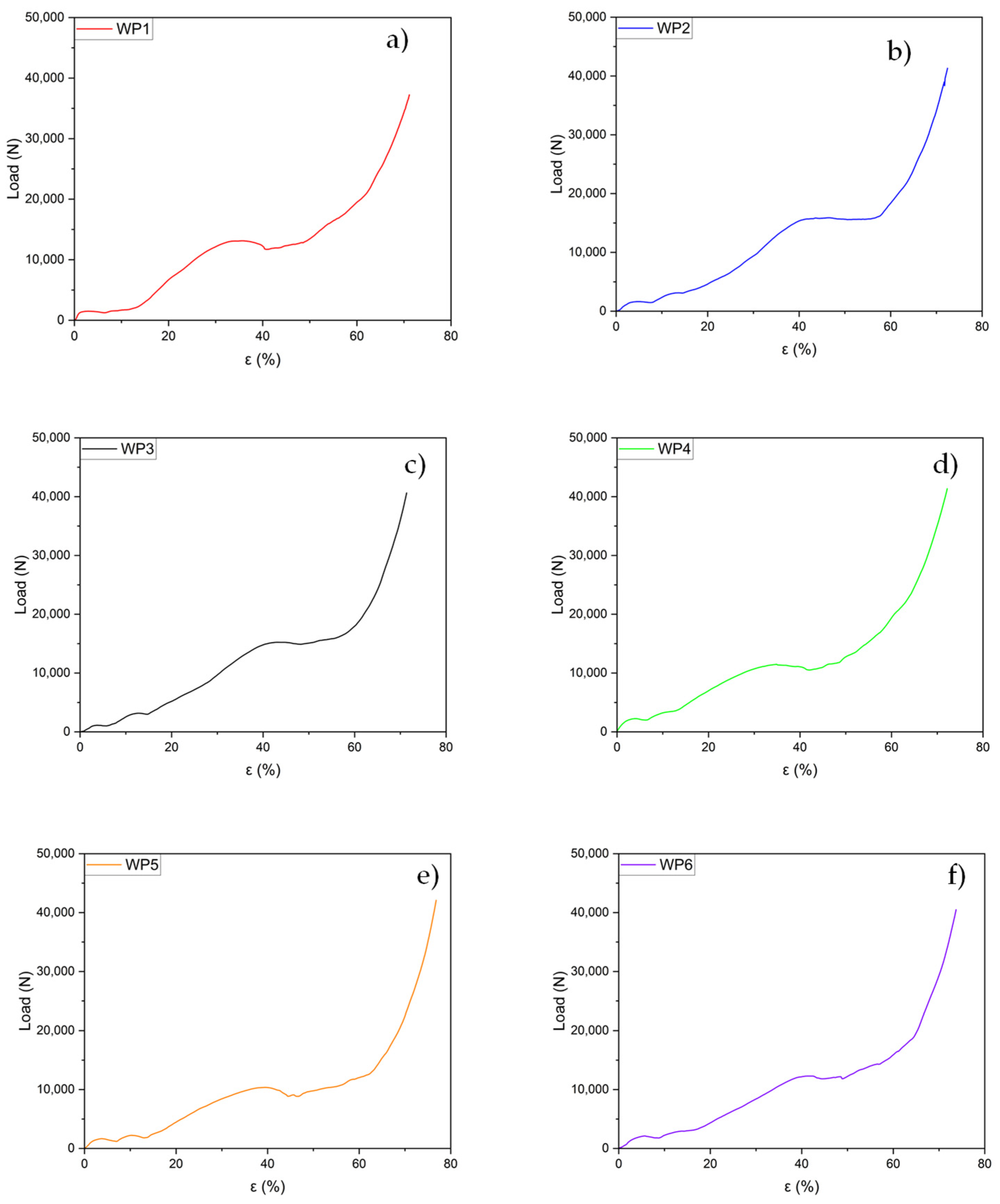
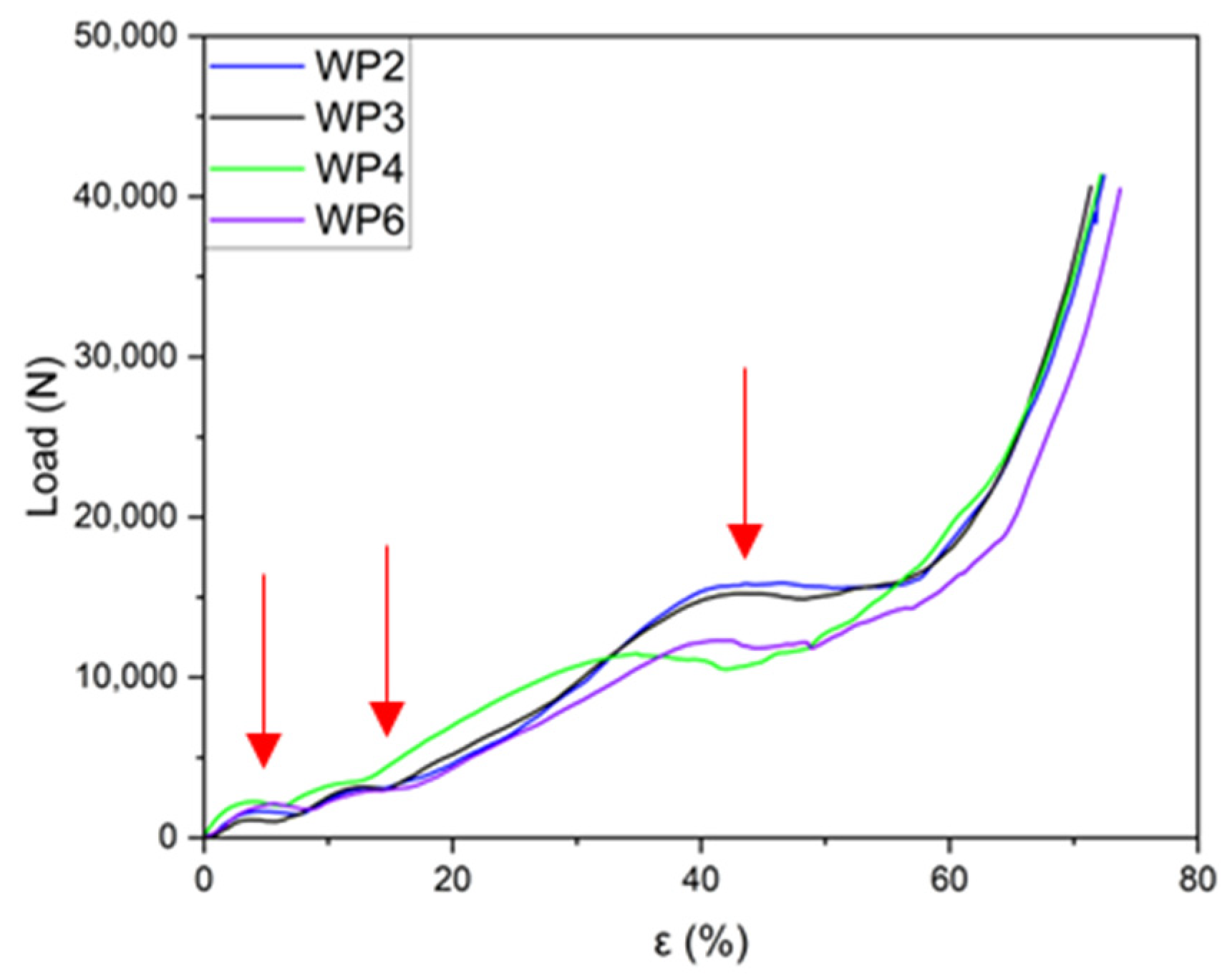
3. Results and Discussion
- Lx = maximum length of the specimen along x;
- Ly = maximum length of the specimen along y;
- Hi = initial height of the specimen;
- Hf = final height of the specimen;
- Wi = initial weight of the specimen;
- Wf = final weight of the specimen;
- SR = resistant section.
4. Conclusions
- (1)
- Geometrical Consistency: The geometric characteristics and weight of the Weaire–Phelan cell structures demonstrate consistent repeatability across the manufacturing process. The theoretical geometric and physical values obtained from the CAD model align closely with the measured values.
- (2)
- Compression Behavior: Static compression tests revealed the typical behavior of open-cell structures. The curves display an initial linear region, followed by three distinct plateaus where the planes progressively collapse as plastic deformation occurs. Final densification takes place when the structure reaches its deformation limit, resulting in a sharp increase in compressive load.
- (3)
- Repeatability of Results: the stress–strain curves exhibit good repeatability, confirming that the manufacturing technique is reliable and that the production process is stable and reproducible.
- (4)
- Specific Absorbed Energy: the specific absorbed energy values are consistently distributed among the six samples, with an average value of 4 J/cm3 and a standard deviation of less than 0.5 J/cm3.
- (5)
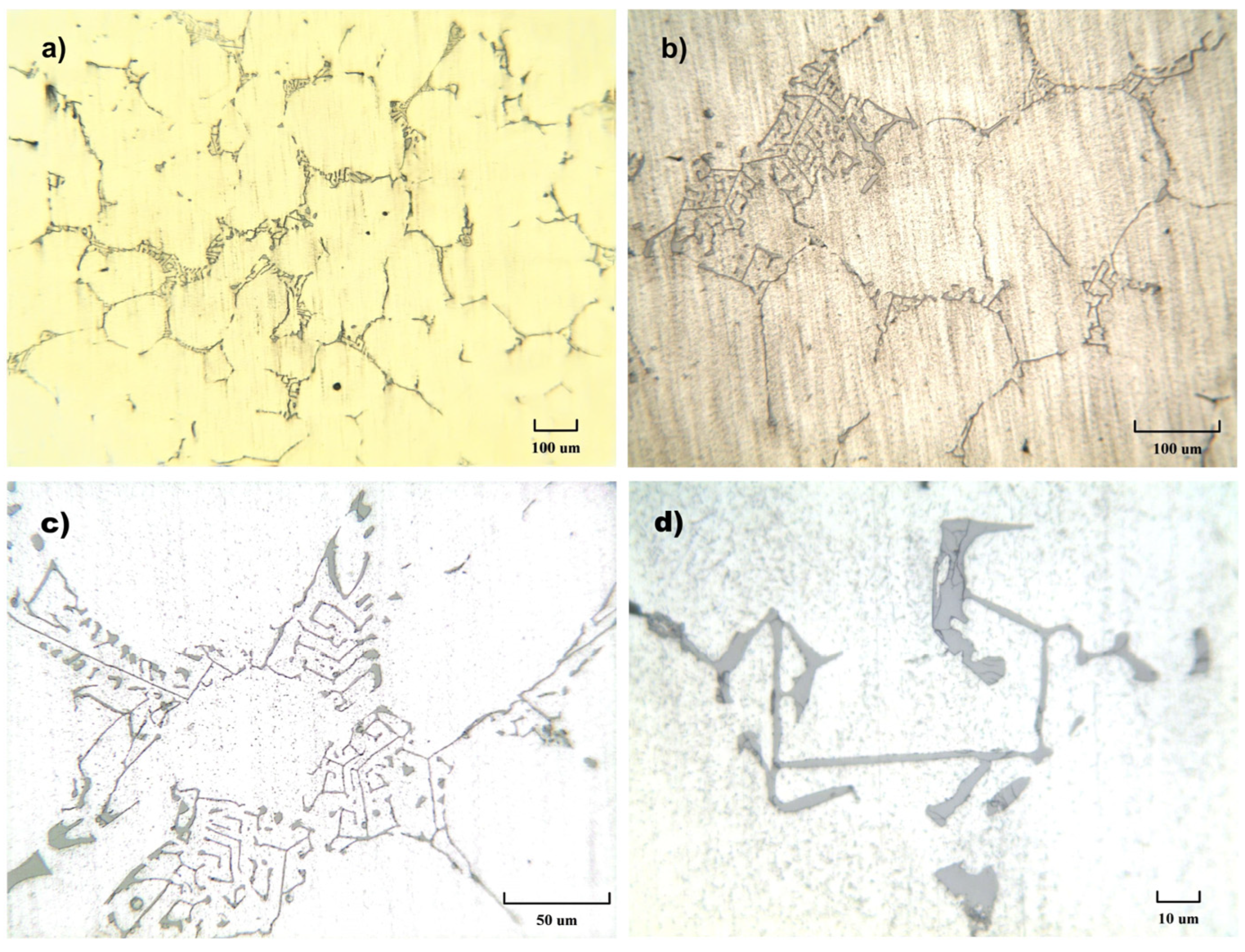
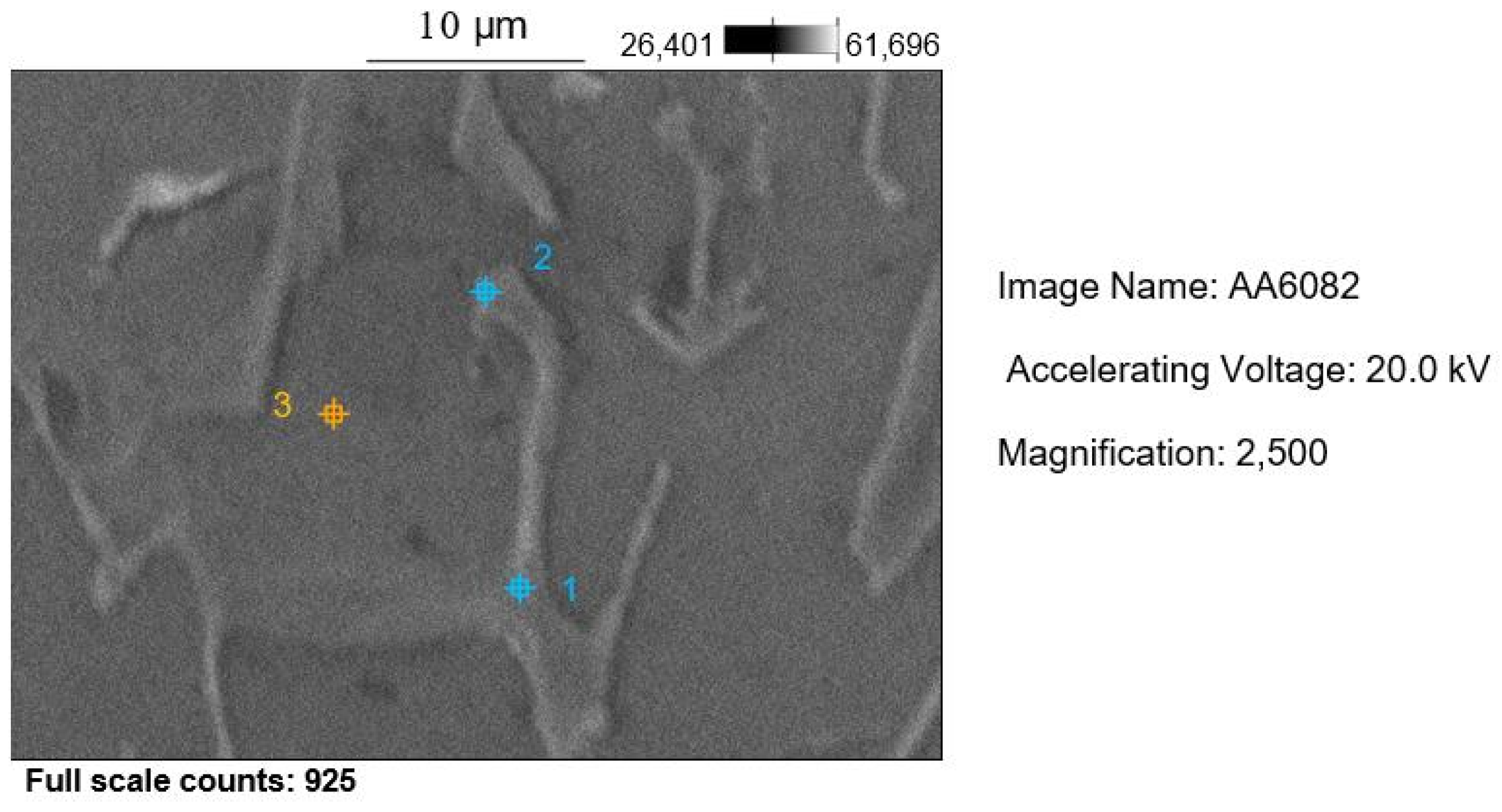
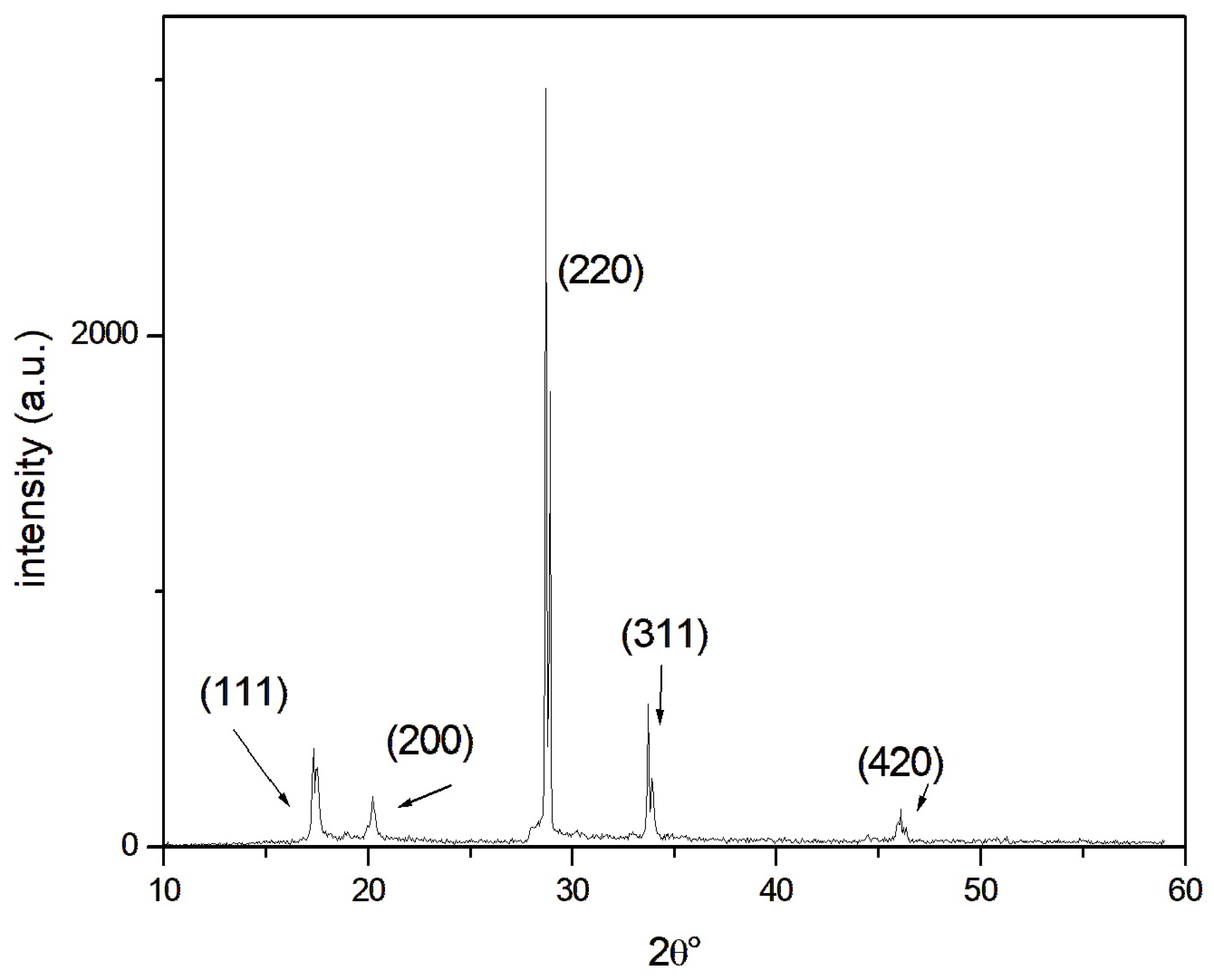
- XRD, OM, SEM, and EDS analyses confirmed the microstructure (α-Al solid solution) deriving from the as-cast condition. The characteristic peaks on the spectrum represent high intensities and are well matched with JCPDS card n. 4-787. Small-size precipitates (AlFeMgMnSi-rich zone), locally identified with EDS analysis, are not detectable with XRD due to their small size and low volume content. The mechanical properties of the alloy, hardness in particular, are in good agreement with the cooling condition.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xue, Z.; Hutchinson, J.W. A Comparative Study of Impulse-Resistant Metal Sandwich Plates. Int. J. Impact Eng. 2004, 30, 1283–1305. [Google Scholar] [CrossRef]
- Ashby, M.F.; Evans, A.; Fleck, N.A.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N.G. Metal Foams A Design Guide; Butterworth-Heinemann: Burlington, MA, USA, 2000; ISBN 978-0-7506-7219-1. [Google Scholar]
- Gibson, L.J. Cellular Solid. Mrs. Bull. 2003, 28, 270–274. [Google Scholar] [CrossRef]
- Costanza, G.; Solaiyappan, D.; Tata, M.E. Properties, Applications and Recent Developments of Cellular Solid Materials: A Review. Materials 2023, 16, 7076. [Google Scholar] [CrossRef] [PubMed]
- Luo, G.; Chen, H.; Li, Y.; Yang, C.; Hu, L.; Ma, S.; Wang, H.; Chen, Z.; Wu, Y.; Wang, M.; et al. Improved Elevated-Temperature Strength and Thermal Stability of Additive Manufactured Al–Ni–Sc–Zr Alloys Reinforced by Cellular Structures. Addit. Manuf. 2024, 90, 104313. [Google Scholar] [CrossRef]
- Yan, H.; Fang, K.; Wu, W.-T.; Zhao, Z.; Feng, F. Thermal Performance Enhancement by Modifying the Spiral Flow and Turbulence Transport in an X-Lattice Cellular Structure. Int. J. Therm. Sci. 2024, 205, 109277. [Google Scholar] [CrossRef]
- Bovesecchi, G.; Coppa, P.; Corasaniti, S.; Costanza, G.; Potenza, M.; Tata, M.E. Experimental Tests of Conduction/Convection Heat Transfer in Very High Porosity Foams with Lattice Structures, Immersed in Different Fluids. Energies 2023, 16, 5959. [Google Scholar] [CrossRef]
- Di Giulio, E.; Nguyen, C.T.; Gloria, A.; Perrot, C.; Dragonetti, R. Three-Dimensional Cellular Structures for Viscous and Thermal Energy Control in Acoustic and Thermoacoustic Applications. Int. J. Heat Mass Transf. 2024, 234, 126076. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, L. Modeling of the Effect of Local Material Imperfection to the Structural Mechanical Property Variability of 2D Finite-Size Cellular Structures. Compos. Struct. 2021, 262, 113610. [Google Scholar] [CrossRef]
- Shuang, X.; Qingtian, D.; Xinbo, L.; Jiabao, Z.; Jinpeng, W.; Zhirong, Y. Energy Absorption and Deformation of Cellular Structures with Dovetail Joints. Mech. Res. Commun. 2025, 143, 104353. [Google Scholar] [CrossRef]
- Bienvenu, Y. Application and Future of Solid Foams. Comptes Rendus. Phys. 2014, 15, 719–730. [Google Scholar] [CrossRef]
- Andrews, E.; Sanders, W.; Gibson, L.J. Compressive and Tensile Behaviour of Aluminum Foams. Mater. Sci. Eng. A 1999, 270, 113–124. [Google Scholar] [CrossRef]
- Bhuvanesh, M.; Costanza, G.; Tata, M.E. Research Progress on Mechanical Behavior of Closed-Cell Al Foams Influenced by Different TiH2 and SiC Additions and Correlation Porosity-Mechanical Properties. Appl. Sci. 2023, 13, 6755. [Google Scholar] [CrossRef]
- Samuel, A.M.; Samuel, E.; Songmene, V.; Samuel, F.H. A Review on Porosity Formation in Aluminum-Based Alloys. Materials 2023, 16, 2047. [Google Scholar] [CrossRef]
- Parveez, B.; Jamal, N.A.; Anuar, H.; Ahmad, Y.; Aabid, A.; Baig, M. Microstructure and Mechanical Properties of Metal Foams Fabricated via Melt Foaming and Powder Metallurgy Technique: A Review. Materials 2022, 15, 5302. [Google Scholar] [CrossRef] [PubMed]
- Pawlowski, P.; Stanczak, M.; Broniszewska-Wojdat, P.; Blanc, L.; Fras, T.; Rusinek, A. Energy-Absorption Capacity of Additively Manufactured AlSi10Mg Cellular Structures Subjected to a Blast-Induced Dynamic Compression—Experimental and Numerical Study. Int. J. Impact Eng. 2025, 198, 105216. [Google Scholar] [CrossRef]
- Ceci, A.; Costanza, G.; Savi, G.; Tata, M.E. Optimization of the Lost PLA Production Process for the Manufacturing of Al-Alloy Porous Structures: Recent Developments, Macrostructural and Microstructural Analysis. Int. J. Lightweight Mater. Manuf. 2024, 7, 662–667. [Google Scholar] [CrossRef]
- Myers, D.; Abdel-Wahab, A.; Hafeez, F.; Kovacev, N.; Essa, K. Optimisation of the Additive Manufacturing Parameters of Polylactic Acid (PLA) Cellular Structures for Biomedical Applications. J. Mech. Behav. Biomed. Mater. 2022, 136, 105447. [Google Scholar] [CrossRef]
- Kumawat, S.; Deshmukh, S.R.; Ghorpade, R.R. Fabrication of Ti-6Al-4v Cellular Lattice Structure Using Selective Laser Melting for Orthopedic Use: A Review. Mater. Today Proc. 2024, 113, 166–172. [Google Scholar] [CrossRef]
- Lin, J.; Yan, A.; Huang, A.; Tang, Q.; Lu, J.; Xu, H.; Huang, Y.; Luo, T.; Chen, Z.; Zeng, A.; et al. Nickel–Titanium Alloy Porous Scaffolds Based on a Dominant Cellular Structure Manufactured by Laser Powder Bed Fusion Have Satisfactory Osteogenic Efficacy. Mater. Today Bio 2024, 29, 101344. [Google Scholar] [CrossRef]
- Kalpakoglou, T.; Yiatros, S. Metal Foams: A Review for Mechanical Properties under Tensile and Shear Stress. Front. Mater. 2022, 9, 998673. [Google Scholar] [CrossRef]
- Ghiani, C.; Linul, E.; Porcu, M.; Marsavina, L.; Movahedi, N.; Aymerich, F. Metal Foam-Filled Tubes as Plastic Dissipaters in Earthquake-Resistant Steel Buildings. IOP Conf. Ser. Mater. Sci. Eng. 2018, 416, 012051. [Google Scholar] [CrossRef]
- Bari, K.; Bollenbach, L. Spiderweb Cellular Structures Manufactured via Additive Layer Manufacturing for Aerospace Application. J. Compos. Sci. 2022, 6, 133. [Google Scholar] [CrossRef]
- Ceci, A.; Costanza, G.; Tata, M.E. Compressive Behavior, Mechanical Properties and Energy Absorption of Al Honeycomb and Al Closed-Cell Foam: A Comparison. Aerospace 2025, 12, 32. [Google Scholar] [CrossRef]
- Shakibanezhad, R.; Sadighi, M.; Hedayati, R. Numerical and Experimental Study of Quasi-Static Loading of Aluminum Closed-Cell Foams Using Weaire–Phelan and Kelvin Tessellations. Transp. Porous Med. 2022, 142, 229–248. [Google Scholar] [CrossRef]
- Grilec, K.; Marić, G.; Jakovljević, S. A Study On Energy Absorption of Aluminium Foam. BHM Berg- Und Hüttenmännische Monatshefte 2010, 155, 231–234. [Google Scholar] [CrossRef]
- Hassanli, F.; Paydar, M.H. Improvement in Energy Absorption Properties of Aluminum Foams by Designing Pore-Density Distribution. J. Mater. Res. Technol. 2021, 14, 609–619. [Google Scholar] [CrossRef]
- Iandiorio, C.; Mattei, G.; Marotta, E.; Costanza, G.; Tata, M.E.; Salvini, P. The Beneficial Effect of a TPMS-Based Fillet Shape on the Mechanical Strength of Metal Cubic Lattice Structures. Materials 2024, 17, 1553. [Google Scholar] [CrossRef]
- Song, Q.; Shi, J.; Chen, X. Acoustic Emission Characterization Analysis of Quasi-Static and Fatigue Compression Properties of Aluminum Foam. Processes 2023, 11, 998. [Google Scholar] [CrossRef]
- Zhang, Z.; Yan, G.; Sun, M.; Li, S.; Zhang, X.; Song, Y.; Liu, Y. Forced Convective Heat Transfer Performance of Foam-like Structures—Comparison of the Weaire-Phelan and the Kelvin Structures with Real Metal Foam. Int. J. Heat Mass Transf. 2024, 227, 125558. [Google Scholar] [CrossRef]
- Cunsolo, S.; Iasiello, M.; Oliviero, M.; Bianco, N.; Chiu, W.K.S.; Naso, V. Lord Kelvin and Weaire–Phelan Foam Models: Heat Transfer and Pressure Drop. J. Heat Transf. 2015, 138, 022601. [Google Scholar] [CrossRef]
- Krishnan, S.; Garimella, S.V.; Murthy, J.Y. Simulation of Thermal Transport in Open-Cell Metal Foams: Effect of Periodic Unit-Cell Structure. J. Heat Transf. 2008, 130, 024503. [Google Scholar] [CrossRef]
- Buffel, B.; Desplentere, F.; Bracke, K.; Verpoest, I. Modelling Open Cell-Foams Based on the Weaire–Phelan Unit Cell with a Minimal Surface Energy Approach. Int. J. Solids Struct. 2014, 51, 3461–3470. [Google Scholar] [CrossRef]
- Weaire, D.; Phelan, R. A Counter-Example to Kelvin’s Conjecture on Minimal Surfaces. Philos. Mag. Lett. 1994, 69, 107–110. [Google Scholar] [CrossRef]
- Zhang, Z.; Yan, G.; Liu, Y.; Zhang, X.; Sun, M.; Li, S.; Song, Y. Study of Forced Convection Heat Transfer Characteristics in Modified Structures Derived from the Weaire-Phelan Foam Geometry. Int. Commun. Heat Mass Transf. 2024, 159, 108134. [Google Scholar] [CrossRef]
- Araujo, A.L.; Celani, G. Exploring Weaire-Phelan through Cellular Automata: A Proposal for a Structural Variance-Producing Engine. In Proceedings of the Blucher Design Proceedings, Editora Blucher, Buenos Aires, Argentina, 9–11 December 2016; pp. 710–714. [Google Scholar]
- Hao, M.; Wei, C.; Liu, X.; Ge, Y.; Cai, J. Quantitative Evaluation on Mechanical Characterization of Ti6Al4V Porous Scaffold Designed Based on Weaire-Phelan Structure via Experimental and Numerical Analysis Methods. J. Alloys Compd. 2021, 885, 160234. [Google Scholar] [CrossRef]
- Șerban, D.A.; Sărăndan, S.; Negru, R.; Belgiu, G.; Marşavina, L. A Parametric Study of the Mechanical Properties of Open-Cell Kelvin Structures. IOP Conf. Ser. Mater. Sci. Eng. 2018, 416, 012108. [Google Scholar] [CrossRef]
- Kaoua, S.A.; Meriem, H.; Djaffar, D.; Azzaz, M. Numerical Modelling of Metal Foams with Weaire-Phelan Cell. Defect. Diffus. Forum 2013, 334–335, 122–126. [Google Scholar] [CrossRef]
- Zhylgeldiyev, A.; Chernyshov, D.; Haider, S.; Mankovits, T. Modelling of Closed-Cell Aluminum Foam Using Weaire–Phelan Unit Cells. Int. Rev. Appl. Sci. Eng. 2024, 15, 390–396. [Google Scholar] [CrossRef]
- File, M.; Cseke, R.; Huri, D.; Balogh, G.; Mankovits, T. Finite Element Analysis of Closed-Cell Aluminum Foam Approximated with Weaire-Phelan Unit Cell Structure. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1246, 012002. [Google Scholar] [CrossRef]
- Ceci, A.; Cerini, C.; Costanza, G.; Tata, M.E. Production of Al Alloys with Kelvin Cells Using the Lost-PLA Technique and Their Mechanical Characterization via Compression Tests. Materials 2025, 18, 296. [Google Scholar] [CrossRef]
- ISO 6507-1:2023; Metallic Materials—Vickers Hardness Test—Part 1: Test Method. ISO: Geneva, Switzerland, 2023.
- Mrówka-Nowotnik, G.; Sieniawski, J. Influence of Heat Treatment on the Microstructure and Mechanical Properties of 6005 and 6082 Aluminium Alloys. J. Mater. Process. Technol. 2005, 162–163, 367–372. [Google Scholar] [CrossRef]








| Sample | PLA [m] | PVA [m] | Weight PLA [g] | Weight PVA [g] | Weight Tot [g] |
|---|---|---|---|---|---|
| Weaire–Phelan | 2.59 | 4.05 | 20.5 | 31.7 | 52.2 |
| Sample | Volume V [mm3] | Surface S [mm2] | S/V [mm−1] | ρ* Theoretical | ρ* Theoretical [%] |
|---|---|---|---|---|---|
| Weaire–Phelan | 9762.3 | 24,693.1 | 2.53 | 0.296 | 29.6 |
| Samples | Lx [mm] | Ly [mm] | Hi [mm] | SR [mm2] | Wi [g] | ρ/ρ0 (%) |
|---|---|---|---|---|---|---|
| WP1 | 39.6 | 39.1 | 39.3 | 1287.7 | 22.6 | 25.4 |
| WP2 | 39.5 | 39.6 | 40.6 | 23.0 | 25.9 | |
| WP3 | 39.7 | 39.7 | 40.1 | 24.9 | 28.0 | |
| WP4 | 39.7 | 39.6 | 39.8 | 23.3 | 26.2 | |
| WP5 | 37.0 | 39.6 | 39.4 | 19.1 | 21.5 | |
| WP6 | 39.5 | 39.5 | 41.2 | 22.6 | 25.4 |
| Samples | Weight [g] | Weight CAD [g] | ΔW [g] | ΔW [%] | ρ/ρ0 | |
|---|---|---|---|---|---|---|
| WP1 | 22.6 | 26.3 | 3.7 | 14 | 14 | 25.4 |
| WP2 | 23.0 | 3.3 | 12 | 25.9 | ||
| WP3 | 24.9 | 1.4 | 5 | 28.0 | ||
| WP4 | 23.3 | 3.0 | 11 | 26.2 | ||
| WP5 | 19.1 | 7.2 | 27 | 21.5 | ||
| WP6 | 22.6 | 3.7 | 14 | 25.4 |
| Samples | Hf [mm] | ΔH [mm] | ε [%] | [%] | Wf [g] | ΔW [g] | [g] |
|---|---|---|---|---|---|---|---|
| WP1 | 12.0 | −26.3 | −67 | −70 | 22.3 | −0.3 | −0.1 |
| WP2 | 12.3 | −28.3 | −70 | 22.9 | −0.1 | ||
| WP3 | 12.6 | −27.5 | −68 | 24.8 | −0.1 | ||
| WP4 | 12.0 | −27.8 | −70 | 23.2 | −0.1 | ||
| WP5 | 10.3 | −29.1 | −74 | 18.9 | −0.2 | ||
| WP6 | 11.7 | −29.5 | −72 | 22.6 | −0.0 |
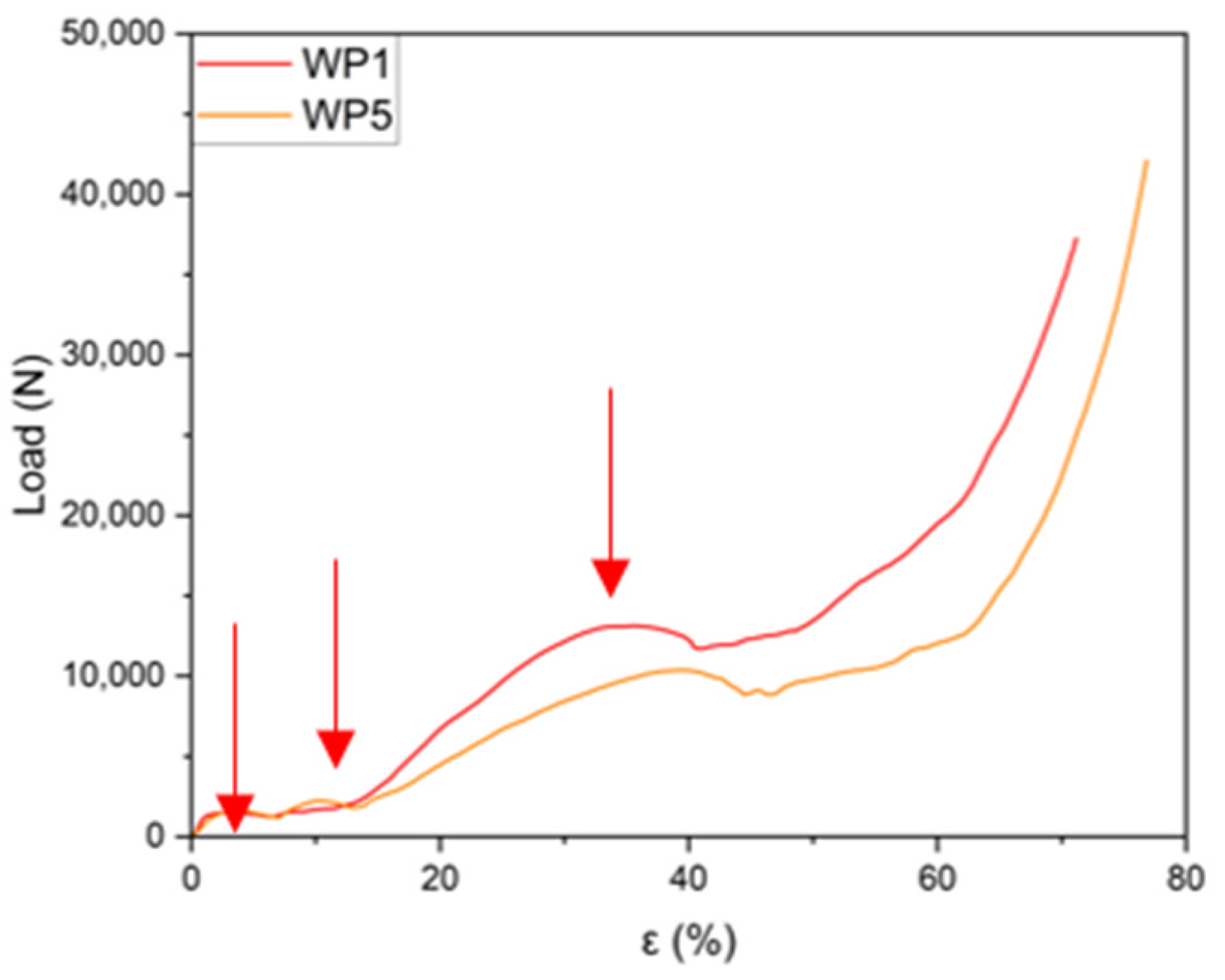
| Samples | Lp1 [kN] | εp1 (%) | Lp2 [kN] | εp2 (%) | Lp3 [kN] | εp3 (%) |
|---|---|---|---|---|---|---|
| WP1 | 1.54 | 1.6–6.7 | 1.67 | 7.3–12.5 | 12.8 | 32.4–48.9 |
| WP2 | 1.67 | 2.5–8.2 | 3.09 | 11.2–14.8 | 15.84 | 40.9–57.1 |
| WP3 | 1.16 | 2.7–5.7 | 3.09 | 11.8–14.6 | 15.20 | 40.3–55.7 |
| WP4 | 2.19 | 2.4–6.2 | 3.60 | 8.1–12.3 | 11.46 | 32.4–47.6 |
| WP5 | 1.67 | 2.3–6.1 | 2.19 | 8.6–12.3 | 10.30 | 39.9–56.0 |
| WP6 | 2.06 | 3.3–7.5 | 2.96 | 10.4–15.8 | 12.23 | 39.3–49.7 |
| WP1 | WP2 | WP3 | WP4 | WP5 | WP6 | |
|---|---|---|---|---|---|---|
| Espec [J/cm3] | 4.34 | 4.35 | 4.32 | 4.18 | 3.15 | 3.69 |
| [J/cm3] | 4.00 | |||||
| Dev stand | 0.49 | |||||
| Al | Mg | Fe | Cu | Si | Mn | |
|---|---|---|---|---|---|---|
| Point 1 | 90.8 | 0.8 | 3.2 | 0.3 | 2.7 | 2.2 |
| Point 2 | 92.4 | 0.6 | 2.6 | 0.2 | 2.4 | 1.8 |
| Point 3 | 99.2 | 0.2 | 0.1 | 0 | 0.4 | 0.1 |
| Samples | HV | Standard Deviation |
|---|---|---|
| As-cast (Air solidified then water cooled) | 50.4 | 3.6 |
| AA 6082 T6 | 109.3 | 1.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ceci, A.; Cerini, C.; Costanza, G.; Tata, M.E. Production and Mechanical Characterization by Compression Tests of Al Alloys with Weaire–Phelan Cells Manufactured by the Lost-PLA Technique. Materials 2025, 18, 1261. https://doi.org/10.3390/ma18061261
Ceci A, Cerini C, Costanza G, Tata ME. Production and Mechanical Characterization by Compression Tests of Al Alloys with Weaire–Phelan Cells Manufactured by the Lost-PLA Technique. Materials. 2025; 18(6):1261. https://doi.org/10.3390/ma18061261
Chicago/Turabian StyleCeci, Alessandra, Corrado Cerini, Girolamo Costanza, and Maria Elisa Tata. 2025. "Production and Mechanical Characterization by Compression Tests of Al Alloys with Weaire–Phelan Cells Manufactured by the Lost-PLA Technique" Materials 18, no. 6: 1261. https://doi.org/10.3390/ma18061261
APA StyleCeci, A., Cerini, C., Costanza, G., & Tata, M. E. (2025). Production and Mechanical Characterization by Compression Tests of Al Alloys with Weaire–Phelan Cells Manufactured by the Lost-PLA Technique. Materials, 18(6), 1261. https://doi.org/10.3390/ma18061261









