Temperature-Dependent Compensation Points in GdxFe1−x Ferrimagnets
Highlights
- We ivestigated the key factors influencing the magnetic compensation temperature (TM) and angular momentum compensation temperature (TA) in GdFe ferrimagnetic alloys and demonstrated their tunability through Gd composition, external magnetic fields, and inter-sublattice exchange strength.
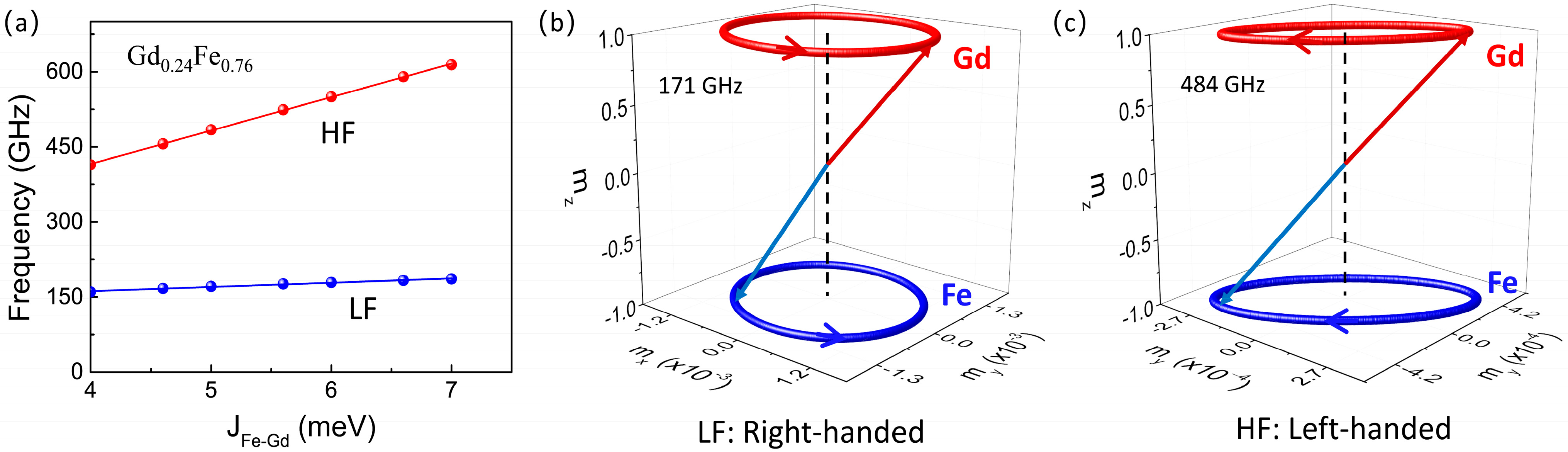
- Analyzed the impact of interlayer coupling between Fe and Gd atoms on resonance frequency and chirality, revealing distinct high- and low-frequency modes with opposite handedness.
Abstract
1. Introduction
2. Atomistic-Level Simulation Model
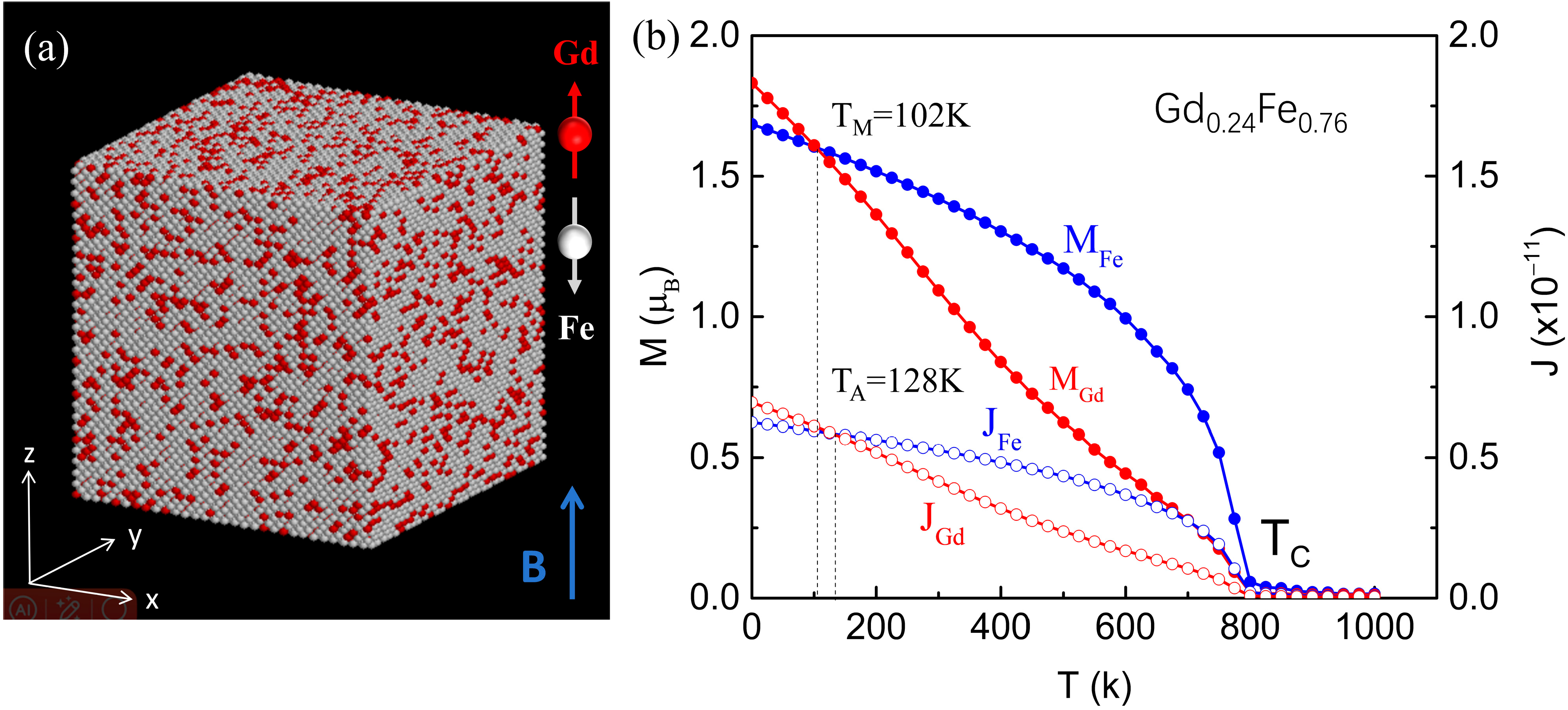
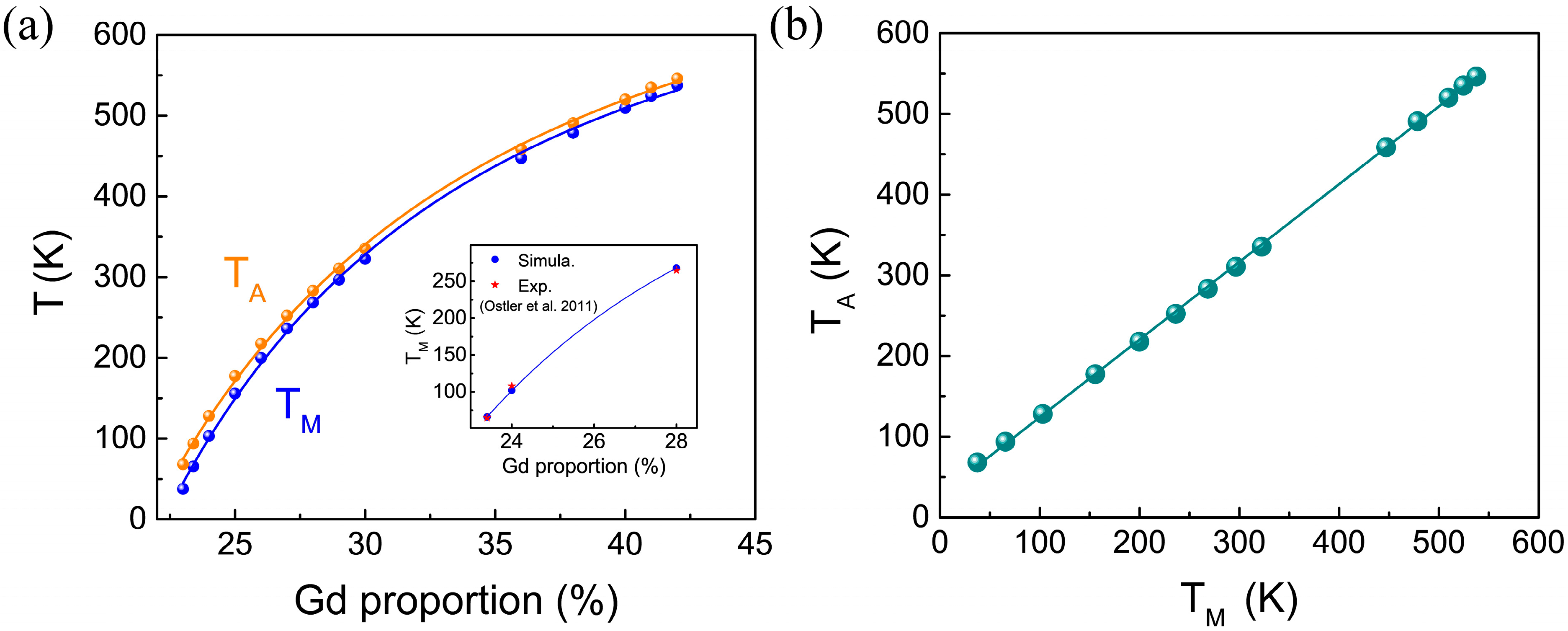
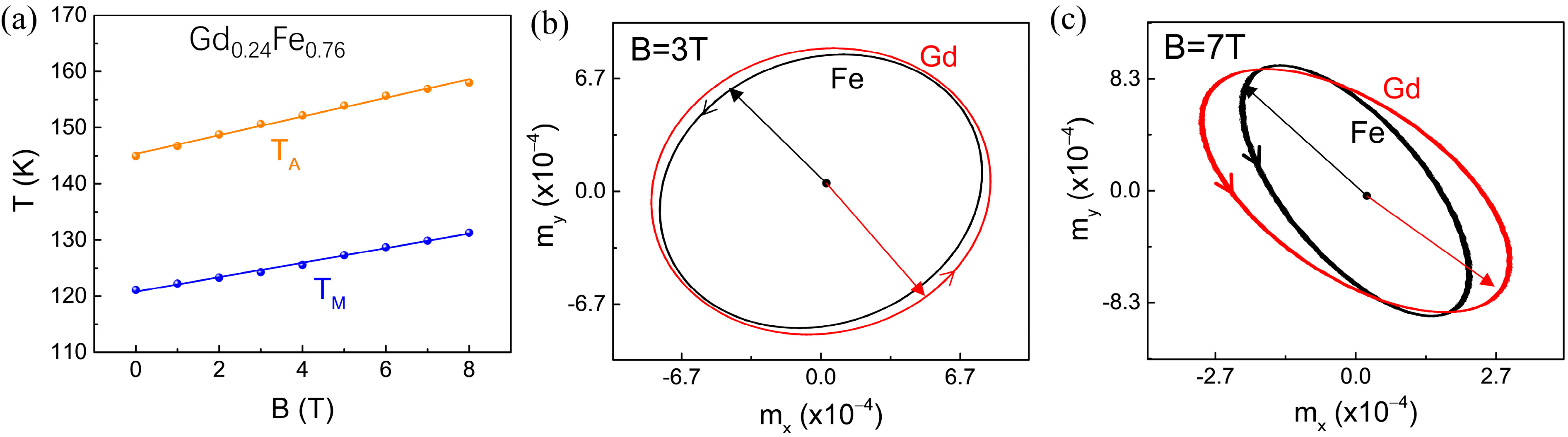
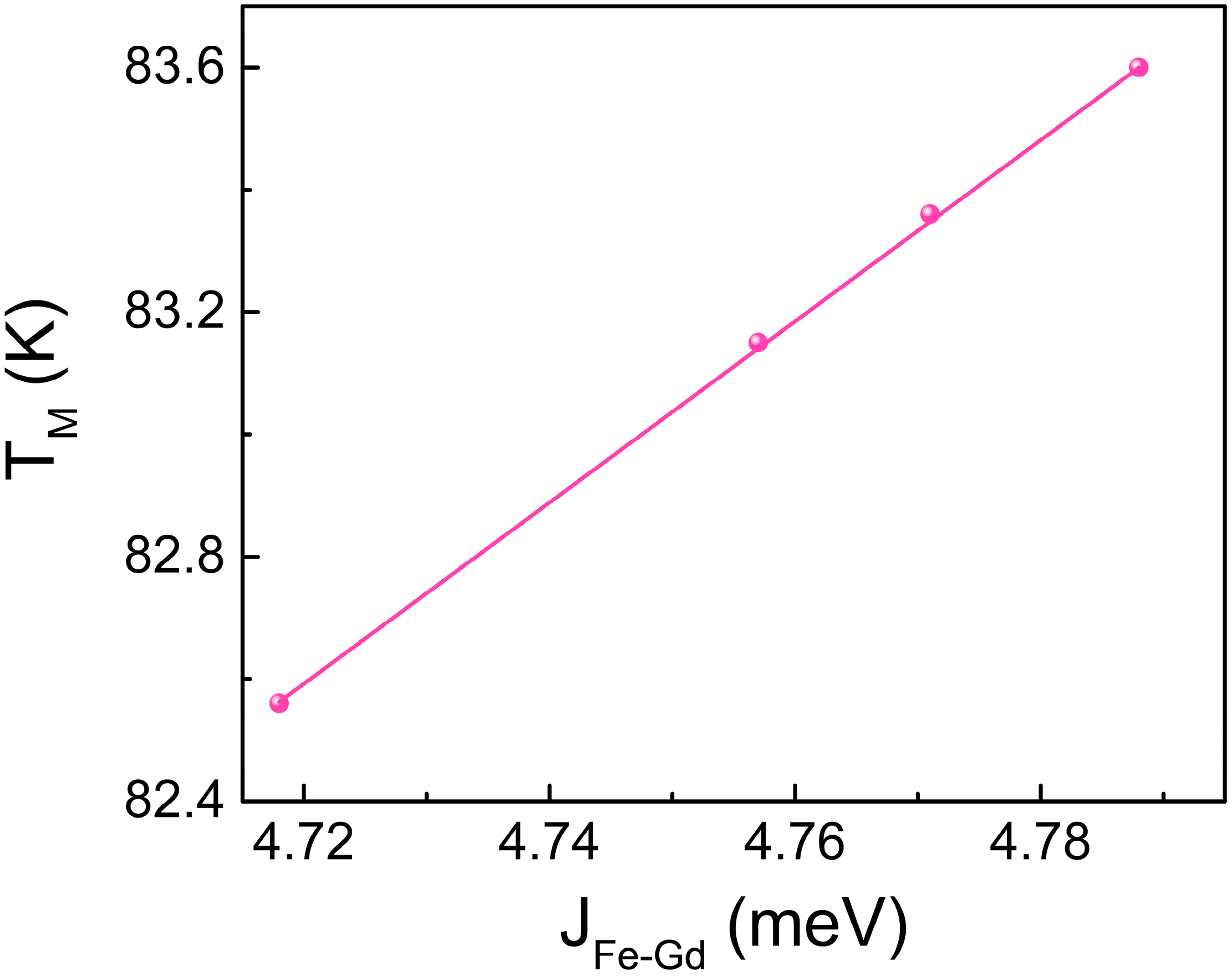
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Back, C.H.; Allenspach, R.; Weber, W.; Parkin, S.S.P.; Weller, D.; Garwin, E.L.; Siegman, H.C. Minimum Field Strength in Precessional Magnetization Reversal. Science 1999, 285, 864. [Google Scholar] [CrossRef] [PubMed]
- Gerrits, T.; Van den Berg, H.A.M.; Hohlfeld, J.; Bär, L.; Rasing, T. Ultrafast precessional magnetization reversal by picosecond magnetic field pulse shaping. Nature 2002, 418, 509–512. [Google Scholar] [CrossRef]
- Kimel, A.V.; Kirilyuk, A.; Tsvetkov, A.; Pisarev, R.V.; Rasing, T. Laser-induced ultrafast spin reorientation in the antiferromagnet TmFeO3. Nature 2004, 429, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Kimel, A.; Kirilyuk, A.; Usachev, P.; Pisarev, R.; Balbashov, A.; Rasing, T. Ultrafast non-thermal control of magnetization by instantaneous photomagnetic pulses. Nature 2005, 435, 655–657. [Google Scholar] [CrossRef]
- Vahaplar, K.; Kalashnikova, A.M.; Kimel, A.V.; Hinzke, D.; Nowak, U.; Chantrell, R.; Tsukamoto, A.; Itoh, A.; Kirilyuk, A.; Rasing, T. Ultrafast path for optical magnetization reversal via a strongly nonequilibrium state. Phys. Rev. Lett. 2009, 103, 117201. [Google Scholar] [CrossRef]
- Ostler, T.A.; Evans, R.F.L.; Chantrell, R.W.; Atxitia, U.; Chubykalo-Fesenko, O.; Radu, I.; Abrudan, R.; Radu, F.; Tsukamoto, A.; Itoh, A.; et al. Crystallographically amorphous ferrimagnetic alloys: Comparing a localized atomistic spin model with experiments. Phys. Rev. B 2011, 84, 024407. [Google Scholar] [CrossRef]
- Yu, T.; Luo, Z.; Bauer, G.E.W. Chirality as generalized spin–orbit interaction in spintronics. Phys. Rep. 2023, 1009, 1–115. [Google Scholar] [CrossRef]
- Lyberatos, A.; Berkov, D.V.; Chantrell, R.W. A method for the numerical simulation of the thermal magnetization fluctuations in micromagnetics. J. Phys. Condens. Matter 1993, 5, 8911. [Google Scholar] [CrossRef]
- Gomonay, E.V.; Loktev, V.M. Spintronics of antiferromagnetic systems (Review Article). Low Temp. Phys. 2014, 40, 17–35. [Google Scholar] [CrossRef]
- Cheng, R.; Daniels, M.W.; Zhu, J.G.; Xiao, D. Antiferromagnetic Spin Wave Field-Effect Transistor. Sci. Rep. 2016, 6, 24223. [Google Scholar] [CrossRef]
- Li, S.; Li, Q.; Xu, J.; Yan, S.; Miao, G.X.; Kang, S.; Dai, Y.; Jiao, J.; Lü, Y. Tunable Optical Mode Ferromagnetic Resonance in FeCoB/Ru/FeCoB Synthetic Antiferromagnetic Trilayers under Uniaxial Magnetic Anisotropy. Adv. Funct. Mater. 2016, 26, 3738–3744. [Google Scholar] [CrossRef]
- Khymyn, R.; Lisenkov, I.; Tiberkevich, V.; Ivanov, B.A.; Slavin, A. Antiferromagnetic THz-frequency Josephson-like Oscillator Driven by Spin Current. Sci. Rep. 2017, 7, 43705. [Google Scholar] [CrossRef] [PubMed]
- Baltz, V.; Manchon, A.; Tsoi, M.; Moriyama, T.; Ono, T.; Tserkovnyak, Y. Antiferromagnetic spintronics. Rev. Mod. Phys. 2018, 90, 015005. [Google Scholar] [CrossRef]
- Duine, R.A.; Lee, K.-J.; Parkin, S.S.P.; Stiles, M.D. Synthetic antiferromagnetic spintronics. Nat. Phys. 2018, 14, 217–219. [Google Scholar] [CrossRef] [PubMed]
- Gomonay, O.; Baltz, V.; Brataas, A.; Tserkovnyak, Y. Antiferromagnetic spin textures and dynamics. Nat. Phys. 2018, 14, 213–216. [Google Scholar] [CrossRef]
- Hu, S.; Zheng, C.; Fan, W.; Liu, Y. Terahertz magnetic excitations in non-collinear antiferromagnetic Mn3Pt: Atomistic-scale dynamical simulations. J. Magn. Magn. Mater. 2023, 588, 171393. [Google Scholar] [CrossRef]
- Hu, S.; Zheng, C.; Chen, C.; Zhou, Y.; Liu, Y. Current-driven spin oscillations in noncollinear antiferromagnetic tunnel junctions. Phys. Rev. B 2024, 109, 174433. [Google Scholar] [CrossRef]
- Zheng, C.; Chen, C.; Hu, S.; Chen, H.-H.; Liu, Y. Terahertz magnetic excitation in a collinear antiferromagnet: Canonical transformation model and atomistic spin simulations. Phys. Lett. A 2024, 516, 129639. [Google Scholar] [CrossRef]
- Kirilyuk, A.; Kimel, A.V.; Rasing, T. Laser-induced magnetization dynamics and reversal in ferrimagnetic alloys. Rep. Prog. Phys. 2013, 76, 026501. [Google Scholar] [CrossRef]
- Fu, Z.; Zhang, Z.; Liu, Y. Temperature-Dependent Magnetization Switching in FeGd Ferrimagnets. SPIN 2018, 8, 1850014. [Google Scholar] [CrossRef]
- Li, W.J.; Wang, C.J.; Zhang, X.M.; Irfan, M.; Khan, U.; Liu, Y.W.; Han, X.F. Experimental investigation and micromagnetic simulations of hybrid CoCr 2 O 4/Ni coaxial nanostructures. Nanotechnology 2018, 29, 245601. [Google Scholar] [CrossRef] [PubMed]
- Stanciu, C.D.; Kimel, A.V.; Hansteen, F.; Tsukamoto, A.; Itoh, A.; Kirilyuk, A.; Rasing, T. Ultrafast spin dynamics across compensation points in ferrimagnetic GdFeCo: The role of angular momentum compensation. Phys. Rev. B 2006, 73, 220402. [Google Scholar] [CrossRef]
- Le Guyader, L.; El Moussaoui, S.; Buzzi, M.; Chopdekar, R.V.; Heyderman, L.J.; Tsukamoto, A.; Itoh, A.; Kirilyuk, A.; Rasing, T.; Kimel, A.V.; et al. Demonstration of laser induced magnetization reversal in GdFeCo nanostructures. Appl. Phys. Lett. 2012, 101, 022410. [Google Scholar] [CrossRef]
- Li, S.; Gao, R.; Cheng, C.; Yan, Y.; Lai, T. Intrinsic subpicosecond magnetization reversal driven by femtosecond laser pulses in GdFeCo amorphous films. Appl. Phys. Lett. 2013, 103, 242411. [Google Scholar] [CrossRef]
- He, W.; Wu, H.-Y.; Cai, J.-W.; Liu, Y.-W.; Cheng, Z.-H. Laser-Induced Magnetization Dynamics of GdFeCo Film Probing by Time Resolved Magneto-Optic Kerr Effect. SPIN 2015, 5, 1540014. [Google Scholar] [CrossRef]
- Wilson, R.B.; Gorchon, J.; Yang, Y.; Lambert, C.-H.; Salahuddin, S.; Bokor, J. Ultrafast magnetic switching of GdFeCo with electronic heat currents. Phys. Rev. B 2017, 95, 180409. [Google Scholar] [CrossRef]
- Stanciu, C.D.; Hansteen, F.; Kimel, A.V.; Kirilyuk, A.; Tsukamoto, A.; Itoh, A.; Rasing, T. All-Optical Magnetic Recording with Circularly Polarized Light. Phys. Rev. Lett. 2007, 99, 047601. [Google Scholar] [CrossRef]
- Radu, I.; Vahaplar, K.; Stamm, C.; Kachel, T.; Pontius, N.; Dürr, H.A.; Ostler, T.A.; Barker, J.; Evans, R.F.L.; Chantrell, R.W.; et al. Transient ferromagnetic-like state mediating ultrafast reversal of antiferromagnetically coupled spins. Nature 2011, 472, 205–208. [Google Scholar] [CrossRef]
- Ostler, T.A.; Barker, J.; Evans, R.F.L.; Chantrell, R.W.; Atxitia, U.; Chubykalo-Fesenko, O.; El Moussaoui, S.; Le Guyader, L.; Mengotti, E.; Heyderman, L.J.; et al. Ultrafast heating as a sufficient stimulus for magnetization reversal in a ferrimagnet. Nat. Commun. 2012, 3, 666. [Google Scholar] [CrossRef]
- Graves, C.E.; Reid, A.H.; Wang, T.; Wu, B.; de Jong, S.; Vahaplar, K.; Radu, I.; Bernstein, D.P.; Messerschmidt, M.; Müller, L.; et al. Nanoscale spin reversal by non-local angular momentum transfer following ultrafast laser excitation in ferrimagnetic GdFeCo. Nat. Mater. 2013, 12, 293–298. [Google Scholar] [CrossRef]
- Mangin, S.; Gottwald, M.; Lambert, C.H.; Steil, D.; Uhlíř, V.; Pang, L.; Hehn, M.; Alebrand, S.; Cinchetti, M.; Malinowski, G.; et al. Engineered materials for all-optical helicity-dependent magnetic switching. Nat. Mater. 2014, 13, 286–292. [Google Scholar] [CrossRef] [PubMed]
- Kirilyuk, A.; Kimel, A.V.; Rasing, T. Ultrafast optical manipulation of magnetic order. Rev. Mod. Phys. 2010, 82, 2731–2784. [Google Scholar] [CrossRef]
- Kim, C.; Lee, S.; Kim, H.G.; Park, J.H.; Moon, K.W.; Park, J.Y.; Yuk, J.M.; Lee, K.J.; Park, B.G.; Kim, S.K.; et al. Distinct handedness of spin wave across the compensation temperatures of ferrimagnets. Nat. Mater. 2020, 19, 980–985. [Google Scholar] [CrossRef]
- Wang, L.; Shen, L.; Bai, H.; Zhou, H.-A.; Shen, K.; Jiang, W. Electrical Excitation and Detection of Chiral Magnons in a Compensated Ferrimagnetic Insulator. Phys. Rev. Lett. 2024, 133, 166705. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, Z.; Liu, L.; Zhang, K.; Meng, Y.; Sun, Y.; Gao, P.; Zhao, H.-W.; Niu, Q.; Li, J. Switching magnon chirality in artificial ferrimagnet. Nat. Commun. 2022, 13, 1264. [Google Scholar] [CrossRef]
- Chen, C.; Zheng, C.; Zhang, J.; Liu, Y. Chirality reversal of resonant modes in GdFe ferrimagnets. Appl. Phys. Lett. 2023, 123, 212403. [Google Scholar] [CrossRef]
- Okamoto, S. Flipping handedness in ferrimagnets. Nat. Mater. 2020, 19, 929–930. [Google Scholar] [CrossRef] [PubMed]
- Hahn, M.B. Temperature in micromagnetism: Cell size and scaling effects of the stochastic Landau–Lifshitz equation. J. Phys. Commun. 2019, 3, 075009. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. On the theory of the dispersion of magnetic permeability in ferromagnetic bodies. Phys. Z. Sowjetunion 1935, 8, 153–169. [Google Scholar]
- Gilbert, T.L.; Kelly, J.M. Anomalous Rotational Damping in Ferromagnetic Sheets. In Proceedings of the First Conference on Magnetism and Magnetic Materials, Pittsburgh, PA, USA, 14–16 June 1955. [Google Scholar]
- Jiao, X.; Zhang, Z.; Liu, Y. Modeling of Temperature Dependence of Magnetization in TbFe Films—An Atomistic Spin Simulation Study. SPIN 2016, 6, 1650003. [Google Scholar] [CrossRef]
- Mekonnen, A.; Cormier, M.; Kimel, A.V.; Kirilyuk, A.; Hrabec, A.; Ranno, L.; Rasing, T. Femtosecond laser excitation of spin resonances in amorphous ferrimagnetic Gd1-xCox alloys. Phys. Rev. Lett. 2011, 107, 117202. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Zheng, C.; Hu, S.; Zhang, J.; Liu, Y. Temperature-Dependent Compensation Points in GdxFe1−x Ferrimagnets. Materials 2025, 18, 1193. https://doi.org/10.3390/ma18061193
Chen C, Zheng C, Hu S, Zhang J, Liu Y. Temperature-Dependent Compensation Points in GdxFe1−x Ferrimagnets. Materials. 2025; 18(6):1193. https://doi.org/10.3390/ma18061193
Chicago/Turabian StyleChen, Chao, Cuixiu Zheng, Shanshan Hu, Jianwei Zhang, and Yaowen Liu. 2025. "Temperature-Dependent Compensation Points in GdxFe1−x Ferrimagnets" Materials 18, no. 6: 1193. https://doi.org/10.3390/ma18061193
APA StyleChen, C., Zheng, C., Hu, S., Zhang, J., & Liu, Y. (2025). Temperature-Dependent Compensation Points in GdxFe1−x Ferrimagnets. Materials, 18(6), 1193. https://doi.org/10.3390/ma18061193





