Interlayer Parallel Connection of Multiple Helmholtz Resonators for Optional Broadband Low Frequency Sound Absorption
Abstract
1. Introduction
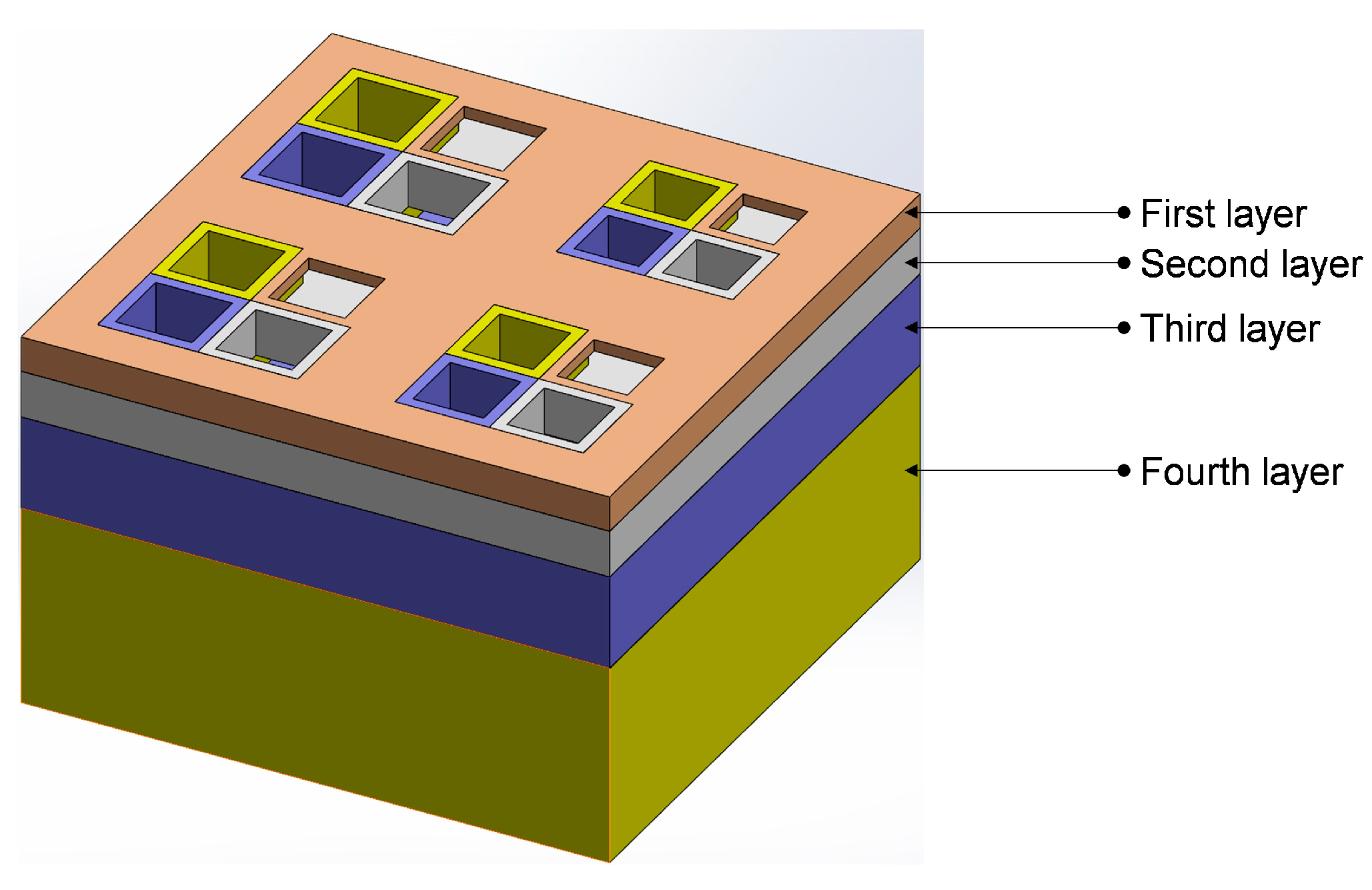
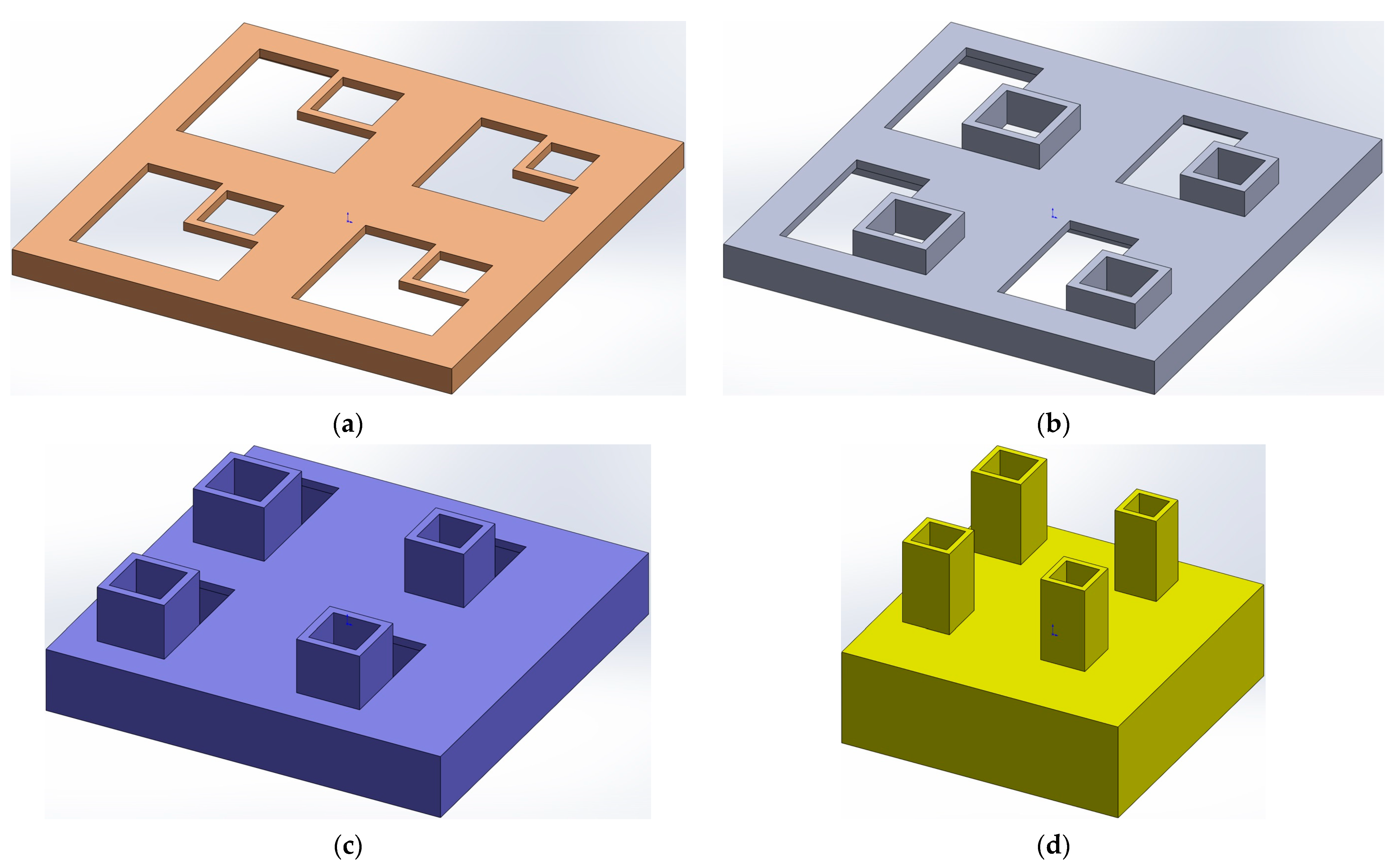
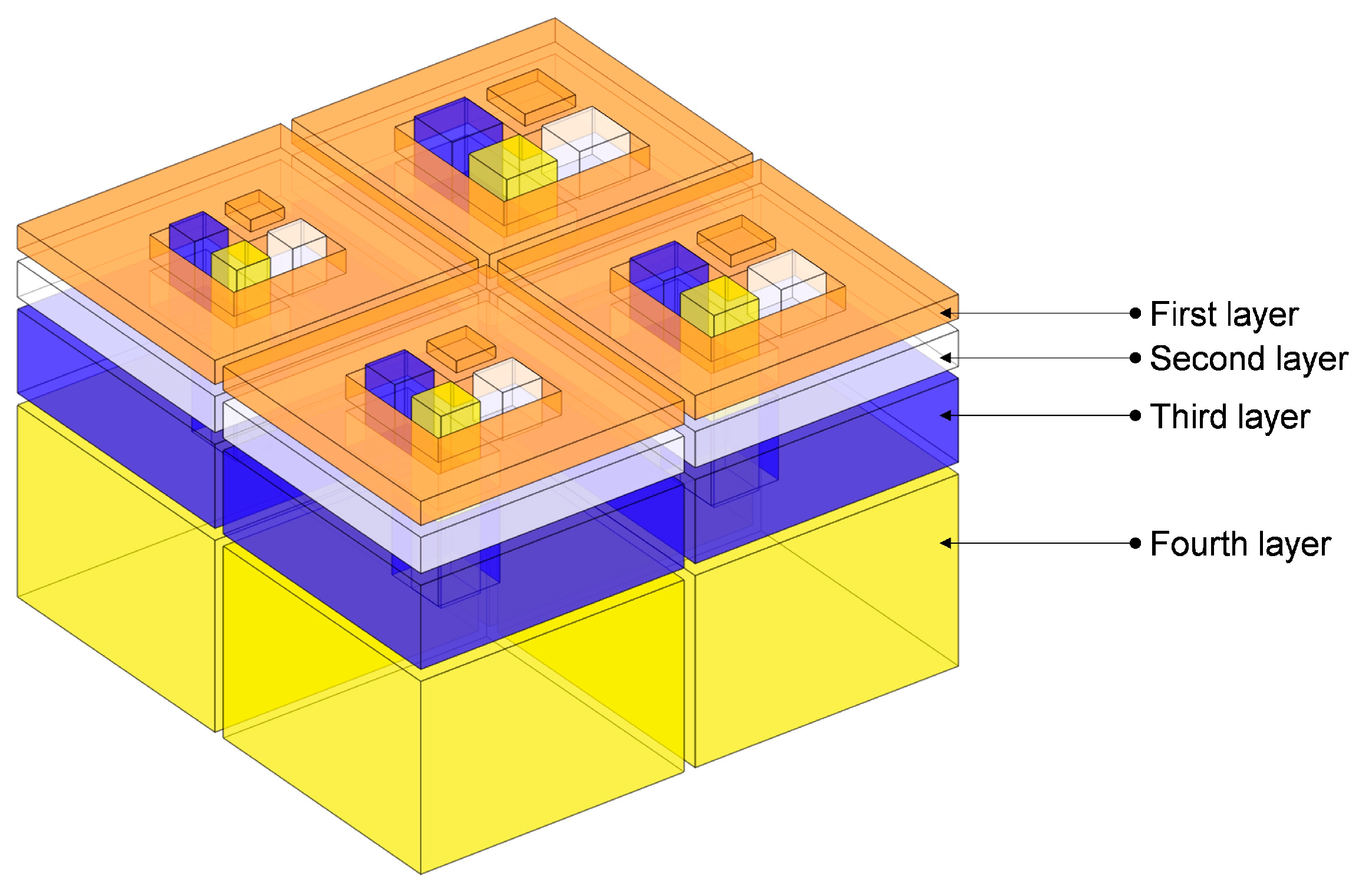
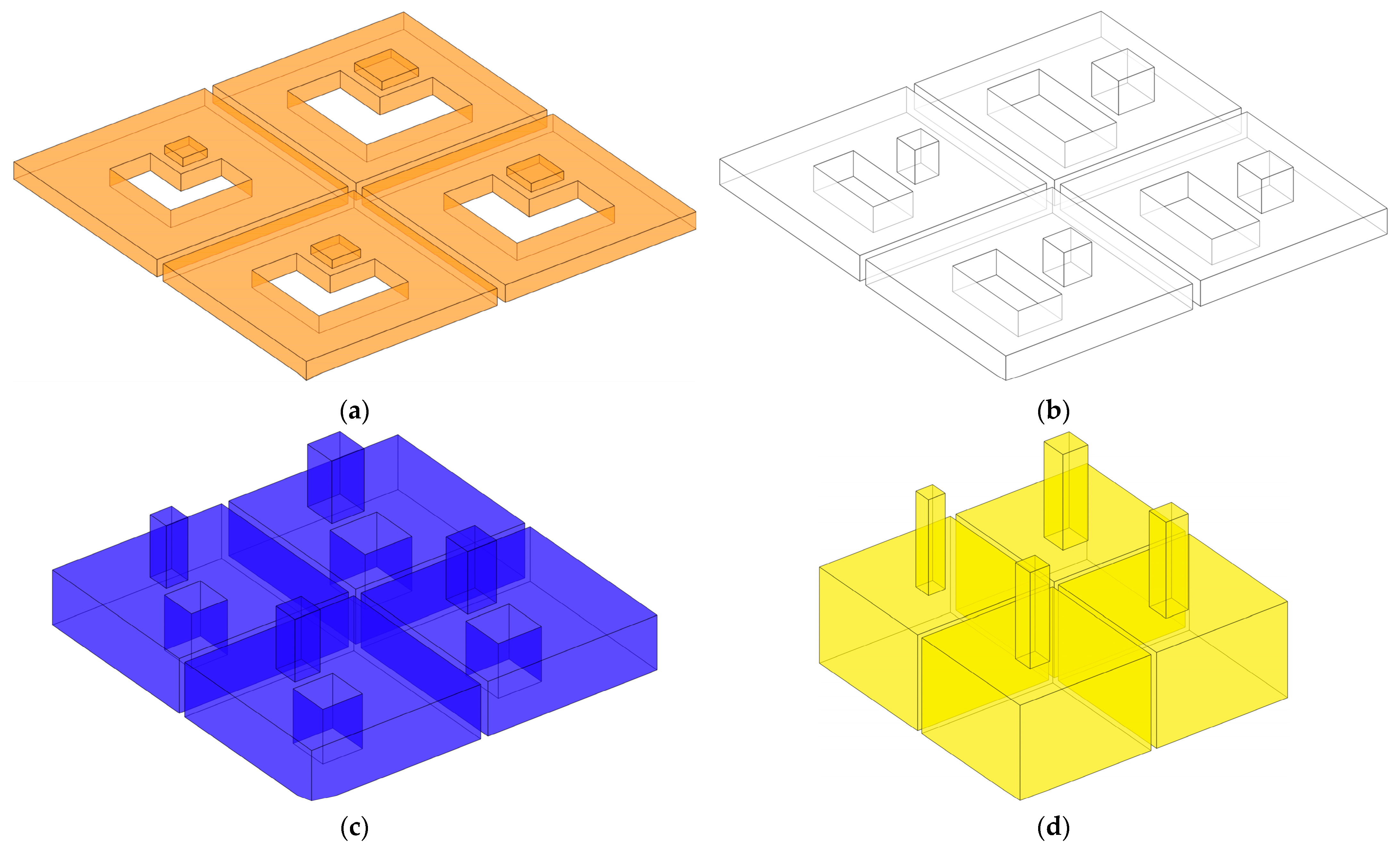
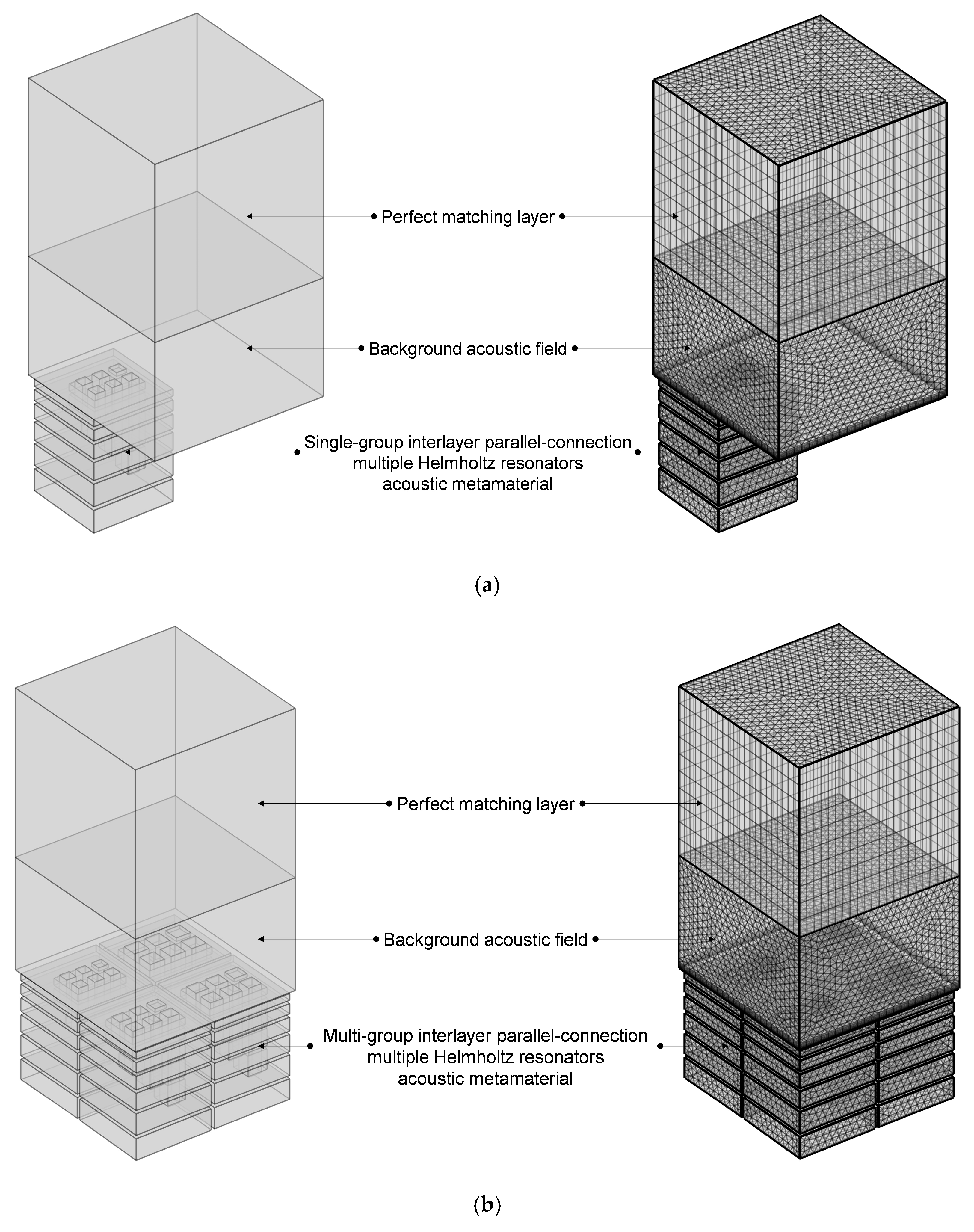
2. Structural Design
3. Acoustic Finite Element Simulation
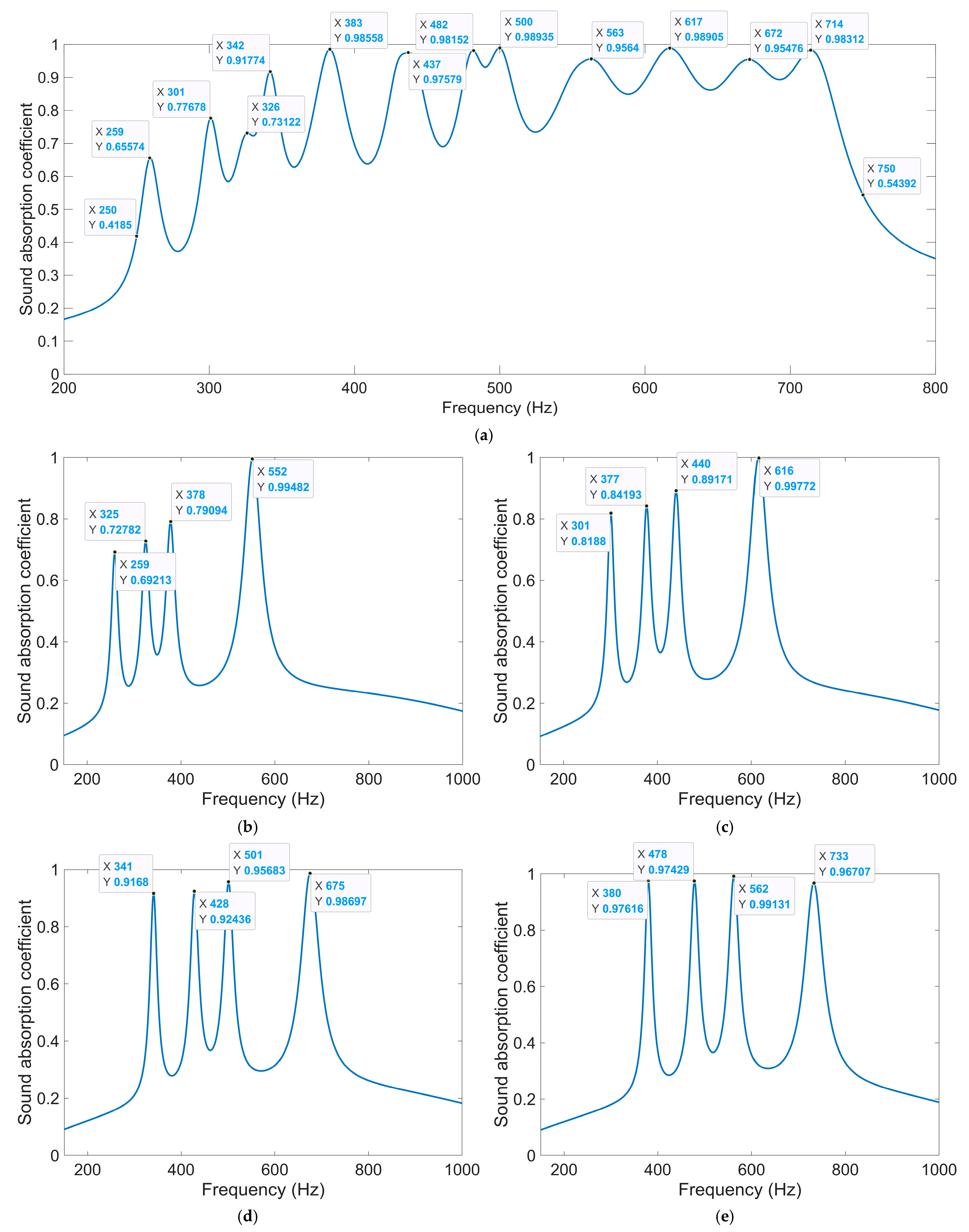
4. Results and Discussions
4.1. Experimental Validation
4.2. Further Investigations and Discussions
4.2.1. Parametric Optimization
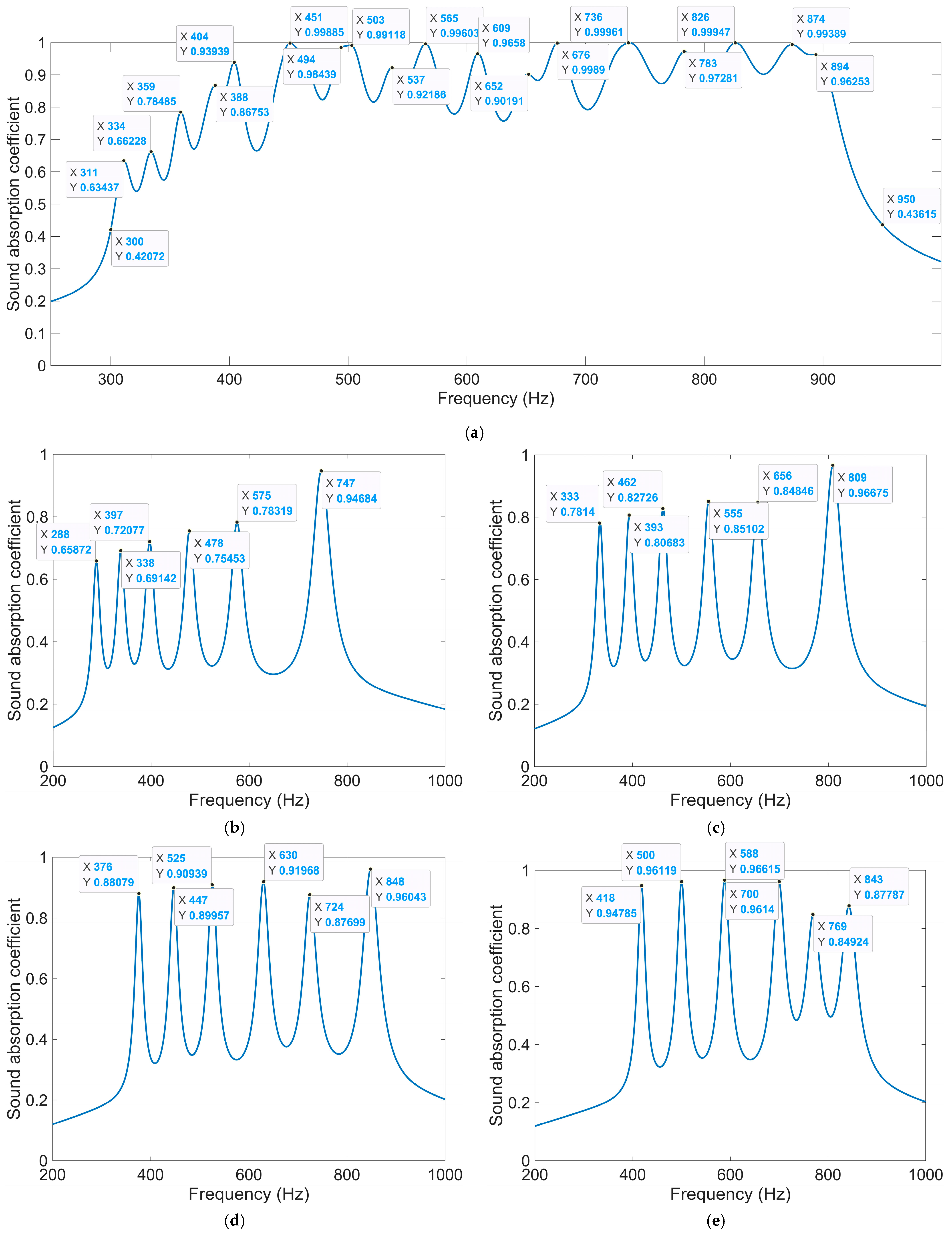
4.2.2. Optimization of Thickness of Each Layer
4.2.3. Alteration of Number of Layers
5. Conclusions
- (1)
- The proposed IPC–MHR acoustic metamaterial consists of several layers, and the Helmholtz resonators among different layers are connected in parallel, which settles the conflict between the number of Helmholtz resonators and the volume of the rear cavity for each chamber with the given front area of the single-layer acoustic metamaterial.
- (2)
- The sound absorption property of IPC–MHR acoustic metamaterial is studied by finite element simulation and further optimized by particle swarm algorithm. The average sound absorption coefficient in the discrete frequency band [200 Hz, 300 Hz] U [400 Hz, 600 Hz] U [800 Hz, 1250 Hz] is 0.7769 for the IPC–MHR with four layers. Through the optimization of the thickness of each layer, the average sound absorption coefficient in 250–750 Hz is up to 0.8068. Similarly, the optimized IPC–MHR with six layers gains an average sound absorption coefficient of 0.8454 in 300–950 Hz, which exhibits an excellent sound absorption performance in the low-frequency range with a wide frequency band.
- (3)
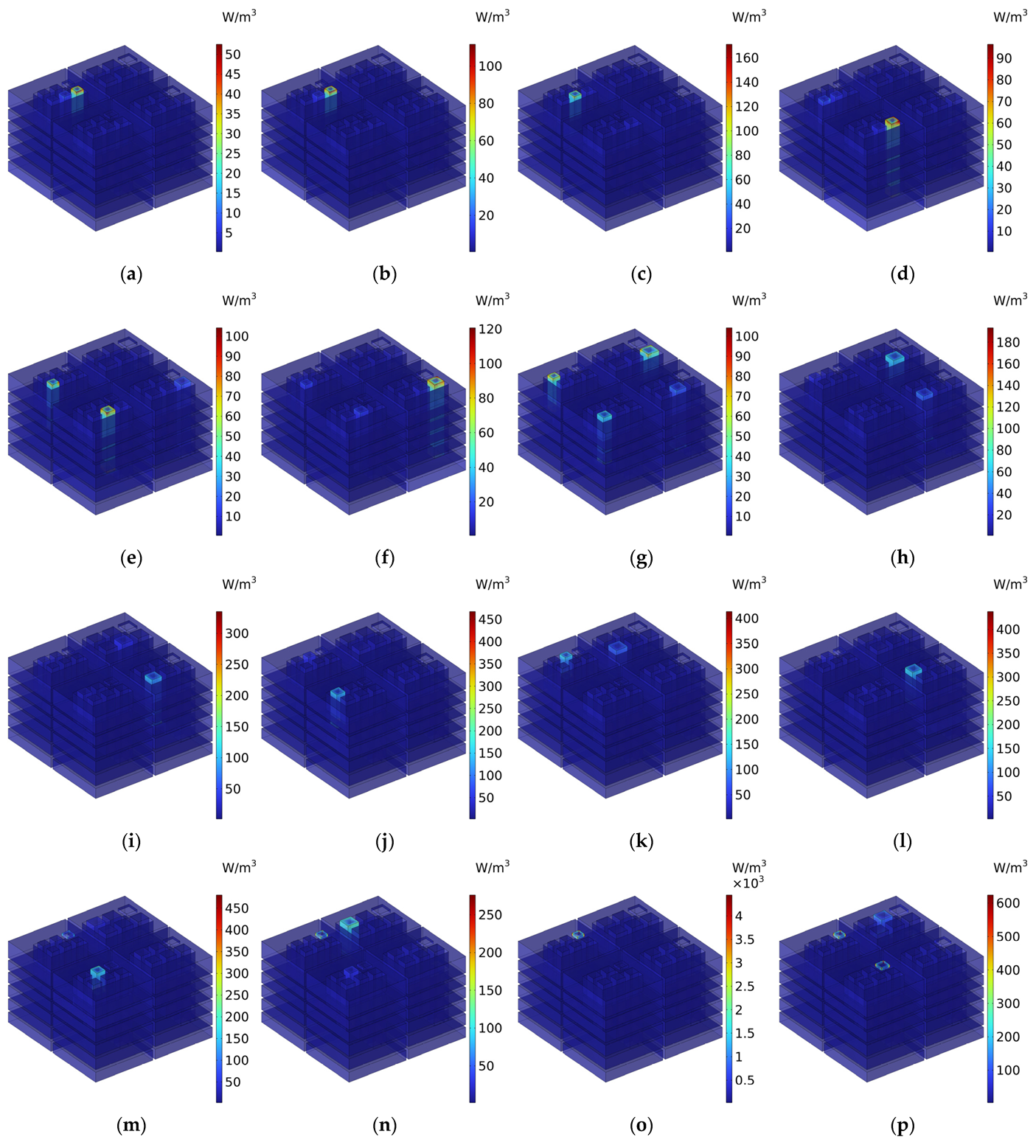
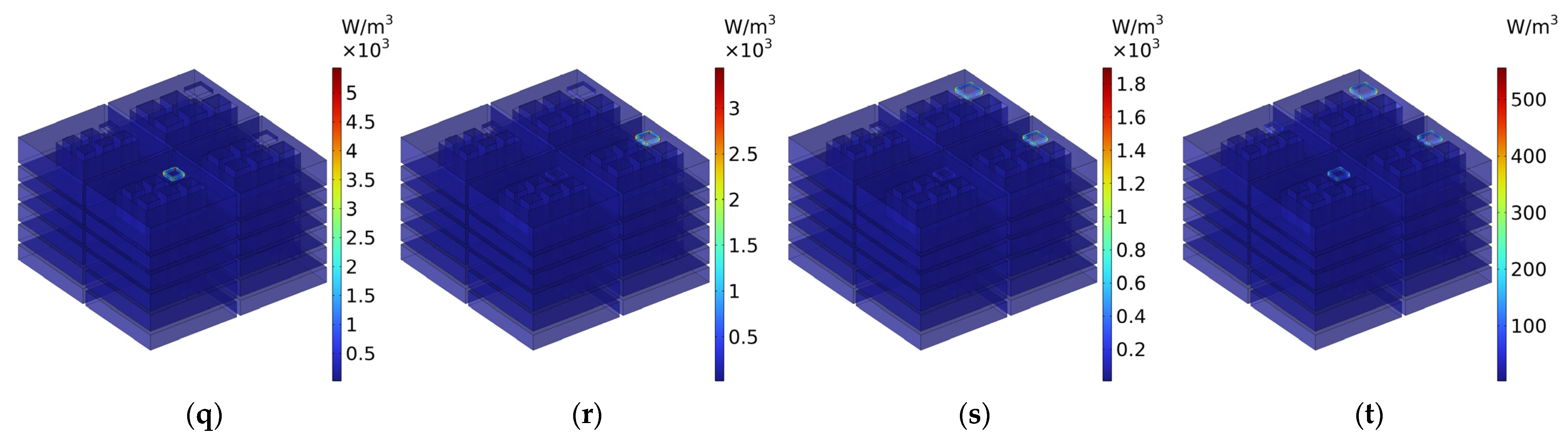
- The sound absorption mechanism of IPC–MHR proposed in this research is displayed intuitively by the distributions of the viscous power densities for representative frequencies, which proves that the final absorption effect is mainly realized by the resonance effect of each resonator and assisted by coupling effect among different resonators.
- (4)
- The actual sound absorption performance of IPC–MHR is validated by standing wave tube measurement with the sample fabricated through the additive manufacturing method. The consistency between the simulation result and the experimental data is satisfactory, which can prove the effectiveness of this IPC–MHR and the accuracy of the finite element simulation model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbols | Meanings |
|---|---|
| α | Sound absorption coefficient |
| Ztotal | The total acoustic impedance of the IPC–MHR acoustic metamaterial |
| Z0 | The acoustic impedance of air under the condition of normal temperature and pressure |
| t0 | The thickness of all the wall |
| S0 | The side length of the cross-sectional shape for the multi-group IPC–MHR |
| T1 | The total thickness of the first layer |
| T2 | The total thickness of the second layer |
| T3 | The total thickness of the third layer |
| T4 | The thickness of the fourth layer |
| a | The side length of the square incident aperture for the single-group IPC–MHR |
| ai | The side length of the square incident aperture for the multi-group IPC–MHR |
References
- Del Rosario-Gilabert, D.; Carbajo, J.; Hernández-Pozo, M.; Valenzuela-Miralles, A.; Ruiz, D.; Poveda-Martínez, P.; Esquiva, G.; Gómez-Vicente, V. Eco-Friendly and Biocompatible Material to Reduce Noise Pollution and Improve Acoustic Comfort in Healthcare Environments. Buildings 2024, 14, 3151. [Google Scholar] [CrossRef]
- Chen, K.; Kang, J.; Ma, H. Evaluation of healthy indoor acoustic environments in residential buildings by the occupants: A mixed-method approach. Build. Environ. 2023, 246, 110950. [Google Scholar] [CrossRef]
- Bonet-Solà, D.; Vidaña-Vila, E.; Alsina-Pagès, R.M. Prediction of the acoustic comfort of a dwelling based on automatic sound event detection. Noise Mapp. 2023, 10, 20220177. [Google Scholar] [CrossRef]
- Vasconcelos, R.O.; Gordillo-Martinez, F.; Ramos, A.; Lau, I.H. Effects of Noise Exposure and Ageing on Anxiety and Social Behaviour in Zebrafish. Biology 2023, 12, 1165. [Google Scholar] [CrossRef]
- Song, J.; Meng, Q.; Kang, J.; Yang, D.; Li, M. Effects of planning variables on urban traffic noise at different scales. Sustain. Cities Soc. 2024, 100, 105006. [Google Scholar] [CrossRef]
- Chen, S.; He, P.; Yu, B.; Wei, D.; Chen, Y. The challenge of noise pollution in high-density urban areas: Relationship between 2D/3D urban morphology and noise perception. Build. Environ. 2024, 253, 111313. [Google Scholar] [CrossRef]
- Yu, C.; Chen, X.; Duan, M.; Li, M.; Wang, X.; Mao, Y.; Zhao, L.; Xin, F.; Lu, T.J. Adjustable sound absorbing metastructures for low-frequency variable discrete sources. Int. J. Mech. Sci. 2024, 267, 108965. [Google Scholar] [CrossRef]
- Wu, C.C.; Loke, S.C.; Lu, Z.; Shrestha, M.; Khoo, B.C.; Lau, G.-K. Transformation from Helmholtz to Membrane Resonance by Electro-Adhesive Zip of a Double-Layer Micro-Slit Acoustic Absorber. Adv. Mater. Technol. 2023, 8, 2201757. [Google Scholar] [CrossRef]
- Xu, L.; Zhu, Z.Q.; Howe, D. Acoustic noise radiated from direct torque controlled induction motor drives. IEE Proc.-Electr. Power Appl. 2000, 147, 491–496. [Google Scholar] [CrossRef]
- Gonzalez, P.; Buigues, G.; Mazon, A.J. Noise in Electric Motors: A Comprehensive Review. Energies 2023, 16, 5311. [Google Scholar] [CrossRef]
- Peng, W.; Zhang, J.; Shi, M.; Li, J.; Guo, S. Low-frequency sound insulation optimisation design of membrane-type acoustic metamaterials based on Kriging surrogate model. Mater. Des. 2023, 225, 111491. [Google Scholar] [CrossRef]
- Ma, Y.; Ye, W. Biomimetic Coupling Structure Increases the Noise Friction and Sound Absorption Effect. Materials 2023, 16, 7148. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Q.Y.; Xu, T.; Liu, Y.; Dusengumuremyi, V.; Cheng, B.Z.; Hou, H. Study on low-mid-frequency broadband sound absorption properties of bending acoustic metamaterials with embedded porous materials. Phys. Scr. 2024, 99, 105912. [Google Scholar] [CrossRef]
- Yang, W.; He, J.; He, C.; Cai, M. Evaluation of Urban Traffic Noise Pollution based on Noise Maps. Transp. Res. Part D Transp. Environ. 2020, 87, 102516. [Google Scholar] [CrossRef]
- Liang, Y.; You, J.; Wang, R.; Qin, B.; Han, S. Urban Transportation Data Research Overview: A Bibliometric Analysis Based on CiteSpace. Sustainability 2024, 16, 9615. [Google Scholar] [CrossRef]
- Chen, J.; He, L.; Li, X.; Zheng, B.; Wang, T.; Wang, D.; Zou, C. Experimental Investigation on Building Sound Environment: Traffic-Induced Air Noise and Structure-Borne Noise. Buildings 2024, 14, 2380. [Google Scholar] [CrossRef]
- Wang, H.; Ma, P.; Fan, X. A Compact Low-Frequency Acoustic Perfect Absorber Constructed with a Folded Slit. Materials 2024, 17, 5992. [Google Scholar] [CrossRef]
- Yang, X.; Shen, X.; Yang, F.; Yin, Z.; Yang, F.; Yang, Q.; Shen, C.; Xu, M.; Wan, J. Acoustic metamaterials of modular nested Helmholtz resonators with multiple tunable absorption peaks. Appl. Acoust. 2023, 213, 109647. [Google Scholar] [CrossRef]
- Althamer, S. Metamaterial beam with dual-action absorbers for tunable and multi-band vibration absorption. J. Intell. Mater. Syst. Struct. 2023, 34, 2257–2267. [Google Scholar] [CrossRef]
- Saatchi, D.; Oh, S.; Yoo, H.; Kim, J.S.; Lee, M.J.; Khan, M.; Wicklein, B.; Mahato, M.; Oh, I. Dynamic Schwarz Meta-Foams: Customizable Solutions for Environmental Noise Reduction. Adv. Sci. 2024. early access. [Google Scholar] [CrossRef]
- Chen, Y.; Shao, Z.R.; Wei, J.L.; Feng, J.; Sareh, P. Geometric design and performance analysis of a foldcore sandwich acoustic metastructure for tunable low-frequency sound absorption. Finite Elem. Anal. Des. 2024, 235, 104150. [Google Scholar] [CrossRef]
- Bezançon, G.; Doutres, O.; Umnova, O.; Leclaire, P.; Dupont, T. Thin metamaterial using acoustic black hole profiles for broadband sound absorption. Appl. Acoust. 2024, 216, 109744. [Google Scholar] [CrossRef]
- Schimidt, C.S.; de Oliveira, L.P.R.; De Marqui, C., Jr. Reconfigurable piezoelectric metamaterial for selective noise directivity. J. Sound Vib. 2024, 585, 118472. [Google Scholar] [CrossRef]
- Ravanbod, M.; Ebrahimi-Nejad, S.; Mollajafari, M. A thin-walled cavity structure with double-layer tapered scatterer locally resonant metamaterial plates for extreme low-frequency attenuation. Int. J. Solids Struct. 2024, 293, 112742. [Google Scholar] [CrossRef]
- Zhang, W.; Xin, F. Broadband low-frequency sound absorption via Helmholtz resonators with porous material lining. J. Sound Vib. 2024, 578, 118330. [Google Scholar] [CrossRef]
- Červenka, M.; Bednařík, M. Maximizing the Absorbing Performance of Rectangular Sonic Black Holes. Appl. Sci. 2024, 14, 7766. [Google Scholar] [CrossRef]
- Kheybari, M.; Daraio, C.; Bilal, O.R. Tunable Auxetic Metamaterials for Simultaneous Attenuation of Airborne Sound and Elastic Vibrations in All Directions. Appl. Phys. Lett. 2022, 121, 081702. [Google Scholar] [CrossRef]
- Bi, S.; Yang, F.; Shen, X.; Zhang, J.; Yang, X.; Zhang, H.; Peng, W. Analysis of Influencing Factors for Stackable and Expandable Acoustic Metamaterial with Multiple Tortuous Channels. Materials 2023, 16, 6643. [Google Scholar] [CrossRef]
- Shendy, M.; Oluyemi, M.; Maftoon, N.; Salehian, A. An Extensive Parametric Analysis and Optimization to Design Unidimensional Periodic Acoustic Metamaterials for Noise Attenuation. Appl. Sci. 2024, 14, 7272. [Google Scholar] [CrossRef]
- Yang, X.; Shen, X.; Peng, W.; Zhu, D.; Song, H.; Hu, D.; Shen, C.; Xu, M.; Zhu, N.; Shi, Q. Online tunable sound absorbing acoustic metamaterial with optional aperture and adjustable cavity. Appl. Acoust. 2025, 231, 110556. [Google Scholar] [CrossRef]
- Nakanishi, S. A study on the optimized area ratio of unit cell assembly for the broadband perfect sound absorption of acoustic metasurface. Acoust. Sci. Technol. 2024, 45, 320–323. [Google Scholar] [CrossRef]
- Nakanishi, S. Broadband sound absorption by acoustic metasurface of planar array of small Helmholtz resonators. Acoust. Sci. Technol. 2024, 45, 234–237. [Google Scholar] [CrossRef]
- Bi, S.; Wang, E.; Shen, X.; Yang, F.; Zhang, X.; Yang, X.; Yin, Q.; Shen, C.; Xu, M.; Wan, J. Enhancement of sound absorption performance of Helmholtz resonators by space division and chamber grouping. Appl. Acoust. 2023, 207, 109352. [Google Scholar] [CrossRef]
- Papadakis, N.M.; Stavroulakis, G.E. Tunable Helmholtz Resonators Using Multiple Necks. Micromachines 2023, 14, 1932. [Google Scholar] [CrossRef] [PubMed]
- Papadakis, N.M.; Stavroulakis, G.E. FEM Investigation of a Multi-Neck Helmholtz Resonator. Appl. Sci. 2023, 13, 10610. [Google Scholar] [CrossRef]
- Hoppen, H.; Langfeldt, F.; Gleine, W.; von Estorff, O. Helmholtz resonator with two resonance frequencies by coupling with a mechanical resonator. J. Sound Vib. 2023, 559, 117747. [Google Scholar] [CrossRef]
- Hedayati, R.; Lakshmanan, S.P. Active Acoustic Metamaterial Based on Helmholtz Resonators to Absorb Broadband Low-Frequency Noise. Materials 2024, 17, 962. [Google Scholar] [CrossRef]
- Langfeldt, F.; Khatokar, A.J.; Gleine, W. Plate-type acoustic metamaterials with integrated Helmholtz resonators. Appl. Acoust. 2022, 199, 109019. [Google Scholar] [CrossRef]
- Herrero-Durá, I.; Cebrecos, A.; Picó, R.; Romero-García, V.; García-Raffi, L.M.; Sánchez-Morcillo, V.J. Sound Absorption and Diffusion by 2D Arrays of Helmholtz Resonators. Appl. Sci. 2020, 10, 1690. [Google Scholar] [CrossRef]
- Li, J.; Shi, Y.; Jiang, R.; Zhang, Z.; Huang, Q. Acoustic Insulation Mechanism of Membrane-Type Acoustic Metamaterials Loaded with Arbitrarily Shaped Mass Blocks of Variable Surface Density. Materials 2022, 15, 1556. [Google Scholar] [CrossRef]
- Mahesh, K.; Mini, R.S. Theoretical investigation on the acoustic performance of Helmholtz resonator integrated microperforated panel absorber. Appl. Acoust. 2021, 178, 108012. [Google Scholar] [CrossRef]
- Gaafer, F.N. Broadband low-frequency sound absorption via a hexagonal acoustic metamaterial in the honeycomb structure. Kuwait J. Sci. 2022, 49, 73–83. [Google Scholar] [CrossRef]
- Ciaburro, G.; Parente, R.; Iannace, G.; Puyana-Romero, V. Design Optimization of Three-Layered Metamaterial Acoustic Absorbers Based on PVC Reused Membrane and Metal Washers. Sustainability 2022, 14, 4218. [Google Scholar] [CrossRef]
- Fang, X.; Pan, X.; Zhang, X.; Li, D.; Yin, X.; Jin, Y.; Wang, W.; Wu, W. Investigation on Low-Frequency and Broadband Sound Absorption of the Compact Anechoic Coating Considering Hydrostatic Pressure. J. Mar. Sci. Eng. 2024, 12, 543. [Google Scholar] [CrossRef]
- Ramírez-Solana, D.; Redondo, J.; Mangini, A.M.; Fanti, M.P. Particle Swarm Optimization of Resonant Sonic Crystals Noise Barriers. IEEE Access 2023, 11, 38426–38435. [Google Scholar] [CrossRef]
- Wang, X.; Ma, L.; Wang, Y.; Guo, H. Design of multilayer sound-absorbing composites with excellent sound absorption properties at medium and low frequency via constructing variable section cavities. Compos. Struct. 2021, 266, 113798. [Google Scholar] [CrossRef]
- Yan, S.; Wu, J.; Chen, J.; Xiong, Y.; Mao, Q.; Zhang, X. Optimization design and analysis of honeycomb micro-perforated plate broadband sound absorber. Appl. Acoust. 2022, 186, 108487. [Google Scholar] [CrossRef]
- Peng, L.; Bao, B. Optimized membrane-type acoustic metamaterials for alleviating engineering fatigue damage via lightweight optimization. Eng. Struct. 2023, 292, 116550. [Google Scholar] [CrossRef]

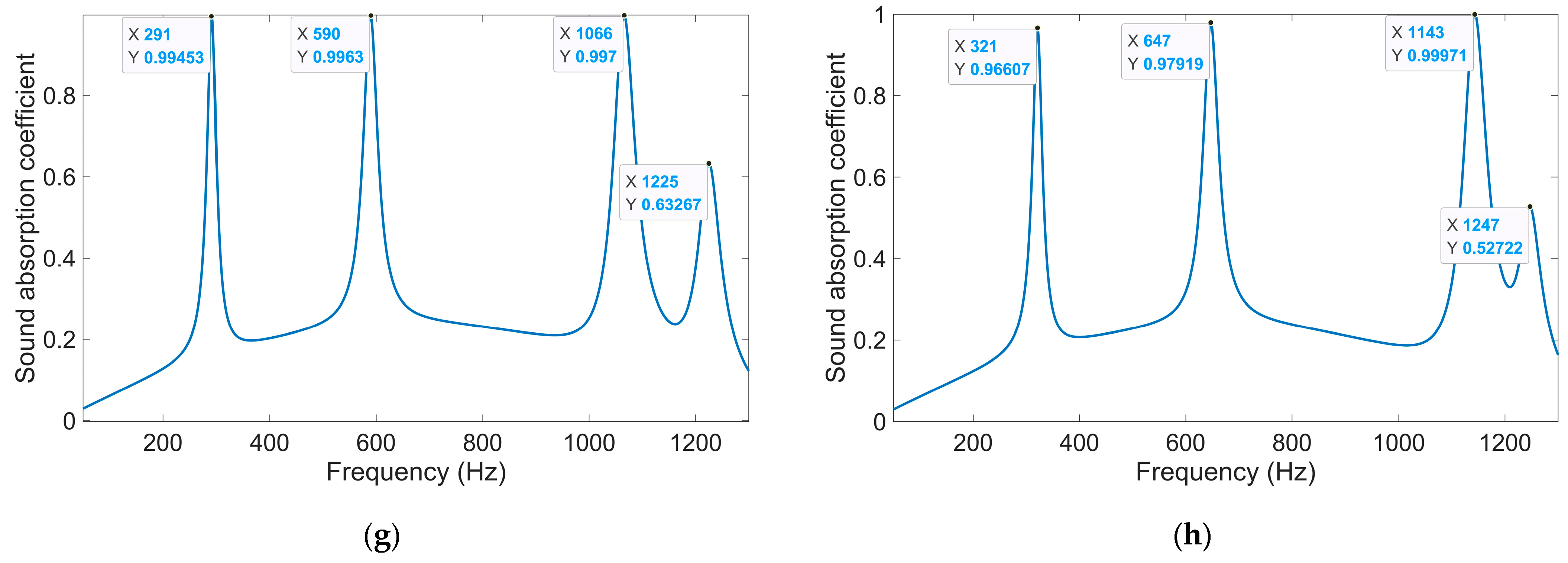
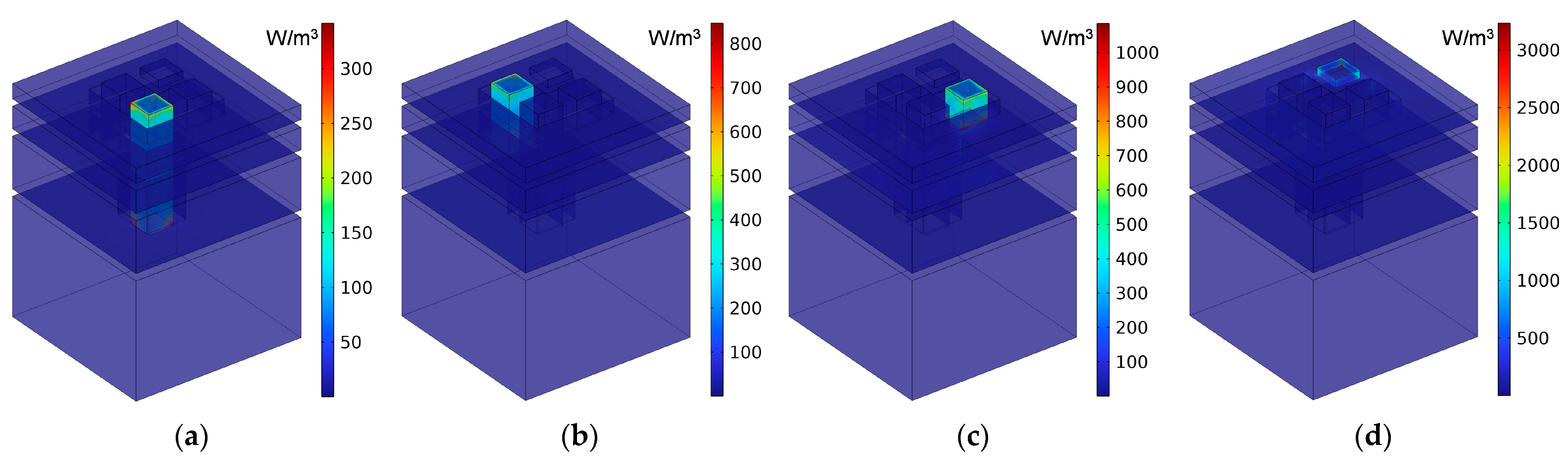
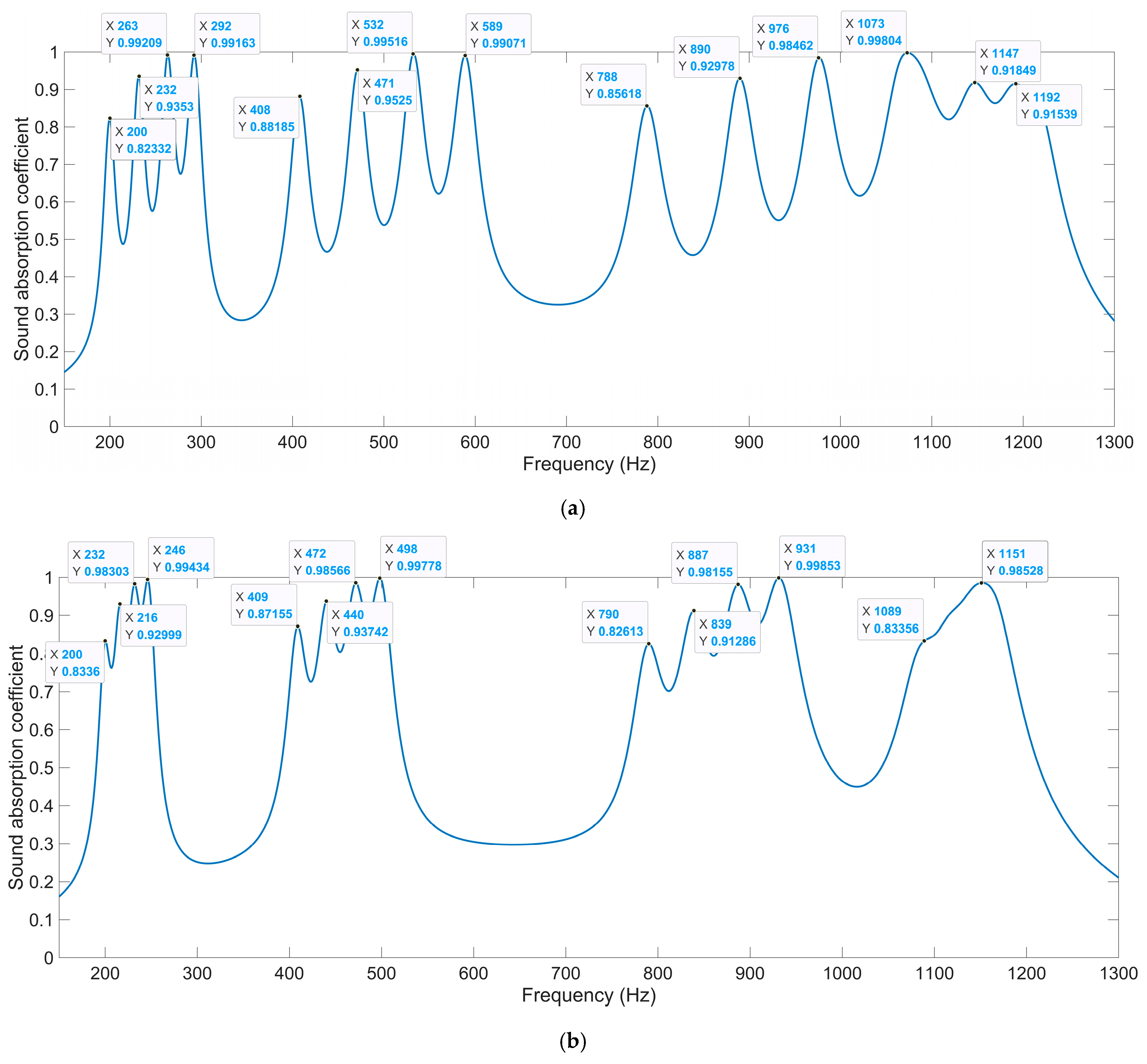
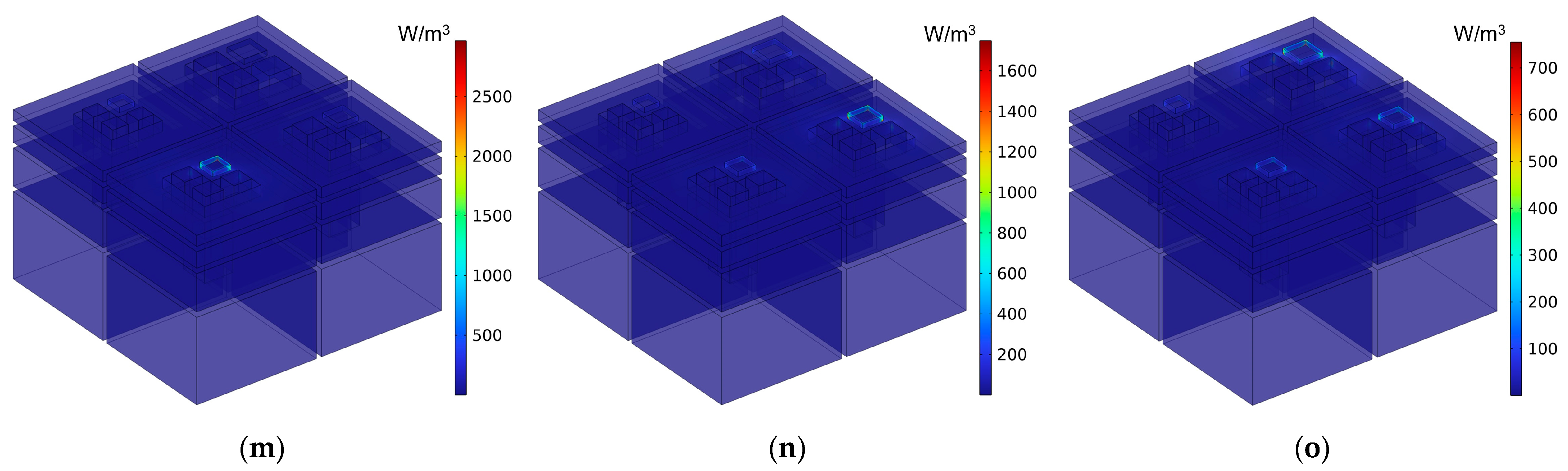

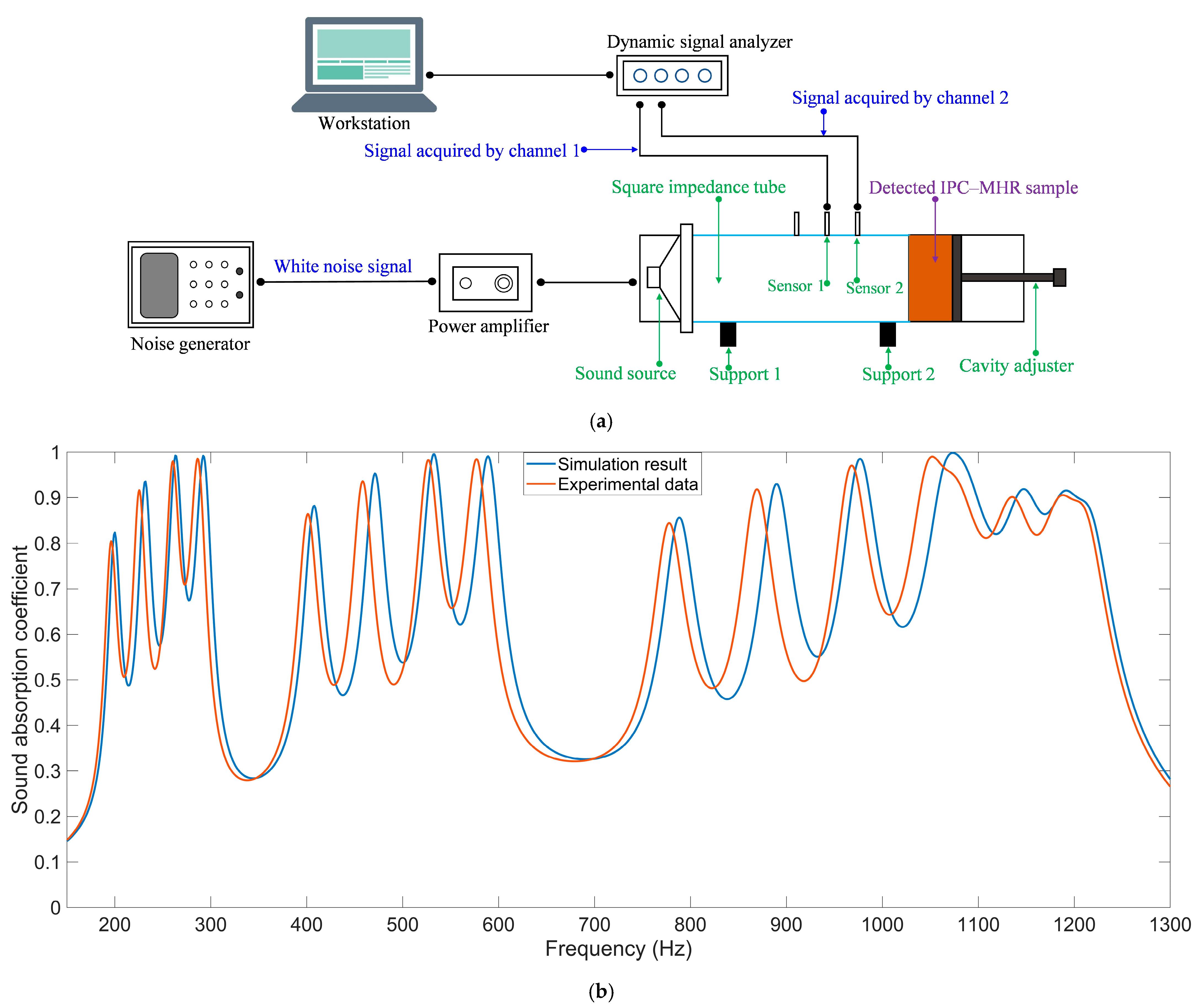

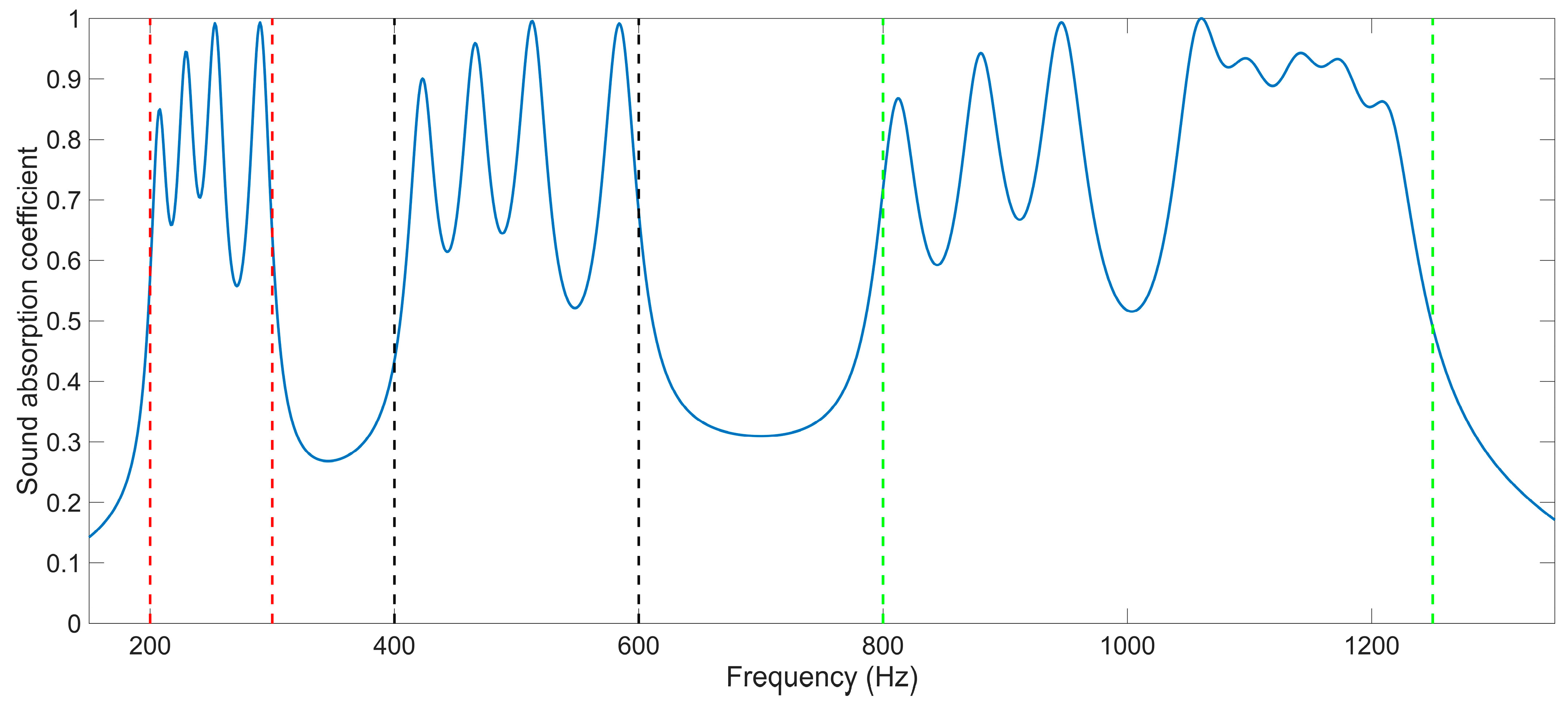
| Meanings | Symbols | Value or Range |
|---|---|---|
| The total thickness of the IPC–MHR acoustic metamaterial | T4 + t0 | 64 mm |
| The thickness of all the wall | t0 | 2 mm |
| The side length of the cross-sectional shape for the multi-group IPC–MHR | S0 | 100 mm |
| The side length of the cross-sectional shape for the single-group IPC–MHR | (S0 − 3t0)/2 | 47 mm |
| The total thickness of the first layer | T1 = 3t0 | 6 mm |
| The length of the front aperture for the first layer | t0 | 2 mm |
| The thickness of the rear chamber for the first layer | T1–t0 | 4 mm |
| The total thickness of the second layer | T2 = 2T1 + t0 | 14 mm |
| The length of the front aperture for the second layer | T1 | 6 mm |
| The thickness of the rear chamber for the second layer | T2–T1–t0 | 6 mm |
| The total thickness of the third layer | T3 = 2T2 + t0 | 30 mm |
| The length of the front aperture for the third layer | T2 | 14 mm |
| The thickness of the rear chamber for the third layer | T3–T2–t0 | 14 mm |
| The thickness of the fourth layer | T4 = 2T3 + t0 | 62 mm |
| The length of the front aperture for the fourth layer | T3 | 30 mm |
| The thickness of the rear chamber for the fourth layer | T4–T3–t0 | 30 mm |
| The side length of the square incident aperture for the single-group IPC–MHR | a | [3 mm, 10 mm] |
| The side length of the square incident aperture for the multi-group IPC–MHR | ai | 6 mm, 7 mm, 8 mm, 9 mm |
| Parameters | Value or Type | Parameters | Value or Type |
|---|---|---|---|
| The type of mesh | Extremely fine mesh | The type of acoustic field | Plane wave |
| The type of grid | Free tetrahedral grid | The amplitude of background field | 1 Pa |
| The selected solver | Steady state solver | The direction of incident wave | (0, 0, −1) |
| The relative tolerance of solver | 0.001 | The thickness of background field | 64 mm |
| The maximum unit size | 4 mm | The thickness of perfect matching layer | 96 mm |
| The minimum unit size | 0.04 mm | The equilibrium pressure | 1 atm |
| The maximal unite growth rate | 1.3 | The equilibrium temperature | 293.15 K |
| The curvature factor | 0.2 | The number of layers in distribution | 10 |
| The resolution of narrow region | 1 | The number of layers in boundary | 10 |
| The investigated frequency range | 50–1300 Hz | The stretch factor in boundary | 1.2 |
| The frequency sampling interval | 1 Hz | The regulation factor for thickness | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Li, Q.; Shen, X.; Zhou, B.; Wang, N.; Wang, E.; Zhang, X.; Shen, C.; Wang, H.; Jiang, S. Interlayer Parallel Connection of Multiple Helmholtz Resonators for Optional Broadband Low Frequency Sound Absorption. Materials 2025, 18, 682. https://doi.org/10.3390/ma18030682
Yang X, Li Q, Shen X, Zhou B, Wang N, Wang E, Zhang X, Shen C, Wang H, Jiang S. Interlayer Parallel Connection of Multiple Helmholtz Resonators for Optional Broadband Low Frequency Sound Absorption. Materials. 2025; 18(3):682. https://doi.org/10.3390/ma18030682
Chicago/Turabian StyleYang, Xiaocui, Qiang Li, Xinmin Shen, Binbin Zhou, Ning Wang, Enshuai Wang, Xiaonan Zhang, Cheng Shen, Hantian Wang, and Shunjie Jiang. 2025. "Interlayer Parallel Connection of Multiple Helmholtz Resonators for Optional Broadband Low Frequency Sound Absorption" Materials 18, no. 3: 682. https://doi.org/10.3390/ma18030682
APA StyleYang, X., Li, Q., Shen, X., Zhou, B., Wang, N., Wang, E., Zhang, X., Shen, C., Wang, H., & Jiang, S. (2025). Interlayer Parallel Connection of Multiple Helmholtz Resonators for Optional Broadband Low Frequency Sound Absorption. Materials, 18(3), 682. https://doi.org/10.3390/ma18030682








