Valley-Related Multipiezo Effect in Altermagnet Monolayer V2STeO
Abstract
1. Introduction
2. Computational Method and Details
3. Results and Discussion
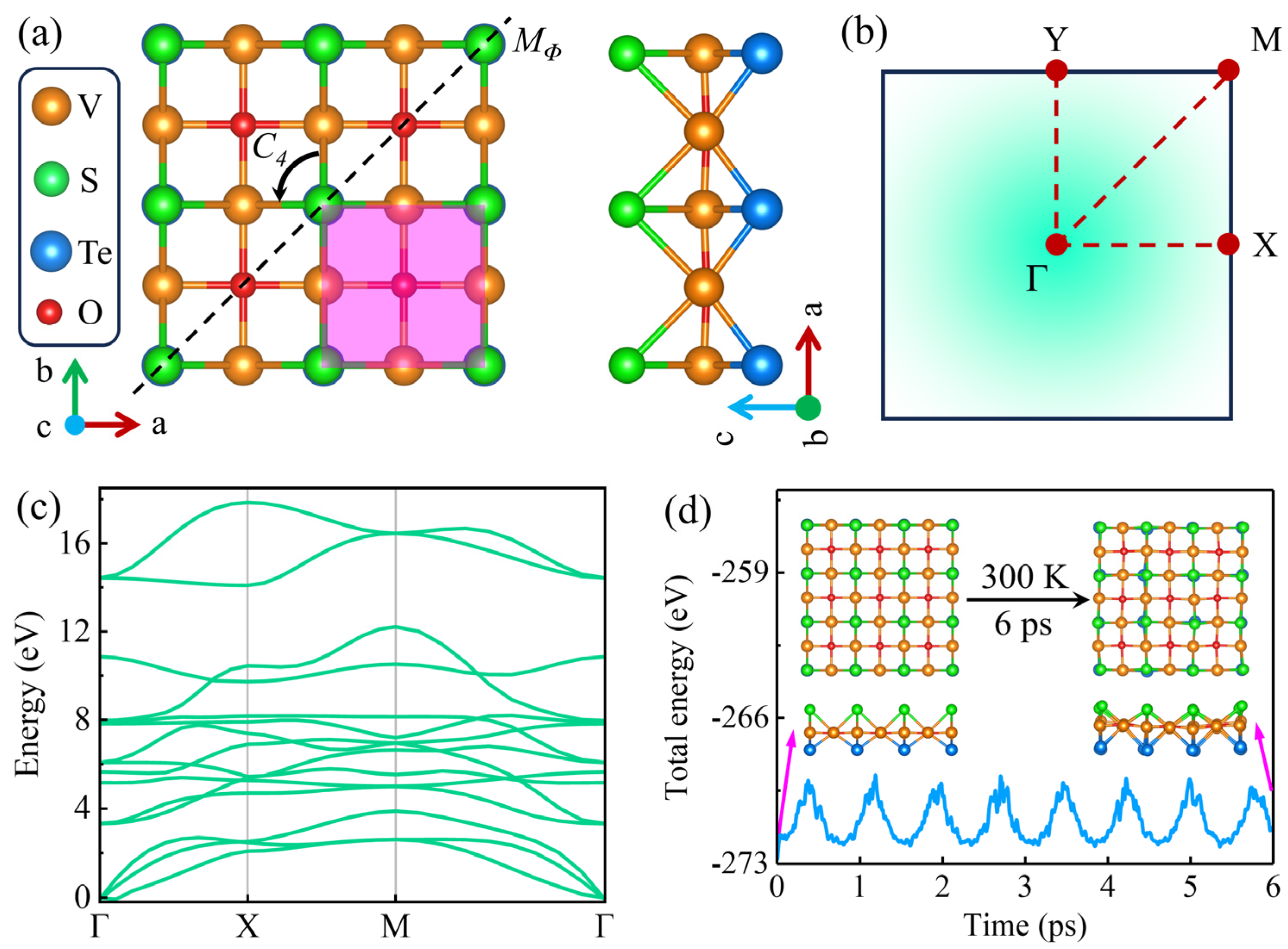
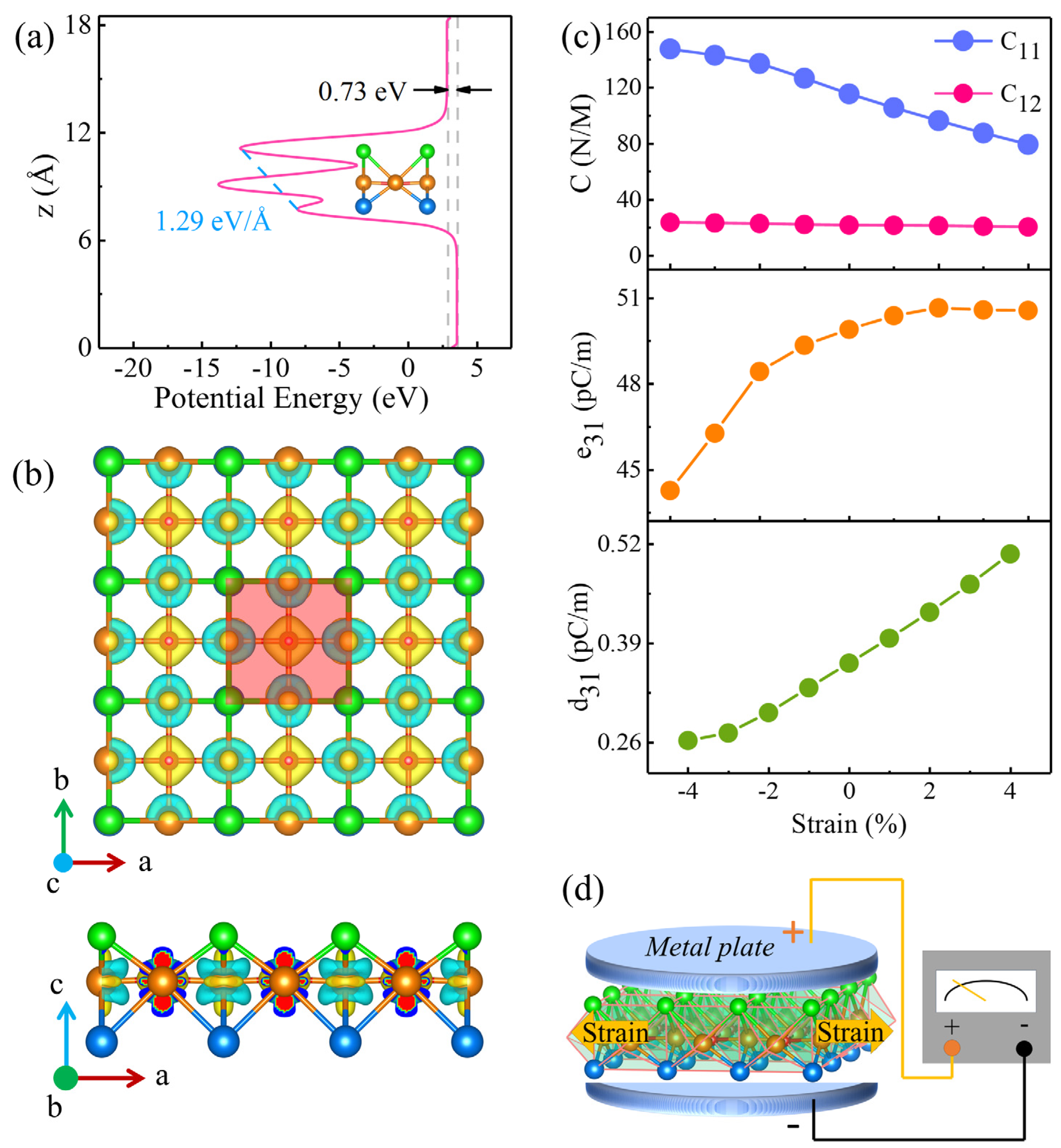
3.1. Stability Property, Magnetic Feature, and Energy Band of Monolayer V2STeO
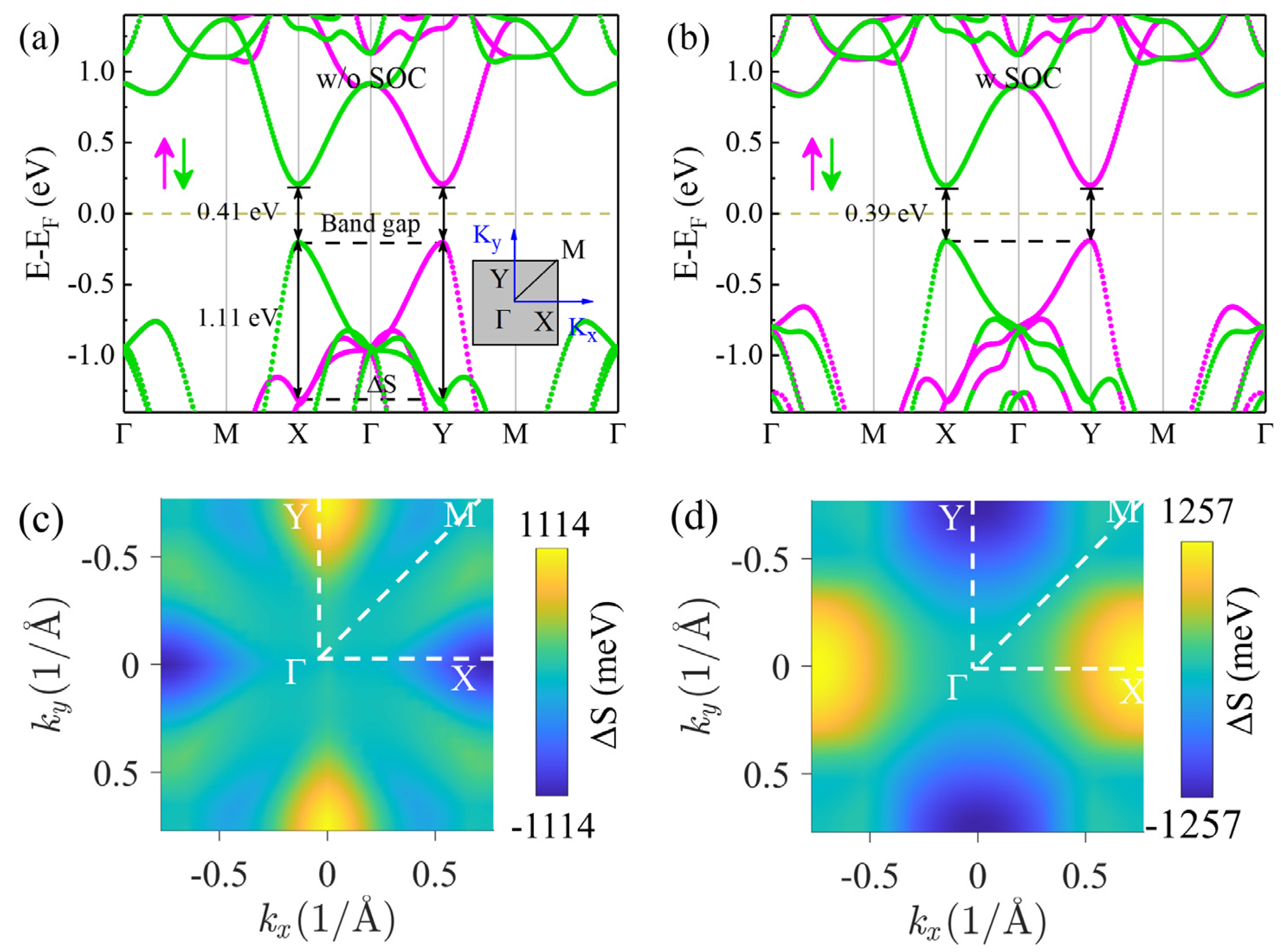
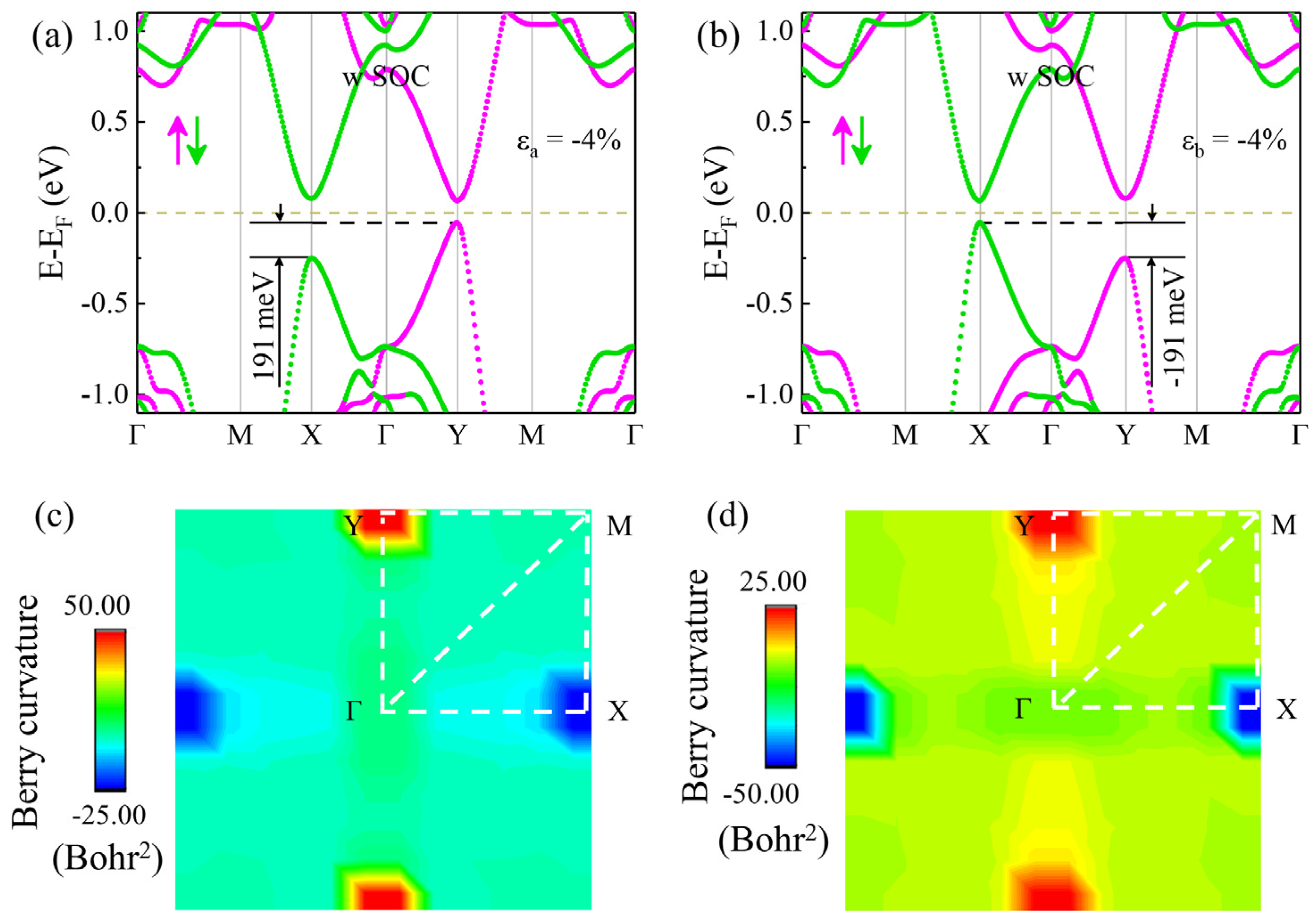
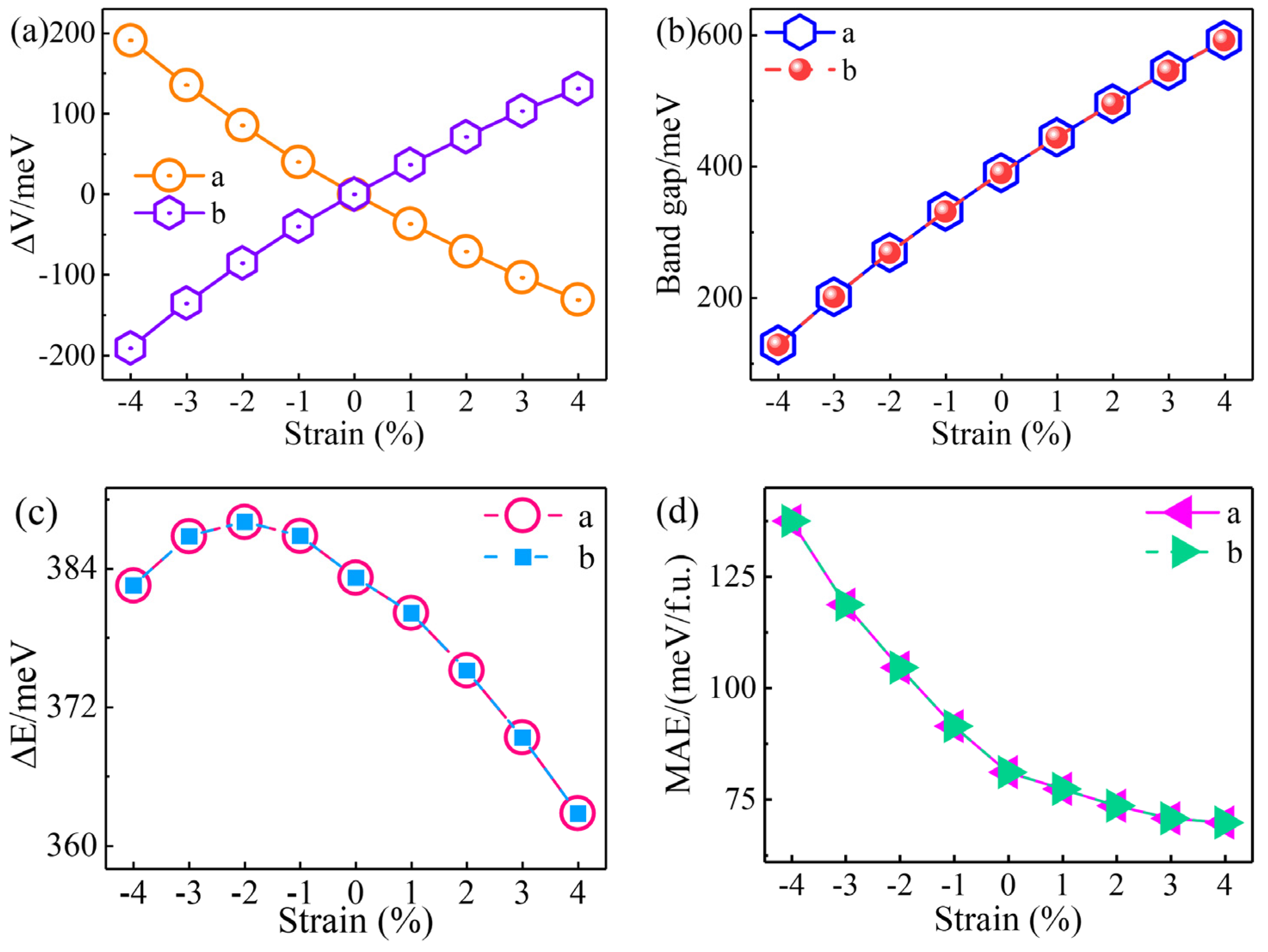
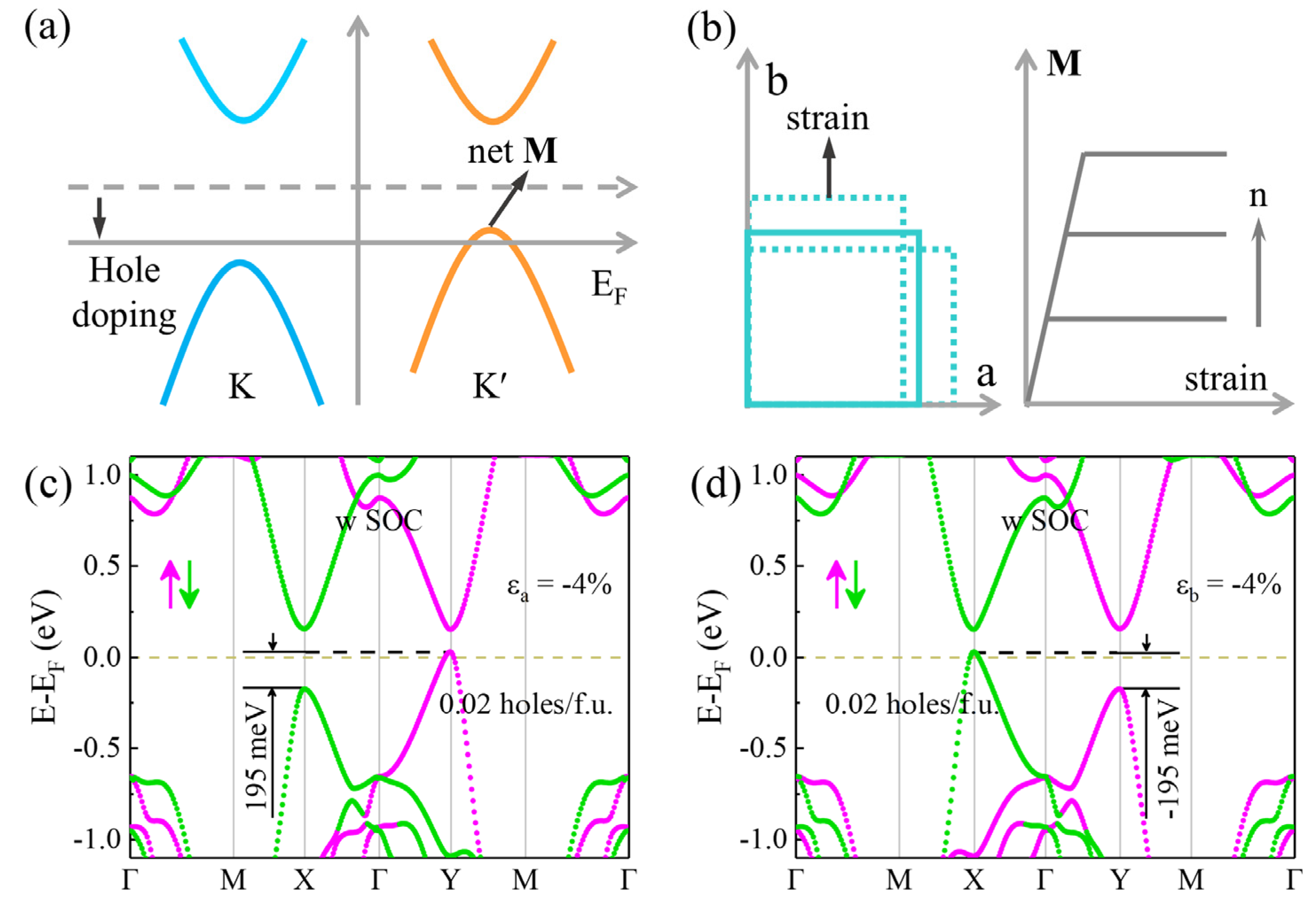
3.2. Piezovalley Effect of Monolayer V2STeO
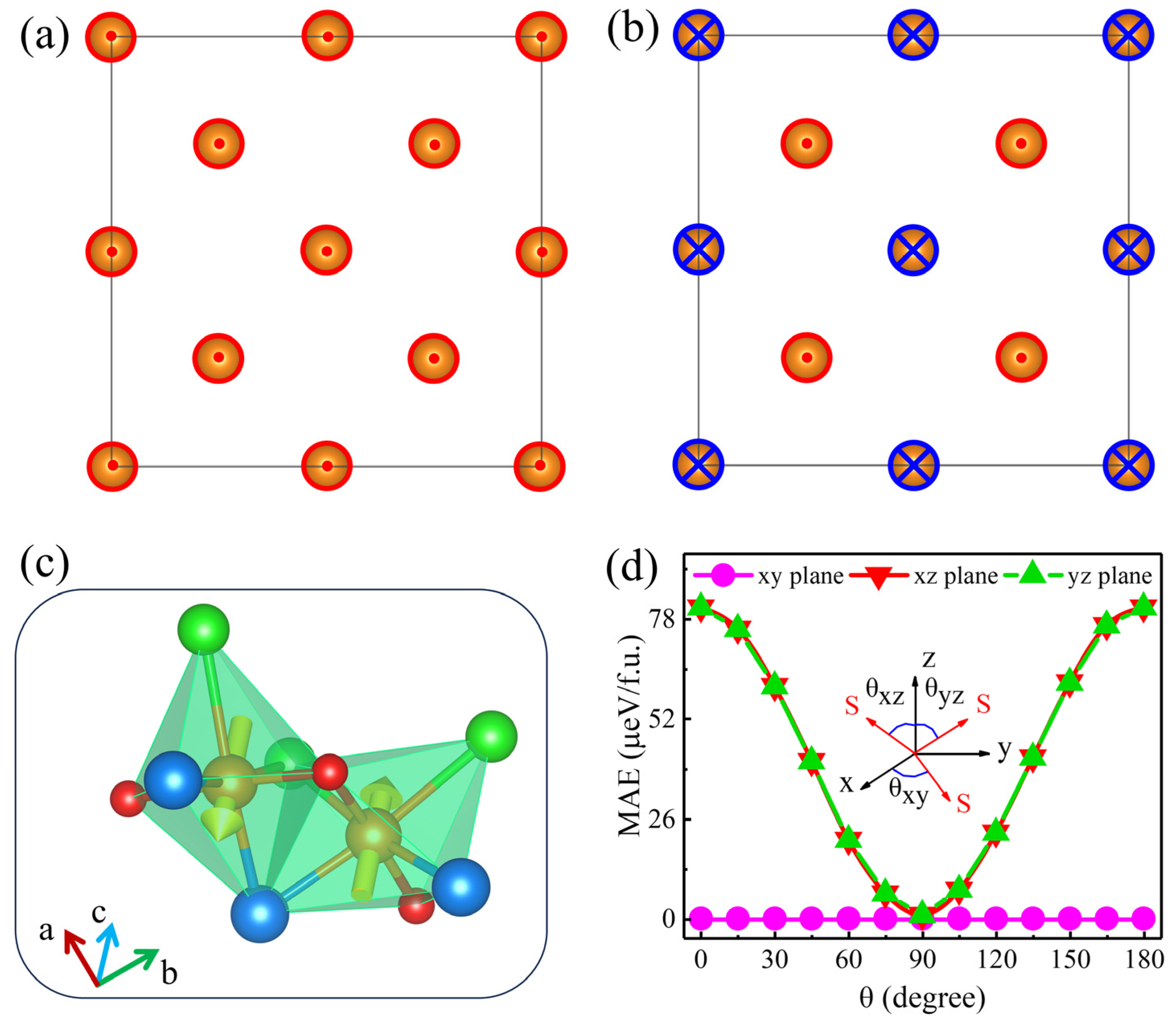
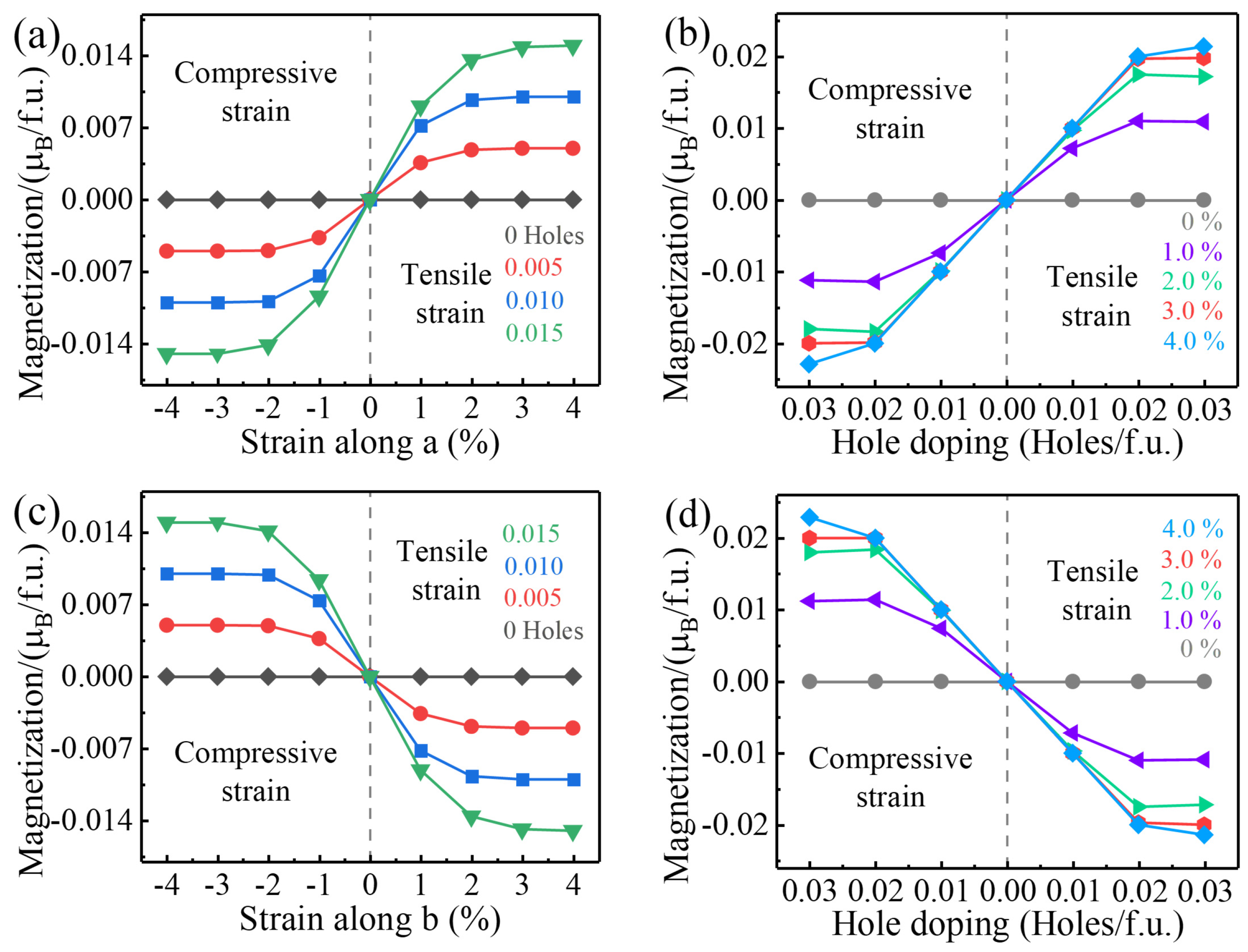
3.3. Piezomagnetic Effect of Monolayer V2STeO
3.4. Piezoelectric Effect of Monolayer V2STeO
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mak, K.F.; McGill, K.L.; Park, J.; McEuen, P.L. The valley Hall effect in MoS2 transistors. Science 2014, 344, 1489. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Ross, J.S.; Liu, G.-B.; Aivazian, G.; Jones, A.; Fei, Z.; Zhu, W.; Xiao, D.; Yao, W.; Cobden, D.; et al. Electrical tuning of valley magnetic moment through symmetry control in bilayer MoS2. Nat. Phys. 2013, 9, 149. [Google Scholar] [CrossRef]
- Schaibley, J.R.; Yu, H.; Clark, G.; Rivera, P.; Ross, J.S.; Seyler, K.L.; Yao, W.; Xu, X. Valleytronics in 2D materials. Nat. Rev. Mater. 2016, 1, 16055. [Google Scholar] [CrossRef]
- Vitale, S.A.; Nezich, D.; Varghese, J.O.; Kim, P.; Gedik, N.; Jarillo-Herrero, P.; Xiao, D.; Rothschild, M. Valleytronics: Opportunities, challenges, and paths forward. Small 2018, 14, 1801483. [Google Scholar] [CrossRef]
- Xiao, D.; Liu, G.-B.; Feng, W.; Xu, X.; Yao, W. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 2012, 108, 196802. [Google Scholar] [CrossRef]
- Tong, W.-Y.; Gong, S.-J.; Wan, X.; Duan, C.-G. Concepts of ferrovalley material and anomalous valley Hall effect. Nat. Commun. 2016, 7, 13612. [Google Scholar] [CrossRef]
- Peng, R.; Ma, Y.; Xu, X.; He, Z.; Huang, B.; Dai, Y. Intrinsic anomalous valley Hall effect in single-layer Nb3I8. Phys. Rev. B 2020, 102, 035412. [Google Scholar] [CrossRef]
- Feng, Y.L.Y.; Zhang, T.; He, Z.; Dai, Y.; Huang, B.; Ma, Y. Strain-valley coupling in 2D antiferromagnetic lattice. Adv. Funct. Mater. 2023, 33, 2305130. [Google Scholar]
- Šmejkal, L.; Sinova, J.; Jungwirth, T. Emerging research landscape of altermagnetism. Phys. Rev. X 2022, 12, 040501. [Google Scholar] [CrossRef]
- Šmejkal, L.; Sinova, J.; Jungwirth, T. Beyond conventional ferromagnetism and antiferromagnetism: A phase with nonrelativistic spin and crystal rotation symmetry. Phys. Rev. X 2022, 12, 031042. [Google Scholar] [CrossRef]
- Zhu, Y.-P.; Chen, X.; Liu, X.-R.; Liu, Y.; Liu, P.; Zha, H.; Qu, G.; Hong, C.; Li, J.; Jiang, Z.; et al. Observation of plaid-like spin splitting in a noncoplanar antiferromagnet. Nature 2024, 626, 523. [Google Scholar] [CrossRef] [PubMed]
- Krempaský, J.; Šmejkal, L.; D’Souza, S.W.; Hajlaoui, M.; Springholz, G.; Uhlířová, K.; Alarab, F.; Constantinou, P.C.; Strocov, V.; Usanov, D.; et al. Altermagnetic lifting of Kramers spin degeneracy. Nature 2024, 626, 517. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Tong, W.-Y.; Shen, Y.-H.; Wan, X.; Duan, C.-G. Concepts of the half-valley-metal and quantum anomalous valley Hall effect. npj Comp. Mater. 2020, 6, 129. [Google Scholar]
- Chang, Y.; Zhang, Z.; Deng, L.; Wu, Y.; Zhang, X. Ferrovalley and quantum anomalous Hall effect in Janus TiTeCl monolayer. Materials 2024, 17, 3331. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, X.; Yang, H.; Han, X.; Yan, Y. Stain controlling transport properties of heterostructure composed of monolayer CrI3. Appl. Phys. Lett. 2019, 114, 192405. [Google Scholar] [CrossRef]
- Shen, T.; Penumatcha, A.V.; Appenzeller, J. Strain engineering for transition metal dichalcogenides based field effect transistors. Acs Nano 2016, 10, 4712. [Google Scholar] [CrossRef]
- Zhao, Y.-F.; Shen, Y.-H.; Hu, H.; Tong, W.-Y.; Duan, C.-G. Combined piezoelectricity and ferrovalley properties in Janus monolayer VClBr. Phys. Rev. B 2021, 103, 115124. [Google Scholar] [CrossRef]
- Shen, S.; Wu, Q.; Liang, Y.; Huang, B.; Dai, Y.; Ma, Y. Single-layer BI: A multifunctional semiconductor with ferroelectricity, ultrahigh carrier mobility, and negative poisson’s ratio. Phys. Rev. Appl. 2021, 15, 014027. [Google Scholar] [CrossRef]
- Ma, H.-Y.; Hu, M.; Li, N.; Liu, J.; Yao, W.; Jia, J.-F.; Liu, J. Multifunctional antiferromagnetic materials with giant piezomagnetism and noncollinear spin current. Nat. Commun. 2021, 12, 2846. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, T.; Li, Y.; Qiao, L.; Ma, X.; Liu, C.; Hu, T.; Gao, H.; Ren, W. Multipiezo effect in altermagnetic V2SeTeO monolayer. Nano Lett. 2024, 24, 472. [Google Scholar] [CrossRef]
- Li, J.-Y.; Fan, A.-D.; Wang, Y.-K.; Zhang, Y.; Li, S. Strain-induced valley polarization; topological states, and piezomagnetism in two-dimensional altermagnetic V2Te2O, V2STeO, V2SSeO, and V2S2O. Appl. Phys. Lett. 2024, 125, 222404. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 169. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Aryasetiawan, F.; Karlsson, K.; Jepsen, O.; Schonberger, U. Calculations of Hubbard U from first-principles. Phys. Rev. B 2006, 74, 125106. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scripta. Mater. 2015, 108, 1. [Google Scholar] [CrossRef]
- Gonze, X.; Lee, C. Dynamical matrices; born effective charges; dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B 1997, 55, 10355. [Google Scholar] [CrossRef]
- Bucher, D.; Pierce, L.C.T.; McCammon, J.A.; Markwick, P.R.L. On the use of accelerated molecular dynamics to enhance configurational sampling in ab initio simulations. J. Chem. Theory. Comput. 2011, 7, 890. [Google Scholar] [CrossRef] [PubMed]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Mostofi, A.A.; Yates, J.R.; Pizzi, G.; Lee, Y.-S.; Souza, I.; Vanderbilt, D.; Marzari, N. An updated version of wannier90: A tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 2014, 185, 2309. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, S.; Song, H.-F.; Troyer, M.; Soluyanov, A.A. WannierTools: An open-source software package for novel topological materials. Comput. Phys. Commun. 2018, 224, 405. [Google Scholar] [CrossRef]
- Hamann, D.R.; Wu, X.; Rabe, K.M.; Vanderbilt, D. Metric tensor formulation of strain in density-functional perturbation theory. Phys. Rev. B 2005, 71, 035117. [Google Scholar] [CrossRef]
- Cheng, H.-X.; Zhou, J.; Ji, W.; Zhang, Y.-N.; Feng, Y.-P. Two-dimensional intrinsic ferrovalley GdI2 with large valley polarization. Phys. Rev. B 2021, 103, 125121. [Google Scholar] [CrossRef]
- Sheng, K.; Chen, Q.; Yuan, H.-K.; Wang, Z.-Y. Monolayer CeI2: An intrinsic room-temperature ferrovalley semiconductor. Phys. Rev. B 2022, 105, 075304. [Google Scholar] [CrossRef]
- Ishizaka, K.; Bahramy, M.S.; Murakawa, H.; Sakano, M.; Shimojima, T.; Sonobe, T.; Koizumi, K.; Shin, S.; Miyahara, H.; Kimura, A.; et al. Giant rashba-type spin splitting in bulk BiTeI. Nat. Mater. 2011, 10, 521. [Google Scholar] [CrossRef]
- Reimers, S.; Odenbreit, L.; Šmejkal, L.; Strocov, V.N.; Constantinou, P.; Hellenes, A.B.; Ubiergo, R.J.; Campos, W.H.; Bharadwaj, V.K.; Chakraborty, A.; et al. Direct observation of altermagnetic band splitting in CrSb thin films. Nat. Commun. 2024, 15, 2116. [Google Scholar] [CrossRef]
- Zhang, F.; Cheng, X.; Yin, Z.; Liu, C.; Deng, L.; Qiao, Y.; Shi, Z.; Zhang, S.; Lin, J.; Liu, Z.; et al. Crystal-symmetry-paired spin-valley locking in a layered room-temperature antiferromagnet. arXiv 2024, arXiv:2407.19555. [Google Scholar]
- Singh, N.; Schwingenschlögl, U. A route to permanent valley polarization in monolayer MoS2. Adv. Mater. 2017, 29, 1600970. [Google Scholar] [CrossRef] [PubMed]
- Xiao, D.; Chang, M.C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959. [Google Scholar] [CrossRef]
- Thouless, D.J.; Kohmoto, M.; Nightingale, M.P.; den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 1982, 49, 405. [Google Scholar] [CrossRef]
- Yuan, H.T.; Shimotani, H.; Tsukazaki, A.; Ohtomo, A.; Kawasaki, M.; Iwasa, Y. High-density carrier accumulation in ZnO eield-effect transistors gated by electric double layers of ionic liquids. Adv. Funct. Mater. 2009, 19, 1046. [Google Scholar] [CrossRef]
- Dhoot, A.S.; Israel, C.; Moya, X.; Mathur, N.; Friend, R.H. Large electric field effect in electrolyte-gated manganites. Phys. Rev. Lett. 2009, 102, 136402. [Google Scholar] [CrossRef]
- Li, Y.Q.; Zhang, X.; Shang, X.; He, Q.W.; Tang, D.S.; Wang, X.C.; Duan, C.G. Magnetic and ferroelectric manipulation of valley physics in Janus piezoelectric materials. Nano Lett. 2023, 23, 10013. [Google Scholar] [CrossRef]
- Guo, S.-D.; Wang, M.-X.; Tao, Y.-L.; Liu, B.-G. Piezoelectric ferromagnetism in Janus monolayer YBrI: A first-principles prediction. Phys. Chem. Chem. Phys. 2023, 25, 796. [Google Scholar] [CrossRef]
- Guo, S.D.; Guo, X.S.; Cheng, K.; Wang, K.; Ang, Y.S. Piezoelectric altermagnetism and spin-valley polarization in Janus monolayer Cr2SO. Appl. Phys. Lett. 2023, 123, 082401. [Google Scholar] [CrossRef]
- Guo, S.-D.; Guo, X.-S.; Cai, X.-X.; Liu, B.-G. Valley polarization transition driven by biaxial strain in Janus GdClF monolayer. Phys. Chem. Chem. Phys. 2022, 24, 715. [Google Scholar] [CrossRef]
- Liao, J.; Ma, X.; Yuan, G.; Xu, P.; Yuan, Z. Coexistence of in- and out-of-plane piezoelectricity in Janus XSSiN2 (X = Cr, Mo, W) monolayers. Appl. Phys. Lett. 2023, 610, 155586. [Google Scholar] [CrossRef]
- Cai, X.; Chen, G.; Li, R.; Pan, Z.; Jia, Y. Novel valleytronic and piezoelectric properties coexisting in Janus MoAZ3H (A = Si, or Ge; Z = N, P, or As) monolayers. J. Mater. Chem. C 2024, 12, 4682. [Google Scholar] [CrossRef]
- Hallil, H.; Cai, W.; Zhang, K.; Yu, P.; Liu, S.; Xu, R.; Zhu, C.; Liu, Z.; Zhang, Q. Strong piezoelectricity in 3R-MoS2 flakes. Adv. Electron. Mater. 2022, 8, 2101131. [Google Scholar] [CrossRef]
- You, J.; Pan, J.; Shang, S.-L.; Xu, X.; Liu, Z.; Li, J.; Liu, H.; Kang, T.; Xu, M.; Li, S.; et al. Salt-assisted selective growth of H phase monolayer VSe2 with apparent hole transport behavior. Nano Lett. 2022, 22, 10167. [Google Scholar] [CrossRef]
- Lin, H.; Si, J.; Zhu, X.; Cai, K.; Li, H.; Kong, L.; Yu, X.; Wen, H.-H. Structure and physical properties of CsV2Se2−xO and V2Se2O. Phys. Rev. B 2018, 98, 075132. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.; Wu, Y.; Deng, L.; Yin, X.; Zhang, X. Valley-Related Multipiezo Effect in Altermagnet Monolayer V2STeO. Materials 2025, 18, 527. https://doi.org/10.3390/ma18030527
Chang Y, Wu Y, Deng L, Yin X, Zhang X. Valley-Related Multipiezo Effect in Altermagnet Monolayer V2STeO. Materials. 2025; 18(3):527. https://doi.org/10.3390/ma18030527
Chicago/Turabian StyleChang, Yufang, Yanzhao Wu, Li Deng, Xiang Yin, and Xianmin Zhang. 2025. "Valley-Related Multipiezo Effect in Altermagnet Monolayer V2STeO" Materials 18, no. 3: 527. https://doi.org/10.3390/ma18030527
APA StyleChang, Y., Wu, Y., Deng, L., Yin, X., & Zhang, X. (2025). Valley-Related Multipiezo Effect in Altermagnet Monolayer V2STeO. Materials, 18(3), 527. https://doi.org/10.3390/ma18030527





