Ultrasonic Melt Processing: Progress, Applications, and Future Directions
Highlights
- Primary crystal fragmentation occurs via a fatigue-like mechanism.
- Ultrasonic bubbles and streaming are visualized with in situ synchrotron imaging.
- Shock waves from bubble implosions are quantified through numerical modeling.
- Interactions in ultrasonic melt processing are simulated using coupling modeling.
Abstract
1. Introduction
2. A Brief over Review of the Historical Development of the Melt Processing
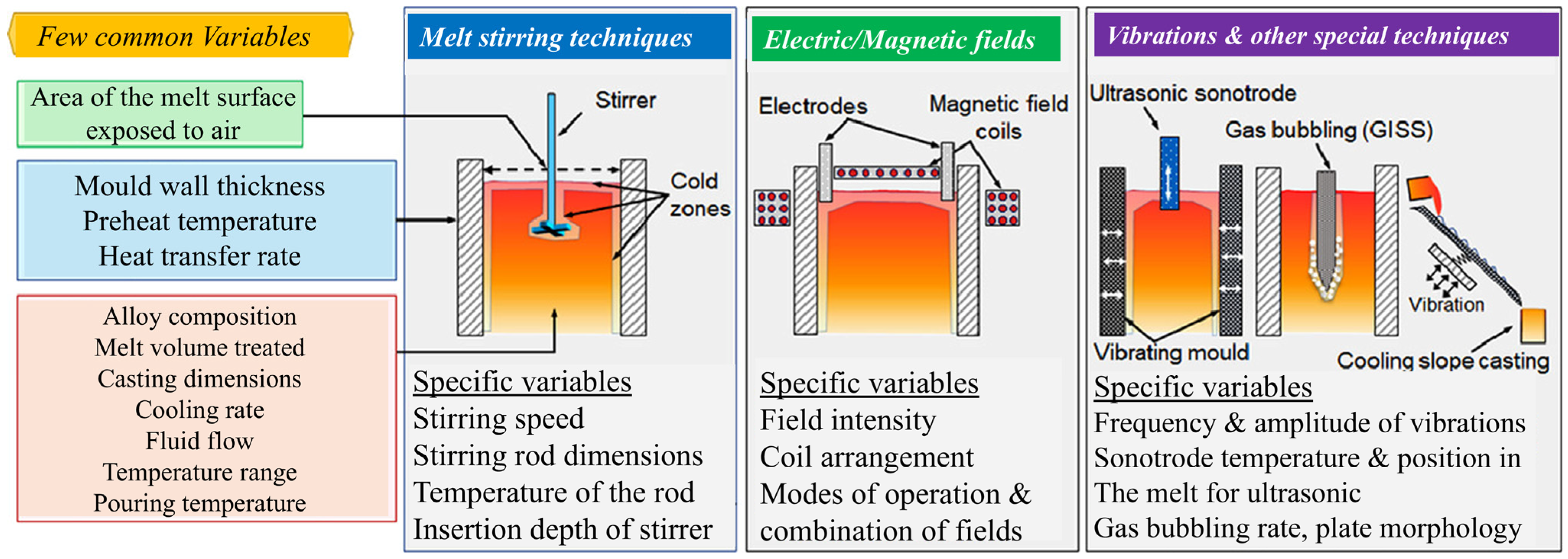
2.1. Electromagnetic Stirring
2.2. Melt Stirring
2.3. Vibration-Assisted Melt Processing
2.4. Gas Bubbling-Assisted Melt Processing
2.5. Ultrasonic-Assisted Melt Processing
3. The Fundamental Issues of Ultrasonic Melt Processing
4. Experimental Techniques for Studying Ultrasonic Melt Processing
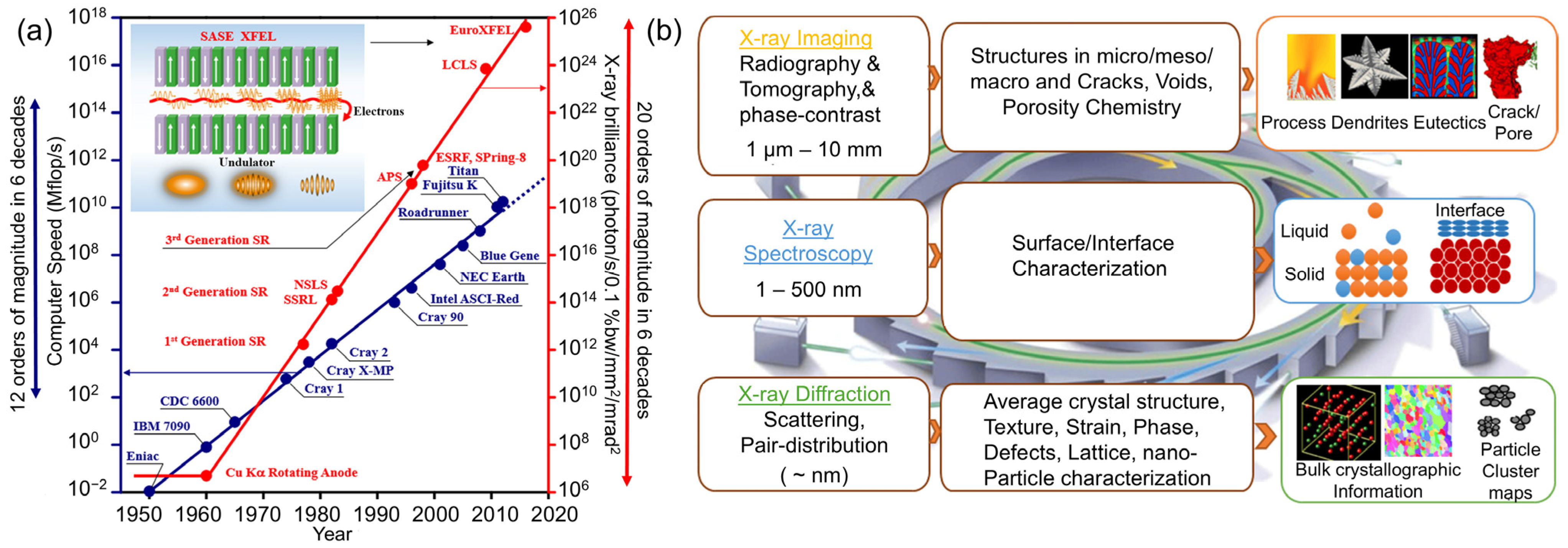
4.1. A Brief Overview of the Development of Synchrotron X-Rays
4.2. Scientific Focuses of the Research on Ultrasonic Melt Processing
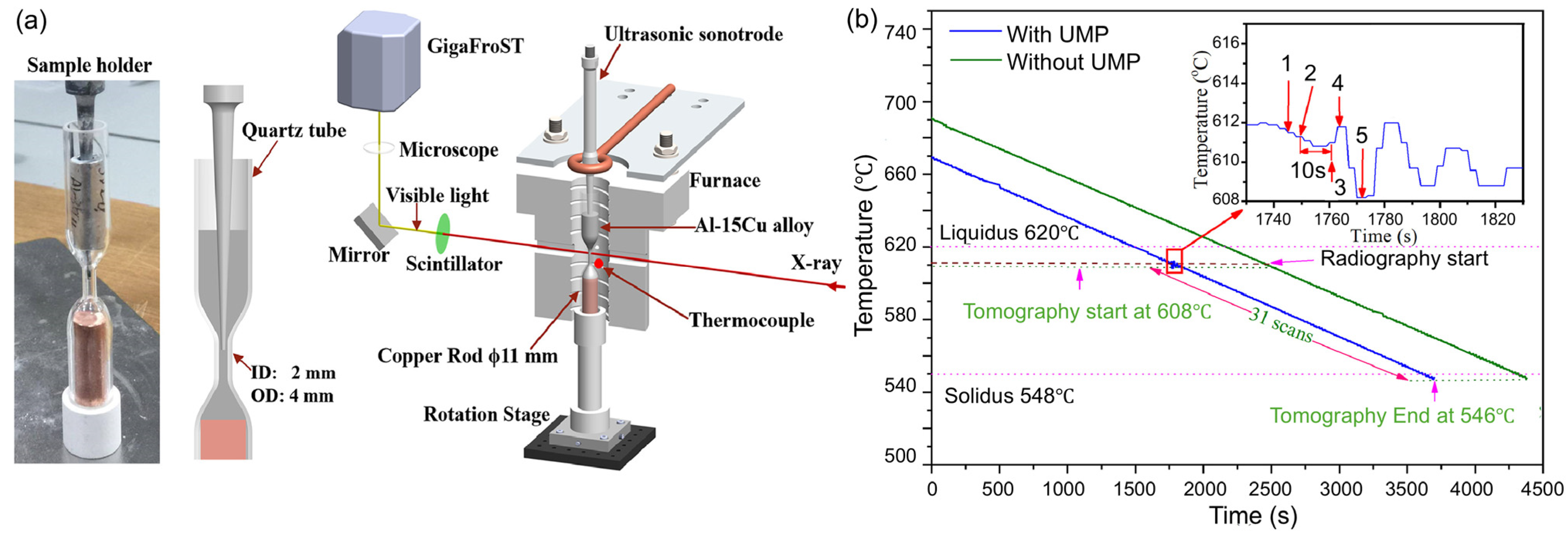
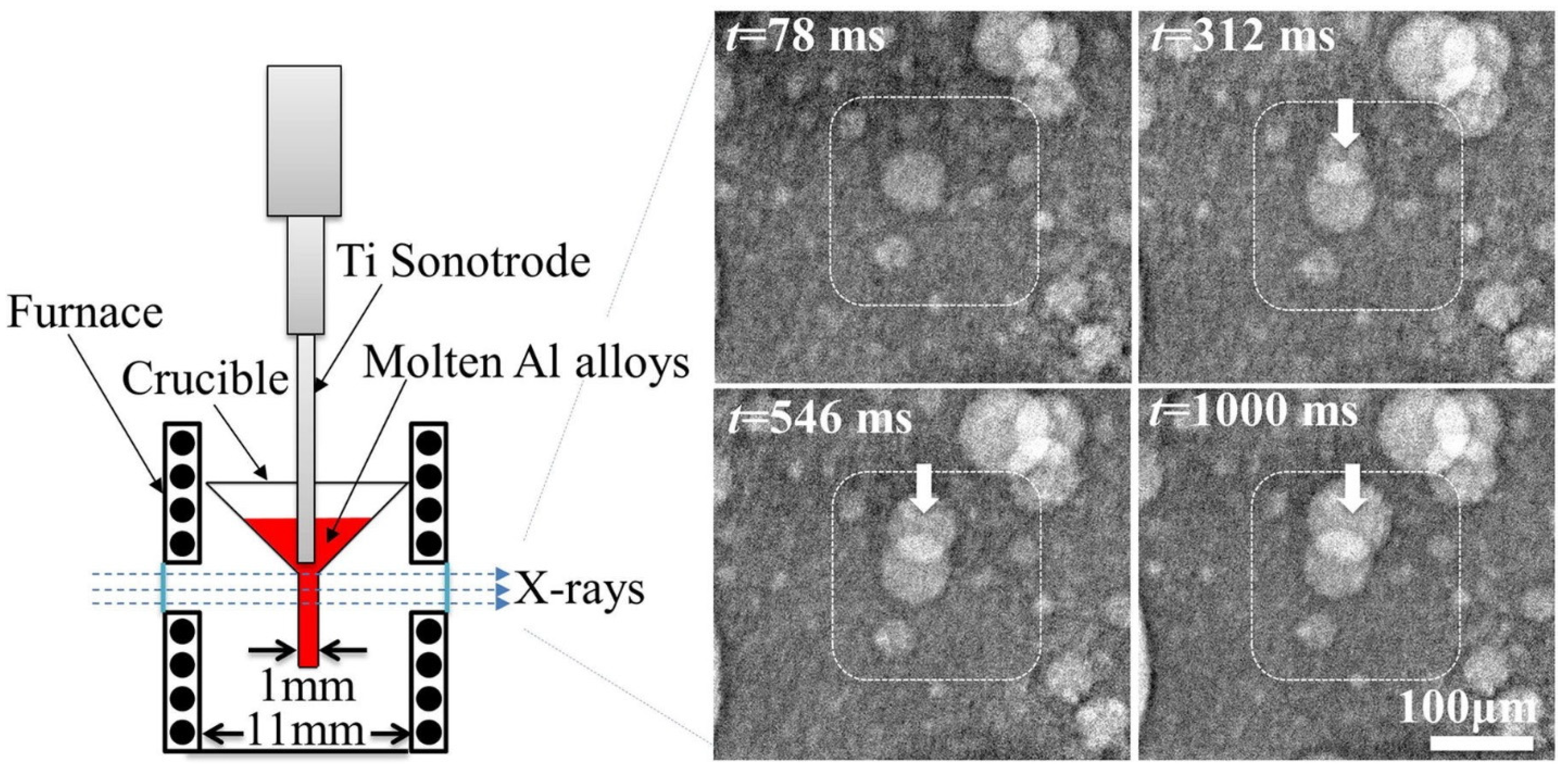
4.2.1. Experiment Setup for Studying Ultrasonic Melt Processing
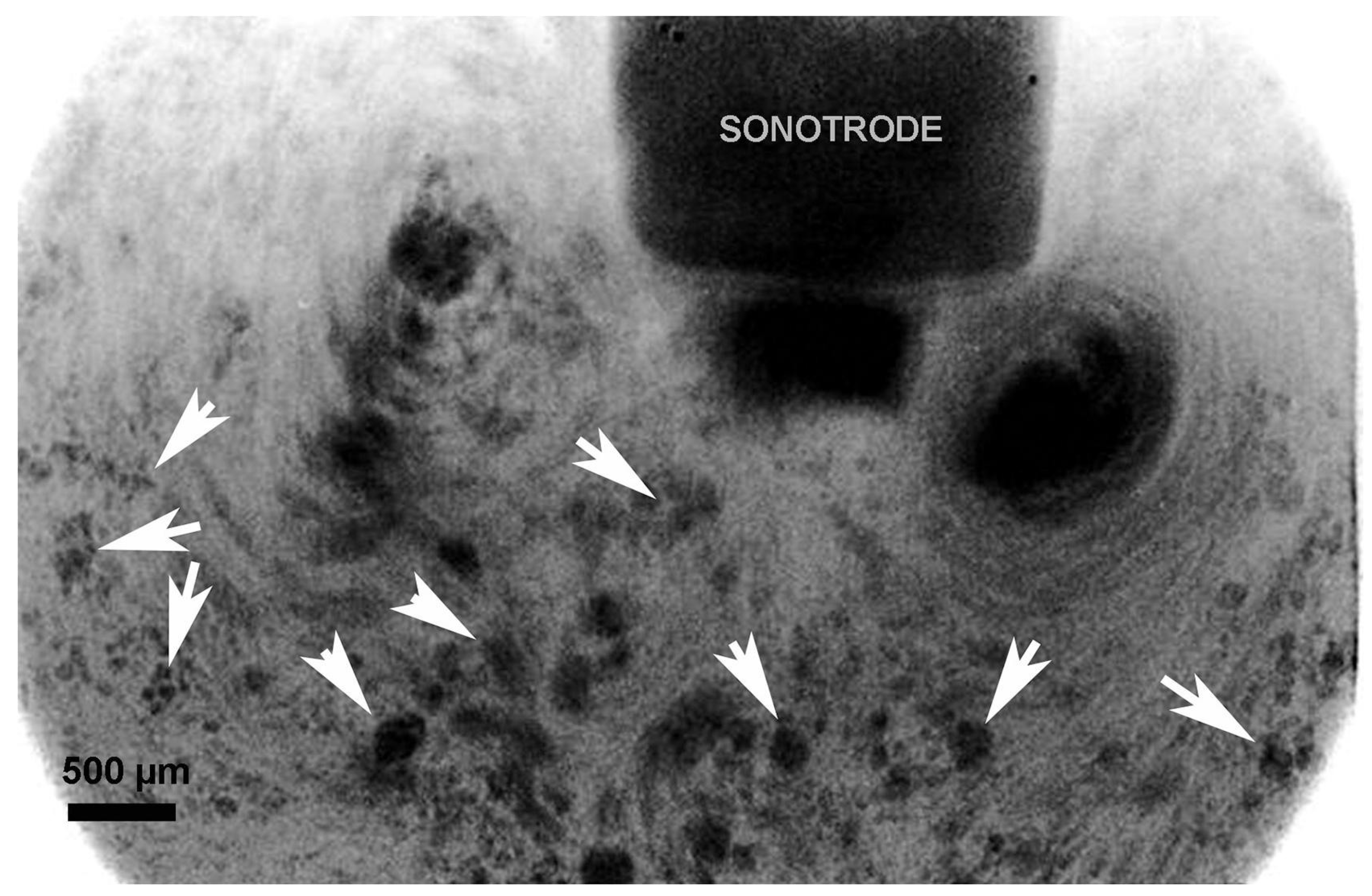
4.2.2. Ultrasonic Bubble in Melt
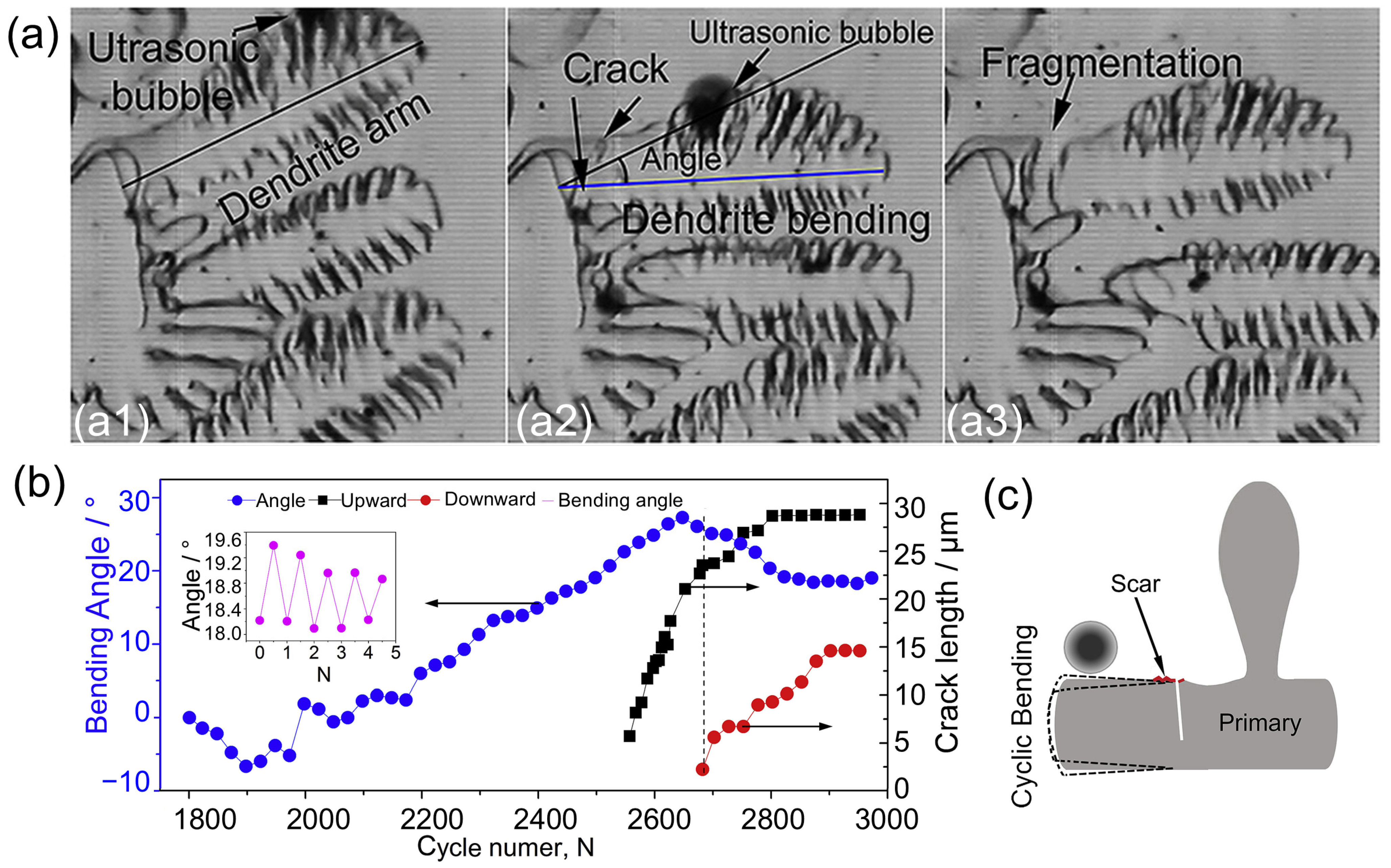
4.2.3. Interaction Between Ultrasound and Solid Phase During Solidification
5. The Modeling and Simulation Methods for Complementing the Experimental Methods
5.1. Analytical Model
5.2. Numerical Modeling
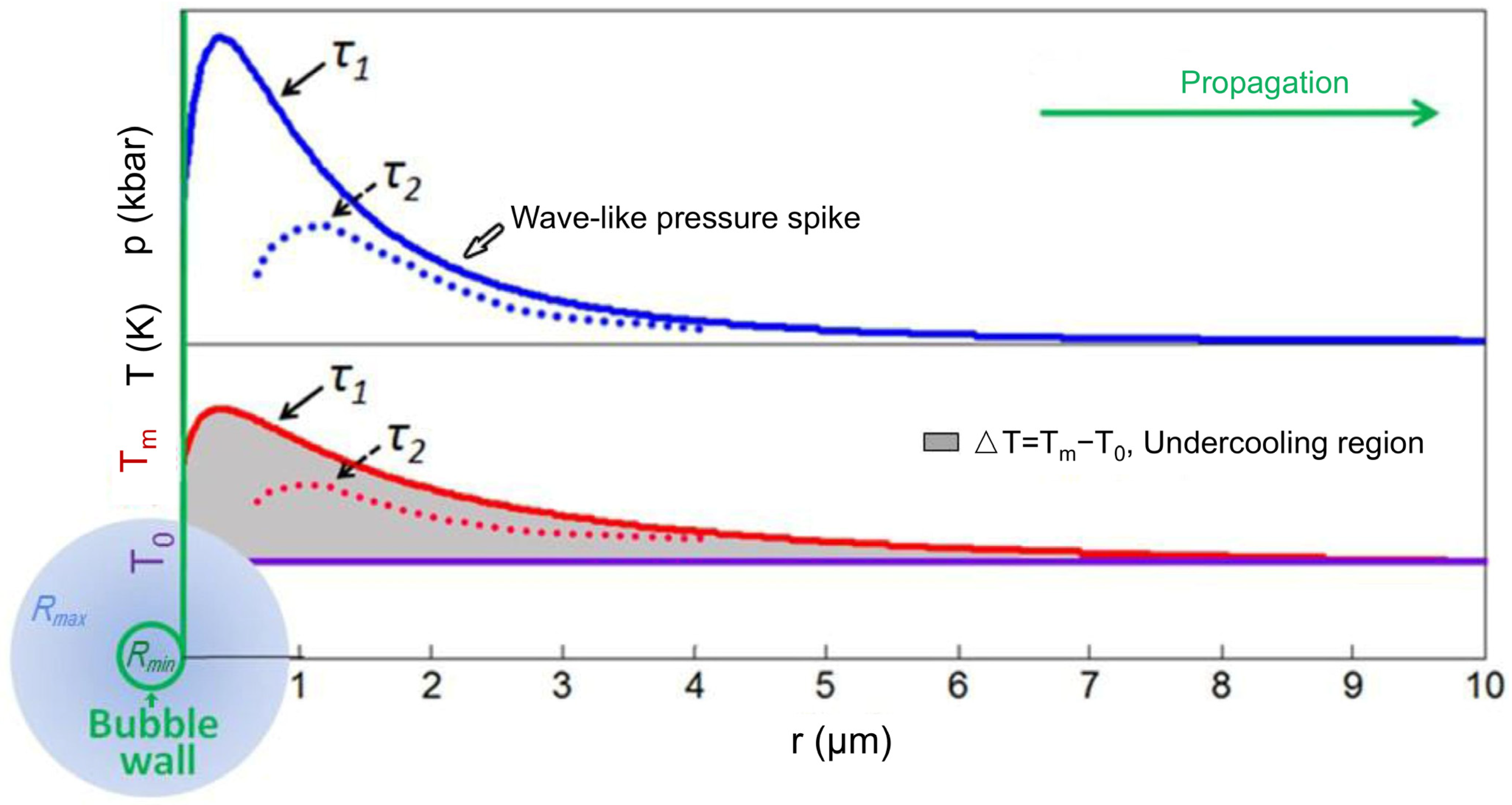
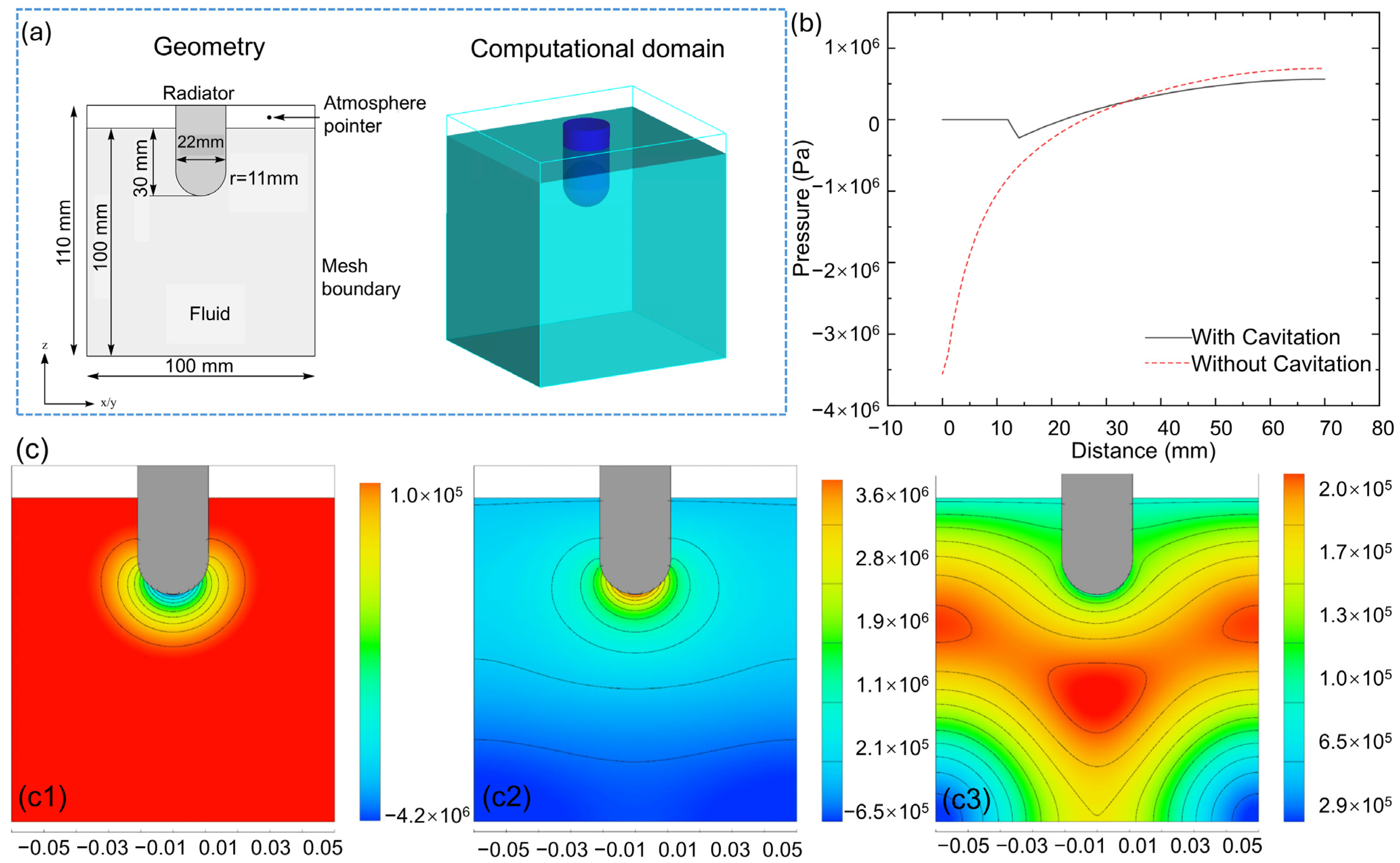
Acoustic Pressure
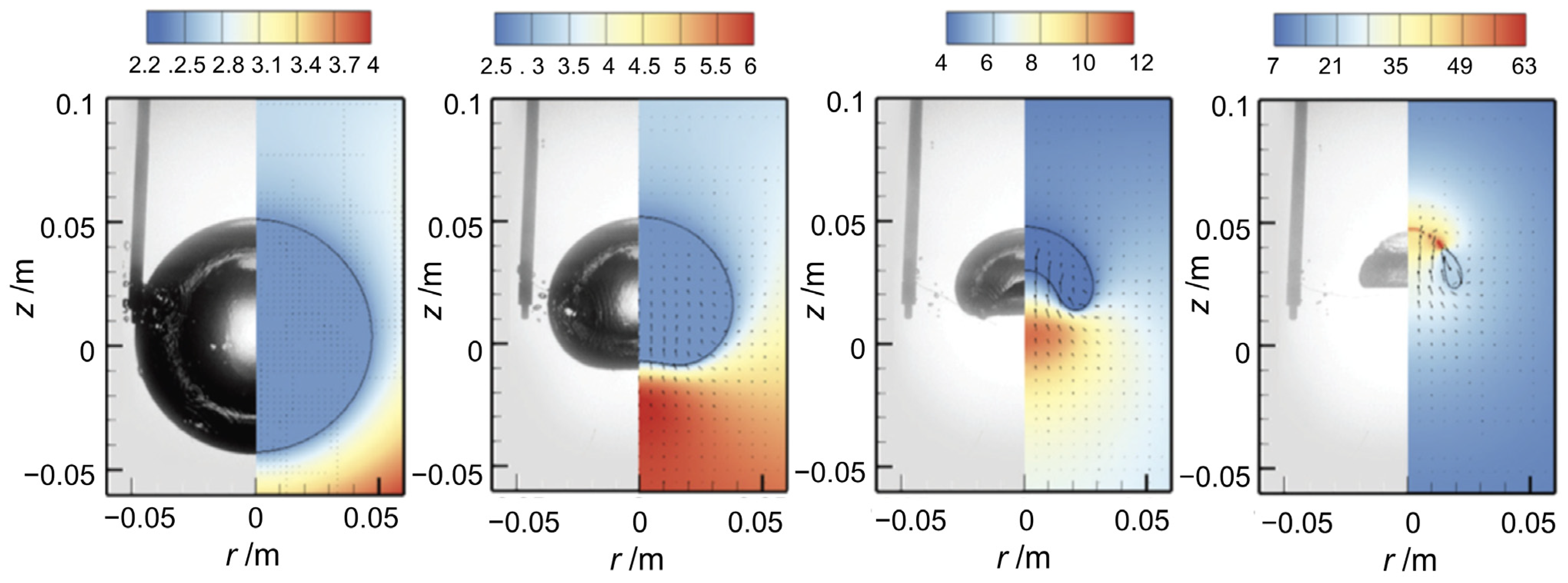
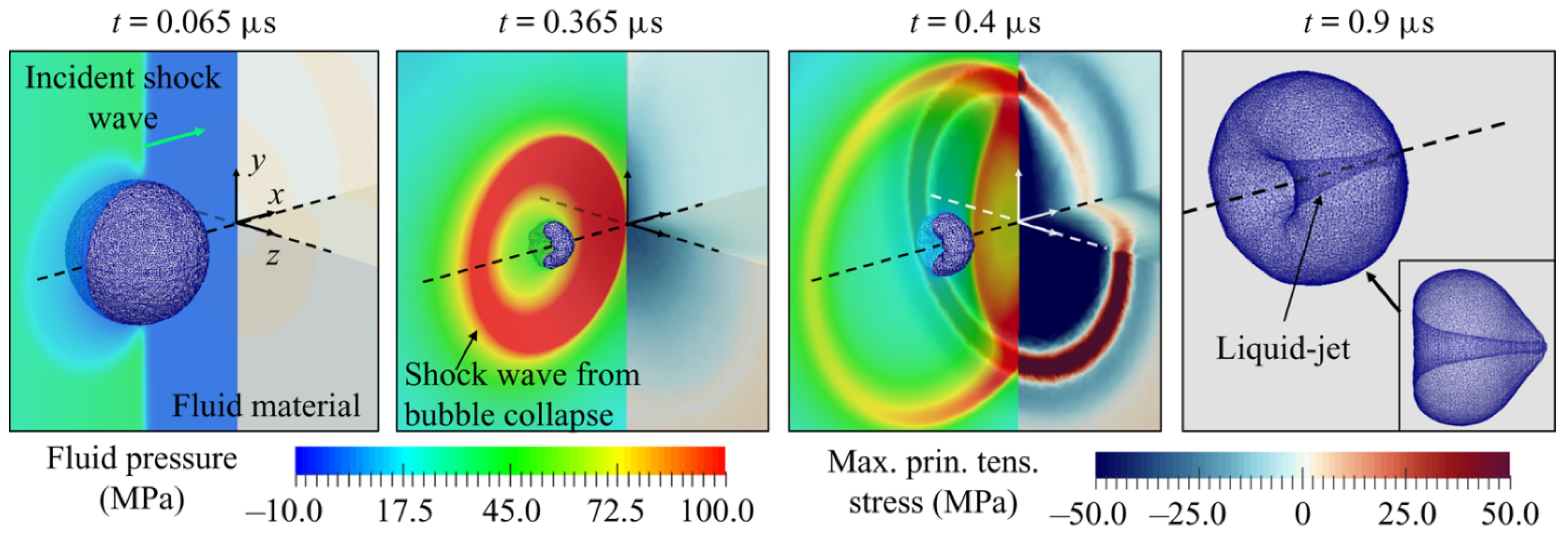
5.3. Ultrasonic Bubble Dynamics
5.3.1. Modeling Based on Navier–Stokes
5.3.2. Modeling Based on Rayleigh–Plesset Equation
5.4. Molecular Dynamics Modeling
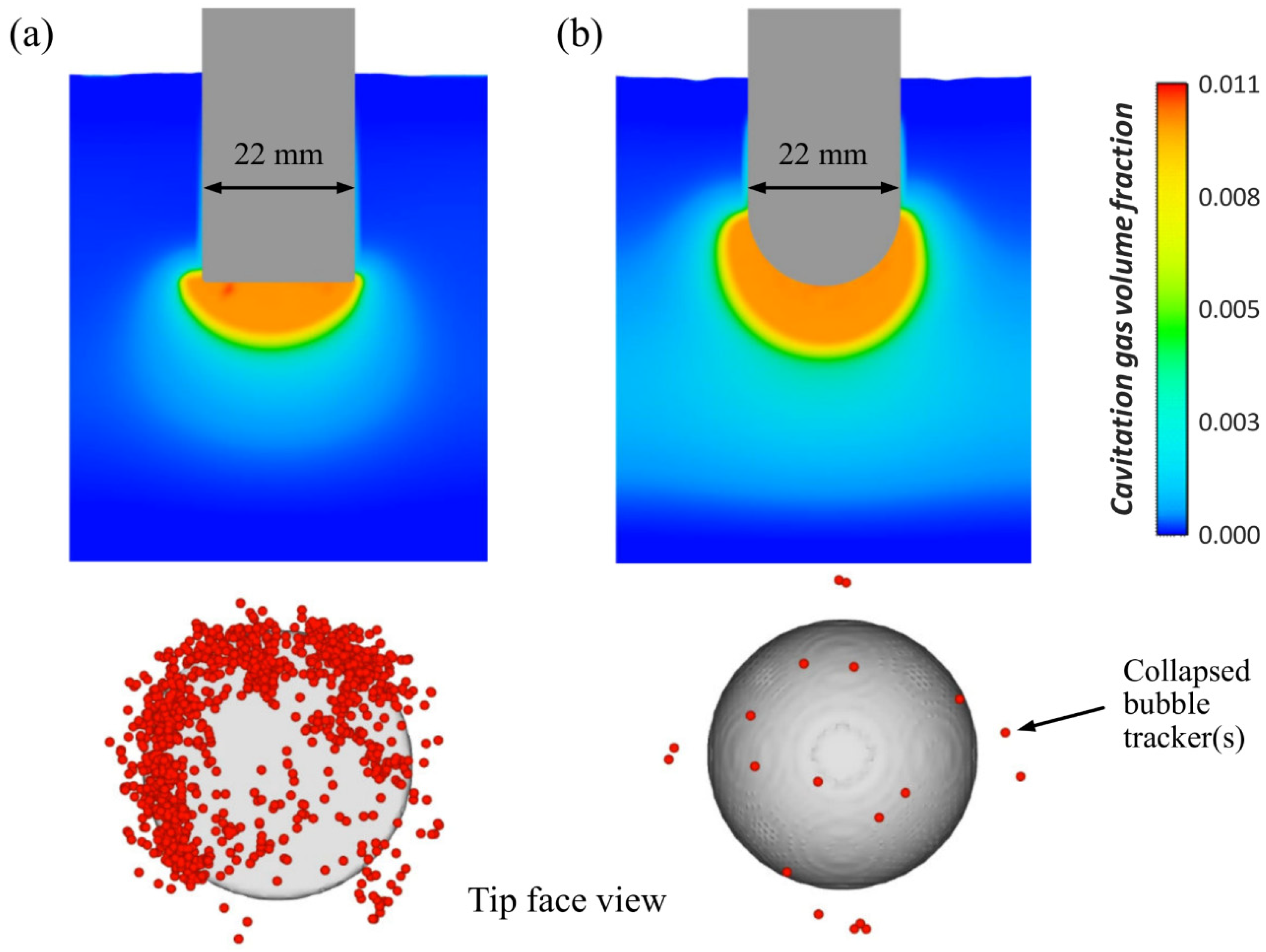
5.5. Interaction Modeling
6. Summary and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Eskin, D.G.; Tzanakis, I. High-frequency vibration and ultrasonic processing. In Solidification Processing of Metallic Alloys Under External Fields; Springer: Berlin/Heidelberg, Germany, 2018; pp. 153–193. [Google Scholar]
- Brodova, I.; Popel, P.; Eskin, G.; Belov, N.; Aksenov, A.; Eskin, D.; Rokhlin, L.; Tonkov, E.Y.; Ponyatovsky, E.; Moiseyev, V.N. Advances in Metallic Alloys; Fridlyander Eskin: New York, NY, USA, 2000. [Google Scholar]
- Eskin, D.G. Ultrasonic melt processing: Achievements and challenges. Mater. Sci. Forum 2015, 828–829, 112–118. [Google Scholar] [CrossRef]
- Eskin, D.G. Ultrasonic processing of molten and solidifying aluminium alloys: Overview and outlook. Mater. Sci. Technol. 2017, 33, 636–645. [Google Scholar] [CrossRef]
- Raoufi, K.; Sutherland, J.W.; Zhao, F.; Clarens, A.F.; Rickli, J.L.; Fan, Z.; Huang, H.; Wang, Y.; Lee, W.J.; Mathur, N.; et al. Current state and emerging trends in advanced manufacturing: Process technologies. Int. J. Adv. Manuf. Technol. 2024, 135, 4089–4118. [Google Scholar] [CrossRef]
- Eskin, D.G. Ultrasonic melt processing: Opportunities and misconceptions. Mater. Sci. Forum 2014, 794–796, 101–106. [Google Scholar] [CrossRef]
- Subroto, T.; Lebon, G.S.; Eskin, D.G.; Skalicky, I.; Roberts, D.; Tzanakis, I.; Pericleous, K. Numerical modelling and experimental validation of the effect of ultrasonic melt treatment in a direct-chill cast AA6008 alloy billet. J. Mater. Res. Technol. 2021, 12, 1582–1596. [Google Scholar] [CrossRef]
- Puga, H.; Costa, S.; Barbosa, J.; Ribeiro, S.; Prokic, M. Influence of ultrasonic melt treatment on microstructure and mechanical properties of AlSi9Cu3 alloy. J. Mater. Process. Technol. 2011, 211, 1729–1735. [Google Scholar] [CrossRef]
- Han, Q. Ultrasonic processing of materials. Metall. Mater. Trans. B 2015, 46, 1603–1614. [Google Scholar] [CrossRef]
- Eskin, G. Cavitation mechanism of ultrasonic melt degassing. Ultrason. Sonochem. 1995, 2, S137–S141. [Google Scholar] [CrossRef]
- Eskin, G.; Eskin, D.G. Effects of ultrasonic (cavitation) melt processing on the structure refinement and property improvement of cast and worked aluminum alloys. Mater. Sci. Forum 2002, 396–402, 77–82. [Google Scholar] [CrossRef]
- Eskin, D.G. Mechanisms and control of macrosegregation in DC casting. Light Metals 2016, 2014, 855–860. [Google Scholar]
- Eskin, D.G. Basics of Solidification Processing of Metallic Alloys. In Solidification Processing of Metallic Alloys Under External Fields; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–17. [Google Scholar]
- Janssens, K. Chapter 4 X-ray based methods of analysis. Compr. Anal. Chem. 2004, 42, 129–226. [Google Scholar]
- Bertrand, L.; Cotte, M.; Stampanoni, M.; Thoury, M.; Marone, F.; Schöder, S. Development and trends in synchrotron studies of ancient and historical materials. Phys. Rep. 2012, 519, 51–96. [Google Scholar] [CrossRef]
- Naohisa, H.; Yasuo, O. X-ray focusing to 62 keV by compound refractive lenses for high-pressure x-ray diffraction. Rev. Sci. Instrum. 2022, 93, 083908. [Google Scholar]
- Haijun, H.; Da, S.; Yanan, F.; Jun, W.; Baode, S. Synchrotron radiation X-ray imaging of cavitation bubbles in Al–Cu alloy melt. Ultrason. Sonochem. 2014, 21, 1275–1278. [Google Scholar]
- Edgar, C.B. The Application of X-Ray Crystal Analysis to Metallurgy. Ind. Eng. Chem. 1924, 16, 692–698. [Google Scholar]
- Mathiesen, R.H.; Arnberg, L.; Mo, F.; Weitkamp, T.; Snigirev, A. Time Resolved X-Ray Imaging of Dendritic Growth in Binary Alloys. Phys. Rev. Lett. 1999, 83, 5062. [Google Scholar] [CrossRef]
- Mirihanage, W.U.; Falch, K.V.; Snigireva, I.; Snigirev, A.; Li, Y.J.; Arnberg, L.; Mathiesen, R.H. Retrieval of three-dimensional spatial information from fast in situ two-dimensional synchrotron radiography of solidification microstructure evolution. Acta Mater. 2014, 81, 241–247. [Google Scholar] [CrossRef]
- Jang, H.S.; Lee, G.H.; Jeon, J.B.; Choi, Y.S.; Shin, S. Effect of ultrasonic melt treatment conditions on melt quality of Al–Mg alloy. J. Mater. Res. Technol. 2022, 19, 2645–2656. [Google Scholar] [CrossRef]
- He, W.; Zhao, Y.; Wei, Q.; Liu, H.; Song, D.; Shen, F.; Sun, Z.; Li, R. Effect of ultrasonic melt processing and cooling rate on microstructure evolution of Al-Cu-Mn-Mg-Fe-Si alloy. J. Mater. Res. Technol. 2023, 27, 3655–3669. [Google Scholar] [CrossRef]
- Zhang, L.; Eskin, D.; Katgerman, L. Influence of ultrasonic melt treatment on the formation of primary intermetallics and related grain refinement in aluminum alloys. J. Mater. Sci. 2011, 46, 5252–5259. [Google Scholar] [CrossRef]
- Atamanenko, T.; Eskin, D.; Zhang, L.; Katgerman, L. Criteria of grain refinement induced by ultrasonic melt treatment of aluminum alloys containing Zr and Ti. Metall. Mater. Trans. A 2010, 41, 2056–2066. [Google Scholar] [CrossRef]
- Yuan, T.; Kou, S.; Luo, Z. Grain refining by ultrasonic stirring of the weld pool. Acta Mater. 2016, 106, 144–154. [Google Scholar] [CrossRef]
- Pola, A.; Arrighini, A.; Roberti, R. Melt Treatment, Grain Refinement & Modification I: Ultrasounds: A New Technology for Alloys Degassing, Grain Refinement and Obtainment of a Thixotropic Structure. Alum. Alloys Phys. Mech. Prop. 2008, 1, 321. [Google Scholar]
- Eskin, D.G. Overview of ultrasonic degassing development. In Light Metals 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 1437–1443. [Google Scholar]
- Eskin, D.; Tzanakis, I.; Wang, F.; Lebon, G.; Subroto, T.; Pericleous, K.; Mi, J. Fundamental studies of ultrasonic melt processing. Ultrason. Sonochem 2019, 52, 455–467. [Google Scholar] [CrossRef]
- Honarvar, F.; Varvani-Farahani, A. A review of ultrasonic testing applications in additive manufacturing: Defect evaluation, material characterization, and process control. Ultrasonics 2020, 108, 106227. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W. Ultrasonic vibration-assisted (UV-A) manufacturing processes: State of the art and future perspectives. J. Manuf. Process. 2020, 51, 174–190. [Google Scholar] [CrossRef]
- Raabe, D. The materials science behind sustainable metals and alloys. Chem. Rev. 2023, 123, 2436–2608. [Google Scholar] [CrossRef]
- Gahan, R.; Zguris, G.C. A review of the melt blown process. In Proceedings of the Fifteenth Annual Battery Conference on Applications and Advances (Cat. No. 00TH8490), Long Beach, CA, USA, 11–14 January 2000; pp. 145–149. [Google Scholar]
- Boljanovic, V. Metal Shaping Processes: Casting and Molding, Particulate Processing, Deformation Processes, and Metal Removal; Industrial Press Inc.: New York, NY, USA, 2009. [Google Scholar]
- Agrawal, A.; Pandelidis, I.; Pecht, M. Injection-molding process control—A review. Polym. Eng. Sci. 1987, 27, 1345–1357. [Google Scholar] [CrossRef]
- Shah, S.; Nautiyal, H.; Gugliani, G.; Kumar, A.; Namboodri, T.; Singla, Y.K. Sustainability in Smart Manufacturing: Trends, Scope, and Challenges; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar]
- Qin, L.; Shen, J.; Li, Q.; Shang, Z. Effects of convection patterns on freckle formation of directionally solidified Nickel-based superalloy casting with abruptly varying cross-sections. J. Cryst. Growth 2017, 466, 45–55. [Google Scholar] [CrossRef]
- Li, Q.; Shen, J.; Qin, L.; Gao, S. Investigation on freckles in directionally solidified CMSX-4 superalloy specimens with abrupt cross section variation. J. Alloys Compd. 2017, 691, 997–1004. [Google Scholar] [CrossRef]
- Qin, L.; Shen, J.; Yang, G.; Li, Q.; Shang, Z. A design of non-uniform thickness mould for controlling temperature gradient and S/L interface shape in directionally solidified superalloy blade. Mater. Des. 2017, 116, 565–576. [Google Scholar] [CrossRef]
- Balasubramani, N.; Venezuela, J.; StJohn, D.; Wang, G.; Dargusch, M. A review of the origin of equiaxed grains during solidification under mechanical stirring, vibration, electromagnetic, electric-current, and ultrasonic treatments. J. Mater. Sci. Technol. 2023, 144, 243–265. [Google Scholar] [CrossRef]
- Tzavaras, A.A.; Brody, H. Electromagnetic stirring and continuous casting—Achievements, problems, and goals. JOM 1984, 36, 31–37. [Google Scholar] [CrossRef]
- Liu, C.-T.; Lin, S.-Y.; Lee, W.-J.; Chen, J.-H. Electromagnetic stirring systems. IEEE Ind. Appl. Mag. 2011, 17, 38–43. [Google Scholar]
- Wang, F.; Wang, E.; Zhang, L.; Jia, P.; Wang, T. Influence of electromagnetic stirring (EMS) on the microstructure and mechanical property of Incoloy825 superalloy. J. Manuf. Process. 2017, 26, 364–371. [Google Scholar] [CrossRef]
- Du, Y.; Lu, Y.; Wang, T.; Li, T.; Zhang, G. Effect of electromagnetic stirring on microstructure and properties of Al0.5CoCrCuFeNi alloy. Procedia Eng. 2012, 27, 1129–1134. [Google Scholar] [CrossRef]
- Li, J.; Wang, B.; Ma, Y.; Cui, J. Effect of complex electromagnetic stirring on inner quality of high carbon steel bloom. Mater. Sci. Eng. A 2006, 425, 201–204. [Google Scholar] [CrossRef]
- Kunstreich, S. Electromagnetic stirring for continuous casting. Metall. Res. Technol. 2003, 100, 395–408. [Google Scholar] [CrossRef]
- Wang, L.; Shen, J.; Qin, L.; Feng, Z.; Wang, L.; Fu, H. The effect of the flow driven by a travelling magnetic field on solidification structure of Sn–Cd peritectic alloys. J. Cryst. Growth 2012, 356, 26–32. [Google Scholar] [CrossRef]
- Li, Q.; Shen, J.; Qin, L.; Xiong, Y.; Yue, X. Effect of traveling magnetic field on freckle formation in directionally solidified CMSX-4 superalloy. J. Mater. Process. Technol. 2019, 274, 116308. [Google Scholar] [CrossRef]
- Fujisaki, K.; Ueyama, T.; Takahashi, K.-i.; Satoh, S. Phase characteristics of electromagnetic stirring. IEEE Trans. Magn. 1997, 33, 4245–4247. [Google Scholar] [CrossRef]
- Qin, L.; Shen, J.; Li, Q.; Shang, Z. Effect of a traveling magnetic field on freckle formation of directionally solidified Pb–Sn alloys. J. Mater. Res. 2017, 32, 2045–2054. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, B.; Jiang, H.; Tan, L.; Weng, Y.; Yang, Y.; Qin, L. Numerical Simulation of Transport Phenomena in Directional Solidification Castings with Changeable Cross-Section and Solidification Interface Control. Metals 2022, 12, 1694. [Google Scholar] [CrossRef]
- Qin, L.; Shen, J.; Fu, H. The Suppression of the Natural Convection in the Directional Solidification Processing of Superalloy by the Introduction of the Traveling Magnetic Field: 2D and 3D Simulation. High Temp. Mater. Process. 2016, 35, 881–893. [Google Scholar] [CrossRef]
- Hanumanth, G.; Irons, G. Particle incorporation by melt stirring for the production of metal-matrix composites. J. Mater. Sci. 1993, 28, 2459–2465. [Google Scholar] [CrossRef]
- Brabazon, D.; Browne, D.; Carr, A. Mechanical stir casting of aluminium alloys from the mushy state: Process, microstructure and mechanical properties. Mater. Sci. Eng. A 2002, 326, 370–381. [Google Scholar] [CrossRef]
- Cross, M.; Campbell, J. Modeling of casting, welding and advanced solidification processes VII. In Proceedings of the 7th Conference in a Series on Modeling, Casting, and Welding Processes, London, UK, 10–15 September 1995. [Google Scholar]
- Abu-Dheir, N.; Khraisheh, M.; Saito, K.; Male, A. Silicon morphology modification in the eutectic Al–Si alloy using mechanical mold vibration. Mater. Sci. Eng. A 2005, 393, 109–117. [Google Scholar] [CrossRef]
- Campbell, J. Effects of vibration during solidification. Int. Met. Rev. 1981, 26, 71–108. [Google Scholar] [CrossRef]
- Guan, R.-G.; Tie, D. A review on grain refinement of aluminum alloys: Progresses, challenges and prospects. Acta Metall. Sin. 2017, 30, 409–432. [Google Scholar] [CrossRef]
- Stern, E.A.; Līvņš, P.; Zhang, Z. Thermal vibration and melting from a local perspective. Phys. Rev. B 1991, 43, 8850–8860. [Google Scholar] [CrossRef]
- Campbell, J. Castings; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Wannasin, J.; Martinez, R.; Flemings, M. Grain refinement of an aluminum alloy by introducing gas bubbles during solidification. Scr. Mater. 2006, 55, 115–118. [Google Scholar] [CrossRef]
- Dunand, D.C. Processing of titanium foams. Adv. Eng. Mater. 2004, 6, 369–376. [Google Scholar] [CrossRef]
- Ma, L.; Song, Z. Cellular structure control of aluminium foams during foaming process of aluminium melt. Scr. Mater. 1998, 39, 1523–1528. [Google Scholar] [CrossRef]
- Soni, S.K.; Manimaran, D.; Thomas, S.B.; Thomas, B. Microstructure and mechanical characterization of Al6061 based composite and nanocomposites prepared via conventional and ultrasonic-assisted melt-stirring techniques. Mater. Today Commun. 2023, 34, 105222. [Google Scholar] [CrossRef]
- Li, X.; Yang, Y.; Cheng, X. Ultrasonic-assisted fabrication of metal matrix nanocomposites. J. Mater. Sci. 2004, 39, 3211–3212. [Google Scholar] [CrossRef]
- Alavi, S.H.; Harimkar, S.P. Melt expulsion during ultrasonic vibration-assisted laser surface processing of austenitic stainless steel. Ultrasonics 2015, 59, 21–30. [Google Scholar] [CrossRef]
- Gao, S.; Qiu, Z.; Ma, Z.; Yang, Y. Flow properties of polymer melt in longitudinal ultrasonic-assisted microinjection molding. Polym. Eng. Sci. 2017, 57, 797–805. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, Y.; Ming, W.; He, W.; Ma, J. The Metal Additive-Manufacturing Technology of the Ultrasonic-Assisted Wire-and-Arc Additive-Manufacturing Process. Metals 2023, 13, 398. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, M.; Zhang, T.; Xie, J.; Wei, K.; Wang, S.; Yin, L.; He, P. Grain refinement and mechanical properties improvement of Inconel 625 alloy fabricated by ultrasonic-assisted wire and arc additive manufacturing. J. Alloys Compd. 2022, 910, 164957. [Google Scholar] [CrossRef]
- Ji, F.; Qin, X.; Hu, Z.; Xiong, X.; Ni, M.; Wu, M. Influence of ultrasonic vibration on molten pool behavior and deposition layer forming morphology for wire and arc additive manufacturing. Int. Commun. Heat Mass Transf. 2022, 130, 105789. [Google Scholar] [CrossRef]
- Qin, L.; Maciejewska, B.M.; Subroto, T.; Morton, J.A.; Porfyrakis, K.; Tzanakis, I.; Eskin, D.G.; Grobert, N.; Fezzaa, K.; Mi, J. Ultrafast synchrotron X-ray imaging and multiphysics modelling of liquid phase fatigue exfoliation of graphite under ultrasound. Carbon 2022, 186, 227–237. [Google Scholar] [CrossRef]
- Morton, J.A.; Khavari, M.; Qin, L.; Maciejewska, B.M.; Tyurnina, A.V.; Grobert, N.; Eskin, D.G.; Mi, J.; Porfyrakis, K.; Prentice, P.; et al. New insights into sono-exfoliation mechanisms of graphite: In situ high-speed imaging studies and acoustic measurements. Mater. Today 2021, 49, 10–22. [Google Scholar] [CrossRef]
- Priyadarshi, A.; Shahrani, S.B.; Choma, T.; Zrodowski, L.; Qin, L.; Leung, C.L.A.; Clark, S.J.; Fezzaa, K.; Mi, J.; Lee, P.D.; et al. New insights into the mechanism of ultrasonic atomization for the production of metal powders in additive manufacturing. Addit. Manuf. 2024, 83, 104033. [Google Scholar] [CrossRef]
- Qin, L.; Zhang, Z.; Guo, B.; Li, W.; Mi, J. Determining the Critical Fracture Stress of Al Dendrites near the Melting Point via Synchrotron X-ray Imaging. Acta Metall. Sin. 2023, 36, 857–864. [Google Scholar] [CrossRef]
- Ng, K.L.; Maciejewska, B.M.; Qin, L.; Johnston, C.; Barrio, J.; Titirici, M.-M.; Tzanakis, I.; Eskin, D.G.; Porfyrakis, K.; Mi, J.; et al. Direct evidence of the exfoliation efficiency and graphene dispersibility of green solvents toward sustainable graphene production. ACS Sustain. Chem. Eng. 2022, 11, 58–66. [Google Scholar] [CrossRef]
- Yu, L.; Lin, Y.; Li, L.; Zong, H.; Zhou, Y.; Zhao, S.; Zhang, Z.; Grobert, N.; Maciejewska, B.M.; Qin, L. Understanding interfacial dynamics: Hydrostatic pressure-induced sono-dispersion of carbon nanotubes. Surf. Interfaces 2024, 51, 104740. [Google Scholar] [CrossRef]
- Riedel, E.; Liepe, M.; Scharf, S. Simulation of ultrasonic induced cavitation and acoustic streaming in liquid and solidifying aluminum. Metals 2020, 10, 476. [Google Scholar] [CrossRef]
- Mobilio, S.; Boscherini, F.; Meneghini, C. Synchrotron Radiation; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Willmott, P. An Introduction to Synchrotron Radiation: Techniques and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Huang, S.; Luo, S.; Qin, L.; Shu, D.; Sun, B.; Lunt, A.J.; Korsunsky, A.M.; Mi, J. 3D local atomic structure evolution in a solidifying Al-0.4 Sc dilute alloy melt revealed in operando by synchrotron X-ray total scattering and modelling. Scr. Mater. 2022, 211, 114484. [Google Scholar] [CrossRef]
- Zhang, Z.; Khong, J.C.; Koe, B.; Luo, S.; Huang, S.; Qin, L.; Cipiccia, S.; Batey, D.; Bodey, A.J.; Rau, C.; et al. Multiscale characterization of the 3D network structure of metal carbides in a Ni superalloy by synchrotron X-ray microtomography and ptychography. Scr. Mater. 2021, 193, 71–76. [Google Scholar] [CrossRef]
- Qin, L.; Du, W.; Cipiccia, S.; Bodey, A.J.; Rau, C.; Mi, J. Synchrotron X-ray operando study and multiphysics modelling of the solidification dynamics of intermetallic phases under electromagnetic pulses. Acta Mater. 2024, 265, 119593. [Google Scholar] [CrossRef]
- Xie, H.; Wang, J.; Li, Y.; Song, J.; Hu, H.; Qin, L.; Zhao, H.; Li, C.; Cui, Y.; Tan, Z.; et al. Fast shot speed induced microstructure and mechanical property evolution of high pressure die casting Mg-Al-Zn-RE alloys. J. Mater. Process. Technol. 2024, 331, 118523. [Google Scholar] [CrossRef]
- Huang, S.; Qin, L.; Zhao, J.; Xiang, K.; Luo, S.; Michalik, S.; Mi, J. Revealing atomic structure evolution of an Al-1.5 Fe alloy in the liquid state using X-ray total scattering and empirical potential structure refinement. Proc. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1274, 012007. [Google Scholar] [CrossRef]
- Karagadde, S.; Leung, C.L.A.; Lee, P.D. Progress on in situ and operando X-ray imaging of solidification processes. Materials 2021, 14, 2374. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wang, C.; Koe, B.; Schlepütz, C.M.; Irvine, S.; Mi, J. Synchrotron X-ray imaging and ultrafast tomography in situ study of the fragmentation and growth dynamics of dendritic microstructures in solidification under ultrasound. Acta Mater. 2021, 209, 116796. [Google Scholar] [CrossRef]
- Huang, H.; Qin, L.; Tang, H.; Shu, D.; Yan, W.; Sun, B.; Mi, J. Ultrasound cavitation induced nucleation in metal solidification: An analytical model and validation by real-time experiments. Ultrason. Sonochem. 2021, 80, 105832. [Google Scholar] [CrossRef]
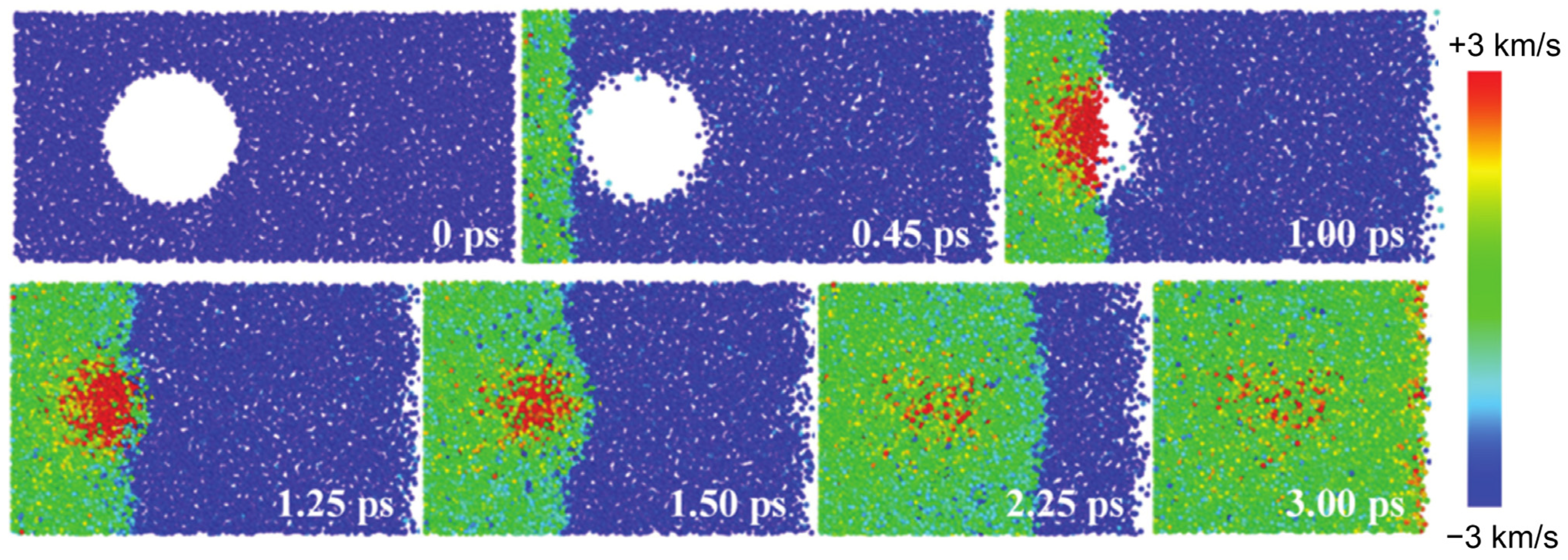
- Qin, L.; Porfyrakis, K.; Tzanakis, I.; Grobert, N.; Eskin, D.G.; Fezzaa, K.; Mi, J. Multiscale interactions of liquid, bubbles and solid phases in ultrasonic fields revealed by multiphysics modelling and ultrafast X-ray imaging. Ultrason. Sonochem. 2022, 89, 106158. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Tzanakis, I.; Srirangam, P.; Mirihanage, W.; Eskin, D.; Bodey, A.; Lee, P. Synchrotron quantification of ultrasound cavitation and bubble dynamics in Al–10Cu melts. Ultrason. Sonochem. 2016, 31, 355–361. [Google Scholar] [CrossRef]
- Wang, B.; Tan, D.; Lee, T.L.; Khong, J.C.; Wang, F.; Eskin, D.; Connolley, T.; Fezzaa, K.; Mi, J. Ultrafast synchrotron X-ray imaging studies of microstructure fragmentation in solidification under ultrasound. Acta Mater. 2018, 144, 505–515. [Google Scholar] [CrossRef]
- Wang, S.; Kang, J.; Guo, Z.; Lee, T.; Zhang, X.; Wang, Q.; Deng, C.; Mi, J. In situ high speed imaging study and modelling of the fatigue fragmentation of dendritic structures in ultrasonic fields. Acta Mater. 2019, 165, 388–397. [Google Scholar] [CrossRef]
- Wang, F.; Eskin, D.; Mi, J.; Wang, C.; Koe, B.; King, A.; Reinhard, C.; Connolley, T. A synchrotron X-radiography study of the fragmentation and refinement of primary intermetallic particles in an Al-35 Cu alloy induced by ultrasonic melt processing. Acta Mater. 2017, 141, 142–153. [Google Scholar] [CrossRef]
- Mokso, R.; Marone, F.; Stampanoni, M. Real time tomography at the Swiss Light Source. AIP Conf. Proc. 2010, 1234, 87–90. [Google Scholar]
- Marone, F.; Mokso, R.; Fife, J.; Irvine, S.; Modregger, P.; Pinzer, B.; Mader, K.; Isenegger, A.; Mikuljan, G.; Stampanoni, M. Synchrotron-based X-ray tomographic microscopy at the Swiss light source for industrial applications. Synchrotron Radiat. News 2011, 24, 24–29. [Google Scholar] [CrossRef]
- Valloton, J.; Gawor, S.; Henein, H. Modelling of nucleation in Impulse atomized undercooled droplets. Comput. Mater. Sci. 2018, 144, 176–180. [Google Scholar] [CrossRef]
- Xu, Y.; Zhao, D.; Li, Y. A thermodynamic study on the effect of solute on the nucleation driving force, solid–liquid interfacial energy, and grain refinement of Al alloys. Metall. Mater. Trans. A 2018, 49, 1770–1781. [Google Scholar] [CrossRef]
- Boehler, R.; Ross, M. Melting curve of aluminum in a diamond cell to 0.8 Mbar: Implications for iron. Earth Planet. Sci. Lett. 1997, 153, 223–227. [Google Scholar] [CrossRef]
- Terasaki, H.; Kato, T.; Urakawa, S.; Funakoshi, K.-i.; Suzuki, A.; Okada, T.; Maeda, M.; Sato, J.; Kubo, T.; Kasai, S. The effect of temperature, pressure, and sulfur content on viscosity of the Fe–FeS melt. Earth Planet. Sci. Lett. 2001, 190, 93–101. [Google Scholar] [CrossRef]
- Postovalov, V.G.e.; Romanov, E.P.; Kondrat’ev, V.P.; Kononenko, V.I. Theory of transport in liquid metals: Calculation of dynamic viscosity. High Temp. 2003, 41, 762–770. [Google Scholar] [CrossRef]
- Yao, X.; Dahle, A.; Davidson, C.; StJohn, D. Effect of solute on the growth rate and the constitutional undercooling ahead of the advancing interface during solidification of an alloy and the implications for nucleation. J. Mater. Res. 2006, 21, 2470–2479. [Google Scholar] [CrossRef]
- Yao, X.; Dahle, A.K.; Davidson, C.J.; StJohn, D.H. Modelling of grain size transition with alloy concentration in solidified Al–Si alloys. J. Mater. Sci. 2007, 42, 9756–9764. [Google Scholar] [CrossRef]
- Shen, P.; Fujii, H.; Matsumoto, T.; Nogi, K. Critical factors affecting the wettability of α-alumina by molten aluminum. J. Am. Ceram. Soc. 2004, 87, 2151–2159. [Google Scholar] [CrossRef]
- Minsier, V.; Proost, J. Shock wave emission upon spherical bubble collapse during cavitation-induced megasonic surface cleaning. Ultrason. Sonochem. 2008, 15, 598–604. [Google Scholar] [CrossRef] [PubMed]
- Shu, D.; Sun, B.; Mi, J.; Grant, P.S. A high-speed imaging and modeling study of dendrite fragmentation caused by ultrasonic cavitation. Metall. Mater. Trans. A 2012, 43, 3755–3766. [Google Scholar] [CrossRef]
- Rashwan, S.S.; Dincer, I.; Mohany, A. Investigation of acoustic and geometric effects on the sonoreactor performance. Ultrason. Sonochem. 2020, 68, 105174. [Google Scholar] [CrossRef] [PubMed]
- Runa, S.; Himadri, C.; Chandan, G. A review on the application of lattice Boltzmann method for melting and solidification problems. Comput. Mater. Sci. 2022, 206, 111288. [Google Scholar]
- Catarino, S.O.; Miranda, J.M.; Lanceros-Mendez, S.; Minas, G. Numerical prediction of acoustic streaming in a microcuvette. Can. J. Chem. Eng. 2014, 92, 1988–1998. [Google Scholar] [CrossRef]
- Mulbah, C.; Kang, C.; Mao, N.; Zhang, W.; Shaikh, A.R.; Teng, S. A review of VOF methods for simulating bubble dynamics. Prog. Nucl. Energy 2022, 154, 104478. [Google Scholar] [CrossRef]
- Vachaparambil, K.J.; Einarsrud, K.E. Comparison of surface tension models for the volume of fluid method. Processes 2019, 7, 542. [Google Scholar] [CrossRef]
- Liu, Y.-L.; Zhang, A.; Tian, Z.-L.; Wang, S.-P. Dynamical behavior of an oscillating bubble initially between two liquids. Phys. Fluids 2019, 31, 092111. [Google Scholar] [CrossRef]
- Cao, S.; Wang, G.; Coutier-Delgosha, O.; Wang, K. Shock-induced bubble collapse near solid materials: Effect of acoustic impedance. J. Fluid Mech. 2021, 907, A17. [Google Scholar] [CrossRef]
- Sharma, S.S.; Parashar, A. A review of molecular dynamic simulations to study the effect of helium bubble formation in metal crystals. Phys. Scr. 2024, 99, 102001. [Google Scholar] [CrossRef]
- Okumura, H.; Ito, N. Nonequilibrium molecular dynamics simulations of a bubble. Phys. Rev. E 2003, 67, 045301. [Google Scholar] [CrossRef] [PubMed]
- Schanz, D.; Metten, B.; Kurz, T.; Lauterborn, W. Molecular dynamics simulations of cavitation bubble collapse and sonoluminescence. New J. Phys. 2012, 14, 113019. [Google Scholar] [CrossRef]
- Zhan, S.; Duan, H.; Pan, L.; Tu, J.; Jia, D.; Yang, T.; Li, J. Molecular dynamics simulation of shock-induced microscopic bubble collapse. Phys. Chem. Chem. Phys. 2021, 23, 8446–8455. [Google Scholar] [CrossRef]
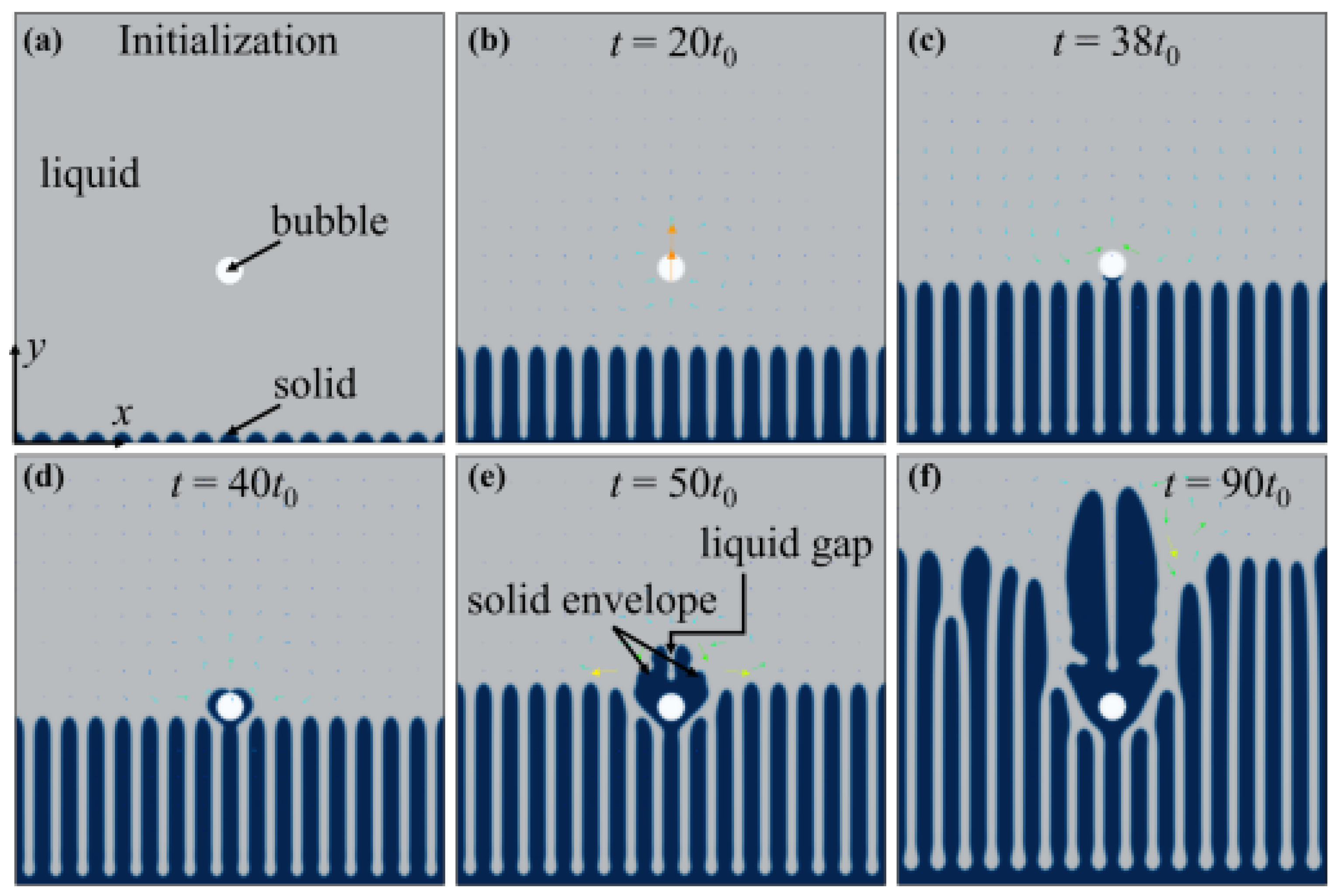
- Zhang, A.; Du, J.; Zhang, X.; Guo, Z.; Wang, Q.; Xiong, S. Phase-field modeling of microstructure evolution in the presence of bubble during solidification. Metall. Mater. Trans. A 2020, 51, 1023–1037. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Weng, Y.; Zhao, Q.; Wu, G.; Deng, Z.; Qin, L. Ultrasonic Melt Processing: Progress, Applications, and Future Directions. Materials 2025, 18, 522. https://doi.org/10.3390/ma18030522
Yang S, Weng Y, Zhao Q, Wu G, Deng Z, Qin L. Ultrasonic Melt Processing: Progress, Applications, and Future Directions. Materials. 2025; 18(3):522. https://doi.org/10.3390/ma18030522
Chicago/Turabian StyleYang, Shuang, Yu Weng, Qin Zhao, Gang Wu, Zhian Deng, and Ling Qin. 2025. "Ultrasonic Melt Processing: Progress, Applications, and Future Directions" Materials 18, no. 3: 522. https://doi.org/10.3390/ma18030522
APA StyleYang, S., Weng, Y., Zhao, Q., Wu, G., Deng, Z., & Qin, L. (2025). Ultrasonic Melt Processing: Progress, Applications, and Future Directions. Materials, 18(3), 522. https://doi.org/10.3390/ma18030522












