Improvement of a Switchable Wide-Incident-Angle Perfect Absorber Incorporating Sb2S3
Abstract
1. Introduction
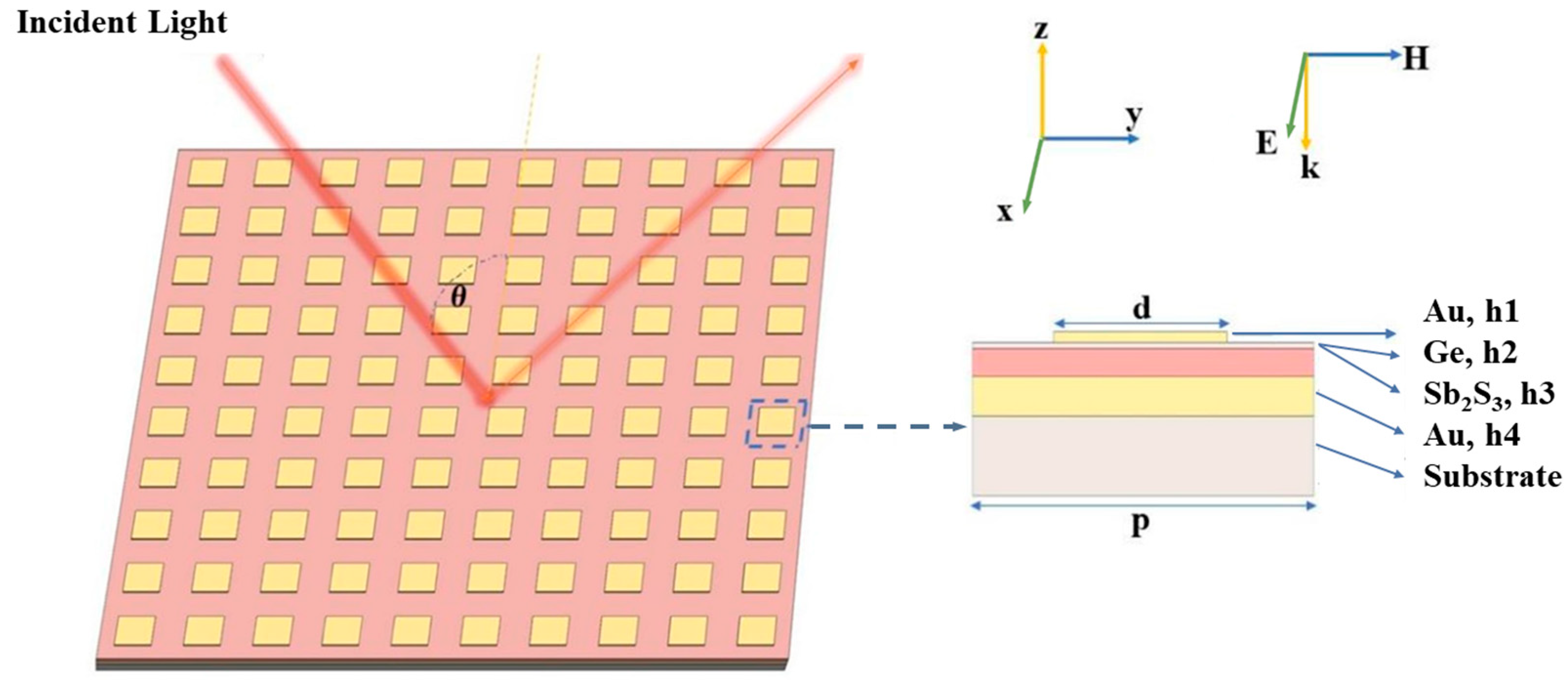
2. Simulation Model
3. Results and Discussion
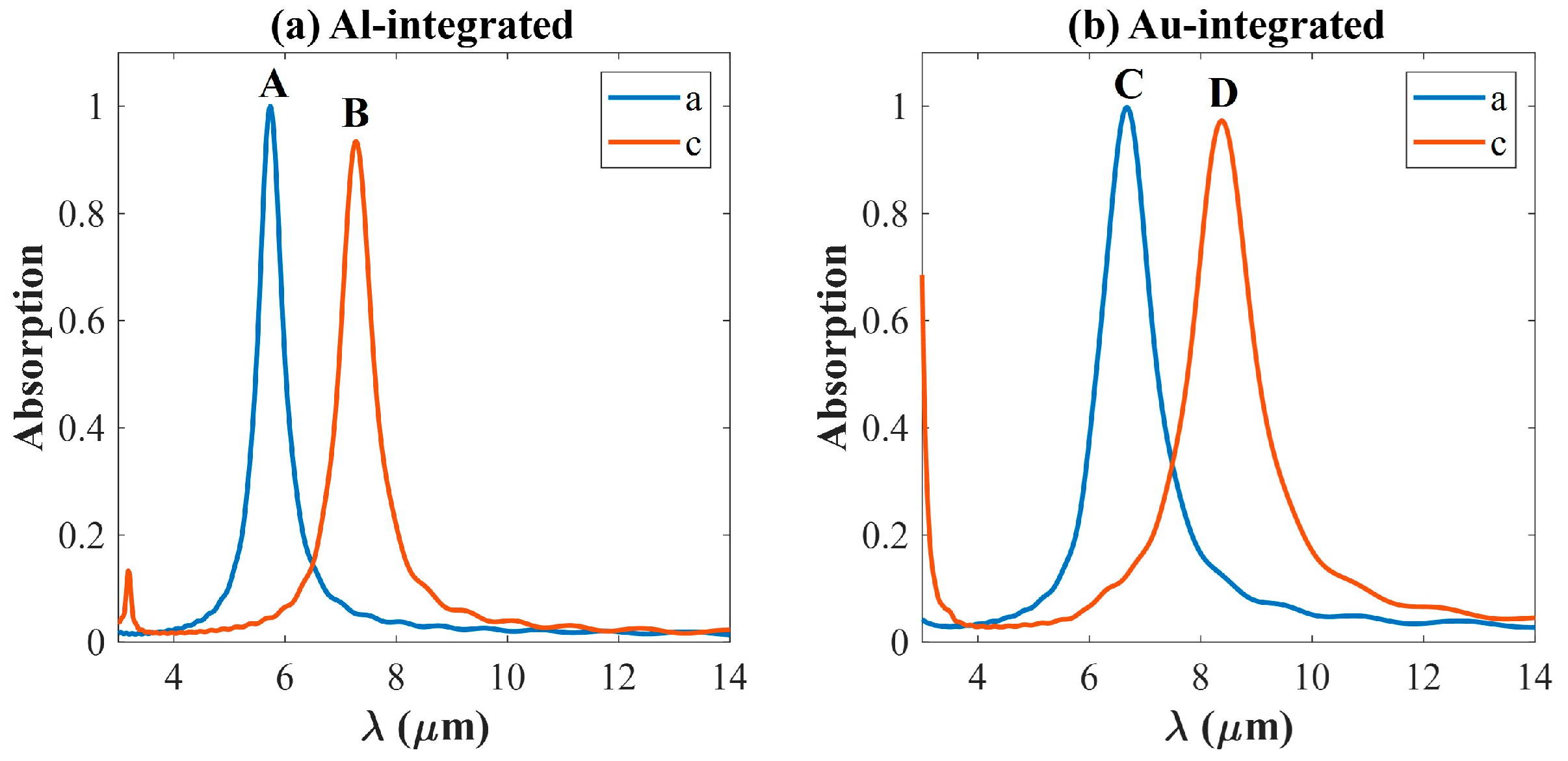
3.1. Narrow-Band Infrared Absorption
3.2. Physical Mechanism of Narrow-Band Infrared Absorption
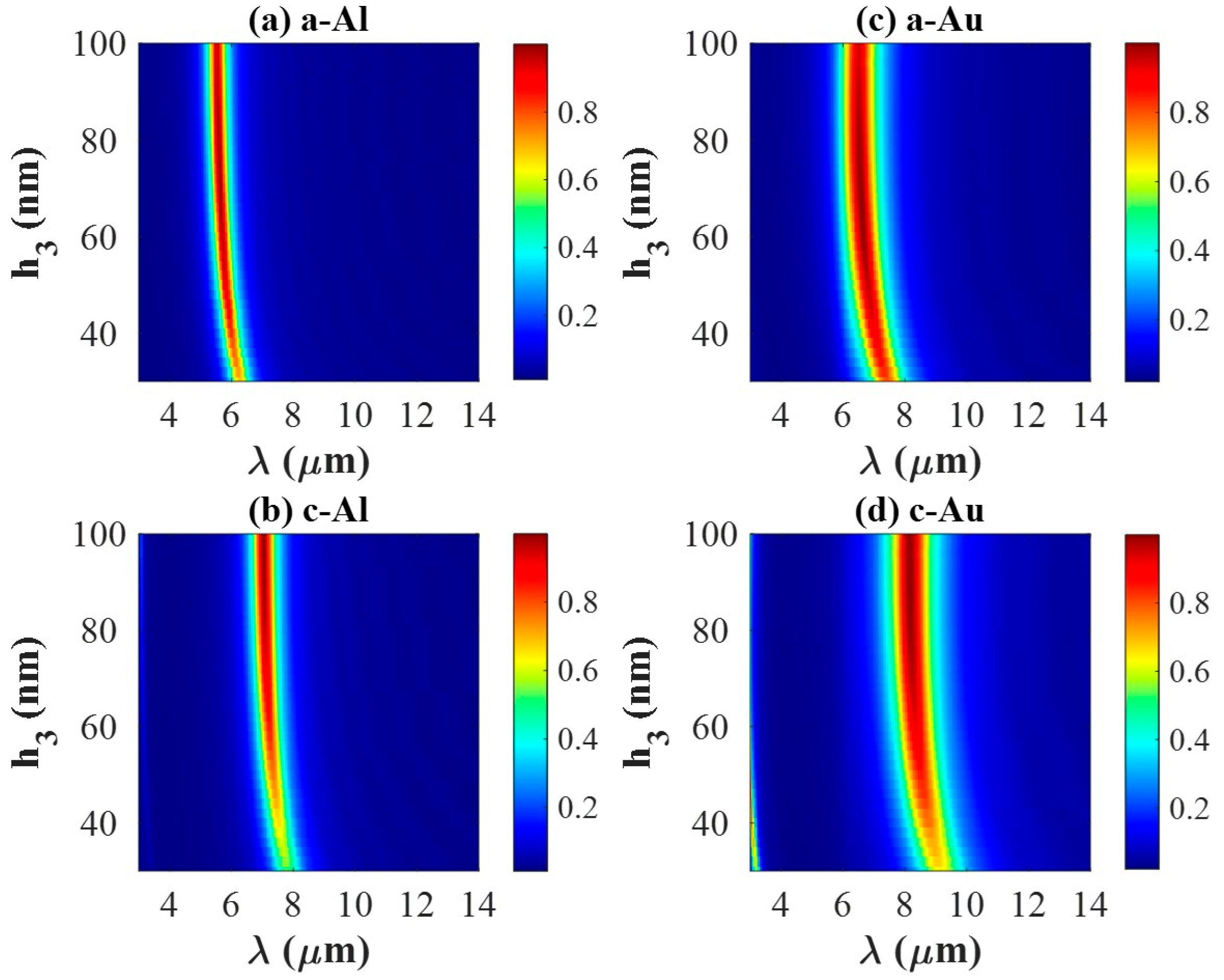
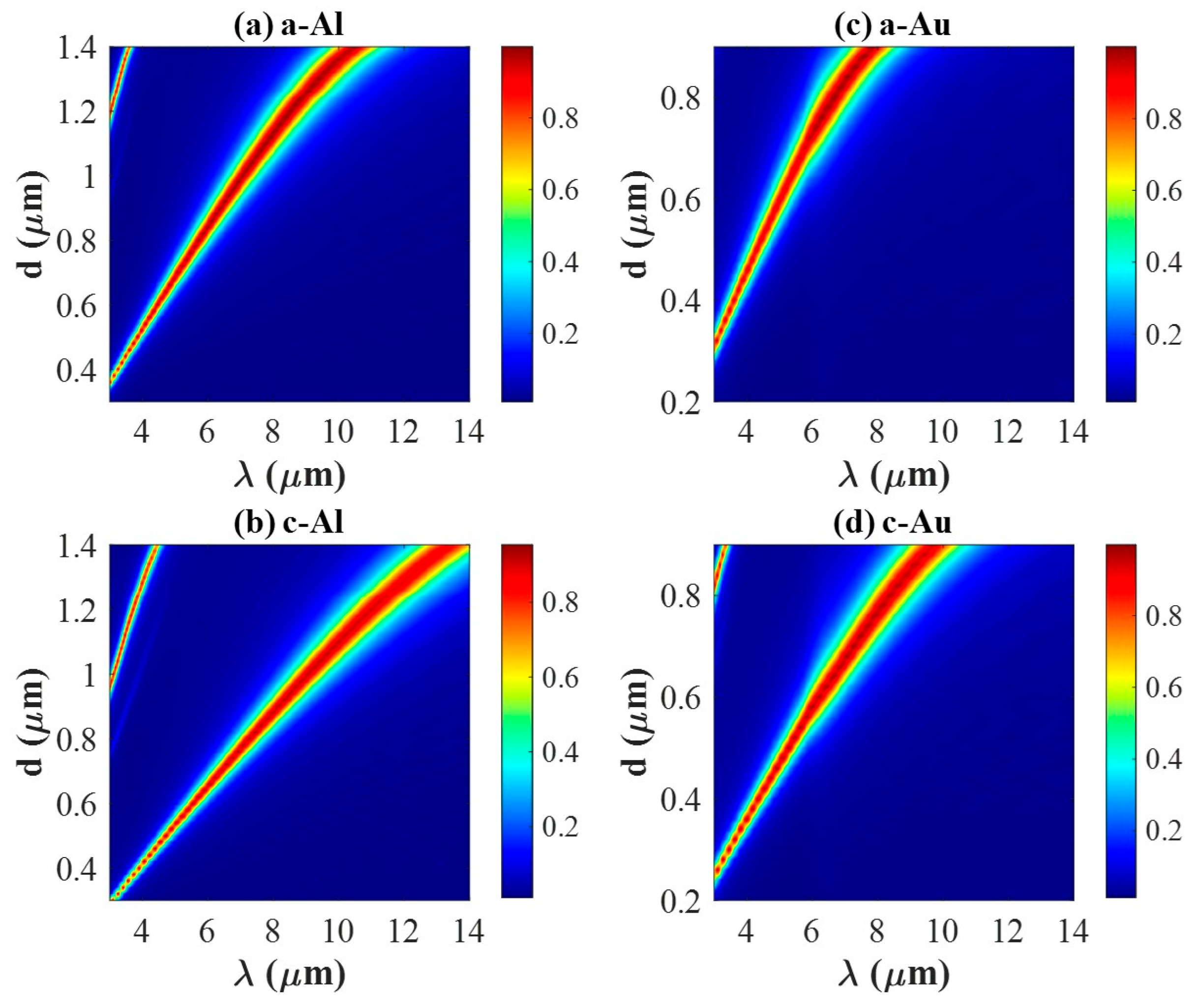
3.3. The Influence of Geometric Parameters
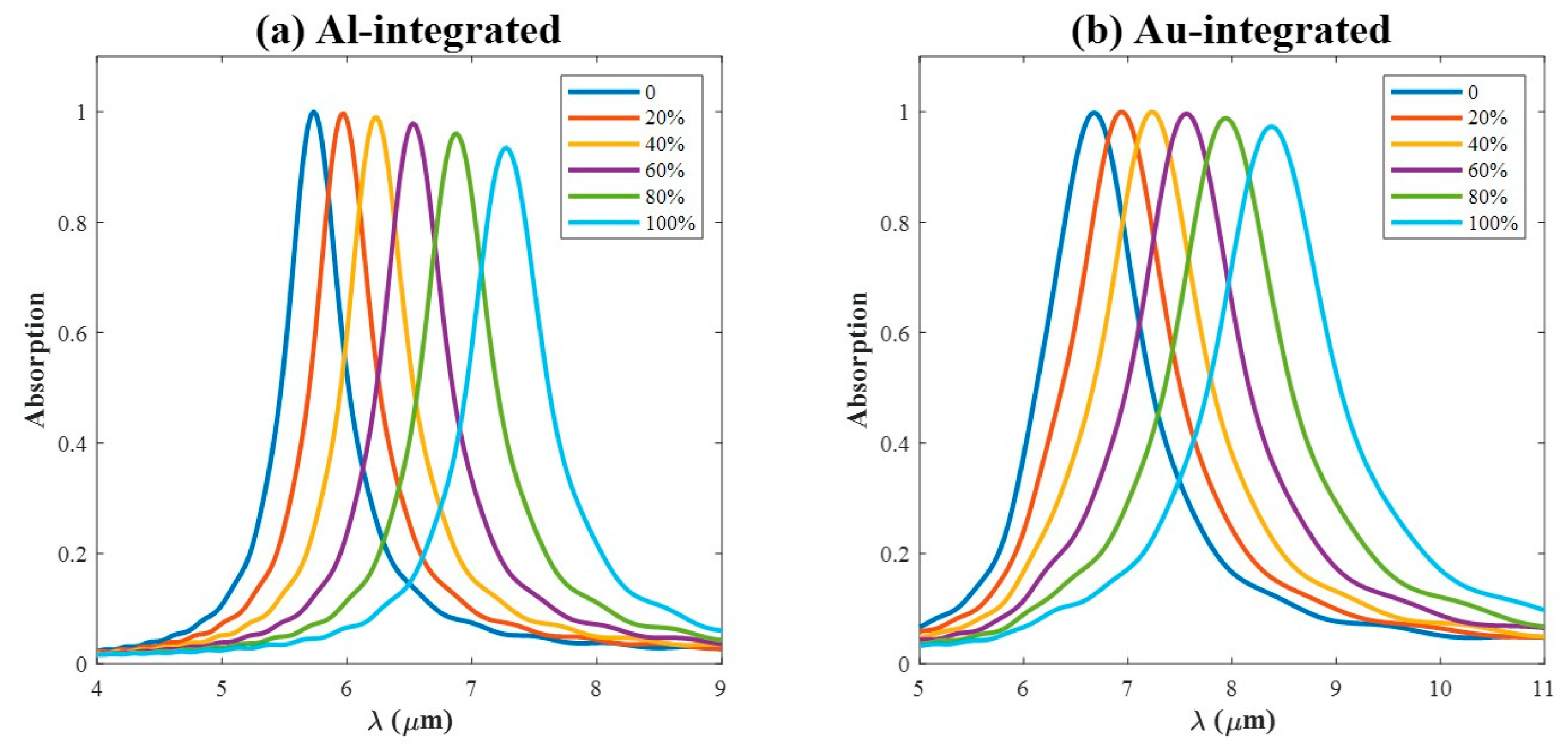
3.4. Crystallization Levels
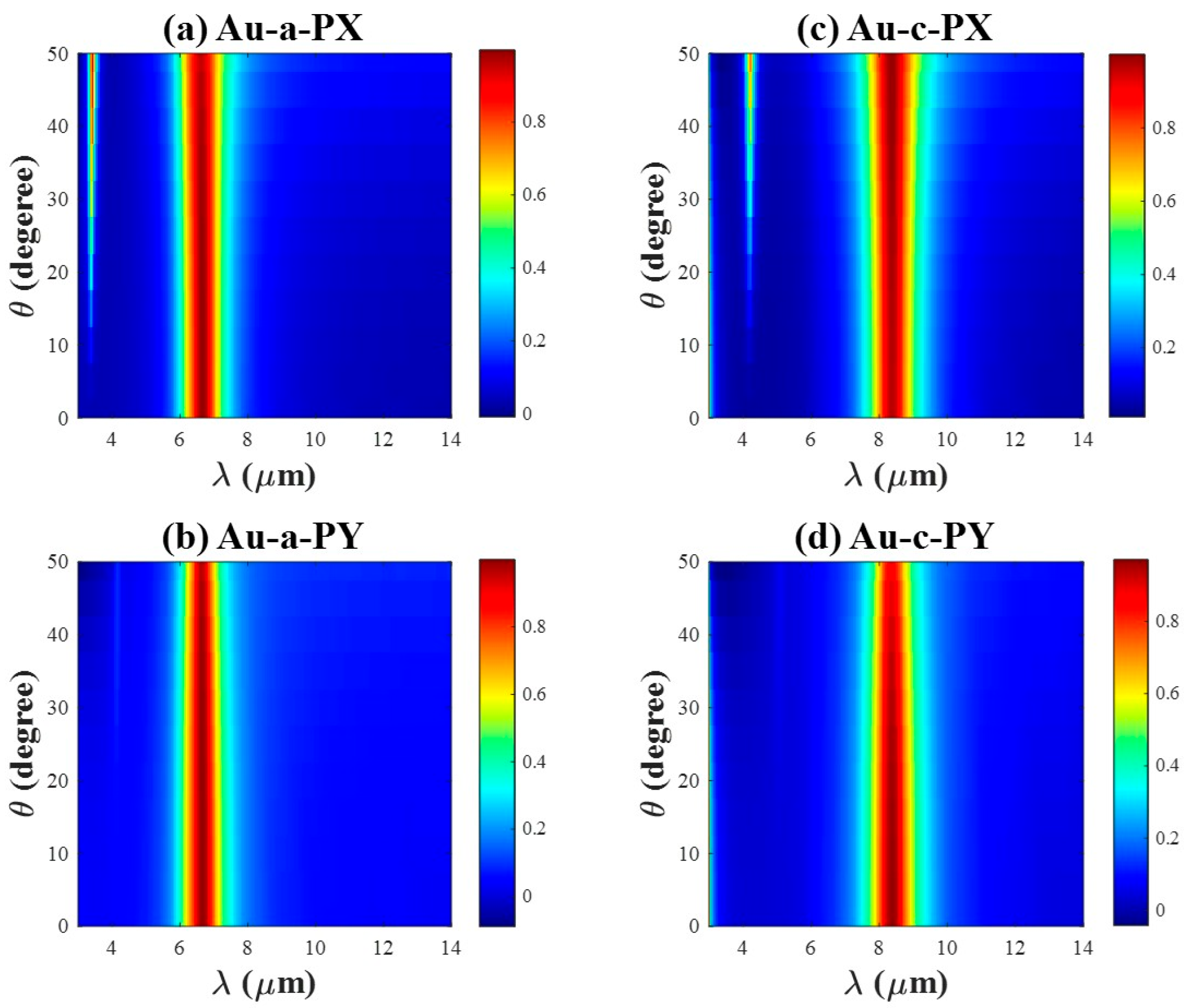
3.5. Incident Angle Dependent
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kossowski, N.; Tahmi, Y.; Loucif, A.; Lepers, M.; Wattellier, B.; Vienne, G.; Khadir, S.; Genevet, P. Metrology of metasurfaces: Optical properties. npj Nanophotonics 2025, 2, 5. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, Z.; Zhang, L.; Wang, Z.; Xie, R.; Zhao, J.; You, R.; You, Z. Review on Metasurfaces: An Alternative Approach to Advanced Devices and Instruments. Adv. Devices Instrum. 2022, 2022, 9765089. [Google Scholar] [CrossRef]
- Wang, R.; Yue, S.; Zhang, Z.; Hou, Y.; Zhao, H.; Qu, S.; Li, M.; Zhang, Z. Broadband Perfect Absorber in the Visible Range Based on Metasurface Composite Structures. Materials 2022, 15, 2612. [Google Scholar] [CrossRef]
- Moreau, A.; Ciracì, C.; Mock, J.J.; Hill, R.T.; Wang, Q.; Wiley, B.J.; Chilkoti, A.; Smith, D.R. Controlled-reflectance surfaces with film-coupled colloidal nanoantennas. Nature 2012, 492, 86–89. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Lee, J.S.; Aggarwal, S.; Farmakidis, N.; He, Y.; Cheng, T.; Bhaskaran, H. Varifocal Metalens Using Tunable and Ultralow-loss Dielectrics. Adv. Sci. 2023, 10, 2204899. [Google Scholar] [CrossRef] [PubMed]
- Tao, J.; You, Q.; Yang, C.; Li, Z.; Deng, L.; Wu, M.; Luo, M.; Wu, L.; Li, C.; Liu, Z.; et al. Beam-steering metasurfaces assisted coherent optical wireless multichannel communication system. Nanophotonics 2023, 12, 3511–3518. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yue, W.; Gao, S. Dielectric diatomic metasurface-assisted versatile bifunctional polarization conversions and incidence-polarization-secured meta-image. Opt. Express 2023, 31, 29900–29911. [Google Scholar] [CrossRef]
- Fang, Y.; Gong, L.; Huang, S.; Yan, S.; Zhang, X. 3-5 μm Mid-Infrared Broadband Perfect Absorber Based on Ti Ring Embedded Structure. IEEE Photonics J. 2023, 15, 4800106. [Google Scholar] [CrossRef]
- Baron, A.; Smith, D.R.; Bowen, P.T. Theory of patch-antenna metamaterial perfect absorbers. Phys. Rev. A 2016, 93, 63849. [Google Scholar] [CrossRef]
- Tittl, A.; Michel, A.K.U.; Schäferling, M.; Yin, X.; Gholipour, B.; Cui, L.; Wuttig, M.; Taubner, T.; Neubrech, F.; Giessen, H. A Switchable Mid-Infrared Plasmonic Perfect Absorber with Multispectral Thermal Imaging Capability. Adv. Mater. 2015, 27, 4597–4603. [Google Scholar] [CrossRef]
- Wu, B.; Wang, M.; Wu, X. Broadband tunable absorption based on phase change materials. Results Phys. 2021, 20, 103704. [Google Scholar] [CrossRef]
- Shi, X.; Chen, C.; Liu, S.; Li, G. Nonvolatile, Reconfigurable and Narrowband Mid-Infrared Filter Based on Surface Lattice Resonance in Phase-Change Ge2Sb2Te5. Nanomaterials 2020, 10, 2530. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, K.; Cheng, Q.; Lu, L.; Li, B.; Song, J.; Luo, Z. Tunable narrowband shortwave-infrared absorber made of a nanodisk-based metasurface and a phase-change material Ge2Sb2Te5 layer. Appl. Opt. 2020, 59, 6309–6314. [Google Scholar] [CrossRef] [PubMed]
- Xiong, L.; Ding, H.; Lu, Y.; Li, G. Extremely narrow and actively tunable Mie surface lattice resonances in GeSbTe metasurfaces: Study. Nanomaterials 2022, 12, 701. [Google Scholar] [CrossRef]
- Alves Oliveira, I.; Gomes De Souza, I.L.; Rodriguez-Esquerre, V.F. Design of hybrid narrow-band plasmonic absorber based on chalcogenide phase change material in the infrared spectrum. Sci. Rep. 2021, 11, 21919. [Google Scholar] [CrossRef]
- Zhu, Y.; Lan, T.; Liu, P.; Yang, J. Broadband near-infrared TiO2 dielectric metamaterial absorbers. Appl. Opt. 2019, 58, 7134–7138. [Google Scholar] [CrossRef]
- Chen, Z.; Weng, Y.; Liu, J.; Guo, N.; Yu, Y.; Xiao, L. Dual-band perfect absorber for a mid-infrared photodetector based on a dielectric metal metasurface. Photonics Res. 2021, 9, 27–33. [Google Scholar] [CrossRef]
- Roy, S.; Debnath, K. Graphene-based electromechanically tunable subwavelength mid-IR perfect absorber. Opt. Quantum Electron. 2023, 55, 1246. [Google Scholar] [CrossRef]
- Zou, M.; Li, Y.; Zhao, W.; Zhang, X.; Wu, Y.; Peng, C.; Fan, L.; Li, J.; Yan, J.; Zhuang, J.; et al. Dynamically tunable perfect absorber based on VO2-Au hybrid nanodisc array. Opt. Eng. 2021, 60, 87103. [Google Scholar] [CrossRef]
- Zografopoulos, D.C.; Sinatkas, G.; Lotfi, E.; Shahada, L.A.; Swillam, M.A.; Kriezis, E.E.; Beccherelli, R. Amplitude modulation in infrared metamaterial absorbers based on electro-optically tunable conducting oxides. Appl. Phys. A 2018, 124, 105. [Google Scholar] [CrossRef]
- Taghinejad, M.; Taghinejad, H.; Xu, Z.; Lee, K.; Rodrigues, S.P.; Yan, J.; Adibi, A.; Lian, T.; Cai, W. Ultrafast Control of Phase and Polarization of Light Expedited by Hot-Electron Transfer. Nano Lett. 2018, 18, 5544–5551. [Google Scholar] [CrossRef]
- Taghinejad, M.; Taghinejad, H.; Xu, Z.; Liu, Y.; Rodrigues, S.P.; Lee, K.; Lian, T.; Adibi, A.; Cai, W. Hot-Electron-Assisted Femtosecond All-Optical Modulation in Plasmonics. Adv. Mater. 2018, 30, 1704915. [Google Scholar] [CrossRef]
- Yuan, D.; Li, J.; Huang, J.; Wang, M.; Xu, S.; Wang, X. Large-Scale Laser Nanopatterning of Multiband Tunable Mid-Infrared Metasurface Absorber. Adv. Opt. Mater. 2022, 10, 2200939. [Google Scholar] [CrossRef]
- Prakash, S.R.; Kumar, R.; Mitra, A. Reconfigurable and spectrally switchable perfect absorber based on a phase-change material. Appl. Opt. 2022, 61, 2888–2895. [Google Scholar] [CrossRef] [PubMed]
- Jiao, S.; Zhao, K.; Jiang, J.; Zhao, K.; Guo, Q.; Wang, J.; Zhang, Y.; Chen, G.; Cheng, Q.; Zuo, P.; et al. Metasurface with all-optical tunability for spatially-resolved and multilevel thermal radiation. Nanophotonics 2024, 13, 1645–1655. [Google Scholar] [CrossRef]
- He, J.; Shi, Z.; Ye, S.; Li, M.; Dong, J. Reconfigurable all-dielectric metasurface based on GSST. Results Phys. 2022, 42, 106017. [Google Scholar] [CrossRef]
- He, J.; Shi, Z.; Ye, S.; Li, M.; Dong, J. Mid-infrared reconfigurable all-dielectric metasurface based on Ge2Sb2Se4Te1 phase-change material. Opt. Express 2022, 30, 34809–34823. [Google Scholar] [CrossRef]
- Gomes De Souza, I.L.; Rodriguez Esquerre, V.F.; Alves Oliveira, I. Design of Planar Reconfigurable, Tunable, and Wide Angle Resonant Absorbers for Applications in the IR Spectrum. Adv. Theory Simul. 2021, 4, 2100002. [Google Scholar] [CrossRef]
- Guo, K.; Li, X.; Ai, H.; Ding, X.; Wang, L.; Wang, W.; Guo, Z. Tunable oriented mid-infrared wave based on metasurface with phase change material of GST. Results Phys. 2022, 34, 105269. [Google Scholar] [CrossRef]
- Meng, Q.; Chen, X.; Xu, W.; Zhu, Z.; Qin, S.; Zhang, J.; Yuan, X. High Q Resonant Graphene Absorber with Lossless Phase Change Material Sb2S3. Nanomaterials 2021, 11, 2820. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chou, J.B.; Li, J.; Li, H.; Du, Q.; Yadav, A.; Zhou, S.; Shalaginov, M.Y.; Fang, Z.; Zhong, H.; et al. Broadband transparent optical phase change materials for high-performance nonvolatile photonics. Nat. Commun. 2019, 10, 4279. [Google Scholar] [CrossRef]
- Biegański, A.; Perestjuk, M.; Armand, R.; Della Torre, A.; Laprais, C.; Saint-Girons, G.; Reboud, V.; Hartmann, J.; Tortai, J.; Moreau, A.; et al. Sb2S3 as a low-loss phase-change material for mid-IR photonics. Opt. Mater. Express 2024, 14, 862–870. [Google Scholar] [CrossRef]
- Delaney, M.; Zeimpekis, I.; Lawson, D.; Hewak, D.W.; Muskens, O.L. A New Family of Ultralow Loss Reversible Phase-Change Materials for Photonic Integrated Circuits: Sb2S3 and Sb2Se3. Adv. Funct. Mater. 2020, 30, 2002447. [Google Scholar] [CrossRef]
- Haynes, W.M. CRC Handbook of Chemistry and Physics, 95th ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: San Diego, CA, USA, 1988. [Google Scholar]
- Tian, X.; Xu, J.; Xu, K.; Ma, X.; Duan, X.; Yang, P.; Ding, P.; Li, Z. Wavelength-selective, tunable and switchable plasmonic perfect absorbers based on phase change materials Ge2Sb2Te5. Europhys. Lett. 2019, 128, 67001. [Google Scholar] [CrossRef]
- Chu, C.H.; Tseng, M.L.; Chen, J.; Wu, P.C.; Chen, Y.H.; Wang, H.C.; Chen, T.Y.; Hsieh, W.T.; Wu, H.J.; Sun, G.; et al. Active dielectric metasurface based on phase-change medium. Laser Photonics Rev. 2016, 10, 986–994. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Z.; Wu, Z.; Zhang, Y. High-efficiency Huygens’ surfaces for electromagnetic wave controlling. In Proceedings of the 2016 IEEE International Conference on Ubiquitous Wireless Broadband (ICUWB), Nanjing, China, 16–19 October 2016; pp. 1–4. [Google Scholar]
- Ma, Y.; Zhou, H.; Huang, Y.; Guo, J.; Zhu, Y.; Wu, Z.; Gu, Q.; Miao, Z.; Yan, C.; Wang, S.; et al. Electrically controllable optical switch metasurface based on vanadium dioxide. Opt. Lett. 2023, 48, 3885–3888. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Wu, P.C.; Sokhoyan, R.; Mauser, K.; Glaudell, R.; Kafaie Shirmanesh, G.; Atwater, H.A. Phase modulation with electrically tunable vanadium dioxide phase-change metasurfaces. Nano Lett. 2019, 19, 3961–3968. [Google Scholar] [CrossRef]
- Cao, T.; Zhang, X.; Dong, W.; Lu, L.; Zhou, X.; Zhuang, X.; Deng, J.; Cheng, X.; Li, G.; Simpson, R.E. Tuneable Thermal Emission Using Chalcogenide Metasurface. Adv. Opt. Mater. 2018, 6, 1800169. [Google Scholar] [CrossRef]
- Ameling, R.; Giessen, H. Cavity Plasmonics: Large Normal Mode Splitting of Electric and Magnetic Particle Plasmons Induced by a Photonic Microcavity. Nano Lett. 2010, 10, 4394–4398. [Google Scholar] [CrossRef]
- Zhu, M.; Abdollahramezani, S.; Li, C.; Fan, T.; Harutyunyan, H.; Adibi, A. Dynamically tunable second-harmonic generation using hybrid nanostructures incorporating phase-change chalcogenides. Nanophotonics 2022, 11, 2727–2735. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Liu, G.; Fu, G.; Liu, X.; Wang, Y. Multi-band light perfect absorption by a metal layer-coupled dielectric metamaterial. Opt. Express 2016, 24, 5020–5025. [Google Scholar] [CrossRef] [PubMed]
- Cao, T.; Zhang, L.; Simpson, R.E.; Cryan, M.J. Mid-infrared tunable polarization-independent perfect absorber using a phase-change metamaterial. J. Opt. Soc. Am. B 2013, 30, 1580–1585. [Google Scholar] [CrossRef]
- Tseng, M.L.; Chen, B.H.; Chu, C.H.; Chang, C.M.; Lin, W.C.; Chu, N.N.; Mansuripur, M.; Liu, A.Q.; Tsai, D.P. Fabrication of phase-change chalcogenide Ge2Sb2Te5 patterns by laser-induced forward transfer. Opt. Express 2011, 19, 16975–16984. [Google Scholar] [CrossRef]
- Gao, K.; Du, K.; Tian, S.; Wang, H.; Zhang, L.; Guo, Y.; Luo, B.; Zhang, W.; Mei, T. Intermediate Phase-Change States with Improved Cycling Durability of Sb2S3 by Femtosecond Multi-Pulse Laser Irradiation. Adv. Funct. Mater. 2021, 31, 2103327. [Google Scholar] [CrossRef]
- Gutiérrez, Y.; Ovvyan, A.P.; Santos, G.; Juan, D.; Rosales, S.A.; Junquera, J.; García-Fernández, P.; Dicorato, S.; Giangregorio, M.M.; Dilonardo, E.; et al. Interlaboratory study on Sb2S3 interplay between structure, dielectric function, and amorphous-to-crystalline phase change for photonics. iScience 2022, 25, 104377. [Google Scholar] [CrossRef]
- Aspnes, D.E. Local-field effects and effective-medium theory: A microscopic perspective. Am. J. Phys. 1982, 50, 704–709. [Google Scholar] [CrossRef]
- Cao, T.; Wei, C.; Simpson, R.E.; Zhang, L.; Cryan, M.J. Rapid phase transition of a phase-change metamaterial perfect absorber. Opt. Mater. Express 2013, 3, 1101–1110. [Google Scholar] [CrossRef]
- Samson, Z.L.; MacDonald, K.F.; De Angelis, F.; Gholipour, B.; Knight, K.; Huang, C.C.; Di Fabrizio, E.; Hewak, D.W.; Zheludev, N.I. Metamaterial electro-optic switch of nanoscale thickness. Appl. Phys. Lett. 2010, 96, 143105. [Google Scholar] [CrossRef]
- Avitzour, Y.; Urzhumov, Y.A.; Shvets, G. Wide-angle infrared absorber based on a negative-index plasmonic metamaterial. Phys. Rev. B 2009, 79, 45131. [Google Scholar] [CrossRef]
- Peng, S.; Tan, Z.; Zhang, J.; Wang, C.; Wen, M.; Zhao, Z.J. High-throughput computational screening of Sb-Te binary alloys for phase-change storage applications. Mater. Res. Technol. 2021, 15, 4243–4256. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Zhang, G.; Li, Y.; Shen, M.; Xiong, Y.; Li, T.; Wang, Y.; Zhao, X.; Ma, C. Improvement of a Switchable Wide-Incident-Angle Perfect Absorber Incorporating Sb2S3. Materials 2025, 18, 5305. https://doi.org/10.3390/ma18235305
Tian Y, Zhang G, Li Y, Shen M, Xiong Y, Li T, Wang Y, Zhao X, Ma C. Improvement of a Switchable Wide-Incident-Angle Perfect Absorber Incorporating Sb2S3. Materials. 2025; 18(23):5305. https://doi.org/10.3390/ma18235305
Chicago/Turabian StyleTian, Yaolan, Guoxu Zhang, Yan Li, Mei Shen, Yufeng Xiong, Ting Li, Yunzheng Wang, Xian Zhao, and Changbao Ma. 2025. "Improvement of a Switchable Wide-Incident-Angle Perfect Absorber Incorporating Sb2S3" Materials 18, no. 23: 5305. https://doi.org/10.3390/ma18235305
APA StyleTian, Y., Zhang, G., Li, Y., Shen, M., Xiong, Y., Li, T., Wang, Y., Zhao, X., & Ma, C. (2025). Improvement of a Switchable Wide-Incident-Angle Perfect Absorber Incorporating Sb2S3. Materials, 18(23), 5305. https://doi.org/10.3390/ma18235305







