Performance Prediction and Process Optimization of Aging-Resistant Rubber-Modified Asphalt via Enhanced BP Neural Network and Multi-Objective NSGA-II
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Database Acquisition
2.1.1. Materials
2.1.2. Experimental Methods
2.1.3. Database Acquisition
2.2. Machine Learning Model Construction
2.2.1. BP Neural Network and Optimization Algorithms
2.2.2. Construction of BP Neural Network Models
2.3. Shapley Additive Explanations
3. Results and Discussion
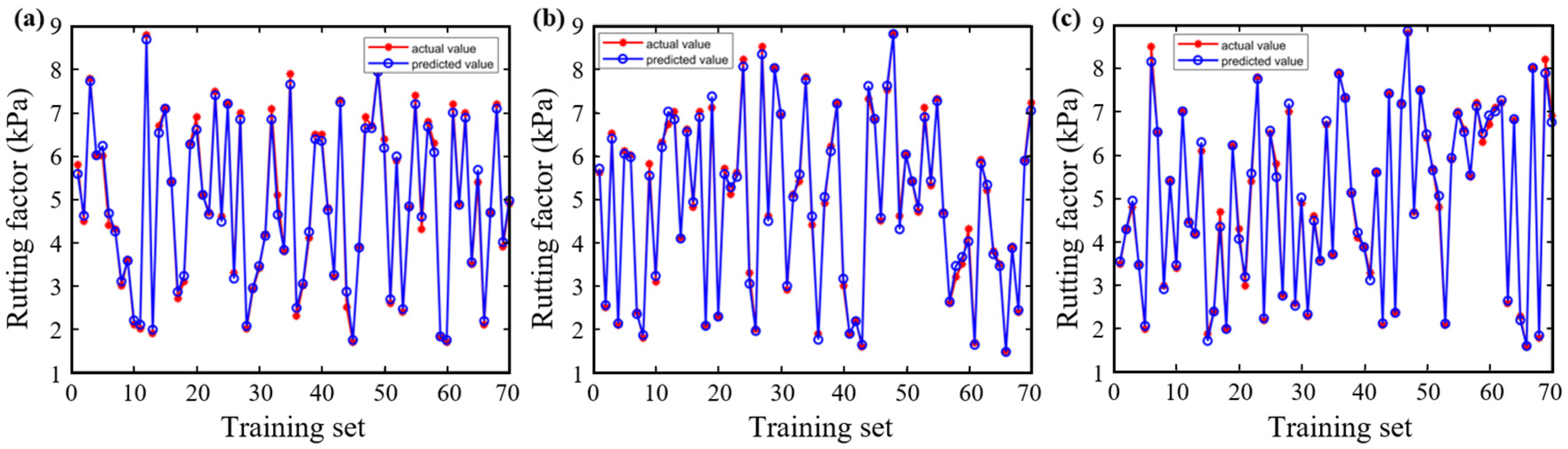
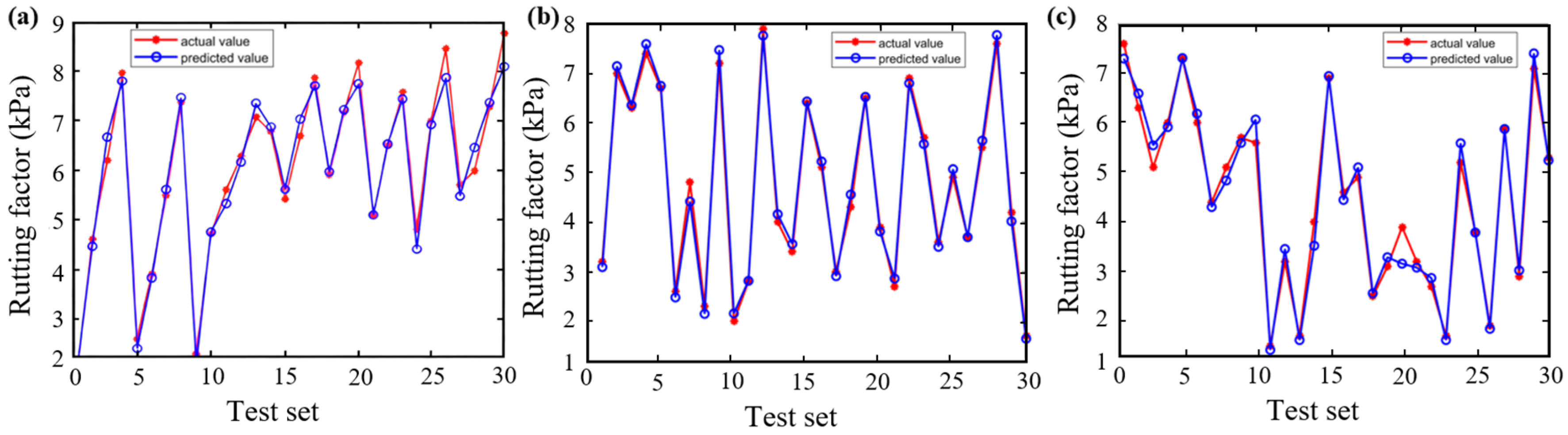
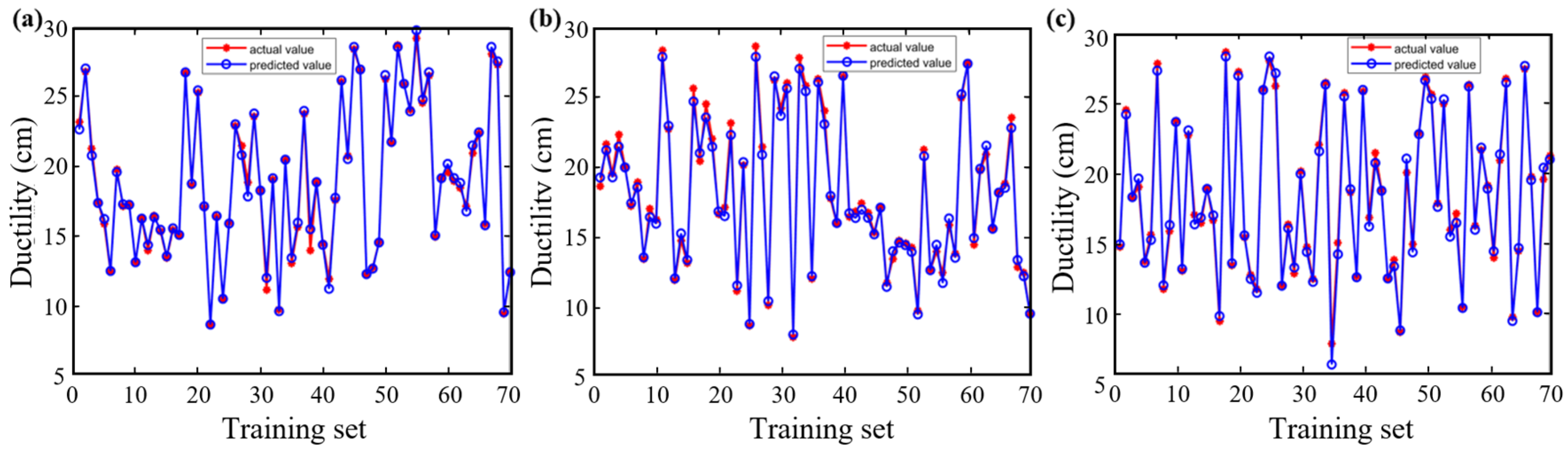
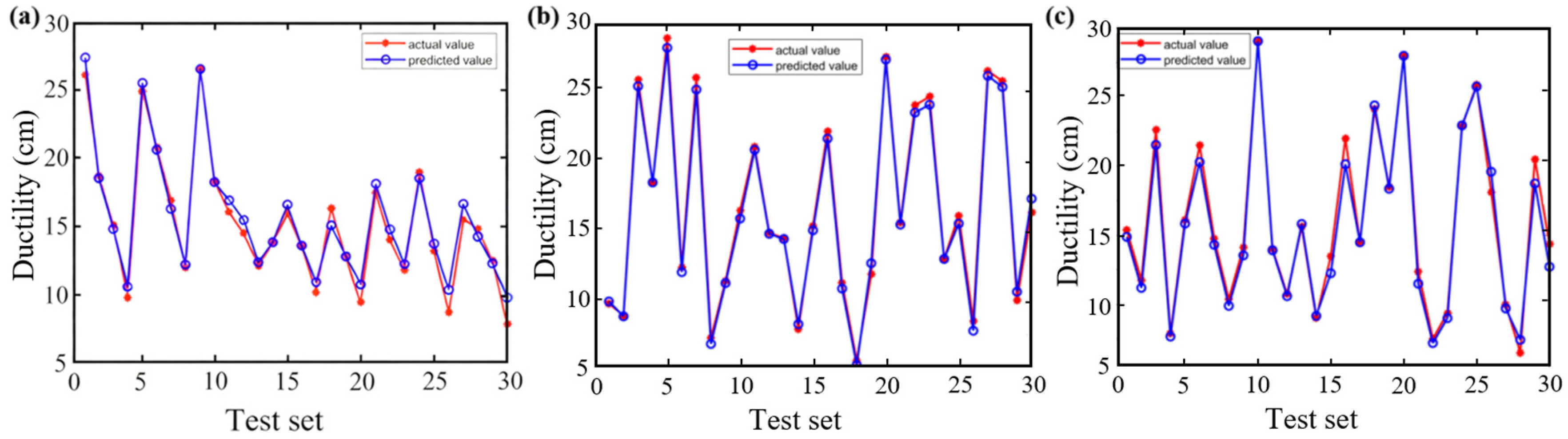
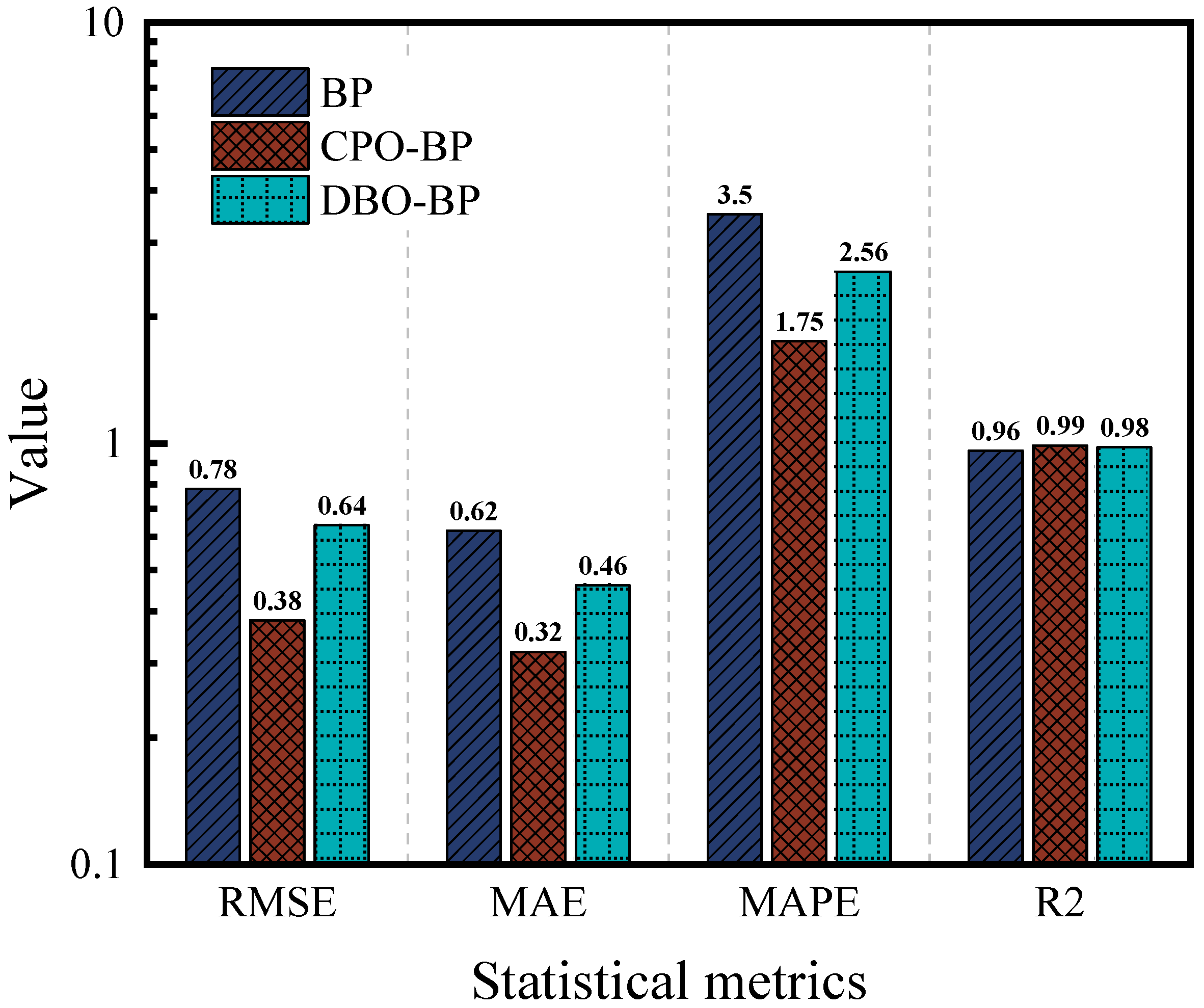
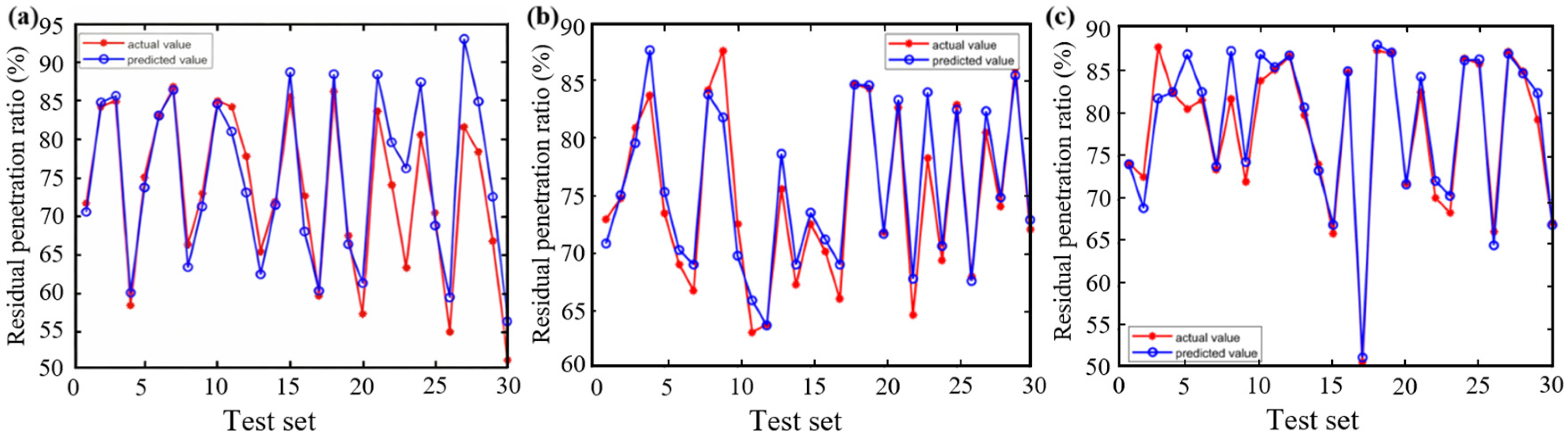
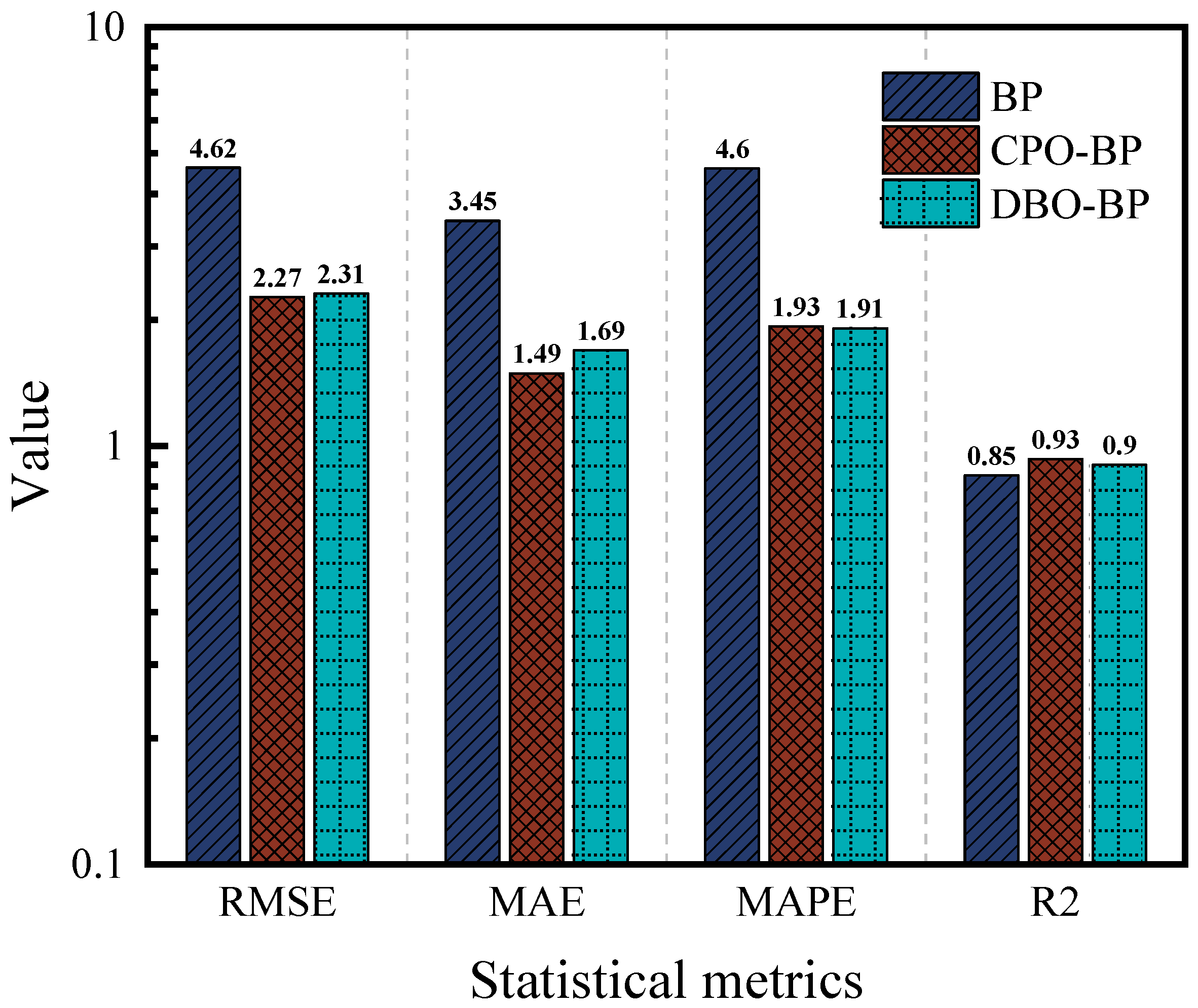
3.1. Neural Network Model Training, Testing and Evaluation
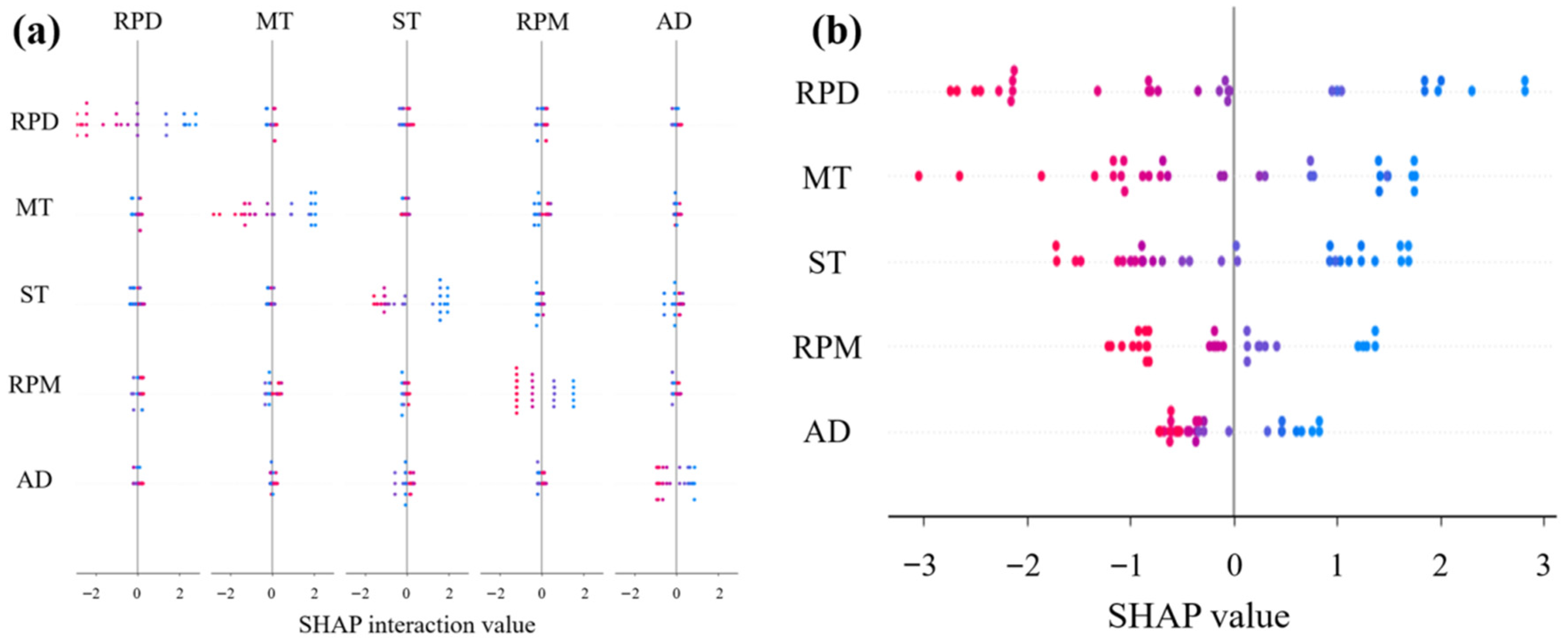
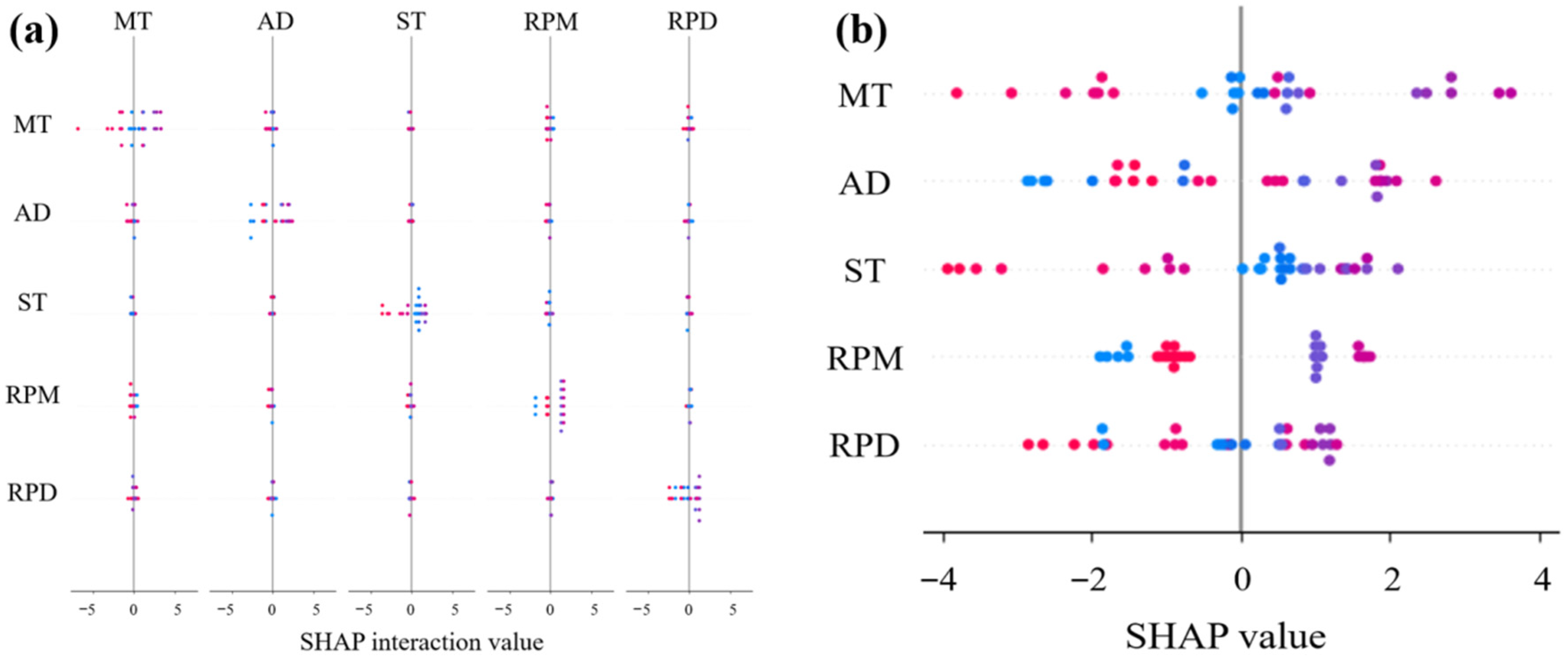
3.2. Interpretability Analysis Based on SHAP
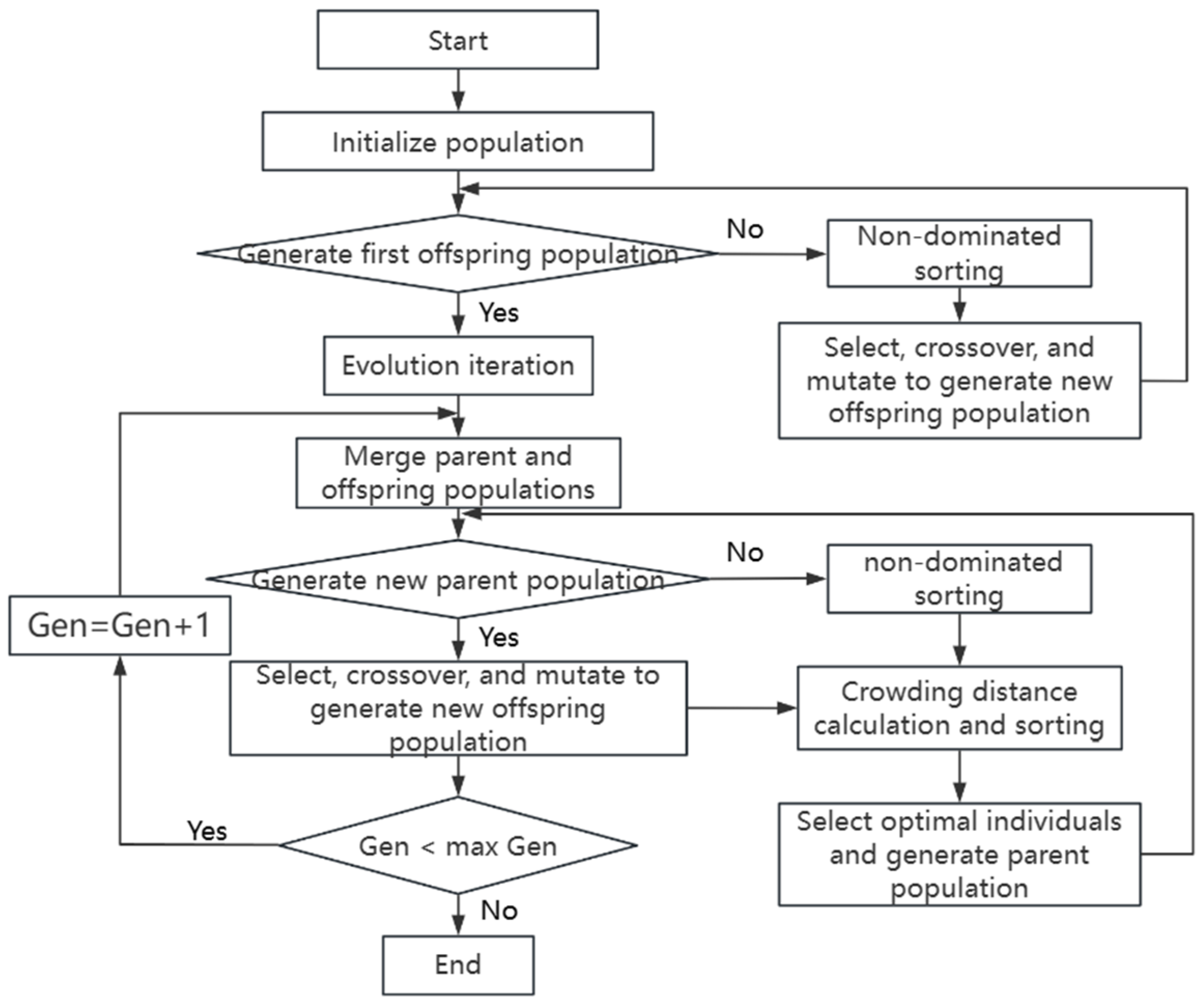
3.3. Multi-Objective Optimization
3.4. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| BP | Backpropagation |
| CPO | Crested Porcupine Optimizer |
| DBO | Dung Beetle Optimizer |
| SHAP | Shapley Additive Explanations |
| CRMA | Crumb Rubber-Modified Asphalt |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| GPR | Gaussian Process Regression |
| RPD | Rubber Powder Dosage |
| RPM | Rubber Powder Mesh size |
| AD | Anti-aging Agent Dosage |
| MT | Mixing Temperature |
| ST | Shearing Time |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Square Error |
| MAPE | Mean Absolute Percentage Error |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| SVM | Support Vector Machine |
| ET | Extremely Randomized Trees |
| KR | Kernel Regression |
| ANN | Artificial Neural Network |
| RNN | Recurrent Neural Network |
| RSM | Response Surface Methodology |
| AFM | Atomic Force Microscopy |
References
- Tian, T.; Jiang, Y.J.; Yi, Y.; Zhang, Y.; Fan, J.T.; Zhang, W.H. Dynamic viscoelastic properties of ultra-large particle size asphalt mixture based on fractional derivative constitutive model. Constr. Build. Mater. 2024, 445, 137893. [Google Scholar] [CrossRef]
- Li, X.Z.; Sha, A.M.; Jiao, W.X.; Cao, Y.S.; Song, R.M. Strain response and creep behavior of asphalt mixture based on multi-damage fractional visco-elasto-plastic constitutive model. Constr. Build. Mater. 2025, 472, 140834. [Google Scholar] [CrossRef]
- Bueno, M.; Luong, J.; Terán, F.; Viñuela, U.; Paje, S.E. Macrotexture influence on vibrational mechanisms of the tyre-road noise of an asphalt rubber pavement. Int. J. Pavement Eng. 2014, 15, 606–613. [Google Scholar] [CrossRef]
- Liu, Y.; Su, P.F.; Li, M.M.; You, Z.P.; Zhao, M.H. Review on evolution and evaluation of asphalt pavement structures and materials. J. Traffic Transp. Eng. Engl. Ed. 2020, 7, 573–599. [Google Scholar] [CrossRef]
- Tian, T.; Jiang, Y.J.; Yi, Y.; Nie, C.L. The splitting fatigue properties of ultra-large particle size asphalt mixture under the coupling effect of temperature and load. Eng. Fract. Mech. 2025, 319, 110990. [Google Scholar] [CrossRef]
- Li, Q.S.; Zhang, H.L.; Sun, C.J.; Li, J.C.; Feng, J.R. Effect of novel warm-mix compound on road performance and aging resistance of SBR-modified bituminous mixture. Constr. Build. Mater. 2025, 464, 140116. [Google Scholar] [CrossRef]
- Sánchez, D.B.; Caro, S.; Santos, M.C. Long-term effectiveness of vegetable-based rejuvenation agents across different aging stages of asphalt pavements. Int. J. Pavement Eng. 2024, 25, 2433619. [Google Scholar] [CrossRef]
- Zhang, M.M.; Su, Q.D.; Li, G.Y.; Cao, D.W.; Yao, Y.C.; Yang, S.Q.; Wang, S.F. Enhancing Reutilization of Waste Tires and Sustainability of Environment: Analysis of the Performance and Emission Reduction Mechanism of High Content Rubber Modified Asphalt. Chem. Eng. J. 2025, 508, 160917. [Google Scholar] [CrossRef]
- Chen, R.P.; Chen, L.; Hu, P.; Zhu, H.Z.; Ou, L. Viscoelasticity stage evolution characteristics and multiphase microstructure of aged crumb rubber-modified asphalt. Constr. Build. Mater. 2025, 469, 140531. [Google Scholar] [CrossRef]
- Gui, W.M.; Wang, L.; Li, C.; Zhan, Y.; Zhang, F. Effects of aging behavior on the adhesion and low-temperature performance of surfactant-crumb rubber modified asphalt binder. Int. J. Pavement Eng. 2025, 26, 2467845. [Google Scholar] [CrossRef]
- He, L.; Tang, J.K.; Rong, H.L.; Xie, J.; Wang, J.P.; Wei, L. Recycling of scrap steel slag and waste rubber in asphalt mixtures: Evaluation of road performance and environmental impact analysis. Road Mater. Pavement Des. 2025, 1–24. [Google Scholar] [CrossRef]
- Xue, Y.H.; Zhang, H.G.; Ge, D.D.; Lv, S.T.; Ju, Z.H. The interaction mechanism of activated crumb rubber modified asphalt during the preparation process. Int. J. Pavement Eng. 2025, 26, 2481919. [Google Scholar] [CrossRef]
- Liu, S.; Lu, P.; Sun, X.C.; Wang, H.C.; Fei, Z. Research on the Durability of Modified Crumb Rubber Asphalt Mixtures in High-Altitude and Seasonally Frozen Regions. Coatings 2025, 15, 102. [Google Scholar] [CrossRef]
- Zhou, Y.X.; Xu, G.; Yu, H.; Fan, Y.L.; Wang, H.Z.; Yang, J.; Wu, Y.; Wang, H.P.; Huang, W. Toughness modification of SBS/CRMA on epoxy asphalt: Curing behaviour and low-temperature cracking characteristic analysis. Int. J. Pavement Eng. 2024, 25, 2320171. [Google Scholar] [CrossRef]
- Cao, L.P.; Su, Z.B.; Liu, R.R.; Zhou, T. Optimized formulation of asphalt compound containing bio-oil and shredded rubber. J. Clean. Prod. 2022, 378, 134591. [Google Scholar] [CrossRef]
- He, H.Q.; Gou, P.F.; Li, R.; Pei, J.Z.; Xie, B.W.; Yang, K. Optimum preparation and rheological properties of liquid rubber modified asphalt binder. Constr. Build. Mater. 2022, 347, 128551. [Google Scholar] [CrossRef]
- Zhang, H.G.; Zhang, Y.P.; Chen, J.; Liu, W.C.; Wang, W.S. Influence of preparation parameters on rheological properties and relation analysis of waste rubber modified bitumen mastic. Front. Mater. 2024, 11, 1435814. [Google Scholar] [CrossRef]
- Krishna, G.G.; Jinesh, N. Synergistic interaction effects of process parameters on surface finish in two-way AFM of SS446. Int. J. Interact. Des. Manuf. 2025, 19, 2367–2384. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Y.J.; Li, C.; Bai, C.F.; Zhang, F.X.; Li, J.X.; Guo, M.Y. Prediction of cement-stabilized recycled concrete aggregate properties by CNN-LSTM incorporating attention mechanism. Mater. Today Commun. 2025, 42, 111137. [Google Scholar] [CrossRef]
- Chu, Y.H.; Zhang, Y.P.; Li, S.Y.; Ma, Y.G.; Yang, S.J. A machine learning approach for identifying vertical temperature gradient in steel-concrete composite beam under solar radiation. Adv. Eng. Softw. 2024, 196, 103695. [Google Scholar] [CrossRef]
- Zhang, H.T.; Fu, X.X.; Jiang, H.Y.; Liu, X.; Lv, L.H. The relationships between asphalt ageing in lab and field based on the neural network. Road Mater. Pavement Des. 2015, 16, 493–504. [Google Scholar] [CrossRef]
- Luo, Y.H.; Guo, P.; Gao, J.F.; Chen, Y.Z.; Zhou, D.J.; Hu, J.Y. Prediction and evaluation the moisture damage resistance of rejuvenated asphalt mixtures based on neural network. Constr. Build. Mater. 2023, 378, 131130. [Google Scholar] [CrossRef]
- Ma, X.Y.; Ma, X.J.; Wang, Z.L.; Song, S.L.; Sheng, Y.P. Investigation of changing SARA and fatigue properties of asphalt bitumen under ageing and analysis of their relation based upon the BP neural network. Constr. Build. Mater. 2023, 394, 132163. [Google Scholar] [CrossRef]
- Rezoug, A.; Bader-El-Den, M.; Boughaci, D. Two-step optimization algorithm operated by heuristic and machine learning methods. Discret. Math. Algorithms Appl. 2024, 17, 2450108. [Google Scholar] [CrossRef]
- Singh, S.K.; Kumar, M.; Singh, J. Integration of Particle Swarm Optimization (PSO) and Machine Learning to Improve Classification Accuracy During Antenna Design. Trans. Electr. Electron. Mater. 2023, 24, 258–266. [Google Scholar] [CrossRef]
- Ding, N.; Ruan, X.; Wang, H.; Liu, Y. Automobile Insurance Fraud Detection Based on PSO-XGBoost Model and Interpretable Machine Learning Method. Insur. Math. Econ. 2025, 120, 51–60. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, B.L.; Li, J.; Wang, Q.; Hu, K.H. Experimental and machine learning study on mechanical properties and frost resistance of nano-TiO2 modified steel fiber reinforced concrete. J. Build. Eng. 2024, 98, 111207. [Google Scholar] [CrossRef]
- Tian, K.M.; Kang, Z.H.; Kang, Z.J. A Productivity Prediction Method of Fracture-Vuggy Reservoirs Based on the PSO-BP Neural Network. Energies 2024, 17, 3482. [Google Scholar] [CrossRef]
- You, G.D.; Chang, Z.C.; Li, X.Y.; Li, Z.F.; Xiao, Z.Y.; Lu, Y.R.; Zhao, S.L. Using enhanced Variational Modal Decomposition and Dung Beetle Optimization Algorithm optimization-kernel Extreme Learning Machine model to forecast short-term wind power. Electr. Power Syst. Res. 2024, 236, 110904. [Google Scholar] [CrossRef]
- Zhang, C.P.; Liu, H.M.; Peng, Y.M.; Ding, W.Y.; Cao, J. Intelligent Prediction and Application Research on Soft Rock Tunnel Deformation Based on the ICPO-LSTM Model. Buildings 2024, 14, 2244. [Google Scholar] [CrossRef]
- Xia, H.Z.; Chen, L.M.; Xu, H.W. Multi-strategy dung beetle optimizer for global optimization and feature selection. Int. J. Mach. Learn. Cybern. 2025, 16, 189–231. [Google Scholar] [CrossRef]
- Wang, R.; Salleh, H.; Li, K.; Abdul-Samad, Z. A conceptual cost estimation model for building construction projects by hybrid Back-Propagation Neural Network and Dung Beetle Optimizer algorithm. J. Asian Arch. Build. Eng. 2024, 24, 5520–5542. [Google Scholar] [CrossRef]
- ASTM D7175; Standard Test Method for Determining the Rheological Properties of Asphalt Binder Using a Dynamic Shear Rheometer. ASTM: West Conshohocken, PA, USA, 2023.
- ASTM D113; Standard Test Method for Ductility of Asphalt Materials. ASTM: West Conshohocken, PA, USA, 2017.
- ASTM D2872; Standard Test Method for Effect of Heat and Air on a Moving Film of Asphalt Binder (Rolling Thin-Film Oven Test). ASTM: West Conshohocken, PA, USA, 2022.
- ASTM D5; Standard Test Method for Penetration of Bituminous Materials. ASTM: West Conshohocken, PA, USA, 2017.
- Xue, Y.Y.; Ge, D.D.; Lv, S.T.; Duan, D.F.; Deng, Y.J. Evaluation of asphalt modified with bio-oil and high rubber content: Low temperature and short mixing time production condition. Constr. Build. Mater. 2023, 408, 133656. [Google Scholar] [CrossRef]
- Zhang, J.W.; Chen, M.Z.; Wu, S.P.; Zhou, X.X.; Zhao, G.Y.; Zhao, Y.C.; Cheng, M. Evaluation of VOCs inhibited effects and rheological properties of asphalt with high-content waste rubber powder. Constr. Build. Mater. 2021, 300, 124320. [Google Scholar] [CrossRef]
- Jamal, M.; Giustozzi, F. Chemo-rheological Investigation on Waste Rubber-Modified Bitumen Response to Various Blending Factors. Int. J. Pavement Res. Technol. 2022, 15, 395–414. [Google Scholar] [CrossRef]
- Sernas, O.; Cygas, D.; Vaitkus, A.; Gumauskait, V. The Influence of Crumb Rubber on Modified Bitumen Properties. In Proceedings of the 10th International Conference on Environmental Engineering (ICEE), Vilnius, Lithuania, 27–28 April 2017. [Google Scholar]
- Li, H.A. Application of BP neural network in logistics forecasting. In Proceedings of the 1st International Conference on Modelling and Simulation, Nanjing, China, 4–7 October 2008; pp. 54–57. [Google Scholar]
- Quan, R.; Zhou, Y.L.; Yao, S.Y.; Wan, H.; Chang, Y.F. Improving the performance of a polygonal automobile exhaust thermoelectric generator with a crested porcupine optimizer. Appl. Therm. Eng. 2025, 268, 125946. [Google Scholar] [CrossRef]
- Lei, W.L.; Gu, Y.F.; Huang, J.Y. An Enhanced Crowned Porcupine Optimization Algorithm Based on Multiple Improvement Strategies. Appl. Sci. 2024, 14, 11414. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested Porcupine Optimizer: A new nature-inspired metaheuristic. Knowl. Based Syst. 2023, 284, 111257. [Google Scholar] [CrossRef]
- Li, C.J.; Li, S.; Xie, Y.; Wu, J.Z.; Zhang, C.Y. Optimization of laser welding process parameters considering carbon emissions and weld quality based on DBO-BP and NSGA-II. Int. J. Precis. Eng. Manuf. Technol. 2025, 12, 1429–1444. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, S.; Mai, S.P. Composite high order super-twisting sliding mode control algorithm for PMSMs based on dung beetle optimization. J. Power Electron. 2025, 25, 1198–1207. [Google Scholar] [CrossRef]
- Dong, A.Q.; Liu, L.J.; Zhao, C.C.; Guan, Y. Neural Network Prediction of Locomotive Engine Parameters Based on the Dung Beetle Optimization Algorithm and Multi-Objective Optimization of Engine Operating Parameters. Sensors 2025, 25, 677. [Google Scholar] [CrossRef]
- Sun, E.Y.; Zhao, Y.Q.; Wang, G.Z. Nano surface evolution properties of crumb rubber modified asphalt due to aging and adhesion failure mechanism. Constr. Build. Mater. 2024, 420, 135564. [Google Scholar] [CrossRef]
- Zhao, Z.B.; Liu, B.; Zhang, C.R.; Liu, H.R. An improved adaptive NSGA-II with multi-population algorithm. Appl. Intell. 2019, 49, 569–580. [Google Scholar] [CrossRef]
- Sun, E.; Zhao, Y.Q.; Cai, R. Characterization of microstructural evolution of asphalt due to water damage using atomic force microscopy. Constr. Build. Mater. 2024, 438, 137175. [Google Scholar] [CrossRef]
- Jegatheesan, N.; Ibrahim, M.R.; Ahmed, A.N.; Koting, S.; El-Shafie, A.; Katman, H.Y.B. Modeling the properties of terminal blend crumb rubber modified bitumen with crosslinking additives. Constr. Build. Mater. 2024, 444, 137648. [Google Scholar] [CrossRef]
- Uwanuakwa, I.D.; Ali, S.I.A.; Hasan, M.R.M.; Akpinar, P.; Sani, A.; Shariff, K.A. Artificial Intelligence Prediction of Rutting and Fatigue Parameters in Modified Asphalt Binders. Appl. Sci. 2020, 10, 7764. [Google Scholar] [CrossRef]
- Al-Sabaeei, A.M.; Alhussian, H.; Abdulkadir, S.J.; Sutanto, M.; Alrashydah, E.; Mabrouk, G.; Bilema, M.; Milad, A.; Abdulrahman, H. Computational modelling for predicting rheological properties of composite modified asphalt binders. Case Stud. Constr. Mater. 2023, 19, e02651. [Google Scholar] [CrossRef]









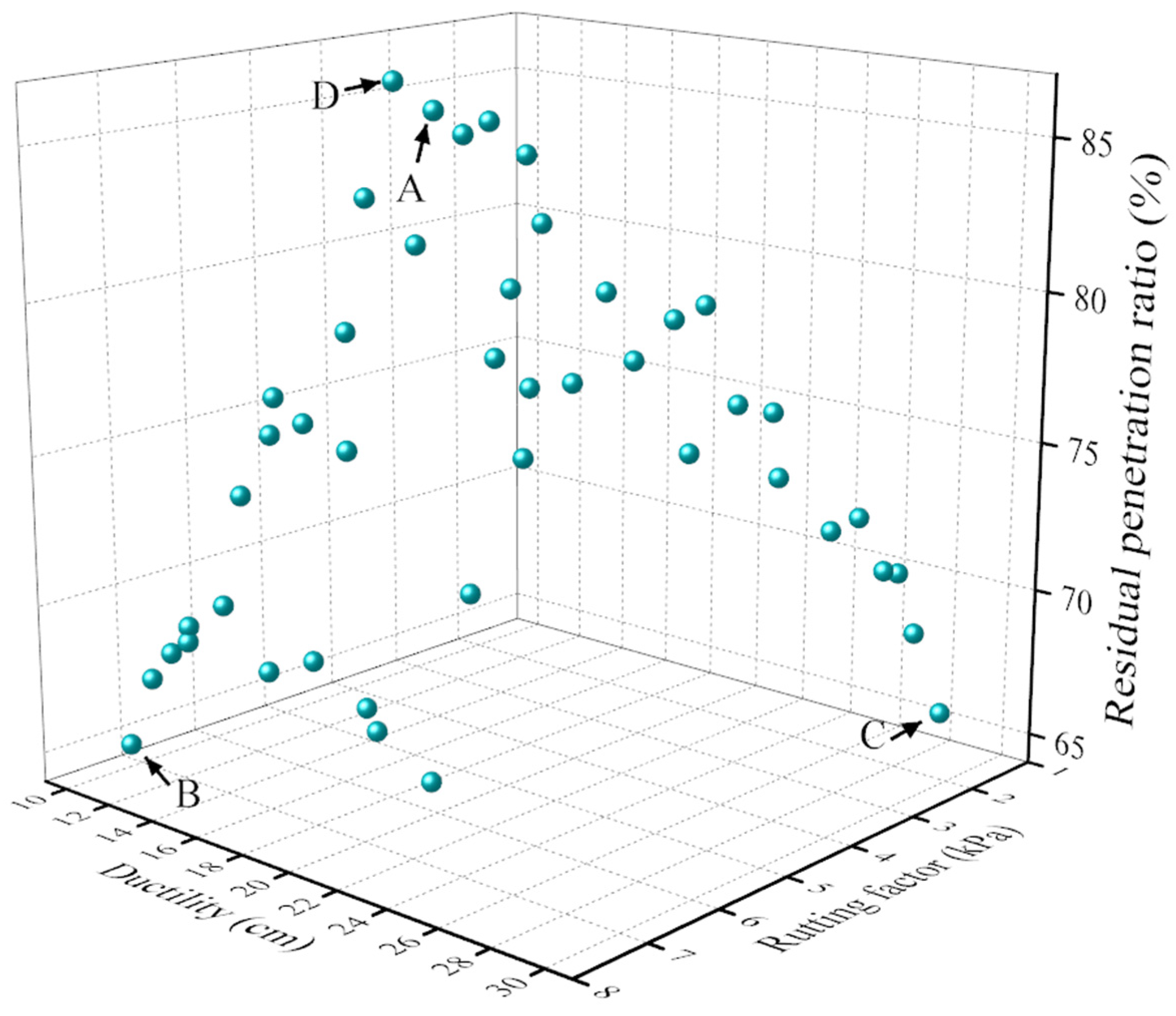


| Index | A | B | C | D | |
|---|---|---|---|---|---|
| RPD (%) | 24.36 | 28.98 | 16.33 | 24.36 | |
| RPM (mesh) | 50.95 | 75.85 | 88.31 | 52.70 | |
| AD (%) | 1.16 | 1.72 | 0.14 | 1.59 | |
| MT (℃) | 180.81 | 194.90 | 160.02 | 187.97 | |
| ST (min) | 74.17 | 132.52 | 25.83 | 74.17 | |
| NSGA-Ⅱ | Rutting factor (kPa) | 5.29 | 7.49 | 1.81 | 5.49 |
| Ductility (cm) | 17.91 | 11.3 | 28.21 | 16.86 | |
| Residual penetration ratio (%) | 86.06 | 65.42 | 68.51 | 86.94 | |
| Test Value | Rutting factor (kPa) | 5.6 | 7.33 | 1.85 | 5.55 |
| Ductility (cm) | 18.32 | 11.48 | 26.33 | 17.2 | |
| Residual penetration ratio (%) | 85.14 | 66.28 | 70.22 | 88.3 | |
| Error | Rutting factor | 5.94% | 2.14% | 2.03% | 1.09% |
| Ductility | 2.18% | 1.59% | 6.07% | 2.02% | |
| Residual penetration ratio | 1.12% | 1.19% | 2.46% | 1.56% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Gao, S.; Fan, J.; Zhang, J.; Li, Y. Performance Prediction and Process Optimization of Aging-Resistant Rubber-Modified Asphalt via Enhanced BP Neural Network and Multi-Objective NSGA-II. Materials 2025, 18, 5292. https://doi.org/10.3390/ma18235292
Li S, Gao S, Fan J, Zhang J, Li Y. Performance Prediction and Process Optimization of Aging-Resistant Rubber-Modified Asphalt via Enhanced BP Neural Network and Multi-Objective NSGA-II. Materials. 2025; 18(23):5292. https://doi.org/10.3390/ma18235292
Chicago/Turabian StyleLi, Shanwei, Shaojie Gao, Jiangtao Fan, Jiupeng Zhang, and Yan Li. 2025. "Performance Prediction and Process Optimization of Aging-Resistant Rubber-Modified Asphalt via Enhanced BP Neural Network and Multi-Objective NSGA-II" Materials 18, no. 23: 5292. https://doi.org/10.3390/ma18235292
APA StyleLi, S., Gao, S., Fan, J., Zhang, J., & Li, Y. (2025). Performance Prediction and Process Optimization of Aging-Resistant Rubber-Modified Asphalt via Enhanced BP Neural Network and Multi-Objective NSGA-II. Materials, 18(23), 5292. https://doi.org/10.3390/ma18235292





