Research on High-Temperature Damage Behavior of Super Martensitic Stainless Steel 04Cr13Ni5Mo Based on Finite Element Simulation
Abstract
1. Introduction
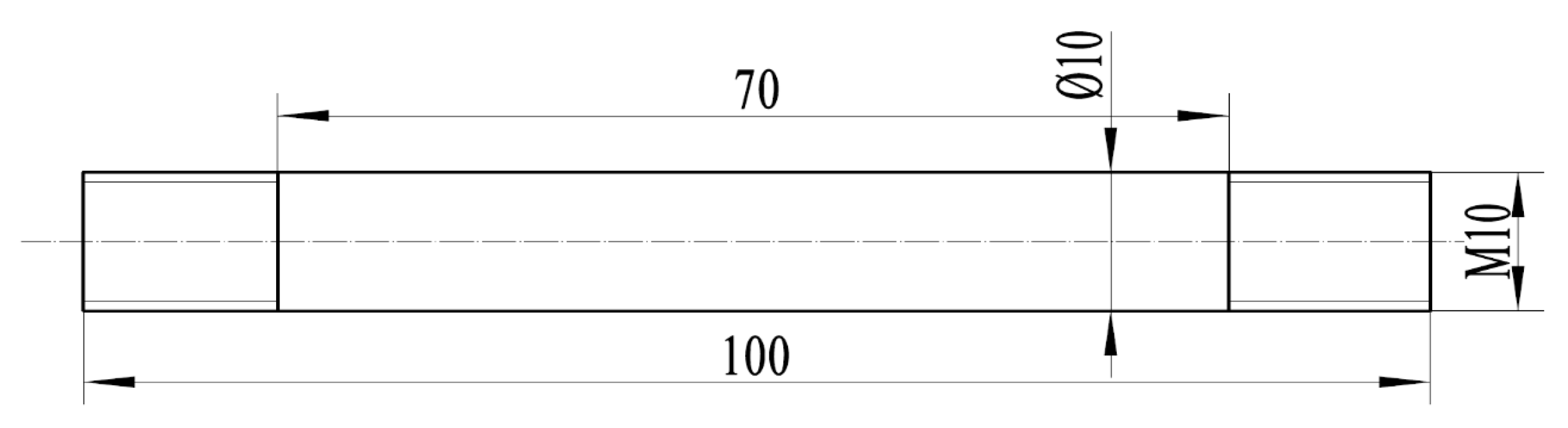
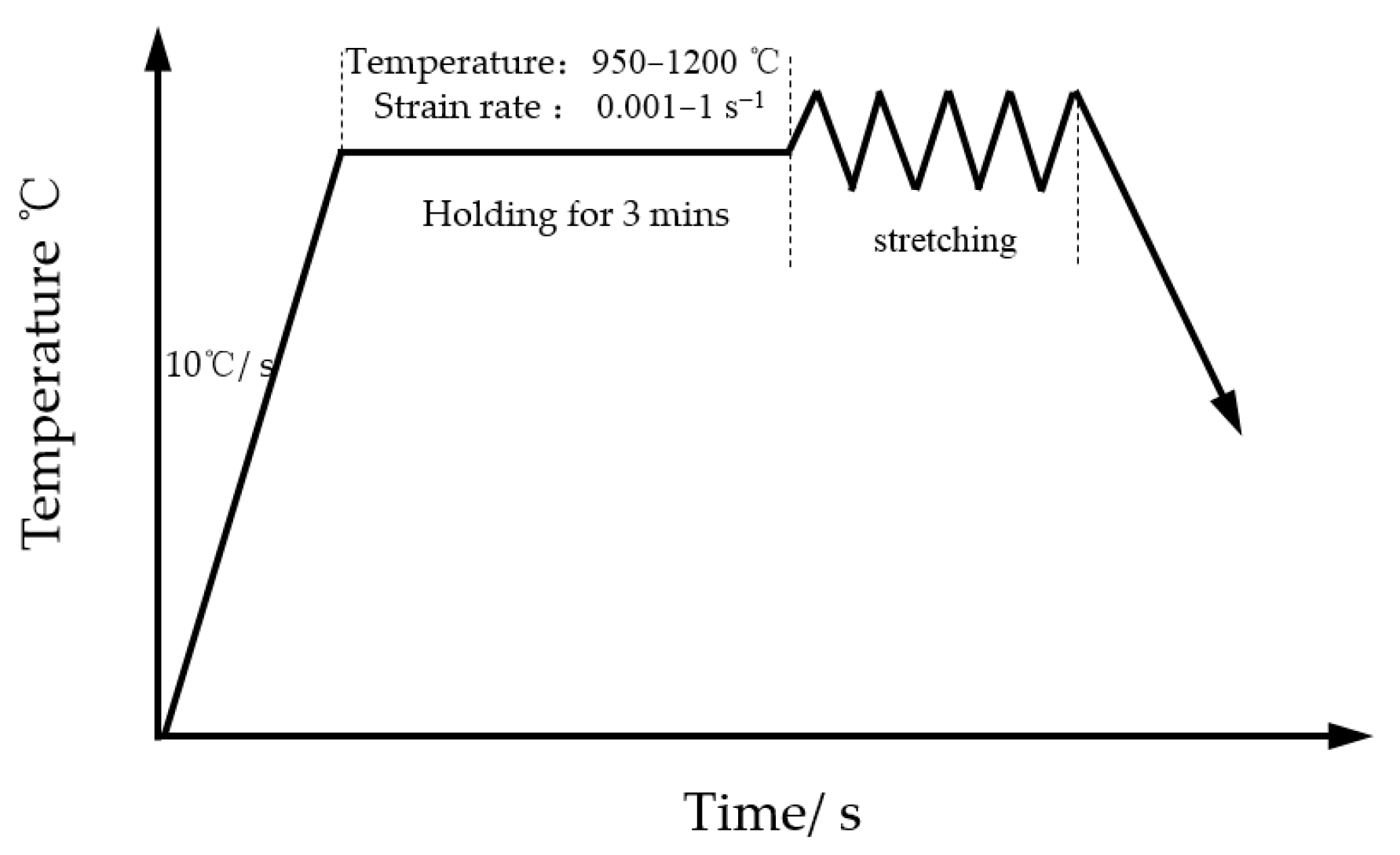
2. Materials and Methods
3. Results
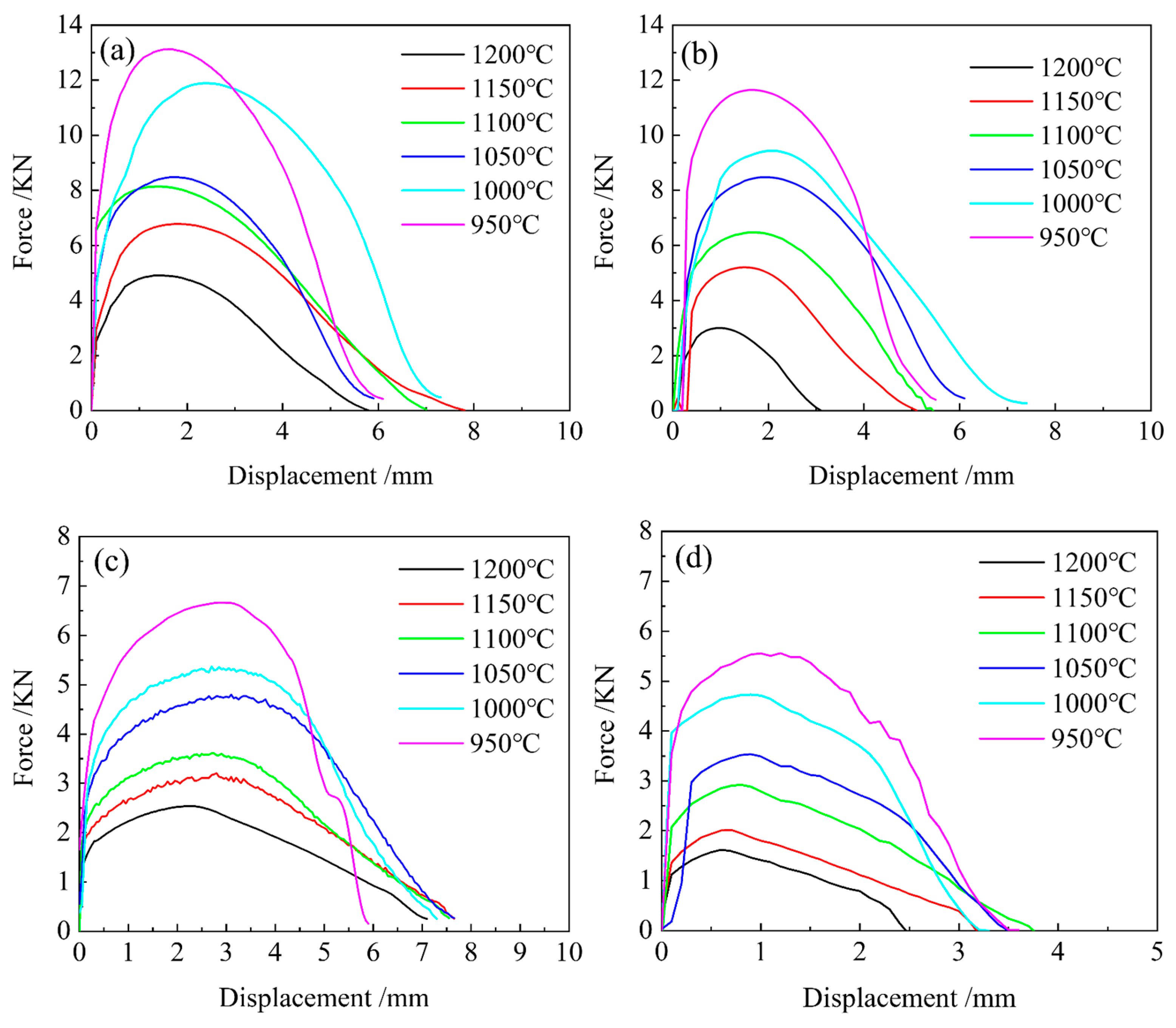
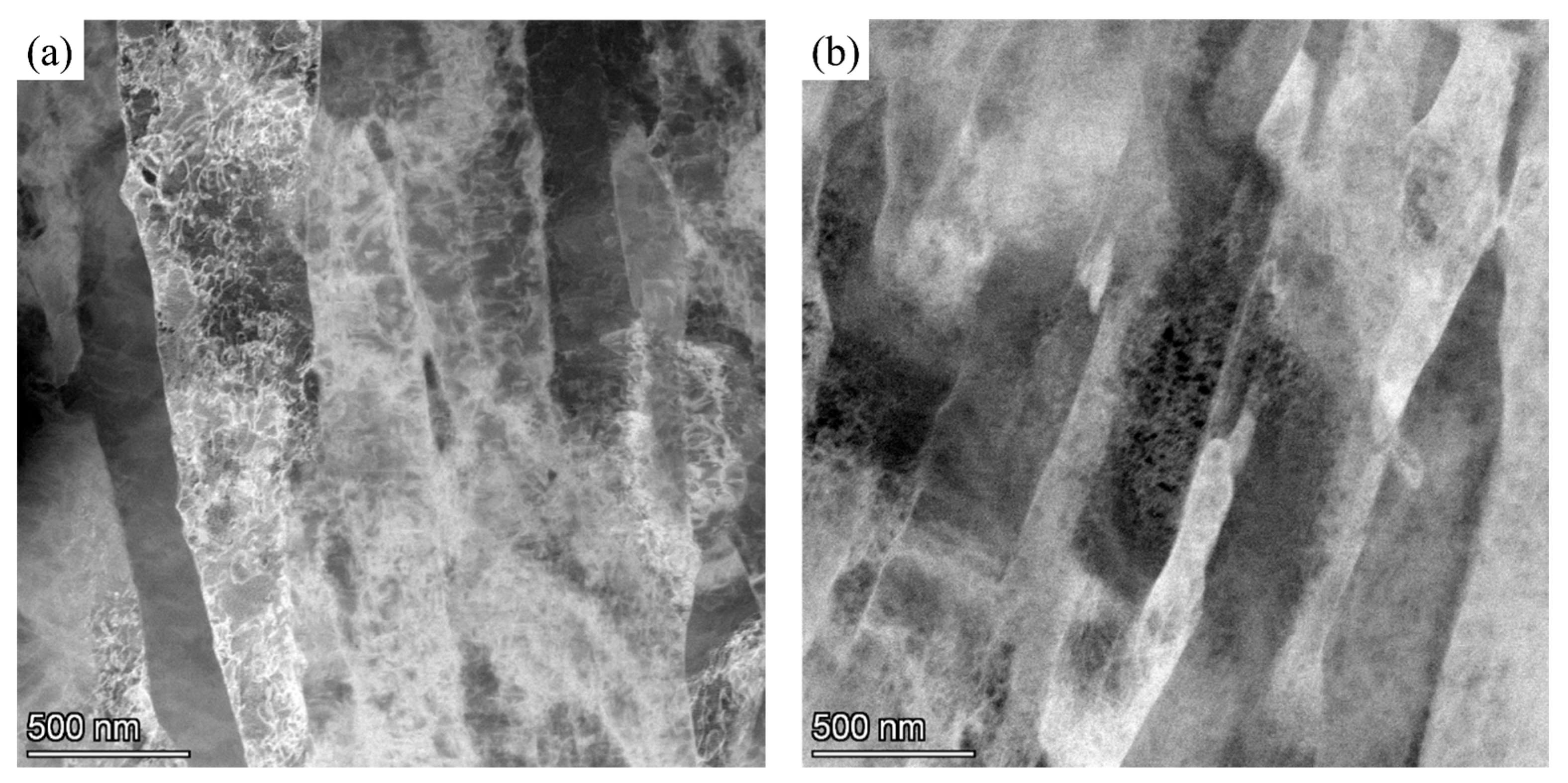
3.1. High-Temperature Damage Behavior and Microstructure Evolution of 04Cr13Ni5Mo Martensitic Stainless Steel
3.2. High-Temperature Damage Behavior and Microstructure Evolution of 04Cr13Ni5Mo Martensitic Stainless Steel
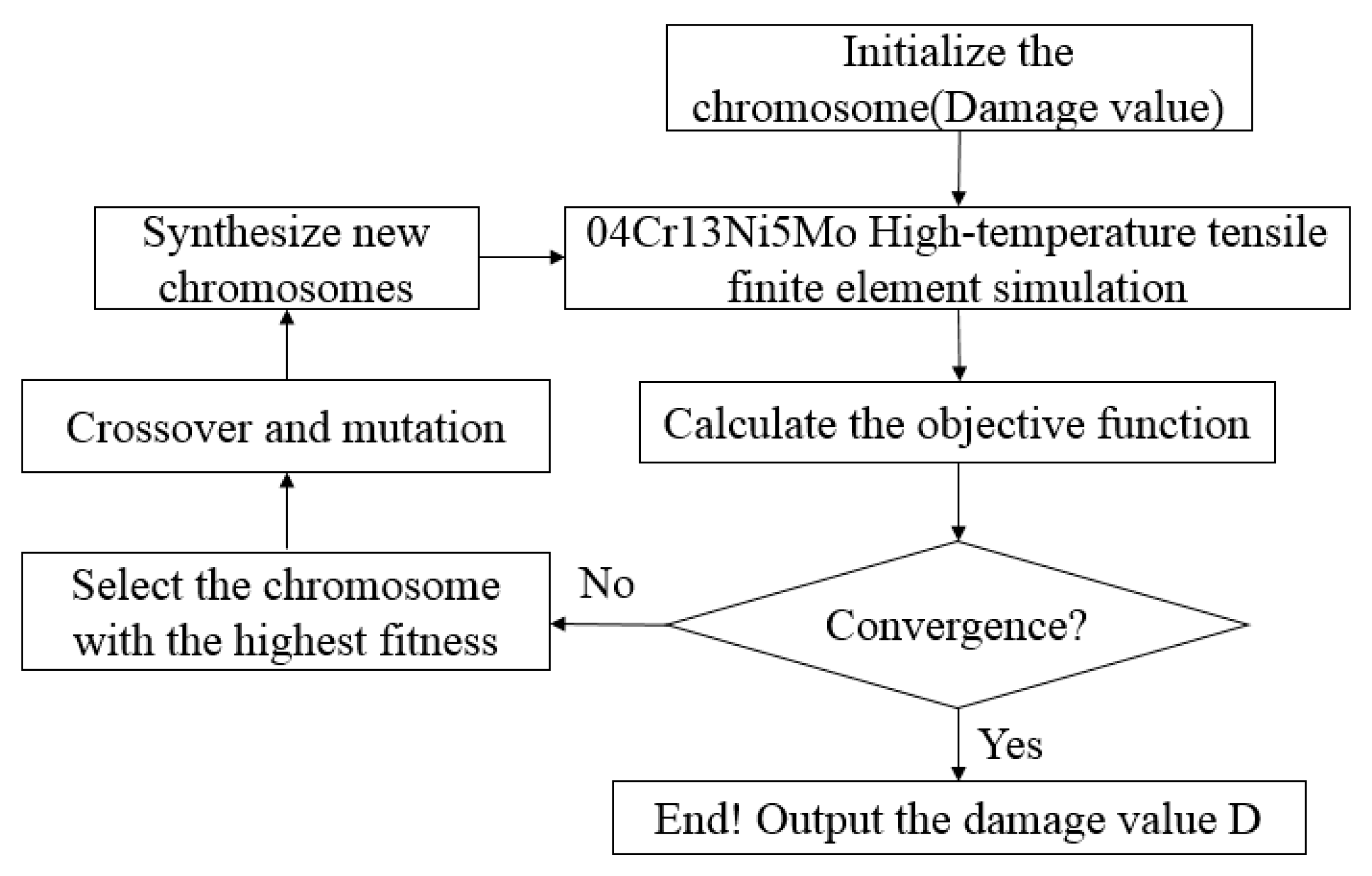
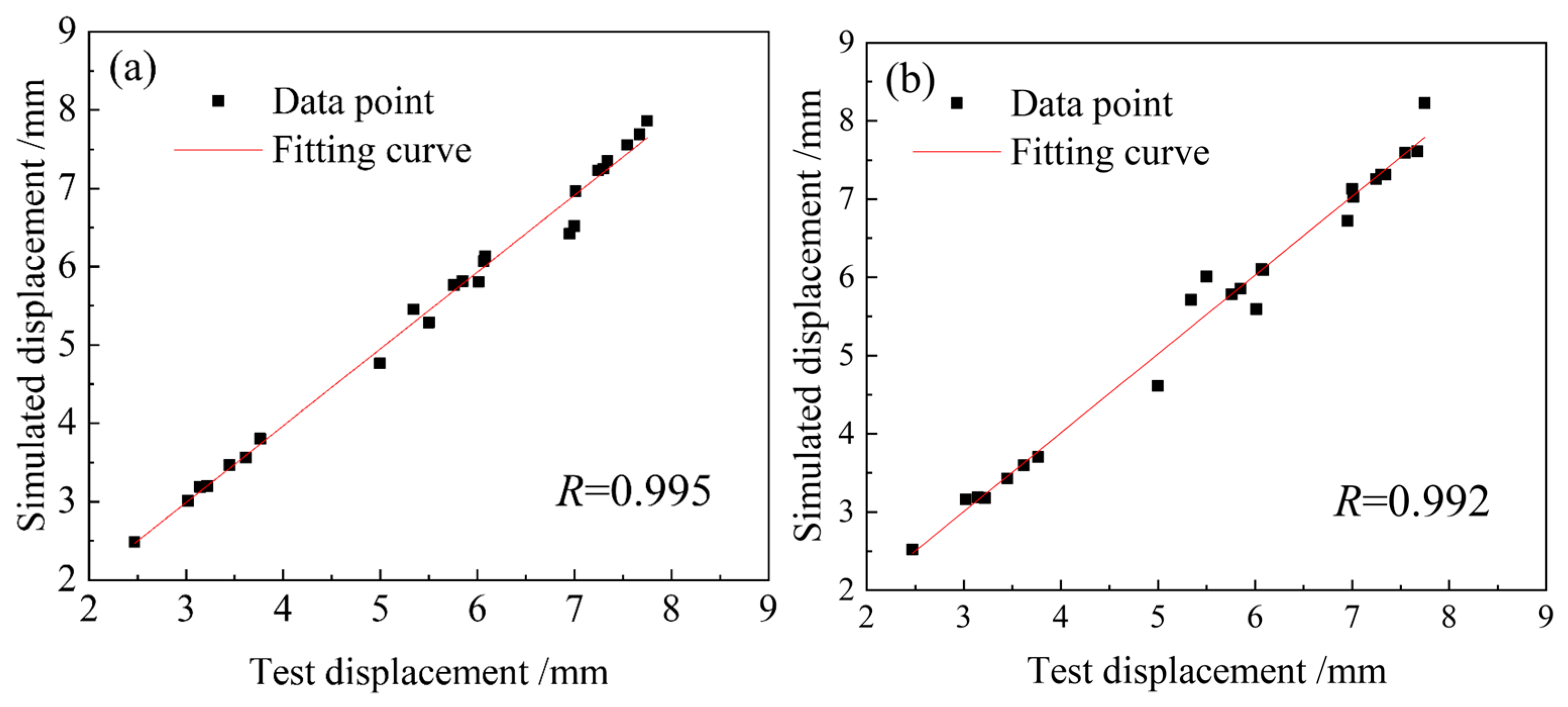
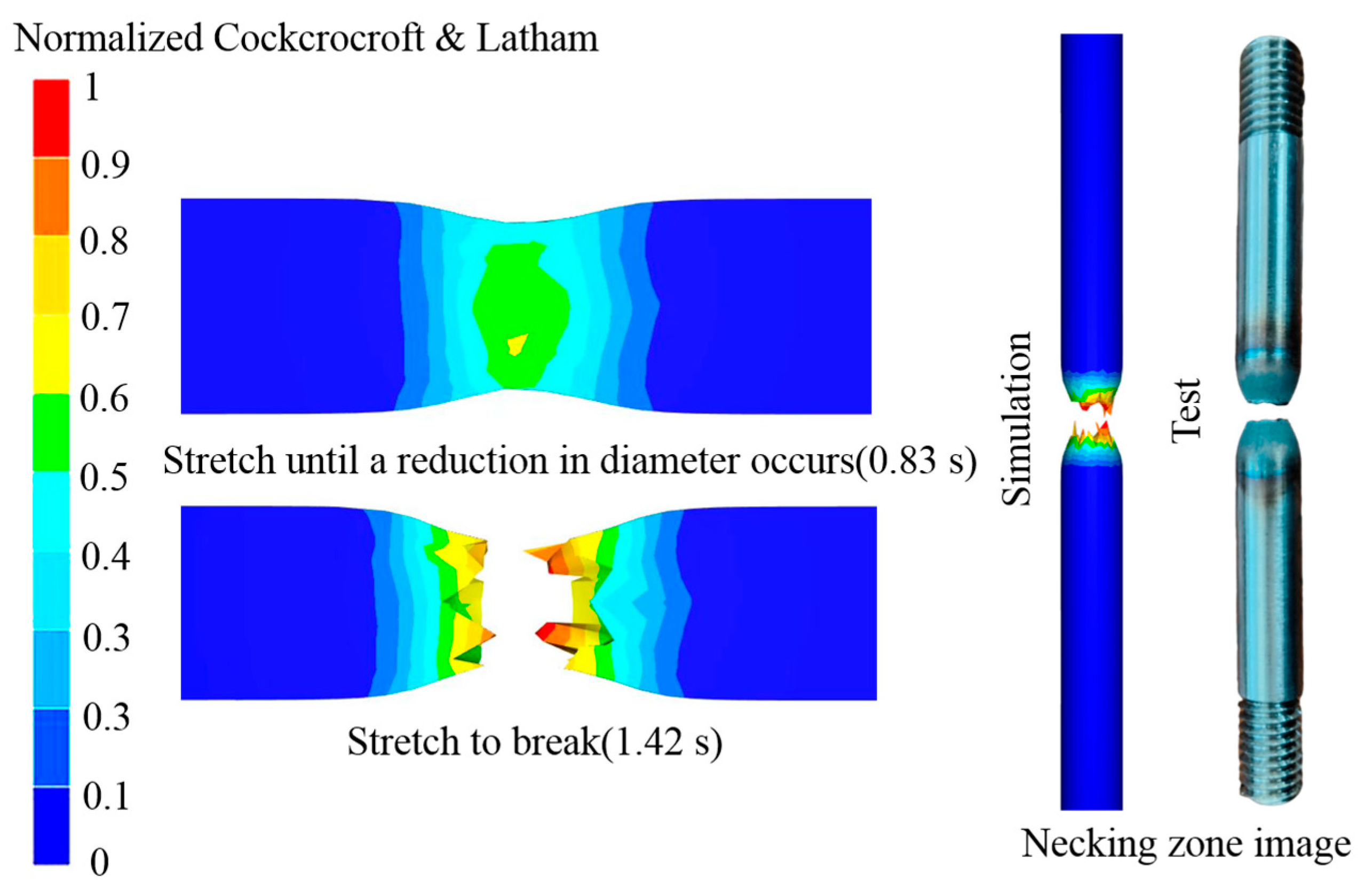
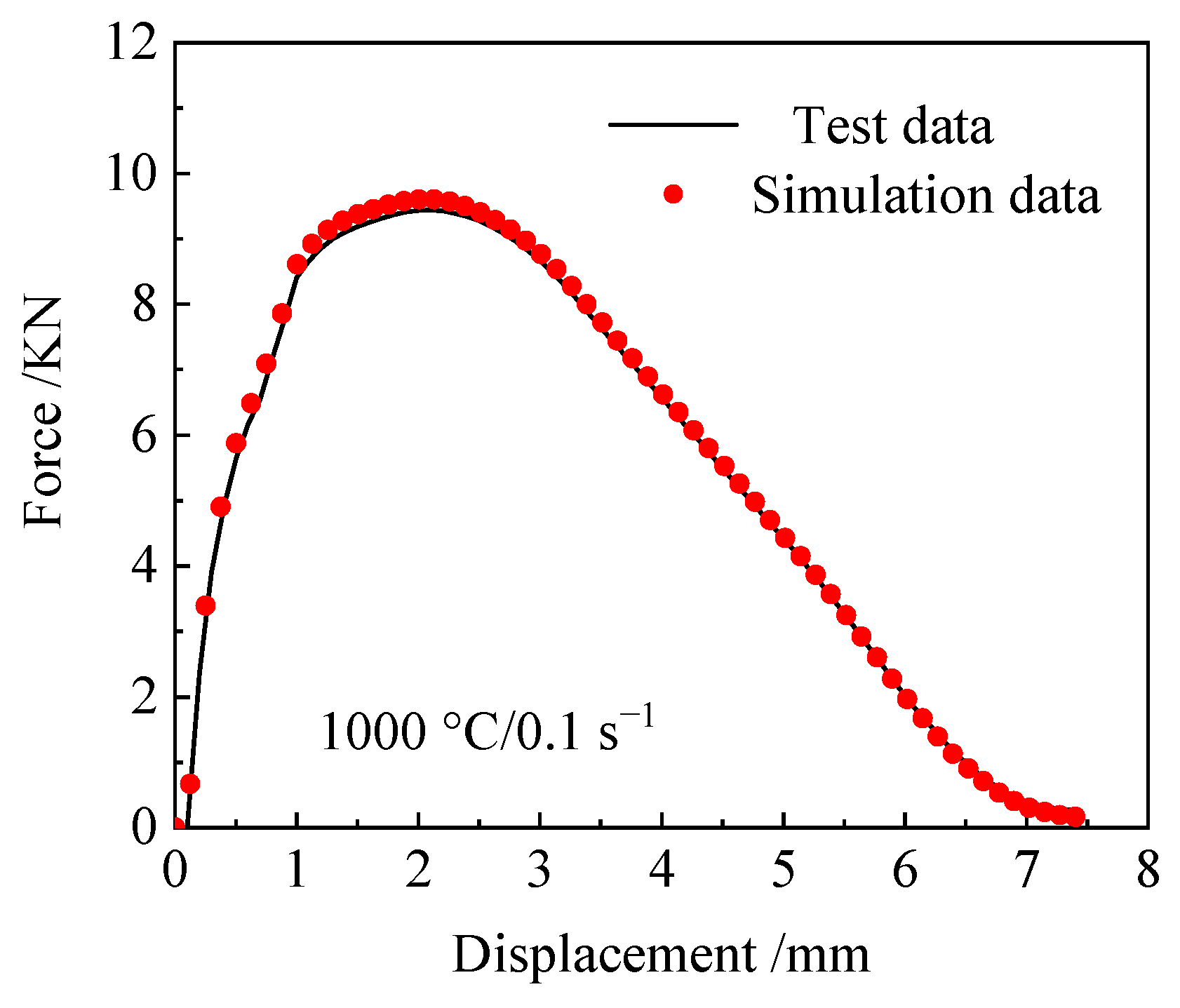
3.2.1. Establishment of a High-Temperature Damage Model for 04Cr13Ni5Mo Martensitic Stainless Steel
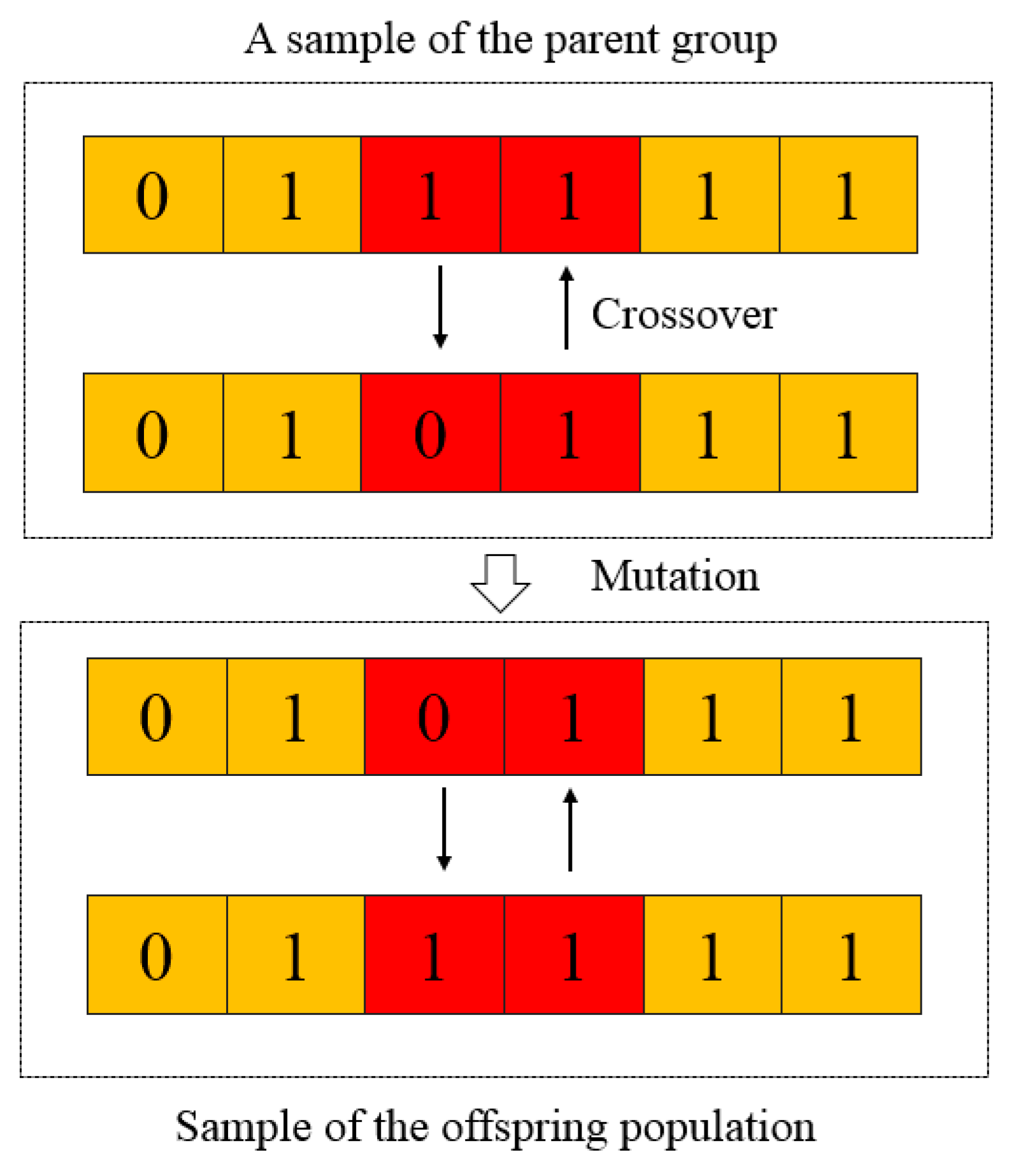
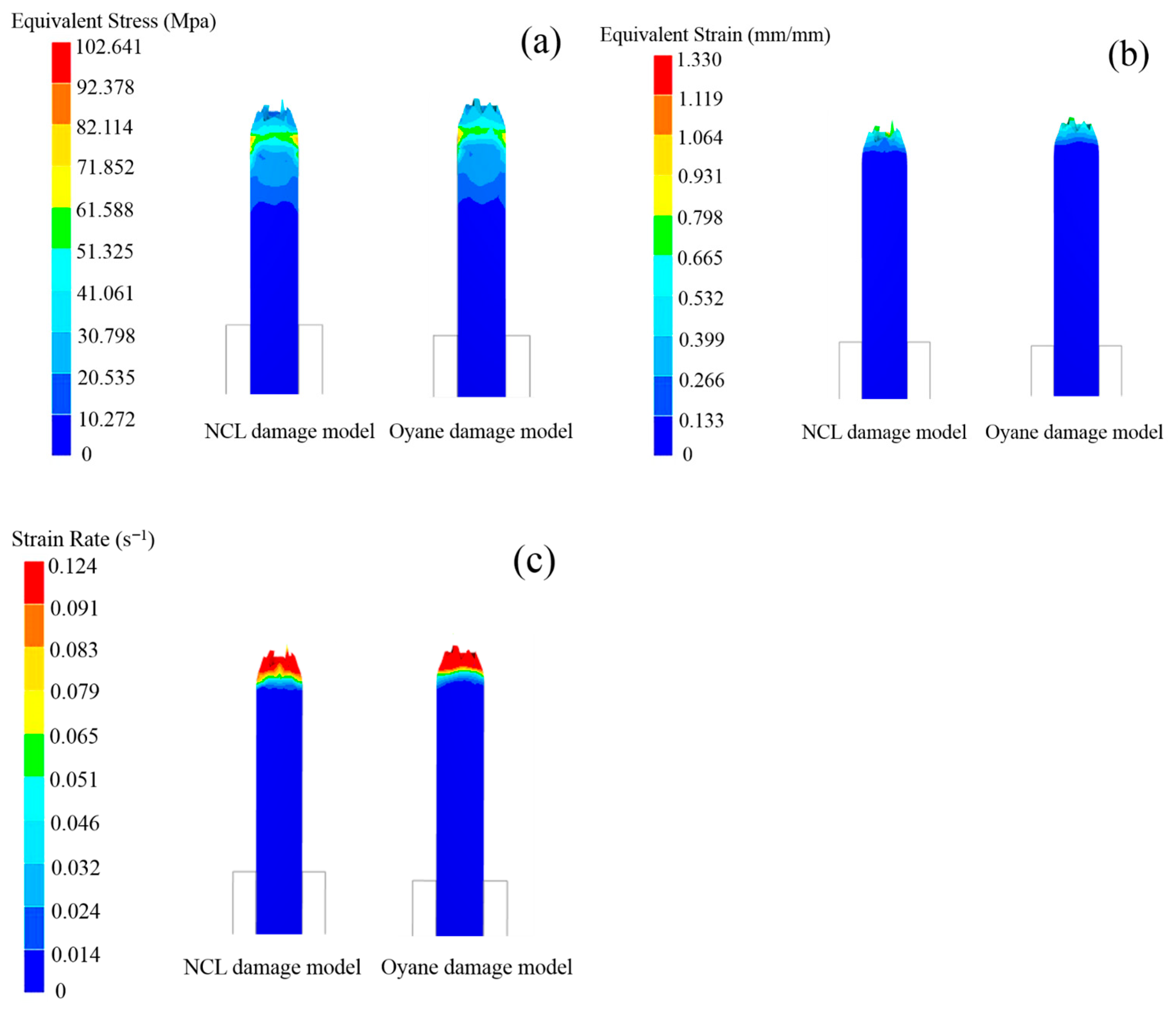
3.2.2. Parameter Characterization for High-Temperature Damage Model of 04Cr13Ni5Mo Martensitic Stainless Steel
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nasir, J.; Javed, A.; Ali, M.; Ullah, K.; Kazmi, S.A.A. Capacity optimization of pumped storage hydropower and its impact on an integrated conventional hydropower plant operation. Appl. Energy 2022, 323, 119561. [Google Scholar] [CrossRef]
- Alimirzazadeh, S.; Kumashiro, T.; Leguizamón, S.; Jahanbakhsh, E.; Maertens, A.; Vessaz, C.; Tani, K.; Avellan, F. GPU-accelerated numerical analysis of jet interference in a six-jet Pelton turbine using Finite Volume Particle Method. Renew. Energy 2020, 148, 234–246. [Google Scholar] [CrossRef]
- Zeng, C.; Xiao, Y.; Wang, Z.; Zhang, J.; Luo, Y. Numerical analysis of a Pelton bucket free surface sheet flow and dynamic performance affected by operating head. Proc. Inst. Mech. Eng. Part A J. Power Energy 2017, 231, 182–196. [Google Scholar] [CrossRef]
- Klein, S.J.W.; Fox, E.L.B. A review of small hydropower performance and cost. Renew. Sustain. Energy Rev. 2022, 169, 112898. [Google Scholar] [CrossRef]
- Lukeš, R.; Honus, S.; Blejchař, T.; Balco, M. Reaction Cross-Flow Turbine for Small Hydropower Plants: Flow Profile Design and CFD Analysis. Renew. Energy 2025, 252, 123560. [Google Scholar] [CrossRef]
- Maika, N.; Lin, W.; Khatamifar, M. A review of gravitational water vortex hydro turbine systems for hydropower generation. Energies 2023, 16, 5394. [Google Scholar] [CrossRef]
- Chaulagain, R.K.; Poudel, L.; Maharjan, S. A review on non-conventional hydropower turbines and their selection for ultra-low-head applications. Heliyon 2023, 9, e17753. [Google Scholar] [CrossRef]
- Li, X.; Dai, Y.; Wang, X.; Liu, Y.; Chen, Y.; Wang, C.; Zhang, H.; Li, L.; Liu, H.; He, C.; et al. Effects of local microstructure on crack initiation in super martensitic stainless steel under very-high-cycle fatigue. Int. J. Fatigue 2022, 163, 107019. [Google Scholar] [CrossRef]
- Chen, A.Y.; Ruan, H.H.; Wang, J.; Chan, H.L.; Wang, Q.; Li, Q.; Lu, J. The influence of strain rate on the microstructure transition of 304 stainless steel. Acta Mater. 2011, 59, 3697–3709. [Google Scholar] [CrossRef]
- Salahi, S.; Kazemipour, M.; Nasiri, A. Effects of microstructural evolution on the corrosion properties of AISI 420 martensitic stainless steel during cold rolling process. Mater. Chem. Phys. 2021, 258, 123916. [Google Scholar] [CrossRef]
- Naghizadeh, M.; Mirzadeh, H. Microstructural evolutions during annealing of plastically deformed AISI 304 austenitic stainless steel: Martensite reversion, grain refinement, recrystallization, and grain growth. Metall. Mater. Trans. A 2016, 47, 4210–4216. [Google Scholar] [CrossRef]
- Liu, Y.R.; Ye, D.; Yong, Q.L.; Su, J.; Zhao, K.Y.; Jiang, W. Effect of heat treatment on microstructure and property of Cr13 super martensitic stainless steel. J. Iron Steel Res. Int. 2011, 18, 60–66. [Google Scholar] [CrossRef]
- Song, Y.; Dong, Q.; Zhang, J.; Li, G.; Xu, D.; Yang, P. A prediction method for fatigue crack growth under high stress levels using accumulative plastic damage properties. Mar. Struct. 2024, 93, 103535. [Google Scholar] [CrossRef]
- Chen, X.; Yang, Z.; Zhang, B.; Sun, J.; Su, Z.; Mao, Y. An Inverse Optimization Method for the Parameter Determination of the High-Temperature Damage Model and High-Temperature Damage Graph of Ti6Al4V Alloy. Materials 2023, 16, 4770. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Chen, X.; Du, K.; Zhou, X.; Xiang, N.; Osaka, A. A modified Bonora damage model for temperature and strain rate-dependent materials in hot forging process. Eng. Fract. Mech. 2020, 235, 107107. [Google Scholar] [CrossRef]
- Rong, H.; Hu, P.; Ying, L.; Hou, W.; Zhang, J. Thermal forming limit diagram (TFLD) of AA7075 aluminum alloy based on a modified continuum damage model: Experimental and theoretical investigations. Int. J. Mech. Sci. 2019, 156, 59–73. [Google Scholar] [CrossRef]
- Jia, W.; Ma, L.; Le, Q.; Zhi, C.; Liu, P. Deformation and fracture behaviors of AZ31B Mg alloy at elevated temperature under uniaxial compression. J. Alloys Compd. 2019, 783, 863–876. [Google Scholar] [CrossRef]
- Alkayem, N.F.; Cao, M.; Zhang, Y.; Bayat, M.; Su, Z. Structural damage detection using finite element model updating with evolutionary algorithms: A survey. Neural Comput. Appl. 2018, 30, 389–411. [Google Scholar] [CrossRef]
- Felder, S.; Kopic-Osmanovic, N.; Holthusen, H.; Brepols, T.; Reese, S. Thermo-mechanically coupled gradient-extended damage-plasticity modeling of metallic materials at finite strains. Int. J. Plast. 2022, 148, 103142. [Google Scholar] [CrossRef]
- Gao, P.F.; Fei, M.Y.; Zhan, M.; Fu, M.W. Microstructure-and damage-nucleation-based crystal plasticity finite element modeling for the nucleation of multi-type voids during plastic deformation of Al alloys. Int. J. Plast. 2023, 165, 103609. [Google Scholar] [CrossRef]
- Oyane, M. Criteria of ductile fracture strain. Bull. JSME 1972, 15, 1507–1513. [Google Scholar] [CrossRef]
- Cockcroft, M.G.; Latham, D.J. Ductility and the workability of metals. J. Inst. Met. 1968, 96, 33–39. [Google Scholar]
- Oh, S.I.; Chen, C.C.; Kobayashi, S. Ductile Fracture in Axisymmetric Extrusion and Drawing Part 1: Deformation Mechanics of Extrusion and Drawing. J. Manuf. Sci. Eng. 1977, 101, 36–44. [Google Scholar]
- Kim, H.K.; Kim, W.J. Failure prediction of magnesium alloy sheets deforming at warm temperatures using the Zener-Holloman parameter. Mech. Mater. 2010, 42, 293–303. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Hao, W. Application of Orthogonal Experimental Design for the Automatic Software Testing. Appl. Mech. Mater. 2013, 347, 812–818. [Google Scholar] [CrossRef]
- Cao, Z.; Sun, Y.; Wan, Z.; Ren, L.; Hu, L. Critical damage model of TiAl alloy during high-temperature deformation process. Chin. J. Nonferr. Met. 2018, 28, 670–676. [Google Scholar] [CrossRef]






| Chemical Composition | Fe | C | Si | Mn | S | P | Cr | Ni | Mo | Cu |
|---|---|---|---|---|---|---|---|---|---|---|
| 04Cr13Ni5Mo | 80.423 | 0.033 | 0.36 | 0.71 | 0.003 | 0.018 | 12.9 | 4.9 | 0.6 | 0.053 |
| Parameter | Young Modulus/Gpa | Strength Stress/MPa | Tensile Strength/MPa | Hardness/HBW |
|---|---|---|---|---|
| 04Cr13Ni5Mo | 201 | 657 | 806 | 307 |
| Population Size | Crossover Rate | Mutation Rate | Target Function Value | Maximum Iterations |
|---|---|---|---|---|
| 25 | 0.8 | 0.05 | 0.03 | 150 |
| Damage Criterion | Deformation Condition | 950 °C | 1000 °C | 1050 °C | 1100 °C | 1150 °C | 1200 °C |
|---|---|---|---|---|---|---|---|
| Normalized Cockcroft and Latham | 0.001 s−1 | 1.573 | 1.692 | 1.861 | 1.342 | 1.307 | 1.107 |
| 0.01 s−1 | 1.534 | 1.663 | 1.816 | 1.214 | 1.211 | 1.085 | |
| 0.1 s−1 | 1.484 | 1.562 | 1.748 | 1.184 | 1.164 | 0.987 | |
| 1 s−1 | 1.457 | 1.529 | 1.717 | 1.143 | 1.116 | 0.957 | |
| Oyane | 0.001 s−1 | 1.604 | 1.687 | 1.833 | 1.360 | 1.297 | 1.061 |
| 0.01 s−1 | 1.579 | 1.709 | 1.800 | 1.253 | 1.226 | 1.070 | |
| 0.1 s−1 | 1.448 | 1.582 | 1.762 | 1.172 | 1.195 | 0.996 | |
| 1 s−1 | 1.497 | 1.579 | 1.746 | 1.136 | 1.163 | 0.948 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.; Tian, J.; Chen, H.; Zhang, B.; Li, F.; Shi, H. Research on High-Temperature Damage Behavior of Super Martensitic Stainless Steel 04Cr13Ni5Mo Based on Finite Element Simulation. Materials 2025, 18, 5262. https://doi.org/10.3390/ma18235262
Sun T, Tian J, Chen H, Zhang B, Li F, Shi H. Research on High-Temperature Damage Behavior of Super Martensitic Stainless Steel 04Cr13Ni5Mo Based on Finite Element Simulation. Materials. 2025; 18(23):5262. https://doi.org/10.3390/ma18235262
Chicago/Turabian StyleSun, Tonghui, Jihong Tian, Huiqin Chen, Bo Zhang, Fei Li, and Hongqiang Shi. 2025. "Research on High-Temperature Damage Behavior of Super Martensitic Stainless Steel 04Cr13Ni5Mo Based on Finite Element Simulation" Materials 18, no. 23: 5262. https://doi.org/10.3390/ma18235262
APA StyleSun, T., Tian, J., Chen, H., Zhang, B., Li, F., & Shi, H. (2025). Research on High-Temperature Damage Behavior of Super Martensitic Stainless Steel 04Cr13Ni5Mo Based on Finite Element Simulation. Materials, 18(23), 5262. https://doi.org/10.3390/ma18235262





