Enhanced Chroma-YOLO Framework for Effective Defect Detection and Fatigue Life Prediction in 3D-Printed Polylactic Acid
Abstract
1. Introduction
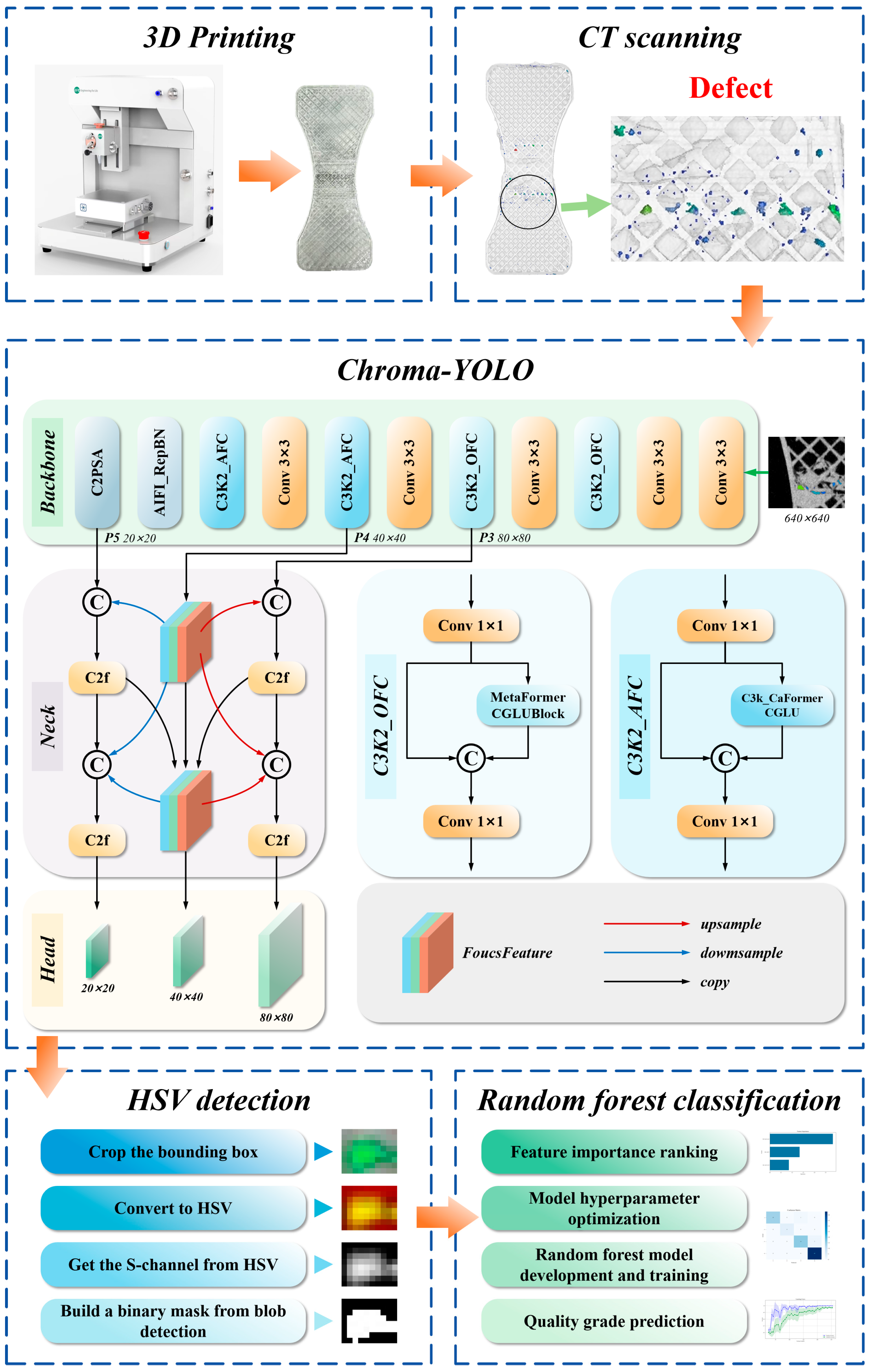
2. Experimental Methods
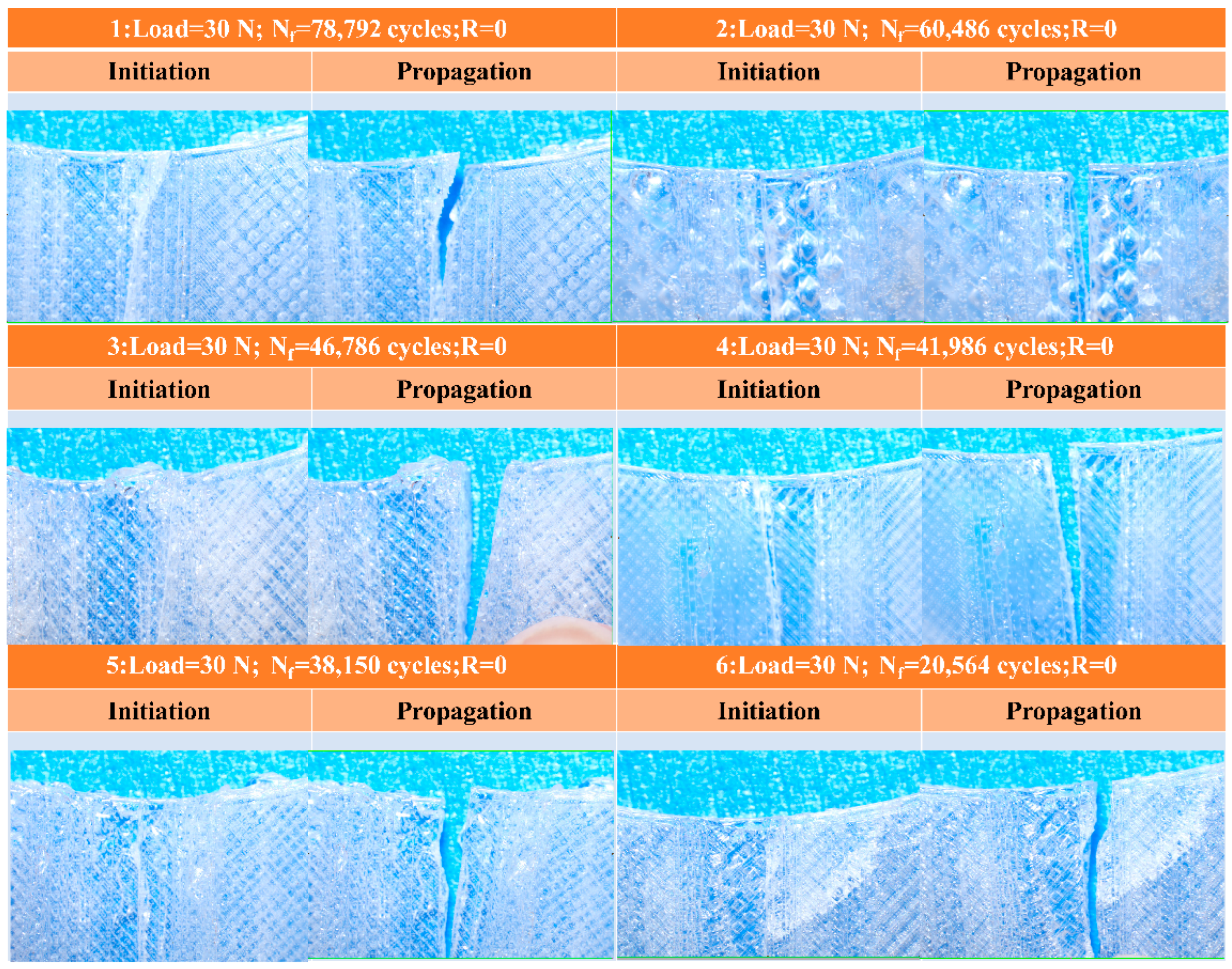
2.1. Internal Defect Characterization and Fatigue Testing of PLA Specimens
2.2. Chroma-YOLO
2.2.1. YOLOv11
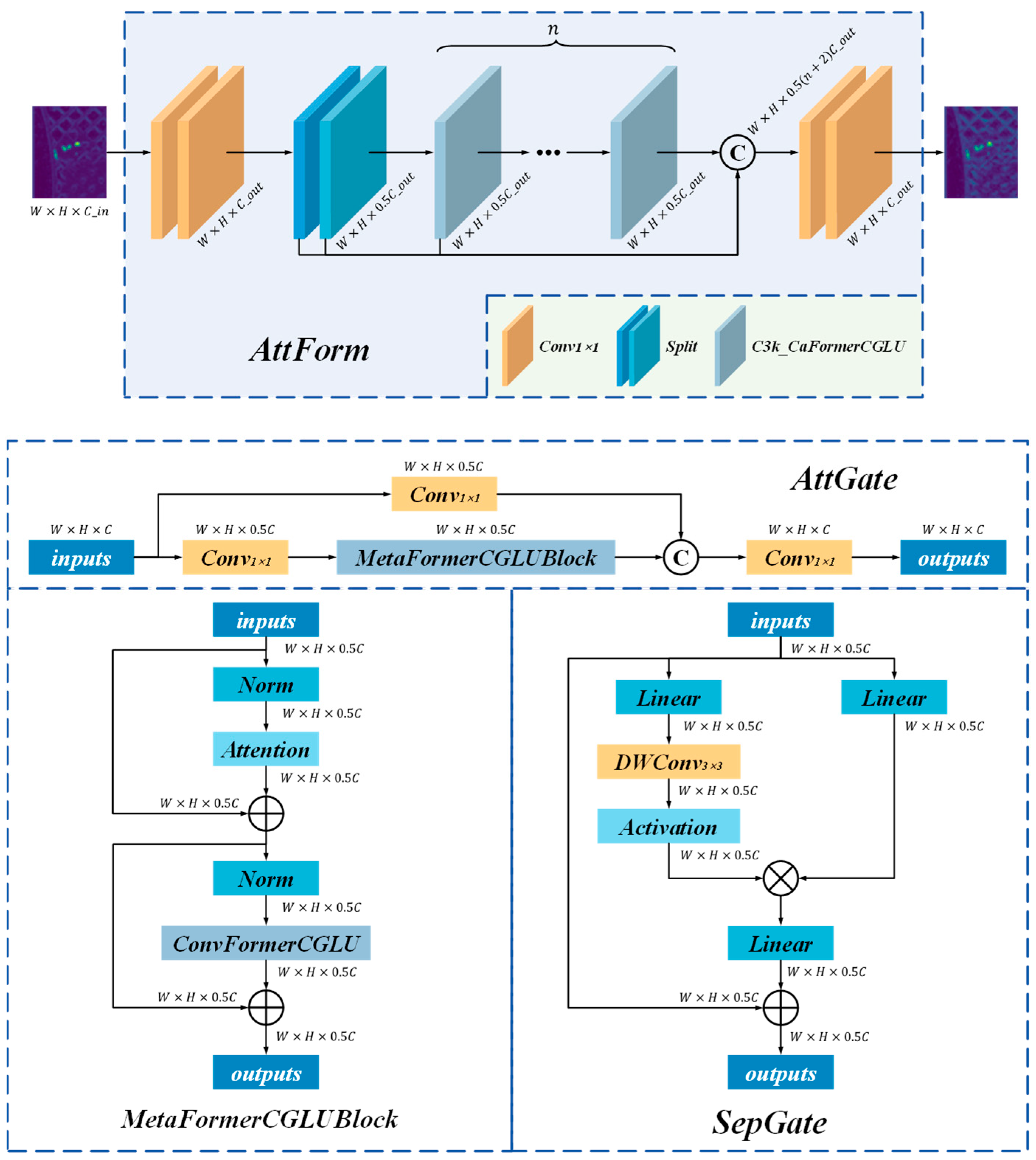
2.2.2. AttForm Attention Enhancement Network
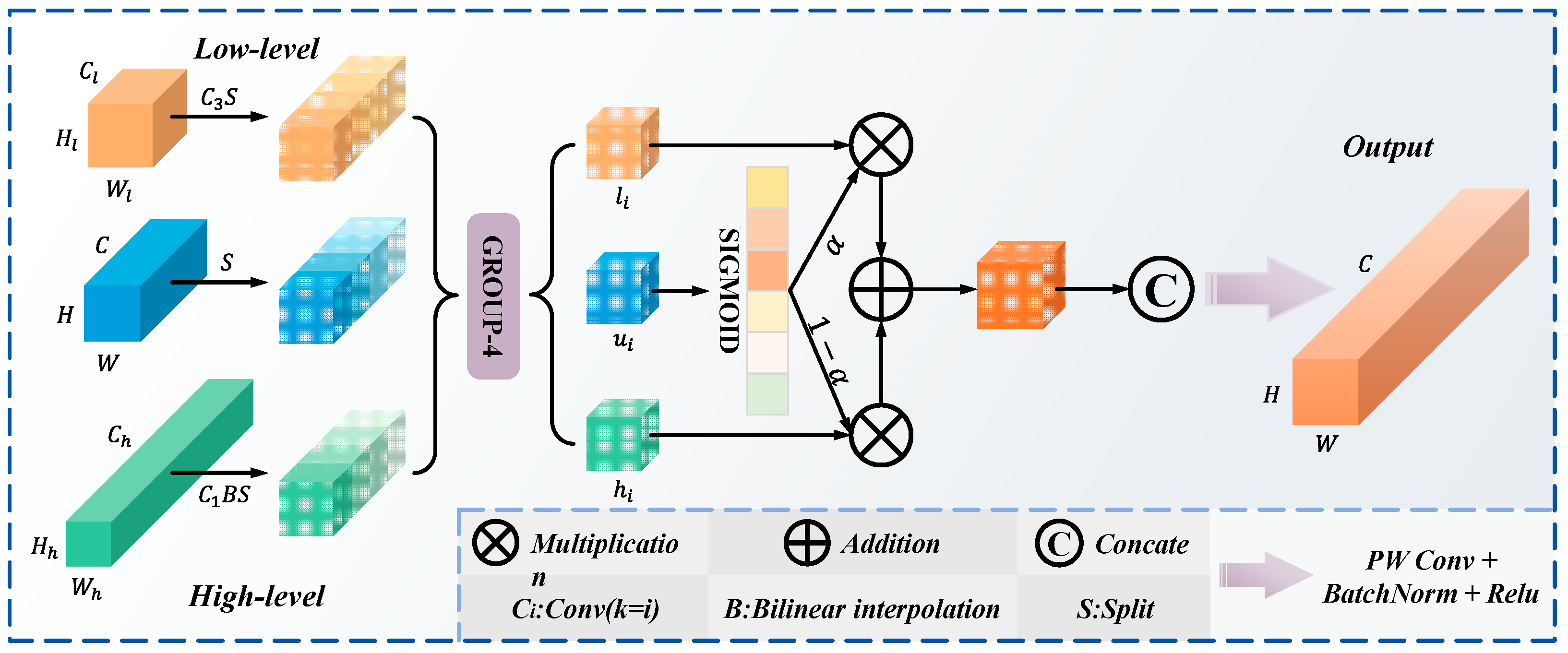
2.2.3. TriFusion Feature Fusion Network
2.2.4. RepFocus Self-Attention Reparameterization Module
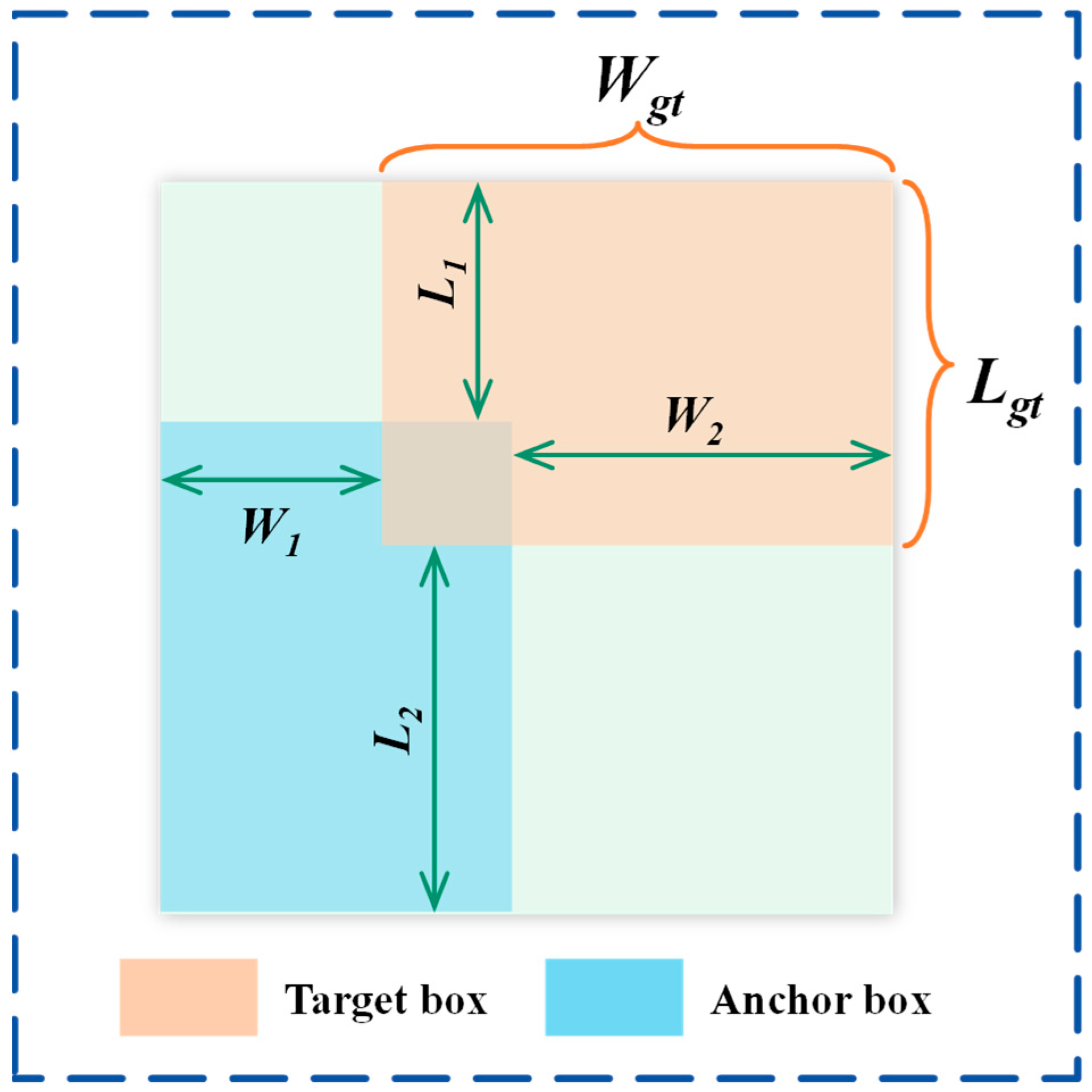
2.2.5. Boundary Penalty Loss Function Module
2.3. HSV Color Space-Based Defect Extraction
2.4. Random Forest Fatigue Life Prediction Model
3. Experiments and Results
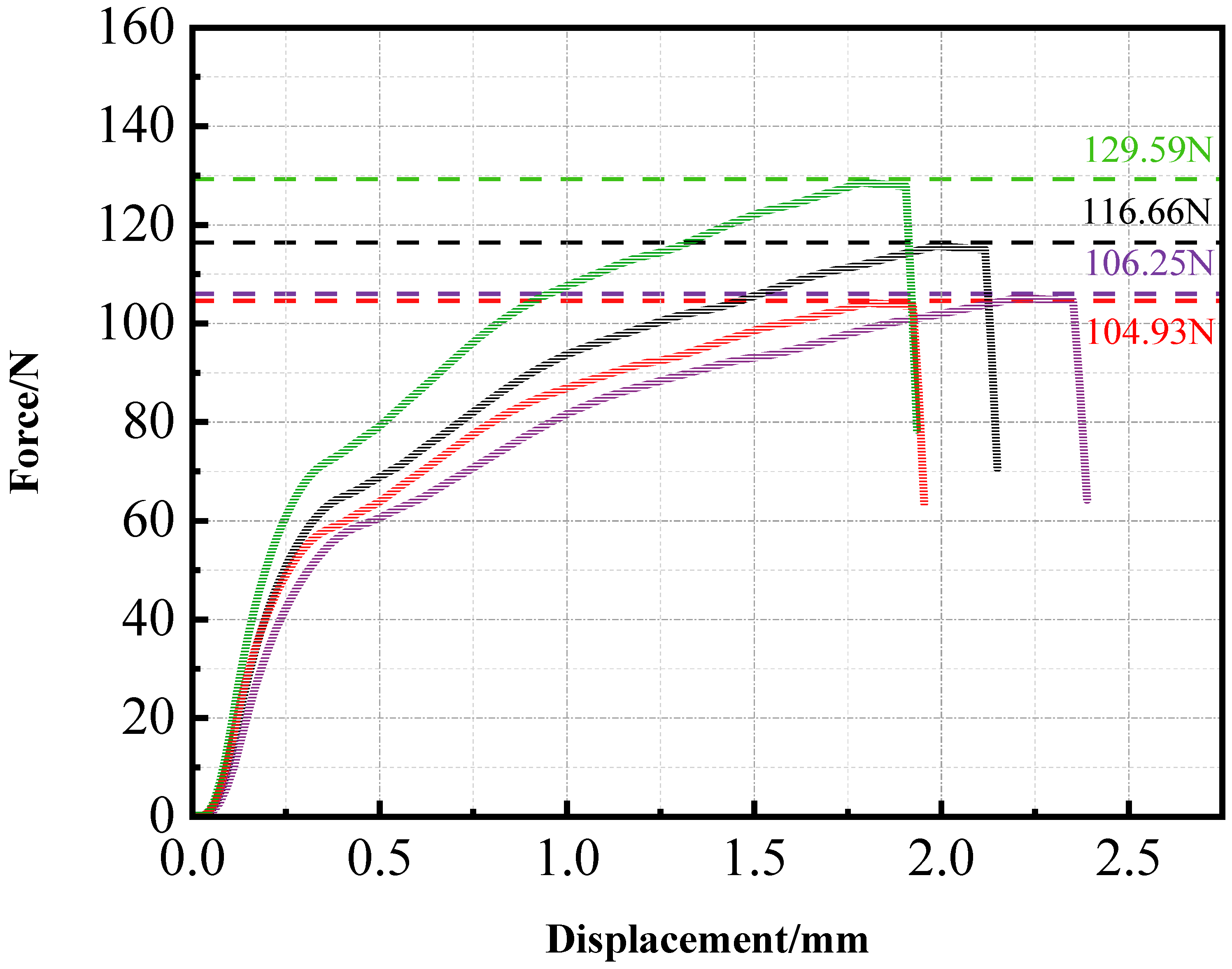
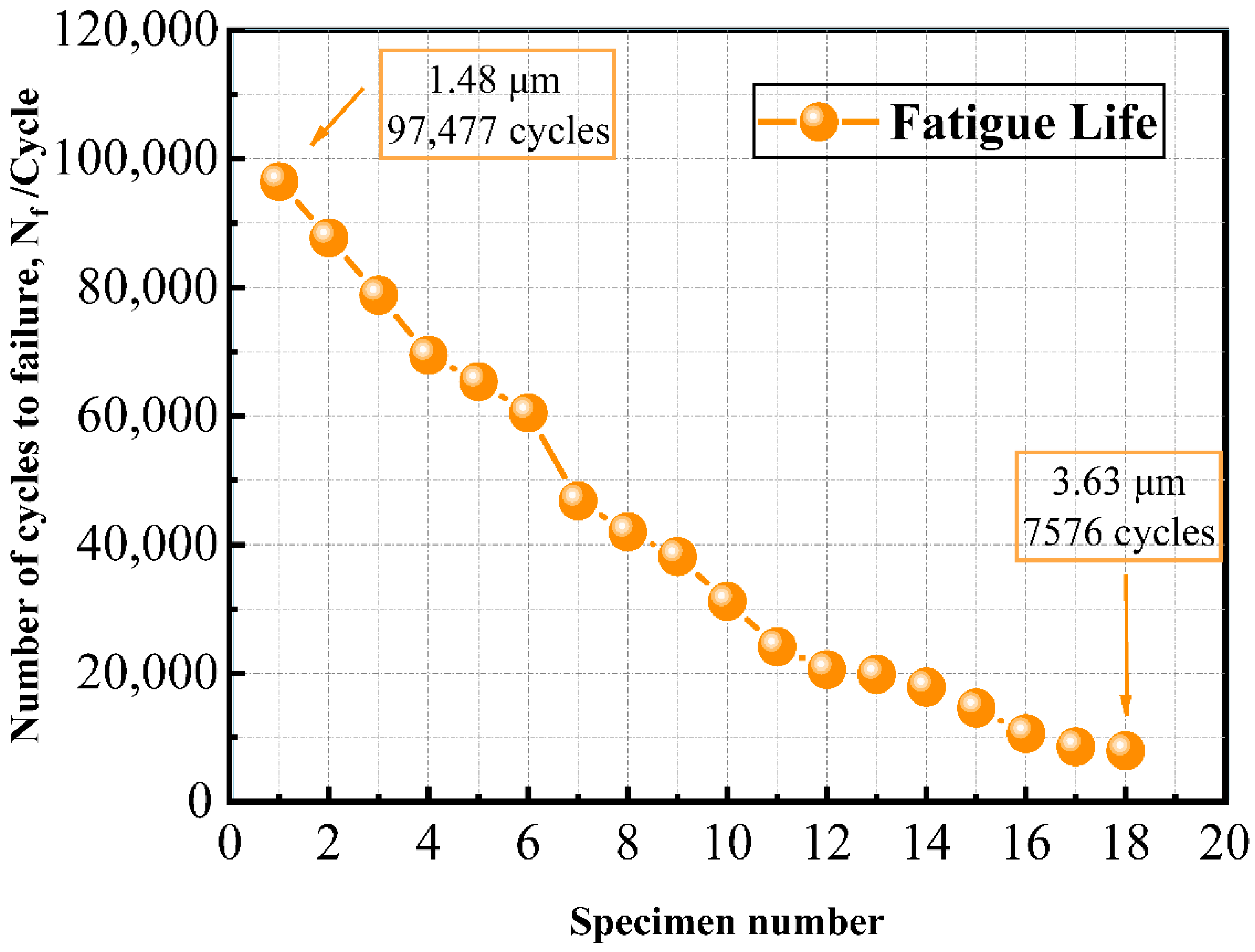
3.1. Tensile, Fatigue, and SEM Results
3.2. Experimental Setup and Model Metrics
- Precision: Precision refers to the proportion of true positive samples among all samples predicted positive. Its formula is given by Equation (20):
- TP (True Positive) is the count of correctly detected targets, and FP (False Positive) is the count of incorrectly detected ones.
- Recall: Recall refers to the proportion of correctly predicted positive samples among all actual positive samples. Its formula is given by Equation (21):where FN (False Negative) represents the number of targets that were not detected.
- mAP50: mAP50 (Mean Average Precision at IoU threshold 0.5) represents the Average Precision when the IoU (Intersection over Union) threshold is set at 0.5. The formula for Average Precision is shown in Equation (22):
- mAP50-95: mAP50-95 is the mean of Average Precision values across IoU thresholds from 0.5 to 0.95, with a step size of 0.05. Its formula is given by Equation (23):where t represents the IoU thresholds from 0.5 to 0.95, with a step size of 0.05.
- Parameters: Parameters refer to the total number of trainable parameters in the model. The total parameter count is typically expressed in millions (M) or billions (B).
- Giga Floating Point Operations Per Second (GFLOPS): GFLOPS is a unit of measurement for assessing the processing capability of computing devices or algorithms.
3.3. Module Comparison Experiments
3.3.1. AttForm Module Comparison Experiments
3.3.2. TriFusion Module Comparison Experiments
3.3.3. RepFocus Module Comparison Experiments
3.3.4. BIoU Loss Function Comparison Experiments
3.4. Ablation Experiments
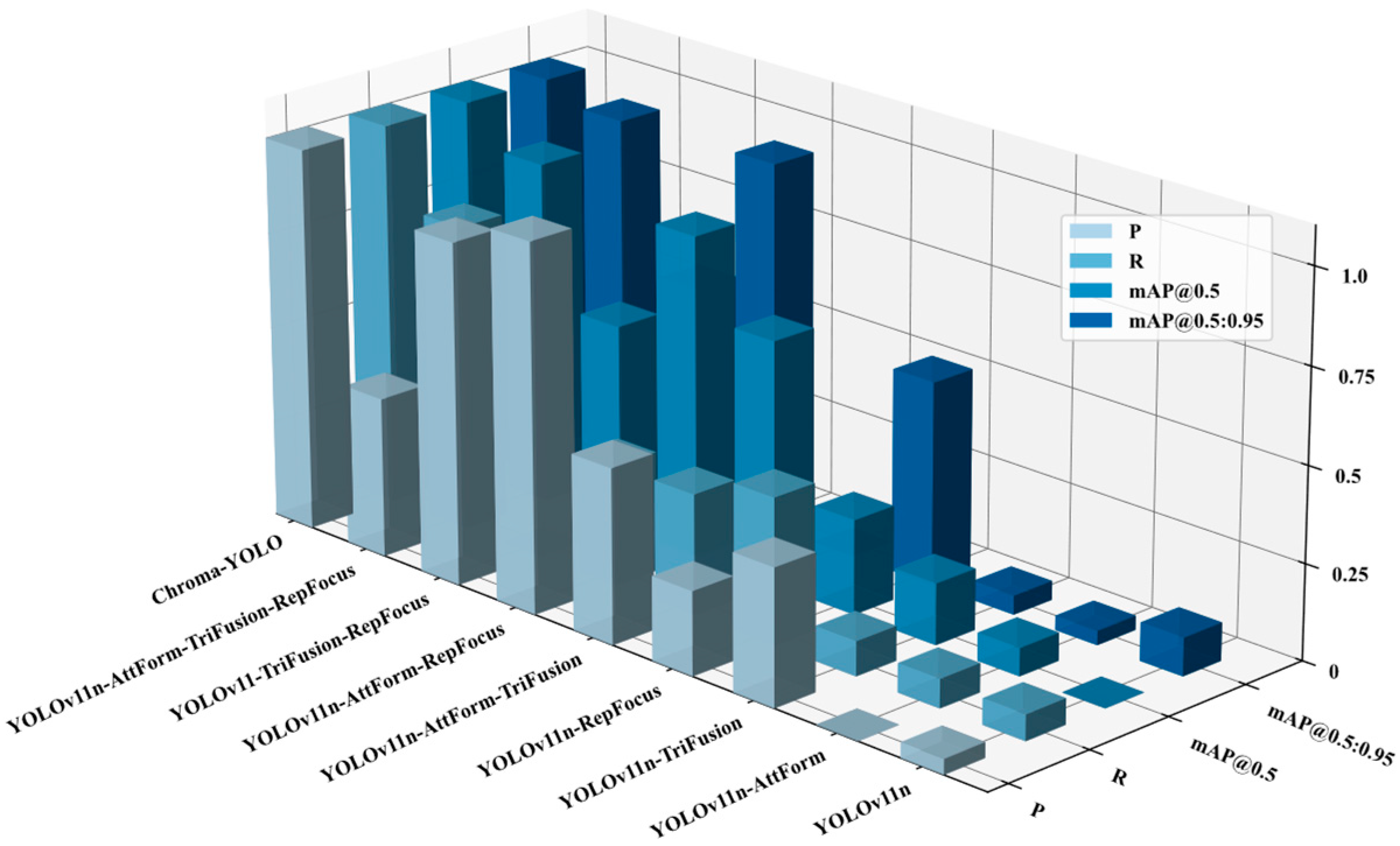
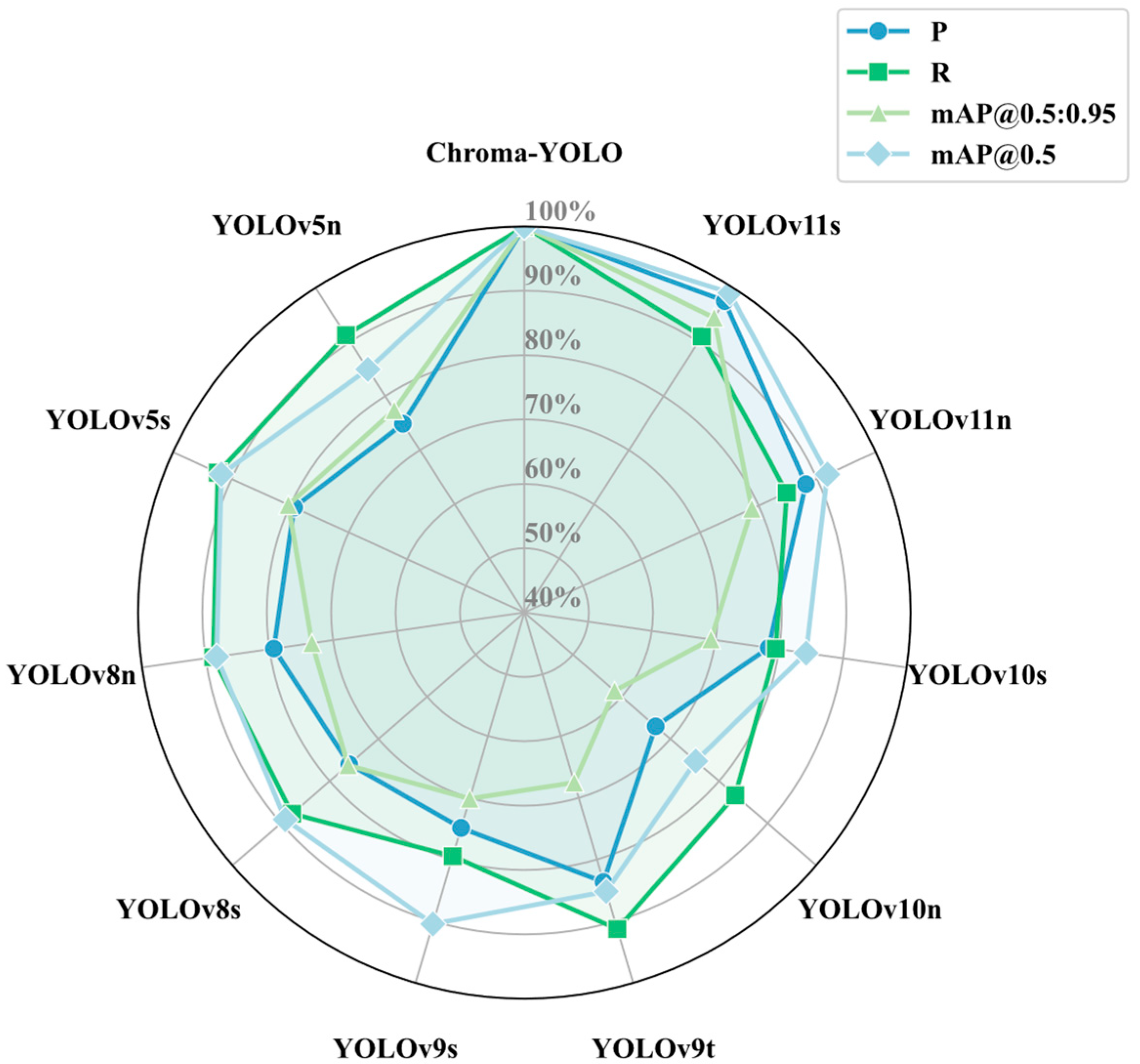
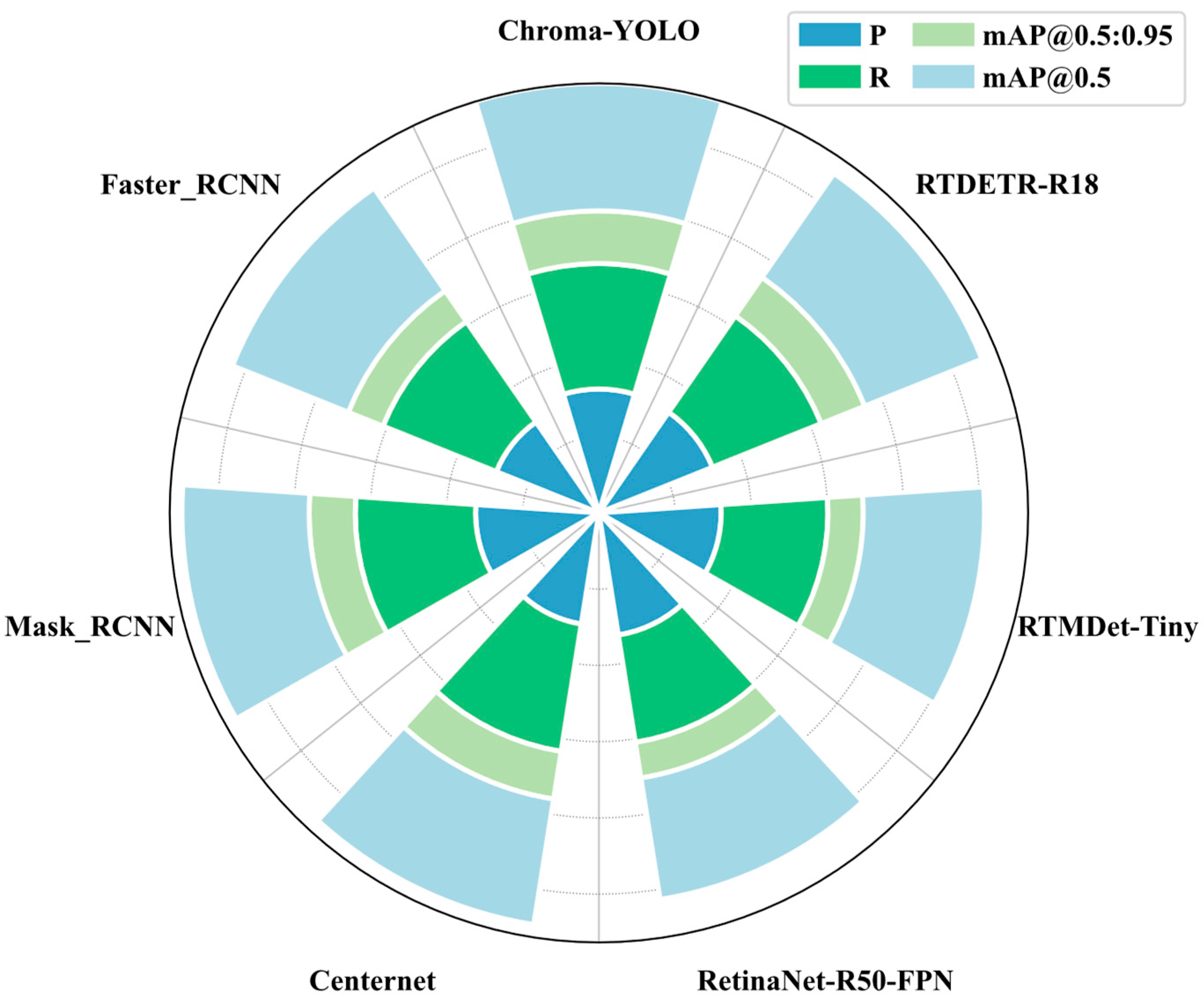
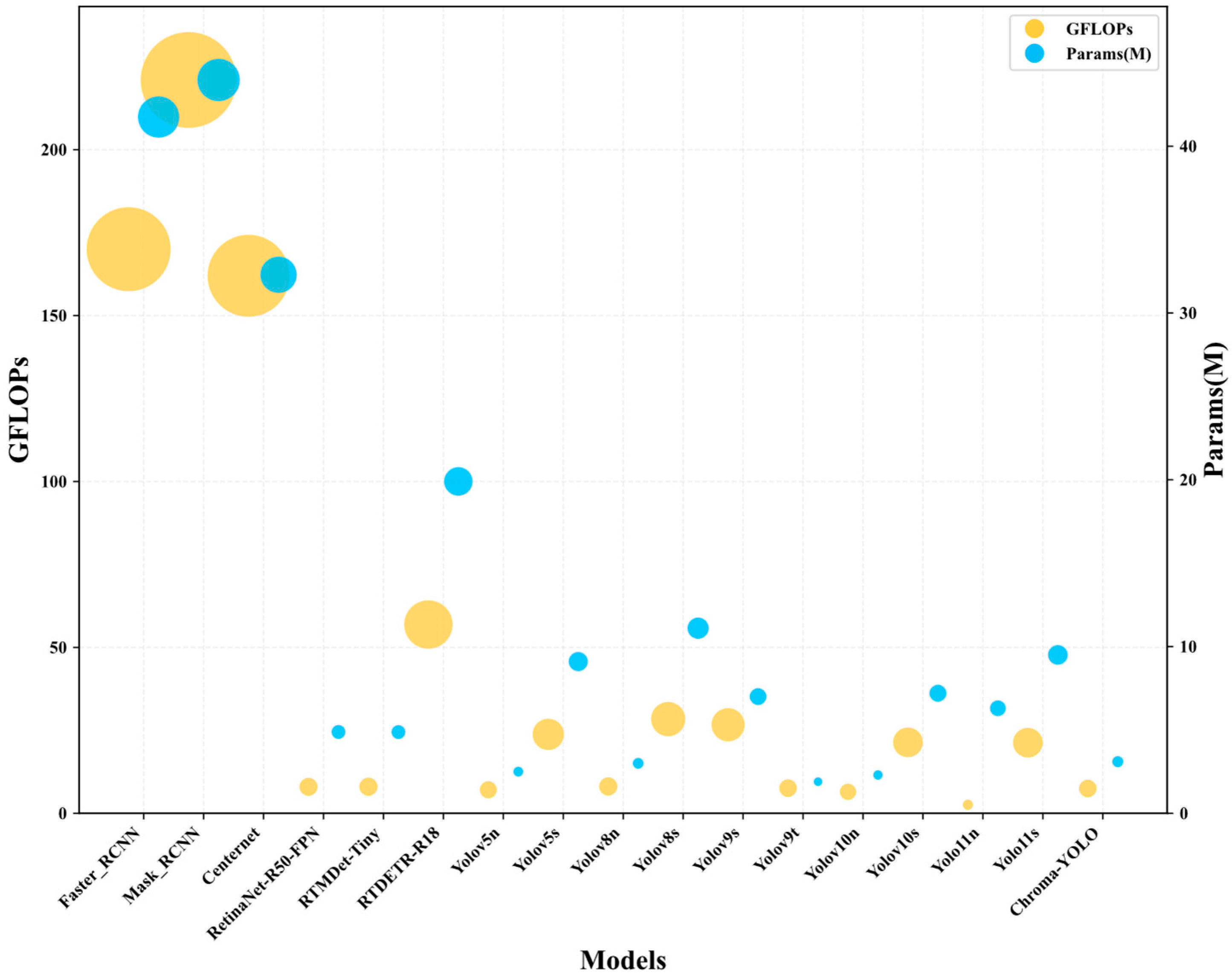
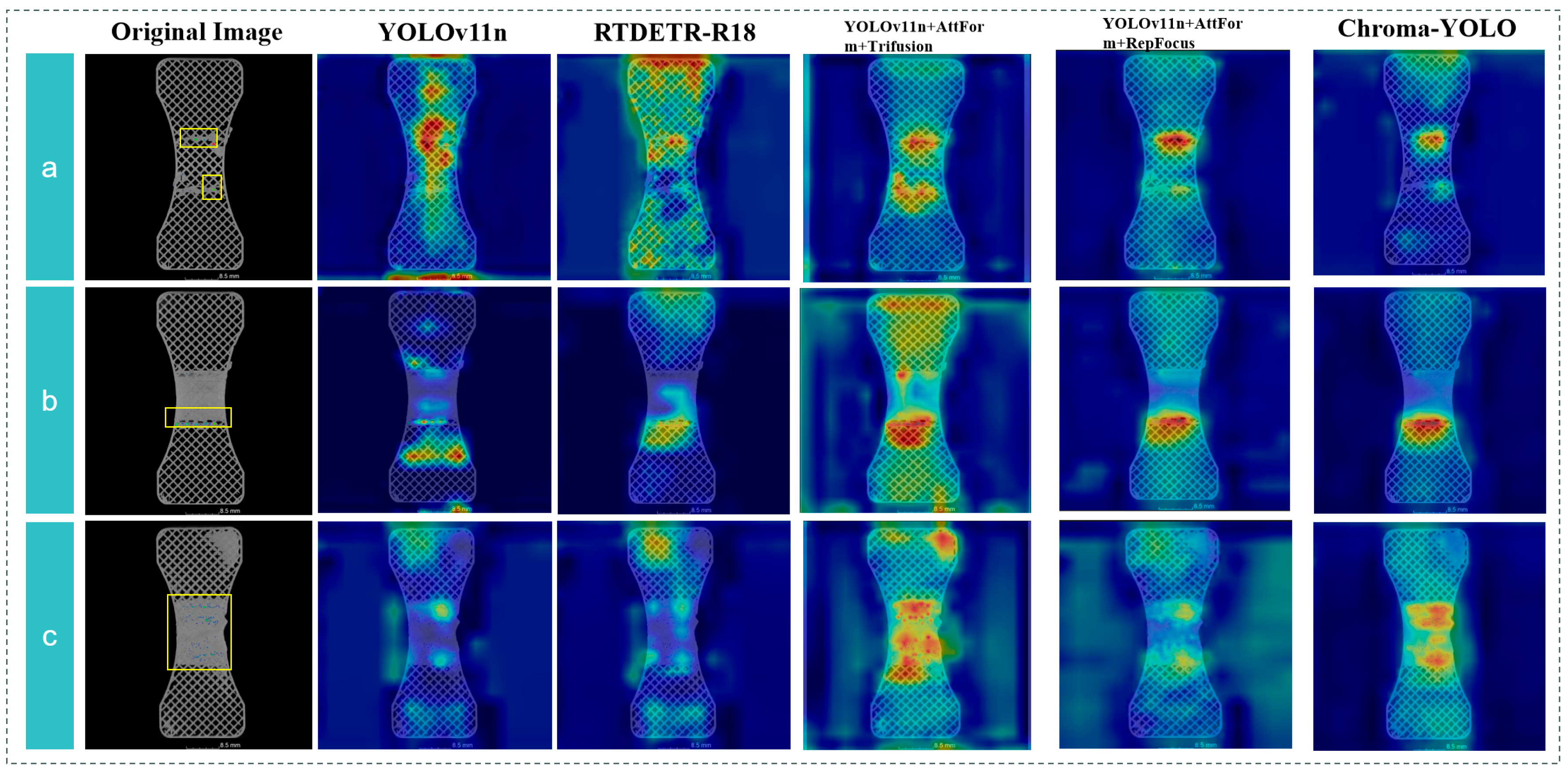
3.5. Comparative Experiments of Different Detection Models
3.6. Defect Extraction in Polylactic Acid Specimens
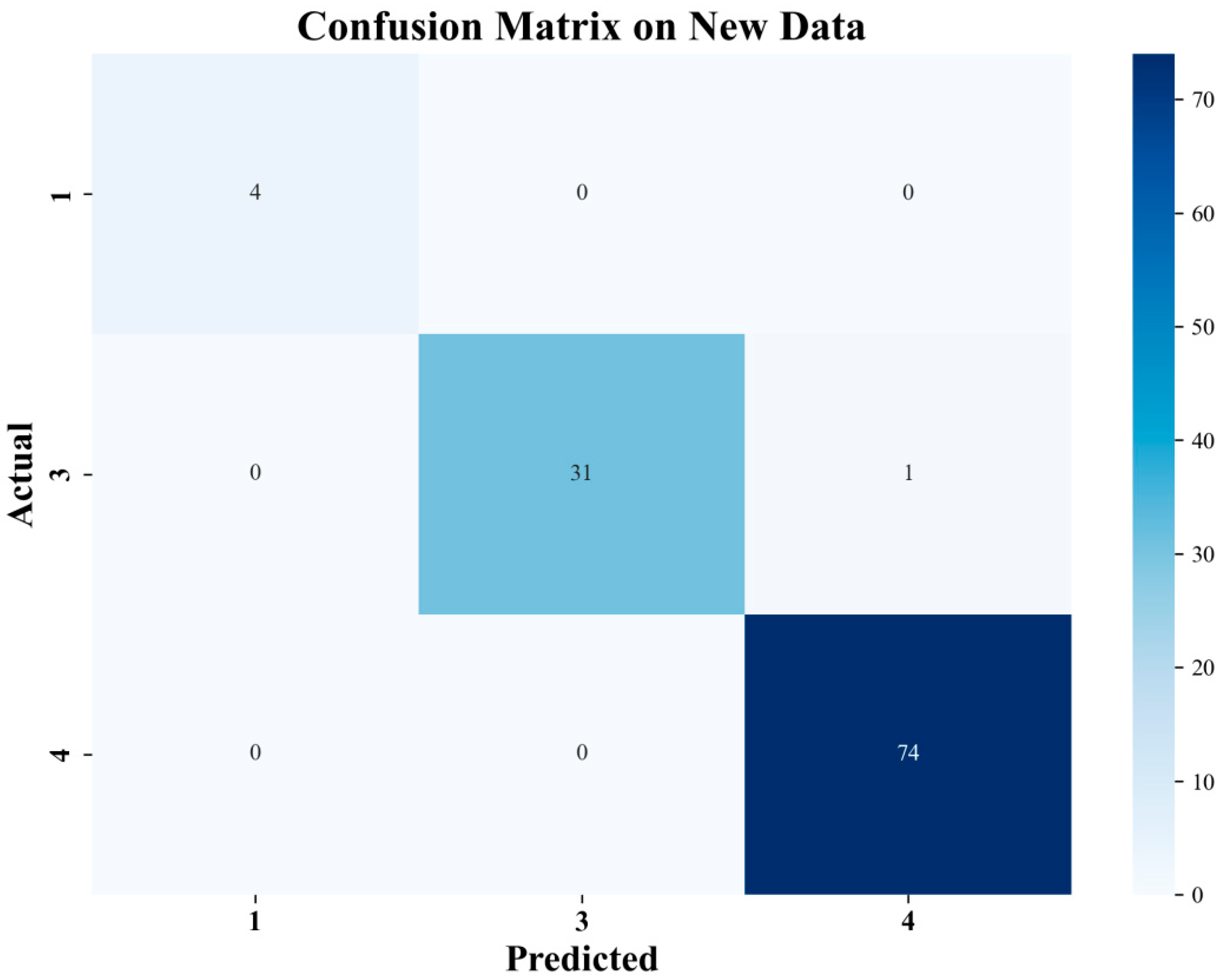
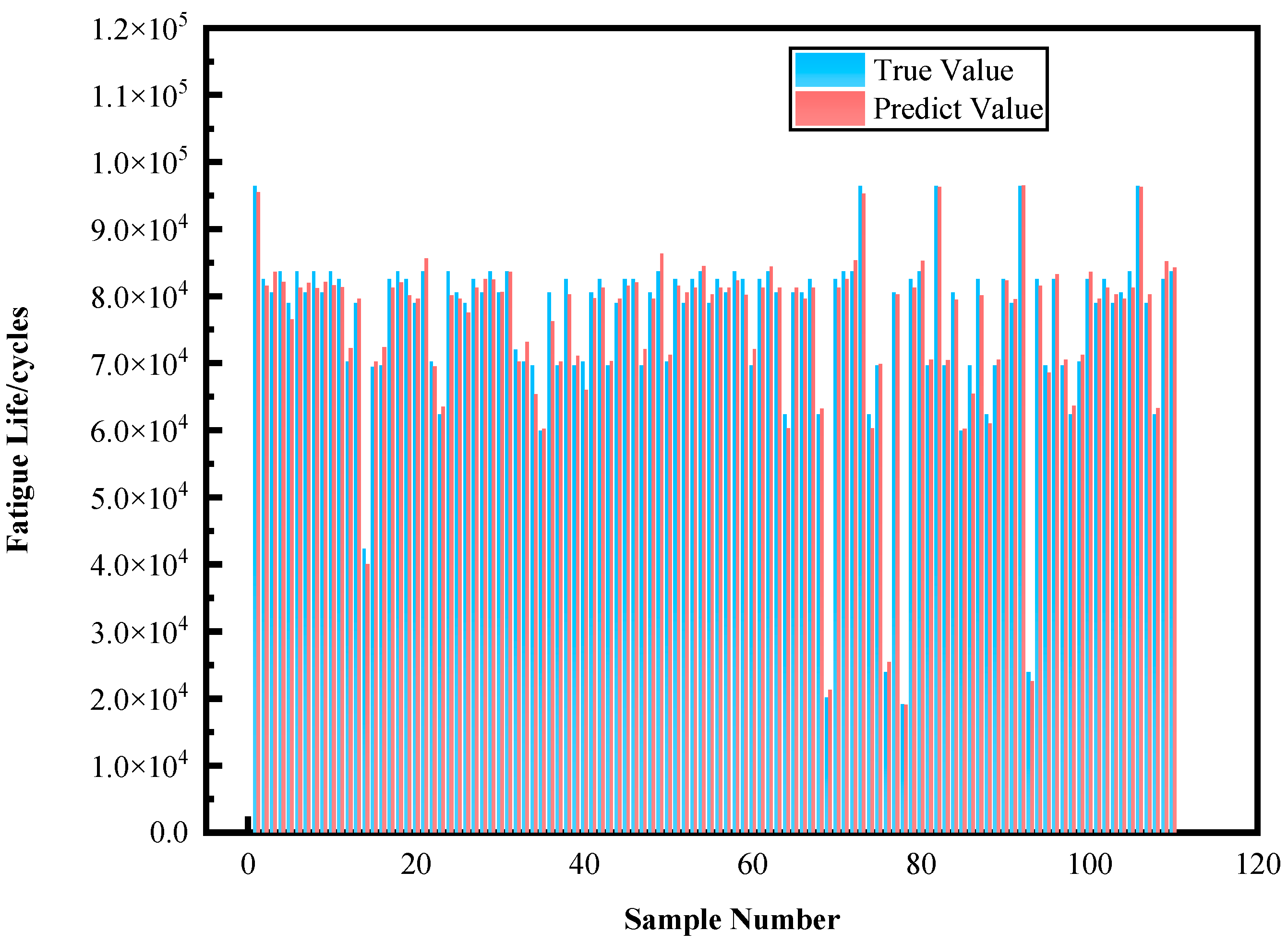
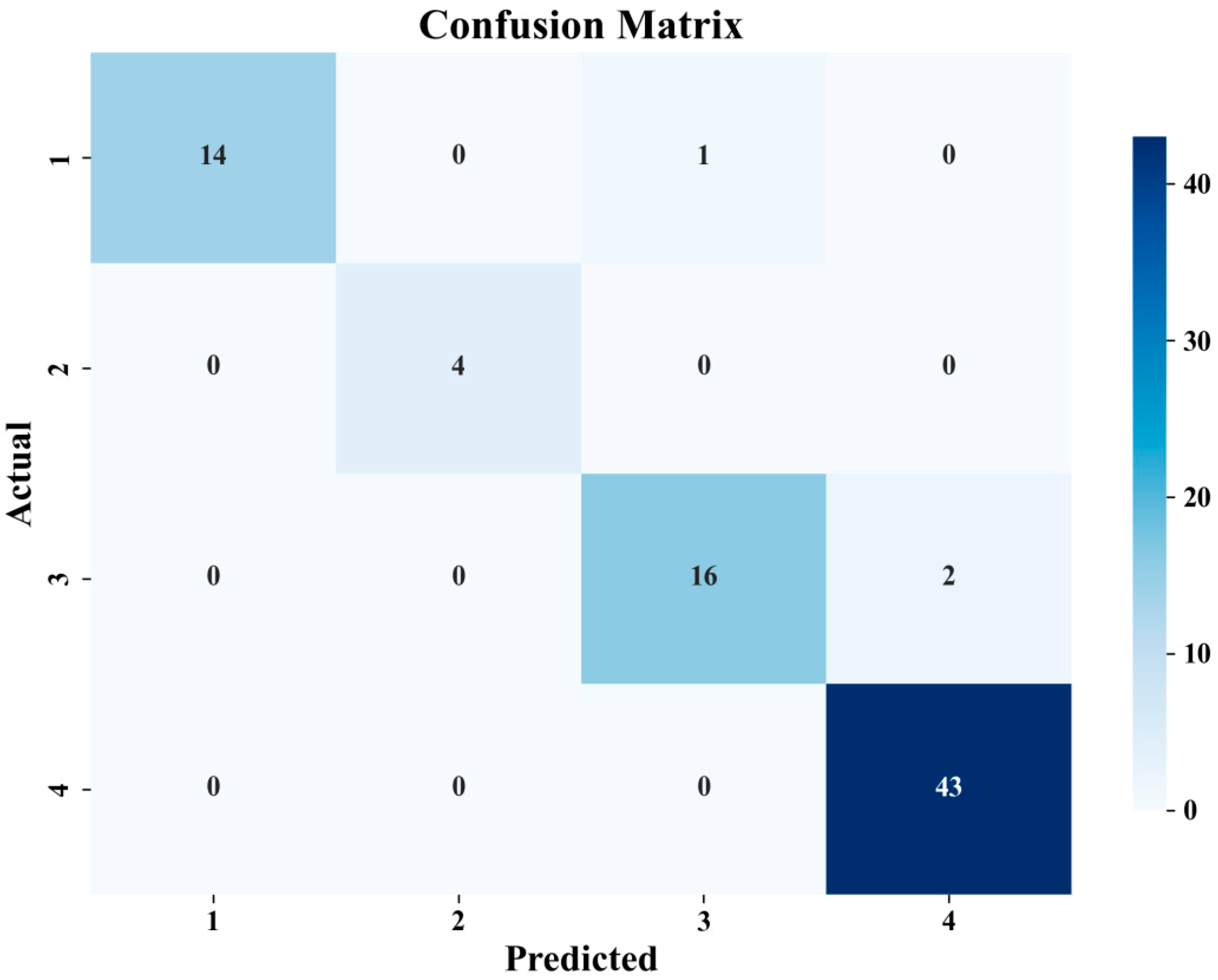
3.7. Fatigue Life Prediction for PLA Specimens
4. Conclusions
- An integrated detection and prediction framework consisting of three major modules: Chroma-YOLO with four core innovations (AttForm attention enhancement network, TriFusion feature fusion architecture, RepFocus self-attention reparameterization module, and BIoU boundary penalty loss function), an HSV defect extraction module, and a random forest fatigue life prediction model.
- Experimental results show that Chroma-YOLO outperforms the baseline YOLOv11n by improving Precision by 9.7% (71.5% to 81.2%), Recall by 12.5% (69.8% to 82.3%), mAP@50 by 6.9% (76.7% to 83.6%), and mAP@50-95 by 7.3% (27.2% to 34.5%).
- The HSV defect detection module increases the contrast between defect regions and the background, significantly improving visibility. The random forest model achieves an accuracy of 96.25% on the test set and 99.09% on the validation set.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PLA | Polylactic Acid |
References
- Yuk, H.; Lu, B.; Lin, S.; Qu, K.; Xu, J.; Luo, J.; Zhao, X. 3D printing of conducting polymers. Nat. Commun. 2020, 11, 1604. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.Q.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Solomon, I.J.; Sevvel, P.; Gunasekaran, J. A review on the various processing parameters in FDM. Mater. Today Proc. 2021, 37, 509–514. [Google Scholar] [CrossRef]
- Li, H.; Liu, B.; Ge, L.; Chen, Y.; Zheng, H.; Fang, D. Mechanical performances of continuous carbon fiber reinforced PLA composites printed in vacuum. Compos. Part B Eng. 2021, 225, 109277. [Google Scholar] [CrossRef]
- Cano-Vicent, A.; Tambuwala, M.M.; Hassan, S.S.; Barh, D.; Aljabali, A.A.A.; Birkett, M.; Arjunan, A.; Serrano-Aroca, Á. Fused deposition modelling: Current status, methodology, applications and future prospects. Addit. Manuf. 2021, 47, 102378. [Google Scholar] [CrossRef]
- Košir, T.; Slavič, J. Manufacturing of single-process 3D-printed piezoelectric sensors with electromagnetic protection using thermoplastic material extrusion. Addit. Manuf. 2023, 73, 103699. [Google Scholar] [CrossRef]
- Jiao, H.; Qu, Z.; Jiao, S.; Gao, Y.; Li, S.; Song, W.-L.; Chen, H.; Zhu, H.; Zhu, R.; Fang, D. A 4D x-ray computer microtomography for high-temperature electrochemistry. Sci. Adv. 2022, 8, eabm5678. [Google Scholar] [CrossRef]
- Sun, X.; Huang, L.; Xiao, B.G.; Zhang, Q.; Li, J.Q.; Ding, Y.H.; Fang, Q.H.; He, W.; Xie, H.M. X-ray computed tomography in metal additive manufacturing: A review on prevention, diagnostic, and prediction of failure. Thin Walled Struct. 2025, 207, 112736. [Google Scholar] [CrossRef]
- Bellens, S.; Vandewalle, P.; Dewulf, W. Deep learning based porosity segmentation in X-ray CT measurements of polymer additive manufacturing parts. Procedia CIRP 2021, 96, 336–341. [Google Scholar] [CrossRef]
- Gobert, C.; Kudzal, A.; Sietins, J.; Mock, C.; Sun, J.; McWilliams, B. Porosity segmentation in X-ray computed tomography scans of metal additively manufactured specimens with machine learning. Addit. Manuf. 2020, 36, 101460. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Fu, K.; Luo, X. Adaptive defect detection for 3-D printed lattice structures based on improved faster R-CNN. IEEE Trans. Instrum. Meas. 2022, 71, 5020509. [Google Scholar] [CrossRef]
- Snow, Z. Correlating in-situ sensor data to defect locations and part quality for additively manufactured parts using machine learning. Addit. Manuf. 2022, 58, 103049. [Google Scholar] [CrossRef]
- Luo, Y.W.; Zhang, B.; Feng, X.; Song, Z.M.; Qi, X.B.; Li, C.P.; Chen, G.F.; Zhang, G.P. Pore-affected fatigue life scattering and prediction of additively manufactured inconel 718: An investigation based on miniature specimen testing and machine learning approach. Mater. Sci. Eng. A 2021, 802, 140693. [Google Scholar] [CrossRef]
- Li, A.; Poudel, A.; Shao, S.; Shamsaei, N.; Liu, J. Nondestructive fatigue life prediction for additively manufactured metal parts through a multimodal transfer learning framework. IISE Trans. 2025, 57, 1344–1359. [Google Scholar] [CrossRef]
- Chauhan, V.K.; Zhou, J.; Lu, P.; Molaei, S.; Clifton, D.A. A brief review of hypernetworks in deep learning. Artif. Intell. Rev. 2024, 57, 250. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Wen, Y.; Fu, K.; Luo, X. Intelligent defect detection method for additive manufactured lattice structures based on a modified YOLOv3 model. J. Nondestruct. Eval. 2022, 41, 3. [Google Scholar] [CrossRef]
- Yu, R.; Wang, R. Learning dynamical systems from data: An introduction to physics-guided deep learning. Proc. Natl. Acad. Sci. USA 2024, 121, e2311808121. [Google Scholar] [CrossRef]
- Zhou, Y. A YOLO-NL object detector for real-time detection. Expert Syst. Appl. 2024, 238, 122256. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 28, 91–99. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. SSD: Single shot MultiBox detector. In Computer Vision—ECCV 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer: Cham, Switzerland, 2016; pp. 21–37. [Google Scholar]
- Wang, D.; Tan, J.; Wang, H.; Kong, L.; Zhang, C.; Pan, D.; Li, T.; Liu, J. SDS-YOLO: An improved vibratory position detection algorithm based on YOLOv11. Measurement 2025, 244, 116518. [Google Scholar] [CrossRef]
- Zhao, C.; Shu, X.; Yan, X.; Zuo, X.; Zhu, F. RDD-YOLO: A modified YOLO for detection of steel surface defects. Measurement 2023, 214, 112776. [Google Scholar] [CrossRef]
- Wu, J.; Huang, C.; Li, Z.; Li, R.; Wang, G.; Zhang, H. An in situ surface defect detection method based on improved you only look once algorithm for wire and arc additive manufacturing. Rapid Prototyp. J. 2023, 29, 910–920. [Google Scholar] [CrossRef]
- Wen, Y.; Cheng, J.; Ren, Y.; Feng, Y.; Zhang, Z.; Zhang, Y. Complex defects detection of 3-D-printed lattice structures: Accuracy and scale improvement in YOLO V7. IEEE Trans. Instrum. Meas. 2024, 73, 5013209. [Google Scholar] [CrossRef]
- Sani, A.R.; Zolfagharian, A.; Kouzani, A.Z. Automated defects detection in extrusion 3D printing using YOLO models. J. Intell. Manuf. 2024, 1–21. [Google Scholar] [CrossRef]
- GB/T 1040.1-2018; Plastics—Determination of Tensile Properties—Part 1: General Principles. National Standard of the People’s Republic of China: Beijing, China, 2018.
- Wang, L.; Liu, Z.; Qiu, T.; Deng, L.; Zhang, Y.; Wang, X. The influence of internal defects on the fatigue behavior of 4032D polylactic acid in fused deposition modeling. J. Mater. Res. Technol. 2025, 36, 548–560. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Hussain, M. YOLO-v1 to YOLO-v8, the rise of YOLO and its complementary nature toward digital manufacturing and industrial defect detection. Machines 2023, 11, 677. [Google Scholar] [CrossRef]
- Khanam, R.; Hussain, M. YOLOv11: An overview of the key architectural enhancements. arXiv 2024, arXiv:2410.17725. [Google Scholar] [CrossRef]
- Zhao, Y.; Lv, W.; Xu, S.; Wei, J.; Wang, G.; Dang, Q.; Liu, Y.; Chen, J. DETRs beat YOLOs on real-time object detection. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 16965–16974. [Google Scholar]
- Yu, W.; Si, C.; Zhou, P.; Luo, M.; Zhou, Y.; Feng, J.; Yan, S.; Wang, X. MetaFormer baselines for vision. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 896–912. [Google Scholar] [CrossRef]
- Xu, S.; Zheng, S.; Xu, W.; Xu, R.; Wang, C.; Zhang, J.; Teng, X.; Li, A.; Guo, L. Hcf-net: Hierarchical context fusion network for infrared small object detection. In Proceedings of the 2024 IEEE International Conference on Multimedia and Expo, Niagara Falls, ON, Canada, 15–19 July 2024; pp. 1–6. [Google Scholar]
- He, W.; Han, K.; Tang, Y.; Wang, C.; Yang, Y.; Guo, T.; Wang, Y. DenseMamba: State space models with dense hidden connection for efficient large language models. arXiv 2024, arXiv:2403.00818. [Google Scholar] [CrossRef]
- Guo, J.; Chen, X.; Tang, Y.; Wang, Y. SLAB: Efficient transsformers with simplified linear attention and progressive re-parameterized batch normalization. arXiv 2024, arXiv:2405.11582. [Google Scholar]
- Dezecot, S.; Maurel, V.; Buffiere, J.-Y.; Szmytka, F.; Koster, A. 3D characterization and modeling of low cycle fatigue damage mechanisms at high temperature in a cast aluminum alloy. Acta Mater. 2017, 123, 24–34. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Iranzad, R.; Liu, X. A review of random forest-based feature selection methods for data science education and applications. Int. J. Data Sci. Anal. 2024, 20, 197–211. [Google Scholar] [CrossRef]
- Serrano-Munoz, I.; Buffiere, J.Y.; Mokso, R.; Verdu, C.; Nadot, Y. Location, location & size: Defects close to surfaces dominate fatigue crack initiation. Sci. Rep. 2017, 7, 45239. [Google Scholar] [CrossRef] [PubMed]





| Model | GFLOPS | Params (M) | Precision (%) | Recall (%) | mAP50 (%) | mAP50-95 (%) |
|---|---|---|---|---|---|---|
| C3k2-EMBC | 6.1 | 2.8 | 67.1 | 76.9 | 69.6 | 24.1 |
| C3k2-iRMB-DRB | 6.2 | 2.4 | 66.5 | 75.7 | 66.0 | 23.1 |
| C3k2-PoolingFormer-CGLU | 5.5 | 2.3 | 70.3 | 74.5 | 76.8 | 25.6 |
| AttForm | 6.0 | 2.3 | 71.1 | 69.9 | 77.2 | 26.7 |
| Model | GFLOPS | Params (M) | Precision (%) | Recall (%) | mAP50 (%) | mAP50-95 (%) |
|---|---|---|---|---|---|---|
| FDPN | 7.6 | 2.7 | 67.4 | 74.5 | 72.4 | 24.8 |
| CGRFPN | 8.6 | 3.3 | 68.1 | 75.3 | 76.3 | 26.0 |
| EMBSFPN | 6.5 | 2.12 | 65.5 | 75.4 | 77.3 | 24.8 |
| TriFusion | 7.4 | 2.7 | 74.7 | 70.1 | 77.8 | 26.8 |
| Model | GFLOPS | Params (M) | Precision (%) | Recall (%) | mAP50 (%) | mAP50-95 (%) |
|---|---|---|---|---|---|---|
| FocalModulation | 7.5 | 2.8 | 70.8 | 76.3 | 74.3 | 27.0 |
| SPPF-LSKA | 7.6 | 2.8 | 70.6 | 75.2 | 74.1 | 27.2 |
| AIFI | 7.5 | 3.15 | 66.2 | 77.8 | 74.1 | 25.1 |
| RepFocus | 6.6 | 3.2 | 73.3 | 74.0 | 78.4 | 30.7 |
| Model | GFLOPS | Params (M) | Precision (%) | Recall (%) | mAP50 (%) | mAP50-95 (%) |
|---|---|---|---|---|---|---|
| Inner shape iou | 7.5 | 3.2 | 81.6 | 63.6 | 77.5 | 31.7 |
| wise_WIoU | 7.5 | 3.1 | 70.3 | 75.8 | 79.8 | 33.7 |
| Inner-Powerful-IoU | 7.5 | 3.2 | 81.8 | 70.7 | 76.1 | 26.2 |
| BIoU | 7.5 | 3.2 | 73.1 | 82.2 | 83.6 | 34.2 |
| Model | GFLOPS | Params (M) | Precision (%) | Recall (%) | mAP50 (%) | mAP50-95 (%) |
|---|---|---|---|---|---|---|
| YOLOv11n | 2.6 | 6.3 | 71.5 | 69.8 | 76.7 | 27.2 |
| YOLOv11n-AttForm | 6.0 | 2.3 | 71.1 | 69.9 | 77.2 | 26.7 |
| YOLOv11n-Trifusion | 7.4 | 2.7 | 74.7 | 70.1 | 77.8 | 26.8 |
| YOLOv11n-RepFocus | 6.6 | 3.2 | 73.3 | 74.0 | 78.4 | 30.7 |
| YOLOv11n-AttForm-Trifusion | 7.2 | 2.5 | 75.7 | 73.1 | 81.1 | 26.4 |
| YOLOv11n-AttForm-RepFocus | 6.3 | 2.9 | 80.8 | 73.1 | 82.5 | 34.2 |
| YOLOv11n-TriFusion-RepFocus | 7.7 | 3.3 | 80.1 | 68.9 | 80.4 | 31.0 |
| YOLOv11n-AttForm-Trifusion-RepFocus | 7.5 | 3.1 | 75.3 | 79.6 | 82.9 | 34.1 |
| Chroma-YOLO | 7.5 | 3.1 | 81.2 | 82.3 | 83.6 | 34.5 |
| Model | GFLOPS | Params (M) | Precision (%) | Recall (%) | mAP50 (%) | mAP50-95 (%) |
|---|---|---|---|---|---|---|
| Yolov5n | 7.1 | 2.5 | 60.8 | 75.1 | 71 | 26.7 |
| yolov5s | 23.8 | 9.1 | 64.4 | 76.0 | 76.7 | 27.7 |
| Yolov8n | 8.1 | 3.0 | 64.4 | 73.1 | 73.8 | 25.3 |
| Yolov8s | 28.4 | 11.1 | 61.7 | 72.2 | 74.5 | 26.3 |
| Yolov9s | 26.7 | 7.0 | 60.8 | 65.4 | 75.6 | 24.2 |
| Yolov9t | 7.6 | 1.9 | 67.9 | 75.1 | 71.2 | 23.3 |
| Yolov10n | 6.5 | 2.3 | 54.4 | 68.6 | 62.9 | 20.2 |
| Yolov10s | 21.4 | 7.2 | 63.6 | 65.4 | 70.4 | 23.9 |
| Yolov11n | 6.3 | 2.6 | 71.5 | 69.8 | 76.7 | 27.2 |
| Yolov11s | 21.3 | 9.5 | 79.2 | 74.9 | 82.8 | 32.6 |
| Faster_RCNN | 170.0 | 41.75 | 72.5 | 80.2 | 81.9 | 24.5 |
| Mask_RCNN | 221.0 | 43.97 | 80.9 | 79.0 | 83.5 | 30.2 |
| Centernet | 162.0 | 32.29 | 73.8 | 84.6 | 83.3 | 31.6 |
| RetinaNet-R50-FPN | 8.0 | 4.88 | 81.1 | 71.3 | 80.6 | 23.6 |
| RTMDet-Tiny | 8.03 | 4.873 | 80.2 | 70.1 | 79.6 | 23.1 |
| RTDETR-R18 | 56.9 | 19.9 | 80.3 | 76.9 | 82.9 | 30.7 |
| Chroma-YOLO | 7.5 | 3.1 | 81.2 | 82.3 | 83.6 | 34.5 |
| Categories | N | S (pixel) | Smax (pixel) | Training Set | Validation Set | Test Set |
|---|---|---|---|---|---|---|
| P1 | N > 20 | S > 300 | Smax ≥ 150 | 45 | 4 | 15 |
| P2 | 10 < N < 20 | 200 < S < 300 | Smax < 150 | 17 | 0 | 4 |
| P3 | 10 < N < 20 | 100 < S < 200 | Smax < 150 | 48 | 32 | 18 |
| P4 | 0 < N < 10 | 0 < S < 100 | Smax < 150 | 208 | 74 | 43 |
| n_estimators | max_depth | min_samples_split | min_samples_leaf | |
|---|---|---|---|---|
| 1 | 22 | NONE | 1 | 1 |
| 2 | 24 | 10 | 2 | 2 |
| 3 | 26 | 20 | 3 | 3 |
| 4 | 28 | 30 | 4 | 4 |
| BEST | 26 | NONE | 1 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Liu, Z.; Lv, T.; Wang, X.; Qiu, T. Enhanced Chroma-YOLO Framework for Effective Defect Detection and Fatigue Life Prediction in 3D-Printed Polylactic Acid. Materials 2025, 18, 5159. https://doi.org/10.3390/ma18225159
Wang L, Liu Z, Lv T, Wang X, Qiu T. Enhanced Chroma-YOLO Framework for Effective Defect Detection and Fatigue Life Prediction in 3D-Printed Polylactic Acid. Materials. 2025; 18(22):5159. https://doi.org/10.3390/ma18225159
Chicago/Turabian StyleWang, Liang, Zhibing Liu, Ting Lv, Xibin Wang, and Tianyang Qiu. 2025. "Enhanced Chroma-YOLO Framework for Effective Defect Detection and Fatigue Life Prediction in 3D-Printed Polylactic Acid" Materials 18, no. 22: 5159. https://doi.org/10.3390/ma18225159
APA StyleWang, L., Liu, Z., Lv, T., Wang, X., & Qiu, T. (2025). Enhanced Chroma-YOLO Framework for Effective Defect Detection and Fatigue Life Prediction in 3D-Printed Polylactic Acid. Materials, 18(22), 5159. https://doi.org/10.3390/ma18225159






