Shear Performance Degradation of Fiber-Reinforced Recycled Aggregate Concrete Beams Under Salt Freeze–Thaw Cycles
Abstract
1. Introduction
2. Experimental Procedure
2.1. Materials and Mixture Proportions
2.1.1. Materials
2.1.2. Mixture Proportions
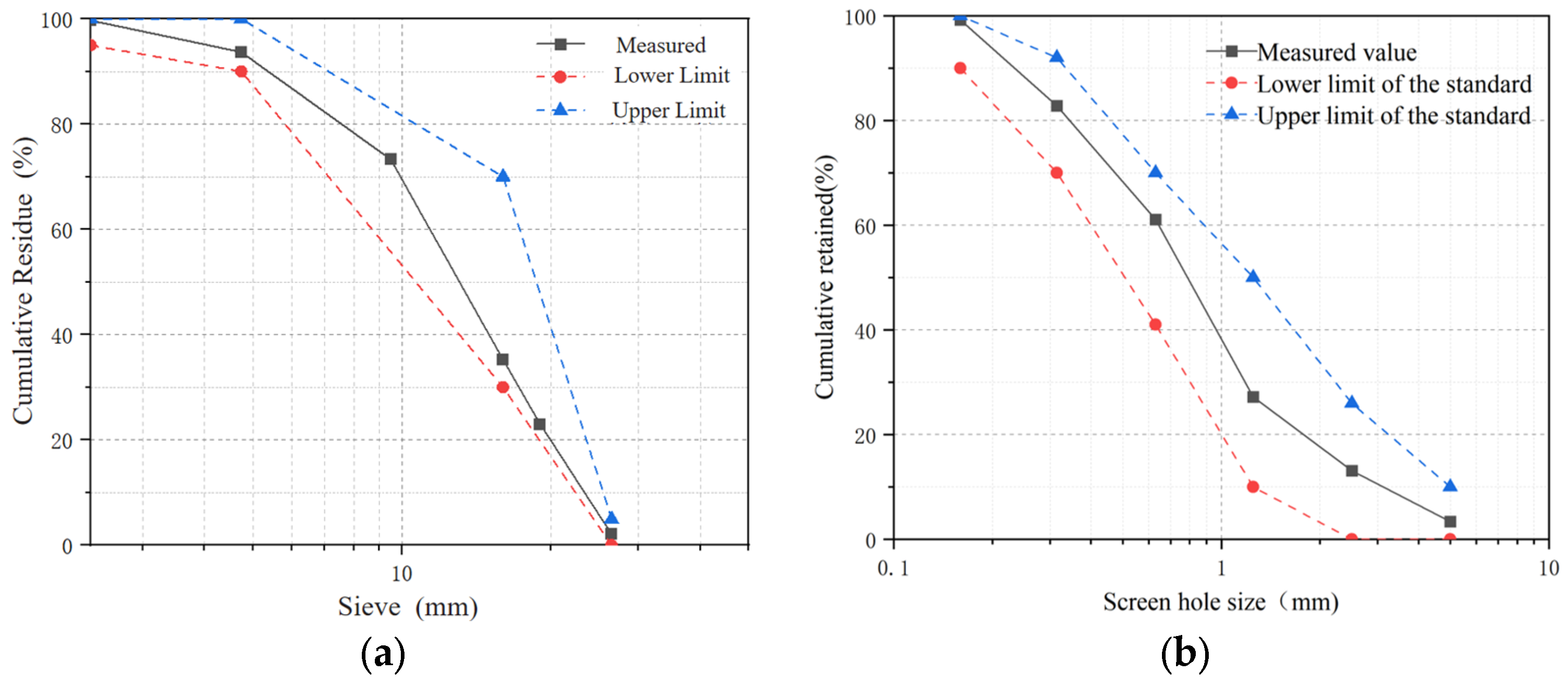
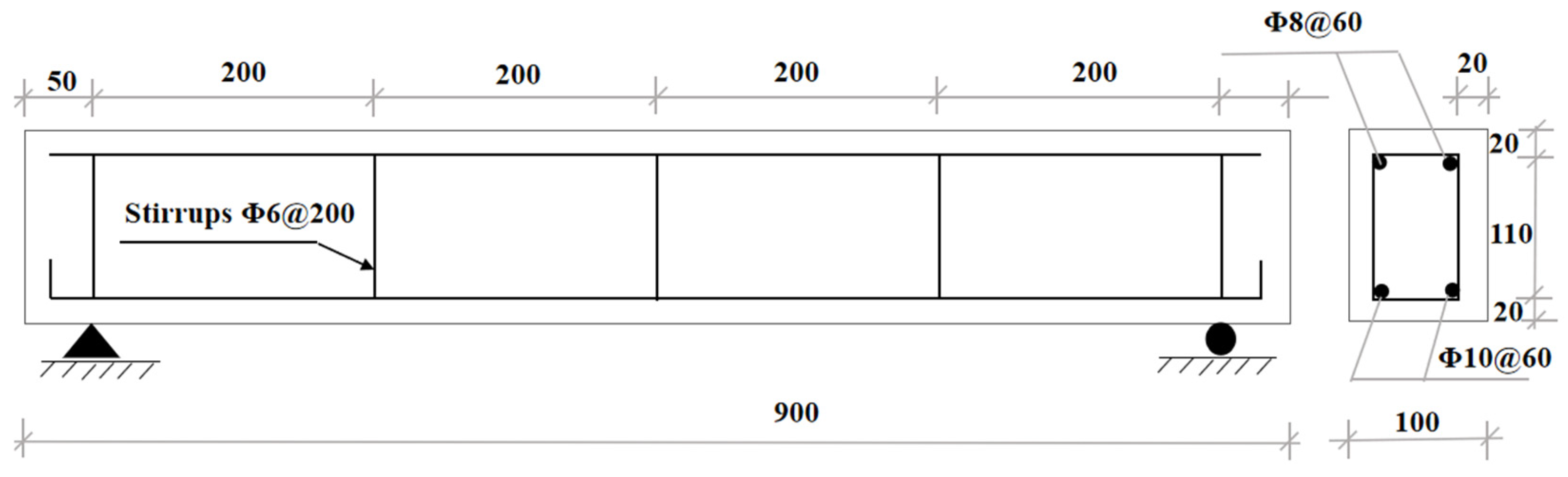
2.2. Specimen Design and Fabrication
2.2.1. Specimen Parameters
2.2.2. Specimen Fabrication
2.3. Freeze–Thaw Cycle Testing
2.3.1. Freeze–Thaw Media
2.3.2. Freeze–Thaw Treatment
2.4. Static Loading Test Method
3. Test Results and Discussion
3.1. Deterioration of Material Properties
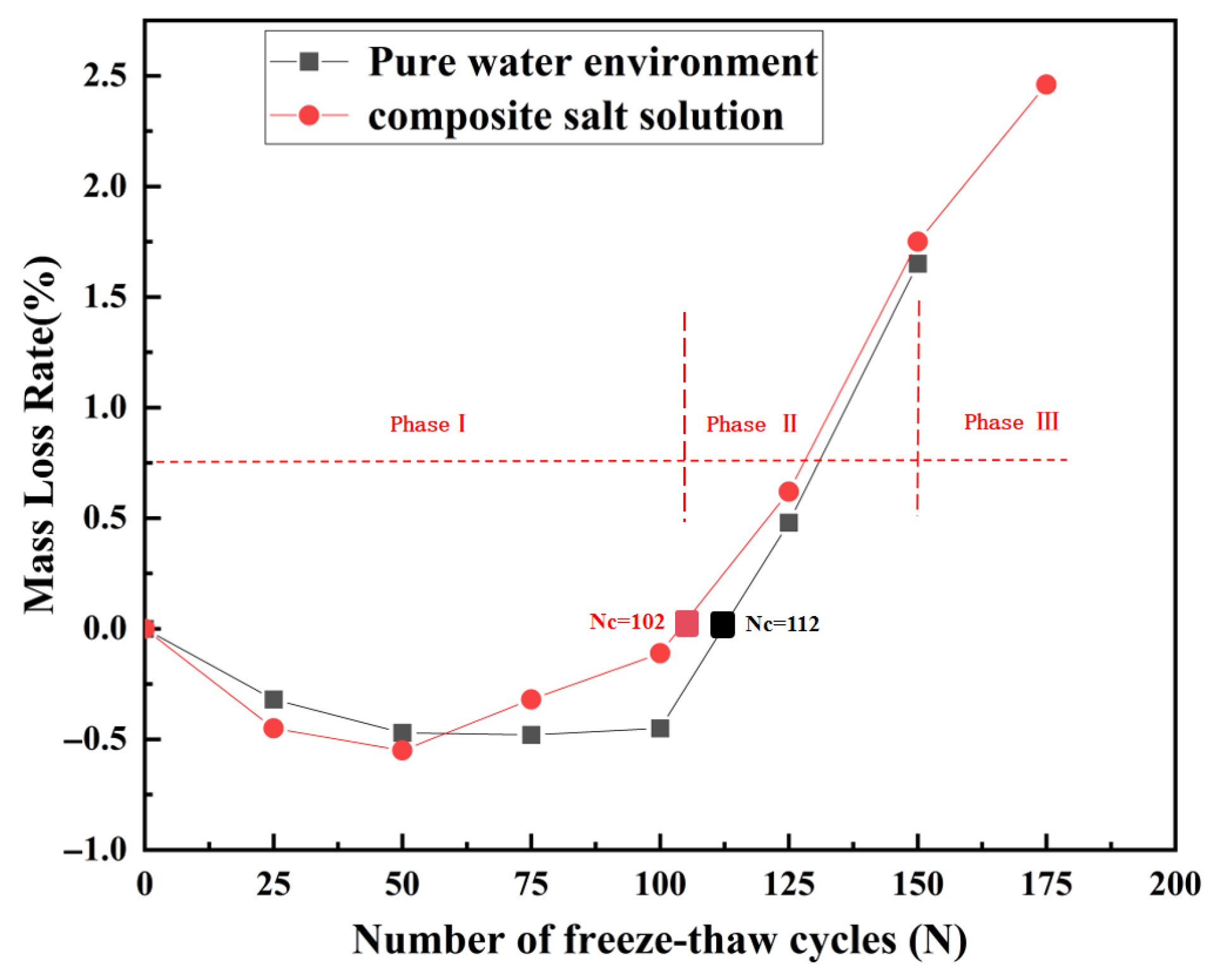
3.1.1. Mass Loss
3.1.2. Relative Dynamic Elastic Modulus (RDEM)
3.1.3. Compressive Strength
- (1)
- Phase I: Ion migration–frost heave dominant stage (0–75 cycles): Strength degradation in this stage is primarily dominated by frost heave effects induced by ion migration, with more severe damage observed in compound salt environments than in freshwater. After 75 cycles, the strength loss rate in compound salt reaches 6.95%, exceeding the freshwater environment by 1.48 percentage points (5.47%). This discrepancy arises because salt ion enrichment accelerates microcrack propagation in ITZ, expediting mechanical performance deterioration. Although sulfate ions temporarily mitigate pure physical frost heave, the combined effects of chemical erosion and synergistic ion interactions result in greater damage in compound salt environments compared to freshwater FT [46]. The synergistic interaction between ion migration and frost heave constitutes the primary degradation mechanism in this stage.
- (2)
- Phase II: Chemical corrosion dominant stage (75–150 cycles): As cycles progress, chemical erosion gradually becomes the dominant factor in strength degradation, with accelerated strength loss observed in compound salt environments. After 100 and 150 cycles, strength loss rates reach 14.95% and 23.83%, respectively. Notably, at 125 cycles, the strength loss rate (13.48%) is significantly lower than the 51.6% reported by Peng et al. [45], indicating substantially improved degradation resistance. While chemical erosion dominates this stage, the inhibitory effect of the hybrid modification system continues to delay damage progression.
- (3)
- Phase III: Structural failure stage (150–175 cycles): This stage witnesses a rapid escalation of structural damage culminating in failure, with strength loss rates exhibiting leapfrog growth. After 175 cycles, the strength loss rate surges to 34.18%, primarily due to preferential deterioration of initial defects in the ITZ and sustained degradation of bond performance, ultimately triggering macroscopic structural collapse [47].
3.2. Compressive Strength Degradation Behavior of Recycled Aggregate Concrete
3.3. Shear Behavior of Test Beams
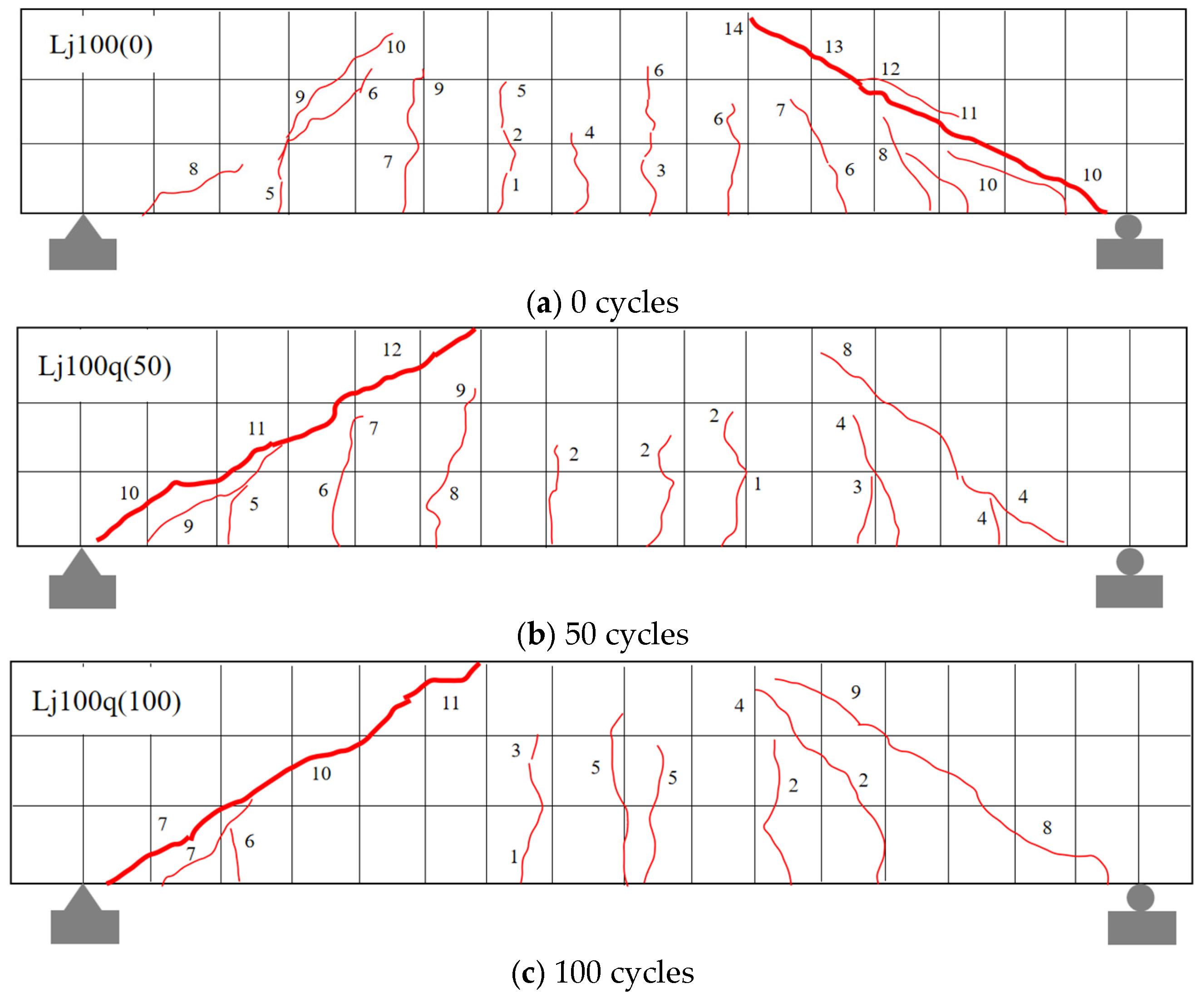
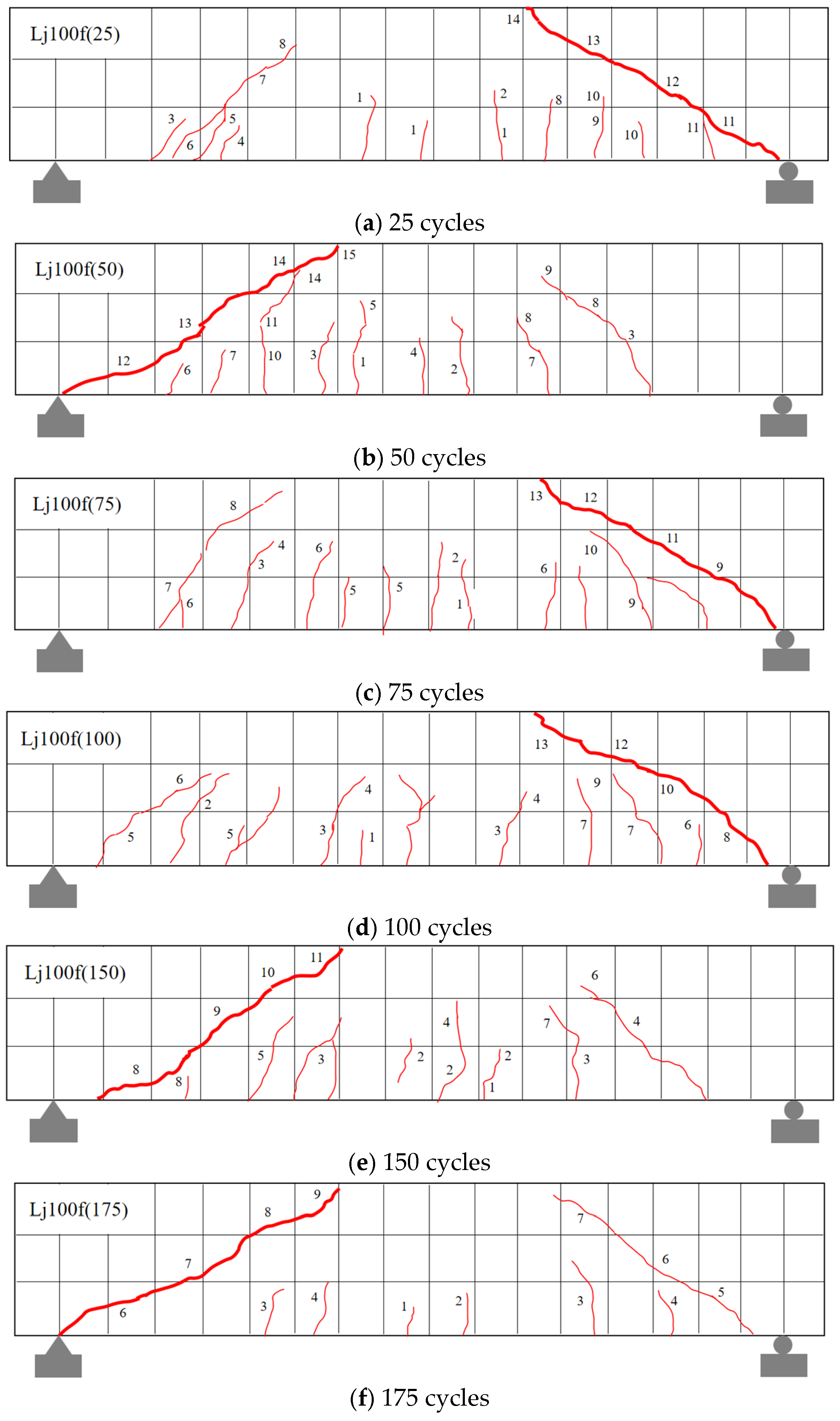
3.3.1. Crack Propagation and Failure Patterns
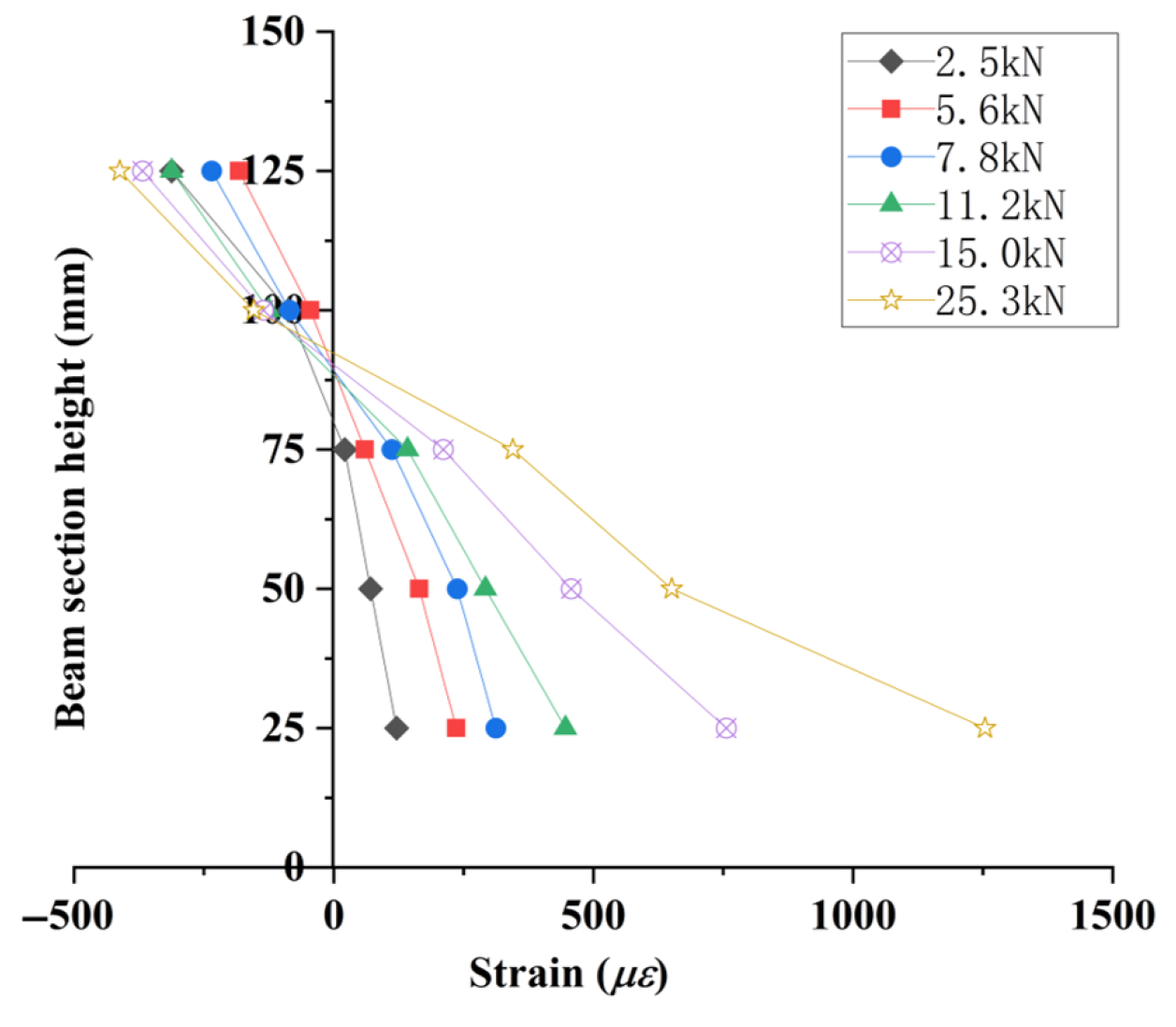
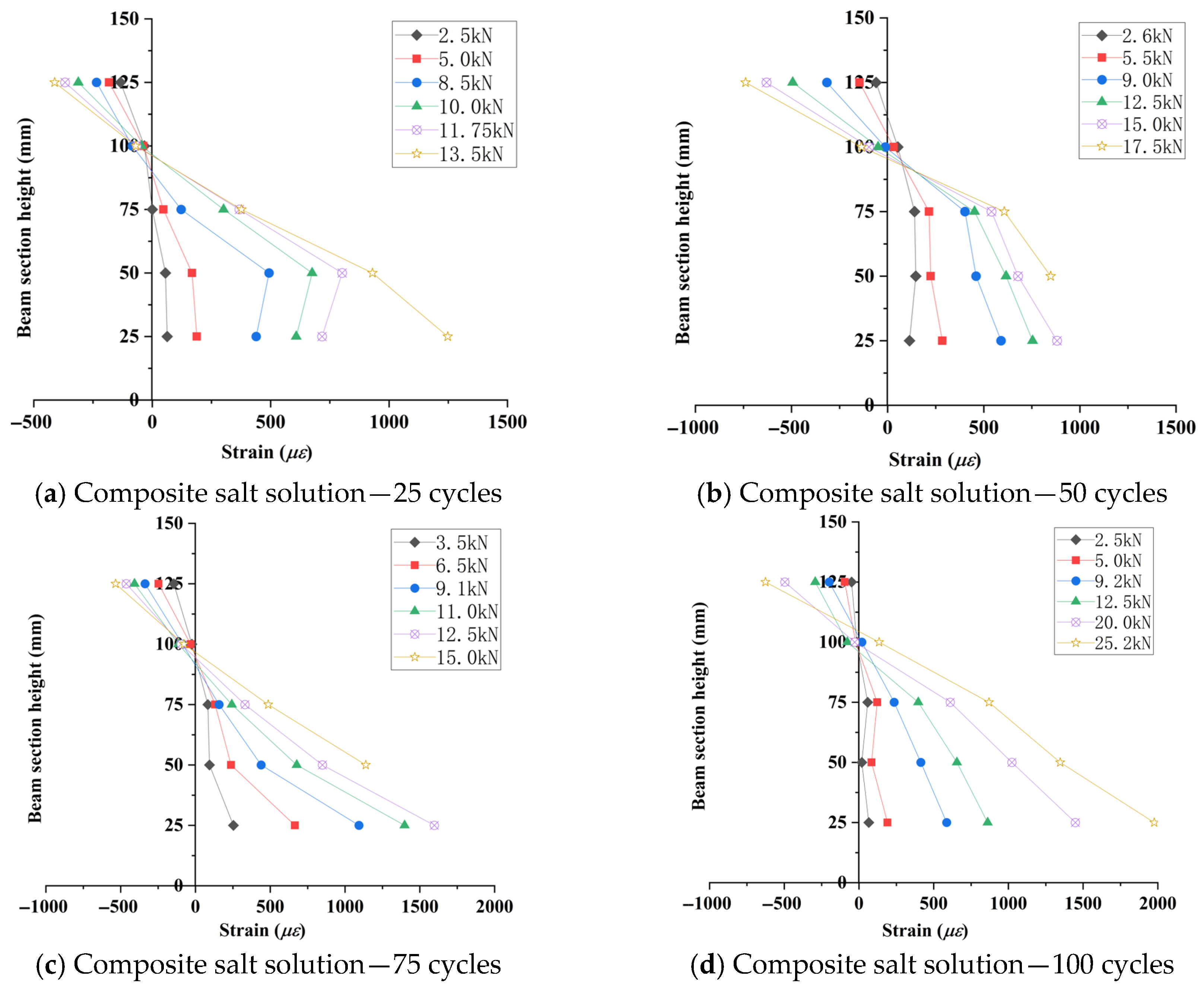
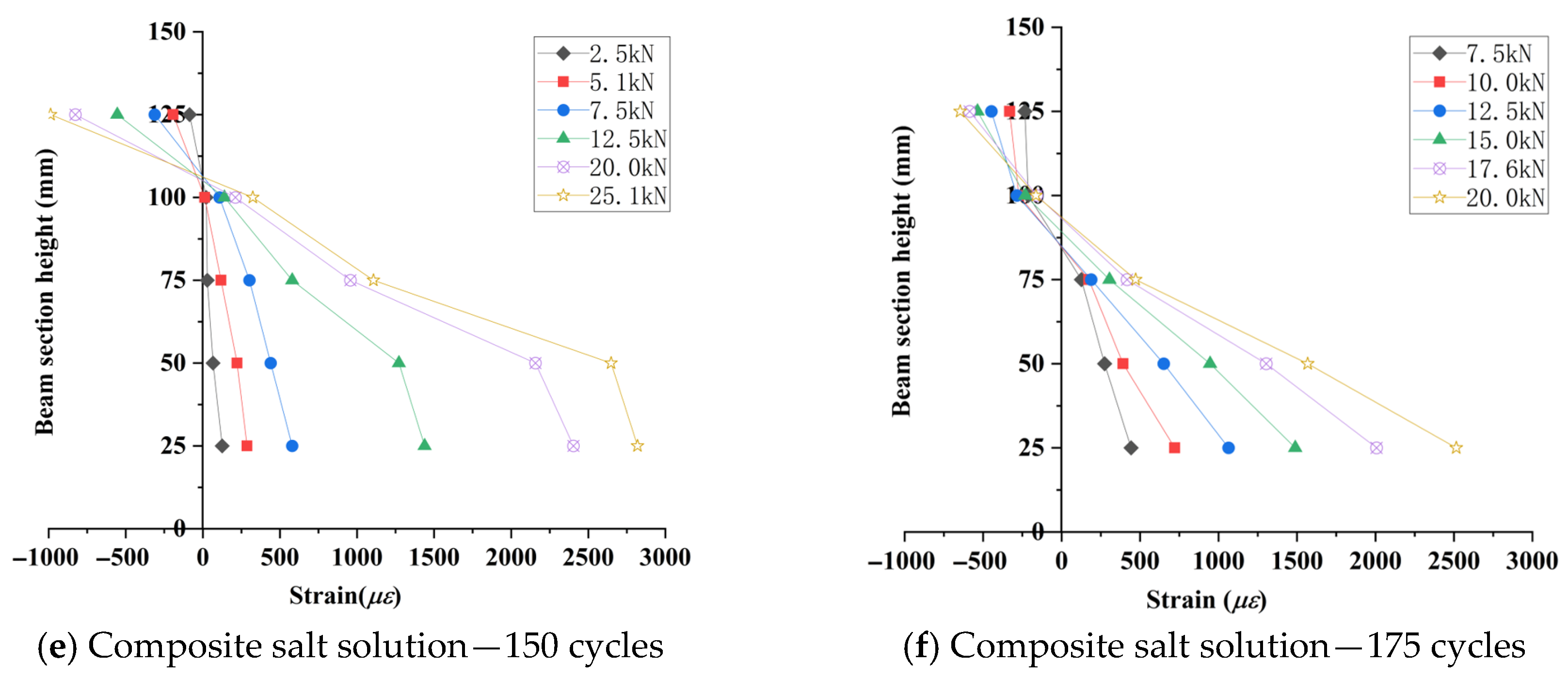
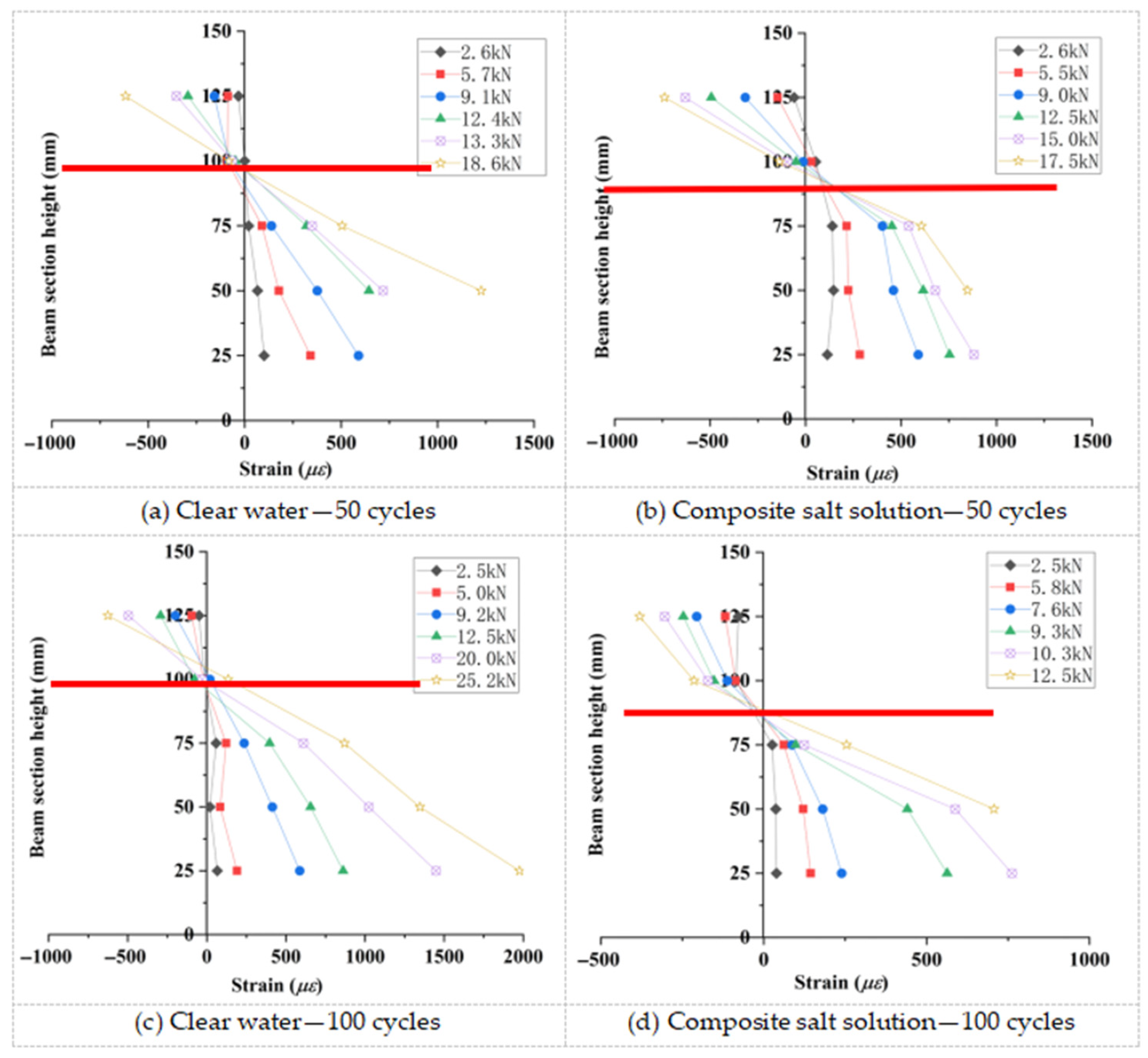
3.3.2. Concrete Strain Distribution in Test Beams
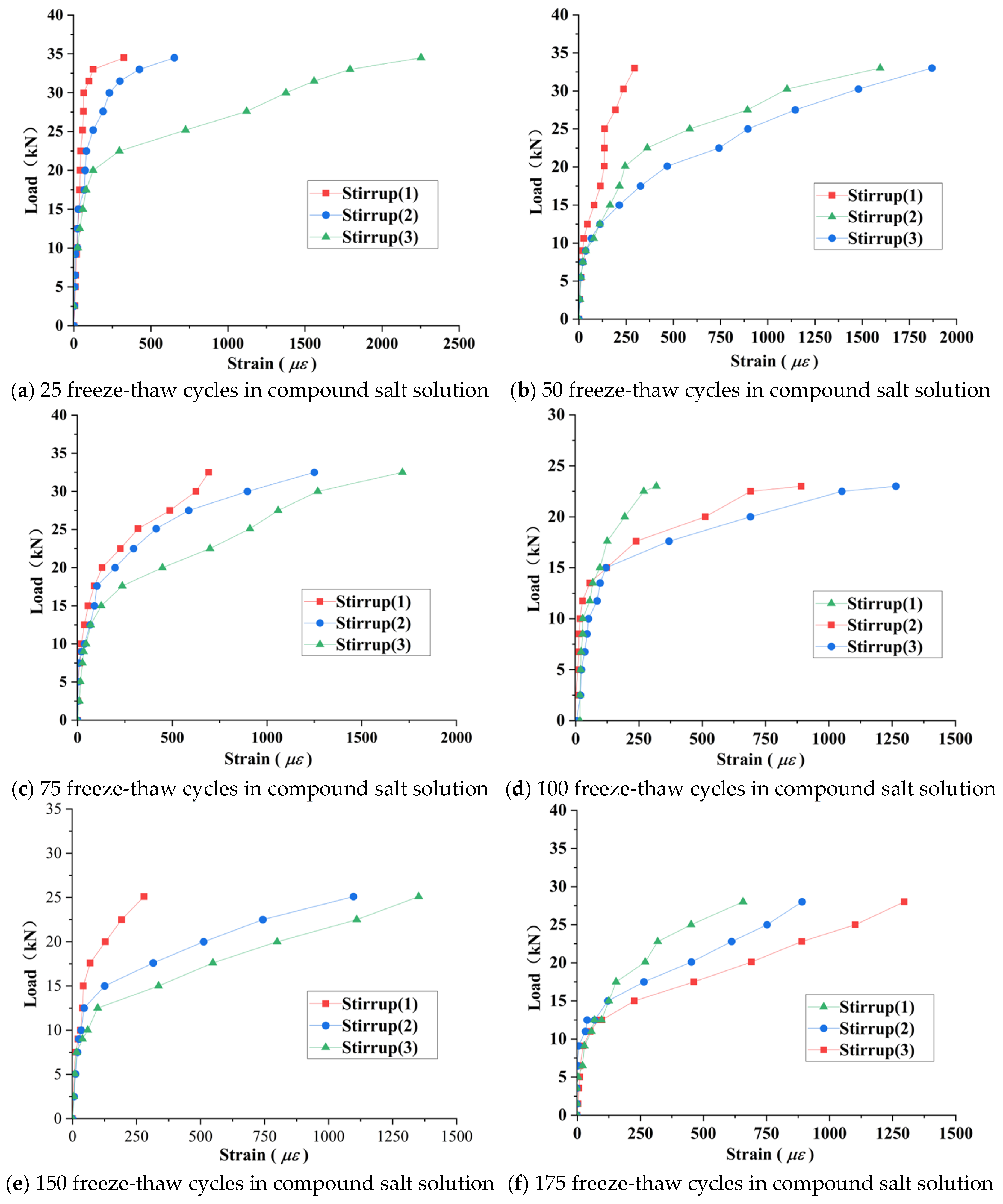
3.3.3. Load–Stirrup Strain Analysis of Test Beams
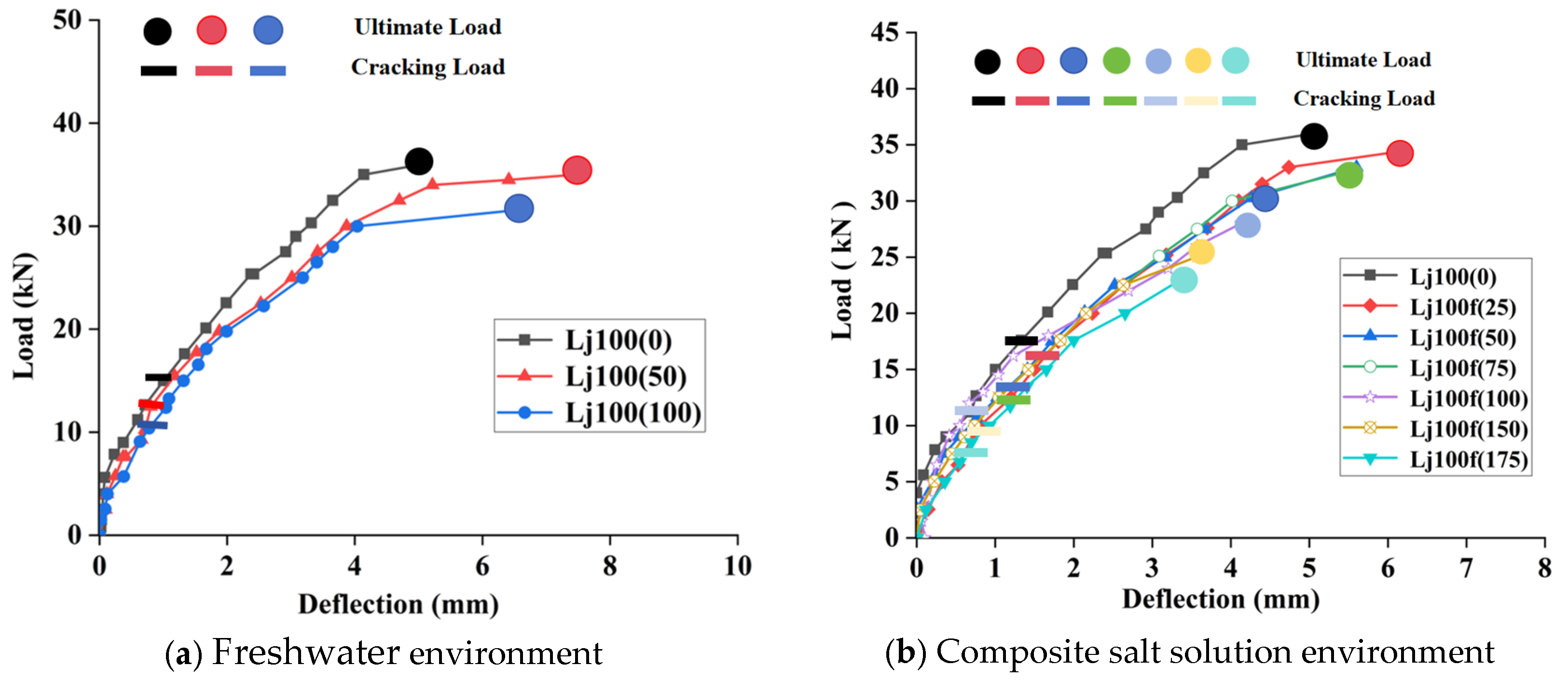
3.3.4. Load–Deflection Response of the Test Beams
3.4. Shear Capacity Prediction Model for Recycled Aggregate Concrete Beams
3.4.1. Necessity of Modifying the Shear Capacity Model for Post-Freeze–Thaw RAC Beams
3.4.2. Modification of Shear Capacity Prediction Model for Post-Freeze–Thaw RAC Beams
3.4.3. Validation of the Modified Models
3.4.4. Validation of Model Applicability
4. Conclusions
- (1)
- In both freshwater and composite salt solution environments, the crack patterns and distribution characteristics of freeze–thaw-damaged PF-RAC beams demonstrated consistent behavior: initial microcracks consistently initiated within the ITZ under tension, with principal cracks propagating along approximately 45° shear paths. The crack bridging effect of PPF effectively restricted disorderly crack propagation, thereby mitigating environmental impacts on crack development. This finding aligns with the conclusions of Yap et al. (2013) [64] regarding the role of fibers in maintaining structural integrity under harsh conditions, confirming the universal applicability of fiber-mediated crack control.
- (2)
- Compressive strength continuously deteriorated with increasing FT cycles in both environments, yet the degradation rate was significantly higher in the composite salt solution. For instance, after 125 cycles, the strength loss reached 22.11% in salt environment versus 13.48% in freshwater; after 175 cycles, the loss increased to 34.18%. This accelerated deterioration is attributed to the synergistic effect of salt crystallization pressure and chemical erosion, as also described by Valenza and Scherer (2007) [65]. Importantly, the incorporation of PPF substantially alleviated strength loss. After 125 cycles, PF-RAC exhibited a loss of only 13.48%, far lower than the 51.6% reported by Peng et al. (2022) [45] for plain RAC under similar conditions, quantitatively confirming that fibers enhance frost resistance through matrix toughening and microcrack restraint.
- (3)
- Both cracking load and shear capacity decreased with freeze–thaw cycles, with more severe degradation in the composite salt environment. After 100 cycles, the shear capacity reduction was 22.22% in salt solution, about 1.70 times that in freshwater. After 175 cycles, the cracking load dropped from 17.6 kN to 7.6 kN in salt solution, compared to 12.2 kN after only 100 cycles in freshwater. These results confirm that Cl− and SO42− ions act synergistically to accelerate stirrup corrosion and concrete matrix damage, significantly impairing residual load capacity. However, it should be noted that the present study employed a fixed PPF content, length, and diameter. The potential existence of a fiber effectiveness threshold under combined salt freeze–thaw conditions, as well as the limitations of fiber reinforcement, remain unexamined and warrant further investigation.
- (4)
- The modified shear capacity model incorporating the comprehensive influence coefficient kv(n) demonstrated high predictive accuracy. In freshwater, errors were below 1%; in composite salt environment, errors remained under 8%. When validated using external data from Su et al., errors stayed below 9%, confirming the model’s broad applicability. This model offers a practical tool for quantifying the coupled effect of freeze–thaw and salt erosion on the shear behavior of fiber-reinforced recycled aggregate concrete members, addressing a gap in current design guidelines.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RCA | Recycled coarse aggregate |
| RAC | Recycled aggregate concrete |
| NAC | Natural aggregate concrete |
| ITZ | Interfacial transition zone |
| FT | Freeze–thaw |
| PPF | Polypropylene fibers |
| FA | Fly ash |
| RDEM | Relative dynamic elastic modulus |
| AFt | Ettringite |
| PF-RAC | Polypropylene fiber-reinforced recycled aggregate concrete |
| C-S-H | Calcium silicate hydrate |
| LVDT | Linear variable differential transformer |
| UNEP | The United Nations Environment Programme |
| ACI | American Concrete Institute |
| DG/TJ | Shanghai Local Technical Specification |
| GB | Guobiao (Chinese National Standard) |
| XJJ | Xinjiang Local Standard |
| RH | Relative humidity |
References
- United Nations Environment Programme (UNEP); Global Alliance for Buildings and Construction (Global ABC). Global Status Report for Buildings and Construction 2023; United Nations Environment Programme: Nairobi, Kenya, 2024. [Google Scholar]
- Hossain, M.U.; Poon, C.S.; Lo, I.M.C.; Cheng, J.C.P. Comparative environmental evaluation of aggregate production from recycled waste materials and virgin sources by LCA. Resour. Conserv. Recycl. 2016, 109, 67–77. [Google Scholar] [CrossRef]
- Duan, Z.; Deng, Q.; Xiao, J.; Zhang, H.; Nasr, A.; Li, L.; Zou, S. Early-stage water-absorbing behavior and mechanism of recycled coarse aggregate. Constr. Build. Mater. 2023, 394, 132138. [Google Scholar] [CrossRef]
- Deng, Q.; Zhang, R.; Liu, C.; Duan, Z.; Xiao, J. Influence of fiber properties on abrasion resistance of recycled aggregate concrete: Length, volume fraction, and types of fibers. Constr. Build. Mater. 2023, 362, 129750. [Google Scholar] [CrossRef]
- Tabsh, S.W.; Abdelfatah, A.S. Influence of recycled concrete aggregates on strength properties of concrete. Constr. Build. Mater. 2009, 23, 1163–1167. [Google Scholar] [CrossRef]
- Şahin, Y.; Akkaya, Y.; Taşdemir, M.A. Effects of freezing conditions on the frost resistance and microstructure of concrete. Constr. Build. Mater. 2021, 270, 121458. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, S.; Wang, Z.; Li, X.; Gong, F.; Nagai, K.; Deng, J.; Ueda, T.; Hu, W. Experimental investigation on electrical response and mechanical performance of cementitious materials at low temperatures. Cem. Concr. Compos. 2023, 143, 105264. [Google Scholar] [CrossRef]
- Zhao, Y.; Lian, S.; Bi, J.; Wang, C.; Zheng, K. Study on Freezing-Thawing damage mechanism and evolution model of concrete. Theor. Appl. Fract. Mech. 2022, 121, 103439. [Google Scholar] [CrossRef]
- Su, T.; Wu, J.; Yang, G.; Jing, X.; Mueller, A. Shear behavior of recycled coarse aggregate concrete beams after freezing-and-thawing cycles. ACI Struct. J. 2019, 116, 67–76. [Google Scholar] [CrossRef]
- Jin, Z.Q.; Sun, W.; Zhang, Y.S.; Jiang, J.Y. Damage of concrete in sulfate and chloride solution. J. Chin. Ceram. Soc. 2006, 34, 630–635. (In Chinese) [Google Scholar] [CrossRef]
- Zou, D.J.; Qin, S.S.; Liu, T.J.; Gong, H.; Zhou, A.O.; Pei, H.F. Chloride Ion Diffusion in Cement Mortar in Multi-Ion Solutions with Various Ions. J. Chin. Ceram. Soc. 2020, 48, 1817–1823. (In Chinese) [Google Scholar] [CrossRef]
- Etxeberria, M.; Marí, A.R.; Vázquez, E. Recycled aggregate concrete as structural material. Mater. Struct. 2007, 40, 529–541. [Google Scholar] [CrossRef]
- Pradhan, S.; Kumar, S.; Barai, S.V. Shear performance of recycled aggregate concrete beams: An insight for design aspects. Constr. Build. Mater. 2018, 178, 593–611. [Google Scholar] [CrossRef]
- Fathifazl, G.; Razaqpur, A.; Isgor, O.B.; Abbas, A.; Fournier, B.; Foo, S. Shear capacity evaluation of steel reinforced recycled concrete (RRC) beams. Eng. Struct. 2011, 33, 1025–1033. [Google Scholar] [CrossRef]
- Cao, D.F.; Zhou, M.; Ge, W.J.; Yuan, S.F. Study on Shear Behavior of Reinforced Concrete Beams after Freeze-Thaw Cycles. Ind. Constr. 2015, 45, 32–37. [Google Scholar] [CrossRef]
- Duan, A.; Li, Z.; Zhang, W.; Jin, W.-L. Flexural Behaviour of Reinforced Concrete Beams under Freeze-Thaw Cycles and Sustained Load. Struct. Infrastruct. Eng. 2017, 13, 1350–1358. [Google Scholar] [CrossRef]
- Wei, Y. The Research of Calculation Model of Concrete Beam and Post-Performance Prediction of Concrete Under Freeze-Thaw Environment. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2010. (In Chinese). [Google Scholar]
- Berto, L.; Saetta, A.; Talledo, D. Constitutive Model of Concrete Damaged by Freeze–Thaw Action for Evaluation of Structural Performance of RC Elements. Constr. Build. Mater. 2015, 98, 559–569. [Google Scholar] [CrossRef]
- Zhang, W. Research on Shear Behavior of Reinforced Concrete Beams with Recycled Coarse Aggregate. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2008. (In Chinese). [Google Scholar]
- Wang, L.D.; Zhou, Z.Y.; Ye, L.F.; Ye, S. Experimental Study on the Effect of Composite Powder and PolypropyleneFiber on the Frost Resistance of Recycled Concrete. J. Univ. Shanghai Sci. Technol. 2017, 39, 301–306. (In Chinese) [Google Scholar] [CrossRef]
- Setkit, M.; Leelatanon, S.; Imjai, T.; Garcia, R.; Limkatanyu, S. Prediction of Shear Strength of Reinforced Recycled Aggregate Concrete Beams without Stirrups. Buildings 2021, 11, 402. [Google Scholar] [CrossRef]
- Rahal, K.N.; Alrefaei, Y.T. Shear strength of longitudinally reinforced recycled aggregate concrete beams. Eng. Struct. 2017, 145, 273–282. [Google Scholar] [CrossRef]
- Hossain, F.M.Z.; Pal, A.; Ahmed, K.S.; Bediwy, A.; Alam, M.S. Shear behavior of polypropylene fiber-reinforced concrete beams containing recycled aggregate and crumb rubber. J. Clean. Prod. 2023, 412, 137370. [Google Scholar] [CrossRef]
- Gao, S.; Ban, S.; Guo, J.; Zou, C.X.; Cong, Y.Y. Effect of Silica Fume on Interfacial Transition Zone of Recycled Concrete. Mater. Rep. 2023, 37, 97–103. (In Chinese) [Google Scholar]
- Yuan, S.; Li, K.; Luo, J.; Yin, W.; Chen, P.; Dong, J.; Liang, W.; Zhu, Z.; Tang, Z. Research on the frost resistance performance of fully recycled pervious concrete reinforced with fly ash and basalt fiber. J. Build. Eng. 2024, 86, 108792. [Google Scholar] [CrossRef]
- Ghoneim, M.; Yehia, A.; Yehia, S.; Abuzaid, W. Shear strength of fiber reinforced recycled aggregate concrete. Materials 2020, 13, 4183. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.-G.; Liu, W.; Yan, Z.-H.; Gu, Z.-C. Effect of ultra-low temperature freeze-thaw cycle on the flexural performance of hybrid fiber RC beams subjected to monotonic and repeated loading. Structures 2024, 59, 105751. [Google Scholar] [CrossRef]
- GB 175-2023; Common Portland Cement. China Architecture & Building Press: Beijing, China, 2023. (In Chinese)
- GB 50119-2013; Code for Concrete Admixture Application. China Architecture & Building Press: Beijing, China, 2014. (In Chinese)
- XJJ 076-2017; Technical Specification for Application of Recycled Aggregate Concrete. Construction Standard Service Center of the Xinjiang Uygur Autonomous Region: Urumqi, China, 2017. (In Chinese)
- Huang, W.; Guo, Y.T.; Ge, P.; Quan, L.W.; Dong, K.L. Mixture ratio optimization of polypropylene fiber recycled brick aggregate concrete based on response surface methodology. J. Cent. South Univ. Sci. Technol. 2022, 53, 2709–2718. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Z.-X.; Yao, Z.-Q.; Liang, H.E.; Wu, H.-H.; Liu, Z.-M. Time-varying Damage of Macro-and-micro Properties of Fly Ash Concrete in Corrosive Media. J. Yangtze River Sci. Res. Inst. 2021, 38, 133–138. (In Chinese) [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2015. (In Chinese)
- GB/T 25177-2010; Recycled Coarse Aggregate for Concrete. Standardization Administration of China: Beijing, China, 2010.
- JGJ 55-2011; Specification for Mix Proportion Design of Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2011. (In Chinese)
- Wu, J.; Jing, X.; Wang, Z. Uni-axial compressive stress-strain relation of recycled coarse aggregate concrete after freezing and thawing cycles. Constr. Build. Mater. 2017, 134, 210–219. [Google Scholar] [CrossRef]
- Na, S.S. The experimental study on coefficient of collapsibility and salt-frost heaving character of strong chlorine saline soil in Lop Nur. Master’s Thesis, Xinjiang Agricultural University, Urumqi, China, 2012. [Google Scholar]
- GB/T 50082-2009; Standard for Test Methods of Long-term Performance and Durability of Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2009; ISBN 978-7-112-10943-8.
- Tian, W.; Han, N. Evaluation of damage in concrete suffered freeze-thaw cycles by CT technique. J. Adv. Concr. Technol. 2016, 14, 679–690. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Guan, Z.; Ding, Q. Elastic modulus damage model of cement mortar under salt freezing circumstance based on X-ray CT scanning. Constr. Build. Mater. 2018, 191, 1201–1209. [Google Scholar] [CrossRef]
- Xiao, Q.H.; Qi, X.; Li, L.L.; Qiu, J.S.; Liu, S.L. Research on composite damage of recycled concrete by the combined action of freeze-thaw and sulfate attack. Concrete 2024, 8, 32–37. [Google Scholar] [CrossRef]
- Cao, Y.Z.; Guo, L.P.; Chen, B.; Wu, J.D. Thermodynamic modelling and experimental investigation on chloride binding in cement exposed to chloride and chloride-sulfate solution. Constr. Build. Mater. 2020, 246, 118398. [Google Scholar] [CrossRef]
- Guan, X.M.; Zhang, G.L.; He, F.Q.; Qiu, J. Study on the formation and stability of Friedel’s salt in cement-based materials in chloride environmen. J. Henan Polytech. Univ. Nat. Sci. 2023, 42, 176–182. [Google Scholar] [CrossRef]
- Liu, H.; Liu, C.; Bai, G.; Zhu, C. Study on the effect of chloride ion ingress on the pore structure of the attached mortar of recycled concrete coarse aggregate. Constr. Build. Mater. 2020, 263, 120123. [Google Scholar] [CrossRef]
- Peng, R.X.; Qiu, W.L.; Teng, F. Investigation on seawater freeze-thaw damage deterioration of marine concrete structures in cold regions from multi-scale. Ocean. Eng. 2022, 248, 110867. [Google Scholar] [CrossRef]
- Xiang-Peng, F.; Li-Ping, G.; Jian-Dong, W.; Bang-Cheng, L.; Ying-Jie, C.; Xu-Yan, S. Impact of temperature, pH value and multiple ions on the physisorption of chloride ion on C-S-H gel surface. Constr. Build. Mater. 2023, 392, 131967. [Google Scholar] [CrossRef]
- Zhao, Y.; Xi, X.; Zheng, Y.; Du, C.; Zhao, Y.; Li, Y. Evaluation indexes of the frost resistance of recycled aggregate concrete and improvement mechanisms: A review. J. Build. Eng. 2024, 95, 110331. [Google Scholar] [CrossRef]
- Maruyama, I.; Sogo, M.; Sogabe, T.; Sato, R.; Kawai, K. Flexural properties of reinforced recycled concrete beams. In Proceedings of the International RILEM Conference on the Use of Recycled Materials in Buildings and Structures; RILEM Publications: Barcelona, Spain, 2004; pp. 315–324. ISBN 978-2-912143-46-5. [Google Scholar]
- Wang, H.; Zhang, B.; Wang, Q. Study on the durability of recycled concrete under the coupling action of freeze-thaw cycles and compound salt erosion. Concrete 2023, 4, 40–44+50. (In Chinese) [Google Scholar] [CrossRef]
- Arezoumandi, M.; Drury, J.; Volz, J.S.; Khayat, K.H. Effect of recycled concrete aggregate replacement level on shear strength of reinforced concrete beams. ACI Mater. J. 2015, 112, 559–568. [Google Scholar] [CrossRef]
- Tošić, N.; Marinković, S.; de Brito, J. Deflection control for reinforced recycled aggregate concrete beams: Experimental database and extension of the fib Model Code 2010 model. Struct. Concr. 2019, 20, 2015–2029. [Google Scholar] [CrossRef]
- Zamanzadeh, Z.; Lourenço, L.; Barros, J. Recycled Steel Fibre Reinforced Concrete failing in bending and in shear. Constr. Build. Mater. 2015, 85, 195–207. [Google Scholar] [CrossRef]
- DG/TJ 08-2018-2007; Technical Code on the Application of Recy—Cled Concrete. Tongji University: Shanghai, China, 2007. (In Chinese)
- Yan, G.X.; Liang, J.L.; Zhang, X.L.; Zhang, L.S. Research ofthe ultim ate shear form ula ofrecycled concrete beam. Concrete 2013, 8, 41–42+46. (In Chinese) [Google Scholar] [CrossRef]
- Rhardane, A.; Sleiman, S.A.H.; Alam, S.Y.; Grondin, F. A quantitative assessment of the parameters involved in the freeze–thaw damage of cement-based materials through numerical modelling. Constr. Build. Mater. 2021, 272, 121838. [Google Scholar] [CrossRef]
- Liu, J.; Huang, X.; Chen, X.; Huang, M.; Wu, Q. An improved design model for the shear capacity of monolithic uncracked interfaces based on the contribution degrees of concrete and shear reinforcements. Structures 2024, 65, 106632. [Google Scholar] [CrossRef]
- Yuan, A.; Zhao, X.; Lu, R. Experimental investigation on shear performance of fiber-reinforced high-strength concrete dry joints. Eng. Struct. 2020, 223, 111159. [Google Scholar] [CrossRef]
- Tian, Y.; Jiang, J.; Wang, S.; Yang, T.; Qi, L.; Geng, J. The mechanical and interfacial properties of concrete prepared by recycled aggregates with chloride corrosion media. Constr. Build. Mater. 2021, 282, 122653. [Google Scholar] [CrossRef]
- del Bosque, I.S.; Heede, P.V.D.; De Belie, N.; de Rojas, M.S.; Medina, C. Freeze-thaw resistance of concrete containing mixed aggregate and construction and demolition waste-additioned cement in water and de-icing salts. Constr. Build. Mater. 2020, 259, 119772. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, B. Repair of ordinary Portland cement concrete using alkali activated slag/fly ash: Freeze-thaw resistance and pore size evolution of adhesive interface. Constr. Build. Mater. 2021, 300, 124334. [Google Scholar] [CrossRef]
- Zou, D.; Wang, Z.; Shen, M.; Liu, T.; Zhou, A. Improvement in freeze-thaw durability of recycled aggregate permeable concrete with silane modification. Constr. Build. Mater. 2021, 268, 121097. [Google Scholar] [CrossRef]
- Hu, B.; Meng, T.-F.; Li, Y.; Li, D.-Z.; Chen, L. Dynamic splitting tensile bond behavior of new-to-old concrete interfaces. Constr. Build. Mater. 2021, 281, 122570. [Google Scholar] [CrossRef]
- Hu, X.; Peng, G.; Niu, D.; Zhao, N. Damage study on service performance of early-age frozen concrete. Constr. Build. Mater. 2019, 210, 22–31. [Google Scholar] [CrossRef]
- Yap, S.P.; Alengaram, U.J.; Jumaat, M.Z. Enhancement of mechanical properties in polypropylene– and nylon–fibre reinforced oil palm shell concrete. Mater. Des. 2013, 49, 1034–1041. [Google Scholar] [CrossRef]
- Valenza, J.J.; Scherer, G.W. A review of salt scaling: II. Mechanisms. Cem. Concr. Res. 2007, 37, 1022–1034. [Google Scholar] [CrossRef]










| Material Name | Fundamental Properties |
|---|---|
| Ordinary Portland Cement (P·O 42.5) | Density: 3.10 g/cm3, specific surface area: 349 m2/kg, loss on ignition (LOI): 3.57%, residue on 80 μm sieve: <10%, chemical composition (wt.s%): CaO 58.62; SiO2 23.08; Al2O3 6.01. |
| Fly Ash (Grade I, FA) | Loss on ignition (LOI): 2.62%; fineness (45 μm sieve residue): 16%; Al2O3 content: 36.8%; SiO2 content: <45.1%; SO3 content: 1.2%; chloride ion content: 0.015%; specific surface area: 420 m2/kg. |
| Polypropylene Fiber (PPF) | Monofilament polypropylene fibers produced by Shandong Jinhongyao Engineering Materials Co., Ltd. (Jinan City, China) were used, with a diameter of approximately 36 μm, a density of about 0.91 g/cm3, a length of approximately 12 mm, a tensile strength > 430 MPa, an elongation > 35%, a breaking strength of 455 MPa, an initial modulus of 4200 MPa, and resistance to acids and alkalis. |
| Mixing Water | No specific performance indicators (meets general tap water quality requirements for concrete mixing). |
| Additives (FK-AE + DFTR-PCE) | Complies with Technical Code for Application of Concrete Admixtures (GB 50119-2013) [29]. |
| Material Type | D10 (μm) | D50 (μm) | D90 (μm) |
|---|---|---|---|
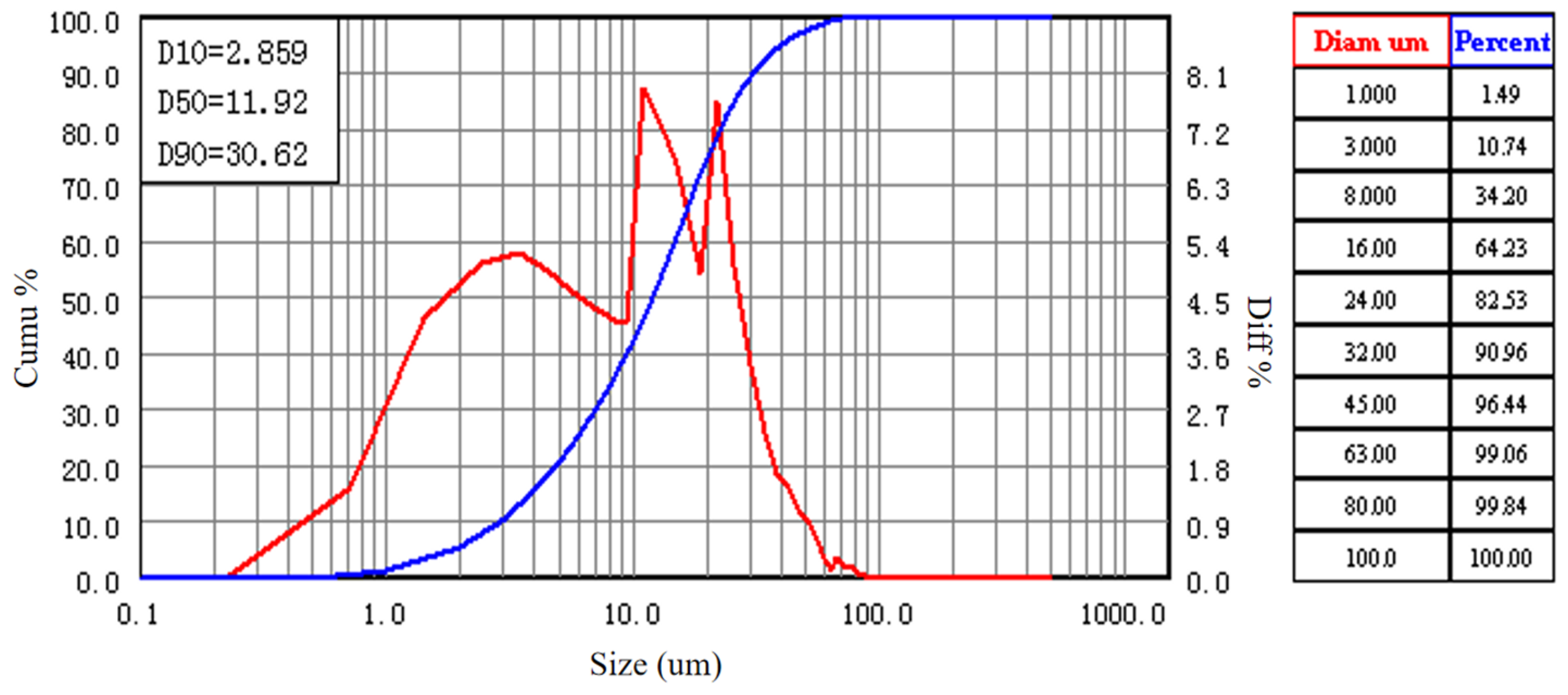
| Fly ash | 2.859 | 11.92 | 30.62 |
| Cement | 2.978 | 14.36 | 46.97 |
| Specimen Type | Cement (kg/m3) | FA (%) | PPF (%) | RCA (kg/m3) | Sand (kg/m3) | Water (kg/m3) | Water Reducer (kg/m3) |
|---|---|---|---|---|---|---|---|
| Test Beam/ Prism/Cube | 418.44 | 20 | 0.9 | 1085 | 535 | 185 | 5.29 |
| Freeze–Thaw Cycle (N) | 0 | 25 | 50 | 75 | 100 | 125 | 150 | 175 |
|---|---|---|---|---|---|---|---|---|
| Measured Strength (MPa) | 33.65 | 33.06 | 32.00 | 30.31 | 28.62 | 26.21 | 25.63 | 22.15 |
| Predicted Strength (MPa) | 35.04 | 32.97 | 31.02 | 29.19 | 27.47 | 25.85 | 24.32 | 22.89 |
| Relative Error (%) | 4.46 | 0.36 | 2.12 | 2.44 | 2.48 | 0.52 | 2.92 | 1.58 |
| Environmental Condition | Unfrozen | Clear Water | Composite Salt Solution | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Freeze–Thaw Cycles | 0 | 50 | 100 | 25 | 50 | 75 | 100 | 150 | 175 |
| Maximum Strain, με | 1852 | 2158 | 1985 | 2219 | 1875 | 1780 | 1310 | 1374 | 1308 |
| Environmental Condition | Specimen ID | Freeze–Thaw Cycles | Fn, kN | Fu, kN | Maximum Inclined Crack Width, mm | Maximum Midspan Deflection, mm |
|---|---|---|---|---|---|---|
| Clear water environment | Lj100(0) | 0 | 17.6 | 36 | 1.15 | 5.05 |
| Lj100q(50) | 50 | 15.4 | 35 | 2.46 | 7.46 | |
| Lj100q(100) | 100 | 12.2 | 31.6 | 1.59 | 6.59 | |
| Composite salt solution environment | Lj100f(25) | 25 | 14.8 | 34.5 | 1.23 | 6.23 |
| Lj100f(50) | 50 | 13.5 | 33 | 1.60 | 5.60 | |
| Lj100f(75) | 75 | 11.35 | 32.5 | 0.41 | 5.41 | |
| Lj100f(100) | 100 | 10.60 | 28 | 0.13 | 4.13 | |
| Lj100f(150) | 150 | 8.85 | 25 | 1.59 | 3.59 | |
| Lj100f(175) | 175 | 7.60 | 23 | 0.36 | 3.36 |
| Freezing and Thawing Cycles | Fue, kN | [48] Fup, kN | Equation (9) Fup, kN | Fue/Fup |
|---|---|---|---|---|
| 0 | 36 | 38.48 | 38.48 | 0.94 |
| 50 | 35 | 38.37 | 35.00 | 1.00 |
| 100 | 31.6 | 35.10 | 31.62 | 1.00 |
| Freezing and Thawing Cycles | Fue, kN | [33] Fup, kN | Equation (10) Fup, kN | Fue/Fup |
|---|---|---|---|---|
| 0 | 36 | 38.48 | 38.48 | 0.94 |
| 25 | 34.5 | 37.22 | 32.33 | 1.07 |
| 50 | 33 | 39.41 | 31.00 | 1.06 |
| 75 | 30.5 | 37.44 | 28.11 | 1.08 |
| 100 | 28 | 36.67 | 26.39 | 1.06 |
| 150 | 25 | 35.76 | 23.67 | 1.06 |
| 175 | 23 | 35.48 | 22.52 | 1.02 |
| Shear–Span Ratio | Cross-Sectional Dimensions (mm × mm) | Freeze–Thaw Cycles | RCA Replacement Rate (%) | Fue, kN | Equation (9) Fup, kN | Fue/Fup |
|---|---|---|---|---|---|---|
| 2.48 | 100 × 150 | 0 | 100 | 72.67 | 74.49 | 0.98 |
| 2.48 | 100 × 150 | 25 | 100 | 64.94 | 66.9 | 0.97 |
| 2.48 | 100 × 150 | 55 | 100 | 61.84 | 60.25 | 1.03 |
| 2.48 | 100 × 150 | 80 | 100 | 58.75 | 55.23 | 1.06 |
| 2.48 | 100 × 150 | 105 | 100 | 57.20 | 52.18 | 1.10 |
| 2.48 | 100 × 150 | 130 | 100 | 52.57 | 48.48 | 1.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Wu, J.; Zhao, J.; Zeng, Z.; Wang, X.; Wang, Y.; Luan, H.; Wang, Y.; Hu, D. Shear Performance Degradation of Fiber-Reinforced Recycled Aggregate Concrete Beams Under Salt Freeze–Thaw Cycles. Materials 2025, 18, 4817. https://doi.org/10.3390/ma18204817
Guo S, Wu J, Zhao J, Zeng Z, Wang X, Wang Y, Luan H, Wang Y, Hu D. Shear Performance Degradation of Fiber-Reinforced Recycled Aggregate Concrete Beams Under Salt Freeze–Thaw Cycles. Materials. 2025; 18(20):4817. https://doi.org/10.3390/ma18204817
Chicago/Turabian StyleGuo, Shefeng, Jin Wu, Jingmiao Zhao, Zhehong Zeng, Xiangyu Wang, Yiyuan Wang, Haoxiang Luan, Yulin Wang, and Dongxia Hu. 2025. "Shear Performance Degradation of Fiber-Reinforced Recycled Aggregate Concrete Beams Under Salt Freeze–Thaw Cycles" Materials 18, no. 20: 4817. https://doi.org/10.3390/ma18204817
APA StyleGuo, S., Wu, J., Zhao, J., Zeng, Z., Wang, X., Wang, Y., Luan, H., Wang, Y., & Hu, D. (2025). Shear Performance Degradation of Fiber-Reinforced Recycled Aggregate Concrete Beams Under Salt Freeze–Thaw Cycles. Materials, 18(20), 4817. https://doi.org/10.3390/ma18204817







