Digital Image Correlation and Numerical Analysis of Mechanical Behavior in Photopolymer Resin Lattice Structures
Abstract
1. Introduction
2. Materials and Methods
3. Experimental Methods
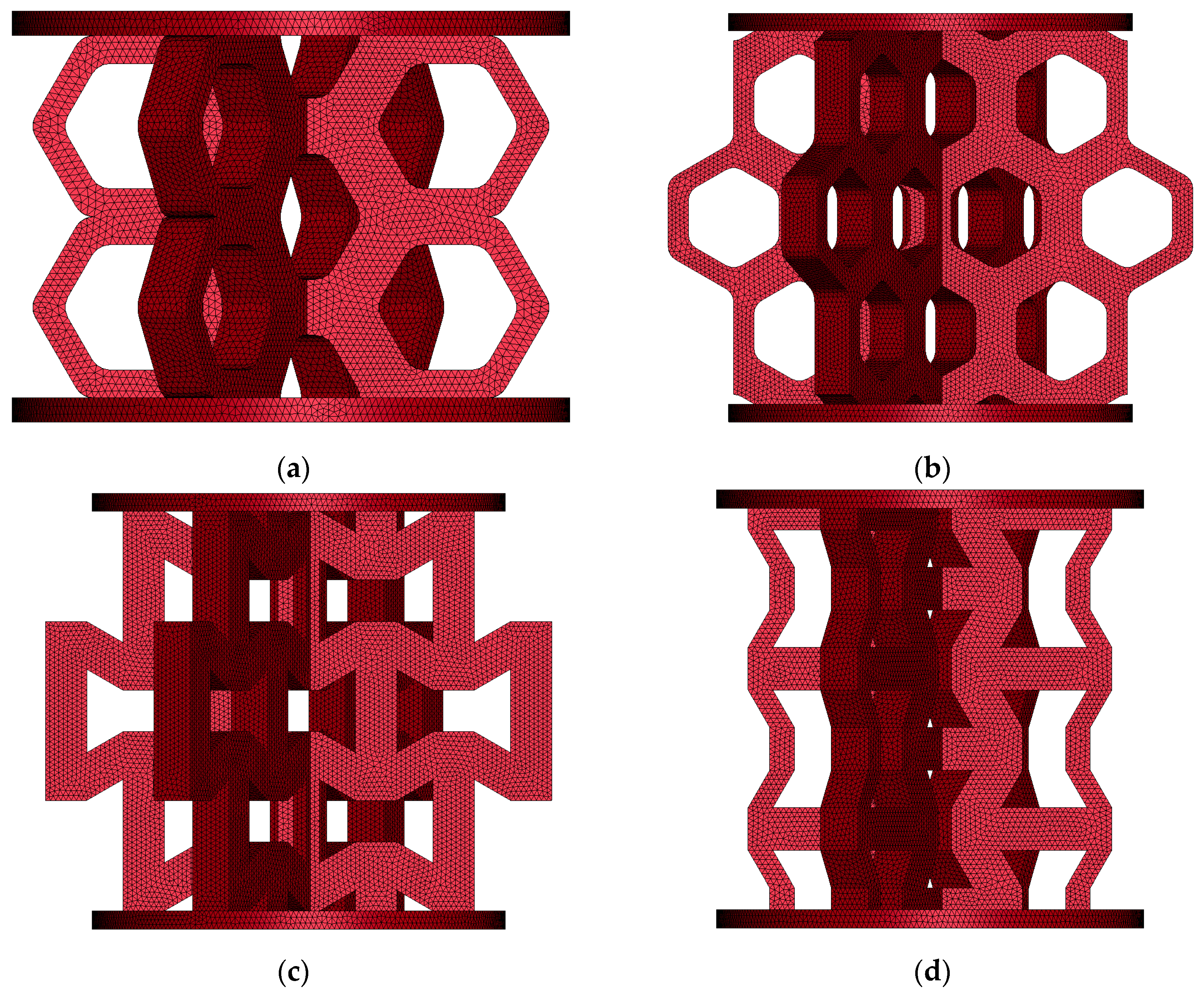
4. Numerical Simulation Procedure
5. Results and Comparisons
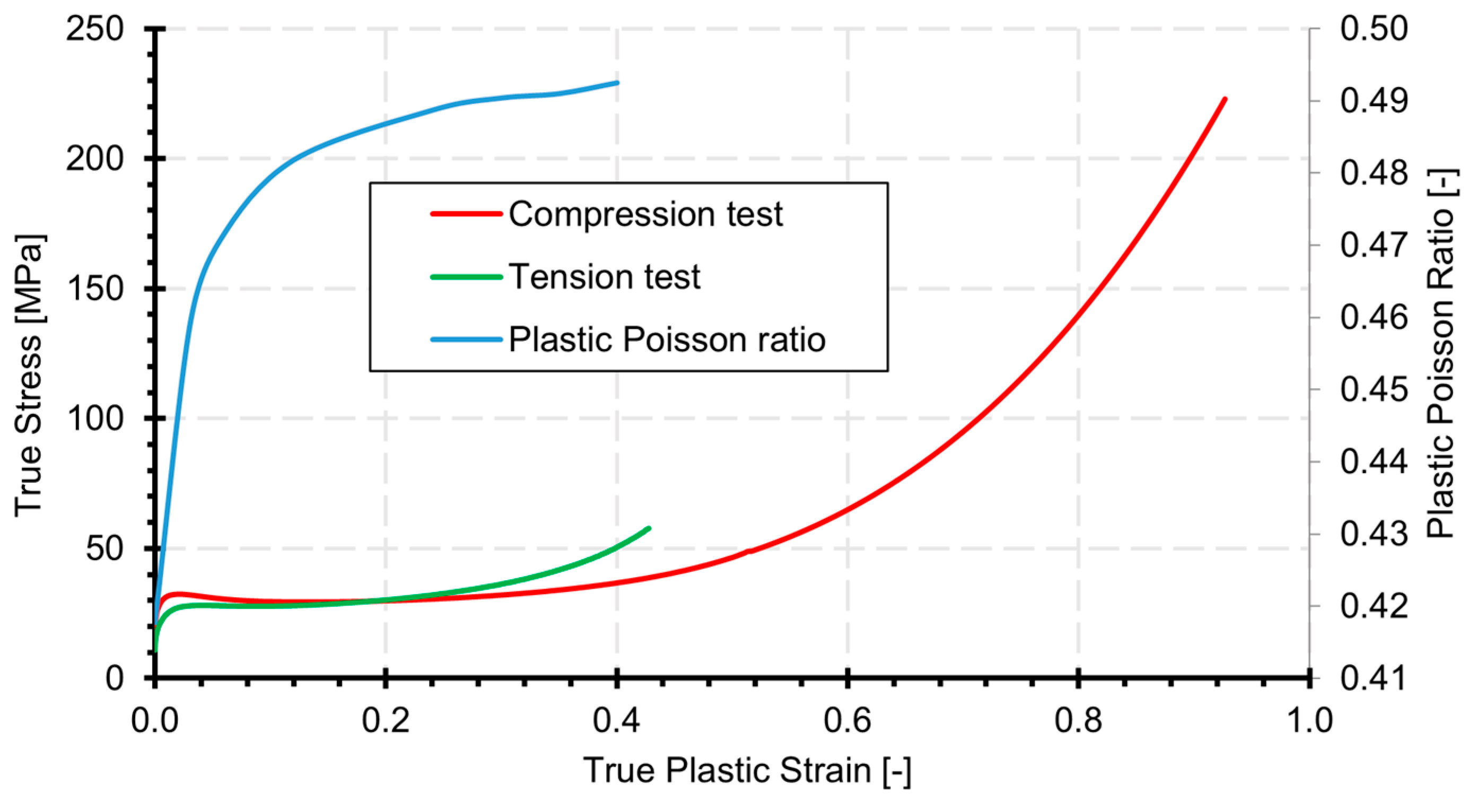
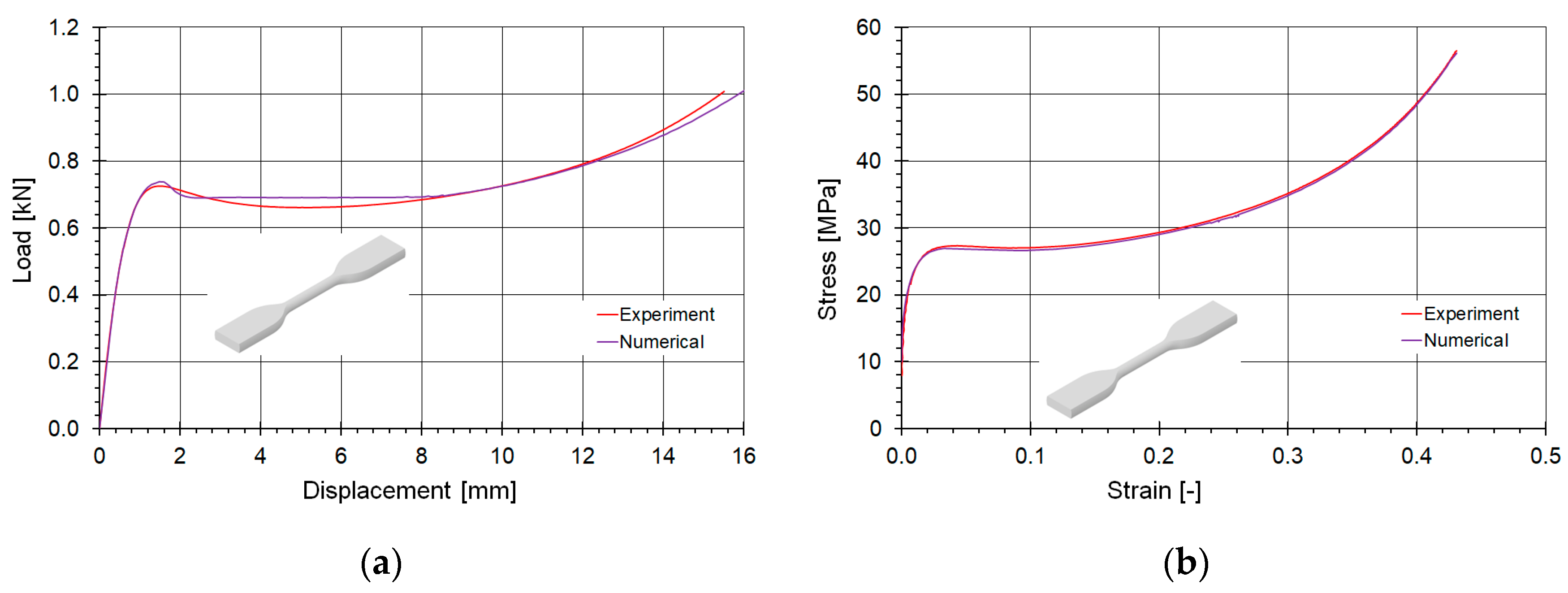
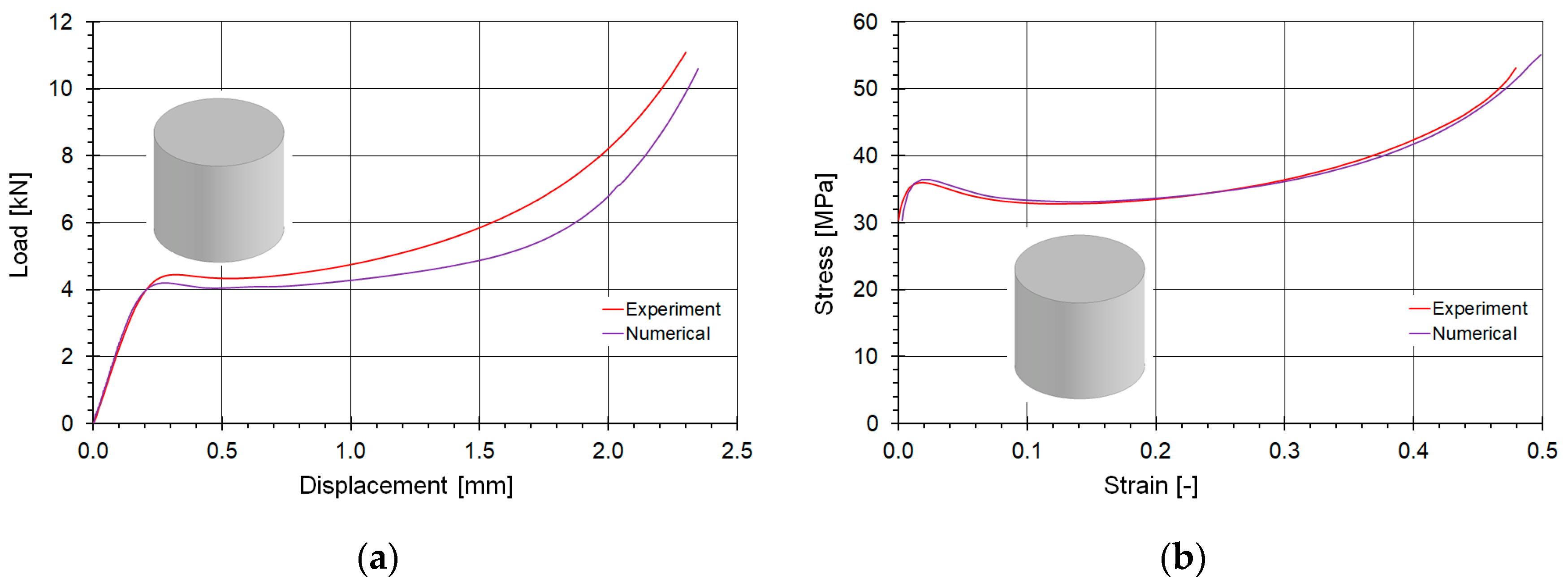
5.1. Development of the SAMP-1 Numerical Material Model from Experimental Data
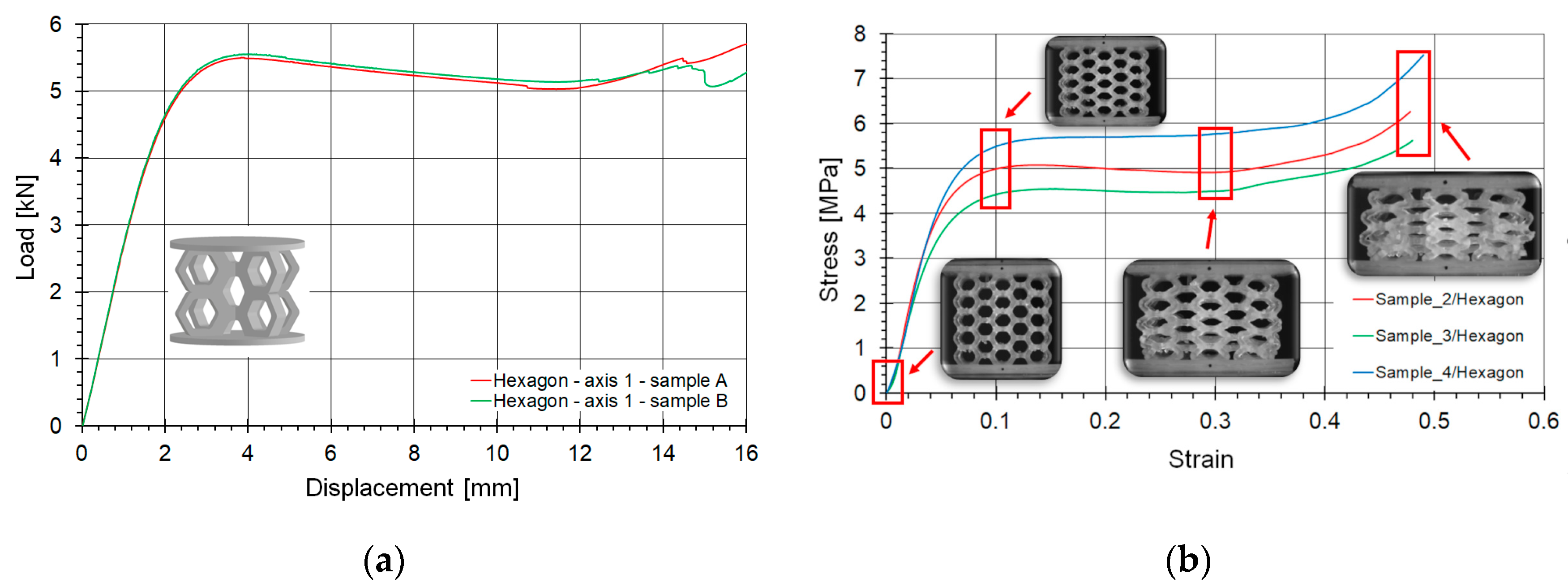
5.2. Comparison of Compression Curves for the Studied Lattice Structures
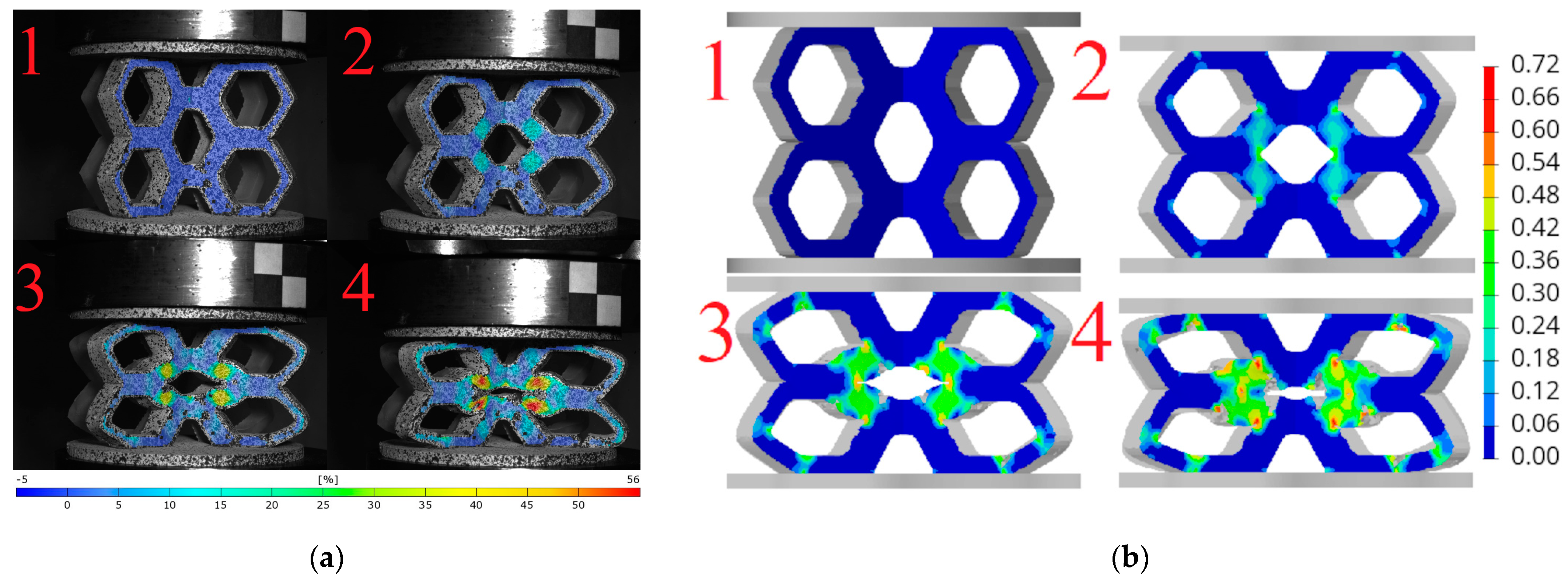
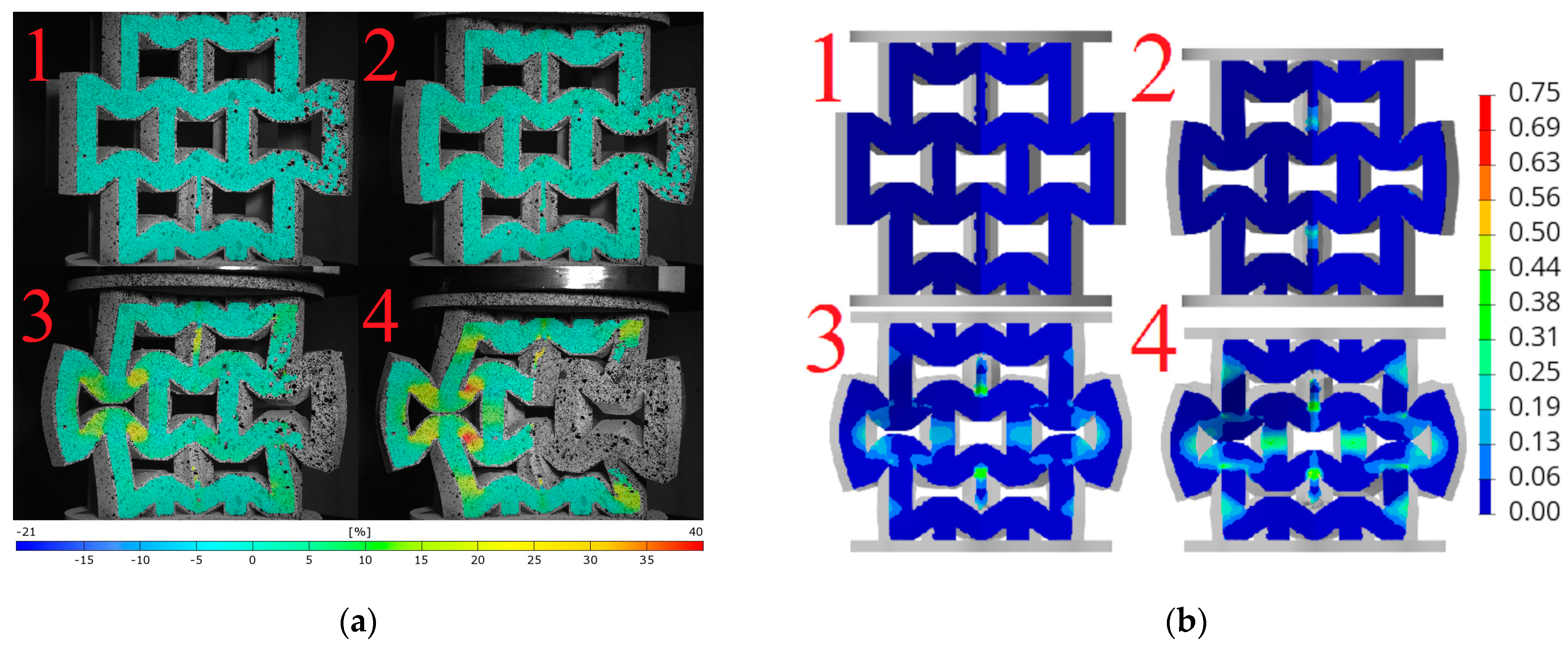
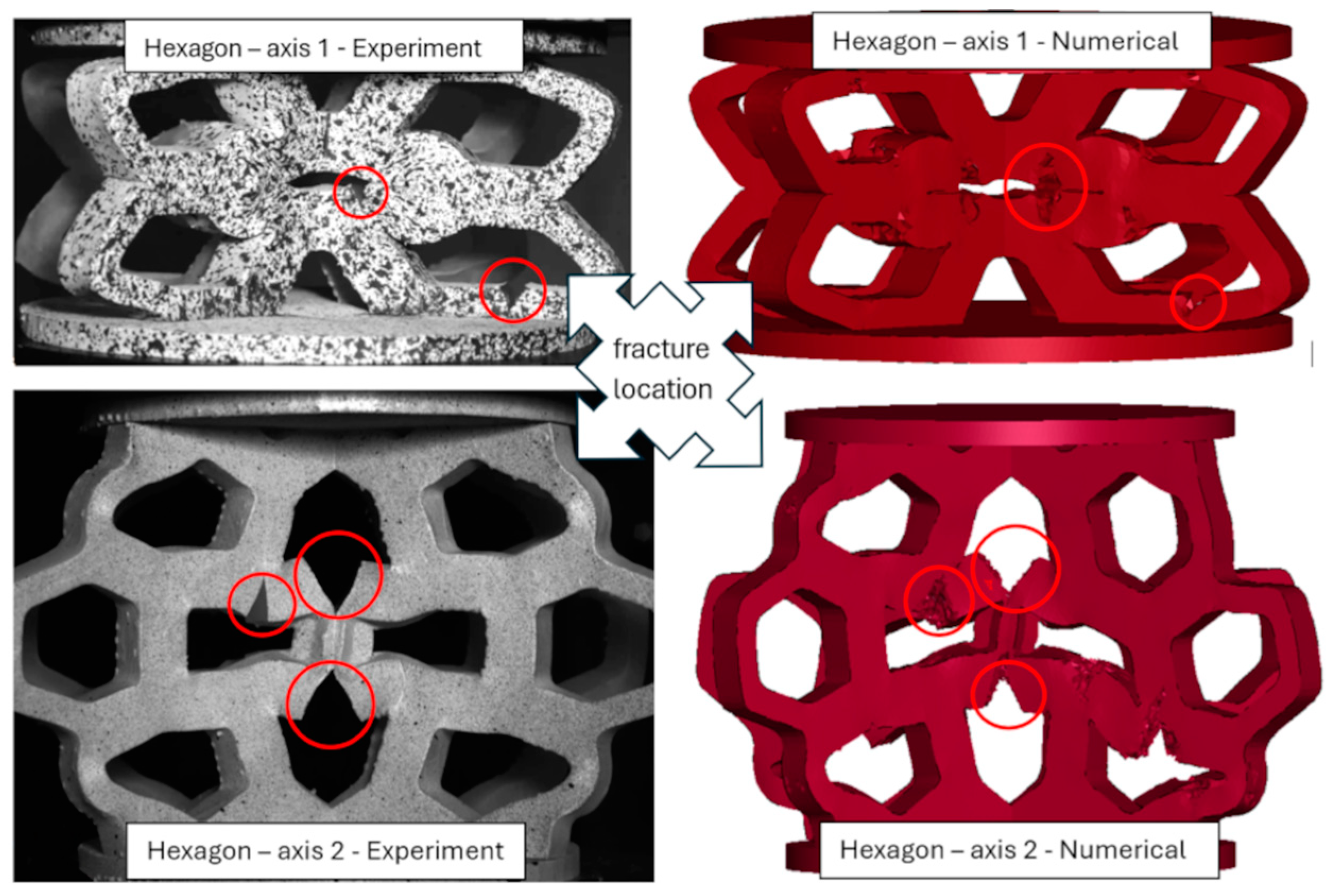
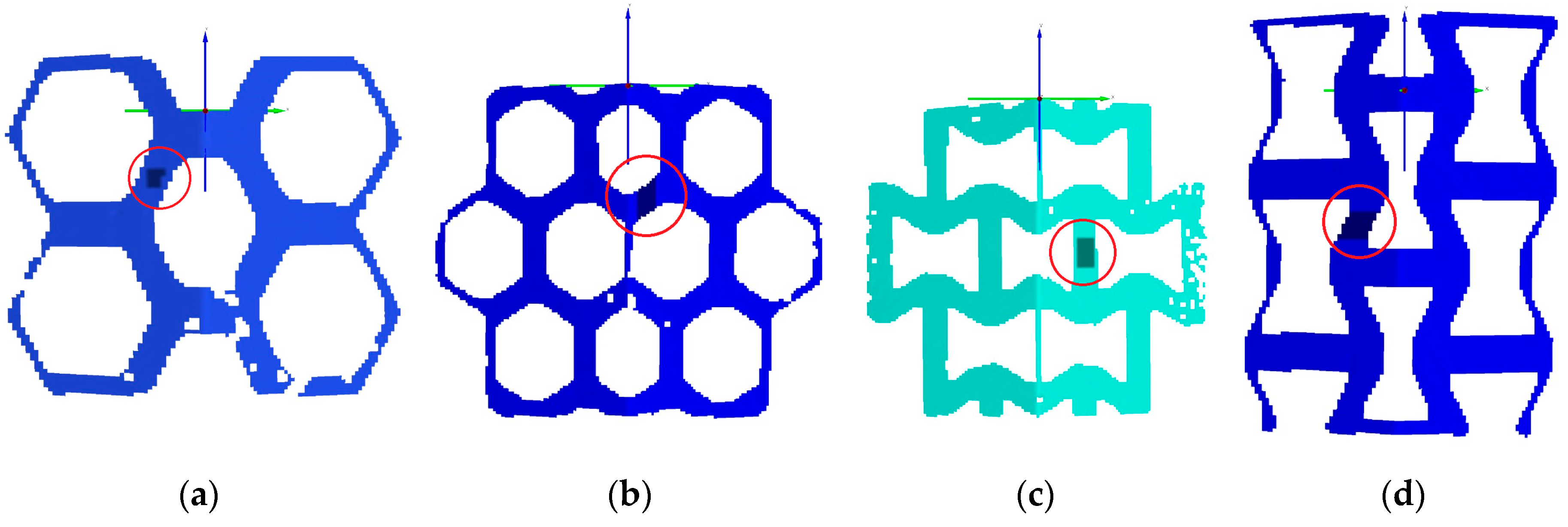
5.3. Comparison of Failure Mechanisms
5.4. Comparison of Major Strain Curves
6. Summary and Conclusions
- During the calibration process, the characteristics of the experimentally determined tensile and compression curves were successfully reproduced in the numerical simulations. The numerical material model SAMP-1 accurately captured the behavior of Durable Resin. A reasonable agreement was observed between the model’s behavior and the experimental strength test results.
- Deformation and failure mechanisms of the lattice structures were evaluated. Various topologies subjected to different loading conditions were considered, highlighting the versatility of the developed model The use of enlarged cells in the studied topologies enabled a detailed DIC analysis of the structural behavior during the compression process. A good agreement was observed between the numerical modeling results and the experimental behavior. The level of agreement varied among different topologies, with the best match achieved for the hexagonal structure compressed along axis 2, where the numerical model’s accuracy for the average force error was below 5%.
- It was noted that during the compression of all considered structures, a complex state of loading occurred. In the hexagonal topology, bending plays a significant role in the regions with the largest major strains. Plastic hinges form in these areas, where the strains are very large and approach crushing levels. In the re-entrant honeycomb structure, shear deformations dominate in the most stressed regions. For axis 2, auxetic behavior was observed for this structure, consistent with the actual behavior.
- In order to confirm the consistency of the numerical calculations with the experimental results, a comparison of the major strain in the areas of maximum stress was performed. Good agreement between the numerical calculations and experimental results was also achieved here. However, the agreement varied for different structures. The hexagonal structure, loaded along axis 2, achieved the best fit, with differences remaining within a range of up to 5%. The weakest fit was observed for the re-entrant honeycomb structure, especially loaded in the axis 1.
- A strain-based failure model was employed in the numerical analyses of both topologies, which satisfactorily captured the failure process of the structures and accurately reflected their global behavior. Failure was observed exclusively in the hexagonal structure (both axes), with fractures occurring in regions of strain and stress concentration, as expected. While the model was active for all four structures, no failure was detected in the re-entrant honeycomb structures, consistent with the experimental results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vesenjak, M.; Öchsner, A.; Hribersek, M.; Ren, Z. Behaviour of Cellular Structures with Fluid Fillers under Impact Loading. Int. J. Multiphys. 2007, 1, 101–122. [Google Scholar] [CrossRef]
- Seif, M.N.; Puppo, J.; Zlatinov, M.; Schaffarzick, D.; Martin, A.; Beck, M.J. Stochastic Mechanical Modeling of Metallic Foams to Determine Onset of Mesoscale Behavior. arXiv 2023, arXiv:2302.14715. [Google Scholar]
- Ráž, K.; Chval, Z.; Pereira, M. Lattice Structures—Mechanical Description with Respect to Additive Manufacturing. Materials 2024, 17, 5298. [Google Scholar] [CrossRef] [PubMed]
- Issabayeva, Z.; Shishkovsky, I. Prediction of The Mechanical Behavior of Polylactic Acid Parts with Shape Memory Effect Fabricated by FDM. Polymers 2023, 15, 1162. [Google Scholar] [CrossRef]
- Schneider, Y.; Guski, V.; Sahin, A.O.; Schmauder, S.; Kadkhodapour, J.; Hufert, J.; Grebhardt, A.; Bonten, C. Investigation of Auxetic Structural Deformation Behavior of PBAT Polymers Using Process and Finite Element Simulation. Polymers 2023, 15, 3142. [Google Scholar] [CrossRef] [PubMed]
- Paredes Pureco, P.; Fuentes-Juvera, L.; Olivas-Alanis, L.H.; Roman-Flores, A.; Cuan-Urquizo, E. Novel Additively Manufactured Dihedral Tiling Architected Metamaterial Conformed with Pentagon and Rhombus: Design and Mechanical Properties. Mater. Res. Express 2023, 10, 065304. [Google Scholar] [CrossRef]
- Gu, G.; Xia, Y.; Lin, C.-H.; Lin, S.; Meng, Y.; Zhou, Q. Experimental study on characterizing damage behavior of thermoplastics. Mater. Des. 2013, 44, 199–207. [Google Scholar] [CrossRef]
- Wu, B.; Chen, Q.; Liu, F.; Chen, M.; Lu, Y.; Jiang, D.; Yi, Y. Study on Dynamic Mechanics of Node-Enhanced Graded Lattice Structure and Application Optimization in Automobile Energy Absorbing Box. Materials 2023, 16, 6893. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Sarasini, F.; Medori, E.; Berto, F.; Razavi, N. Scale-Dependent Mechanical Performance Variations in Polylactic Acid Lattice Structures Fabricated via Additive Manufacturing. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 3561–3583. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, D.Z.; Zheng, X. Revealing the excellent properties of minimal surface lattice structures based on additive manufacturing through the principle of least action. Int. J. Adv. Manuf. Technol. 2022, 121, 1575–1588. [Google Scholar] [CrossRef]
- Olmos, D.; González-Benito, J. Polymeric Materials with Antibacterial Activity: A Review. Polymers 2021, 13, 613. [Google Scholar] [CrossRef] [PubMed]
- Kechagias, J.; Chaidas, D.; Vidakis, N.; Salonitis, K.; Vaxevanidis, N.M. Key Parameters Controlling Surface Quality and Dimensional Accuracy: A Critical Review of FFF Process. Mater. Manuf. Process. 2022, 37, 963–984. [Google Scholar] [CrossRef]
- Yelamanchi, B.; Mummareddy, B.; Santiago, C.C.; Ojoawo, B.; Metsger, K.; Helfferich, B.; Zapka, J.; Silani, F.; MacDonald, E.; Cortes, P. Mechanical and fatigue performance of pressurized vessels fabricated with multi jet fusion™ for automotive applications. Addit. Manuf. 2021, 44, 102048. [Google Scholar] [CrossRef]
- Chua, C.K.; Wong, C.H.; Yeong, W.Y. Benchmarking for Additive Manufacturing. In Standards, Quality Control and Measurement Sciences in 3D Printing and Additive Manufacturing, 1st ed.; Academic Press: Cambridge, MA, USA, 2017; pp. 181–212. [Google Scholar]
- Shahrubudin, N.; Lee, T.C.; Ramlan, R. An Overview on 3D Printing Technology: Technological, Materials, and Applications. Procedia Manuf. 2019, 35, 1286–1296. [Google Scholar] [CrossRef]
- Farkas, A.Z.; Galatanu, S.-V.; Nagib, R. The Influence of Printing Layer Thickness and Orientation on the Mechanical Properties of DLP 3D-Printed Dental Resin. Polymers 2023, 15, 1113. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Tey, W.S.; Choo, J.Y.C.; Chen, J.; Tan, P.; Cai, C.; Ong, A.; Zhao, L.; Zhou, K. Enhancing the mechanical strength of multi jet fusion–printed polyamide 12 and its glass fiber-reinforced composite via high-temperature annealing. Addit. Manuf. 2021, 46, 102205. [Google Scholar] [CrossRef]
- Khan, N.; Riccio, A. A systematic review of design for additive manufacturing of aerospace lattice structures: Current trends and future directions. Prog. Aerosp. Sci. 2024, 149, 101021. [Google Scholar] [CrossRef]
- Panowicz, R.; Jeschke, A.; Durejko, T.; Zachman, M.; Konarzewski, M. The Mechanical Properties and Energy Absorption of AuxHex Structures. Materials 2024, 17, 6073. [Google Scholar] [CrossRef]
- Ansari, A.I.; Sheikh, N.A.; Kumar, N. Simulation and Experimental Energy Absorption Behavior of ABS-M30i-Based Three Distinct Lattice Structures Fabricated by Polymer 3D Printer. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 509. [Google Scholar] [CrossRef]
- Li, Y.; Long, S.; Liu, Q.; Lv, H.; Liu, M. Resistive Switching Performance Improvement via Modulating Nanoscale Conductive Filament, Involving the Application of Two-Dimensional Layered Materials. Small 2017, 13, 1604306. [Google Scholar] [CrossRef] [PubMed]
- Cai, C.; Tey, W.S.; Chen, J.; Zhu, W.; Liu, X.; Liu, T.; Zhao, L.; Zhou, K. Comparative study on 3d printing of polyamide 12 by selective laser sintering and multi jet fusion. J. Mater. Process. Technol. 2021, 228, 116882. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, F.; Fu, G.; Zhang, D.; Zhang, T.; Zhou, H. Improved Mechanical Properties and Energy Absorption of BCC Lattice Structures with Triply Periodic Minimal Surfaces Fabricated by SLM. Materials 2018, 11, 2411. [Google Scholar] [CrossRef]
- Moon, S.K.; Tan, Y.E.; Hwang, J.; Yoon, Y.-J. Application of 3D Printing Technology for Designing Light-Weight Unmanned Aerial Vehicle Wing Structures. Int. J. Precis. Eng. Manuf.-Green Technol. 2014, 1, 223–228. [Google Scholar] [CrossRef]
- Bogusz, P.; Popławski, A.; Stankiewicz, M.; Kowalski, B. Experimental Research of Selected Lattice Structures Developed with 3D Printing Technology. Materials 2022, 15, 378. [Google Scholar] [CrossRef] [PubMed]
- Dan, X.; Li, J.; Zhao, Q.; Sun, F.; Wang, Y.; Yang, L. A Cross-Dichroic-Prism-Based Multi-Perspective Digital Image Correlation System. Appl. Sci. 2019, 9, 673. [Google Scholar] [CrossRef]
- Chu, T.C.; Ranson, W.F.; Sutton, M.A. Applications of digital-image-correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Tang, Z.; Liang, J.; Xiao, Z.; Guo, C.; Hu, H. Three-dimensional digital image correlation system for deformation measurement in experimental mechanics. Opt. Eng. 2010, 49, 103601. [Google Scholar] [CrossRef]
- Li, J.; Xin, X.; Yang, G.; Zhang, G.; Siebert, T.; Yang, L. Whole-field thickness strain measurement using multiple camera digital image correlation system. Opt. Lasers Eng. 2017, 90, 19–25. [Google Scholar] [CrossRef]
- Tang, C.; Luo, J.; Hao, W.; Yuanyuan, W. Flexural Properties of 3D Printed Graded Lattice Reinforced Cementitious Composites Using Digital Image Correlation. Mater. Des. 2023, 227, 111734. [Google Scholar] [CrossRef]
- Kolling, S.; Haufe, A.; Feucht, M.; Du Bois, P. SAMP-1: A Semi-Analytical Model for the Simulation of Polymers. In Proceedings of the 4th German Forum on LS-DYNA 2005, Bamberg, Germany, 21 October 2005. [Google Scholar]
- Kurudimath, K.; Godthi, V.; Dasappa, P.; Bobba, S. Benefits of Semi-Analytical Model Polymer Techniques (SAMP-1 with GISSMO Failure) for Crashworthiness of Critical Thermoplastic Automotive Structural Parts; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2021. [Google Scholar] [CrossRef]
- Magazzù, A.; Marcuello, C. Investigation of Soft Matter Nanomechanics by Atomic Force Microscopy and Optical Tweezers: A Comprehensive Review. Nanomaterials 2023, 13, 963. [Google Scholar] [CrossRef] [PubMed]
- Hoerig, C.; Ghaboussi, J.; Wang, Y.; Insana, M.F. Machine Learning in Model-free Mechanical Property Imaging: Novel Integration of Physics with the Constrained Optimization Process. Front. Phys. 2021, 9, 600718. [Google Scholar] [CrossRef]
- Masłowska-Lipowicz, I.; Wyrębska, Ł.; Szałek, B.; Olszewski, P.; Gajewski, R. Materiały auksetyczne–struktury, potencjalne zastosowanie. Technol. I Jakość Wyr. 2020, 65, 116–119. [Google Scholar]
- Using Durable Resin. Available online: https://support.formlabs.com/s/article/Using-Durable-Resin?language=en_US (accessed on 18 November 2021).
- GOM mbH. ARAMIS Podręcznik Użytkownika—Oprogramowanie; GOM mbH: Braunschweig, Germany, 2010. [Google Scholar]
- Maddah, H.A. Polypropylene as a Promising Plastic: A Review. Am. J. Polym. Sci. 2016, 6, 1–11. [Google Scholar] [CrossRef]
- Livermore Software Technology Corporation (LSTC). LS-DYNA® Keyword User’s Manual. Volume II: Material Models; Livermore Software Technology Corporation: Livermore, CA, USA, 2024. [Google Scholar]
- Daiyan, H.; Grytten, F.; Andreassen, E.; Osnes, H.; Lyngstad, O.V. Numerical Simulation of Low-Velocity Impact Loading of a Ductile Polymer Material. Mater. Des. 2012, 42, 450–458. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Rolfes, R.; Vucetic, M.; Reinoso, J.; Vogler, M.; Grbic, N. Material Modelling of Short Fiber Reinforced Thermoplastic for the FEA of a Clinching Test. Procedia CIRP 2014, 18, 250–255. [Google Scholar] [CrossRef]
- Ngueveu, Y.; Miyagano, S.; Lauro, F.; Balieu, R. Modelling of Ductile Polymer Model for Crash Application. In Proceedings of the 11th European LS-DYNA Conference, Salzburg, Austria, 9–11 May 2017; Available online: https://www.researchgate.net/publication/316973186 (accessed on 27 December 2024).
- Haufe, A.; Du Bois, P.A.; Kolling, S.; Feucht, M. A Semi-Analytical Model for Polymers Subjected to High Strain Rates. In Proceedings of the 5th European LS-DYNA Users Conference, Stuttgart, Germany, 25–26 May 2005. [Google Scholar]
- Popławski, A.; Kędzierski, P.; Morka, A. Identification of Armox 500T Steel Failure Properties in the Modeling of Perforation Problems. Mater. Des. 2020, 190, 108536. [Google Scholar] [CrossRef]



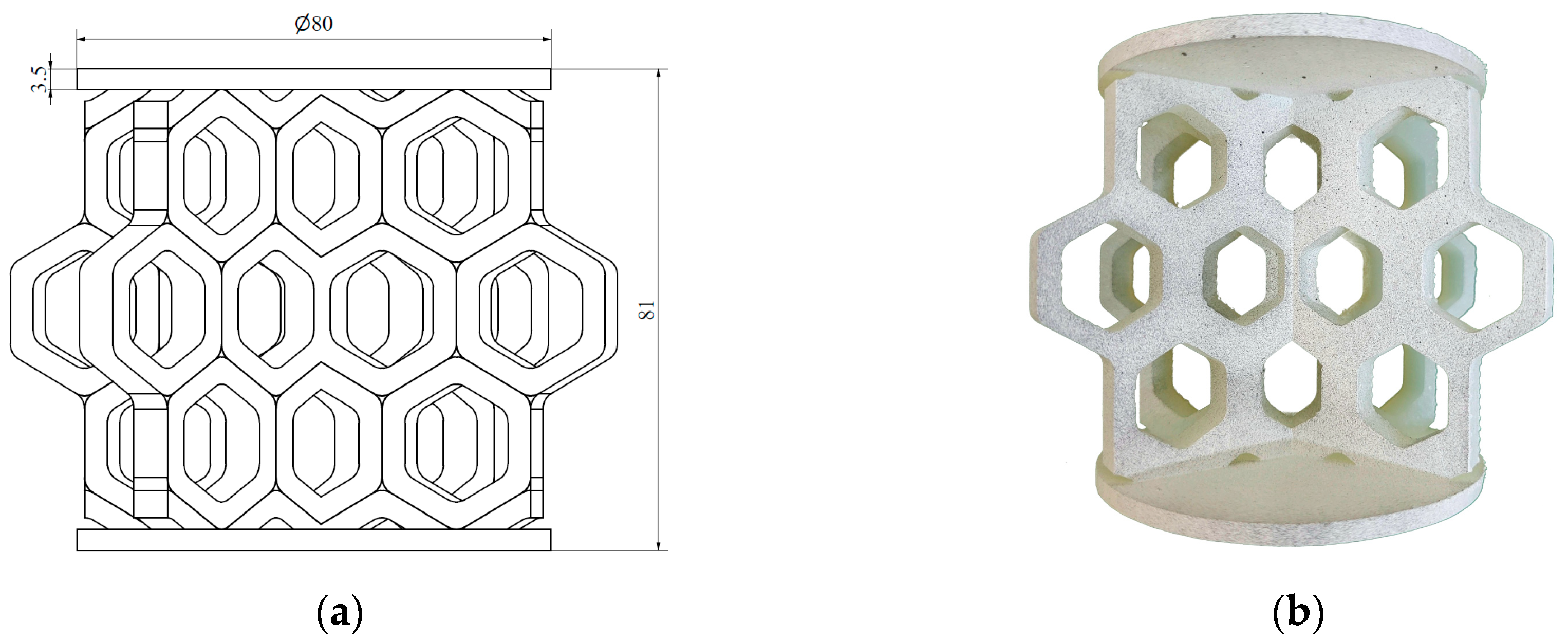

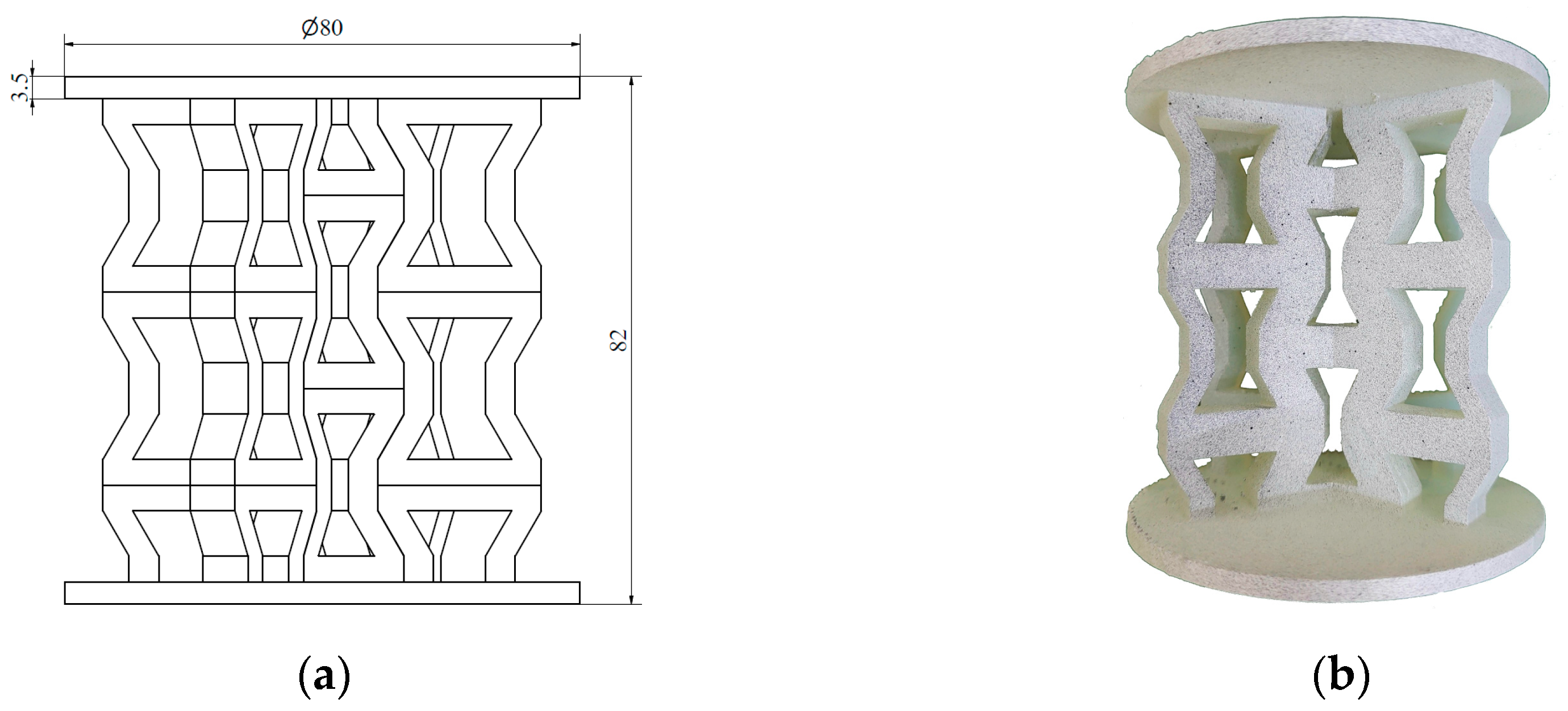






| Properties | Literature Values [36] | Experimental Values | Standard Deviation |
|---|---|---|---|
| Tensile strength [MPa] | 28 | 25 | 0.3 |
| Tensile modulus [MPa] | 1000 | 999 | 6 |
| Shear modulus [MPa] | - | 353 | 4 |
| Elongation [%] | 55 | 58 | 2 |
| Heat Deflection Temperature HDT [°C] | 41 | - | - |
| Liquid density [g/cm3] | 1.06 | - | - |
| Cured density [g/cm3] | 1.13 | - | - |
| Sample | High [mm] | Mass [g] | Load (max) [kN] | ΔLoad (max) [%] | Load (avg) [kN] | ΔLoad (avg) [%] |
|---|---|---|---|---|---|---|
| Hexagon_axis 1—exp. (avg) | 52.0 | 70.40 | 5.53 | 8.88 | 4.95 | 9.03 |
| Hexagon_axis 1—num. | - | 6.02 | 5.40 | |||
| Hexagon_axis 2—exp. (avg) | 74.0 | 100.67 | 8.99 | 5.56 | 7.01 | 4.17 |
| Hexagon_axis 2—num. | - | 9.49 | 7.31 | |||
| Re-entrant honeycomb_axis 1—exp. (avg) | 77.3 | 114.60 | 7.96 | 12.93 | 6.07 | 8.98 |
| Re-entrant honeycomb_axis 1—num. | - | 8.98 | 6.61 | |||
| Re-entrant honeycomb_axis 2—exp. (avg) | 75.0 | 93.28 | 8.74 | 6.93 | 8.30 | 1.40 |
| Re-entrant honeycomb_axis 2—num. | - | 8.14 | 8.41 |
| Sample | Sample Hight Reduction (16mm) [%] | Major Strain (16 mm) [%] | Δ Major Strain (16 mm) [%] | Major Strain (avg) [%] | Δ Major Strain (avg) [%] |
|---|---|---|---|---|---|
| Hexagon_axis 1—exp. (avg) | 30.8 | 50.71 | 7.42 | 25.15 | 6.01 |
| Hexagon_axis 1—num. | 46.95 | 23.64 | |||
| Hexagon_axis 2—exp. (avg) | 21.6 | 29.53 | 4.37 | 12.56 | 5.17 |
| Hexagon_axis 2—num. | 28.24 | 11.91 | |||
| Re-entrant honeycomb_axis 1—exp. (avg) | 20.7 | 11.60 | 22.36 | 4.46 | 9.91 |
| Re-entrant honeycomb_axis 1—num. | 9.01 | 4.02 | |||
| Re-entrant honeycomb_axis 2—exp. (avg) | 21.3 | 23.23 | 11.29 | 11.27 | 1.99 |
| Re-entrant honeycomb_axis 2—num. | 20.61 | 11.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popławski, A.; Bogusz, P.; Grudnik, M. Digital Image Correlation and Numerical Analysis of Mechanical Behavior in Photopolymer Resin Lattice Structures. Materials 2025, 18, 384. https://doi.org/10.3390/ma18020384
Popławski A, Bogusz P, Grudnik M. Digital Image Correlation and Numerical Analysis of Mechanical Behavior in Photopolymer Resin Lattice Structures. Materials. 2025; 18(2):384. https://doi.org/10.3390/ma18020384
Chicago/Turabian StylePopławski, Arkadiusz, Paweł Bogusz, and Maciej Grudnik. 2025. "Digital Image Correlation and Numerical Analysis of Mechanical Behavior in Photopolymer Resin Lattice Structures" Materials 18, no. 2: 384. https://doi.org/10.3390/ma18020384
APA StylePopławski, A., Bogusz, P., & Grudnik, M. (2025). Digital Image Correlation and Numerical Analysis of Mechanical Behavior in Photopolymer Resin Lattice Structures. Materials, 18(2), 384. https://doi.org/10.3390/ma18020384








