Finite Element Simulation of Hot Rolling for Large-Scale AISI 430 Ferritic Stainless-Steel Slabs Using Industrial Rolling Schedules—Part 1: Set-Up, Optimization, and Validation of Numerical Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Procedure
2.2. Material
2.3. FEM Simulation
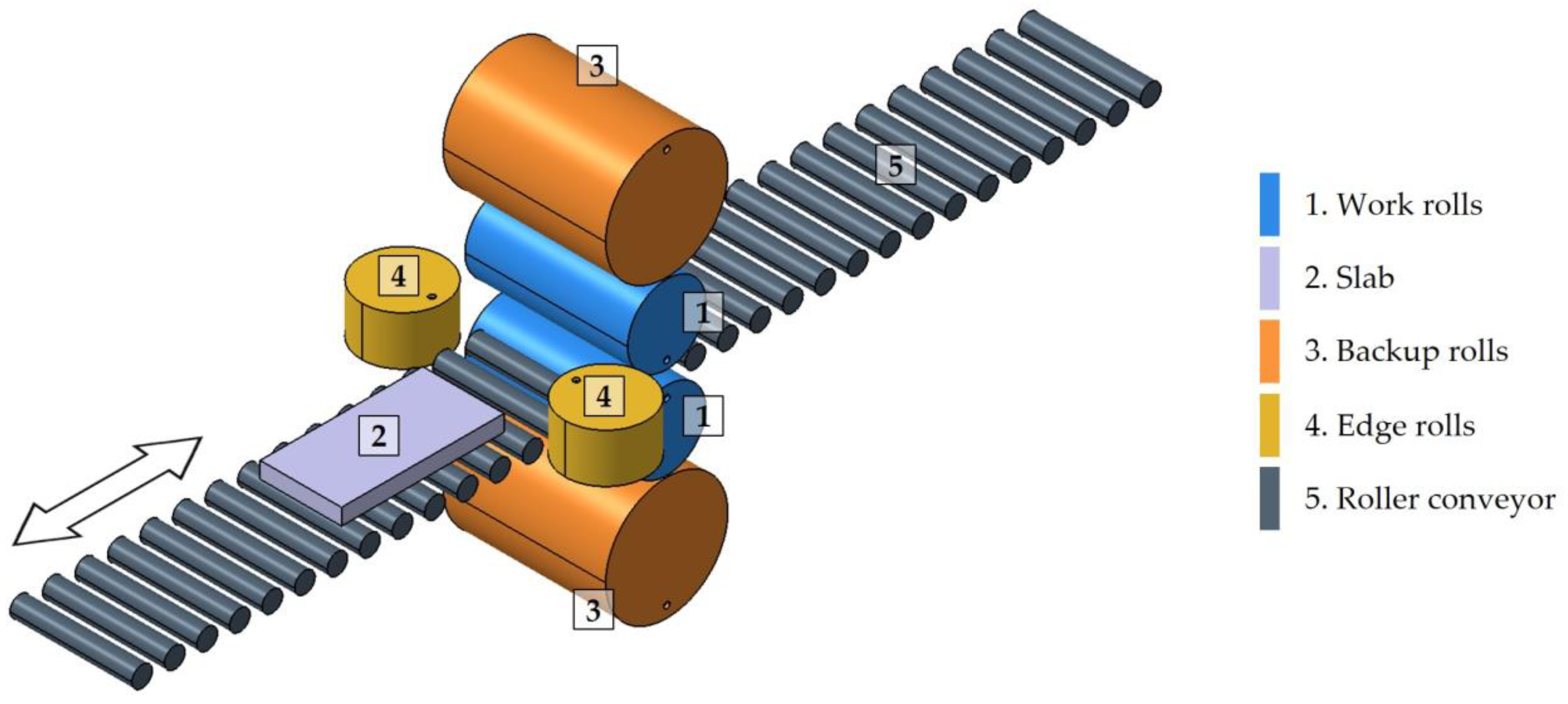
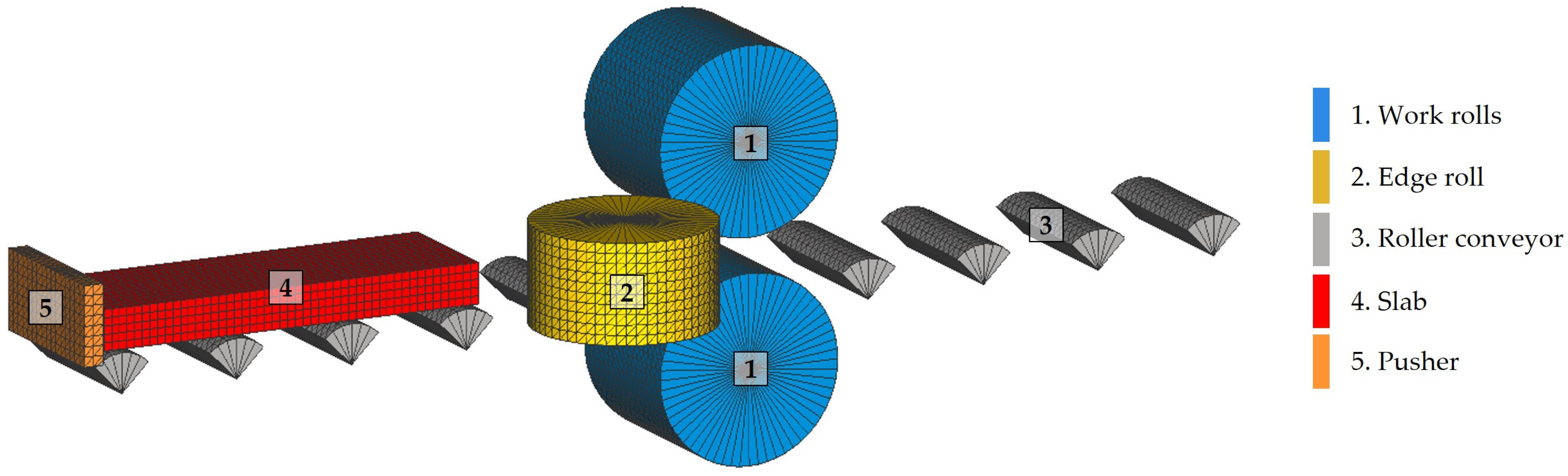
2.3.1. Establishment of FEM Model
- The work rolls, the edge rolls, and the roller conveyor were considered as rigid bodies because of their minimal deformation compared with the slab. Therefore, no material was defined for the rolls.
- The slab was assumed to be a uniform and isotropic visco-plastic body at the beginning of the simulation.
- The rolls were assigned a four-node thermally coupled tetrahedral element mesh. In addition, an element type analysis was performed using two different element types for the slab. Specifically, a four-node thermally coupled tetrahedral element mesh and an eight-node thermally coupled hexahedral element mesh were used. A remeshing condition was implemented to avoid mesh distortion caused by deformations occurring during rolling. Thus, the mesh effectively adapted to the changing geometry of the slab, without compromising its integrity or the accuracy of the results obtained.
- During hot rolling, there is friction between the rolls and the slab. Therefore, the friction coefficient of each pair of contact surfaces was defined.
- The thermal effects were considered for the thermo-mechanical calculations, including the heat transfer between the slab and rolls and the slab and the environment. Therefore, the heat transfer coefficients were defined. In addition, the temperature of the environment and the temperature of the rolls were also defined.
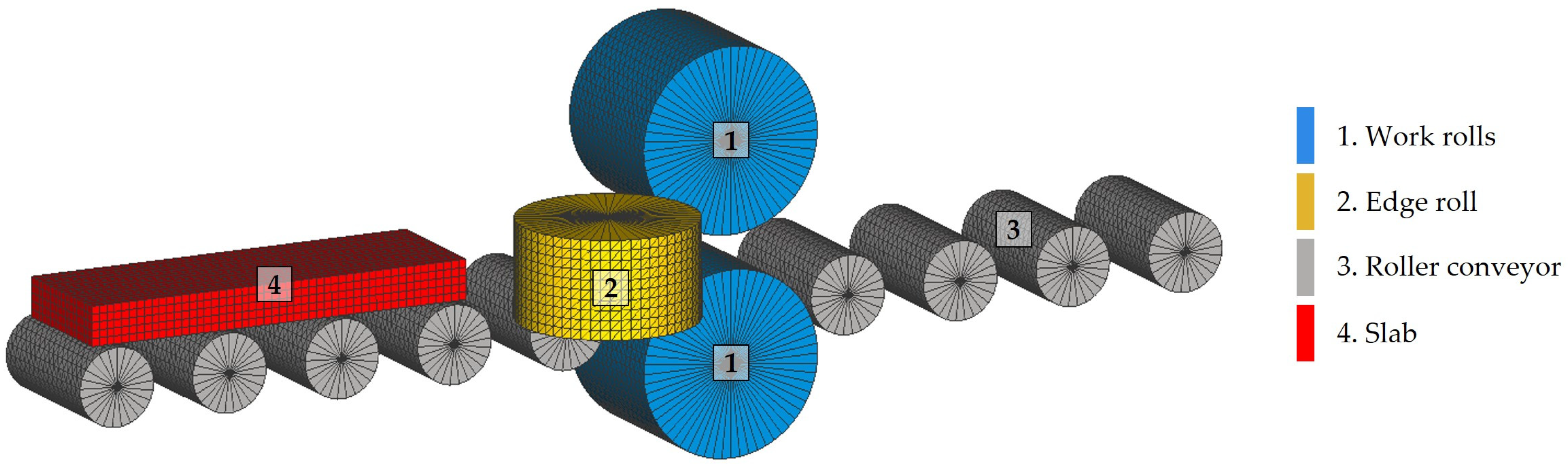
2.3.2. Model Description
2.3.3. Model Meshing
2.3.4. The Mathematical Model of the Material
2.3.5. Rolling Process Parameters
3. Results and Discussion
3.1. Model Optimization
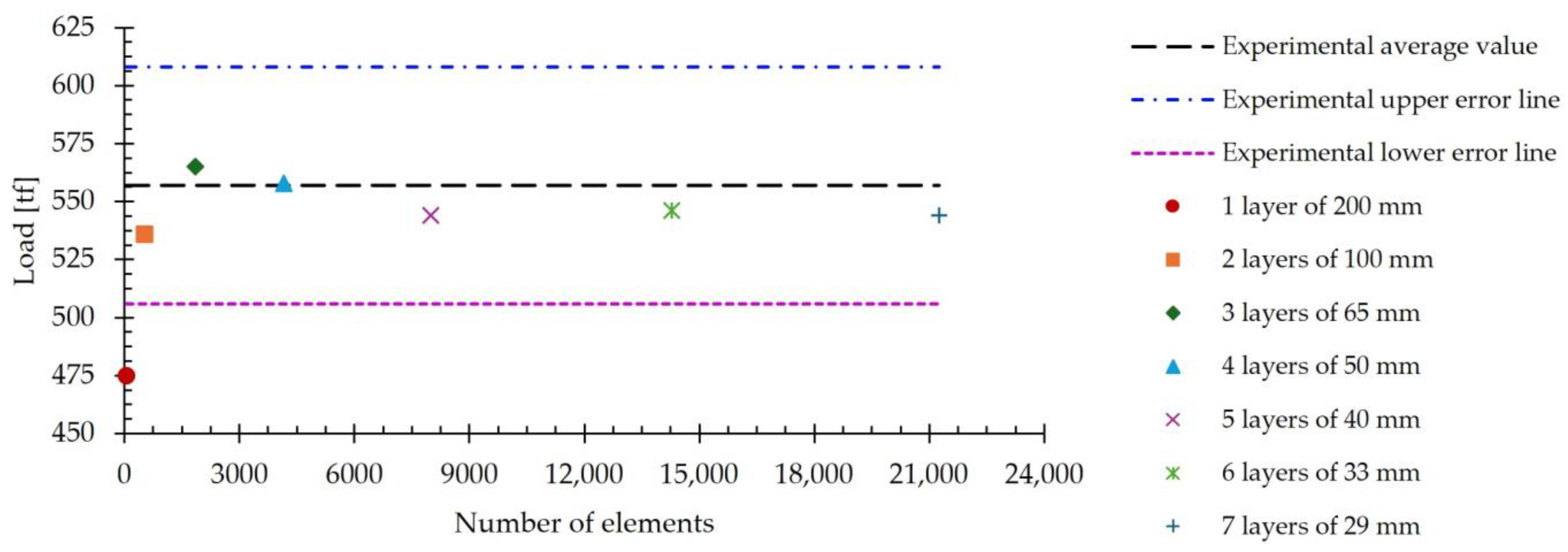
3.1.1. Mesh Sensitivity Analysis
3.1.2. Element Type Analysis
3.1.3. Symmetry Usage Analysis
3.1.4. The Simplification of the Model
3.2. Validation of Simulations
3.2.1. Thickness
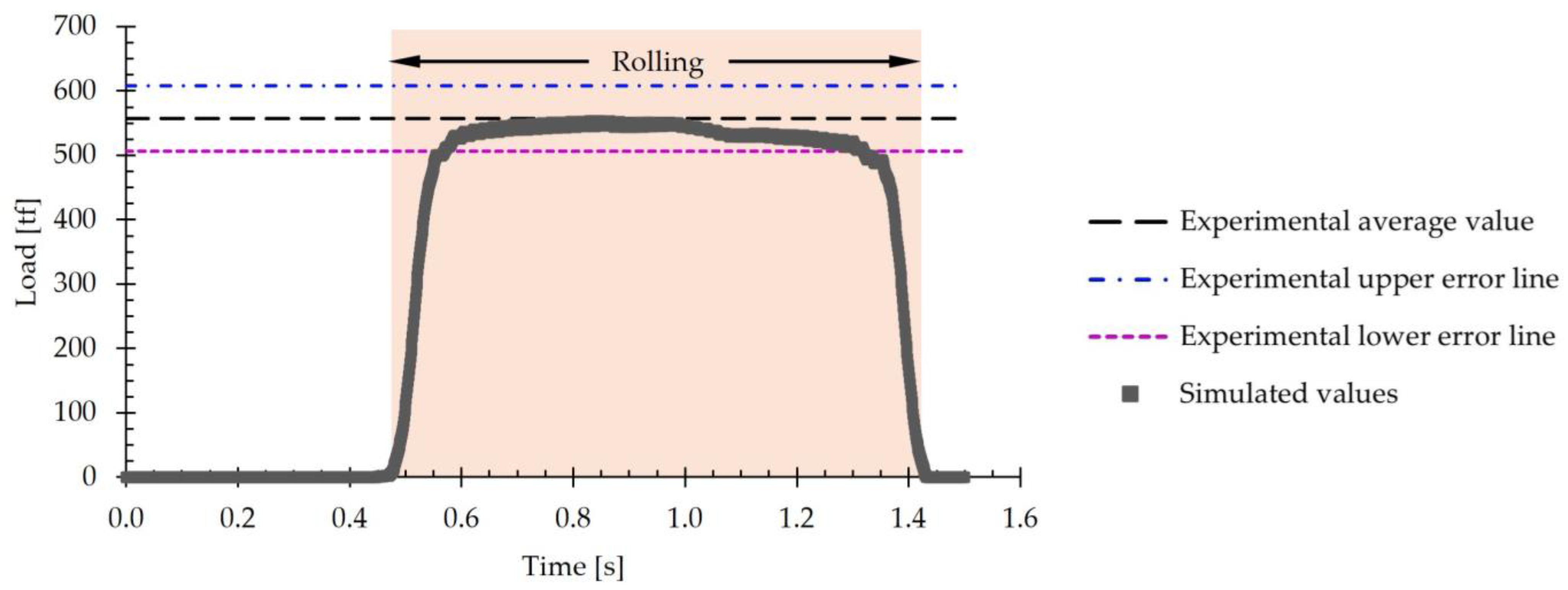
3.2.2. Load
3.3. Simulation Results
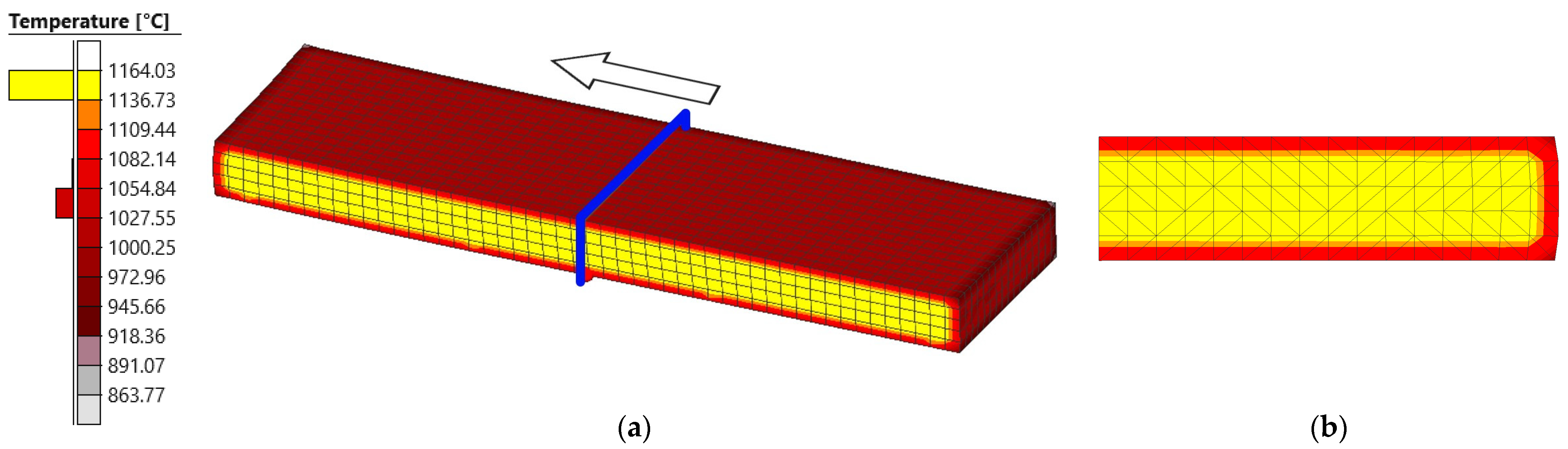
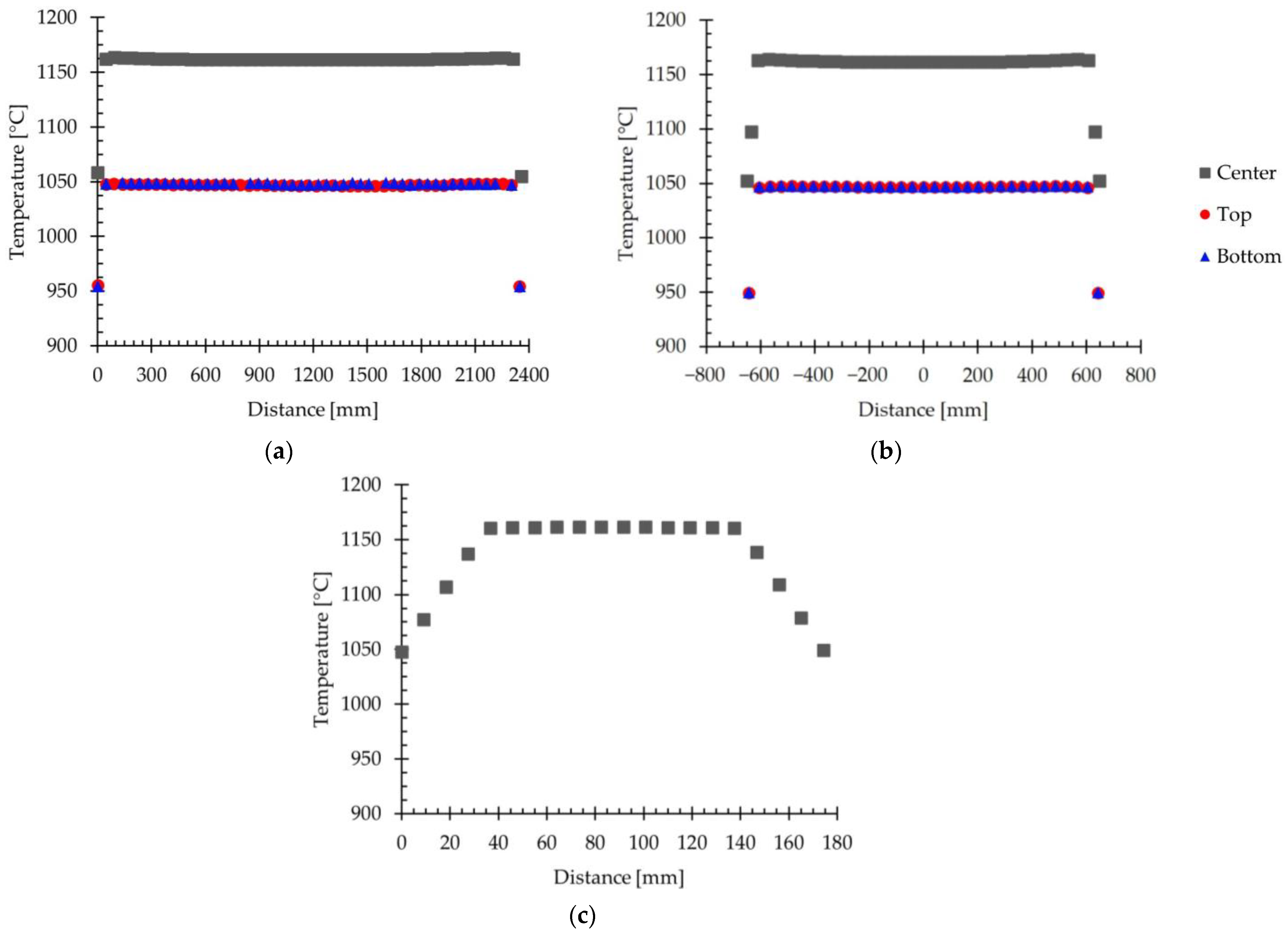
3.3.1. Temperature
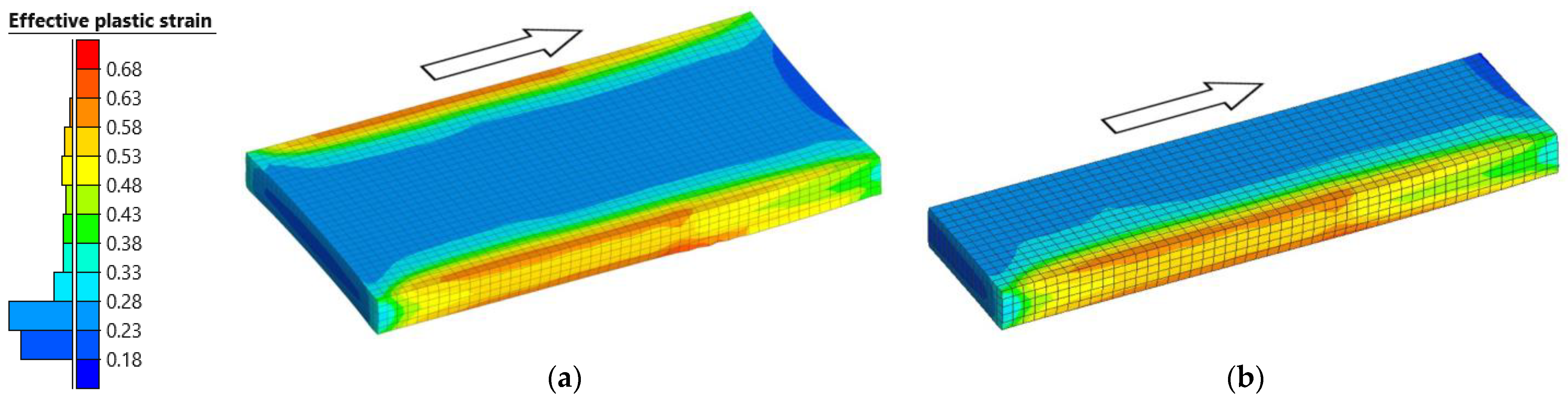
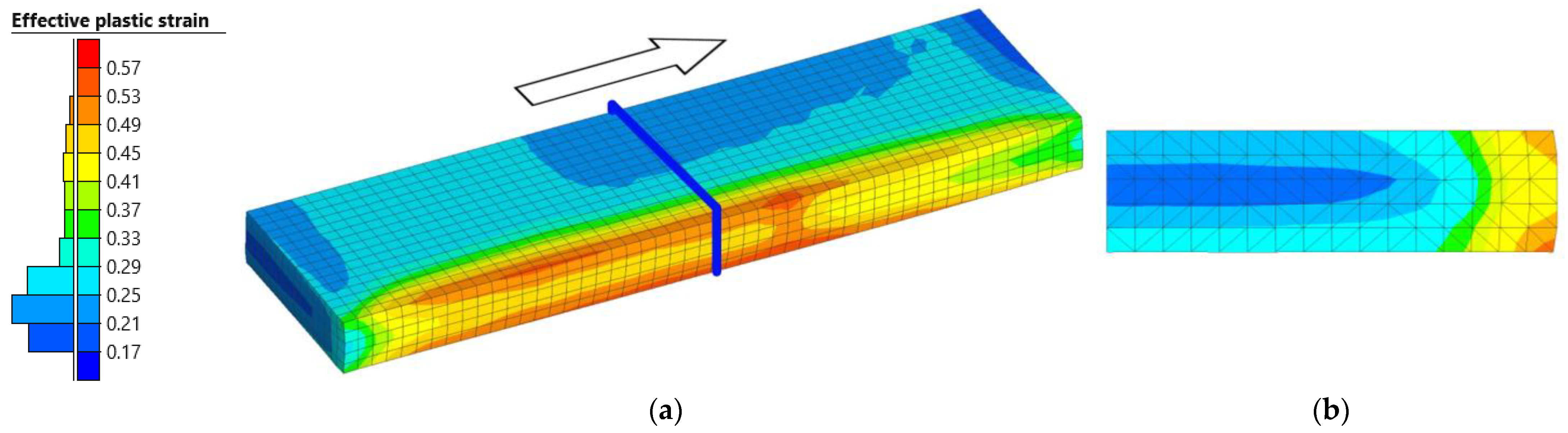
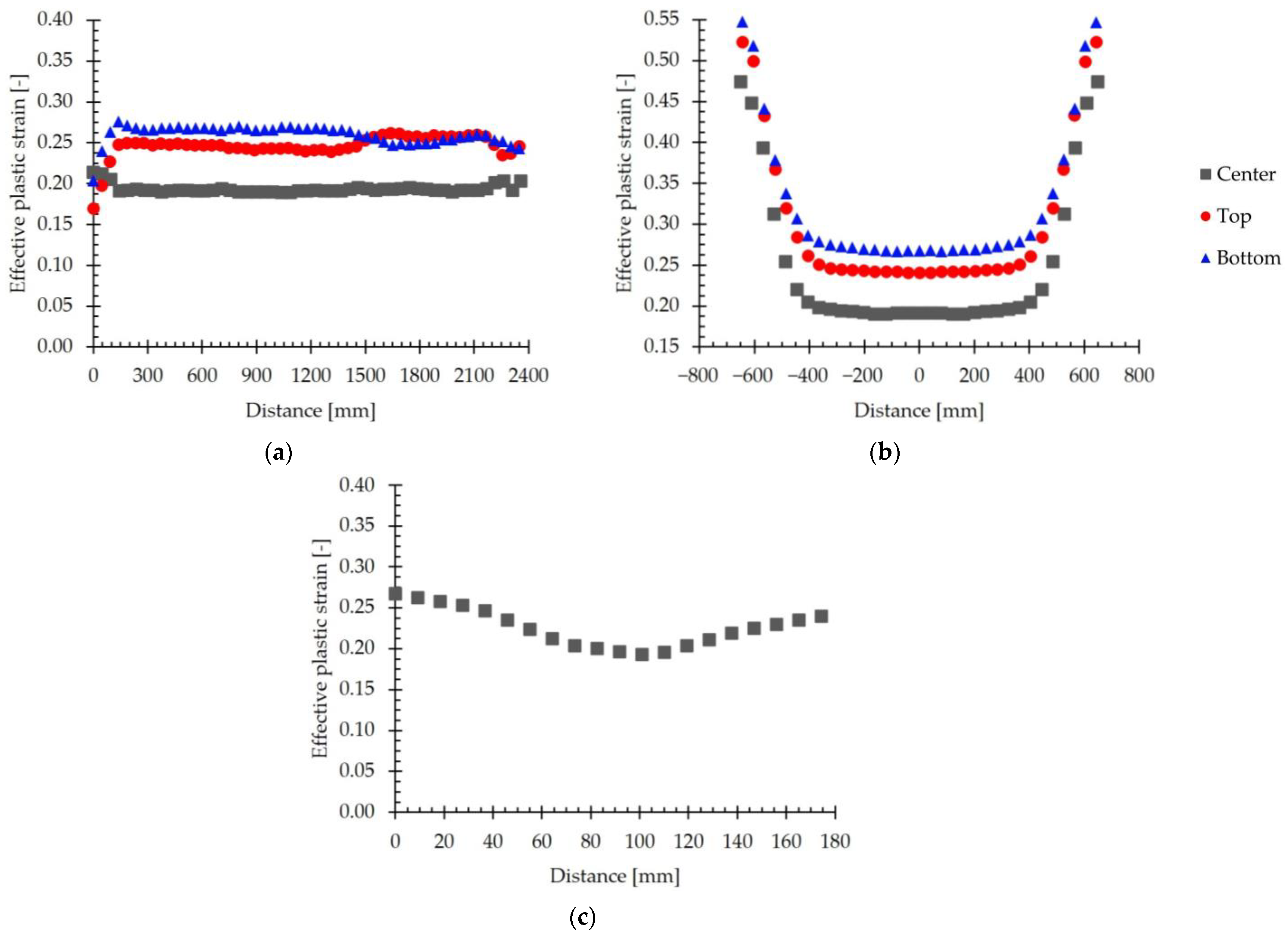
3.3.2. Effective Plastic Strain
4. Conclusions
- The literature review conducted revealed no previous studies in which simulations of the hot rolling of large format stainless-steel flat products using industrial rolling schedules by means of three-dimensional FEM models have been performed.
- A numerical finite element model was proposed for the simulation of the roughing stage of the hot rolling process of large-scale AISI 430 ferritic stainless-steel slabs. This model was used to simulate the first pass of the rolling schedule used in the industry in the manufacturing of flat products.
- The initial model was enhanced by means of a mesh sensitivity analysis, an element type analysis, the application of symmetry, and a simplification of the model. In this way, the computation time required to simulate the first pass was reduced from the 27,723 s needed to simulate the initial model to the 2727 s used to simulate the improved model. Thus, the computation time was reduced by 90.2%.
- The results obtained indicate that the reduction in computation time does not affect the accuracy of the numerical data, indicating that the model used represents a good compromise between computational time and the accuracy of the results.
- It was estimated that the error obtained in the thickness prediction was 0.3%, whereas the error in the rolling load prediction was 3.4%. These results show that the optimized numerical model can predict with sufficient precision and accuracy the hot rolling process of large-scale AISI 430 ferritic stainless-steel slabs using industrial rolling schedules.
- Results on the distribution of temperature and effective plastic strain were obtained from the simulations performed. Based on the results, it was found that the optimized model is able to correctly represent gradients of these magnitudes, it being possible to appreciate their variations in the longitudinal, transverse, and thickness directions.
- Numerical simulations were conducted for the first roughing pass of steel slabs with a length of 2000 mm. In the case of the studied AISI 430 stainless-steel products, slabs could reach lengths of up to 11,000 mm, which would require significantly longer simulation times. This challenge would become even more pronounced when simulating consecutive passes, where the thickness is substantially reduced. Such reductions necessitate a finer discretization of the finite element mesh to accurately capture the variations in the results along the thickness direction. Future work aims to employ the proposed optimized model to simulate the complete rolling schedule, which consists of seven passes. It is expected that the reduction obtained in the calculation time will allow us to study the complete process in a reasonable timeframe.
- The simulation of the first pass was performed using hexahedral elements. This type of element is well suited to regular geometries, such as the slab, and offers higher accuracy with fewer elements compared to tetrahedral elements. However, meshing complex geometries is more challenging. In industrial hot rolling process, significant deformation is observed at the front and tail of the slab, resulting in the characteristic “fishtailing” effect. These regions exhibit considerable geometric distortions, which can compromise the results of simulations using hexahedral meshes. This aspect should be studied in future work.
- Regarding the material mathematical model, an analytical GMT model was employed. The constants used in this model were calibrated for a temperature range of 700 °C to 1300 °C and an effective plastic strain of up to 2. In the simulation of the first pass, a maximum effective plastic strain value of 0.57 was obtained, suggesting that values exceeding 2 are expected in consecutive passes. Therefore, future studies will need to assess the validity and applicability of the analytical model used.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mehtonen, S.V.; Karjalainen, L.P.; Porter, D.A. Hot Deformation Behavior and Microstructure Evolution of a Stabilized High-Cr Ferritic Stainless Steel. Mater. Sci. Eng. A 2013, 571, 1–12. [Google Scholar] [CrossRef]
- Feng, C.-C.; Lin, M.-H.; Chen, Y.-C.; Ou, S.-F.; Huang, C.-C. Optimization of Continuous Casting for Preventing Surface Peeling Defects on Titanium-Containing Ferrite Stainless Steel. Materials 2023, 16, 1461. [Google Scholar] [CrossRef]
- Collado García, I. Origen de La Oxidación En Bordes Del AISI 430 Tras Recocido En Atmósfera Reductora; Universidad de Cádiz: Puerto Real, Spain, 2022. [Google Scholar]
- Ray, S. Principles and Applications of Metal Rolling; Cambridge University Press: Delhi, India, 2016; ISBN 978-1-107-07609-9. [Google Scholar]
- Ikumapayi, O.M.; Akinlabi, E.T.; Onu, P.; Abolusoro, O.P. Rolling Operation in Metal Forming: Process and Principles—A Brief Study. Mater. Today Proc. 2020, 26, 1644–1649. [Google Scholar] [CrossRef]
- Black, J.T.; Kohser, R.A. DeGarmo’s Materials and Processes in Manufacturing, 11th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; ISBN 978-0-470-92467-9. [Google Scholar]
- Shahani, A.R.; Nodamaie, S.A.; Salehinia, I. Parametric Study of Hot Rolling Process by the Finite Element Method. Sci. Iran. 2009, 16, 130–139. [Google Scholar]
- Jo, S.Y.; Hong, S.; Han, H.N.; Lee, M.G. Modeling and Simulation of Steel Rolling with Microstructure Evolution: An Overview. Steel Res. Int. 2023, 94, 2200260. [Google Scholar] [CrossRef]
- Koo, B.S. Longitudinal Bending Behaviors of Hot-Rolled H-Beams by Quenching and Self-Tempering. Eng. Fail. Anal. 2022, 133, 106009. [Google Scholar] [CrossRef]
- Pérez-Alvarado, A.; Arreola-Villa, S.A.; Calderón-Ramos, I.; Servín Castañeda, R.; Mendoza de la Rosa, L.A.; Chattopadhyay, K.; Morales, R. Numerical Simulation of the Hot Rolling Process of Steel Beams. Materials 2021, 14, 7038. [Google Scholar] [CrossRef]
- Serajzadeh, S. Hot Rolling and Direct Cooling. In Comprehensive Materials Processing; Hashmi, S., Batalha, G.F., Van Tyne, C.J., Yilbas, B., Eds.; Elsevier: Oxford, UK, 2014; Volume 3, pp. 377–396. [Google Scholar]
- Yuan, S.; Zhang, L.; Liao, S.; Li, M.; Qi, M.; Zhen, Y.; Guo, S. Materials Static and Dynamic Finite Element Analysis of 304 Stainless Steel Rod and Wire Hot Continuous Rolling Process. J. Univ. Sci. Technol. Beijing 2008, 15, 324–329. [Google Scholar] [CrossRef]
- Nomoto, S.; Oba, M.; Mori, K.; Yamanaka, A. Microstructure-Based Multiscale Analysis of Hot Rolling of Duplex Stainless Steel Using Various Simulation Software. Integr. Mater. Manuf. Innov. 2017, 6, 69–82. [Google Scholar] [CrossRef]
- Rout, M.; Pal, S.K.; Singh, S.B. Finite Element Simulation of a Cross Rolling Process. J. Manuf. Process. 2016, 24, 283–292. [Google Scholar] [CrossRef]
- Ojeda-López, A.; Botana-Galvín, M.; González-Rovira, L.; Botana, F.J. Numerical Simulation as a Tool for the Study, Development, and Optimization of Rolling Processes: A Review. Metals 2024, 14, 737. [Google Scholar] [CrossRef]
- McLaren, A.J.; Sellars, C.M. Modelling Distribution of Microstructure during Hot Rolling of Stainless Steel. Inst. Mater. 1992, 8, 1090–1094. [Google Scholar] [CrossRef]
- Zhang, X.J.; Hodgson, P.D.; Thomson, P.F. The Effect of Through-Thickness Strain Distribution on the Static Recrystallization of Hot Rolled Austenitic Stainless Steel Strip. J. Mater. Process. Technol. 1996, 60, 615–619. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Howard, I.C.; Sellars, C.M. Development and Validation of a Finite Element Model for Hot Rolling Using ABAQUS/STANDARD. Mater. Sci. Technol. 2004, 20, 1123–1133. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Howard, I.C.; Sellars, C.M. Finite Element Modelling of Effects of Roll Gap Geometry in Hot Rolling. Mater. Sci. Technol. 2005, 21, 901–911. [Google Scholar] [CrossRef]
- Sun, C.-G.; Lee, J.-S.; Lee, J.-H.; Hwang, S.-M. Mechanism of Edge Seam Defects of Stainless Steel Generated during Hot Plate Rolling. ISIJ Int. 2006, 46, 93–99. [Google Scholar] [CrossRef][Green Version]
- Mukhopadhyay, A.; Higginson, R.L.; Howard, I.C.; Sellars, C.M. Strain Summation in Finite Element Modelling of Multipass Hot Rolling. Mater. Sci. Technol. 2007, 23, 29–37. [Google Scholar] [CrossRef]
- Kang, H.G.; Huh, M.Y.; Park, S.H.; Engler, O. Effect of Lubrication during Hot Rolling on the Evolution of Through-Thickness Textures in 18%Cr Ferritic Stainless Steel Sheet. Steel Res. Int. 2008, 79, 489–496. [Google Scholar] [CrossRef]
- Sadiq, T.O.; Fadara, T.G.; Aiyedun, P.O.; Idris, J. Numerical Estimation of Rolling Load and Torque for Hot Flat Rolling of Hcss316 at Low Strain Rates Based on Mean Temperature. Int. J. Eng. Res. Afr. 2016, 26, 11–29. [Google Scholar]
- Pourabdollah, P.; Serajzadeh, S. An Upper-Bound Finite Element Solution for Rolling of Stainless Steel 304L under Warm and Hot Deformation Conditions. Multidiscip. Model. Mater. Struct. 2016, 12, 514–533. [Google Scholar] [CrossRef]
- Pourabdollah, P.; Serajzadeh, S. A Study on Deformation Behavior of 304L Stainless Steel during and after Plate Rolling at Elevated Temperatures. J. Mater. Eng. Perform. 2017, 26, 885–893. [Google Scholar] [CrossRef]
- Faini, F.; Attanasio, A.; Ceretti, E. Experimental and FE Analysis of Void Closure in Hot Rolling of Stainless Steel. J. Mater. Process. Technol. 2018, 259, 235–242. [Google Scholar] [CrossRef]
- Rout, M.; Singh, S.B.; Pal, S.K. Microstructure and Texture Evolution in Austenitic Stainless Steel during Low Strain Rate Deformation at Elevated Temperature. Int. J. Mater. Form. 2020, 13, 605–621. [Google Scholar] [CrossRef]
- Mancini, S.; Langellotto, L.; Di Nunzio, P.E.; Zitelli, C.; Di Schino, A. Defect Reduction and Quality Optimization by Modeling Plastic Deformation and Metallurgical Evolution in Ferritic Stainless Steels. Metals 2020, 10, 186. [Google Scholar] [CrossRef]
- Zhou, L.H.; Bi, H.Y.; Sui, F.L.; Du, W.; Fang, X.S. Influence of Finish Rolling Temperature on Microstructure and Properties of Hot-Rolled SUS436L Stainless Steel. J. Mater. Eng. Perform. 2023, 32, 8441–8451. [Google Scholar] [CrossRef]
- Wang, Z.; Tang, G.; Lei, Z.; Wang, H.; Xu, Z.; Yu, H. Research on the Analytical Model of Rolling Force for TiAl Alloy Pack Rolling. Metall. Res. Technol. 2024, 121, 110. [Google Scholar] [CrossRef]
- Du, W.; Jiang, L.; Sun, Q.; Liu, Z.; Zhang, X. Microstructure, Texture, and Formability of Nb+Ti Stabilized High Purity Ferritic Stainless Steel. J. Iron Steel Res. Int. 2010, 17, 47–52. [Google Scholar] [CrossRef]
- Han, Y.; Sun, J.; Sun, J.; Zu, G.; Zhu, W.; Ran, X. High-Temperature Creep Behavior and Microstructural Evolution of a Cu-Nb Co-Alloyed Ferritic Heat-Resistant Stainless Steel. Acta Metall. Sin. 2021, 34, 789–801. [Google Scholar] [CrossRef]
- Sinclair, C.W.; Mithieux, J.D.; Schmitt, J.H.; Bréchet, Y. Recrystallization of Stabilized Ferritic Stainless Steel Sheet. Metall. Mater. Trans. A 2005, 36, 3205–3215. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, B.; Lin, L.; Feng, P.; Zhou, J.; Shen, J. Numerical Analysis and Experimental Trial of Axial Feed Skew Rolling for Forming Bars. Arch. Civ. Mech. Eng. 2022, 22, 17. [Google Scholar] [CrossRef]
- Wang, F.; Ning, L.; Zhu, Q.; Lin, J.; Dean, T.A. An Investigation of Descaling Spray on Microstructural Evolution in Hot Rolling. Int. J. Adv. Manuf. Technol. 2008, 38, 38–47. [Google Scholar] [CrossRef]
- Singh, G.; Singh, P.K. Improving the Energy Efficiency and Process Scrap in Grooved Hot Rolling of SAE 52100 Steel Billets. CIRP J. Manuf. Sci. Technol. 2023, 41, 55–68. [Google Scholar] [CrossRef]
- Topa, A.; Cerik, B.C.; Kim, D.K. A Useful Manufacturing Guide for Rotary Piercing Seamless Pipe by ALE Method. J. Mar. Sci. Eng. 2020, 8, 756. [Google Scholar] [CrossRef]
- Phaniraj, M.P.; Behera, B.B.; Lahiri, A.K. Thermo-Mechanical Modeling of Two Phase Rolling and Microstructure Evolution in the Hot Strip Mill: Part I. Prediction of Rolling Loads and Finish Rolling Temperature. J. Mater. Process. Technol. 2005, 170, 323–335. [Google Scholar] [CrossRef]
- Soulami, A.; Burkes, D.E.; Joshi, V.V.; Lavender, C.A.; Paxton, D. Finite-Element Model to Predict Roll-Separation Force and Defects during Rolling of U-10Mo Alloys. J. Nucl. Mater. 2017, 494, 182–191. [Google Scholar] [CrossRef]
- Hu, K.; Shi, Q.; Han, W.; Zhu, F.; Chen, J. On the Evolution of Temperature and Combined Stress in a Work Roll under Cyclic Thermo-Mechanical Loadings during Hot Strip Rolling and Idling. Materials 2020, 13, 5054. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Guo, L.; Wang, C.; Zhao, Y.; Qi, W.; Yun, X. Prediction of Dynamically Recrystallized Microstructure of AZ31 Magnesium Alloys in Hot Rolling Using an Expanded Dislocation Density Model. J. Mater. Eng. Perform. 2023, 32, 2607–2615. [Google Scholar] [CrossRef]
- Kache, H.; Stonis, M.; Behrens, B.A. Development of a Warm Cross Wedge Rolling Process Using FEA and Downsized Experimental Trials. Prod. Eng. 2012, 6, 339–348. [Google Scholar] [CrossRef]
- Xiangyu, G.; Wenquan, N.; Wenle, P.; Zhiquan, H.; Tao, W.; Lifeng, M. Deformation Behavior and Bonding Properties of Cu/Al Laminated Composite Plate by Corrugated Cold Roll Bonding. J. Mater. Res. Technol. 2023, 22, 3207–3217. [Google Scholar] [CrossRef]
- Jiang, L.-Y.; Chen, Y.-F.; Liang, J.-L.; Li, Z.-L.; Wang, T.; Ma, L.-F. Modeling of Layer Thickness and Strain for the Two-Layered Metal Clad Plate Rolling with the Different Roll Diameters. J. Mater. Res. Technol. 2024, 28, 3849–3864. [Google Scholar] [CrossRef]






| Ref. | Material | Length [mm] | Width [mm] | Thickness [mm] | Passes | Numerical Method | Discretization |
|---|---|---|---|---|---|---|---|
| [16] | AISI 316L | 120 | 50 | 30 | 1 | FEM; FDM | 2D |
| [17] | AISI 304 | N/S | N/S | 2 | 1 | FEM | 2D |
| [18] | AISI 316L | 100 | 30 | 18 | 1 | FEM | 2D |
| [19] | AISI 316L | N/S | N/S | <50 | 1 | FEM | 2D |
| [20] | AISI 304 | 1260 | N/S | 200 | 4 | FEM | 2D |
| [21] | AISI 316L | N/S | N/S | 14.3; 20 | 2 | FEM | 2D |
| [22] | 18%Cr FSS | N/S | N/S | 10 | 3 | FEM | 2D |
| [23] | AISI 316 | N/S | N/S | N/S | N/S | N/S | N/S |
| [24] | AISI 304L | 140 | 40 | 4 | 1 | FEM | 2D |
| [25] | AISI 304L | 120 | 60 | 4 | 1 | FEM | 2D |
| [26] | AISI 316L | 1000 | 340 | 280 | 1 | FEM | 3D |
| [27] | AISI 304LN | 78 | 10 | 10 | 1 | FEM | 3D |
| [28] | 1.4512 FSS | N/S | N/S | N/S | 5 | N/S | N/S |
| [29] | AISI 436L | N/S | N/S | 90 | 3 | FEM | 2D |
| [30] | AISI 304 | N/S | N/S | N/S | 1 | FEM | 3D |
| Pass Number | Initial Thickness [mm] | Final Thickness [mm] | Reduction Ratio [%] | Roll Gap [mm] | Edge Roll Gap [mm] | Linear Velocity [m·min−1] |
|---|---|---|---|---|---|---|
| 1 | 200.0 | 174.5 | 12.8 | 175.2 | 1269.0 | 156 |
| 2 | 174.5 | 145.6 | 16.6 | 147.9 | N/A | 180 |
| 3 | 145.6 | 116.2 | 20.2 | 116.2 | 1253.0 | 196 |
| 4 | 116.2 | 87.4 | 24.8 | 87.0 | N/A | 214 |
| 5 | 87.4 | 61.8 | 29.3 | 60.7 | 1253.0 | 270 |
| 6 | 61.8 | 41.4 | 33.0 | 39.9 | N/A | 279 |
| 7 | 41.4 | 27.0 | 34.8 | 24.9 | 1268.0 | 245 |
| Fe | Cr | Cu | Mn | Mo | Ni | Si | C | N | P | S |
|---|---|---|---|---|---|---|---|---|---|---|
| Balance | 16.7 | 0.09 | 0.37 | 0.016 | 0.22 | 0.41 | 0.027 | 0.029 | 0.022 | 0.001 |
| Parameters | Values [mm] |
|---|---|
| Diameter of the work rolls | 940 |
| Length of the work rolls | 1930 |
| Diameter of the edge rolls | 910 |
| Height of the edge rolls | 250 |
| Diameter of the rolls of the roller conveyor | 400 |
| Length of the rolls of the roller conveyor | 1930 |
| Length of the slab | 2000 |
| Width of the slab | 1280 |
| Thickness of the slab | 200 |
| c1 | c2 | n1 | n2 | l1 | l2 | m1 | m2 |
|---|---|---|---|---|---|---|---|
| 5862.37 N·m−2·s(m1T+m2) | −4.69 × 10−3 °C−1 | −3.02 × 10−4 °C−1 | 3.66 × 10−1 | −8.78 × 10−5 °C−1 | 7.24 × 10−2 | 1.96 × 10−4 °C−1 | −5.47 × 10−2 |
| No. of Elements in Thickness Direction | Element Size [mm] | No. of Elements of the Slab | Computation Time [s] | Average Load [tf] | Error [%] |
|---|---|---|---|---|---|
| 1 | 200 | 60 | 7098 | 475 | 14.7 |
| 2 | 100 | 520 | 7050 | 536 | 3.8 |
| 3 | 65 | 1860 | 11,063 | 565 | 1.4 |
| 4 | 50 | 4160 | 15,741 | 558 | 0.2 |
| 5 | 40 | 8000 | 27,723 | 544 | 2.3 |
| 6 | 33 | 14,274 | 43,468 | 546 | 2.0 |
| 7 | 29 | 21,252 | 69,558 | 544 | 2.3 |
| Model | No. of Elements of the Slab | No. of Elements of the Mill | Total No. of Elements | Computation Time [s] | Time Reduction [%] |
|---|---|---|---|---|---|
| Tetrahedral Elements, Figure 5b | 59,700 | 47,495 | 107,195 | 33,730 | - |
| Hexahedral Elements, Figure 5a | 8000 | 47,495 | 55,495 | 27,723 | 17.8 |
| Symmetrical, Figure 7 | 4000 | 17,718 | 21,718 | 4748 | 85.9 |
| Simplified, Figure 9 | 4000 | 13,782 | 17,782 | 2727 | 91.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ojeda-López, A.; Botana-Galvín, M.; Collado-García, I.; González-Rovira, L.; Botana, F.J. Finite Element Simulation of Hot Rolling for Large-Scale AISI 430 Ferritic Stainless-Steel Slabs Using Industrial Rolling Schedules—Part 1: Set-Up, Optimization, and Validation of Numerical Model. Materials 2025, 18, 383. https://doi.org/10.3390/ma18020383
Ojeda-López A, Botana-Galvín M, Collado-García I, González-Rovira L, Botana FJ. Finite Element Simulation of Hot Rolling for Large-Scale AISI 430 Ferritic Stainless-Steel Slabs Using Industrial Rolling Schedules—Part 1: Set-Up, Optimization, and Validation of Numerical Model. Materials. 2025; 18(2):383. https://doi.org/10.3390/ma18020383
Chicago/Turabian StyleOjeda-López, Adrián, Marta Botana-Galvín, Irene Collado-García, Leandro González-Rovira, and Francisco Javier Botana. 2025. "Finite Element Simulation of Hot Rolling for Large-Scale AISI 430 Ferritic Stainless-Steel Slabs Using Industrial Rolling Schedules—Part 1: Set-Up, Optimization, and Validation of Numerical Model" Materials 18, no. 2: 383. https://doi.org/10.3390/ma18020383
APA StyleOjeda-López, A., Botana-Galvín, M., Collado-García, I., González-Rovira, L., & Botana, F. J. (2025). Finite Element Simulation of Hot Rolling for Large-Scale AISI 430 Ferritic Stainless-Steel Slabs Using Industrial Rolling Schedules—Part 1: Set-Up, Optimization, and Validation of Numerical Model. Materials, 18(2), 383. https://doi.org/10.3390/ma18020383









