The Effect of Varying Abutment Heights on Stress Distribution in Different Bone Densities: A Finite Element Analysis Study
Abstract
1. Introduction
2. Materials and Methods
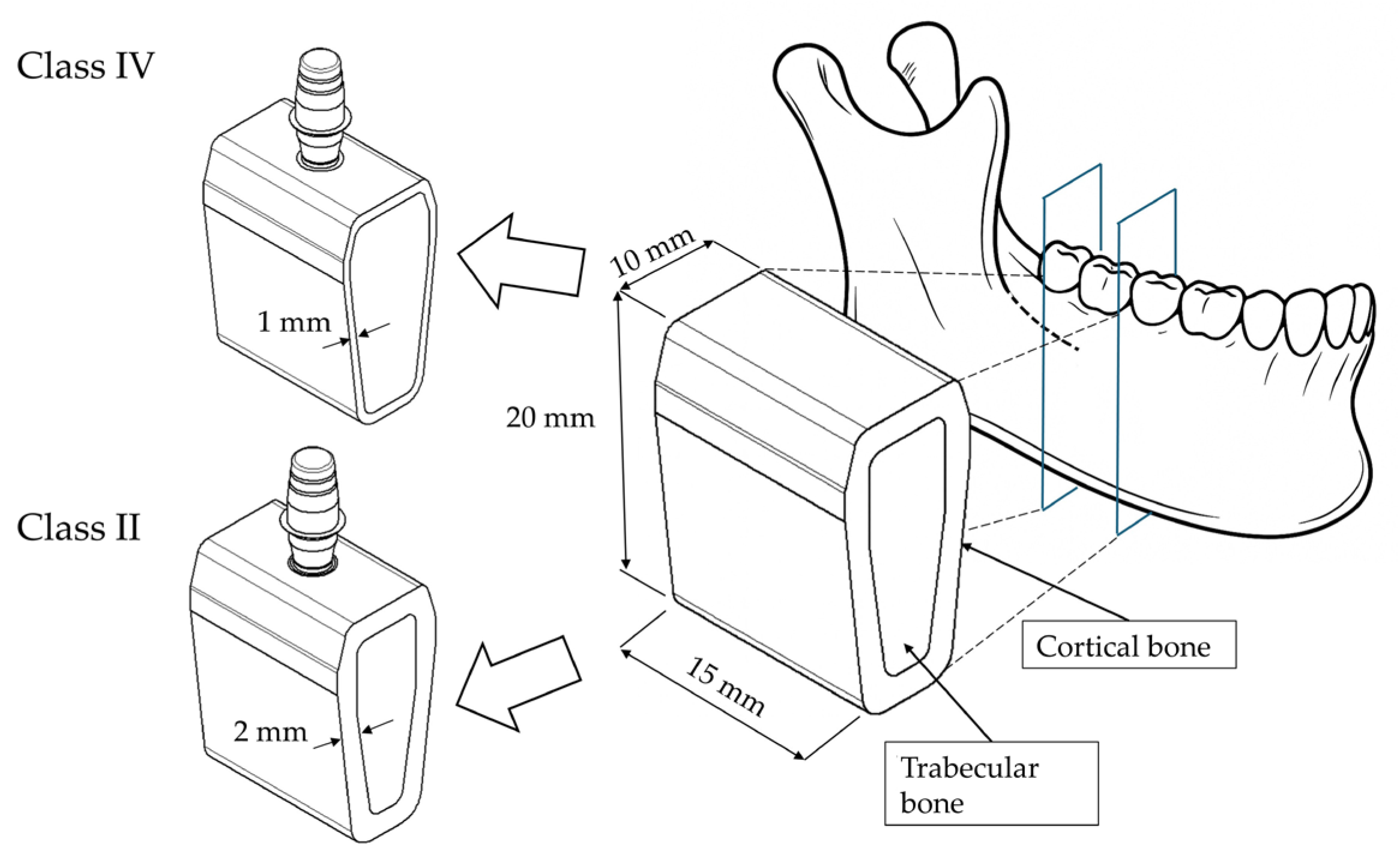
2.1. Modeling
2.2. Materials
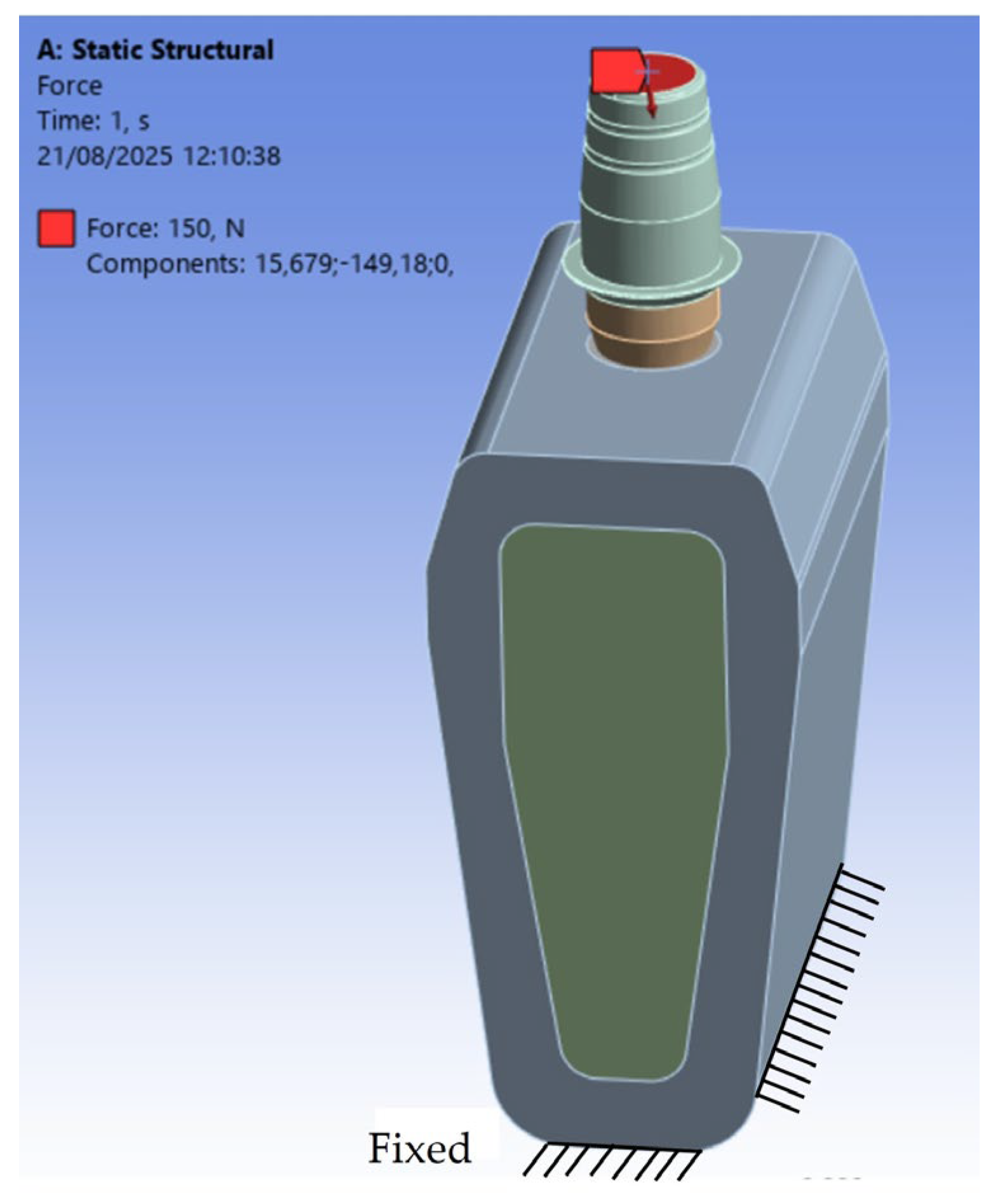
2.3. Constraints and Loading Conditions
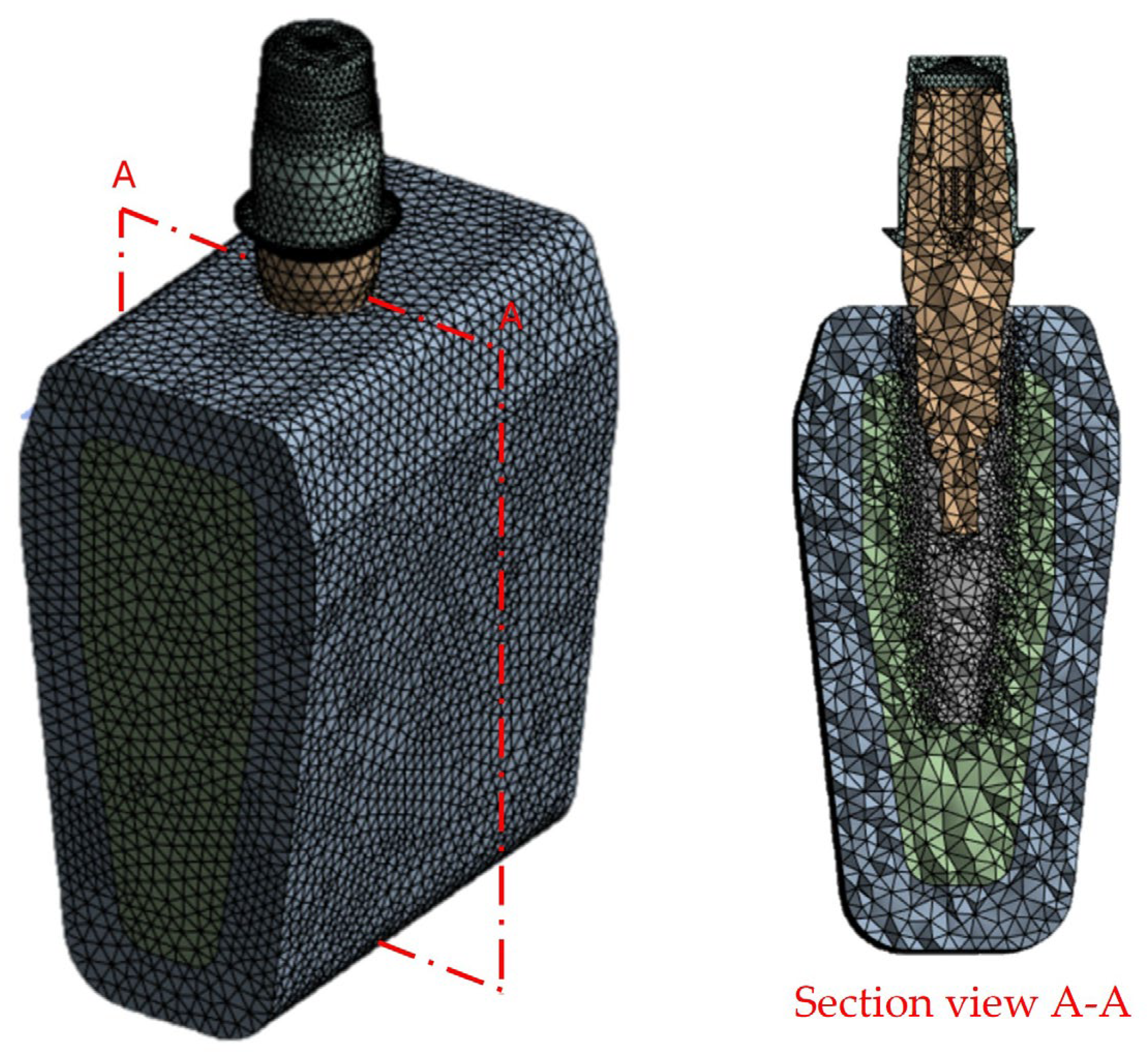
2.4. Finite Element Analysis (FEA)
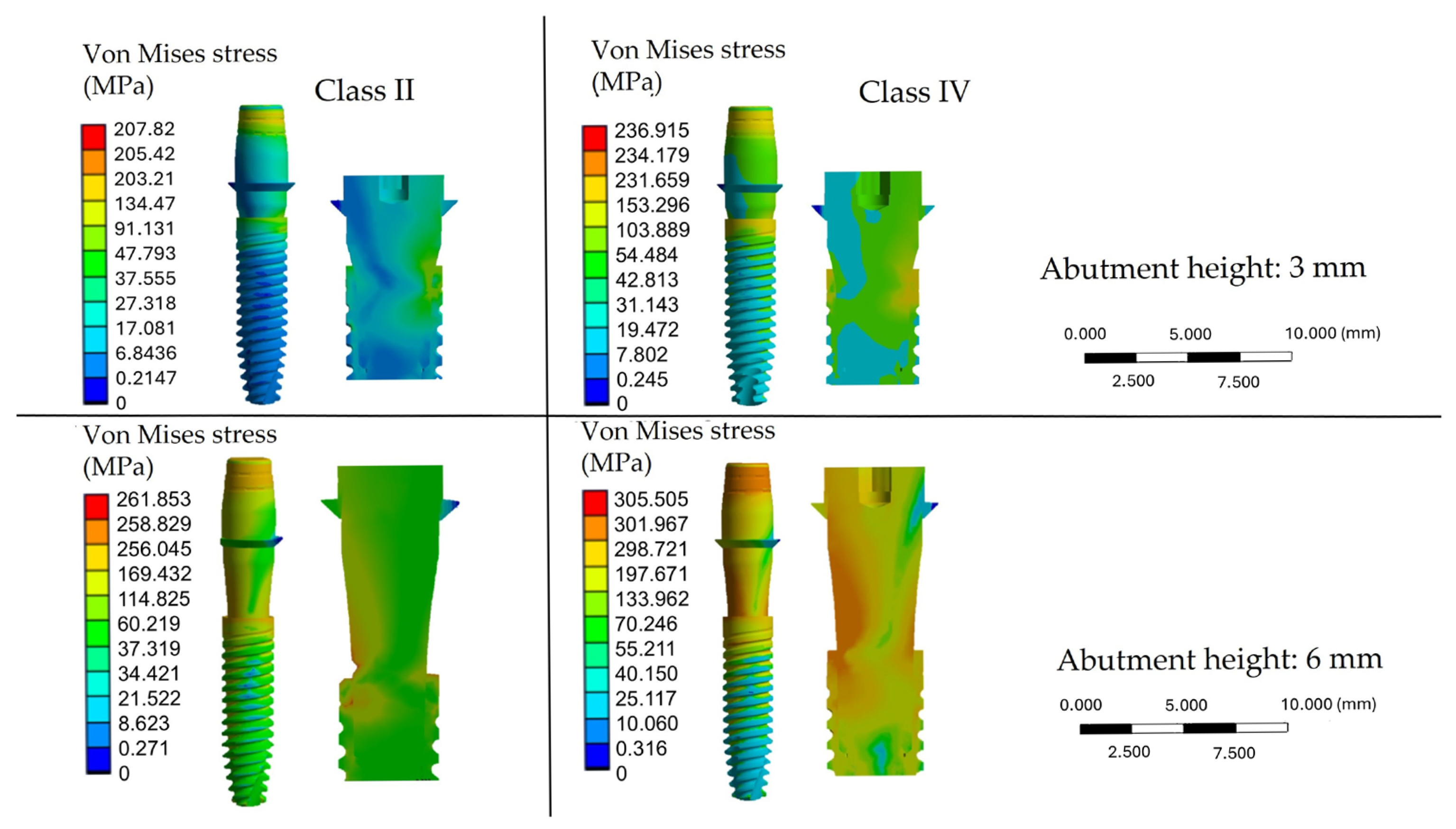
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BIC | Bone-implant contact |
| MBL | Marginal bone loss |
| FEA | Finite element analysis |
| 3D | Three-dimensional |
| CAD | Computer-aided design |
| CT | Computed tomography |
References
- Papaspyridakos, P.; Chen, C.J.; Singh, M.; Weber, H.P.; Gallucci, G. Success criteria in implant dentistry: A systematic review. J. Dent. Res. 2012, 91, 242–248. [Google Scholar] [CrossRef]
- Sartoretto, S.C.; Shibli, J.A.; Javid, K.; Cotrim, K.; Canabarro, A.; Louro, R.S.; Lowenstein, A.; Mourão, C.F.; Moraschini, V. Comparing the long-term success rates of tooth preservation and dental implants: A critical review. J. Funct. Biomater. 2023, 14, 142. [Google Scholar] [CrossRef]
- Alfaraj, T.A.; Al-Madani, S.; Alqahtani, N.S.; Almohammadi, A.A.; Alqahtani, A.M.; AlQabbani, H.S.; Bajunaid, M.K.; Alharthy, B.A.; Aljalfan, N. Optimizing osseointegration in dental implantology: A cross-disciplinary review of current and emerging strategies. Cureus 2023, 15, e47943. [Google Scholar] [CrossRef] [PubMed]
- Kochar, S.P.; Reche, A.; Paul, P. The etiology and management of dental implant failure: A review. Cureus 2022, 14, e30455. [Google Scholar] [CrossRef] [PubMed]
- Donos, N.; Akcali, A.; Padhye, N.; Sculean, A.; Calciolari, E. Bone regeneration in implant dentistry: Which are the factors affecting the clinical outcome? Periodontol. 2000 2023, 93, 26–55. [Google Scholar] [CrossRef]
- Fiorillo, L.; Cicciù, M.; Tözüm, T.F.; D’Amico, C.; Oteri, G.; Cervino, G. Impact of bisphosphonate drugs on dental implant healing and peri-implant hard and soft tissues: A systematic review. BMC Oral Health 2022, 22, 291. [Google Scholar] [CrossRef]
- De Francesco, M.; Ferrara, E.; Inchingolo, F.; Dalmaschio, G.; Pispero, A.; Inchingolo, A.M.; Dipalma, G.; Testori, T.; Tartaglia, G.M.; Rapone, B. Soft-Tissue Management Dental Implants with Digitally Customized Healing Abutments: A Pilot Study. Prosthesis 2024, 6, 596–618. [Google Scholar] [CrossRef]
- Wang, L.; Wang, T.; Lu, Y.; Fan, Z. Comparing the Clinical Outcome of Peri-implant Hard and Soft Tissue Treated with Immediate Individualized CAD/CAM Healing Abutments and Conventional Healing Abutments for Single-Tooth Implants in Esthetic Areas Over 12 Months: A Randomized Clinical Trial. Int. J. Oral Maxillofac. Implants 2021, 36, 984–997. [Google Scholar] [CrossRef]
- Chang, H.H.; Yeh, C.L.; Wang, Y.L.; Huang, Y.C.; Tsai, S.J.; Li, Y.T.; Lin, C.P.; Yang, J.H. Differences in the biomechanical behaviors of natural teeth and dental implants. Dent. Mater. 2021, 37, 682–689. [Google Scholar] [CrossRef] [PubMed]
- Sheba, M.; Floriani, F.; Nimmo, A.; Ercoli, C.; Hosney, S. Interproximal contact loss between implant restorations and adjacent natural teeth: A systematic review and meta-analysis. J. Prosthodont. 2024, 33, 313–323. [Google Scholar] [CrossRef]
- Nimmawitt, P.; Aliyu, A.A.A.; Lohwongwatana, B.; Arunjaroensuk, S.; Puncreobutr, C.; Mattheos, N.; Pimkhaokham, A. Understanding the stress distribution on anatomic customized root-analog dental implant at bone-implant interface for different bone densities. Materials 2022, 15, 6379. [Google Scholar] [CrossRef] [PubMed]
- Pandey, C.; Rokaya, D.; Bhattarai, B.P. Contemporary concepts in osseointegration of dental implants: A review. BioMed Res. Int. 2022, 2022, 6170452. [Google Scholar] [CrossRef]
- Kreve, S.; Ferreira, I.; da Costa Valente, M.L.; Dos Reis, A.C. Relationship between dental implant macro-design and osseointegration: A systematic review. Oral Maxillofac. Surg. 2024, 28, 1–14. [Google Scholar] [CrossRef]
- Sayed, M.E.; Mugri, M.H.; Almasri, M.A.; Al-Ahmari, M.M.; Bhandi, S.; Madapusi, T.B.; Varadarajan, S.; Raj, A.T.; Reda, R.; Testarelli, L.; et al. Role of stem cells in augmenting dental implant osseointegration: A systematic review. Coatings 2021, 11, 1035. [Google Scholar] [CrossRef]
- Cooper, L.F.; Shirazi, S. Osseointegration—The biological reality of successful dental implant therapy: A narrative review. Front. Oral Maxillofac. Med. 2022, 4, 39. [Google Scholar] [CrossRef]
- Insua, A.; Monje, A.; Wang, H.L.; Miron, R.J. Basis of bone metabolism around dental implants during osseointegration and peri-implant bone loss. J. Biomed. Mater. Res. Part A 2017, 105, 2075–2089. [Google Scholar] [CrossRef]
- Shemtov-Yona, K.; Rittel, D. An overview of the mechanical integrity of dental implants. BioMed Res. Int. 2015, 2015, 547384. [Google Scholar] [CrossRef]
- Schwarz, M.S. Mechanical complications of dental implants. Clin. Oral Implants Res. 2000, 11, 156–158. [Google Scholar] [CrossRef]
- Verma, A.; Singh, S.V.; Arya, D.; Shivakumar, S.; Chand, P. Mechanical failures of dental implants and supported prostheses: A systematic review. J. Oral Biol. Craniofacial Res. 2023, 13, 306–314. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.J.; Lee, J.H.; Kim, J.C.; Lee, J.B.; Yeo, I.L. Biological Responses to the Transitional Area of Dental Implants: Material- and Structure-Dependent Responses of Peri-Implant Tissue to Abutments. Materials 2019, 13, 72. [Google Scholar] [CrossRef] [PubMed]
- Romanos, G.E.; Traini, T.; Johansson, C.B.; Piattelli, A. Biologic width and morphologic characteristics of soft tissues around immediately loaded implants: Studies performed on human autopsy specimens. J. Periodontol. 2010, 81, 70–78. [Google Scholar] [CrossRef]
- Piattelli, A.; Scarano, A.; Piattelli, M.; Bertolai, R.; Panzoni, E. Histologic aspects of the bone and soft tissues surrounding three titanium non-submerged plasma-sprayed implants retrieved at autopsy: A case report. J. Periodontol. 1997, 68, 694–700. [Google Scholar] [CrossRef]
- Nimbalkar, S.; Dhatrak, P.; Gherde, C.; Joshi, S. A review article on factors affecting bone loss in dental implants. Mater. Today Proc. 2021, 43, 970–976. [Google Scholar] [CrossRef]
- Chung, D.M.; Oh, T.J.; Lee, J.; Misch, C.E.; Wang, H.L. Factors affecting late implant bone loss: A retrospective analysis. Int. J. Oral Maxillofac. Implants 2007, 22, 117–126. [Google Scholar] [PubMed]
- Hultin, M.; Fischer, J.; Gustafsson, A.; Kallus, T.; Klinge, B. Factors affecting late fixture loss and marginal bone loss around teeth and dental implants. Clin. Implants Dent. Relat. Res. 2000, 2, 203–208. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Lin, C.Y.; Li, J.; Wang, H.L.; Yu, H. Influence of abutment height on peri-implant marginal bone loss: A systematic review and meta-analysis. J. Prosthet. Dent. 2019, 122, 14–21. [Google Scholar] [CrossRef]
- Monje, A.; Kan, J.Y.; Borgnakke, W. Impact of local predisposing/precipitating factors and systemic drivers on peri-implant diseases. Clin. Implants Dent. Relat. Res. 2023, 25, 640–660. [Google Scholar] [CrossRef] [PubMed]
- Amo, F.S.L.D.; Romero-Bustillos, M.; Catena, A.; Galindo-Moreno, P.; Sánchez-Suárez, J.M.; Sánchez, R.; Garaicoa-Pazmino, C. Effect of Abutment Height on Marginal Bone Loss Around Dental Implants: A Systematic Review. Int. J. Prosthodont. 2024, 37, 95–102G. [Google Scholar] [CrossRef]
- Spinato, S.; Galindo-Moreno, P.; Bernardello, F.; Zaffe, D. Minimum Abutment Height to Eliminate Bone Loss: Influence of Implant Neck Design and Platform Switching. Int. J. Oral Maxillofac. Implants 2018, 33, 405–411. [Google Scholar] [CrossRef]
- Lin, G.H.; Lee, E.; Barootchi, S.; Rosen, P.S.; Curtis, D.; Kan, J.; Wang, H.L. The influence of prosthetic designs on peri-implant bone loss: An AO/AAP systematic review and meta-analysis. J. Periodontol. 2025, 96, 634–651. [Google Scholar] [CrossRef]
- Bulaqi, H.A.; Mashhadi, M.M.; Safari, H.; Samandari, M.M.; Geramipanah, F. Effect of increased crown height on stress distribution in short dental implant components and their surrounding bone: A finite element analysis. J. Prosthet. Dent. 2015, 113, 548–557. [Google Scholar] [CrossRef]
- Sunil, S.; Dhatrak, P. Biomechanical consideration of bone density and its influence on stress distribution characteristics of dental implants. Mater. Today Proc. 2021, 46, 478–483. [Google Scholar] [CrossRef]
- Premnath, K.; Sridevi, J.; Kalavathy, N.; Nagaranjani, P.; Sharmila, M.R. Evaluation of stress distribution in bone of different densities using different implant designs: A three-dimensional finite element analysis. J. Indian Prosthodont. Soc. 2013, 13, 555–559. [Google Scholar] [CrossRef]
- Ceddia, M.; Romasco, T.; De Bortoli Jr, N.; Mello, B.F.; Piattelli, A.; Mijiritsky, E.; Di Pietro, N.; Trentadue, B. Biomechanical Finite Element Analysis of Two Types of Short-Angled Implants Across Various Bone Classifications. Materials 2024, 17, 5680. [Google Scholar] [CrossRef] [PubMed]
- Ceddia, M.; Solarino, G.; Cassano, G.D.; Trentadue, B. Finite Element Study on Stability in the Femoral Neck and Head Connection to Varying Geometric Parameters with the Relates Implications on the Effect of Wear. J. Compos. Sci. 2023, 7, 387. [Google Scholar] [CrossRef]
- Ceddia, M.; Trentadue, B. A review of carbon fiber-reinforced polymer composite used to solve stress shielding in total hip replacement. AIMS Mater. Sci. 2024, 11, 449–462. [Google Scholar] [CrossRef]
- Ceddia, M.; Lamberti, L.; Trentadue, B. FEA comparison of the mechanical behavior of three dental crown materials: Enamel, ceramic, and zirconia. Materials 2024, 17, 673. [Google Scholar] [CrossRef]
- Ceddia, M.; Romasco, T.; Comuzzi, L.; Cipollina, A.; Piattelli, A.; Dipalma, G.; Inchingolo, A.M.; Inchingolo, F.; Di Pietro, N.; Trentadue, B. The influence of cement thickness within the cap on stress distribution for dental implants. J. Funct. Biomater. 2024, 15, 199. [Google Scholar] [CrossRef]
- Comuzzi, L.; Tumedei, M.; Di Pietro, N.; Romasco, T.; Hossein, H.H.S.; Montesani, L.; Inchingolo, F.; Piattelli, A.; Covani, U. A comparison of conical and cylindrical implants inserted in an in vitro post-extraction model using low-density polyurethane foam blocks. Materials 2023, 16, 5064. [Google Scholar] [CrossRef]
- Comuzzi, L.; Tumedei, M.; Romasco, T.; Petrini, M.; Afrashtehfar, K.I.; Inchingolo, F.; Piattelli, A.; Di Pietro, N. Insertion torque, removal torque, and resonance frequency analysis values of ultrashort, short, and standard dental implants: An in vitro study on polyurethane foam sheets. J. Funct. Biomater. 2022, 14, 10. [Google Scholar] [CrossRef] [PubMed]
- Bressan, E.; Lops, D.; Tomasi, C.; Ricci, S.; Stocchero, M.; Carniel, E.L. Experimental and computational investigation of Morse taper conometric system reliability for the definition of fixed connections between dental implants and prostheses. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2014, 228, 674–681. [Google Scholar] [CrossRef]
- Alla, I.; Scarano, A.; Sinjari, B.; Xhajanka, E.; Lorusso, F. Peri-Implant Bone Stability Around Tapered Implant Prosthetic Connection: A Systematic Review and Meta-Analysis Comparing Different Cone Morse and Conometric Implants Angle Contact and Coupling Interface Designs. Appl. Sci. 2025, 15, 1237. [Google Scholar] [CrossRef]
- Oliveira, M.R.; Gonçalves, A.; Gabrielli, M.A.C.; de Andrade, C.R.; Vieira, E.H.; Pereira-Filho, V.A. Evaluation of alveolar bone quality: Correlation between histomorphometric analysis and Lekholm and Zarb classification. J. Craniofacial Surg. 2021, 32, 2114–2118. [Google Scholar] [CrossRef] [PubMed]
- Alemayehu, D.B.; Jeng, Y.R. Three-dimensional finite element investigation into effects of implant thread design and loading rate on stress distribution in dental implants and anisotropic bone. Materials 2021, 14, 6974. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Fang, J.; Zhu, W.; Zhong, C.; Ye, D.; Zhu, M.; Lu, X.; Zhao, Y.; Ren, F. Bioinspired highly anisotropic, ultrastrong and stiff, and osteoconductive mineralized wood hydrogel composites for bone repair. Adv. Funct. Mater. 2021, 31, 2010068. [Google Scholar] [CrossRef]
- Liao, S.H.; Tong, R.F.; Dong, J.X. Anisotropic finite element modeling for patient-specific mandible. Comput. Methods Programs Biomed. 2007, 88, 197–209. [Google Scholar] [CrossRef]
- Dong, X.N.; Guo, X.E. The dependence of transversely isotropic elasticity of human femoral cortical bone on porosity. J. Biomech. 2004, 37, 1281–1287. [Google Scholar] [CrossRef]
- Zhang, G.; Jia, X.; Li, Z.; Wang, Q.; Gu, H.; Liu, Y.; Bai, Z.; Mao, H. Comprehensively characterizing heterogeneous and transversely isotropic properties of femur cortical bones. J. Mech. Behav. Biomed. Mater. 2024, 151, 106387. [Google Scholar] [CrossRef]
- Chen, J.; Lan, H.; Macciotta, R.; Wu, Y.; Li, Q.; Zhao, X. Anisotropy rather than transverse isotropy in Longmaxi shale and the potential role of tectonic stress. Eng. Geol. 2018, 247, 38–47. [Google Scholar] [CrossRef]
- O’Mahony, A.M.; Williams, J.L.; Spencer, P. Anisotropic elasticity of cortical and cancellous bone in the posterior mandible increases peri-implant stress and strain under oblique loading. Clin. Oral Implants Res. 2001, 12, 648–657. [Google Scholar] [CrossRef]
- Petrie, C.S.; Williams, J.L. Comparative evaluation of implant designs: Influence of diameter, length, and taper on strains in the alveolar crest. A three-dimensional finite-element analysis. Clin. Oral Implants Res. 2005, 16, 486–494. [Google Scholar] [CrossRef]
- Di Pietro, N.; Ceddia, M.; Romasco, T.; Junior, N.D.B.; Mello, B.F.; Tumedei, M.; Specchiulli, A.; Piattelli, A.; Trentadue, B. Finite element analysis (FEA) of the stress and strain distribution in cone-morse implant-abutment connection implants placed equicrestally and subcrestally. Appl. Sci. 2023, 13, 8147. [Google Scholar] [CrossRef]
- Watanabe, M.; Hattori, Y.; Satoh, C. Biological and biomechanical perspectives of normal dental occlusion. Int. Congr. Series 2005, 1284, 21–27. [Google Scholar] [CrossRef]
- Beltrán-Guijarro, M.; Pérez-Pevida, E.; Chávarri-Prado, D.; Estrada-Martínez, A.; Diéguez-Pereira, M.; Sánchez-Lasheras, F.; Brizuela-Velasco, A. Biomechanical Effects of Ti-Base Abutment Height on the Dental Implant System: A Finite Element Analysis. J. Funct. Biomater. 2024, 15, 101. [Google Scholar] [CrossRef]
- Hosseini-Faradonbeh, S.A.; Katoozian, H.R. Biomechanical evaluations of the long-term stability of dental implant using finite element modeling method: A systematic review. J. Adv. Prosthodont. 2022, 14, 182–202. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Mondragon, M.; Urriolagoitia-Sosa, G.; Romero-Ángeles, B.; García-Laguna, M.A.; Laguna-Canales, A.S.; Pérez-Partida, J.C.; Mireles-Hernández, J.; Carrasco-Hernández, F.; Urriolagoitia-Calderón, G.M. Biomechanical Fatigue Behavior of a Dental Implant Due to Chewing Forces: A Finite Element Analysis. Materials 2024, 17, 1669. [Google Scholar] [CrossRef]
- Reddy, M.S.; Sundram, R.; Abdemagyd, H.A.E. Application of finite element model in implant dentistry: A systematic review. J. Pharmcological Bioallied Sci. 2019, 11, S85–S92. [Google Scholar] [CrossRef]
- Qiu, P.; Cao, R.; Li, Z.; Fan, Z. A comprehensive biomechanical evaluation of length and diameter of dental implants using finite element analyses: A systematic review. Heliyon 2024, 10, e26876. [Google Scholar] [CrossRef]
- Falcinelli, C.; Valente, F.; Vasta, M.; Traini, T. Finite element analysis in implant dentistry: State of the art and future directions. Dent. Mater. 2023, 39, 539–556. [Google Scholar] [CrossRef]
- Chang, Y.; Tambe, A.A.; Maeda, Y.; Wada, M.; Gonda, T. Finite element analysis of dental implants with validation: To what extent can we expect the model to predict biological phenomena? A literature review and proposal for classification of a validation process. Int. J. Implants Dent. 2018, 4, 7. [Google Scholar] [CrossRef] [PubMed]
- Van Staden, R.C.; Guan, H.; Loo, Y.C. Application of the finite element method in dental implant research. Comput. Methods Biomech. Biomed. Eng. 2006, 9, 257–270. [Google Scholar] [CrossRef]
- Helgason, B.; Perilli, E.; Schileo, E.; Taddei, F.; Brynjólfsson, S.; Viceconti, M. Mathematical relationships between bone density and mechanical properties: A literature review. Clin. Biomech. 2008, 23, 135–146. [Google Scholar] [CrossRef] [PubMed]
- Kurniawan, D.; Nor, F.M.; Lee, H.Y.; Lim, J.Y. Finite element analysis of bone-implant biomechanics: Refinement through featuring various osseointegration conditions. Int. J. Oral Maxillofac. Surg. 2012, 1, 1090–1096. [Google Scholar] [CrossRef] [PubMed]
- Schoenbaum, T.R.; Karateew, E.D.; Schmidt, A.; Jadsadakraisorn, C.; Neugebauer, J.; Stanford, C.M. Implant-Abutment Connections and Their Effect on Implant Survival Rates and Changes in Marginal Bone Levels (ΔMBL): A Systematic Review and Meta-Analysis of 45,347 Oral Implants. Int. J. Oral Maxillofac. Implants 2023, 38, 37–45. [Google Scholar] [CrossRef]
- Spinato, S.; Stacchi, C.; Lombardi, T.; Bernardello, F.; Messina, M.; Dovigo, S.; Zaffe, D. Influence of abutment height and vertical mucosal thickness on early marginal bone loss around implants: A randomised clinical trial with an 18-month post-loading clinical and radiographic evaluation. Int. J. Oral Implantol. 2020, 13, 279–290. [Google Scholar]
- Galindo-Moreno, P.; León-Cano, A.; Ortega-Oller, I.; Monje, A.; Suárez, F.; ÓValle, F.; Spinato, S.; Catena, A. Prosthetic Abutment Height is a Key Factor in Peri-implant Marginal Bone Loss. J. Dent. Res. 2014, 93, 80S–85S. [Google Scholar] [CrossRef]
- Munoz, M.; Vilarrasa, J.; Ruíz-Magaz, V.; Albertini, M.; Nart, J. Influence of the abutment height on marginal bone level changes around two-piece dental implants: Meta-analysis and trial sequential analysis of randomized clinical trials. Clin. Oral Implants Res. 2023, 34, 81–94. [Google Scholar] [CrossRef]
- Laleman, I.; Lambert, F. Implant connection and abutment selection as a predisposing and/or precipitating factor for peri-implant diseases: A review. Clin. Implants Dent. Relat. Res. 2023, 25, 723–733. [Google Scholar] [CrossRef]
- Yoon, Y.; Kim, J.-E.; Kim, E.; Park, S.; Kang, I.; Kwon, Y.-D. Stability of the Implant–Alveolar Bone Complex According to the Peri-Implant Bone Loss and Bone Quality: A Finite Element Analysis Study. Appl. Sci. 2024, 14, 11674. [Google Scholar] [CrossRef]
- Okumura, N.; Stegaroiu, R.; Kitamura, E.; Kurokawa, K.; Nomura, S. Influence of maxillary cortical bone thickness, implant design and implant diameter on stress around implants: A three-dimensional finite element analysis. J. Prosthodont. Res. 2010, 54, 133–142. [Google Scholar] [CrossRef]
- Matsuoka, T.; Nakano, T.; Yamaguchi, S.; Ono, S.; Watanabe, S.; Sato, T.; Yatani, H. Effects of implant-abutment connection type and inter-implant distance on inter-implant bone stress and microgap: Three-dimensional finite element analysis. Materials 2021, 14, 2421. [Google Scholar] [CrossRef]
- Fernández-Asián, I.; Torres-Lagares, D.; Serrera-Figallo, M.Á.; Gutiérrez-Pérez, J.L. Relationship Between Implant Connection and Implant Fracture: Systematic Review. Bioengineering 2025, 12, 333. [Google Scholar] [CrossRef]
- Lorusso, F.; Gehrke, S.A.; Tari, S.R.; Scarano, A. Fracture Strength of Conometric Joint Implants Vs. Internal Hexagon Abutment Joint Design: An In Vitro Study. J. Oral Implants 2025, 51, 356–360. [Google Scholar]
- Germán-Sandoval, R.; Ortiz-Magdaleno, M.; Sánchez-Robles, P.; Zavala-Alonso, N.; Fernando Romo-Ramírez, G. Analysis of the mechanical behavior and effect of cyclic fatigue on the implant-abutment Interface. Odovtos Int. J. Dent. Sci. 2021, 23, 104–114. [Google Scholar] [CrossRef]
- Zhang, N.; Karl, M.; Wendler, F. Finite Element Analysis on Stress Development in Alveolar Bone During Insertion of a Novel Dental Implant Design. Appl. Sci. 2025, 15, 8366. [Google Scholar] [CrossRef]
- Rousseau, N.; Msolli, I.; Chabrand, P.; Destainville, A.; Richart, O.; Milan, J.L. Local tissue effects and peri-implant bone healing induced by implant surface treatment: An in vivo study in the sheep. J. Periodontal Res. 2021, 56, 789–803. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Yuan, X.; Ren, M.; Chen, X.; Luo, L.; Zheng, L.; Liu, Y. Three-dimensional finite element analysis of stress distribution on short implants with different bone conditions and osseointegration rates. BMC Oral Health 2023, 23, 220. [Google Scholar] [CrossRef] [PubMed]
- Kasari, M.S.; Yousefi, H.; Shirazi, A.E.; Geramy, A. Effect of bone quality and osseointegration on stress distribution in the bone tissue surrounding dental implant. A finite element analysis. J. Osseointegr. 2023, 15, 106–112. [Google Scholar]
- Falcinelli, C.; Schileo, E.; Balistreri, L.; Baruffaldi, F.; Bordini, B.; Viceconti, M.; Albisinni, U.; Ceccarelli, F.; Milandri, L.; Toni, A.; et al. Multiple loading conditions analysis can improve the association between finite element bone strength estimates and proximal femur fractures: A preliminary study in elderly women. Bone 2014, 67, 71–80. [Google Scholar] [CrossRef]
- Satpathy, M.; Duan, Y.; Betts, L.; Priddy, M.; Griggs, J.A. Effect of bone remodeling on dental implant fatigue limit predicted using 3D finite element analysis. J. Dent. Oral Epidemiol. 2022, 2, 10–54289. [Google Scholar]
- Erdoğdu, M.; Demirel, M.G.; Mohammadi, R.; Güntekin, N. Assessment of the Impact of Bone Quality and Abutment Configuration on the Fatigue Performance of Dental Implant Systems Using Finite Element Analysis (FEA). J. Pers. Med. 2024, 14, 1040. [Google Scholar] [CrossRef] [PubMed]
- Serrato-Pedrosa, J.A.; Villanueva-Fierro, I.; Marquet-Rivera, R.A.; Hernández-Vázquez, R.A.; Cruz-Lopez, S.; Loera-Castañeda, V. Non-Linear Biomechanical evaluation and comparison in the assessment of three different piece dental implant systems for the molar region: A finite element study. J. Funct. Biomater. 2025, 16, 17. [Google Scholar] [CrossRef] [PubMed]
- Kayabaşı, O.; Yüzbasıoğlu, E.; Erzincanlı, F. Static, dynamic and fatigue behaviors of dental implant using finite element method. Adv. Eng. Softw. 2006, 37, 649–658. [Google Scholar] [CrossRef]


| Properties (MPa) | High-Density Trabecular Bone (Class II) | Low-Density Trabecular Bone (Class IV) | Cortical Bone |
|---|---|---|---|
| Ex 1 | 1148 | 230 | 12,600 |
| Ey | 210 | 42 | 12,600 |
| Ez | 1148 | 230 | 19,400 |
| 2 | 0.05 | 0.05 | 0.300 |
| 0.32 | 0.32 | 0.253 | |
| 0.01 | 0.01 | 0.253 | |
| Gxy 3 | 17 | 14 | 4850 |
| Gxz | 108.50 | 87 | 5700 |
| Gyz | 17 | 14 | 5700 |
| Model | Material | Young’s Modulus (GPa) | (ν) |
|---|---|---|---|
| Implant | Ti-6Al-4V | 110 | 0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ceddia, M.; Romasco, T.; Marchioli, G.; Cipollina, A.; Comuzzi, L.; Piattelli, A.; Di Pietro, N.; Trentadue, B. The Effect of Varying Abutment Heights on Stress Distribution in Different Bone Densities: A Finite Element Analysis Study. Materials 2025, 18, 4561. https://doi.org/10.3390/ma18194561
Ceddia M, Romasco T, Marchioli G, Cipollina A, Comuzzi L, Piattelli A, Di Pietro N, Trentadue B. The Effect of Varying Abutment Heights on Stress Distribution in Different Bone Densities: A Finite Element Analysis Study. Materials. 2025; 18(19):4561. https://doi.org/10.3390/ma18194561
Chicago/Turabian StyleCeddia, Mario, Tea Romasco, Giulia Marchioli, Alessandro Cipollina, Luca Comuzzi, Adriano Piattelli, Natalia Di Pietro, and Bartolomeo Trentadue. 2025. "The Effect of Varying Abutment Heights on Stress Distribution in Different Bone Densities: A Finite Element Analysis Study" Materials 18, no. 19: 4561. https://doi.org/10.3390/ma18194561
APA StyleCeddia, M., Romasco, T., Marchioli, G., Cipollina, A., Comuzzi, L., Piattelli, A., Di Pietro, N., & Trentadue, B. (2025). The Effect of Varying Abutment Heights on Stress Distribution in Different Bone Densities: A Finite Element Analysis Study. Materials, 18(19), 4561. https://doi.org/10.3390/ma18194561









