Ab Initio Calculations of Spin Waves: A Review of Theoretical Approaches and Applications
Abstract
1. Introduction
2. Theoretical Background
2.1. Time-Dependent Density-Functional Theory
2.2. Many-Body Perturbation Theory
3. Results and Discussion
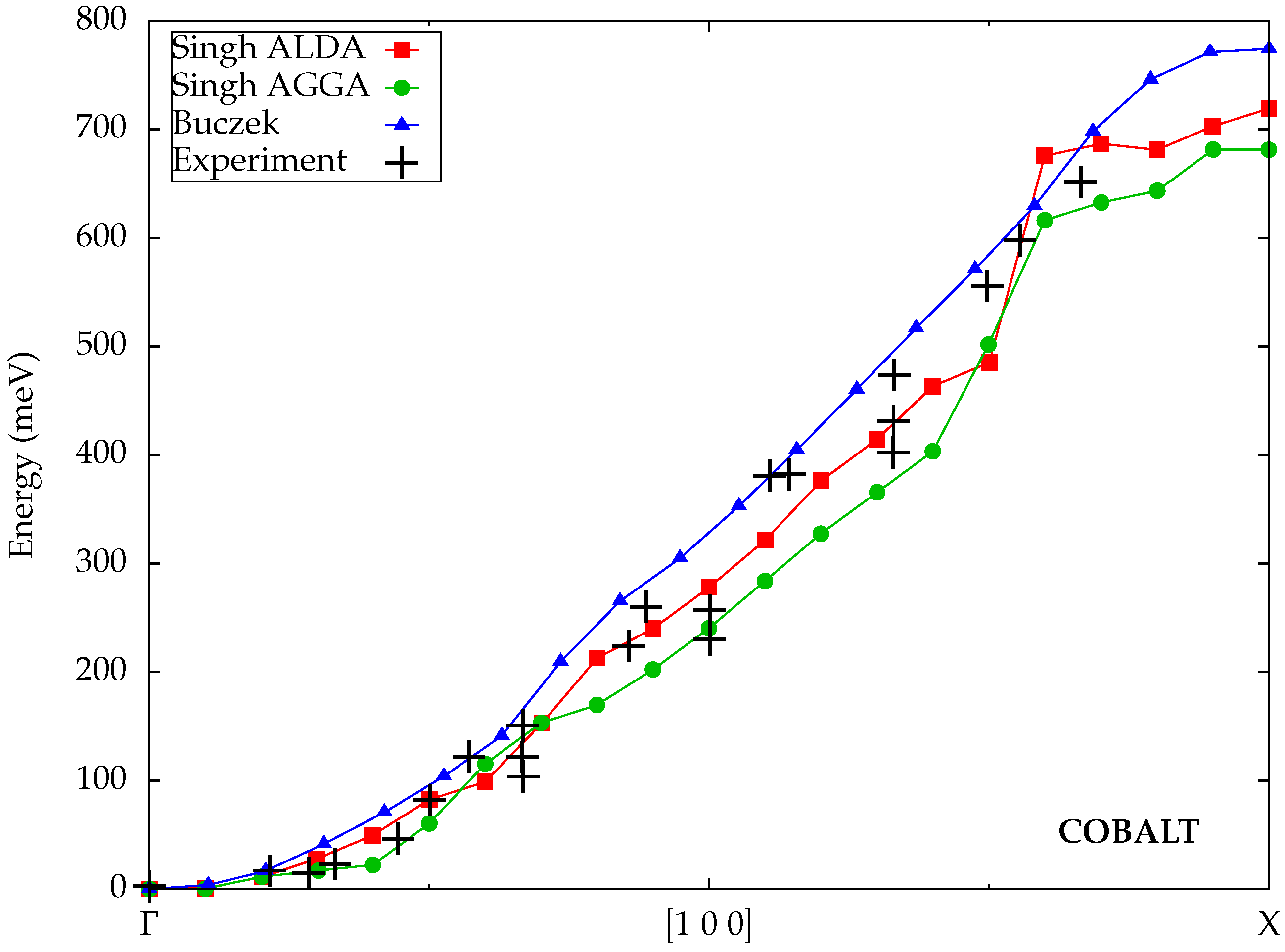
3.1. Cobalt (fcc)
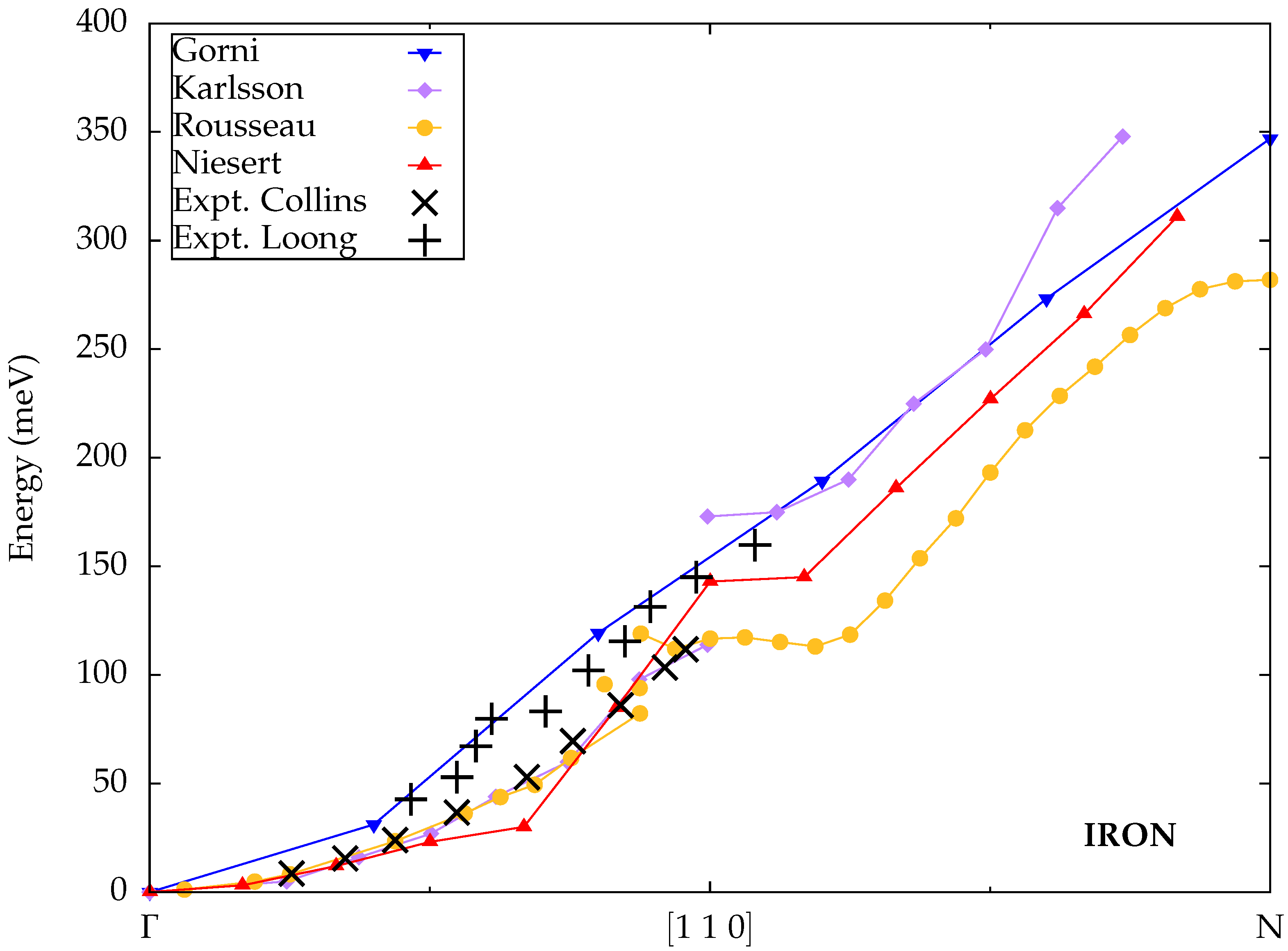
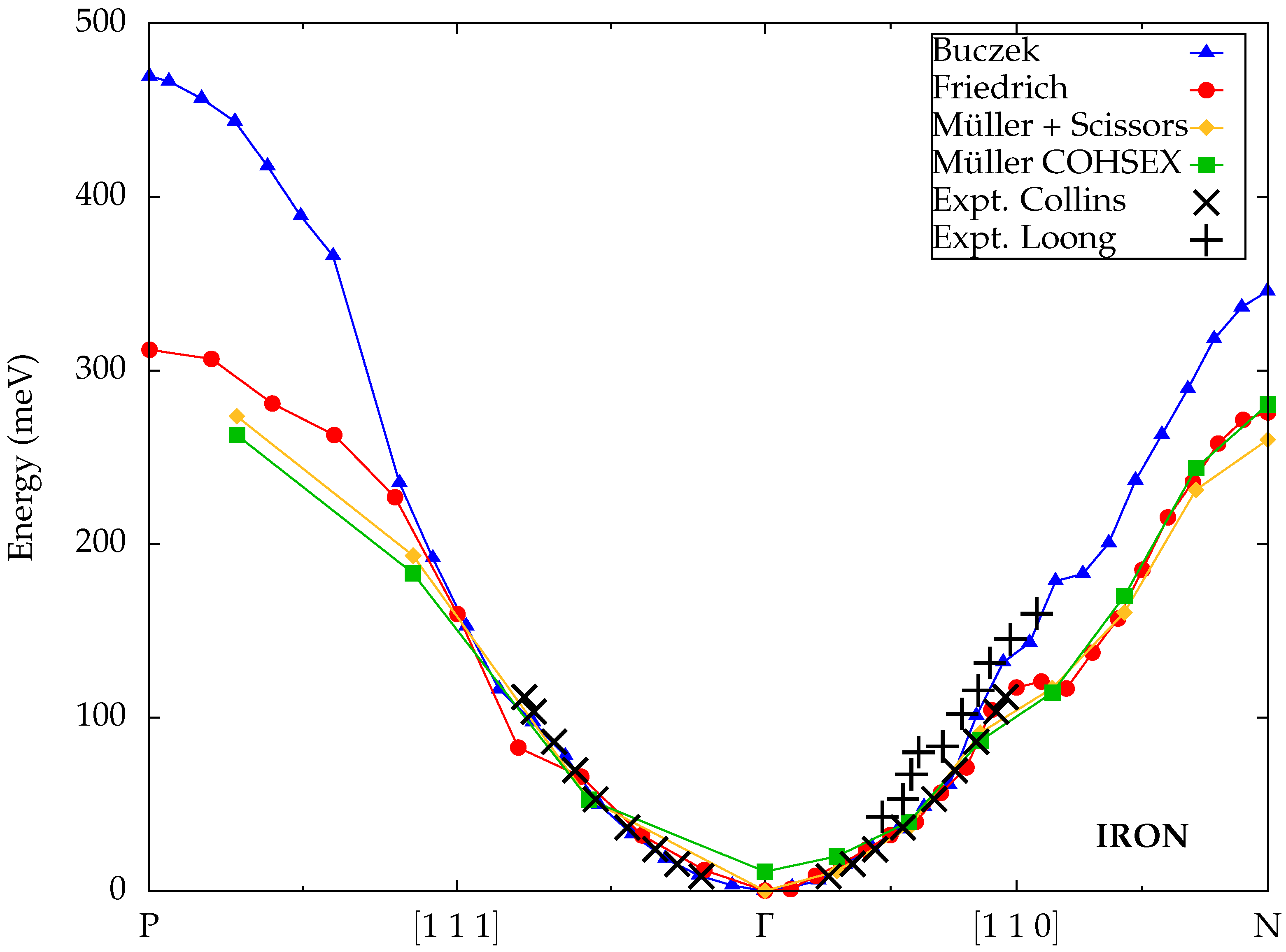
3.2. Iron (bcc)
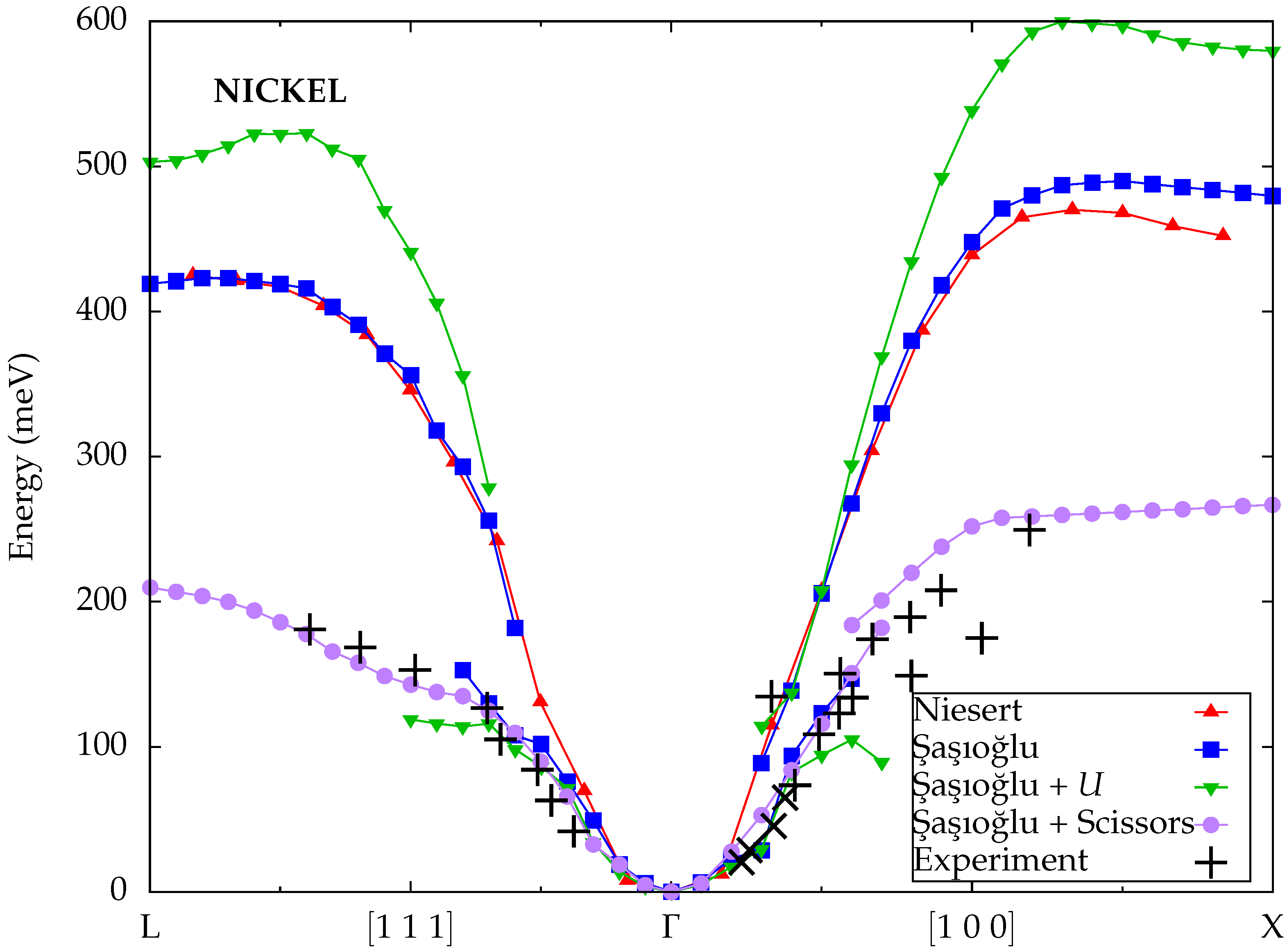
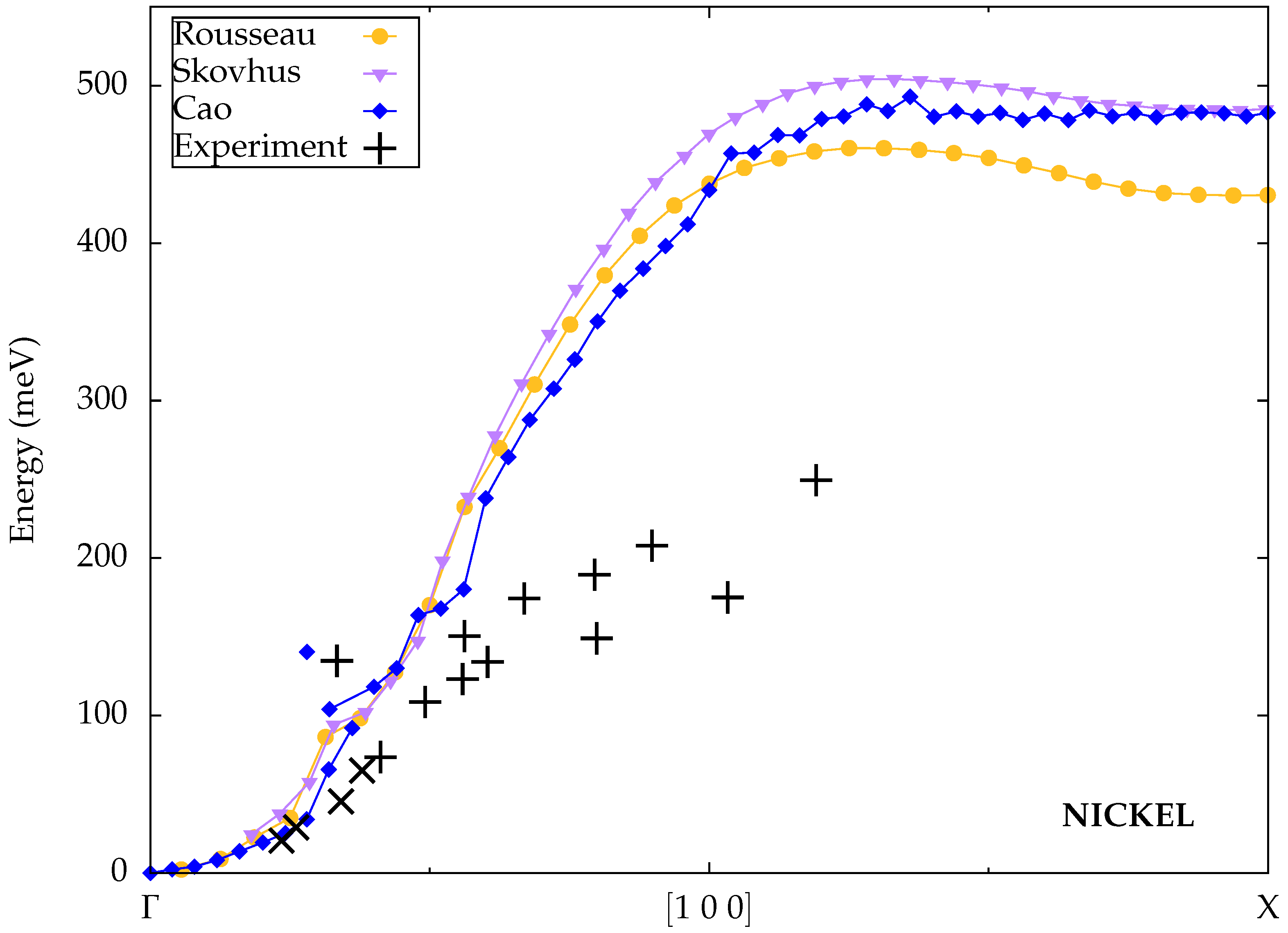
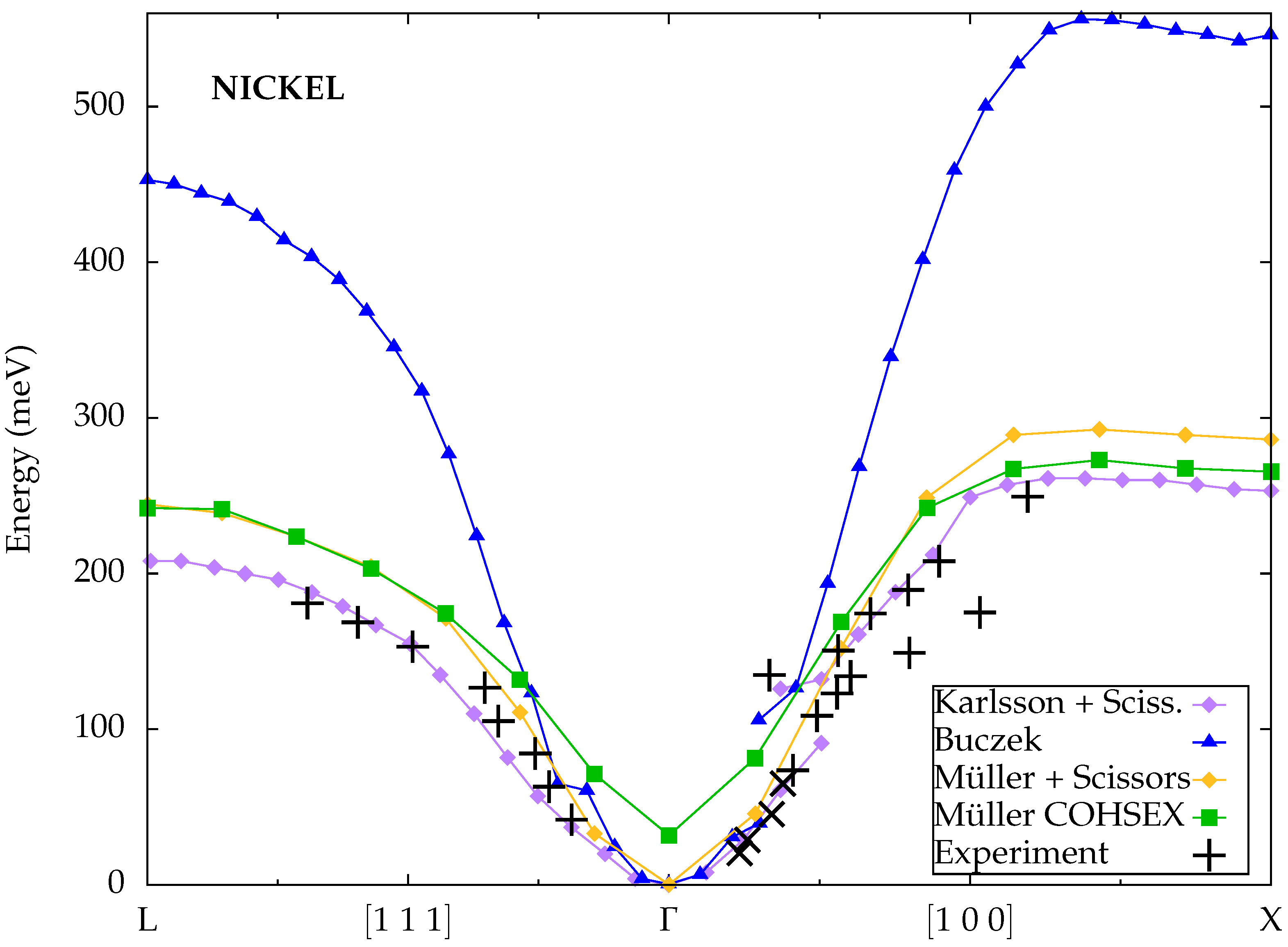
3.3. Nickel (fcc)
3.4. Other Materials
3.4.1. Heusler Alloys
3.4.2. Bulk Transition Metals and Their Binary Compounds
3.4.3. Transition Metal Thin Films
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AGGA | adiabatic generalized gradient approximation |
| ALDA | adiabatic local-density approximation |
| COHSEX | Coulomb-hole screened-exchange |
| DFT | density-functional theory |
| FLAPW | full-potential linearized augmented plane wave |
| GGA | generalized gradient approximation |
| KKR | Korringa–Kohn–Rostoker |
| LDA | local-density approximation |
| LMTO | linear muffin-tin orbital |
| MBPT | many-body perturbation theory |
| PAW | projector augmented wave |
| TDDFT | time-dependent density-functional theory |
References
- Stancil, D.D.; Prabhakar, A. Spin Waves; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Bloch, F. Zur Theorie des Ferromagnetismus. Z. Phys. 1930, 61, 206–219. [Google Scholar] [CrossRef]
- Hofmann, A.; Cui, X.Y.; Schäfer, J.; Meyer, S.; Höpfner, P.; Blumenstein, C.; Paul, M.; Patthey, L.; Rotenberg, E.; Bünemann, J.; et al. Renormalization of bulk magnetic electron states at high binding energies. Phys. Rev. Lett. 2009, 102, 187204. [Google Scholar] [CrossRef] [PubMed]
- Raquet, B.; Viret, M.; Sondergard, E.; Cespedes, O.; Mamy, R. Electron-magnon scattering and magnetic resistivity in 3d ferromagnets. Phys. Rev. B 2002, 66, 024433. [Google Scholar] [CrossRef]
- Jansen, R.; Anil Kumar, P.S.; van’t Erve, O.M.J.; Vlutters, R.; de Haan, P.; Lodder, J.C. Thermal spin-wave scattering in hot-electron magnetotransport across a spin valve. Phys. Rev. Lett. 2000, 85, 3277–3280. [Google Scholar] [CrossRef]
- Eschrig, M. The effect of collective spin-1 excitations on electronic spectra in high-Tc superconductors. Adv. Phys. 2006, 55, 47–183. [Google Scholar] [CrossRef]
- Dahm, T.; Hinkov, V.; Borisenko, S.V.; Kordyuk, A.A.; Zabolotnyy, V.B.; Fink, J.; Büchner, B.; Scalapino, D.J.; Hanke, W.; Keimer, B. Strength of the spin-fluctuation-mediated pairing interaction in a high-temperature superconductor. Nat. Phys. 2009, 5, 217–221. [Google Scholar] [CrossRef]
- Le Tacon, M.; Ghiringhelli, G.; Chaloupka, J.; Moretti Sala, M.; Hinkov, V.; Haverkort, M.W.; Minola, M.; Bakr, M.; Zhou, K.J.; Blanco-Canosa, S.; et al. Intense paramagnon excitations in a large family of high-temperature superconductors. Nat. Phys. 2011, 7, 725–730. [Google Scholar] [CrossRef]
- Karchev, N. Magnon exchange mechanism of ferromagnetic superconductivity. Phys. Rev. B 2003, 67, 054416. [Google Scholar] [CrossRef][Green Version]
- Hattori, K.; Tsunetsugu, H. p-wave superconductivity near a transverse saturation field. Phys. Rev. B 2013, 87, 064501. [Google Scholar] [CrossRef]
- Kruglyak, V.V.; Demokritov, S.O.; Grundler, D. Magnonics. J. Phys. D 2010, 43, 264001. [Google Scholar] [CrossRef]
- Flebus, B.; Grundler, D.; Rana, B.; Otani, Y.; Barsukov, I.; Barman, A.; Gubbiotti, G.; Landeros, P.; Akerman, J.; Ebels, U.; et al. The 2024 magnonics roadmap. J. Phys. Condens. Matter 2024, 36, 363501. [Google Scholar] [CrossRef]
- Chumak, A.V.; Serga, A.A.; Hillebrands, B. Magnon transistor for all-magnon data processing. Nat. Commun. 2014, 5, 4700. [Google Scholar] [CrossRef]
- Liechtenstein, A.I.; Katsnelson, M.I.; Antropov, V.P.; Gubanov, V.A. Local spin density functional approach to the theory of exchange interactions in ferromagnetic metals and alloys. J. Magn. Magn. Mater. 1987, 67, 65–74. [Google Scholar] [CrossRef]
- Bruno, P. Exchange interaction parameters and adiabatic spin-wave spectra of ferromagnets: A “renormalized magnetic force theorem”. Phys. Rev. Lett. 2003, 90, 087205. [Google Scholar] [CrossRef] [PubMed]
- Katsnelson, M.I.; Lichtenstein, A.I. Magnetic susceptibility, exchange interactions and spin-wave spectra in the local spin density approximation. J. Phys. Condens. Matter 2004, 16, 7439–7446. [Google Scholar] [CrossRef]
- Turek, I.; Kudrnovský, J.; Drchal, V.; Bruno, P. Exchange interactions, spin waves, and transition temperatures in itinerant magnets. Philos. Mag. 2006, 86, 1713–1752. [Google Scholar] [CrossRef]
- Ležaić, M.; Mavropoulos, P.; Bihlmayer, G.; Blügel, S. Exchange interactions and local-moment fluctuation corrections in ferromagnets at finite temperatures based on noncollinear density-functional calculations. Phys. Rev. B 2013, 88, 134403. [Google Scholar] [CrossRef]
- Šabani, D.; Bacaksiz, C.; Milošević, M.V. Ab initio methodology for magnetic exchange parameters: Generic four-state energy mapping onto a Heisenberg spin Hamiltonian. Phys. Rev. B 2020, 102, 014457. [Google Scholar] [CrossRef]
- Solovyev, I.V. Exchange interactions and magnetic force theorem. Phys. Rev. B 2021, 103, 104428. [Google Scholar] [CrossRef]
- Halilov, S.V.; Eschrig, H.; Perlov, A.Y.; Oppeneer, P.M. Adiabatic spin dynamics from spin-density-functional theory: Application to Fe, Co, and Ni. Phys. Rev. B 1998, 58, 293–302. [Google Scholar] [CrossRef]
- Brown, R.H.; Nicholson, D.M.C.; Wang, X.; Schulthess, T.C. First principles theory of spin waves in Fe, Co, and Ni. J. Appl. Phys. 1999, 85, 4830–4832. [Google Scholar] [CrossRef]
- Gebauer, R.; Baroni, S. Magnons in real materials from density-functional theory. Phys. Rev. B 2000, 61, R6459–R6462. [Google Scholar] [CrossRef]
- Bylander, D.M.; Niu, Q.; Kleinman, L. Fe magnon dispersion curve calculated with the frozen spin-wave method. Phys. Rev. B 2000, 61, R11875–R11878. [Google Scholar] [CrossRef][Green Version]
- Mook, H.A.; Paul, D.M. Neutron-scattering measurement of the spin-wave spectra for nickel. Phys. Rev. Lett. 1985, 54, 227–229. [Google Scholar] [CrossRef]
- Aryasetiawan, F.; Karlsson, K. Green’s function formalism for calculating spin-wave spectra. Phys. Rev. B 1999, 60, 7419–7428. [Google Scholar] [CrossRef]
- Friedrich, C.; Şaşıoğlu, E.; Müller, M.; Schindlmayr, A.; Blügel, S. Spin excitations in solids from many-body perturbation theory. In First Principles Approaches to Spectroscopic Properties of Complex Materials; Di Valentin, C., Botti, S., Cococcioni, M., Eds.; Number 347 in Topics in Current Chemistry; Springer: Berlin/Heidelberg, Germany, 2014; pp. 259–301. [Google Scholar] [CrossRef]
- Runge, E.; Gross, E.K.U. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar] [CrossRef]
- Niesert, M. Ab Initio Calculations of Spin-Wave Excitation Spectra from Time-Dependent Density-Functional Theory; Number 38 in Schriften des Forschungszentrums Jülich: Schlüsseltechnologien/Key Technologies; Forschungszentrum Jülich: Jülich, Germany, 2012; Available online: https://hdl.handle.net/2128/16523 (accessed on 16 September 2025).
- Buczek, P.; Ernst, A.; Sandratskii, L.M. Interface electronic complexes and Landau damping of magnons in ultrathin magnets. Phys. Rev. Lett. 2011, 106, 157204. [Google Scholar] [CrossRef] [PubMed]
- Rousseau, B.; Eiguren, A.; Bergara, A. Efficient computation of magnon dispersions within time-dependent density functional theory using maximally localized Wannier functions. Phys. Rev. B 2012, 85, 054305. [Google Scholar] [CrossRef]
- Singh, N.; Elliott, P.; Nautiyal, T.; Dewhurst, J.K.; Sharma, S. Adiabatic generalized gradient approximation kernel in time-dependent density functional theory. Phys. Rev. B 2019, 99, 035151. [Google Scholar] [CrossRef]
- Skovhus, T.; Olsen, T. Dynamic transverse magnetic susceptibility in the projector augmented-wave method: Application to Fe, Ni, and Co. Phys. Rev. B 2021, 103, 245110. [Google Scholar] [CrossRef]
- Savrasov, S.Y. Linear response calculations of spin fluctuations. Phys. Rev. Lett. 1998, 81, 2570–2573. [Google Scholar] [CrossRef]
- Cao, K.; Lambert, H.; Radaelli, P.G.; Giustino, F. Ab initio calculation of spin fluctuation spectra using time-dependent density functional perturbation theory, plane waves, and pseudopotentials. Phys. Rev. B 2018, 97, 024420. [Google Scholar] [CrossRef]
- Gorni, T.; Timrov, I.; Baroni, S. Spin dynamics from time-dependent density functional perturbation theory. Eur. Phys. J. B 2018, 91, 249. [Google Scholar] [CrossRef]
- Schindlmayr, A. Exact formulation of the transverse dynamic spin susceptibility as an initial-value problem. Adv. Math. Phys. 2018, 2018, 3732892. [Google Scholar] [CrossRef]
- Singh, N.; Elliott, P.; Dewhurst, J.K.; Gross, E.K.U.; Sharma, S. Ab-initio real-time magnon dynamics in ferromagnetic and ferrimagnetic systems. Phys. Status Solidi B 2020, 257, 1900654. [Google Scholar] [CrossRef]
- Tancogne-Dejean, N.; Eich, F.G.; Rubio, A. Time-dependent magnons from first principles. J. Chem. Theory Comput. 2020, 16, 1007–1017. [Google Scholar] [CrossRef] [PubMed]
- Mahan, G.D. Many-Particle Physics; Springer: New York, NY, USA, 1990. [Google Scholar] [CrossRef]
- Schindlmayr, A. The GW approximation for the electronic self-energy. In Many-Electron Approaches in Physics, Chemistry and Mathematics; Bach, V., Delle Site, L., Eds.; Number 29 in Mathematical Physics Studies; Springer: Cham, Switzerland, 2014; pp. 343–357. [Google Scholar] [CrossRef]
- Karlsson, K.; Aryasetiawan, F. A many-body approach to spin-wave excitations in itinerant magnetic systems. J. Phys. Condens. Matter 2000, 12, 7617–7631. [Google Scholar] [CrossRef]
- Şaşıoğlu, E.; Schindlmayr, A.; Friedrich, C.; Freimuth, F.; Blügel, S. Wannier-function approach to spin excitations in solids. Phys. Rev. B 2010, 81, 054434. [Google Scholar] [CrossRef]
- Moriya, T. Spin Fluctuations in Itinerant Electron Magnetism; Number 56 in Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar] [CrossRef]
- Müller, M.C.T.D.; Friedrich, C.; Blügel, S. Acoustic magnons in the long-wavelength limit: Investigating the Goldstone violation in many-body perturbation theory. Phys. Rev. B 2016, 94, 064433. [Google Scholar] [CrossRef]
- Skovhus, T.; Olsen, T. Magnons in antiferromagnetic bcc Cr and Cr2O3 from time-dependent density functional theory. Phys. Rev. B 2022, 106, 085131. [Google Scholar] [CrossRef]
- Balashov, T. Inelastic Scanning Tunneling Spectroscopy: Magnetic Excitations on the Nanoscale. Ph.D. Thesis, Universität Karlsruhe (TH), Karlsruhe, Germany, 2009. [Google Scholar] [CrossRef]
- The Elk Code. Available online: http://elk.sourceforge.net/ (accessed on 16 September 2025).
- Buczek, P.; Ernst, A.; Sandratskii, L.M. Different dimensionality trends in the Landau damping of magnons in iron, cobalt, and nickel: Time-dependent density functional study. Phys. Rev. B 2011, 84, 174418. [Google Scholar] [CrossRef]
- Buczek, P.A. Spin Dynamics of Complex Itinerant Magnets. Ph.D. Thesis, Universität Halle-Wittenberg, Halle, Germany, 2009. [Google Scholar] [CrossRef]
- Buczek, P.; Ernst, A.; Bruno, P.; Sandratskii, L.M. Energies and lifetimes of magnons in complex ferromagnets: A first-principle study of Heusler alloys. Phys. Rev. Lett. 2009, 102, 247206. [Google Scholar] [CrossRef] [PubMed]
- Buczek, P.; Ernst, A.; Sandratskii, L.; Bruno, P. The energies and life times of magnons in bulk iron and one-monolayer Fe film. J. Magn. Magn. Mater. 2010, 322, 1396–1398. [Google Scholar] [CrossRef]
- Schmidt, A.B.; Pickel, M.; Donath, M.; Buczek, P.; Ernst, A.; Zhukov, V.P.; Echenique, P.M.; Sandratskii, L.M.; Chulkov, E.V.; Weinelt, M. Ultrafast magnon generation in an Fe film on Cu(100). Phys. Rev. Lett. 2010, 105, 197401. [Google Scholar] [CrossRef] [PubMed]
- Buczek, P.; Ernst, A.; Sandratskii, L.M. Spin dynamics of half-metallic Co2MnSi. J. Phys. Conf. Ser. 2010, 200, 042006. [Google Scholar] [CrossRef]
- Mortensen, J.J.; Larsen, A.H.; Kuisma, M.; Ivanov, A.V.; Taghizadeh, A.; Peterson, A.; Haldar, A.; Dohn, A.O.; Schäfer, C.; Jónsson, E.O.; et al. GPAW: An open Python package for electronic structure calculations. J. Chem. Phys. 2024, 160, 092503. [Google Scholar] [CrossRef]
- The FLEUR Project. Available online: https://www.flapw.de/ (accessed on 16 September 2025).
- Friedrich, C.; Schindlmayr, A.; Blügel, S. Efficient calculation of the Coulomb matrix and its expansion around k = 0 within the FLAPW method. Comput. Phys. Commun. 2009, 180, 347–359. [Google Scholar] [CrossRef]
- Friedrich, C.; Blügel, S.; Schindlmayr, A. Efficient implementation of the GW approximation within the all-electron FLAPW method. Phys. Rev. B 2010, 81, 125102. [Google Scholar] [CrossRef]
- Collins, M.F.; Minkiewicz, V.J.; Nathans, R.; Passell, L.; Shirane, G. Critical and spin-wave scattering of neutrons from iron. Phys. Rev. 1969, 179, 417–430. [Google Scholar] [CrossRef]
- Loong, C.; Carpenter, J.M.; Lynn, J.W.; Robinson, R.A.; Mook, H.A. Neutron scattering study of the magnetic excitations in ferromagnetic iron at high energy transfers. J. Appl. Phys. 1984, 55, 1895–1897. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with QUANTUM ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Baroni, S.; Gebauer, R. The Liouville–Lanczos approach to time-dependent density-functional (perturbation) theory. In Fundamentals of Time-Dependent Density Functional Theory; Number 837 in Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2012; pp. 375–390. [Google Scholar] [CrossRef]
- Gorni, T.; Baseggio, O.; Delugas, P.; Baroni, S.; Timrov, I. turboMagnon—A code for the simulation of spin-wave spectra using the Liouville–Lanczos approach to time-dependent density-functional perturbation theory. Comput. Phys. Commun. 2022, 280, 108500. [Google Scholar] [CrossRef]
- Ododo, J.C.; Anyakoha, M.W. Magnetic excitations in nickel and iron. J. Phys. F Met. Phys. 1983, 13, 2335–2349. [Google Scholar] [CrossRef]
- Schindlmayr, A.; Friedrich, C.; Şaşıoğlu, E.; Blügel, S. First-principles calculation of electronic excitations in solids with SPEX. Z. Phys. Chem. 2010, 224, 357–368. [Google Scholar] [CrossRef]
- Lynn, J.W.; Mook, H.A. Temperature dependence of the dynamic susceptibility of nickel. Phys. Rev. B 1981, 23, 198–206. [Google Scholar] [CrossRef]
- Cooke, J.F.; Blackman, J.A.; Morgan, T. New interpretation of spin-wave behavior in nickel. Phys. Rev. Lett. 1985, 54, 718–721. [Google Scholar] [CrossRef]
- Cooke, J.F. Neutron scattering from itinerant-electron ferromagnets. Phys. Rev. B 1973, 7, 1108–1116. [Google Scholar] [CrossRef]
- Cooke, J.F.; Lynn, J.W.; Davis, H.L. Calculations of the dynamic susceptibility of nickel and iron. Phys. Rev. B 1980, 21, 4118–4131. [Google Scholar] [CrossRef]
- Callaway, J.; Chatterjee, A.K.; Singhal, S.P.; Ziegler, A. Magnetic susceptibility of ferromagnetic metals: Application to nickel. Phys. Rev. B 1983, 28, 3818–3830. [Google Scholar] [CrossRef]
- Okumura, H.; Sato, K.; Kotani, T. Spin-wave dispersion of 3d ferromagnets based on quasiparticle self-consistent GW calculations. Phys. Rev. B 2019, 100, 054419. [Google Scholar] [CrossRef]
- van Schilfgaarde, M.; Kotani, T.; Faleev, S. Quasiparticle self-consistent GW theory. Phys. Rev. Lett. 2006, 96, 226402. [Google Scholar] [CrossRef]
- Kotani, T.; van Schilfgaarde, M.; Faleev, S.V. Quasiparticle self-consistent GW method: A basis for the independent-particle approximation. Phys. Rev. B 2007, 76, 165106. [Google Scholar] [CrossRef]
- Liu, X.; Lin, Y.; Feng, J. Implementation of the density functional perturbation theory for generalized susceptibility in the projector augmented wave framework. Phys. Rev. B 2023, 108, 094405. [Google Scholar] [CrossRef]
- Okumura, H.; Sato, K.; Suzuki, K.; Kotani, T. Electronic structure and spin-wave dispersion of Cu2MnAl, Ni2MnSn, and Pd2MnSn based on quasi-particle self-consistent GW calculations. J. Phys. Soc. Jpn. 2020, 89, 034704. [Google Scholar] [CrossRef]
- Odashima, M.M.; Marmodoro, A.; Buczek, P.; Ernst, A.; Sandratskii, L. Chirality-dependent magnon lifetime in a compensated half-metallic ferrimagnet. Phys. Rev. B 2013, 87, 174420. [Google Scholar] [CrossRef]
- Şaşıoğlu, E.; Friedrich, C.; Blügel, S. Strong magnon softening in tetragonal FeCo compounds. Phys. Rev. B 2013, 87, 020410. [Google Scholar] [CrossRef]
- Sandratskii, L.M.; Buczek, P. Lifetimes and chirality of spin waves in antiferromagnetic and ferromagnetic FeRh from the perspective of time-dependent density functional theory. Phys. Rev. B 2012, 85, 020406. [Google Scholar] [CrossRef]
- Skovhus, T.; Olsen, T.; Rønnow, H.M. Influence of static correlation on the magnon dynamics of an itinerant ferromagnet with competing exchange interactions: First-principles study of MnBi. Phys. Rev. Mater. 2022, 6, 054402. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Ni, X.S.; Datta, T.; Wang, M.; Yao, D.X.; Cao, K. Ab initio study of spin fluctuations in the itinerant kagome magnet FeSn. Phys. Rev. B 2022, 106, 184422. [Google Scholar] [CrossRef]
- Tang, H.; Plihal, M.; Mills, D.L. Theory of the spin dynamics of bulk Fe and ultrathin Fe(100) films. J. Magn. Magn. Mater. 1998, 187, 23–46. [Google Scholar] [CrossRef]
- Muniz, R.B.; Mills, D.L. Theory of spin excitations in Fe(110) monolayers. Phys. Rev. B 2002, 66, 174417. [Google Scholar] [CrossRef]
- Botti, S.; Schindlmayr, A.; Del Sole, R.; Reining, L. Time-dependent density-functional theory for extended systems. Rep. Prog. Phys. 2007, 70, 357–407. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neugum, M.; Schindlmayr, A. Ab Initio Calculations of Spin Waves: A Review of Theoretical Approaches and Applications. Materials 2025, 18, 4431. https://doi.org/10.3390/ma18184431
Neugum M, Schindlmayr A. Ab Initio Calculations of Spin Waves: A Review of Theoretical Approaches and Applications. Materials. 2025; 18(18):4431. https://doi.org/10.3390/ma18184431
Chicago/Turabian StyleNeugum, Michael, and Arno Schindlmayr. 2025. "Ab Initio Calculations of Spin Waves: A Review of Theoretical Approaches and Applications" Materials 18, no. 18: 4431. https://doi.org/10.3390/ma18184431
APA StyleNeugum, M., & Schindlmayr, A. (2025). Ab Initio Calculations of Spin Waves: A Review of Theoretical Approaches and Applications. Materials, 18(18), 4431. https://doi.org/10.3390/ma18184431