Deterioration of Concrete Under the Combined Action of Sulfate Attack and Freeze–Thaw Cycles: A Review
Abstract
1. Introduction
2. Deterioration Mechanisms of Concrete Under Combined Action of Sulfate Attack and Freeze–Thaw Cycles
2.1. Deterioration Mechanism of Concrete Under Freeze–Thaw Cycles
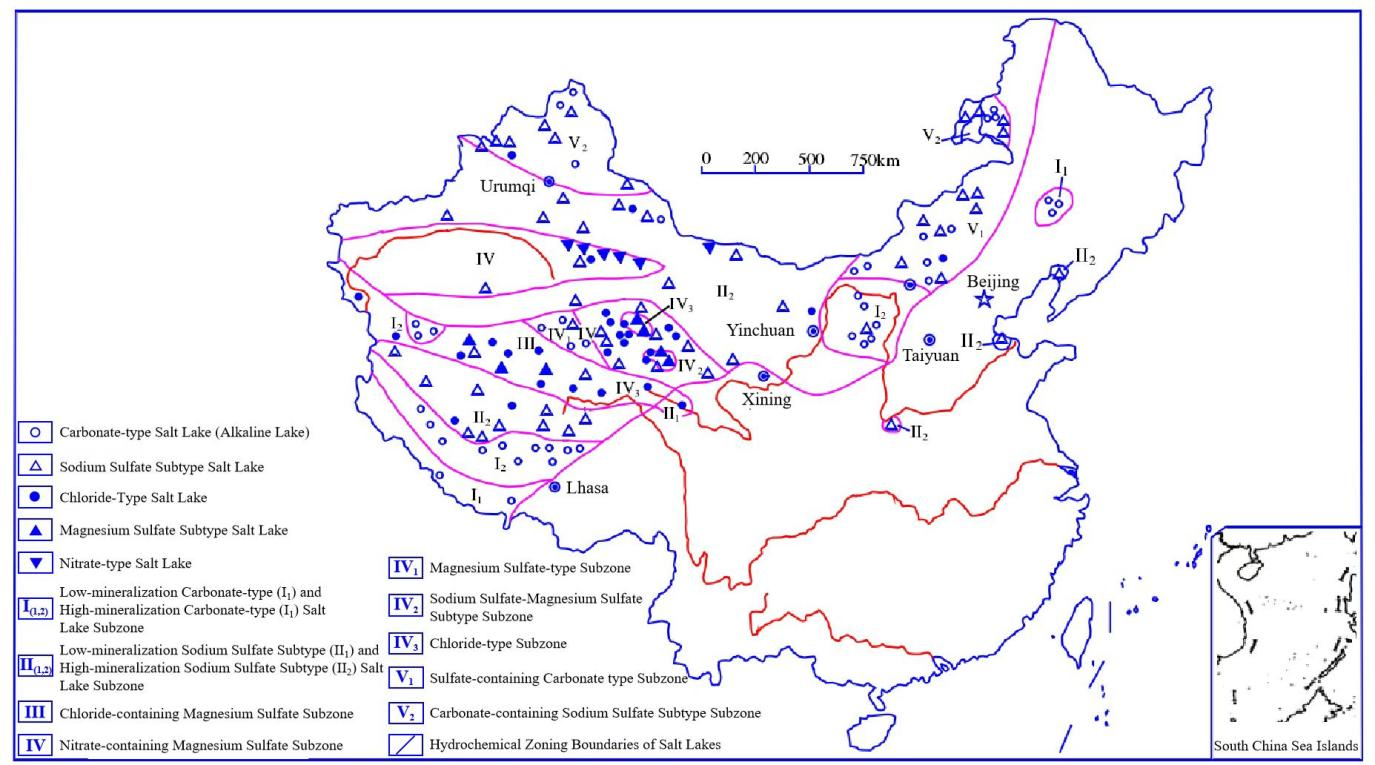
2.2. Deterioration Mechanism of Concrete Under Sulfate Attack
2.3. Deterioration Mechanism of Concrete Under Coupled Sulfate Attack and Freeze–Thaw Cycles
3. Damage Model of Concrete Durability Under Combined Action of Sulfate Attack and Freeze–Thaw Cycles
3.1. Experimental Research
3.2. Erosion Models
3.2.1. Durability Damage Models Based on Macro-Test Indicators
3.2.2. Models Based on Damage Accumulation and Probability Distribution
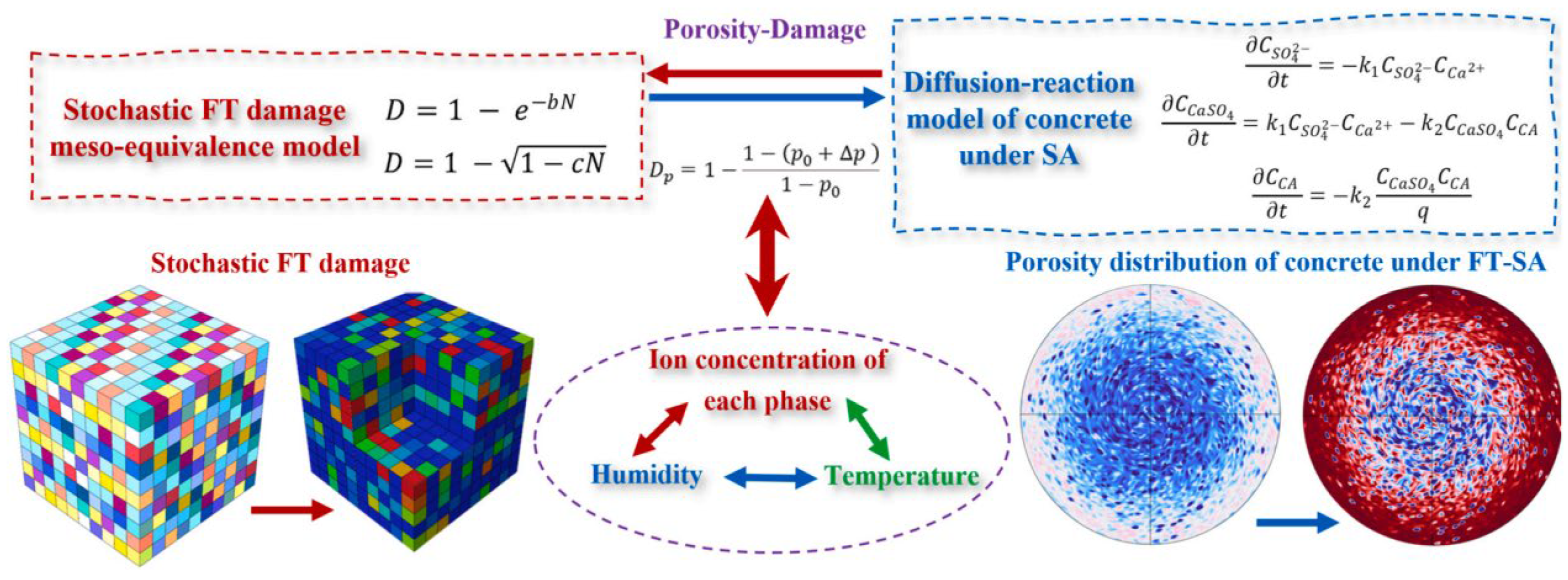
4. Numerical Simulation of Concrete Damage Under Combined Sulfate Attack and Freeze–Thaw Cycles
5. Conclusions
- (1)
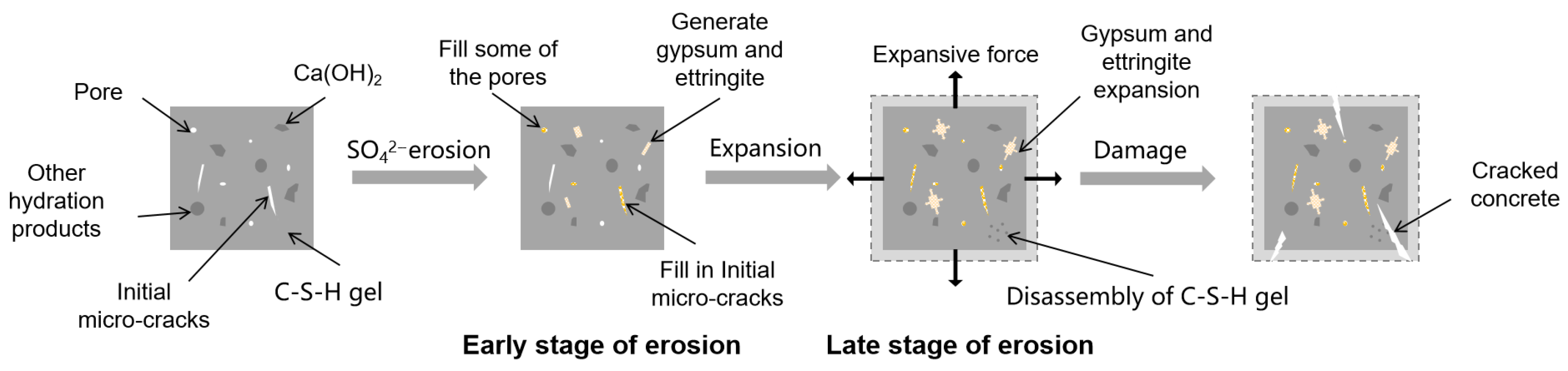
- Complexity and Stage-Specificity of Damage Mechanisms: Compared to isolated SA or FTC exposure, durability deterioration under coupled SA-FTC involves synergistic interactions, including fatigue stress from FTCs, physical salt crystallization, and chemical expansion from sulfate–cement reactions. Key interactive effects—such as sulfate-induced freezing-point depression, increased initial saturation, and temperature-dependent sulfate transport—lead to a highly complex physicochemical deterioration process. Critically, these mechanisms exhibit time-variant synergistic/antagonistic interactions during damage evolution. Current research widely acknowledges that the deterioration process exhibits distinct stage-specific characteristics (e.g., three- or four-stage models). A consensus on concrete degradation mechanisms under combined SA-FTC exposure remains elusive. A unified and quantitative understanding remains lacking regarding transition thresholds between stages, the dominant versus secondary roles of various factors (such as salt type, concentration, and thermal history) in specific stages, and their interactive mechanisms (whether synergistic or antagonistic).
- (2)
- Experimental Research and Limitations: Studies examining factors (e.g., solution concentration/type, test protocols, w/c ratio, air entrainment, fly ash, fiber reinforcement) have established standardized methodologies for quantifying SA-FTC damage via deterioration indicators (mass loss, relative dynamic modulus, compressive strength). However, current experimentation remains confined to material-level properties that rely on simplified laboratory conditions (e.g., water freezing–thawing under constant salt concentration), which diverge significantly from real-world exposure involving air freezing–water thawing, wet–dry cycles, and varying concentration–temperature histories, thereby constraining the extrapolation of laboratory findings to engineering practice. Moreover, studies remain largely focused on the material level, with a lack of systematic linkage to component- and structural-level performance (e.g., load-bearing capacity and stiffness degradation). Furthermore, systematic investigations into the effects of key environmental variables (e.g., cooling rate, minimum temperature and duration, humidity) and compound salt erosion mechanisms remain insufficient, hindering a comprehensive understanding and accurate prediction of durability in realistic service environments.
- (3)
- Damage Modeling and Challenges: To quantify SA-FTC coupled damage, researchers have developed empirical and probabilistic models. Macroscale damage models derived from SA-FTC experimental data—typically formulated using exponential or Weibull functions—inadequately characterize concrete frost damage due to limitations in test duration and indicator selection, which curtails their generalizability and mechanistic insight. For models employing damage accumulation or probability distribution theories (e.g., Wiener or Weibull distributions), the definition and selection of damage variables critically govern model reliability. Moreover, both model types fail to explicitly capture the intrinsic mechanisms through which multifactorial influences govern concrete frost resistance, ultimately hindering mechanistic interpretation and broader applicability.
- (4)
- Numerical Simulation and Current Bottlenecks: Both traditional (e.g., finite element method) and novel peridynamics (PD)-based methods have been applied to simulate concrete behavior under combined SA-FTCs. Nonetheless, research achievements remain sparse and constrained by reliance on limited experimental datasets for validation and parameterization. A major bottleneck is the absence of a predictive, multiscale simulation framework capable of integrating microstructural evolution with macroscopic performance under these complex environmental conditions. Critically, no multiscale numerical framework spanning micro-to-macro levels has been established to fully elucidate the durability damage mechanisms of SA-FTC. Consequently, developing a comprehensive theoretical damage model that integrates multifactorial mechanistic actions, supported by robust numerical simulations of durability degradation, represents a crucial direction for future research.
- (5)
- Perspectives for Future Research: Future research must develop advanced testing protocols replicating real-field conditions, such as varying salt concentrations, thermal cycles, and wet–dry actions. Research progress hinges on advanced damage identification techniques, including post-exposure assessment methods and quantitative damage metrics. Cross-scale studies enabling multiscale characterization of concrete damage require deeper exploration. Such advancements are essential to clarify internal damage propagation processes, thereby providing theoretical and computational foundations for establishing multiscale damage models. High-fidelity multiscale numerical simulations, integrating chemo-thermo-mechanical coupling and phase-field modeling, should be established to bridge physicochemical processes with structural performance for predictive durability analysis.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jin, W.L.; Zhao, Y.X. Durability of Concrete Structures; Science Press: Beijing, China, 2002. [Google Scholar]
- Decky, M.; Hodasova, K.; Papanova, Z.; Remisova, E. Sustainable adaptive cycle pavements using composite foam concrete at high altitudes in central Europe. Sustainability 2022, 14, 9034. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Shou, Q. Saline Soils of China; Science Press: Beijing, China, 1993. [Google Scholar]
- Yu, H.F. Durability, Mechanism and Service Life Prediction Method of High-Performance Concrete in Salt Lake Areas. Ph.D. Thesis, Southeast University, Nanjing, China, 2004. [Google Scholar]
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstructure, Properties, and Materials, 3rd ed.; China Electric Power Press: Beijing, China, 2008. [Google Scholar]
- Powers, T.C. A working hypothesis for further studies of frost resistance of concrete. ACI J. Proc. 1945, 16, 245–272. [Google Scholar]
- Powers, T.C.; Helmuth, R.A. Theory of volume change in hardened Portland cement paste during freezing. Proc. Highw. Res. Board 1953, 32, 285–297. [Google Scholar]
- Jiang, L.; Niu, D.T. Study on Constitutive Relation of Concrete Under Sulfate Attack and Freeze-thaw Environment. J. Sichuan Univ. Eng. Sci. Ed. 2016, 48, 71–78. [Google Scholar]
- Zheng, M.P. On Salt Lakes in China. Miner. Depos. 2001, 2, 181–189+128. [Google Scholar]
- Wu, H.R.; Jin, W.L.; Zhang, F.J.; Wang, Y. Research progress on freeze-thaw damage characteristics of concrete concerned with environmental effects. J. Civ. Eng. 2018, 51, 37–46. [Google Scholar]
- Pigeon, M.; Lachance, M. Critical air void spacing factor for concretes submitted to slow freeze-thaw cycle. ACI J. 1981, 78, 282–291. [Google Scholar]
- Tian, W.; Xie, Y.; Dang, F. Experimental study on meso damage mechanism of concrete Xieunder freezing and thawing environment based on CT technology. J. Wuhan Univ. Eng. Sci. 2016, 49, 397–401. [Google Scholar]
- Zuo, X.; Sun, W. Full process analysis of damage and failure of concrete subjected to external sulfate attack. J. Chin. Ceram. Soc. 2009, 37, 1063–1067. [Google Scholar]
- Moradllo, M.K.; Qiao, C.; Ghantous, R.M.; Zaw, M.; Hall, H.; Ley, M.T.; Weiss, W.J. Quantifying the freeze-thaw performance of air-entrained concrete using the time to reach critical saturation modelling approach. Cem. Concr. Compos. 2020, 106, 103479. [Google Scholar]
- Zuber, B.; Marchand, J. Modeling the deterioration of hydrated cement systems exposed to frost action Part 1: Description of the mathematical model. Cem. Concr. Res. 2000, 30, 1929–1939. [Google Scholar] [CrossRef]
- Jiang, J.Y.; Zheng, H.R.; Sun, G.W.; Wang, F.J.; Liu, Z.Y. Numerical simulation of sulfate attack on concrete. J. Build. Mater. 2023, 26, 1047–1053. [Google Scholar]
- Li, Z.G.; Wang, Y.; Guo, B.B.; Hong, M.S.; Niu, D.T. Numerical simulation of sulfate attack behavior of concrete under temperature influence. J. Build. Mater. 2025, 28, 315–322. [Google Scholar]
- Jiang, L.; Niu, D.T.; Yuan, L.D.; Fei, Q.N. Durability of concrete under sulfate attack exposed to freeze-thaw cycles. Cold Reg. Sci. Technol. 2015, 112, 112–117. [Google Scholar] [CrossRef]
- Jiang, L.; Niu, D.T. Deterioration law of concrete under combined sulfate and freeze-thaw action. J. Cent. South Univ. Nat. Sci. Ed. 2016, 47, 3208–3216. [Google Scholar]
- Hu, S.W.; Yin, Y.Y. Fracture properties of concrete under freeze-thaw cycles and sulfate attack. Constr. Build. Mater. 2022, 350, 128856. [Google Scholar] [CrossRef]
- Liu, J.Z.; Sun, W.; Miao, C.W.; Liu, J.P. Freeze-thaw damage of concrete under combined bending load and salt solution. J. Southeast Univ. Nat. Sci. Ed. 2006, 36, 243–247. [Google Scholar]
- Zhu, X.C.; Zhang, Y.S.; Liu, Z.Y.; Qiao, H.X.; Xue, C.Z.; Feng, Q.; Zhou, Q.M. Study on pore structure evolution of manufactured sand concrete under sulfate freeze-thaw based on NMR technology. Acta Mater. Compos. Sin. 2024, 41, 5478–5491. [Google Scholar]
- Li, S.; Li, H.; Tian, J.; Sun, H.; Ding, Y.F.; Zhang, X.S. Experimental and Numerical Modeling of the Freeze–thaw Response of U-Shaped Channel Lining on Sulfate Saline Soil Foundation. KSCE J. Civ. Eng. 2024, 28, 1280–1294. [Google Scholar] [CrossRef]
- Gan, L.; Xu, W.C.; Shen, Z.Z.; Xu, L.Q.; Zhang, W.B.; Zhang, H.W.; Abbas, M.A.; Chen, G.Y. Experimental and numerical investigations on damage evolution of concrete under sulfate attack and freeze-thaw cycles. J. Build. Eng. 2023, 71, 106469. [Google Scholar] [CrossRef]
- Gong, L.S.; Liu, C.P. Durability of Concrete and Its Protective Repair; China Building and Construction Press: Beijing, China, 1990. [Google Scholar]
- Fagerlund, G. Significance of critical degree of saturation at freezing of porous and brittle materials. ACI Struct. J. 1973, 70, 13–65. [Google Scholar]
- Setzer, M.J. Micro-ice-lens formation in porous solid. J. Colloid Interface Sci. 2001, 243, 193–201. [Google Scholar] [CrossRef]
- Hime, W.G.; Mather, B. “Sulfate attack,” or is it? Cem. Concr. Res. 1999, 29, 789–791. [Google Scholar] [CrossRef]
- Correns, C.W. Growth and dissolution of crystals under linear pressure. Discuss. Faraday Soc. 1949, 5, 267–271. [Google Scholar] [CrossRef]
- Wei, Y.M.; Chen, X.Z.; Chai, J.R.; Qin, Y. Correlation between mechanical properties and pore structure deterioration of recycled concrete under sulfate freeze-thaw cycles: An experimental study. Constr. Build. Mater. 2024, 412, 134794. [Google Scholar] [CrossRef]
- Liang, Y.N.; Yuan, Y.S. Mechanism of concrete corrosion damage in sodium sulfate and magnesium sulfate solutions. J. Chin. Ceram. Soc. 2007, 35, 504–508. [Google Scholar]
- Thaulow, N.; Sahu, S. Mechanism of concrete deterioration due to salt crystallization. Mater. Charact. 2004, 53, 123–128. [Google Scholar] [CrossRef]
- Al-Amoudi, O.S.B. Sulfate attack and reinforcement corrosion in plain and blended cements exposed to sulfate environments. Build. Environ. 1998, 33, 53–61. [Google Scholar] [CrossRef]
- Al-Amoudi, O.S.B. Attack on plain and blended cements exposed to aggressive sulfate environments. Cem. Concr. Compos. 2002, 24, 305–316. [Google Scholar] [CrossRef]
- Liu, Z.Q. Study on Basic Mechanism of Concrete Sulfate Attack. Ph.D. Thesis, Central South University, Changsha, China, 2010. [Google Scholar]
- Wu, J.T.; He, R.; Wang, X.F.; Yang, B.; Wang, Z.J. Research progress on internal and external factors and mechanisms of sulfate attack concrete. Bull. Silic. 2019, 38, 110–117. [Google Scholar]
- Chen, Y.; Liu, P.; Yin, J.; Wang, D.; He, S.S.; Zhang, X.Q.; Yu, Z.W. Progress of chemical thermodynamics and multi-scale research on sulfate erosion of concrete. Concrete 2024, 3, 35–41. [Google Scholar]
- Chen, F. Study on Sulfate Attack Mechanism of Cement-Based Materials in Harsh Environments. Ph.D. Thesis, Southeast University, Nanjing, China, 2025. [Google Scholar]
- Zhang, S.Y. Mechanism of Concrete Sulfate Attack Under Complex Environment. Ph.D. Thesis, Qingdao University of Technology, Qingdao, China, 2014. [Google Scholar]
- Yu, H.F.; Sun, W.; Wu, W.F.; Yang, S.; Yan, L.H. Frost resistance and damage mechanism of ordinary concrete in salt lake brine environment. J. Chin. Ceram. Soc. 2003, 8, 763–769. [Google Scholar]
- Sun, W.; Miao, C.W. Modern Concrete Theory and Technology; Science Press: Beijing, China, 2012. [Google Scholar]
- Dong, W.; Wang, J.F. Research on capillary water absorption characteristics of aeolian sand concrete under sulfate freeze-thaw coupling based on fractal theory. Constr. Build. Mater. 2024, 455, 139184. [Google Scholar] [CrossRef]
- Yuan, L.D. Experimental Study on Concrete Durability Under the Combined Action of Sulfate Erosion and Freeze-Thaw Cycle. Ph.D. Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2013. [Google Scholar]
- Wang, B.X.; Pan, J.J.; Fang, R.C.; Wang, Q. Damage model of concrete subjected to coupling chemical attacks and freeze-thaw cycles in saline soil area. Constr. Build. Mater. 2020, 242, 118205. [Google Scholar] [CrossRef]
- Gan, L.; Liu, Y.; Shen, Z.Z.; Chen, G.Y. Damage evolution law of concrete under sulfate erosion and freeze-thaw cycles. J. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 2023, 51, 134–141. [Google Scholar]
- Xiao, Q.H.; Cao, Z.Y.; Guan, X.; Li, Q.; Liu, X.L. Damage to recycled concrete with different aggregate substitution rates from the coupled action of freeze-thaw cycles and sulfate attack. Constr. Build. Mater. 2019, 221, 74–83. [Google Scholar] [CrossRef]
- Xiao, Q.H.; Li, Q.; Cao, Z.Y.; Tian, W.Y. The deterioration law of recycled concrete under the combined effects of freeze-thaw and sulfate attack. Constr. Build. Mater. 2019, 200, 344–355. [Google Scholar] [CrossRef]
- Xue, W.P.; Peng, X.B.; Alam, M.S.; Wang, Z.J.; Wu, H.; Lin, J. Pore structure, mechanical property and permeability of concrete under sulfate attack exposed to freeze-thaw cycles. Arch. Civ. Mech. Eng. 2024, 24, 130. [Google Scholar] [CrossRef]
- Li, F.L.; Ma, L.H.; Gao, R.D.; Zhao, S.B. Effect of erosion mode on transport of sulfate ions in concrete. J. Yangtze River Sci. Res. Inst. 2010, 27, 62–65. [Google Scholar]
- Bao, W.X.; Yin, Y.; Mi, W.J.; Chen, R.; Lin, X.H. Durability and microstructural evolution of high-performance ecological geopolymer concrete under low-pressure-salt-erosion-freeze-thaw cycling conditions. Constr. Build. Mater. 2024, 426, 136197. [Google Scholar] [CrossRef]
- Su, D.Y. Study on Mechanical Properties and Damage Constitutive Relationship of Waste Glass Concrete Under Sulfate Freeze-Thaw Coupling Environment. Ph.D. Thesis, Anhui University of Science and Technology, Huainan, China, 2023. [Google Scholar]
- Lu, C.G. Research on Durability Test and Life Prediction and Evaluation of Concrete Structure Materials in Northwest Saline Environment. Ph.D. Thesis, Lanzhou University of Technology, Lanzhou, China, 2022. [Google Scholar]
- Deng, L.J. Mechanism analysis of frost resistance of concrete under different sulfate concentrations. Water Conserv. Tech. Superv. 2023, 8, 119–121+223+227. [Google Scholar]
- Wang, H.L.; Dong, Y.S.; Sun, X.Y.; Jin, W.L. Mechanism of concrete degradation by sulfate attack in alternating dry and wet environment. J. Zhejiang Univ. Eng. Technol. 2012, 46, 1255–1261. [Google Scholar]
- Mu, R.; Miao, C.W.; Liu, J.P.; Sun, W. Effects and mechanisms of sodium chloride and sodium sulfate solutions on frost resistance of concrete. J. Chin. Ceram. Soc. 2001, 29, 523–529. [Google Scholar]
- Zheng, F.; Qing, G.S. Research status of environmental factors of concrete subjected to sulfate attack. J. Xuzhou Inst. Technol. Nat. Sci. Ed. 2010, 25, 21–28. [Google Scholar]
- Zheng, X.N.; Diao, B. Study on the deterioration mechanism of concrete mechanical properties under the action of mixed erosion and freeze-thaw cycle. J. Archit. Struct. 2010, 31, 111–116. [Google Scholar]
- Li, Y.D.; Ye, Y.H. Degradation test of concrete performance under the alternating action of mixed erosion and freeze-thaw. Ind. Constr. 2011, 41, 120–123. [Google Scholar]
- Yuan, L.D.; Niu, D.T.; Jiang, L.; Sun, Y.Z.; Fei, Q.N. Study on concrete damage under combined sulfate erosion and freeze-thaw cycles. Bull. Chin. Ceram. Soc. 2013, 32, 1171–1176. [Google Scholar]
- Yuan, X.Q. Study on the mechanism of freeze-thaw cycle and sulphate erosion damage hydraulic concrete. Heilongjiang Water Sci. Technol. 2022, 50, 10–13+31. [Google Scholar]
- Jin, Z.Q.; Chen, H.S.; Zhao, T.J.; Gao, S. Damage and ion transport of concrete under sulfate freeze-thaw. J. Build. Mater. 2015, 18, 493–498. [Google Scholar]
- Tian, W.; Li, X.S.; Wang, F. Experimental study on deterioration mechanism of concrete under coupling action of freeze-thaw cycles and sulfate solution. Bull. Chin. Ceram. Soc. 2019, 38, 702–710. [Google Scholar]
- Chen, Z.M.; Yang, Z.Q.; Liu, J.H.; Yuan, Q.L.; Zhang, M.; Zheng, P.J. Mechanism of silica fume improving concrete life in Qinghai freeze-thaw-erosion environment. Concrete 2024, 12, 133–137+144. [Google Scholar]
- Duan, M.H.; Qin, Y.; Li, Y. Durability of fiber-reinforced concrete under salt-freeze/thaw-dry/wet cycles. J. Chin. Ceram. Soc. 2024, 52, 3703–3717. [Google Scholar]
- Xie, D.J.; Qi, Y.L.; Zhao, J.H.; Wu, P. Study on deterioration mechanism of fiber-reinforced aeolian sand concrete under salt-freeze-thaw coupling. J. Railw. Sci. Eng. 2025, 22, 3086–3097. [Google Scholar]
- Wang, Y.; Yang, Z.F.; Quan, Z.P.; Zhang, S.H.; Niu, D.T.; Wu, J. Sulfate resistance and life prediction of UHPC in western saline soil environment. Constr. Build. Mater. 2025, 458, 139756. [Google Scholar] [CrossRef]
- Zhang, X.P.; Zhang, R.L.; Yang, B.; Xiao, P.Z.; Wang, X.P.; Long, C.F. Strength evolution and prediction model of early-age concrete under freeze-thaw-sulfate corrosion coupling. Mater. Rep. 2024, 38, 205–213. [Google Scholar]
- Zhang, R.L.; Zhang, X.P.; Xue, Y.J.; Wang, X.P.; Xiao, P.Z.; Song, Y. Research on the durability degradation mechanism of early-age concrete and life prediction model under freeze-thaw-salt erosion coupling effect. Structures 2025, 71, 107986. [Google Scholar] [CrossRef]
- Dong, W.; Wang, J.F. Deterioration law and life prediction of aeolian sand concrete under sulfate freeze-thaw cycles. Constr. Build. Mater. 2024, 411, 134593. [Google Scholar] [CrossRef]
- Zhu, X.C.; Wang, D.F.; Zhang, Y.S.; Liu, Z.Y.; Qiao, H.X.; Zhou, Q.M.; Ye, F.K. Study on sulfate diffusion test and mathematical model of manufactured sand concrete under typical freeze-thaw environment in Northwest China. Constr. Build. Mater. 2024, 419, 135559. [Google Scholar] [CrossRef]
- Tanyildizi, H. Durability of concrete exposed to combined freeze-thaw, sulfate, and acid attacks after two years. Rev. Constr. 2023, 22, 102–121. [Google Scholar] [CrossRef]
- Zhu, F.F.; Qiao, H.X.; Fu, Y.; Wang, X.K. Freeze-thaw test and numerical analysis of basalt fiber reinforced concrete in western saline soil regions. J. Chin. Ceram. Soc. 2024, 52, 3431–3443. [Google Scholar]
- GB/T 50082-2009; Standard for Test Methods of Long-Term Performance and Durability of Ordinary Concrete. Ministry of Housing and Urban-Rural Development of China; China Architecture & Building Press: Beijing, China, 2009.
- ASTM C666/C666M-03; Standard Test Method for Resistance of Concrete to Rapid Freezing and Thawing. ASTM International: West Conshohocken, PA, USA, 2003.
- Xiong, B.B.; Gao, L.; Lu, X.C.; Tian, B.; Chen, B.F. Evolution model of concrete freeze-thaw damage based on hydrostatic pressure theory. J. Eng. Mech. 2023, 40, 184–192. [Google Scholar]
- Jiang, L.; Niu, D.T. Study on damage failure criterion of concrete under sulfate and freeze-thaw environment. J. Disaster Prev. Mitig. Eng. 2017, 37, 148–153. [Google Scholar]
- Cai, H. Prediction Model for Frost Durability of Concrete. Ph.D. Thesis, Tsinghua University, Beijing, China, 1998. [Google Scholar]
- Guan, Y.G.; Sun, W.; Miao, C.W. Service life prediction model of concrete based on reliability and damage theory I: Model description and establishment. J. Chin. Ceram. Soc. 2001, 6, 530–534. [Google Scholar]
- Guan, Y.G.; Sun, W.; Miao, C.W. Service life prediction model of concrete based on reliability and damage theory II: Model verification and application. J. Chin. Ceram. Soc. 2001, 6, 535–540. [Google Scholar]
- Qiu, W.L.; Teng, F.; Pan, S.S. Damage constitutive model of concrete under repeated load after seawater freeze-thaw cycles. Constr. Build. Mater. 2020, 236, 117560. [Google Scholar] [CrossRef]
- Liu, L.; Ye, G.; Schlangen, E.; Chen, H.S.; Qian, Z.W.; Sun, W.; Breuge, K. Modeling of the internal damage of saturated cement paste due to ice crystallization pressure during freezing. Cem. Concr. Compos. 2011, 33, 562–571. [Google Scholar] [CrossRef]
- Dong, H.L.; Li, H.J.; Yang, Z.Q.; Wen, J.X.; Huang, F.L.; Wang, Z.; Yi, Z.L. Freeze-thaw damage mechanism and life prediction methods of concrete. Mater. Rep. 2024, 38, 143–153. [Google Scholar]
- Ikumi, T.; Segura, I. Numerical assessment of external sulfate attack in concrete structures: A review. Cem. Concr. Res. 2019, 121, 91–105. [Google Scholar] [CrossRef]
- Yu, Y.G.; Gao, W.; Feng, Y.; Castel, A.; Chen, X.J.; Liu, A.R. On the competitive antagonism effect in combined chloride-sulfate attack: A numerical exploration. Cem. Concr. Res. 2021, 144, 106406. [Google Scholar] [CrossRef]
- Xu, J.; Mo, R.; Wang, P.G.; Zhou, J.G. Coupled transport of sulfate and chloride ions with adsorption effect: A numerical analysis. Front. Mater. 2020, 7, 536517. [Google Scholar] [CrossRef]
- Liu, Y.J.; Li, W.J.; Guan, J.W.; Zhou, X.; Guo, L. Fully coupled peridynamic model for analyzing the chemo-diffusion-mechanical behavior of sulfate attack in concrete. Constr. Build. Mater. 2023, 409, 133874. [Google Scholar] [CrossRef]
- Liang, Y.; Wang, Z. Investigation on performance degradation analysis method of offshore concrete structures under freeze-thaw and sulfate attack. Ocean Eng. 2025, 316, 119935. [Google Scholar] [CrossRef]
- Peng, R.; Qiu, W.; Teng, F. Research on performance degradation analysis method of offshore concrete piers in cold regions. Ocean Eng. 2022, 263, 112304. [Google Scholar] [CrossRef]
- Zheng, C.L.; Wan, S.Y.; Zong, Z.H. Durability evaluation and lifetime prediction of recycled coarse aggregate self-compacting concrete after freeze-thaw and sulfate erosion coupling. Mater. Today Commun. 2024, 39, 109115. [Google Scholar] [CrossRef]




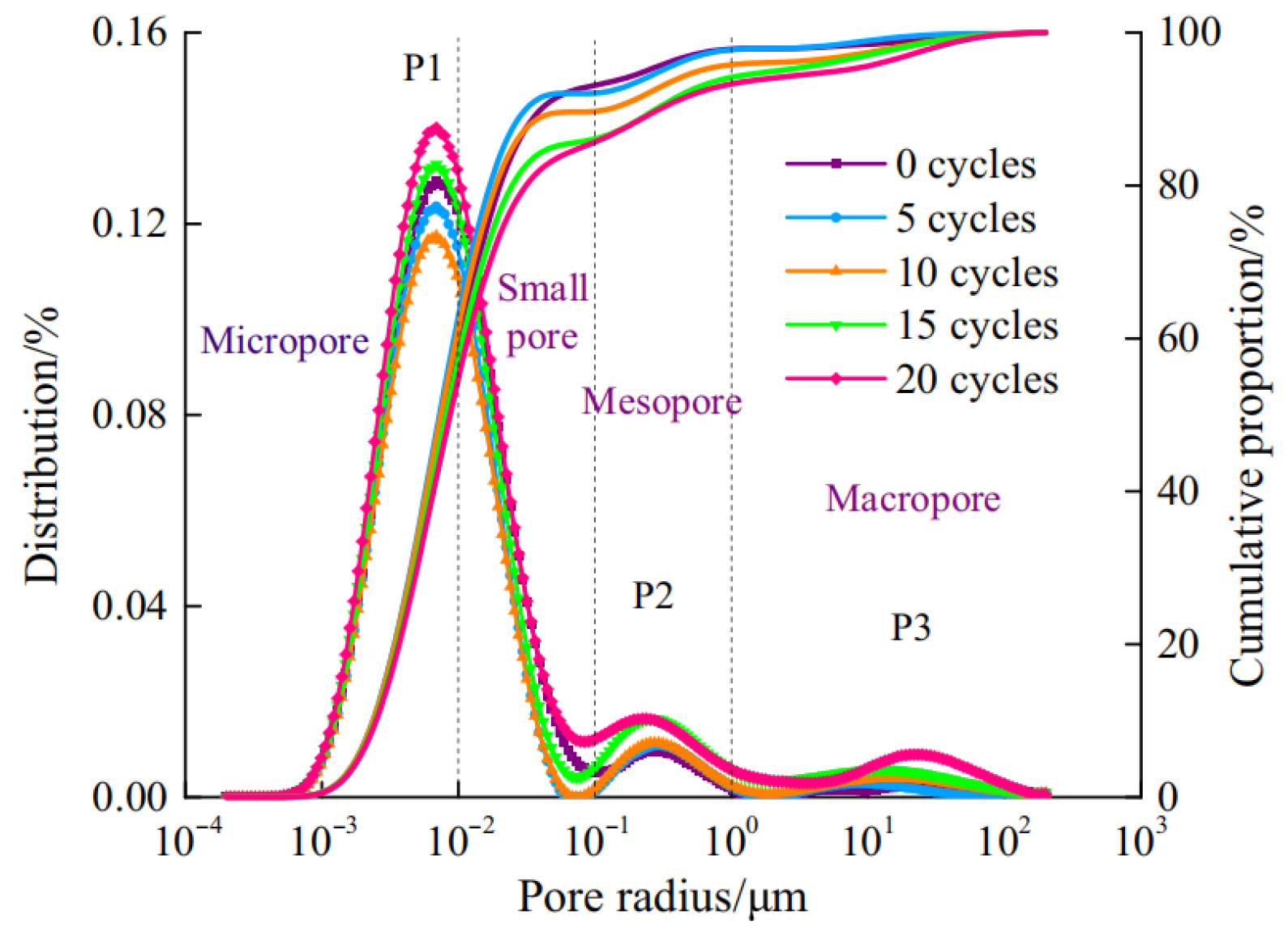

| Salt Solutions | Specimen Dimension, Age | Scholar | w/b Ratio | Evaluation Indicators | Freeze–Thaw Method | Testing Intervals | Key Results |
|---|---|---|---|---|---|---|---|
| 5% Na2SO4 (mass fraction) | 40 mm × 40 mm × 160 mm, 28 d | Mu et al. [55] | 0.44, 0.32, 0.26 | Mass loss, RDEM | Rapid freeze–thaw (water freezing and water melting) | Every 20 cycles (≤300 cycles) | During the initial freeze–thaw phase, sulfate-induced damage is less severe compared to pure water exposure; however, in later stages, concrete with low water–binder ratio exhibits the most significant deterioration under sulfate freeze–thaw conditions. |
| 3% NaCl and 5% Na2SO4 (mass fraction) | 100 mm × l00 mm × l00 mm, 28 d | Zheng et al. [57] | 0.44 | Compressive strength, SEM, XRD | Rapid freeze–thaw (air freezing and air melting, −15 °C~8 °C), 12 h solution immersion every 10 cycles | Every 100 cycles (≤400 cycles) | Mechanical properties of concrete materials experience accelerated deterioration. |
| 100 mm × l00 mm × l00 mm and 100 mm × l00 mm × 300 mm, 28 d | Li et al. [58] | 0.4 | Mass loss, RDEM, compressive strength, elastic modulus | Slow freeze–thaw (air freezing and water melting), 4 h freezing in air at −18 °C to −20 °C, 4 h thawing while fully immersed in the mixed erosion solution at 18–20 °C | Every 100 cycles (≤300 cycles) | With the increase in freeze–thaw cycles, increased erosion of concrete specimen surface, and the apparent quality and relative dynamic modulus did not change significantly when both compressive strength and elastic modulus decreased significantly. Compressive strength and elastic modulus decreased by 26% and 35.1% after 300 freeze–thaw cycles. | |
| 1% Na2SO4, 5% Na2SO4 or 5% MgSO4 (mass fraction) | 100 mm × l00 mm × 400 mm, 28 d + 60 d natural curing | Yuan et al. [59] | 0.45 | Damage layer thickness | Rapid freeze–thaw (water freezing and water melting) | Start at 150 cycles, then every 50 cycles (≤400 cycles) | With the increase of solution concentration, the promoting effect of freeze–thaw damage for the concrete with sulfate solution change to an inhibitory effect. |
| 100 mm × 100 mm × 400 mm for relatively elastic modulus and damage layer thickness test; 100 mm × 100 mm × 100 mm for compressive strength and SEM analysis | Jiang et al. [19] | 0.45 | RDEM, compressive strength, damage layer thickness, SEM | Rapid freeze–thaw (water freezing and water melting) | Start at 100 cycles, then every 50 cycles (≤400 cycles) | Concrete degradation rate in 1% Na2SO4 solution is faster than that in 5% Na2SO4 solution and in water. | |
| 12 prisms of 100 mm × 100 mm × 400 mm, 28 d | Yuan et al. [60] | 0.45 | Damage layer thickness | Rapid freeze–thaw (water freezing and water melting) | Start at 150 cycles, then every 50 cycles (≤350 cycles) | Sodium sulfate acts as a promoter at low concentrations and an inhibitor at high ones. | |
| 3% NaCl and 3% Na2SO4 (mass fraction) | 100 mm × 100 mm × 100 mm, 28 d | Lu et al. [52] | 0.34 | Mass, ultrasonic sound velocity value, NMR, SEM, XRD | Air freeze–water thaw–air freeze–air thaw cycle, specifically: 6 h in freezing chamber at −20 °C, 6 h immersed in salt solution at 20 °C, 6 h in freezing chamber at −20 °C, 6 h in ambient air at 20 °C | Every 25 cycles (≤300 cycles) | Durability life prediction model for concrete was established based on the Birnbaum–Saunders distribution. |
| Brine from a salt lake | 40 mm × 40 mm × 160 mm, 28 d | Yu et al. [40] | 0.60 | RDEM, speed of sound in ultrasonic waves, Mass loss, XRD | Rapid freeze–thaw (water freezing and water melting) | Every 25 cycles | Salt solution has a positive effect by lowering the freezing point, while its negative effect is accelerating salt crystallization. |
| 5% Na2SO4, 3.5% NaCl and 5% Na2SO4 (mass fraction) | 100 mm × 100 mm × 400 mm, 28 d | Jin et al. [61] | 0.46, 0.32 | Ultrasonic transit time, mass fraction of water-soluble and acid-soluble components, pore structure evolution, thermogravimetric curve | Rapid freeze–thaw (water freezing and water melting) | 0, 50, 150, 200 cycles | An increase to double the sulfate ion reactivity and a 2.2-times enlargement of capillary pores were observed in concrete under mixed solution frost, compared to exposure to a 5% Na2SO4 solution. |
| 10% Na2SO4,15% Na2SO4 | 100 mm × 100 mm × 100 mm, 28 d | Tian et al. [62] | 0.45 | Mass, RDEM, uniaxial compressive strength, CT | Slow freeze–thaw (air freeze: −18~−20 °C/4 h; solution thaw: 18~20 °C/4 h) | 0, 20, 40, 60, 80, 100 cycles | Sulfate and freeze–thaw interaction exhibits two-stage deterioration: initial mitigation followed by later acceleration. |
| 5% Na2SO4 | 120 cubes of 100 mm × 100 mm × 100 mm and 36 prisms of 100 mm × 100 mm × 400 mm, 28 d | Chen et al. [63] | 0.35 | Mass loss, RDEM, uniaxial compressive strength | Sulfate dry–wet cycling → Freeze–thaw cycling. Dry–wet cycle (24 h): 16 h immersion in 5% Na2SO4 solution, 6 h drying at 80 °C, 2 h cooling; Freeze–thaw cycle (6 h): Freezing 4 h at −20 ± 2 °C, Thawing 2 h at 5 ± 2 °C Alternating protocol: 16 days = 1 combined cycle (dry–wet + freeze–thaw) | Every cycle (16 d), 80 days (5 cycles) | Compressive strength-based GM(1,1) modeling for service life prediction of concrete. |
| 5% Na2SO4, 5% MgSO4, and 3.5% NaCl compound salt solution | Φ100 × 50 mm, 150 d outdoor exposure | Duan et al. [64] | 0.32 (fiber content is 0.9, 1.2, and 1.4 kg/m3) | Ultrasonic velocity, splitting tensile strength, SEM | Rapid freeze–thaw (water freezing and water melting), 2.5 h freeze/1.5 h thaw | Every 25 cycles (≤200 cycles) | Concrete damage degradation model with ultrasonic pulse velocity damage quantity as independent variable and relative splitting tensile strength as dependent variable. |
| 5% Na2SO4, 10% Na2SO4 | 100 mm × 100 mm × 100 mm, 28 d | Xie et al. [65] | 0.4 (fine aggregate selected 20% of the wind-sediment sand to replace the river sand) | Mass loss, compressive strength, SEM | Rapid freeze–thaw (−20 °C~20 °C, 4 h cycle) | 0, 20, 40, 60, 80 cycles | Weibull function-based constitutive model for concrete damage using micro-damage variables. |
| 3%, 6%, 9% Na2SO4 | 288 cube of 100 mm × 100 mm × 100 mm, 28 d | Gan et al. [24,45] | 0.4 | Mass change, compressive strength, splitting tensile strength, RDEM, CT | Salt immersion (15 d) + freeze–thaw cycling (25 cycles) | Every 25 cycles (≤200 cycles) | Expression for damage evolution of concrete under cyclic salt–freeze–thaw action with number of freeze–thaw cycles as independent variable. |
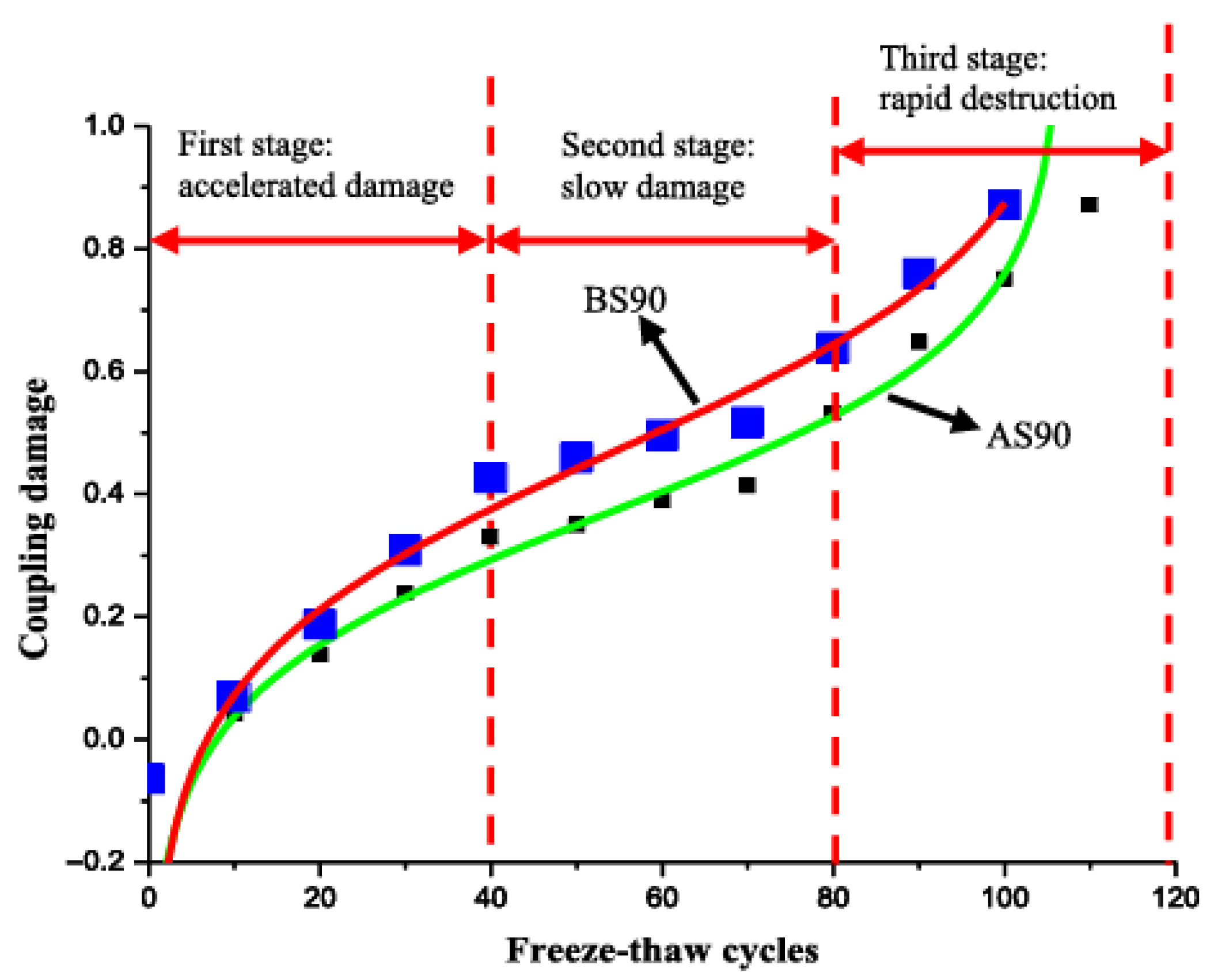
| 20% Na2SO4 | Φ50 × 100 mm, 28 d + 150 d immersion + 3 d drying | Xue et al. [48] | 0.57 | NMR, compressive permeability | Cyclic: 10 h 20% Na2SO4 solution immersion/8 h freeze (−20 °C)/6 h dry (65 °C) | 0, 5, 10, 15, 20 cycles | Proportion of mesopores and macropores in concrete increases with the number of salt–freeze–thaw cycles. |
| 10% Na2SO4 | 40 mm × 40 mm × 40 mm (compression) 40 mm × 40 mm × 160 mm (flexure) | Wang et al. [66] | 0.18, 0.20, 0.22 (different amounts of silica powder and fiber) | Compressive/flexural strength, mass change, RDEM, SEM, XRD, TG-DTG, MIP | Multi-stage: 3 d high-temp + 30 d dry–wet + 2 d freeze–thaw + 2 d sulfate + 3 d low-temp (40 d/cycle ≈ 5 years) | Every cycle (≤6 cycles) | Wiener stochastic process-based life expectancy model using compressive strength as the state variable. |
| 5% Na2SO4, mass fraction | 40 mm × 40 mm × 160 mm | Liu et al. [21] | 0.38 | RDEM | Rapid freeze–thaw | Every 20 cycles (≤200 cycles) | Expression for freeze–thaw damage in concrete with dynamic elastic modulus as the variable. |
| 6% Na2SO4, mass fraction | 100 mm × 100 mm × 100 mm, 7 d | Zhang et al. [67] | 0.26, 0.32, 0.38 | Compressive strength | Rapid freeze–thaw (−23.3 °C~43.1 °C, 6 h freeze/8 h thaw, 24 h/cycle ≈ 1 year) | Every 10 cycles (≤100 cycles) | Variable-weighted buffer gm(1,1) model for early-age concrete strength using anti-corrosion coefficient as the parameter. |
| 6% Na2SO4, mass fraction | 100 mm × 100 mm × 100 mm, 7 d | Zhang et al. [68] | 0.32 (inhibitor content of 0.00%, 0.05%, 0.10%, and 0.15%) | Appearance, mass loss, compressive strength, dynamic modulus | Rapid freeze–thaw (−23.3 °C~43.1 °C, 6 h freeze/8 h thaw, 24 h/cycle ≈ 1 year) | Every 10 cycles (≤100 cycles) | GM-GA-BP Model for early-age concrete service life prediction using number of freeze–thaw cycles as the parameter. |
| 5% Na2SO4, 10% Na2SO4, mass fraction | 100 mm × 100 mm × 100 mm 100 mm × 100 mm × 400 mm (RDME) | Dong et al. [42,69] | 0.54 | Compressive strength, dynamic elastic modulus, Mass, SEM, XRD, NMR | Rapid freeze–thaw | Every 25 cycles | Weibull stochastic probability distribution model for concrete service life prediction using compressive strength as the degradation index. |
| 5% Na2SO4, mass fraction | 100 mm × 100 mm × 100 mm 100 mm × 100 mm × 400 mm (RDME), 28 d | Xiao et al. [46] | 0.45 (0%, 30%, 50%, 100% replacement rate of coarse recycled concrete aggregate) | Mass, RDEM, compressive strength | ASTM C666 (8 ± 2 °C to 17 ± 2 °C) | Every 25 cycles | Freeze–thaw random damage model for recycled concrete using a two-parameter Weibull probability distribution. |
| 5% Na2SO4, mass fraction | 100 mm × 100 mm × 100 mm 100 mm × 100 mm × 400 mm (RDME), 28 d | Wei et al. [30] | 0.38 (0%, 50%, 100% replacement rate of coarse recycled concrete aggregate) | Mass, dynamic elastic modulus, NMR, Vickers hardness of ITZs | The specimen center’s temperature range during the freeze–thaw cycle test is − 18 °C to 5 °C | Every 25 cycles (≤300 cycles) | Pore structure damage model for concrete with comprehensive porosity parameters as variables. |
| 0.89%, 3.7%, 7.4% Na2SO4, mass fraction | 100 mm × 100 mm × 100 mm, 28 d | Zhu et al. [70] | 0.38 (manufactured sand) | Sulfate content | Rapid freeze–thaw (−20 ± 2 °C to 8 ± 2 °C, 3–5 h/cycle) | Every 25 cycles (≤150 cycles) | Diffusion equation for concrete under sulfate freeze–thaw cycles with sulfate ion content as the independent variable. |
| 5% Na2SO4 and 5% MgSO4, mass fraction | 100 mm × 100 mm × 100 mm, cured in water for 28 d after demolding, and then cured for 23 months +2 d under laboratory conditions. Total curing time is 2 years. | Tanyildizi [71] | 0.47 | Mechanical properties, Mass, RDEM, SEM, EDS | Slow freeze–thaw (7 h at −20 ± 2 °C and 5 h at 20 ± 2 °C) | After 56 cycles | Samples exposed to sodium sulfate and freeze–thaw were less affected by the increase in cement dosage. |
| 23 g/L Na2SO4, mass fraction | 100 mm × 100 mm × 100 mm | Zhu et al. [72] | 0.38 (0.1%, 0.2%, and 0.3% bulk accumulative amount of basalt fiber) | RDEM, mass loss, compressive/splitting strength | Rapid freeze–thaw (−20 ± 2 °C/6 h + 20 ± 2 °C/2 h) | Every 15 cycles (≤200 cycles) | Durability of concrete is improved by incorporating an appropriate amount of BF into the concrete to reduce the initial defects and slow down the rate of corrosive ions into the interior of the concrete. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Lv, C.; Xu, Y.; Sun, Y.; Qu, S.; Zhou, X. Deterioration of Concrete Under the Combined Action of Sulfate Attack and Freeze–Thaw Cycles: A Review. Materials 2025, 18, 4309. https://doi.org/10.3390/ma18184309
Wu H, Lv C, Xu Y, Sun Y, Qu S, Zhou X. Deterioration of Concrete Under the Combined Action of Sulfate Attack and Freeze–Thaw Cycles: A Review. Materials. 2025; 18(18):4309. https://doi.org/10.3390/ma18184309
Chicago/Turabian StyleWu, Hairong, Chenjie Lv, Youliang Xu, Yuzhou Sun, Songzhao Qu, and Xiangming Zhou. 2025. "Deterioration of Concrete Under the Combined Action of Sulfate Attack and Freeze–Thaw Cycles: A Review" Materials 18, no. 18: 4309. https://doi.org/10.3390/ma18184309
APA StyleWu, H., Lv, C., Xu, Y., Sun, Y., Qu, S., & Zhou, X. (2025). Deterioration of Concrete Under the Combined Action of Sulfate Attack and Freeze–Thaw Cycles: A Review. Materials, 18(18), 4309. https://doi.org/10.3390/ma18184309