Dry–Wet Cycle Fracture Performance of Recycled Concrete Sulfate Based on Computerized Tomographic Images
Abstract
1. Introduction
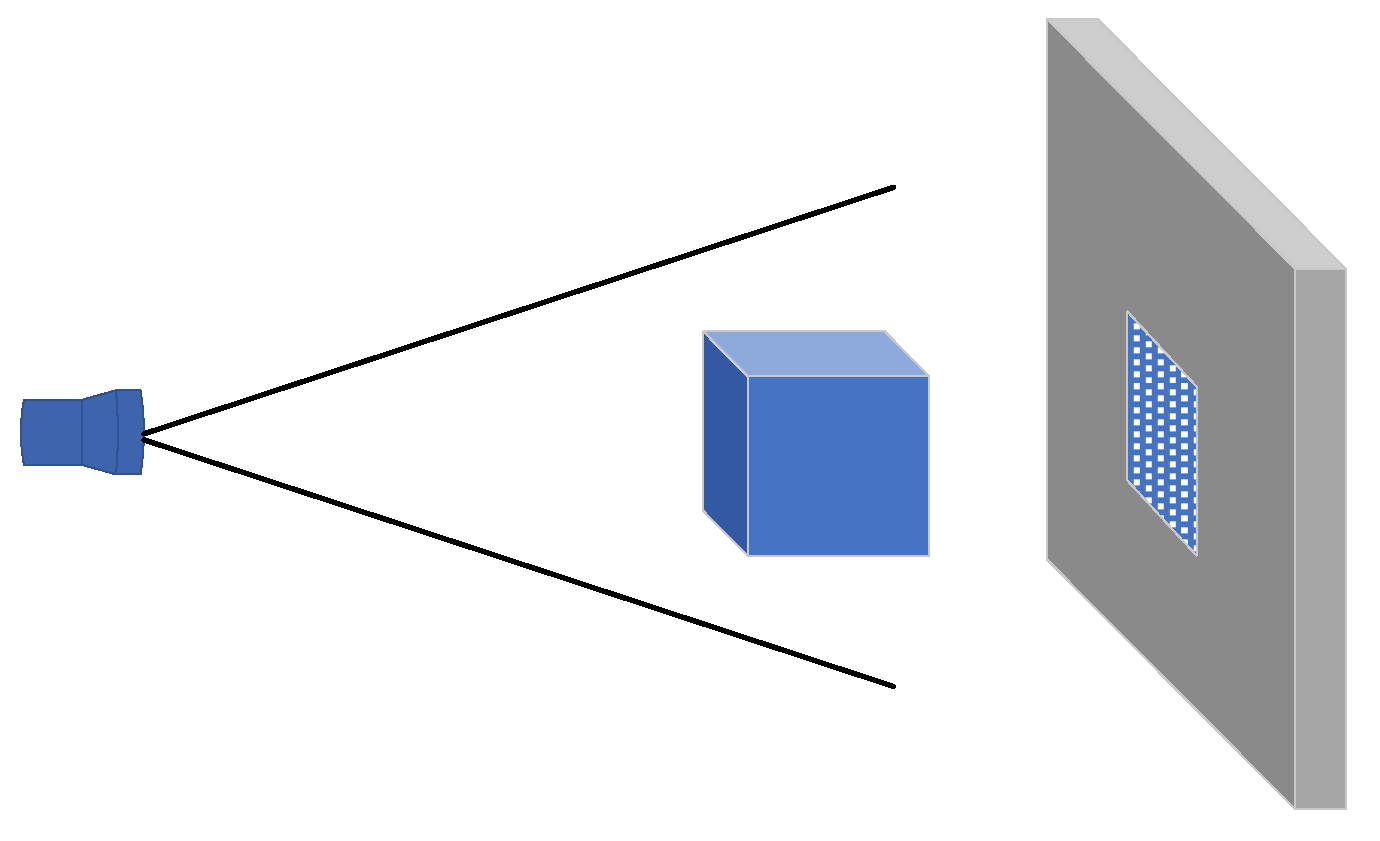
2. CT Scanning Principle
3. Materials and Methods
4. Results and Discussion
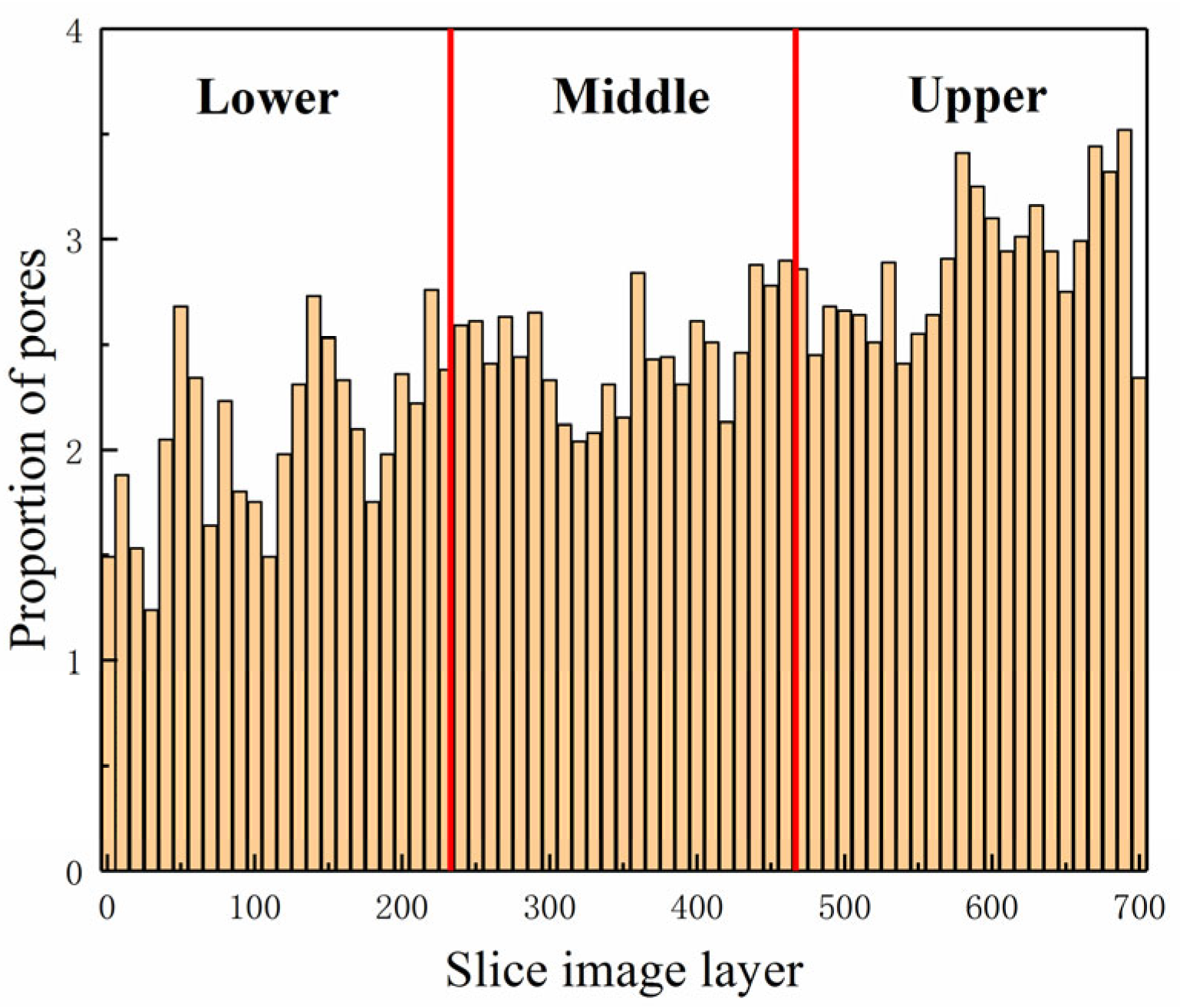
4.1. Analysis of Pore Distribution
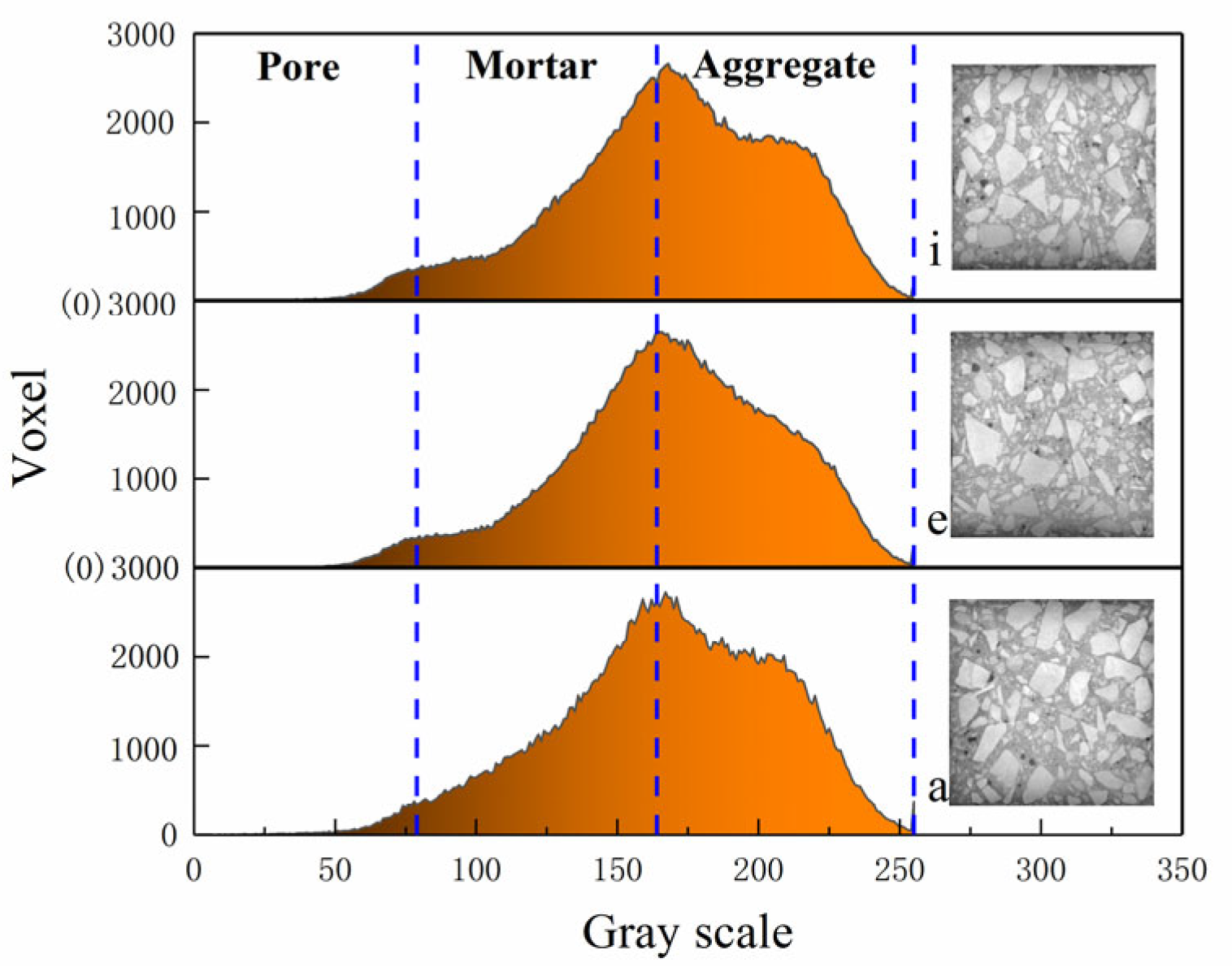
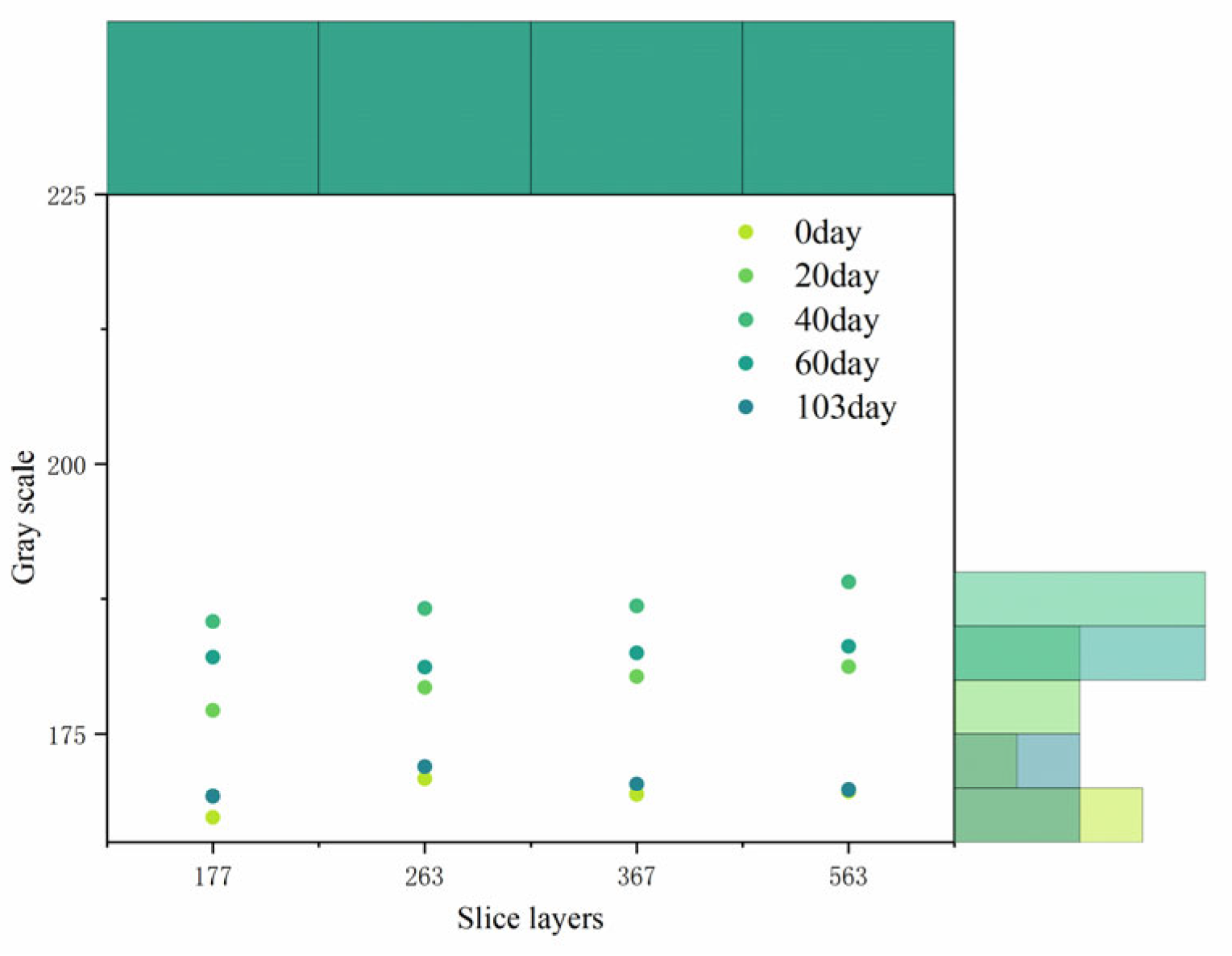
4.2. Gray Analysis
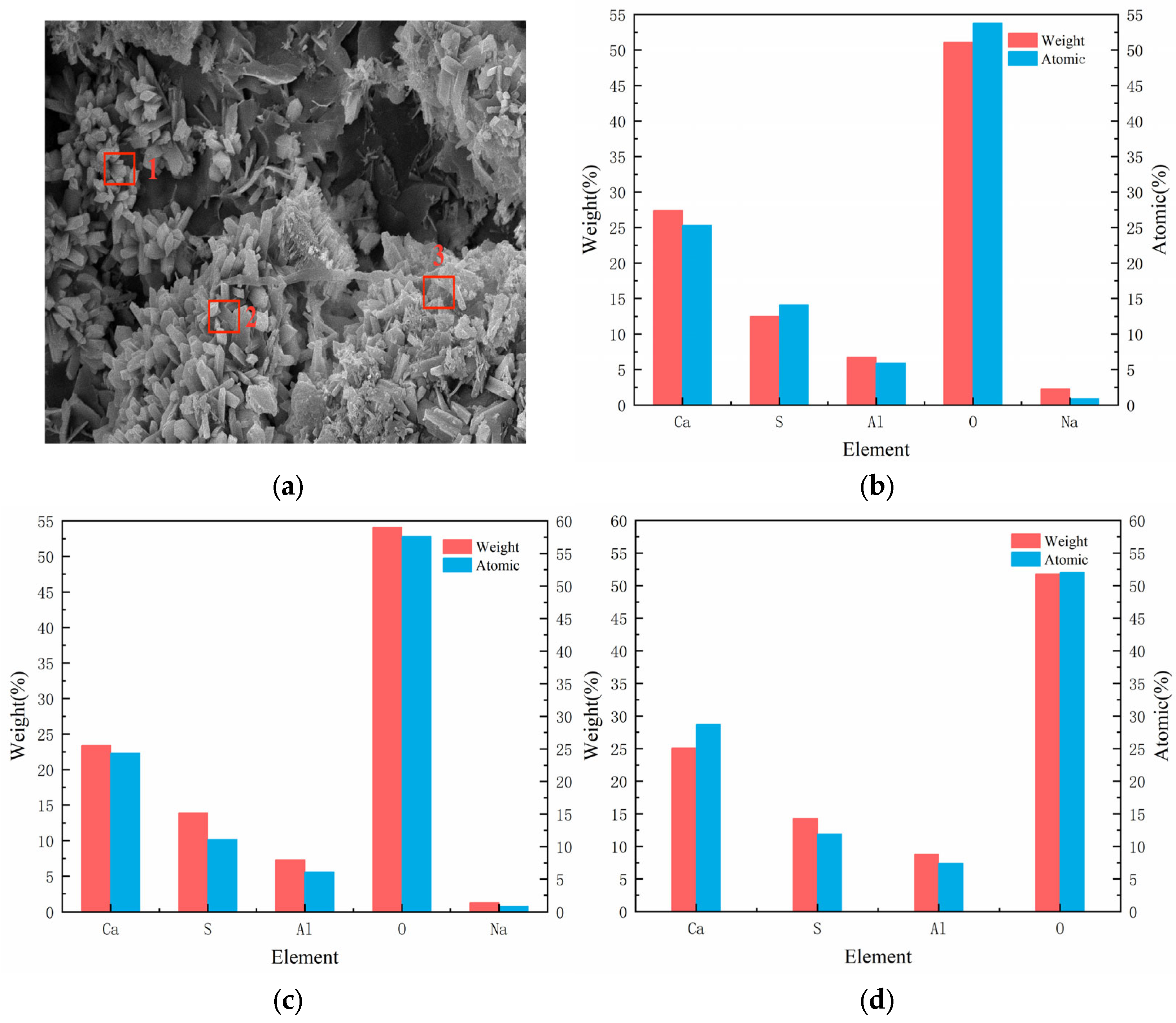
4.3. Micro Analysis
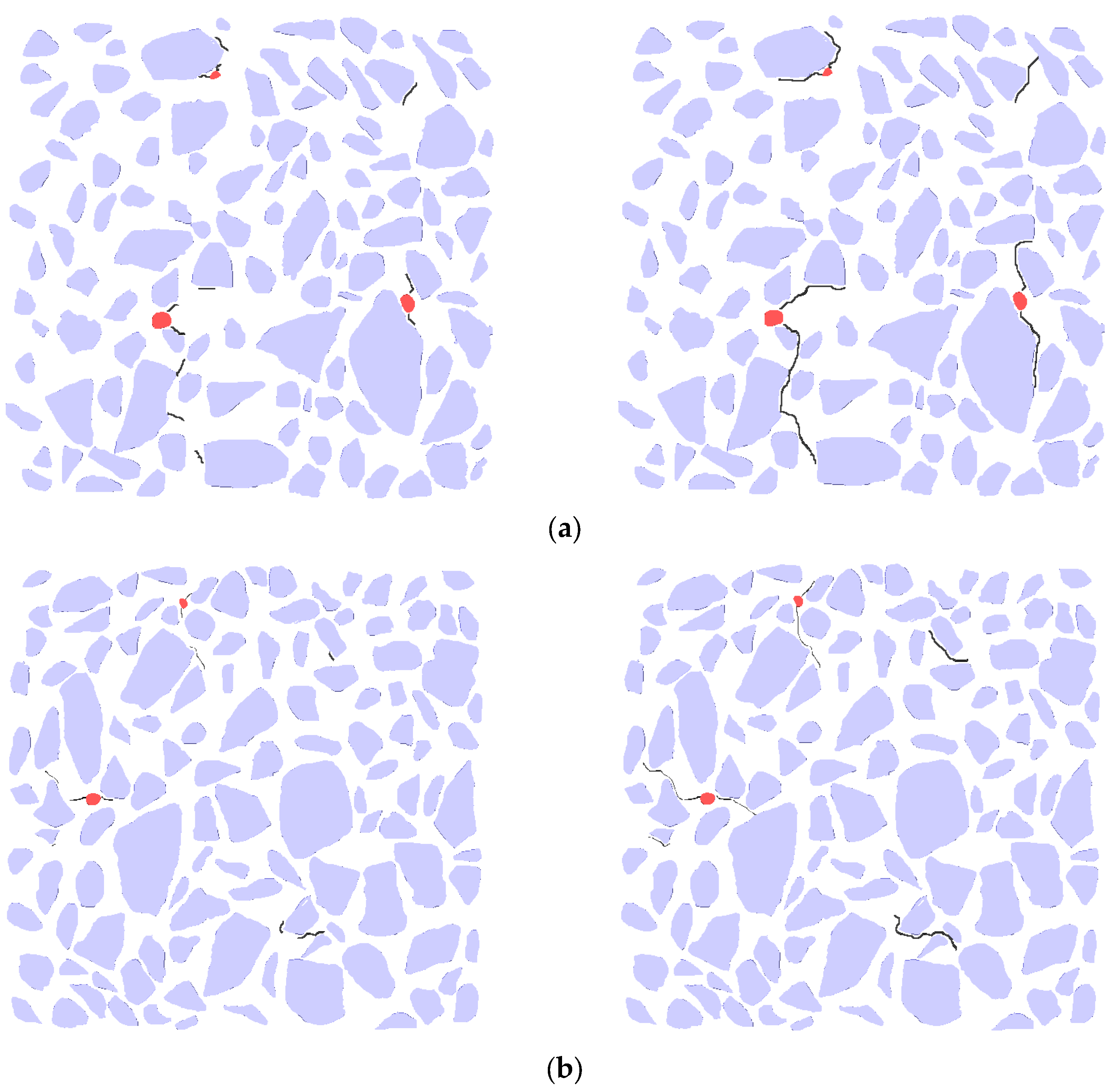
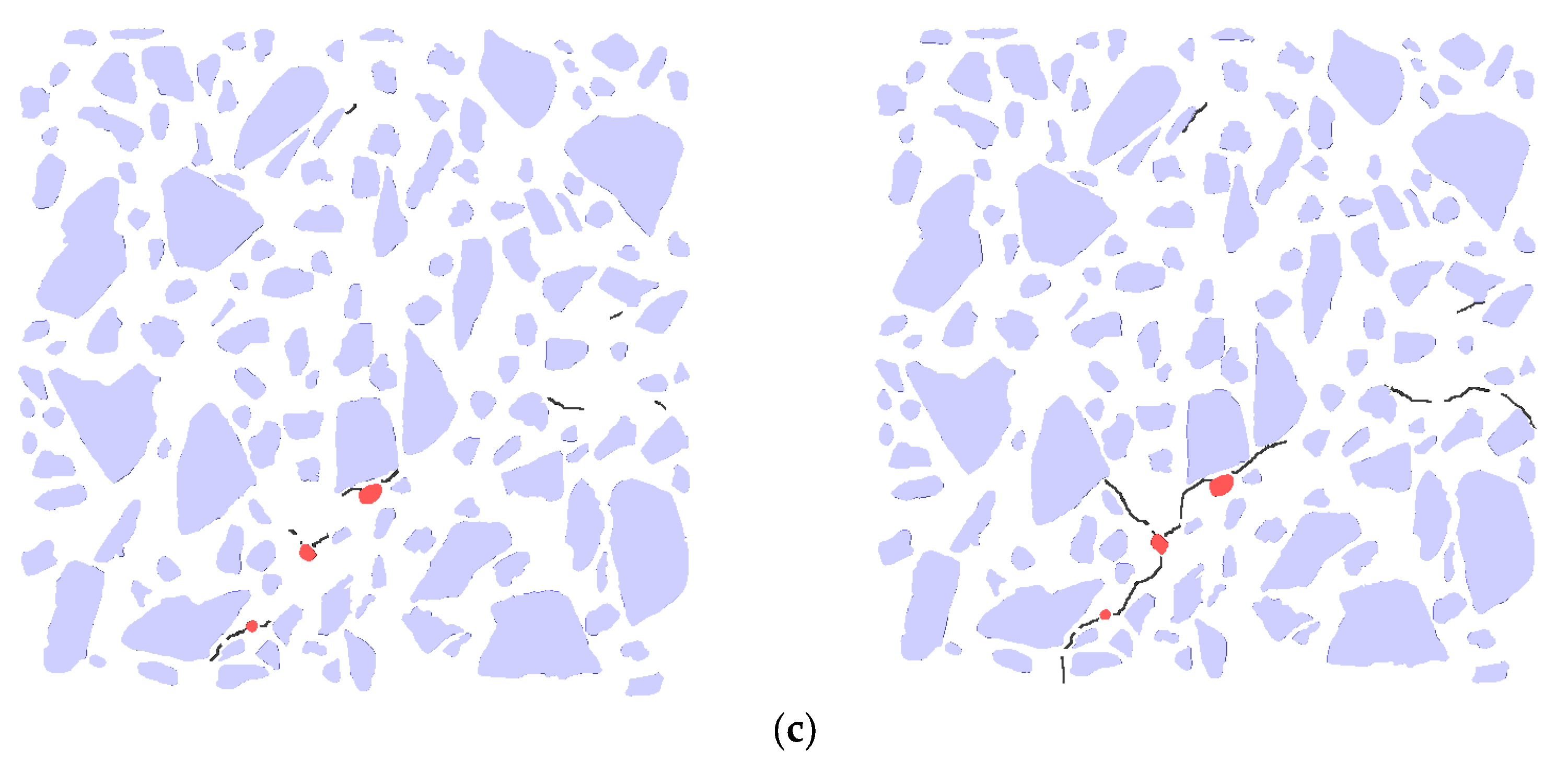
4.4. Crack Growth Analysis
5. Fracture Performance Analysis
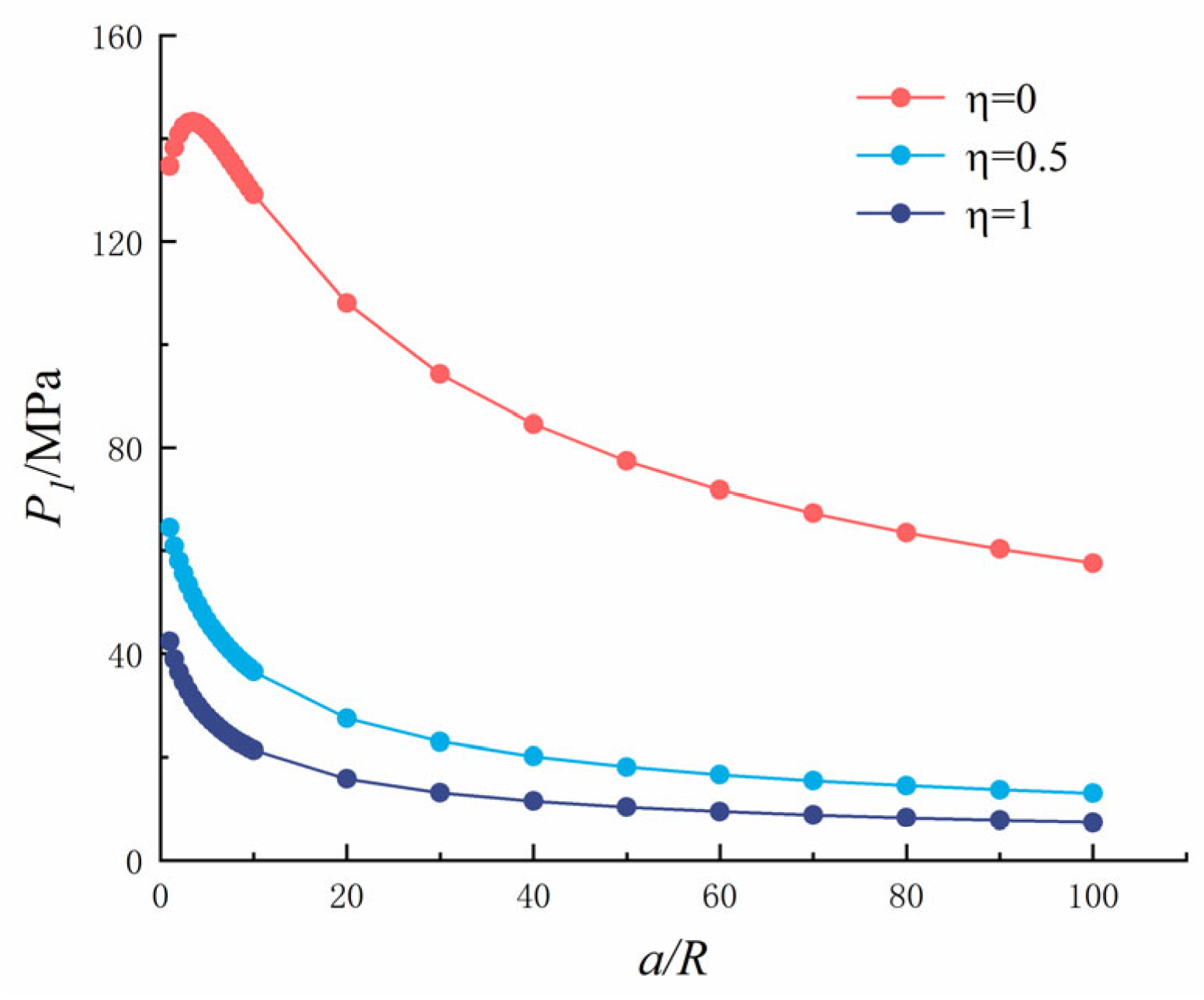
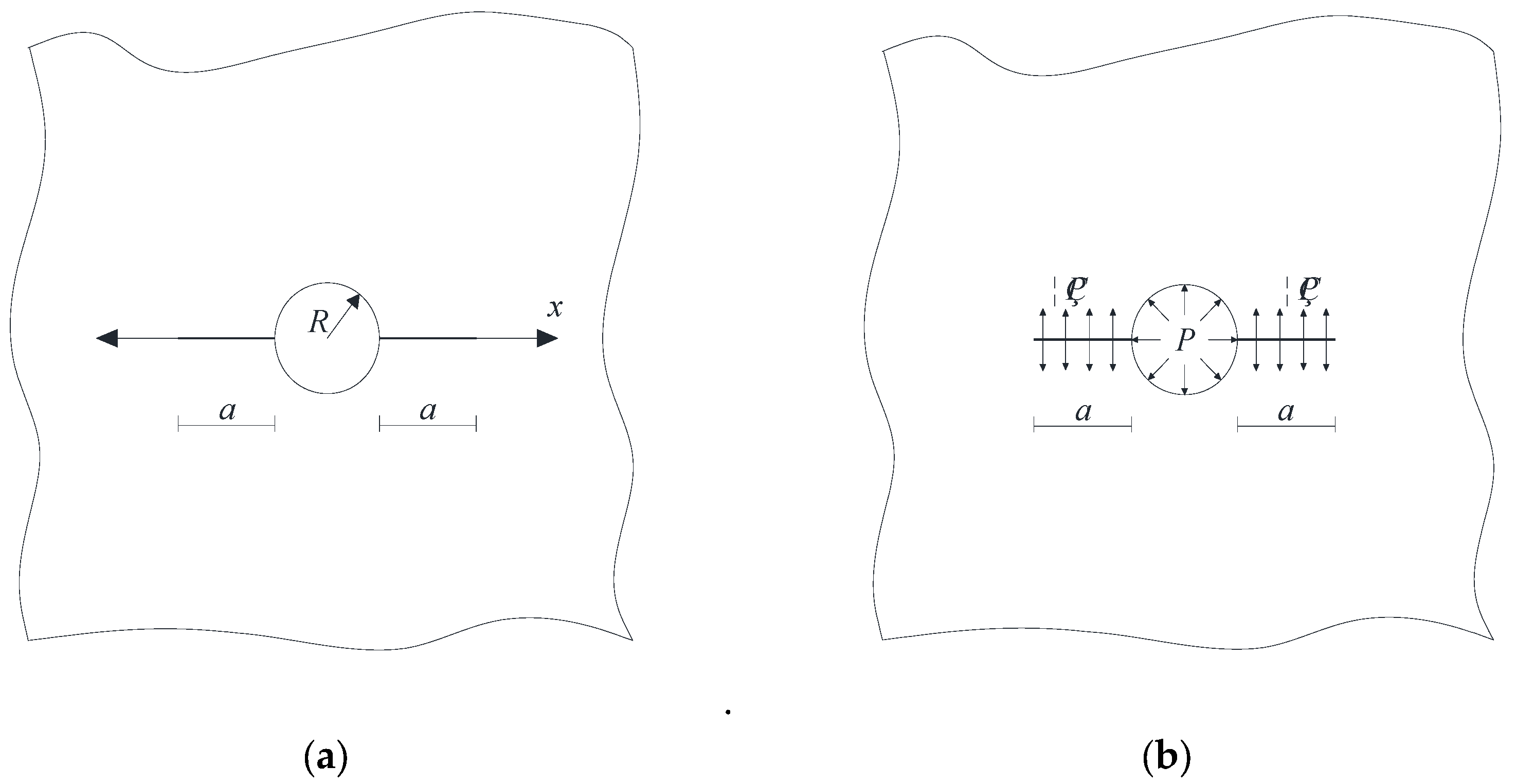
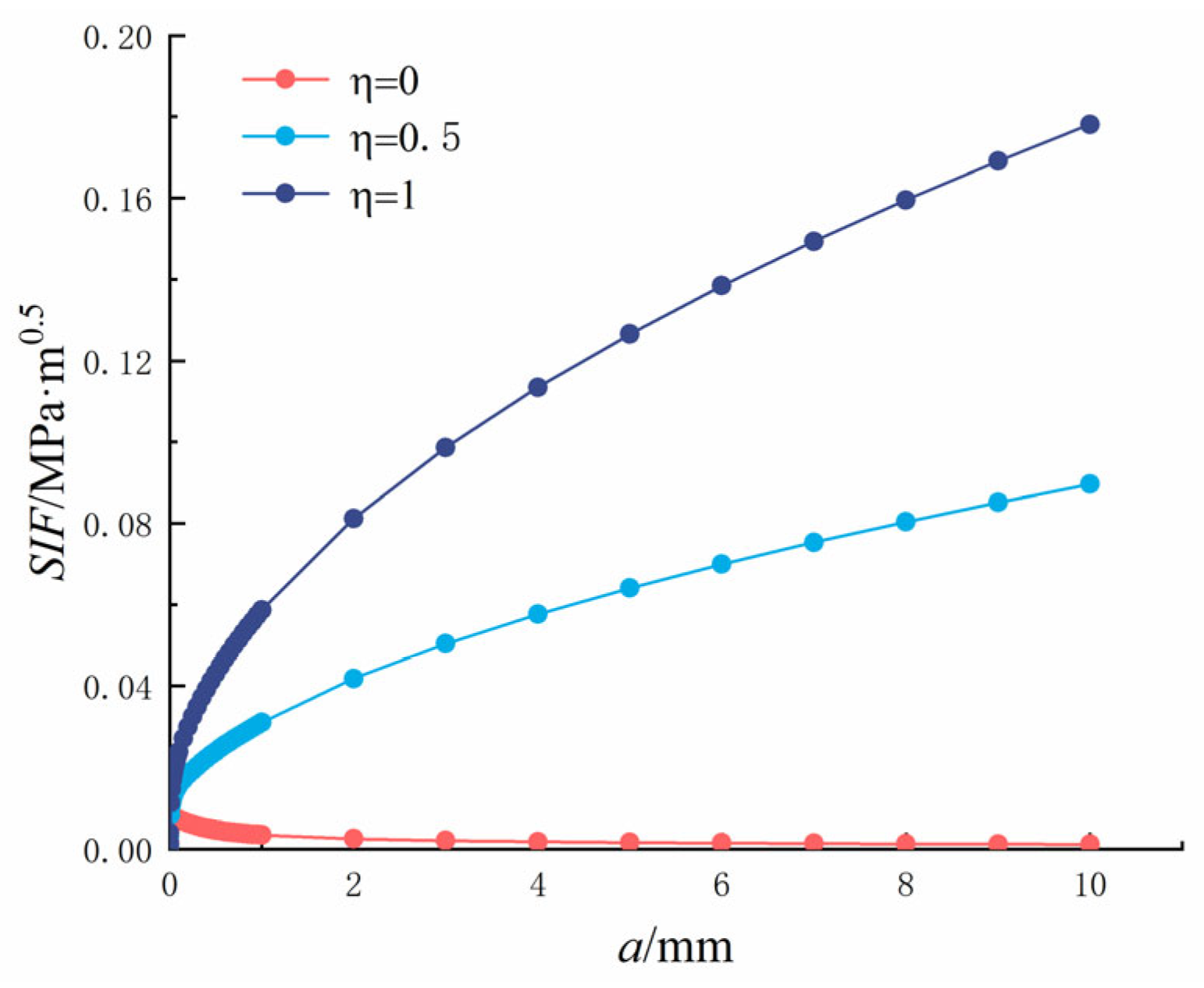
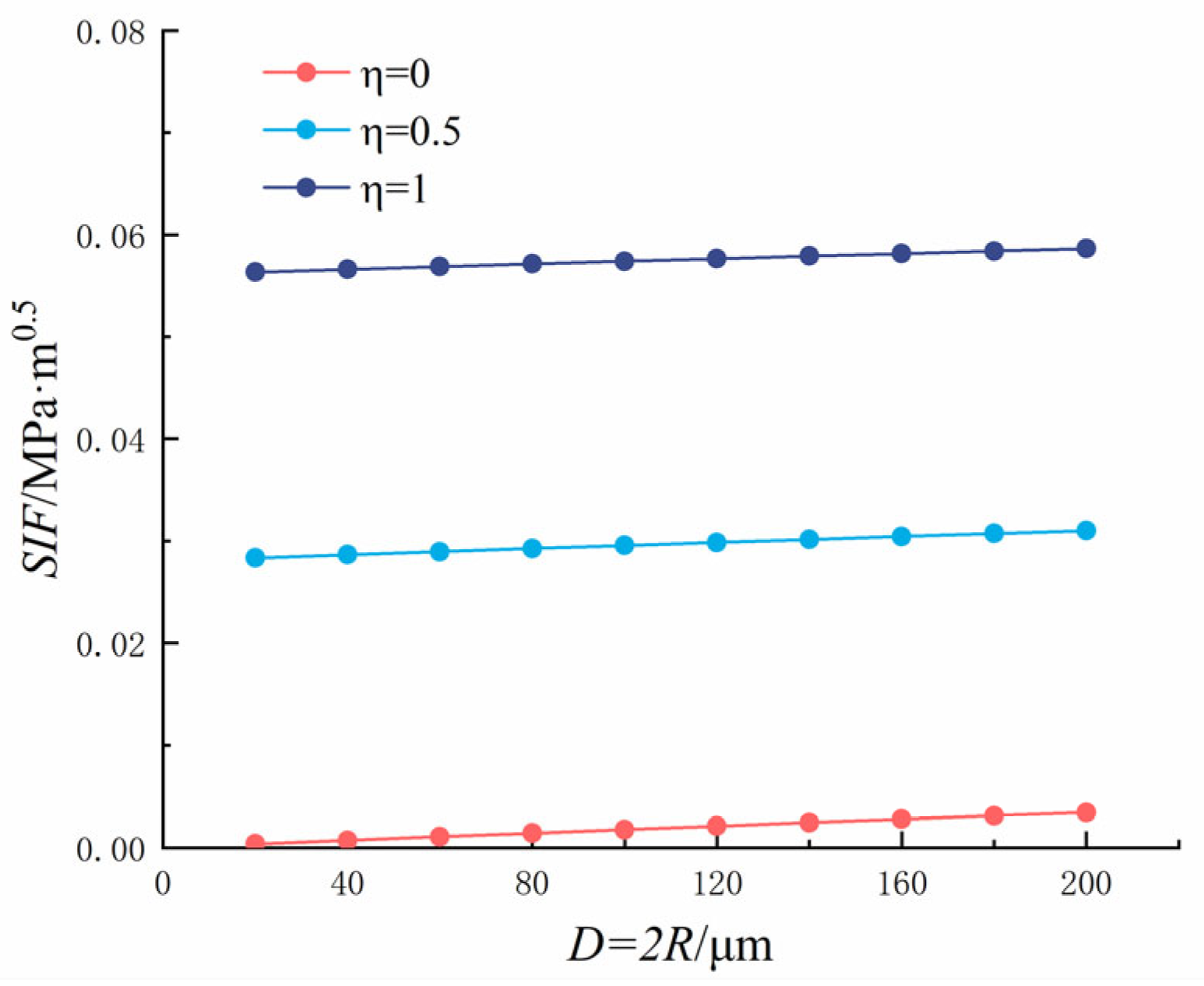
5.1. Analysis of Single Crack at the Hole Edge
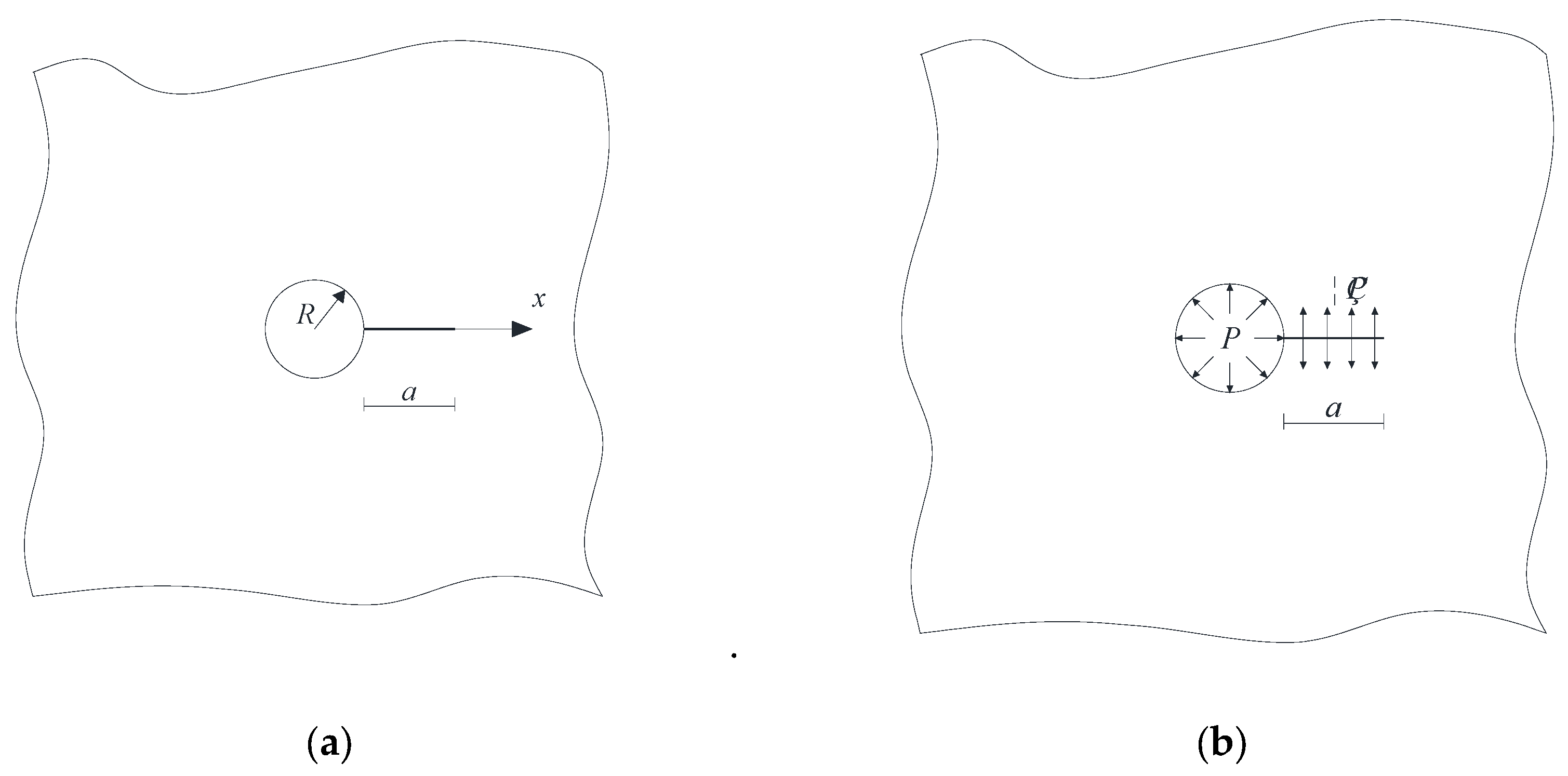


5.2. Analysis of Symmetrical Crack at the Hole Edge
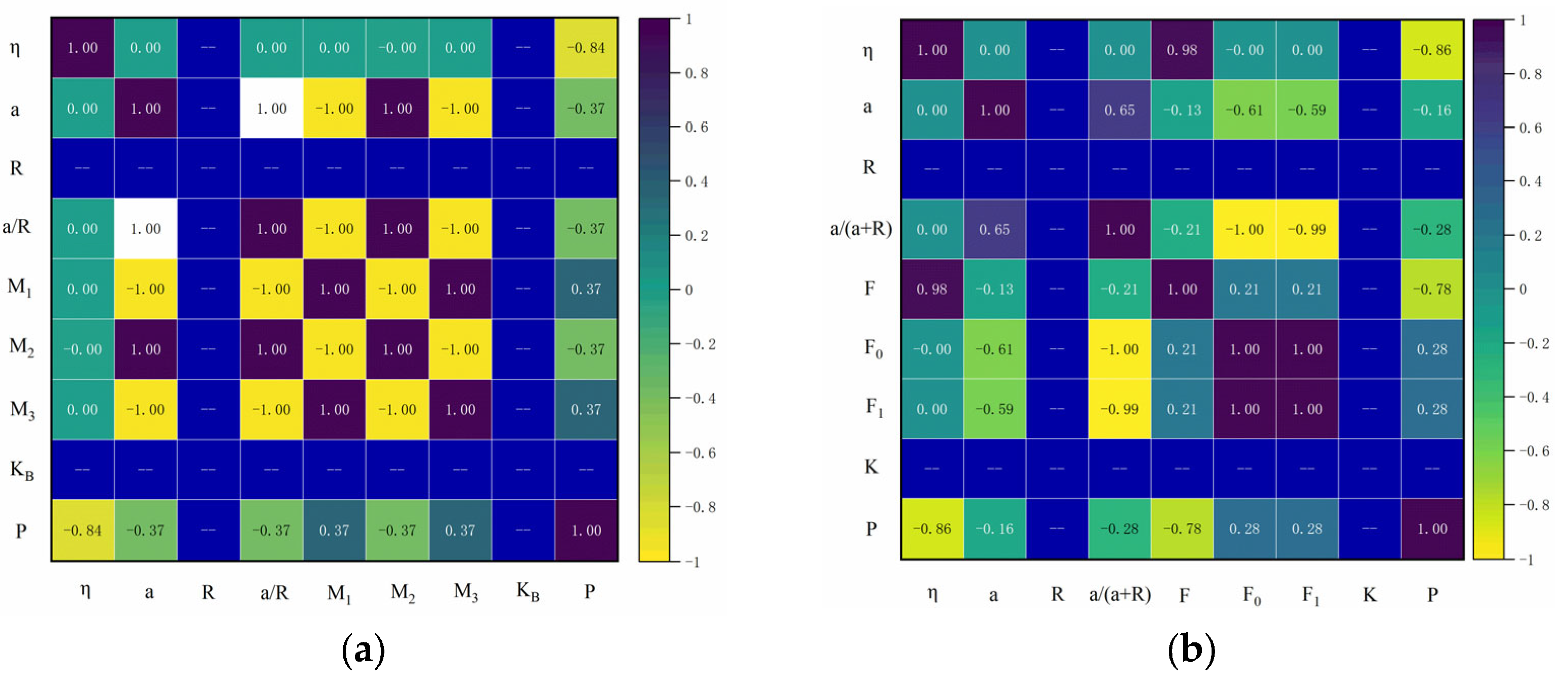
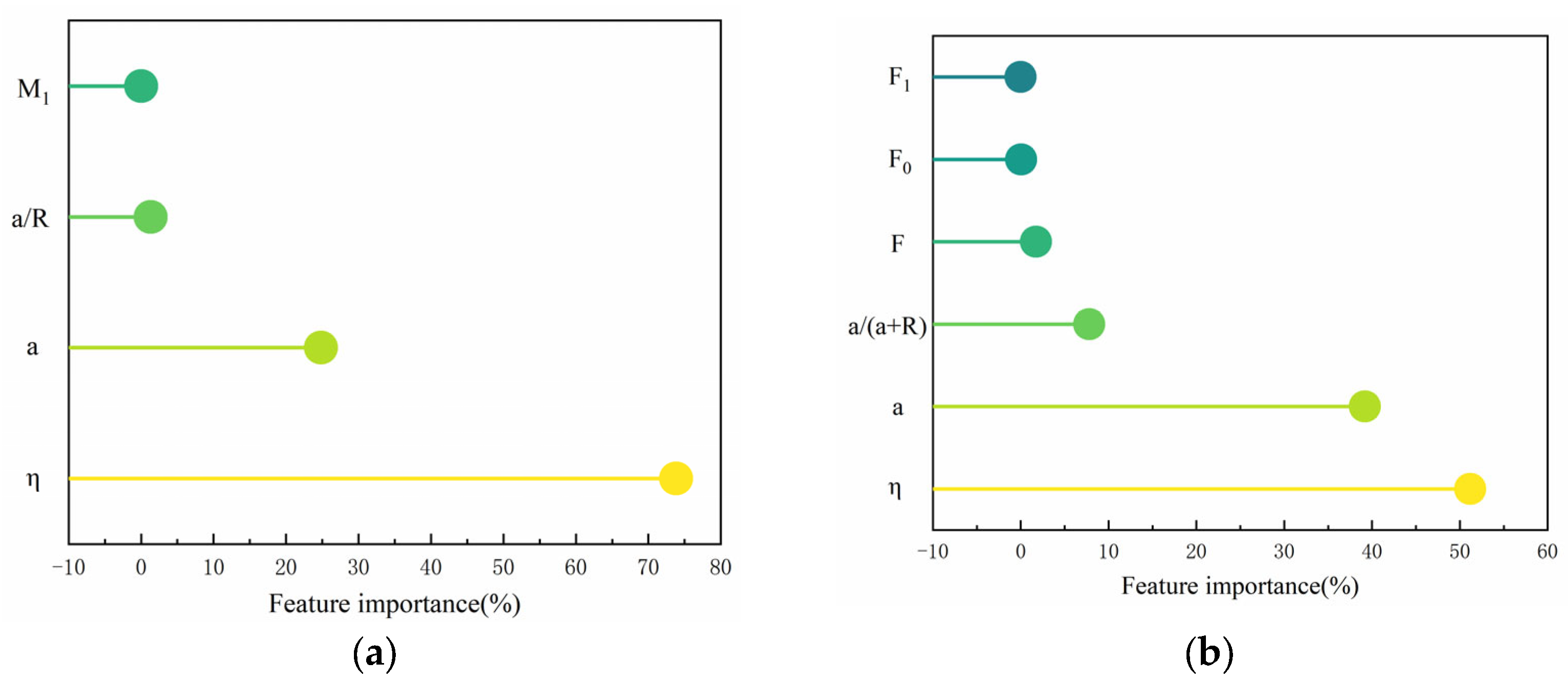
5.3. Principal Component Analysis
6. Conclusions and Recommendations
- (1)
- Pore Distribution and Material Characterization. The analysis revealed that the pores were primarily concentrated in the middle and upper layers of the concrete. The gray levels of the aggregate, mortar, and pores exhibited distinct differences, with the aggregate appearing predominantly bright white (gray levels between 165 and 255), the mortar being gray, and the pores being dark black. These variations in gray levels effectively differentiated the three material phases in the concrete.
- (2)
- Impact of Dry–Wet Cycling on Pore Structure and Crack Formation. The dry–wet cycle tests demonstrated that both the number and size of pores decreased, while expansion stress increased. Cracks appeared first in the internal interface transition zone around large pores and within dense small pores. The evolution of the pore structure and the propagation of cracks were consistent with the changes in the gray levels observed during X-CT scanning. This suggests that monitoring gray level variation is a reliable and effective method for assessing the degradation of RAC following sulfate dry–wet cycling.
- (3)
- Crack Propagation and Stress Intensity Factors (SIFs). As crack length increased, the Stress Intensity Factor (SIF) of both single cracks and symmetric crack tips showed an upward trend. Similarly, the SIF increased with pore diameter, although the change was relatively small. Furthermore, as the crack length increased, the critical expansion force gradually decreased. Notably, the critical expansion force at the symmetric crack tip near the pore edge was 53 times greater than that of a single crack, highlighting the significant role of pore edges in crack resistance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Benhelal, E.; Rashid, M.; Zahedi, G. Reducing environmental impact of cement production. J. Clean. Prod. 2012, 33, 93–101. [Google Scholar]
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstructure, Properties, and Materials, 4th ed.; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
- Neville, A.M. Properties of Concrete, 5th ed.; Pearson: London, UK, 2011. [Google Scholar]
- de Brito, J.; Kurda, R. The past and future of sustainable concrete: A critical review and new strategies on cement-based materials. J. Clean. Prod. 2020, 281, 123558. [Google Scholar] [CrossRef]
- Gao, X.; Yu, Q.; Brouwers, H.J.H. Properties of alkali-activated slag–fly ash blends with limestone. Cem. Concr. Compos. 2015, 59, 119–128. [Google Scholar] [CrossRef]
- Tang, S.; Cai, L.; He, Z. Digital twin for predicting concrete durability. Autom. Constr. 2023, 148, 104732. [Google Scholar]
- Tam, V.W.Y.; Tam, C.M.; Zeng, S.X. Sustainable construction waste recycling. J. Clean. Prod. 2013, 131, 1–9. [Google Scholar]
- Li, Z.; Yao, Y.; Basheer, P.A.M. Modelling sulfate transport in cement-based materials. Cem. Concr. Compos. 2020, 113, 103718. [Google Scholar]
- Zhao, X.; Zhang, Y. Life-cycle assessment of sulfate-resistant recycled concrete. J. Clean. Prod. 2025, 407, 137203. [Google Scholar]
- Cardinale, T.; D’Amato, M.; Sulla, R.; Cardinale, N. Mechanical and physical characterization of papercrete as new eco-friendly construction material. Appl. Sci. 2021, 11, 1011. [Google Scholar] [CrossRef]
- Ferrándiz-Mas, V.; Bond, T.; García-Alcocel, E.; Cheeseman, C.R. Lightweight mortars containing expanded polystyrene and paper sludge ash. Constr. Build. Mater. 2014, 61, 285–292. [Google Scholar] [CrossRef]
- Kim, Y.; Eo, S. 3D-printed recycled concrete exposed to sulfate solutions. Addit. Manuf. 2022, 45, 102071. [Google Scholar]
- Santhanam, M.; Cohen, M.D.; Olek, J. Mechanism of sulfate attack: A critical review. Cem. Concr. Res. 2001, 31, 845–851. [Google Scholar] [CrossRef]
- Qian, X.; Li, Z. Sulfate attack on cement and concrete: A review. Mater. Struct. 2012, 45, 879–896. [Google Scholar]
- Folliard, K.J.; Barrett, T.; Ideker, J. Sulfate attack in concrete. In Handbook of Materials Failure; De Belie, D., Ed.; Woodhead: Cambridge, UK, 2015; pp. 233–260. [Google Scholar]
- Rajabipour, F. Effects of internal sulfate on concrete durability. Cem. Concr. Compos. 2020, 104, 103318. [Google Scholar]
- Zhao, T.; Liu, W. Coupled effects of chloride and sulfate during dry–wet cycles on recycled concrete. Materials 2023, 16, 3892. [Google Scholar]
- Guo, J.-J.; Liu, P.-Q.; Wu, C.-L.; Wang, K. Effect of dry–wet cycle periods on properties of concrete under sulfate attack. Appl. Sci. 2021, 11, 888. [Google Scholar] [CrossRef]
- Jang, S.; Park, Y. Wet–dry cycles on pore structure of UHPC. Materials 2024, 17, 890. [Google Scholar]
- Abbas, S.; Nehdi, M.L.; Salem, A. Hybrid fiber-reinforced concrete: A review. Constr. Build. Mater. 2015, 24, 447–456. [Google Scholar]
- Leite, M.B.; Monteiro, P.J.M. Microstructural analysis of recycled concrete using X-ray microtomography. Constr. Build. Mater. 2016, 68, 445–452. [Google Scholar] [CrossRef]
- Li, H.; Xiao, J.; Skanska, L. Performance of recycled aggregate concrete under sulfate attack and flexural loading. Mater. Struct. 2019, 52, 34. [Google Scholar]
- Taylor, A.; Fenton, M. A study on the performance of recycled aggregate concrete under sulfate attack. Constr. Build. Mater. 2016, 120, 206–214. [Google Scholar] [CrossRef]
- Guan, B.; Zhang, S.; Wang, F.; Li, L. Numerical Simulation of Concrete Attacked by Sulfate under Drying–Wetting Cycles and Alternating Loads. Buildings 2023, 13, 82. [Google Scholar] [CrossRef]
- Yuan, J.; Liu, Y.; Tan, Z.; Zhang, B. Investigating the failure process of concrete under coupled sulfate attack and drying–wetting cycles by X-ray CT. Constr. Build. Mater. 2016, 108, 129–138. [Google Scholar] [CrossRef]
- du Plessis, A.; Olawuyi, B.J.; Boshoff, W.P.; le Roux, S.G. Simple and fast porosity analysis of concrete using X-ray computed tomography. Mater. Struct. 2016, 49, 553–562. [Google Scholar] [CrossRef]
- Sun, L.; Tao, G. Application of X-ray CT in the investigation of the microstructure of recycled concrete. Cem. Concr. Compos. 2019, 98, 134–142. [Google Scholar] [CrossRef]
- Yi, C.; Chen, Z.; Yu, J.; Bindiganavile, V. A Three-Phase Model to Evaluate Effects of Phase Diffusivity and Volume Fraction upon the Crack Propagation in Concrete Subjected to External Sulphate Attack. CivilEng 2023, 4, 12–33. [Google Scholar] [CrossRef]
- Zuo, X.; Li, X.; Zheng, Z.; Zou, Y.; Zhang, Y. Mesoscale modeling and simulation on the chemo-mechanical behavior of concrete in sulfate-rich environments. Eng. Fract. Mech. 2024, 109982. [Google Scholar] [CrossRef]
- Ohno, M.; Maekawa, K. Fully coupled physicochemical-mechanical modeling of sulfate attack-induced expansion in cement-based materials. Cem. Concr. Compos. 2025, 161, 106076. [Google Scholar] [CrossRef]
- Wu, J.; Ke, Q.; Wei, J.; Hu, J.; Zhu, W.; Huang, H. Tracking the observations of volume deformation of concrete under sulfate attack through 3d digital image correlation. J. Test. Eval. 2023, 51, 11. [Google Scholar] [CrossRef]
- Yao, J.; Chen, J.; Lu, C. Fractal Cracking Patterns in Concretes Exposed to Sulfate Attack. Materials 2019, 12, 2338. [Google Scholar] [CrossRef]
- Suryawanshi, R.; Bhattacharjee, S. Multi-scale porosity assessment of recycled concrete aggregates under sulfate attack. Constr. Build. Mater. 2014, 89, 324–332. [Google Scholar] [CrossRef]
- Morozova, N.; Shibano, K.; Shimamoto, Y.; Tayfur, S.; Alver, N.; Suzuki, T. Visualization and evaluation of concrete damage in-service headworks by X-ray CT and non-destructive inspection methods. Front. Built Environ. 2022, 8, 947759. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, H.; Long, W.; Guo, X.; Ji, Y.; Qin, Z.; Xing, F.; Sui, S. Investigation on the sulfate attack of metakaolin-blended recycled concrete based on percolation theory. J. Mater. Res. Technol. 2023, 27, 2615–2626. [Google Scholar] [CrossRef]
- Taylor, A.; Fenton, M. Mechanical properties and durability of recycled aggregate concrete under sulfate attack. Constr. Build. Mater. 2016, 105, 189–197. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, X. Experimental investigation of recycled concrete durability under sulfate attack and drying-wetting cycles. J. Mater. Sci. Technol. 2025, 80, 92–100. [Google Scholar] [CrossRef]
- Hilloulin, B.; Hafidi, A.; Boudache, S.; Loukili, A. Interpretable ensemble machine learning for the prediction of the expansion of cementitious materials under external sulfate attack. J. Build. Eng. 2023, 80, 107951. [Google Scholar] [CrossRef]
- Liu, D.; Gong, C.; Tang, Y.; Jian, Y.; Cao, K. Evaluation of Corrosion Damage in Sulfate-Attacked Concrete by CT, Ultrasonic Pulse Velocity Testing and AHP Methods. Sensors 2022, 22, 3037. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.; Wang, H. Modeling crack propagation in recycled concrete under sulfate attack using fracture mechanics. Mater. Sci. Eng. A 2020, 786, 139–147. [Google Scholar] [CrossRef]
- Zhang, M.; Gu, Z.; Zhao, Y.; Fu, Y.; Kong, X. Compressive strength prediction of cement base under sulfate attack by machine learning approach. Case Stud. Constr. Mater. 2024, 21, e03652. [Google Scholar] [CrossRef]
- Li, Y.; Shi, J.; Shen, J.; Jin, K. Prediction of the Sulfate Attack Resistance of Concrete Based on Machine-Learning Algorithms. J. Comput. Civ. Eng. 2024, 38. [Google Scholar] [CrossRef]
- Tian, W.; Dang, F.N.; Ding, W.H. Based on CT Technology, the Mesoscopic Damage Evolution Analysis of Concrete Materials; China Building Industry Press: Beijing, China, 2016. [Google Scholar]
- Hsieh, J. Computed Tomography: Principles, Design, Artifacts, and Recent Advances; Science Press: Beijing, China, 2006. [Google Scholar]
- ASTM C1012/C1012M-18b; Standard Test Method for Length Change of Hydraulic-Cement Mortars Exposed to a Sulfate Solution. ASTM International: West Conshohocken, PA, USA, 2018.
- GB/T 50082-2009; Standard for Test Methods of Long-Term Performance and Durability of Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2009.
- EN 1992; Eurocode 2: Design of Concrete Structures. European Committee for Standardization: Brussels, Belgium, 2004.
- ACI 224; Control of Cracking in Concrete Structures. American Concrete Institute: Farmington Hills, MI, USA, 2001.
- GB 50010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2015.
- Chen, K.F.; Qiao, H.X.; Wang, P.H.; Peng, K.; Zhu, X.C. Fracture Behavior Analysis of Magnesium Oxychloride Cement Reinforced Concrete under Electric Corrosion. J. Build. Mater. 2020, 23, 557–562. [Google Scholar]
- Wang, H.L.; Li, Q.B. Micro-mechanism of static and dynamic strengths for saturated concrete. J. Hydraul. Eng. 2006, 37, 958–962. [Google Scholar]
- Tada, H.; Paris, P.C.; Irwin, G.R.; Tada, H. The Stress Analysis of Cracks Handbook; ASME Press: New York, NY, USA, 2000. [Google Scholar]
- Van, Q.T.; Viet, Q.D.; Lanh, S.H. Evaluating compressive strength of concrete made with recycled concrete aggregates using machine learning approach. Constr. Build. Mater. 2022, 323, 126578. [Google Scholar] [CrossRef]
- Gao, H.X. Applied Multivariate Statistical Analysis; Peking University Press: Beijing, China, 2005. [Google Scholar]











| Water Absorption Rate (%) | Mud Content (%) | Crushing Index (%) | Bulk Density (%) | Apparent Density (kg/m3) |
|---|---|---|---|---|
| 2.2 | 0.5 | 9.6 | 1488 | 2452 |
| Cement | Coarse Aggregate | Fine Aggregate | Recycled Coarse Aggregate | Water Reducer | Water |
|---|---|---|---|---|---|
| 424 | 933.6 | 614 | 233.4 | 12.72 | 180 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.; He, Z.; Qiao, H. Dry–Wet Cycle Fracture Performance of Recycled Concrete Sulfate Based on Computerized Tomographic Images. Materials 2025, 18, 3998. https://doi.org/10.3390/ma18173998
Chen K, He Z, Qiao H. Dry–Wet Cycle Fracture Performance of Recycled Concrete Sulfate Based on Computerized Tomographic Images. Materials. 2025; 18(17):3998. https://doi.org/10.3390/ma18173998
Chicago/Turabian StyleChen, Kefan, Zhaoyi He, and Hongxia Qiao. 2025. "Dry–Wet Cycle Fracture Performance of Recycled Concrete Sulfate Based on Computerized Tomographic Images" Materials 18, no. 17: 3998. https://doi.org/10.3390/ma18173998
APA StyleChen, K., He, Z., & Qiao, H. (2025). Dry–Wet Cycle Fracture Performance of Recycled Concrete Sulfate Based on Computerized Tomographic Images. Materials, 18(17), 3998. https://doi.org/10.3390/ma18173998






