Study of the Tooth Contact Pattern for Double-Enveloping Worm Gear
Abstract
1. Introduction
- Theoretical methods include analytical and numerical approaches. enabling the determination of contact points, contact lines, and their trajectories. The finite element method (FEM) is particularly valuable for analysing the influence of elastic deformations on contact location and corresponding stress distribution.
- Simulation-based methods, primarily utilizing Computer-Aided Design (CAD) tools, involve analysing 3D models of gear sets for mutual intersection of tooth surfaces. CAD-based methods facilitate the visualization of the contact pattern throughout meshing and the definition of its geometric characteristics. Specialized Computer-Aided Engineering (CAE) tools (e.g., KISSsoft, KIMOS) further support qualitative evaluation of contact quality.
- Experimental methods include techniques such as the widely used marking compound method, which provides a visual representation of the actual contact area.
2. Materials and Methods
2.1. Kinematic System of Gear Mesh
2.1.1. Parameters of the Gear Set
2.1.2. Contact Pattern Determined Using CAD-Based Method
2.2. Experimental Procedure
2.2.1. Globoid Worm Gear Manufacturing
2.2.2. Test Stand
2.2.3. Experimental Method: Chalk Paint, Liquid Tracing and Deformation Freezing
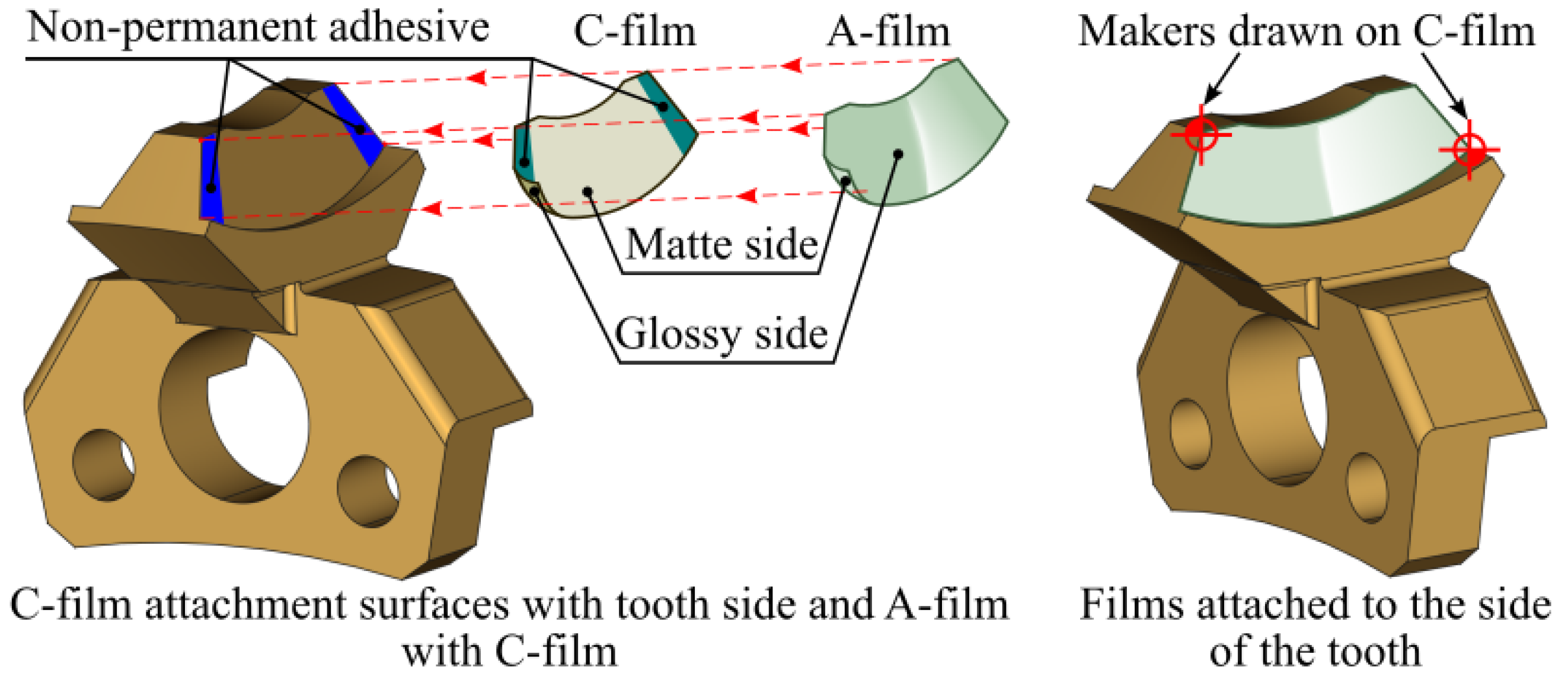
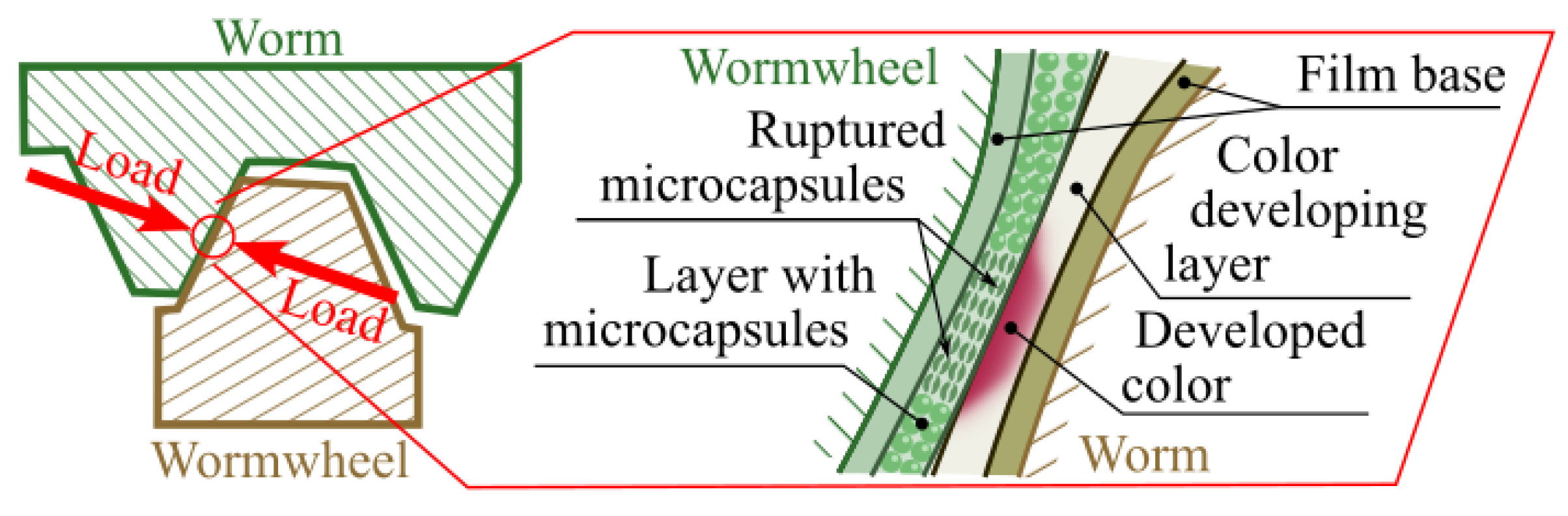
2.2.4. Method Based on Pressure Measurement Using Two-Sheet Type Film
3. Results and Discussion
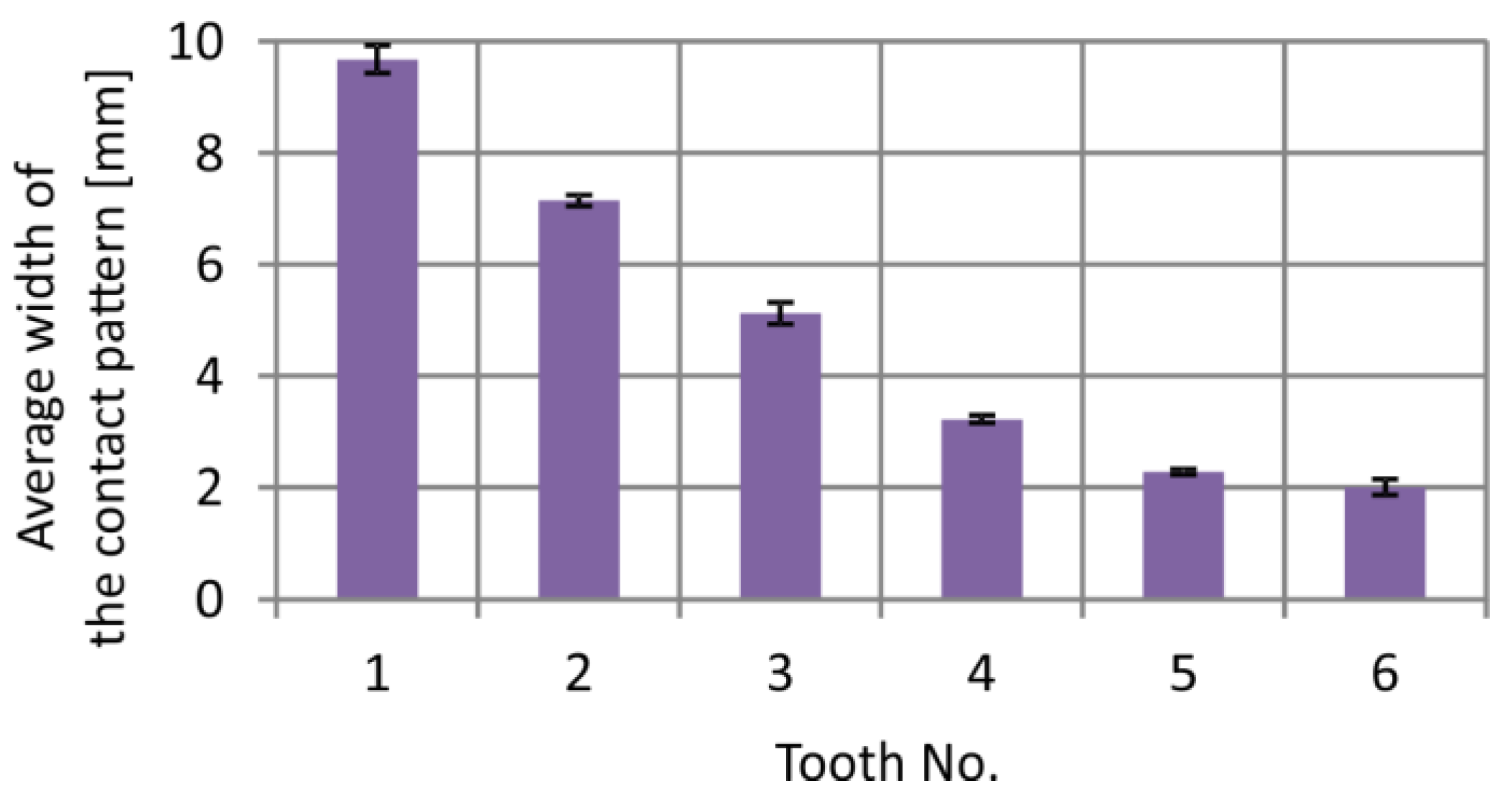
3.1. CAD Analysis of Tooth Contact
3.2. Experimental Method Using Chalk Paint
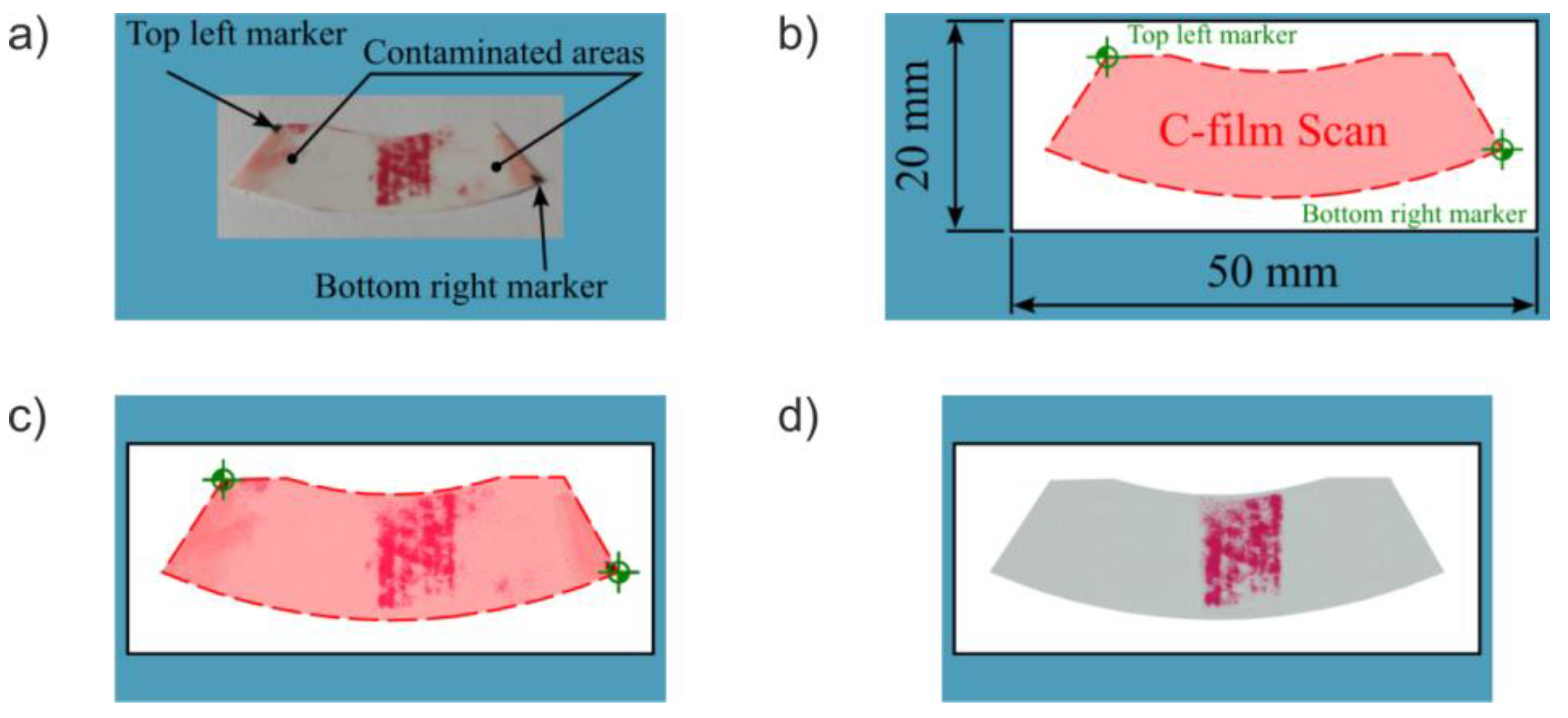
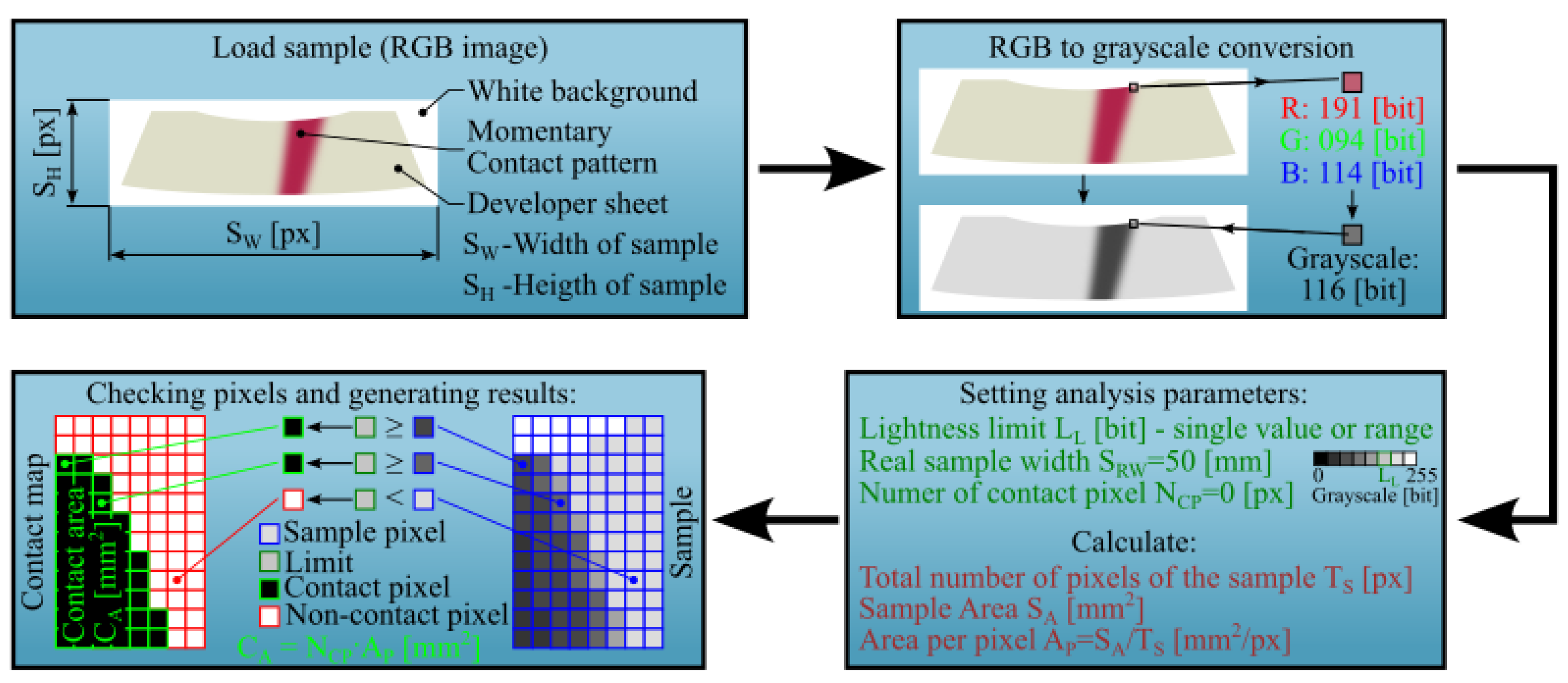
3.3. Analysis of Tooth Contact Pattern Using Two-Sheet Pressure Measurement Film
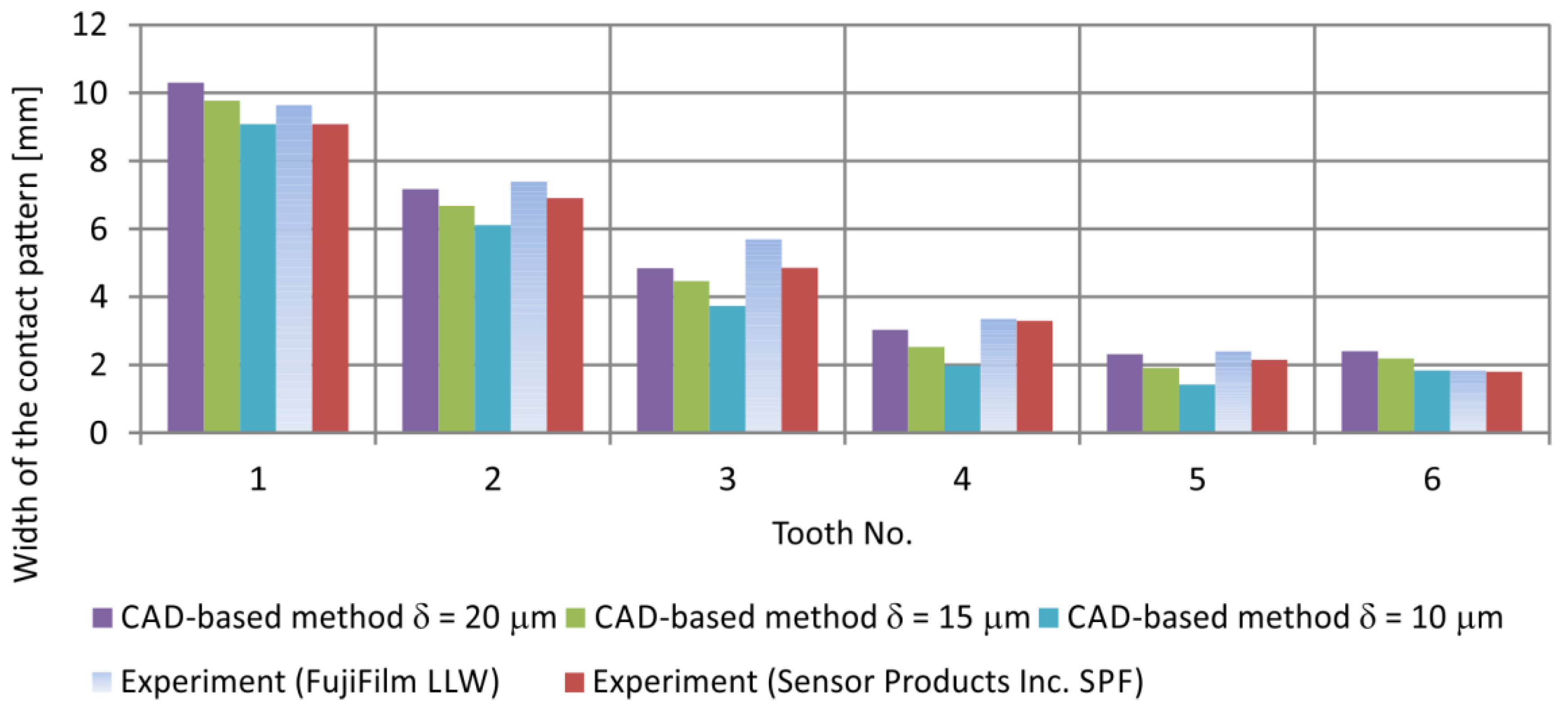
3.4. Comparison
4. Conclusion
- The CAD-based method for determining the contact pattern can be successfully applied to evaluate the form, size, and position of the contact pattern.
- The novel method of contact area measurement using two-sheet pressure measurement film can be successfully applied to evaluate the size and position of contact patterns.
- The experimental method using chalk paint can be applied under workshop conditions, without the need for digital analysis of scanned samples, to quickly assess the correctness of gearbox assembly
- Differences in the resulting contact pattern areas depend, among other factors, on the penetration depth in the CAD method and the intensity threshold used in the digital image processing of experimental data.
- The developed image analysis algorithm enables contact pattern evaluation using a standard office scanner, eliminating the need for dedicated scanning devices and proprietary software typically offered by pressure film manufacturers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sobolak, M. Analysis and Synthesis of Mating Gear Tooth Surface by Discrete Methods; Rzeszów University of Technology Publ.: Rzeszów, Poland, 2006. [Google Scholar]
- Wu, Y.; Luo, P.; Bai, Q.; Liang, S.; Fan, Q.; Hou, L. Modelling and analyzing of loaded meshing characteristics of cylindrical gear transmission with curvilinear-shaped teeth. Meccanica 2023, 58, 1555–1580. [Google Scholar] [CrossRef]
- Batsch, M.; Wydrzyński, D.; Przeszłowski, L. Tooth contact analysis of cylindrical gears with an unconventional tooth profile. Adv. Sci. Technol. Res. J. 2022, 16, 119–129. [Google Scholar] [CrossRef]
- Batsch, M.; Markowski, T.; Legutko, S.; Królczyk, G.M. Measurement and mathematical model of convexo-concave novikov gear mesh. Measurement 2018, 125, 516–526. [Google Scholar] [CrossRef]
- Fuentes-Aznar, A.; Ruiz-Orzaez, R.; Gonzalez-Perez, I. Comparison of spur, helical and curvilinear gear drives by means of stress and tooth contact analyses. Meccanica 2017, 52, 1721–1738. [Google Scholar] [CrossRef]
- Fuentes-Aznar, A.; Nagamoto, H.; Litvin, F.L.; Gonzalez-Perez, I.; Hayasaka, K. Computerized design of modified helical gears finished by plunge shaving. Comput. Methods Appl. Mech. Eng. 2010, 199, 1677–1690. [Google Scholar] [CrossRef]
- Fudali, P.; Markowski, T.; Pacana, J. Machining Simulation of Novikov Profile Gear Models for Analysis and Computational Calculations. Materials 2025, 18, 1155. [Google Scholar] [CrossRef]
- Marciniec, A.; Pacana, J.; Pisula, J.; Fudali, P. Comparative analysis of numerical methods for the determination of contact pattern of spiral bevel gears. Aircr. Eng. Aerosp. Technol. 2018, 90, 359–367. [Google Scholar] [CrossRef]
- Argyris, J.; Fuentes-Aznar, A.; Litvin, F.L. Computerized integrated approach for design and stress analysis of spiral bevel gears. Comput. Methods Appl. Mech. Eng. 2002, 191, 1057–1095. [Google Scholar] [CrossRef]
- Bracci, A.; Gabiccini, M.; Artoni, A.; Guiggiani, M. Geometric contact pattern estimation for gear drives. Comput. Methods Appl. Mech. Eng. 2009, 198, 1563–1571. [Google Scholar] [CrossRef]
- Batsch, M. Mathematical model and tooth contact analysis of convexo-concave helical bevel Novikov gear mesh. Mech. Mach. Theory 2020, 149, 103842. [Google Scholar] [CrossRef]
- Rong, K.; Chen, J.; Gao, F.; Zhou, Z.; Tang, J.; Zhang, J.; Ding, H. Contact pattern expansion regulation model for spiral bevel gear transmission. Int. J. Mech. Sci. 2023, 254, 108459. [Google Scholar] [CrossRef]
- Liu, Z.; Li, F.; Xu, Z.; He, Q. Semi-analytical loaded tooth contact analysis method for spiral bevel gears. Int. J. Mech. Sci. 2023, 253, 108329. [Google Scholar] [CrossRef]
- Miltenović, A.; Banić, M.; Vitković, N.; Simonović, M.; Perić, M.; Rangelov, D. Investigation of the influence of contact patterns of worm-gear sets on friction heat generation during meshing. Appl. Sci. 2024, 14, 738. [Google Scholar] [CrossRef]
- Dudás, L. Modelling and simulation of a new worm gear drive having point-like contact. Eng. Comput. 2013, 29, 251–272. [Google Scholar] [CrossRef]
- Rong, K.B.; Tang, J.Y.; Song, B.Y.; Bu, X.Q.; Zou, X.P. A novel tooth contact analysis method for conical worm drives: An enhanced ease-off topography-based approach with conforming grid and TE-clearance assessment. Mech. Mach. Theory 2025, 205, 105837. [Google Scholar] [CrossRef]
- Rong, K.; Tang, J.; Tian, Z.; Song, B.; Li, H.; Ding, H. A novel accurate–efficient loaded contact analysis method for hypoid gears based on ease-off topography discretization and TE-interference assessment. Mech. Mach. Theory 2025, 209, 106012. [Google Scholar] [CrossRef]
- Gonzalez-Perez, I.; Fuentes-Aznar, A. An exact system of generation for face-milled hypoid gears with uniform depth taper: Application to hypoid gear drives with high gear ratio. Mech. Mach. Theory 2024, 196, 105629. [Google Scholar] [CrossRef]
- Crosher, W.P. Design and Application of the Worm Gear; ASME Press: New York, NY, USA, 2002. [Google Scholar]
- Litvin, F.L.; Fuentes-Aznar, A. Gear Geometry and Applied Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Dudás, L. New technology for manufacturing quasi-globoid worm gearings. Mater. Sci. Eng. 2018, 448, 012035. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, Y.; Luo, W.; Zhang, G. Development and classification of worm drive. In Proceedings of the 14th IFToMM World Congress, Taipei, Taiwan, 25–30 October 2015; pp. 265–273. [Google Scholar] [CrossRef]
- Dudás, L. The Theory and Practice of Worm Gear Drives; Penton Press: London, UK, 2000. [Google Scholar]
- Litvin, F.L. Development of Gear Technology and Theory of Gearing; Levis Research Center: Cleveland, OH, USA, 1999. [Google Scholar]
- Simon, V. Characteristics of a Modified Double Enveloping Worm Gear Drive. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Scottsdale, AZ, USA, 13–16 September 1992; ASME: Washington, DC, USA, 1992; pp. 73–79. [Google Scholar] [CrossRef]
- Simon, V. Load Distribution in Double Enveloping Worm Gears. J. Mech. Design. 1993, 115, 496–501. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Y. Novel methods for curvature analysis and their application to TA worm. Mech. Mach. Theory 2016, 97, 155–170. [Google Scholar] [CrossRef]
- Zhao, Y. Meshing analysis for TA worm. Mech. Mach. Sci. 2016, 43, 13–20. [Google Scholar] [CrossRef]
- Zhao, Y.; Huai, C.; Zhang, Y. Compound Modification of Globoidal Worm Drive with Variable Parameters. Appl. Math. Model. 2017, 50, 17–38. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, Y. Computing method for induced curvature parameters based on normal vector of instantaneous contact line and its application to Hindley worm pair. Adv. Mech. Eng. 2017, 9, 168781401772188. [Google Scholar] [CrossRef]
- Huai, C.; Zhao, Y. Variable height modification of TA worm drive. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 233, 0954406218757269. [Google Scholar] [CrossRef]
- Mohan, L.V.; Shunmugam, M.S. Geometrical aspects of double enveloping worm gear drive. Mech. Mach. Theory 2009, 44, 2053–2065. [Google Scholar] [CrossRef]
- Chen, K.Y.; Tsay, C.B. Mathematical model and worm wheel tooth working surfaces of the ZN-type hourglass worm gear set. Mech. Mach. Theory 2009, 44, 1701–1712. [Google Scholar] [CrossRef]
- Zheng, Z.; Chen, Y.; Chen, B.; Du, X.; Li, C. Meshing performance investigations on a novel point-contact hourglass worm drive with backlash-adjustable. Mech. Mach. Theory 2020, 149, 103841. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, W.; Chen, Y.; Zhang, G. Study on the spur involute gear meshing with planar enveloping hourglass worm based on local conjugate. Proc. Instit. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 1737–1745. [Google Scholar] [CrossRef]
- He, F.; Shi, Z.; Yu, B. Effects of tooth surface modification on planar double-enveloping hourglass worm gear drives. J. Adv. Mech. Des. Syst. Manuf. 2018, 12, JAMDSM0040. [Google Scholar] [CrossRef]
- Peng, Q.; Li, M. Meshing theory and contact analysis of double enveloping hourglass worm drive with planar generatrix. Sci. Rep. 2024, 14, 8023. [Google Scholar] [CrossRef]
- Chi, Y.; Zhao, Y.; Zhu, X.; Li, G.; Chen, X. Geometry, kinematics and synthesis of abnormal hourglass worm gearing with centering bearing contact and lower error sensitivity. Mech. Mach. Theory 2022, 178, 105089. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.; Luo, W.; Chen, B. Study on the meshing evolving mechanism of a novel self-evolution hourglass worm drive. Mech. Mach. Theory 2022, 178, 105074. [Google Scholar] [CrossRef]
- Chen, H.; Ju, Z.; Qu, C.; Cai, X.; Zhang, Y.; Liu, J. Error-sensitivity analysis of hourglass worm gearing with spherical meshing elements. Mech. Mach. Theory 2013, 70, 91–105. [Google Scholar] [CrossRef]
- Zhao, Y.; Su, D.; Zhang, Z. Meshing analysis and technological parameters selection of dual tori double-enveloping toroidal worm drive. Mech. Mach. Theory 2010, 45, 1269–1285. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.; Luo, W.; Chen, B. Study on meshing performance of a novel point-contact hourglass worm drive based on modified involute. Mech. Mach. Theory 2023, 185, 105339. [Google Scholar] [CrossRef]
- Gao, S.; Wang, X. Theoretical modeling and transmission characteristics analysis of a novel double-roller hourglass worm drive based on enveloping principle. Discover Mech. Eng. 2023, 2, 20. [Google Scholar] [CrossRef]
- Haragâs, S.; Ninacs, R.; Buiga, O.; Tudose, L.; Haragâs, A.; Sas-Boca, I.M.; Cristea, F.A. An Attempt to Establish a Mathematical Model for an Unconventional Worm Gear with Bearings. Appl. Sci. 2024, 14, 10833. [Google Scholar] [CrossRef]
- Lei, Z.; Bi, Q.; Wang, Y.; Ding, H. Five-Axis Flank Milling Method of Plane Double Enveloping Hourglass Worm. Adv. Mater. Res. 2011, 314–316, 1523–1532. [Google Scholar] [CrossRef]
- Dong, L.; Wang, J.; Liu, P.; Wei, W.; Li, H. An NC rough turning method of an enveloping toroidal worm. Prod. Eng. 2012, 6, 129–135. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, H.; Yu, G.; Wang, S. A novel CNC machining method for enveloping surface. Int. J. Adv. Manuf. Technol. 2015, 85, 779–790. [Google Scholar] [CrossRef]
- Rui, C.; Xu, J.; Zhang, Y. Study on relief grinding interference checking method of toroidal worm wheel hob. Adv. Mech. Eng. 2022, 14, 10. [Google Scholar] [CrossRef]
- Andrianto, M.; Wu, Y.R.; Arifin, A. A novel manufacturing method for double-enveloping worms using a whirl-machining process. Mech. Mach. Theory 2023, 179, 105099. [Google Scholar] [CrossRef]
- AGMA 6135-A02; Design, Rating and Application of Industrial Globoidal Wormgearing (Metric Edition). American National Standards Institute: Washington, DC, USA, 2002.
- Połowniak, P.; Sobolak, M.; Marciniec, A. Double enveloping worm gear modelling using CAD environment. Bull. Pol. Acad. Sci. Tech. Sci. 2021, 69, e136736. [Google Scholar] [CrossRef]
- Stratasys–3D Printing & Additive Manufacturing Solutions. Available online: https://www.stratasys.com (accessed on 10 March 2025).
- Sobolak, M.; Budzik, G. Experimental method of tooth contact analysis (TCA) with Rapid Prototyping (RP) use. Rapid Prototyp. J. 2008, 14, 197–201. [Google Scholar] [CrossRef]
- Sobolak, M.; Jagiełowicz, P.E. Using rapid prototyping for prototyping and research of polymer transmissions. Mechanika 2010, 7, 107. [Google Scholar]
- FujiFilm Prescale Pressure Measurement Film. Available online: https://www.fujifilm.com/pl/en/business/inspection/measurement-film/prescale (accessed on 10 March 2025).
- Sensor Product Surface Profiler Film. Available online: https://www.sensorprod.com/surface-profiler-film (accessed on 10 March 2025).
- Bachus, K.N.; DeMarco, A.L.; Judd, K.T.; Horwitz, D.S.; Brodke, D.S. Measuring contact area, force, and pressure for bioengineering applications: Using Fuji Film and TekScan systems. Med. Eng. Phys. 2006, 28, 483–488. [Google Scholar] [CrossRef]
- Ng, T.W.; Yeong, W.K. Inexpensive color evaluation of dye-based pressure-sensitive films for plantar studies. J. Biomech. 2005, 38, 2130–2133. [Google Scholar] [CrossRef]
- Lee, Y.K.; Oh, Y.S.; Lee, D.K.; Lee, M.J.; Song, Y.N.; Lee, H.S.; Yeo, E.D. Evaluation of Contact Area and Pressure After Malreduction in Isolated Medial Malleolar Fractures with 2 mm of Displacement: A Cadaveric Study. J. Foot Ankle Surg. 2023, 62, 774–778. [Google Scholar] [CrossRef]
- Clark, A.L.; Herzog, W.; Leonard, T.R. Contact area and pressure distribution in the feline patellofemoral joint under physiologically meaningful loading conditions. J. Biomech. 2002, 35, 53–60. [Google Scholar] [CrossRef]

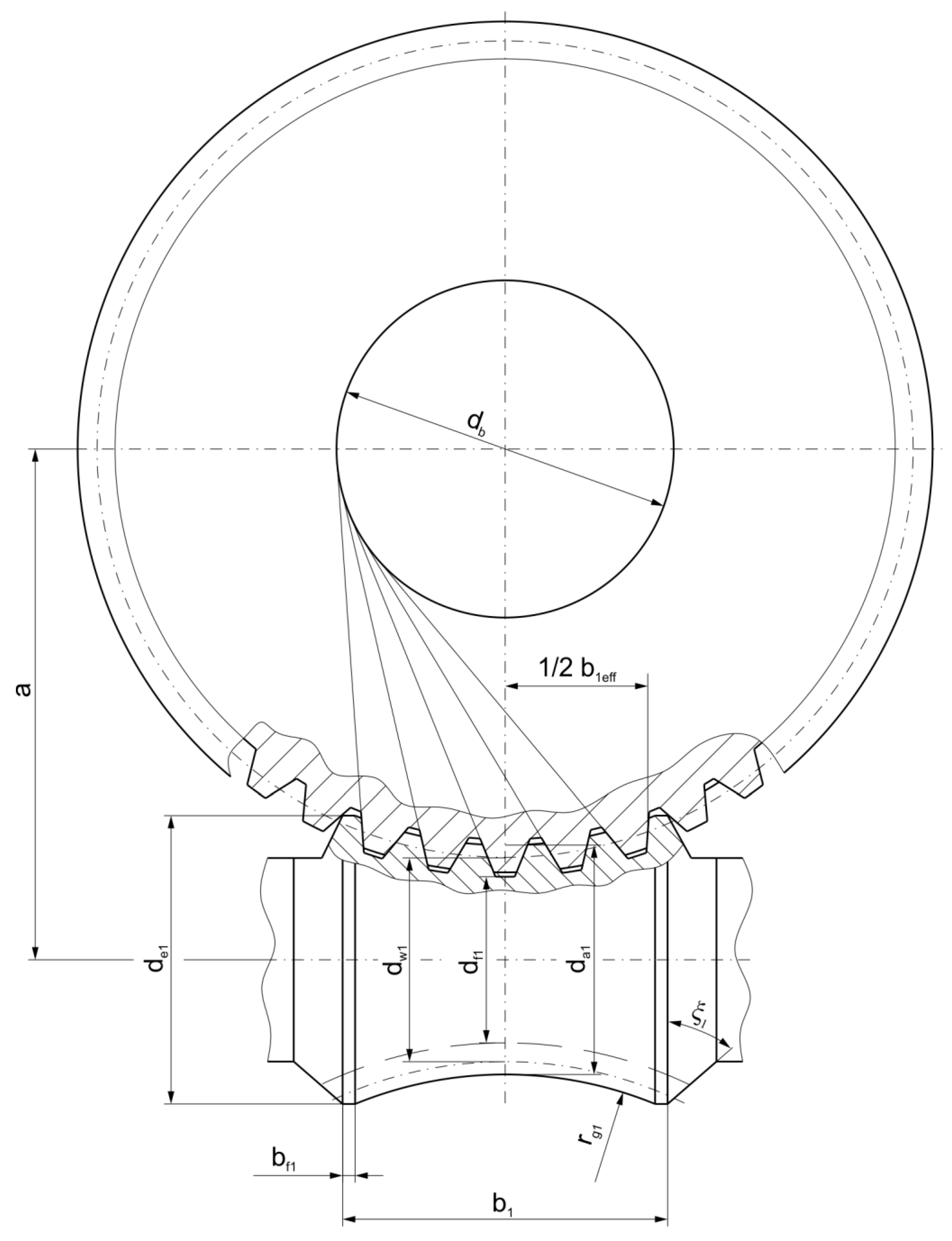
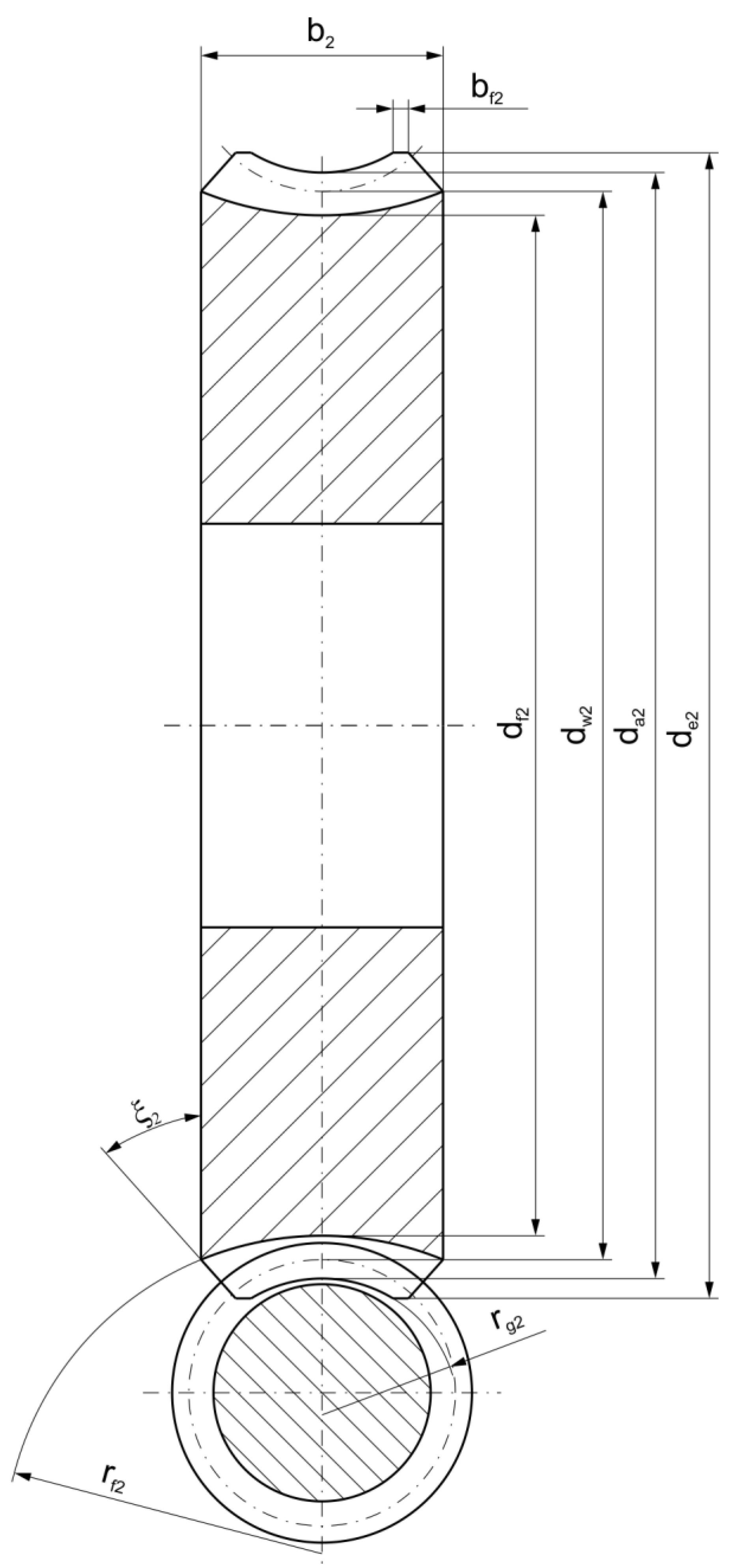
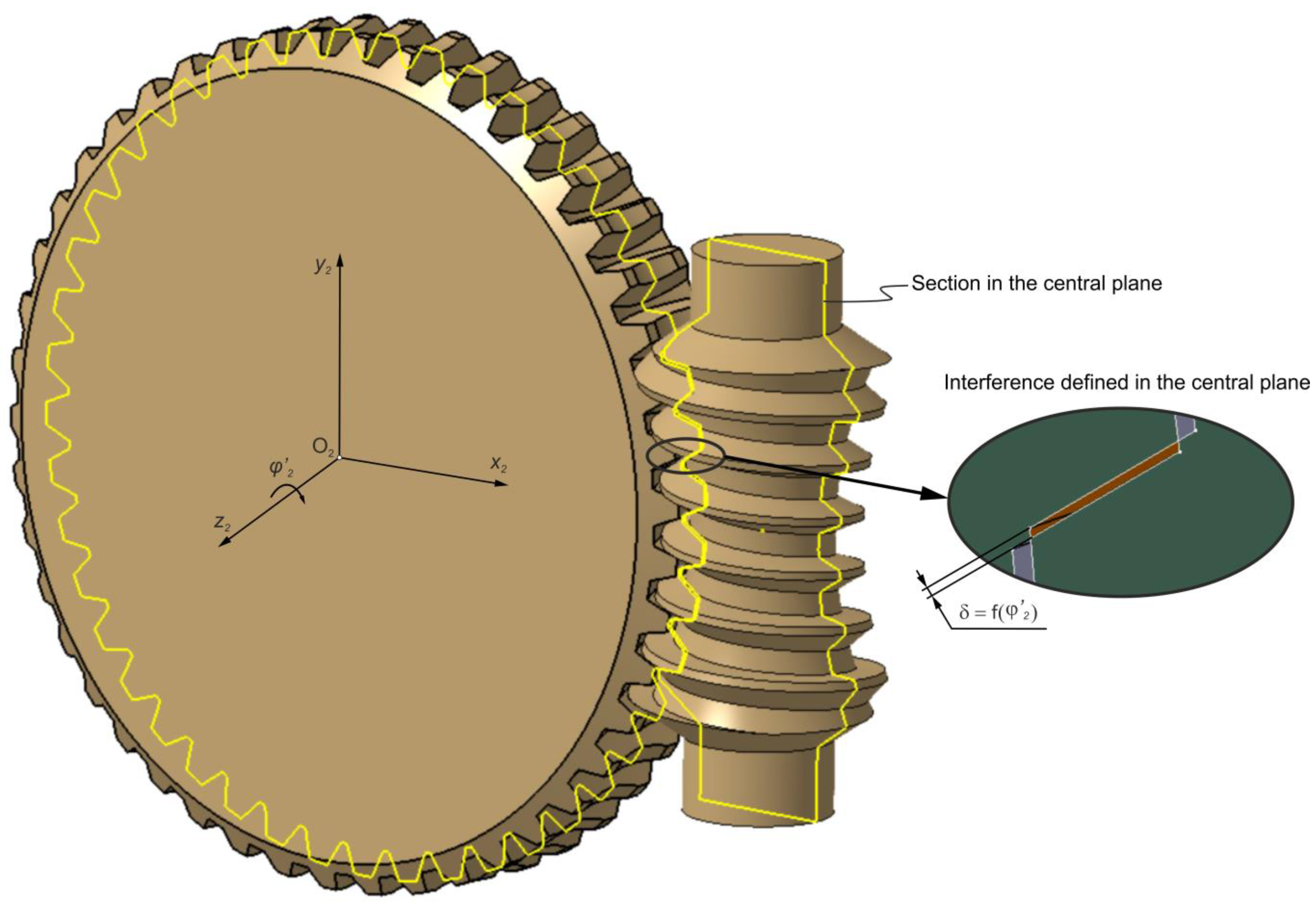
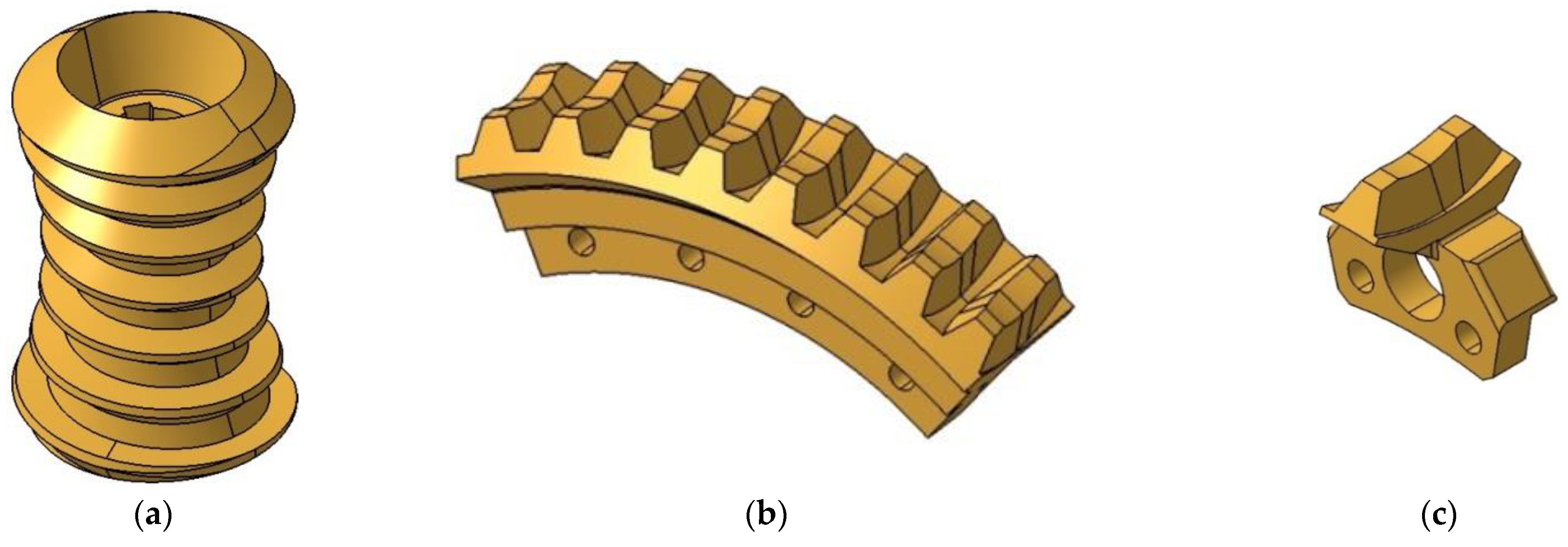






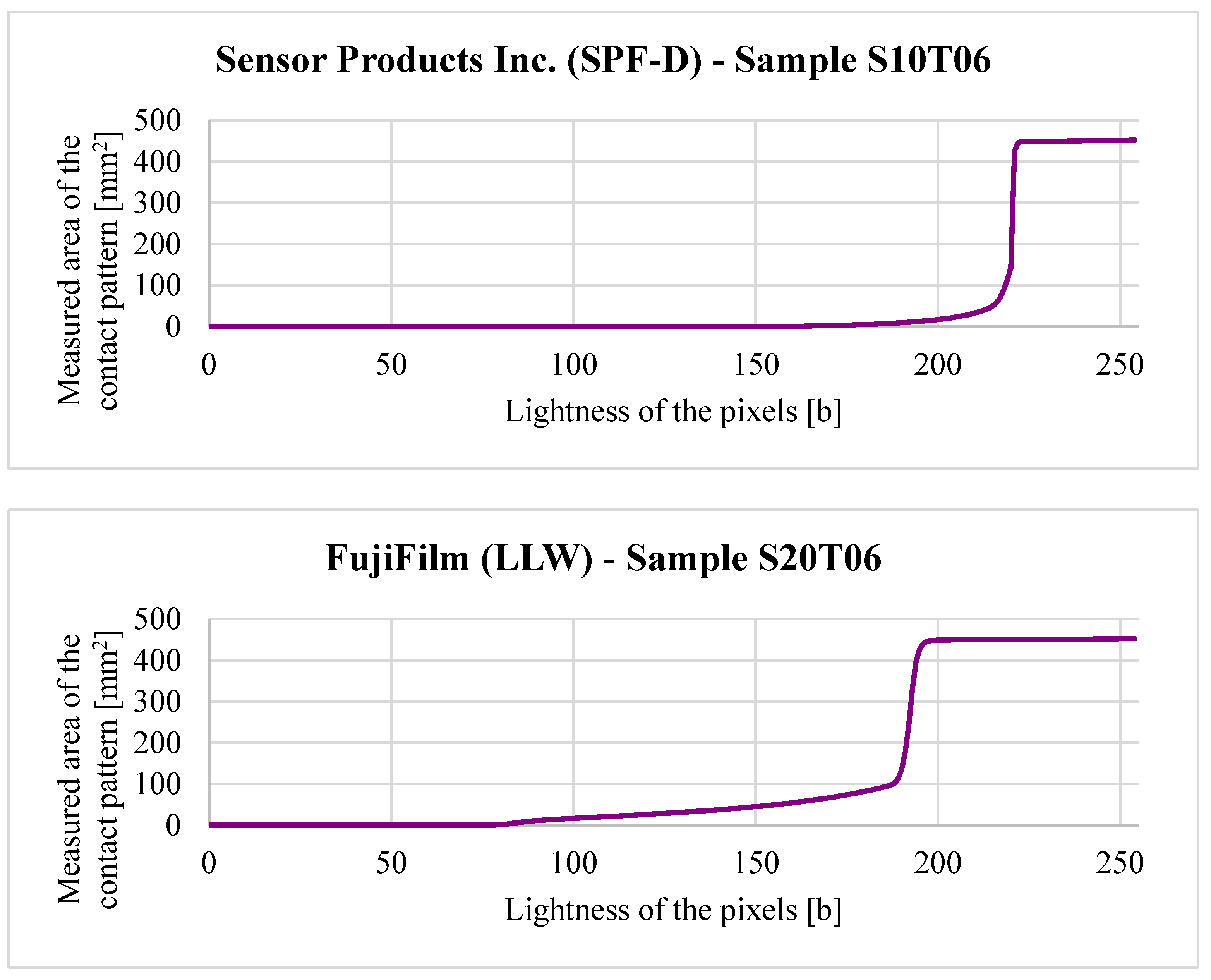
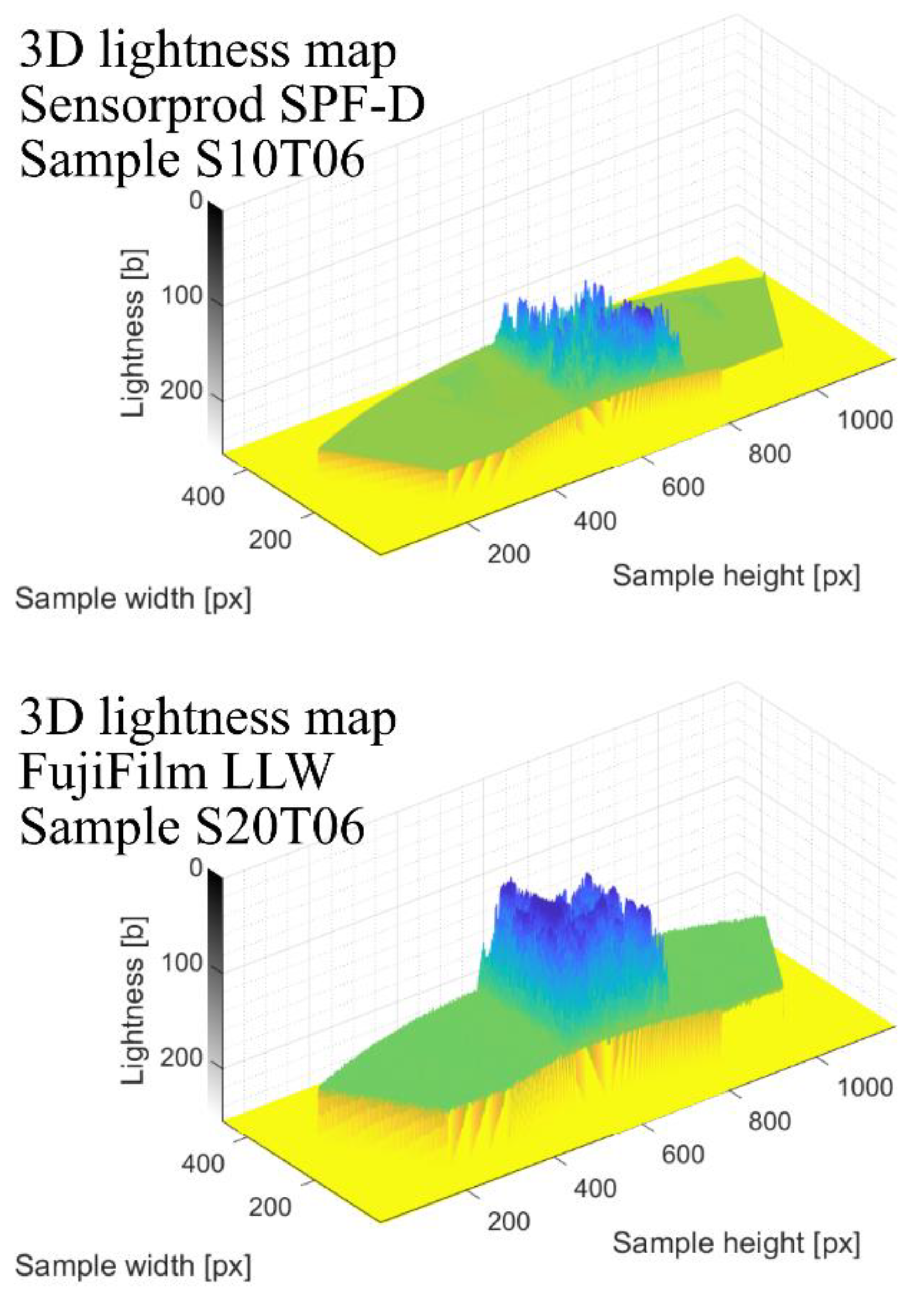





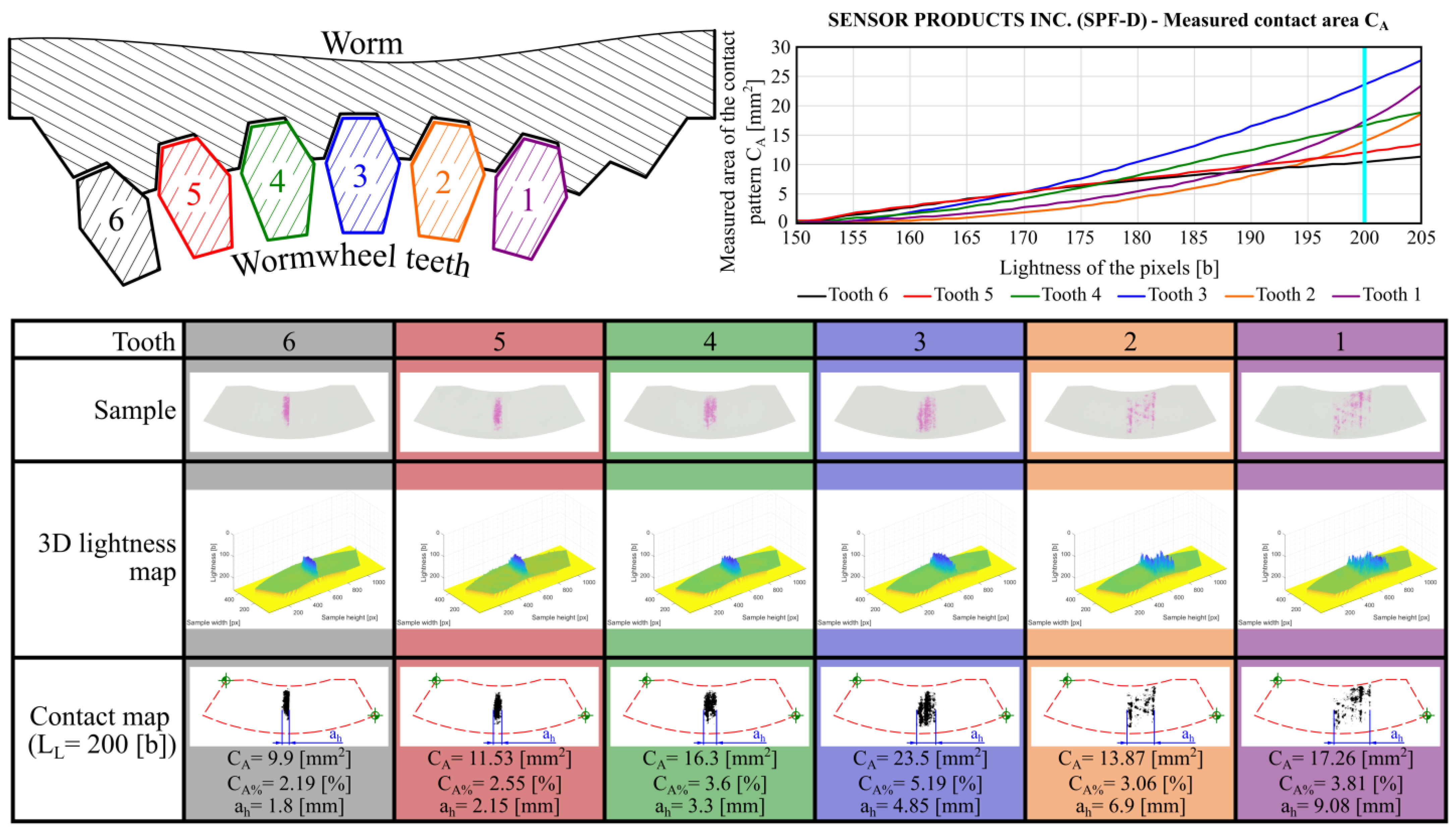



| Parameter | Worm | Worm Wheel |
|---|---|---|
| Normal module [mm] | ||
| Number of teeth [–] | ||
| Normal pleasure angle [°] | ||
| Base diameter [mm] | ||
| Pitch diameter [mm] | ||
| Throat diameter [mm] | ||
| Root diameter [mm] | ||
| Outside diameter [mm] | ||
| Effective worm thread length [mm] | – | |
| Face width [mm] | ||
| Length of flat on outside diameter | ||
| Face angle [°] | ||
| Root form radius [mm] | – | |
| Throat form radius [mm] | ||
| Centre distance [mm] | ||
| Parameter | Value |
|---|---|
| Modulus of elasticity [MPa] | 2000 |
| Ultimate tensile strength [MPa] | 50 |
| Density [g/cm3] | 1.185 |
| Elongation at break [%] | 15 |
| Hardness Shore D | 83 |
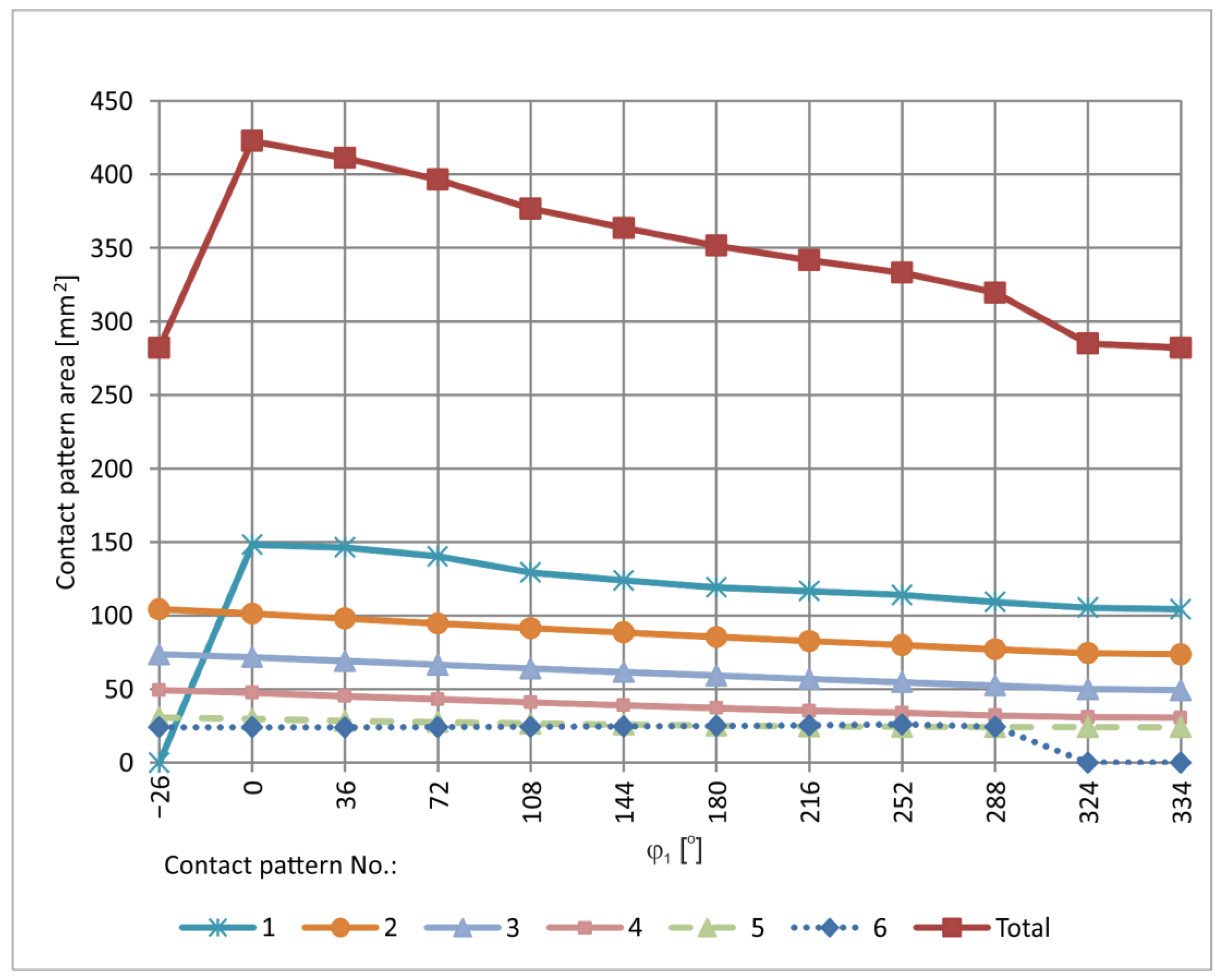
| φ1 [°] | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −26 | 0 | 36 | 72 | 108 | 144 | 180 | 216 | 252 | 288 | 324 | 334 | |
| No. | Contact Pattern Area [mm2] | |||||||||||
| 1 | 0.0 | 148.2 | 146.4 | 140.3 | 129.4 | 123.9 | 119.2 | 116.7 | 114.0 | 109.3 | 105.4 | 104.3 |
| 2 | 104.3 | 101.4 | 98.0 | 94.7 | 91.5 | 88.6 | 85.5 | 82.7 | 79.9 | 77.1 | 74.5 | 73.8 |
| 3 | 73.8 | 71.8 | 69.1 | 66.6 | 64.0 | 61.6 | 59.2 | 56.9 | 54.8 | 52.4 | 50.0 | 49.3 |
| 4 | 49.3 | 47.6 | 45.3 | 43.1 | 41.0 | 39.0 | 37.3 | 35.3 | 33.9 | 32.2 | 31.0 | 30.7 |
| 5 | 30.7 | 29.7 | 28.4 | 27.6 | 26.5 | 25.9 | 25.2 | 24.7 | 24.4 | 24.2 | 24.2 | 24.1 |
| 6 | 24.1 | 24.1 | 24.0 | 24.2 | 24.5 | 24.7 | 25.1 | 25.3 | 26.1 | 24.5 | 0.0 | 0.0 |
| Σ | 282.1 | 422.7 | 411.2 | 396.4 | 376.8 | 363.7 | 351.5 | 341.6 | 333.2 | 319.7 | 285.0 | 282.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalina, A.; Połowniak, P.; Sobolak, M. Study of the Tooth Contact Pattern for Double-Enveloping Worm Gear. Materials 2025, 18, 3997. https://doi.org/10.3390/ma18173997
Kalina A, Połowniak P, Sobolak M. Study of the Tooth Contact Pattern for Double-Enveloping Worm Gear. Materials. 2025; 18(17):3997. https://doi.org/10.3390/ma18173997
Chicago/Turabian StyleKalina, Adam, Piotr Połowniak, and Mariusz Sobolak. 2025. "Study of the Tooth Contact Pattern for Double-Enveloping Worm Gear" Materials 18, no. 17: 3997. https://doi.org/10.3390/ma18173997
APA StyleKalina, A., Połowniak, P., & Sobolak, M. (2025). Study of the Tooth Contact Pattern for Double-Enveloping Worm Gear. Materials, 18(17), 3997. https://doi.org/10.3390/ma18173997






