Comparative Evaluation of Stress Distribution and Permeability Characteristics in Bentonite Cutoff Walls Using CPTU and ABAQUS Methods
Abstract
1. Introduction
2. Materials and Methods
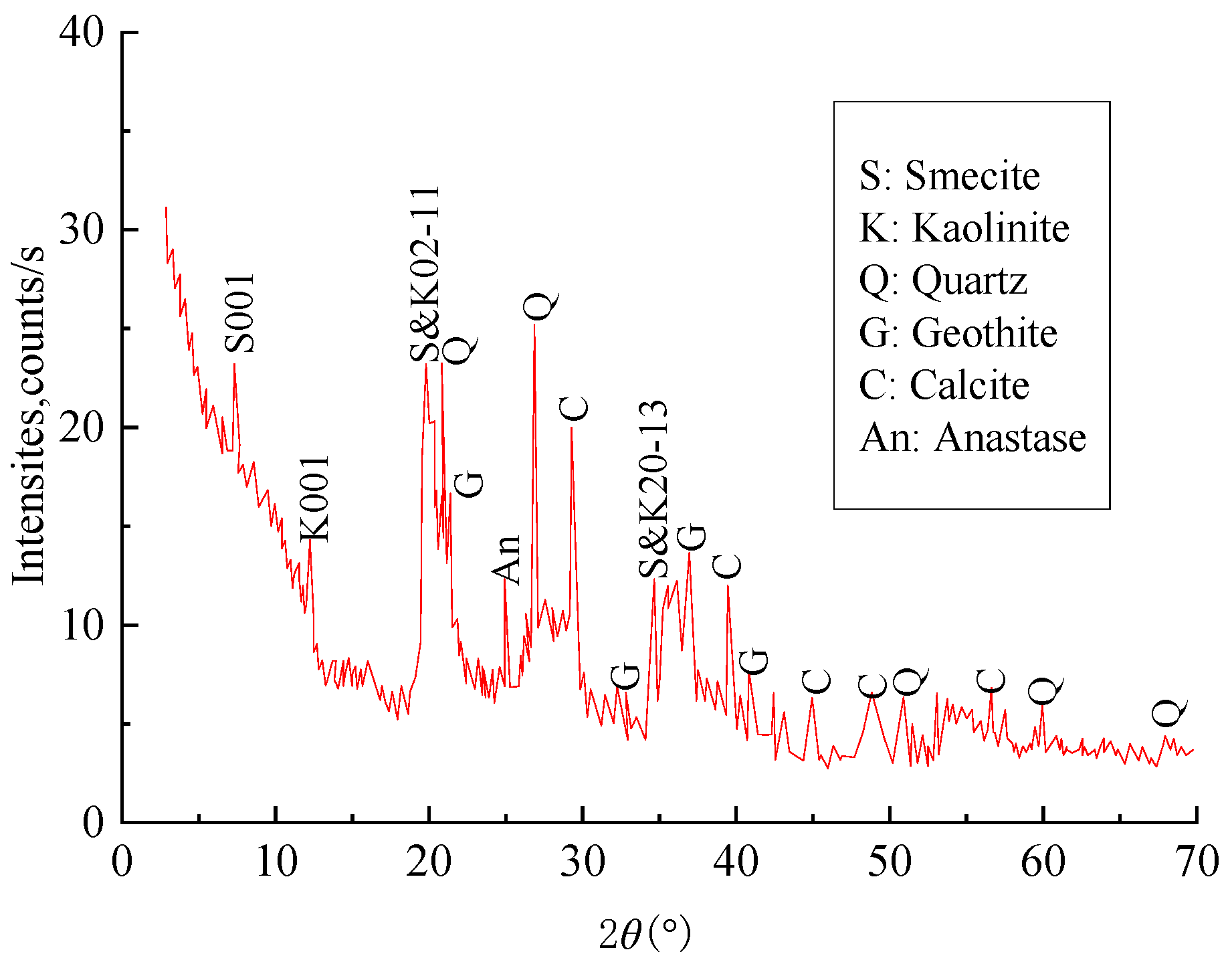
2.1. Test Materials
2.2. CPTU
2.3. ABAQUS
3. Results and Analysis
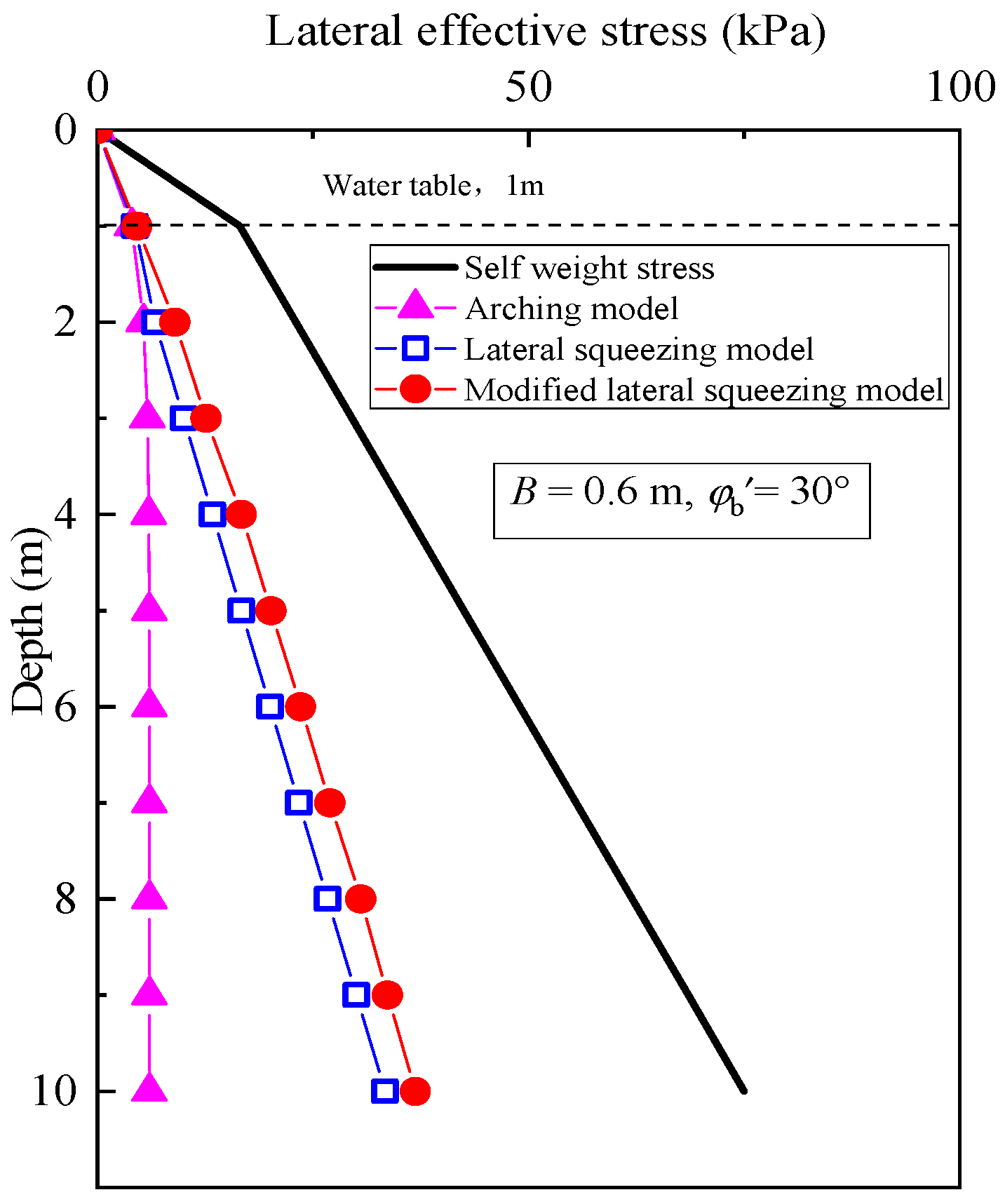
3.1. Lateral Effective Stress
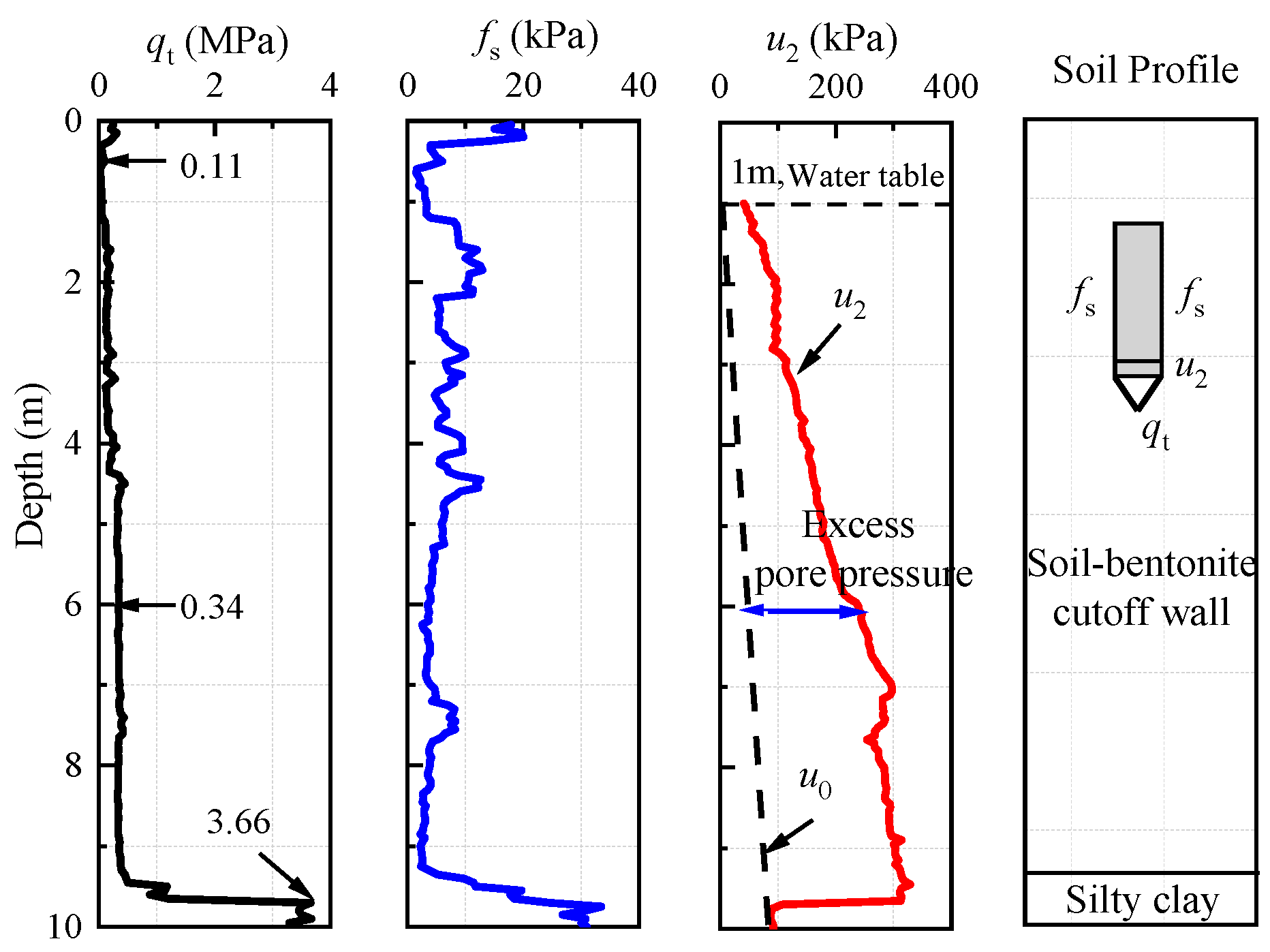
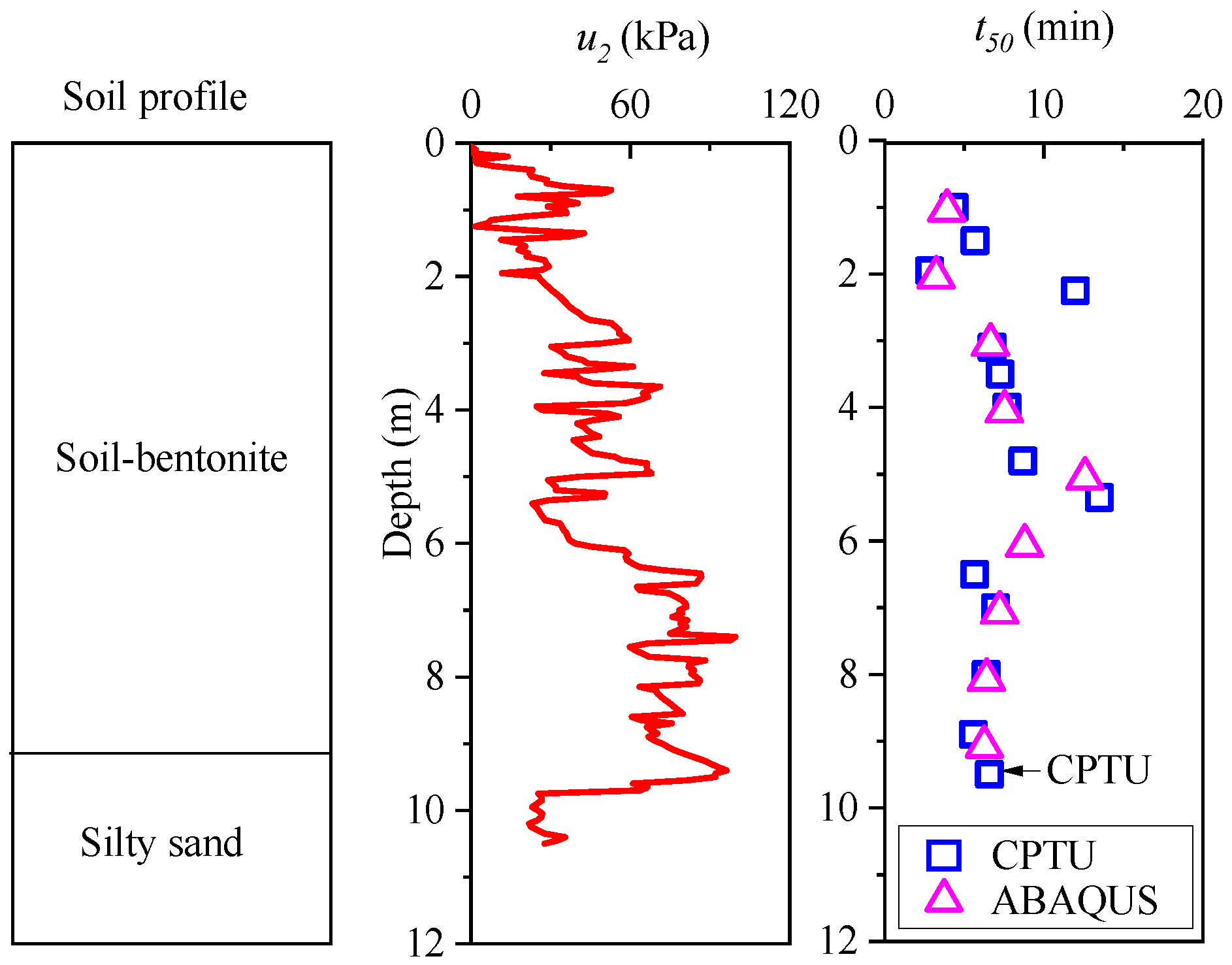
3.2. CPTU Results
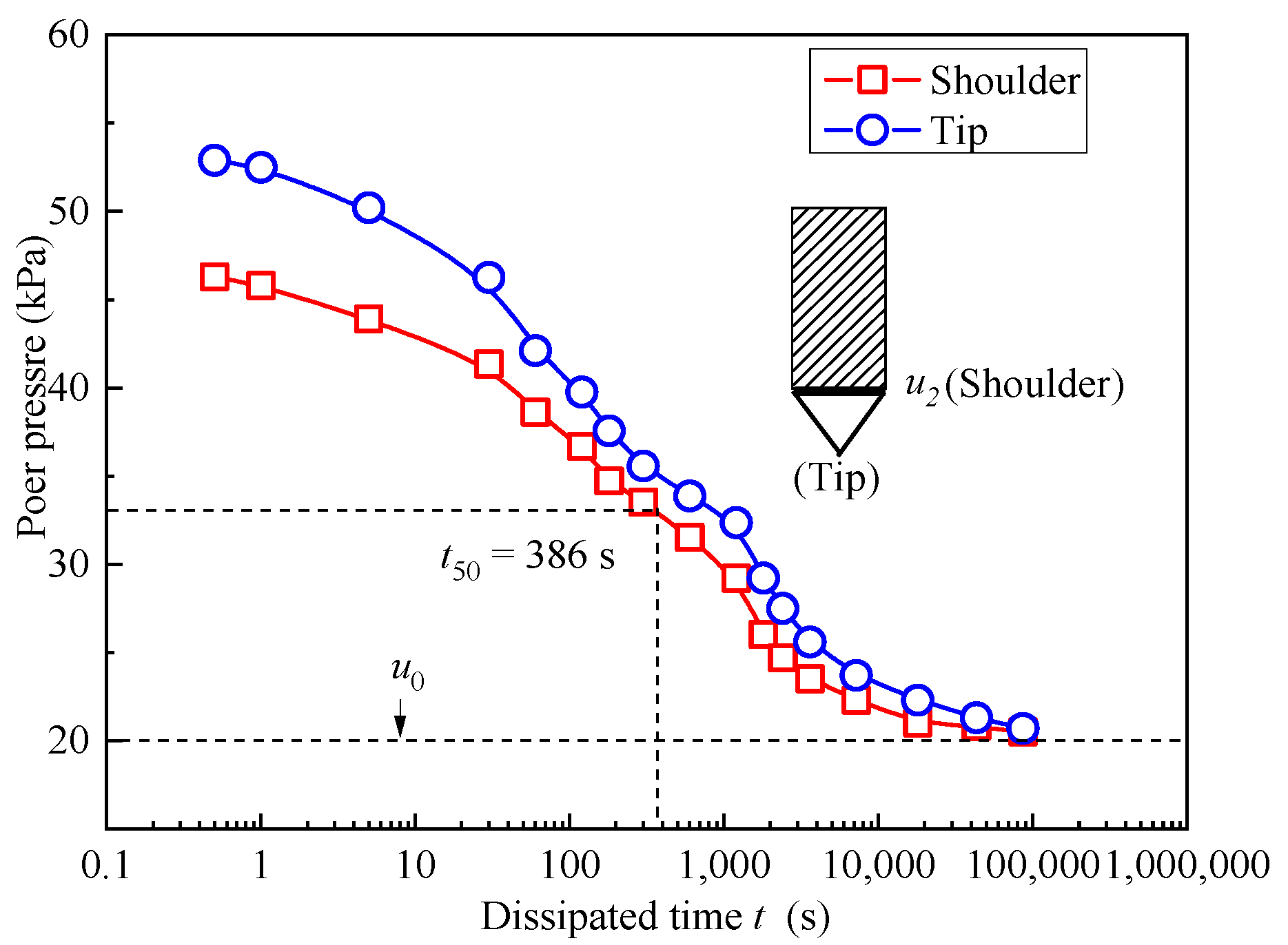
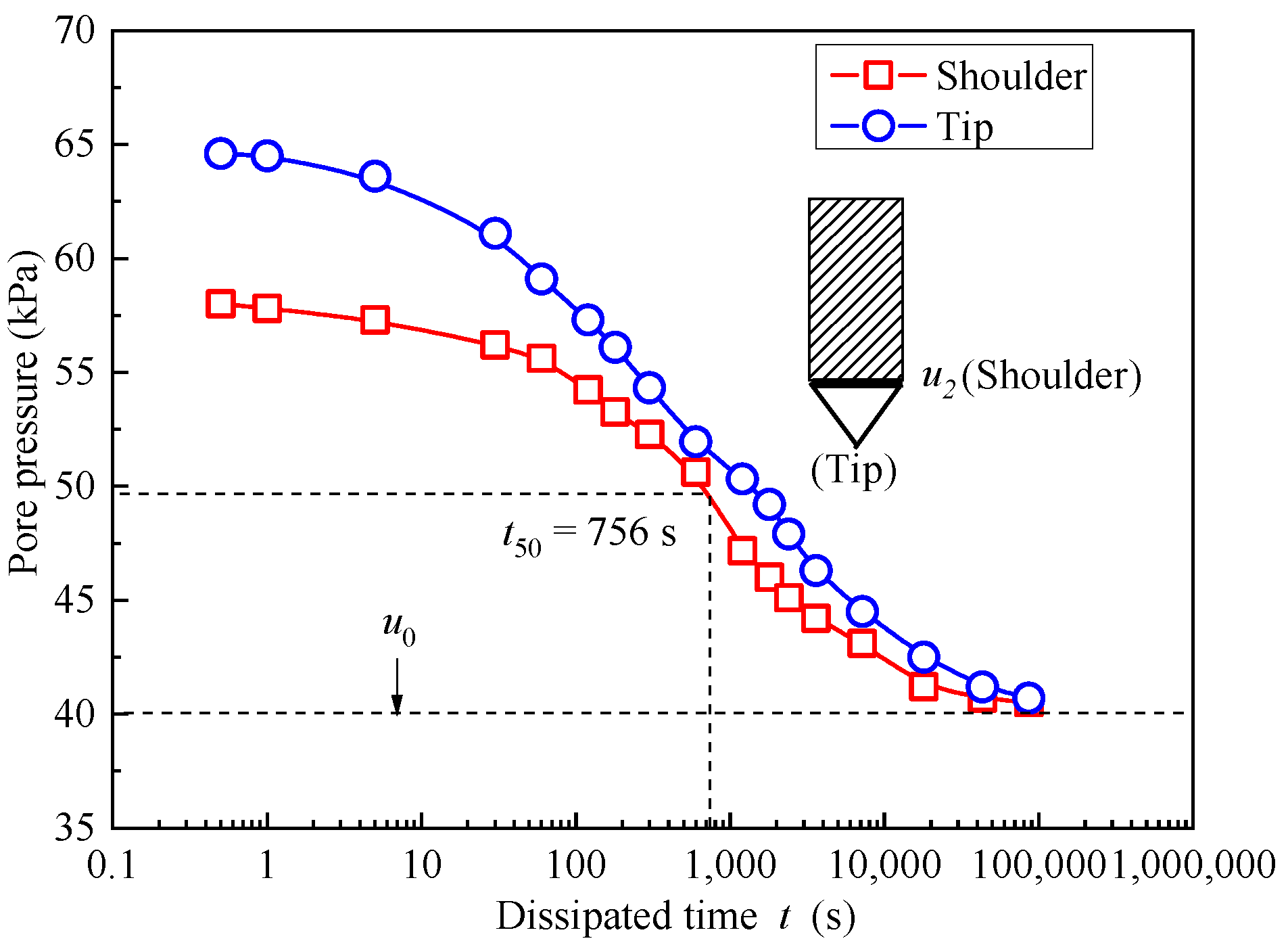
3.3. Pore Pressure Dissipation Types
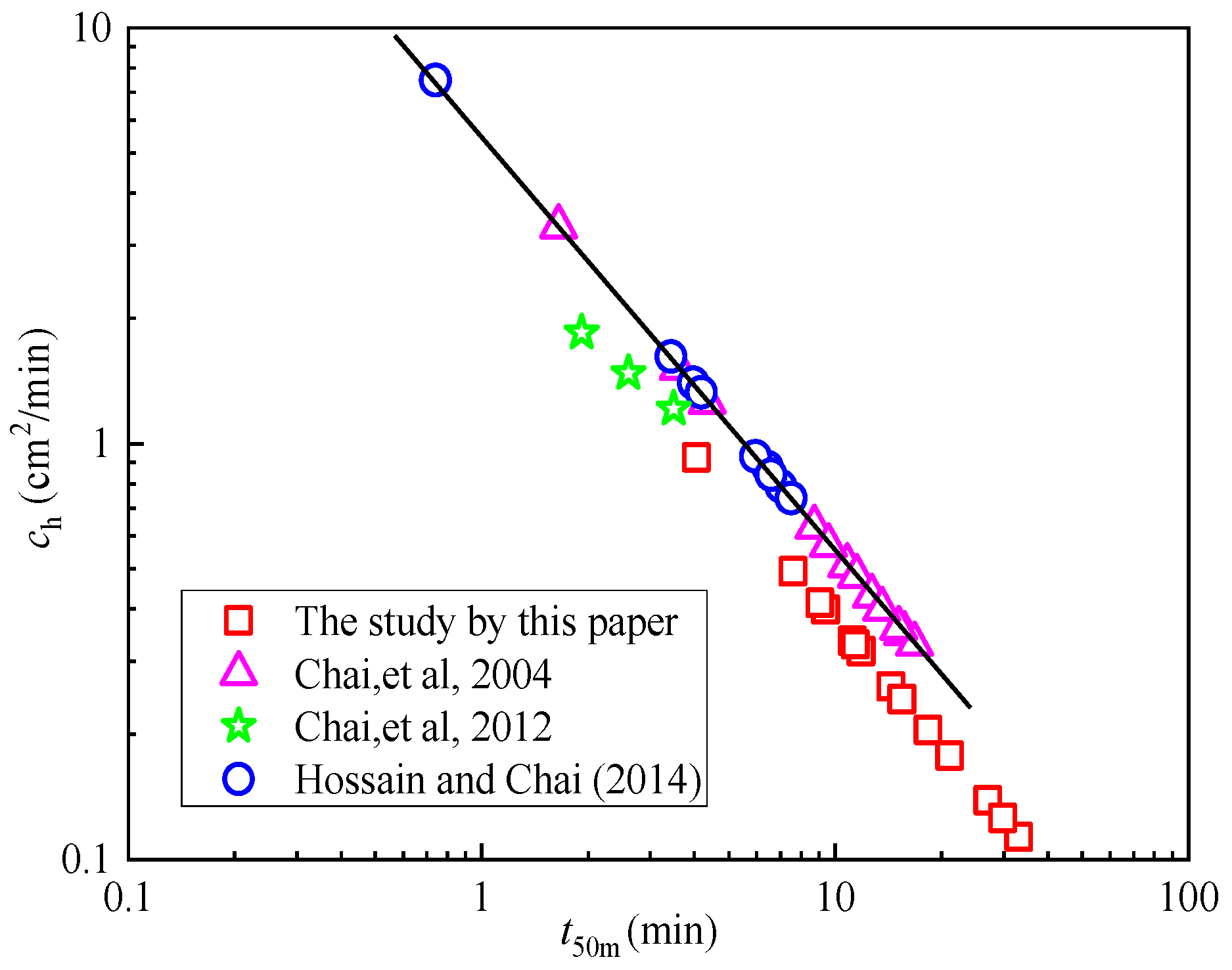
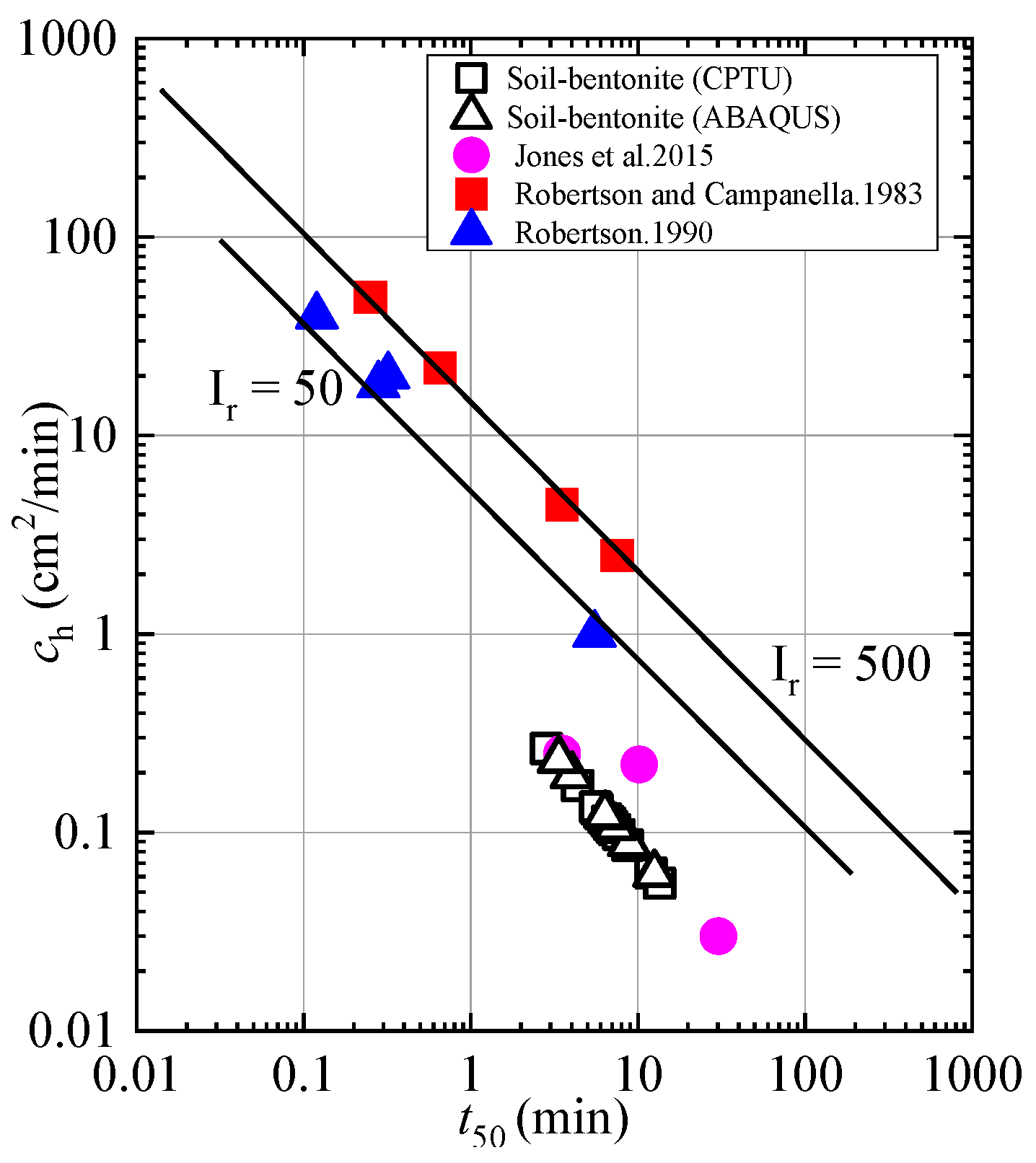
3.4. Coefficient of Consolidation and Permeability
4. Conclusions
- The lateral effective stress of the soil–bentonite mixtures, determined by the arching model, is lower than that calculated using the lateral squeezing model and the modified lateral squeezing model.
- The t50 parameter is crucial for evaluating ch and kh. This paper provides the t50 values at various depths using the CPTU method. The t50 value is 810 s at 5.35 m for the standard dissipation type and 305 s at 7.10 m for the non-dissipation type. The t50 values obtained from CPTU are relatively close to those simulated by ABAQUS.
- The kh values (<1.0 × 10−7 cm/s) of the materials used, obtained through various methods, indicate that they meet the isolation requirements when compared with previous research results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, L.; Liu, T.; Liu, X.; Li, Z.; Cai, G. Key influencing factors and prediction model for the tensile strength of compacted clayey loess. Bull. Eng. Geol. Environ. 2025, 84, 404. [Google Scholar] [CrossRef]
- Liu, L.; Li, Z.; Guo, J.; Lv, S.; Liu, X.; Cai, G.; Fan, G. Compression characteristics and microscopic mechanism of high-temperature sintered loess. Constr. Build. Mater. 2025, 490, 142456. [Google Scholar] [CrossRef]
- Li, Z.; Ma, J.; Liu, X.; Liu, L.; Cai, G.; Peng, L.; Xiong, H. Exploring the temperature, humidity, and deformation characteristics of gravel replacement foundations in seasonally frozen zones: A model testing study. Bull. Eng. Geol. Environ. 2025, 84, 141. [Google Scholar] [CrossRef]
- Garvin, S.L.; Hayles, C.S. The chemical compatibility of cement–bentonite cut-off wall material. Constr. Build. Mater. 1999, 13, 329–341. [Google Scholar] [CrossRef]
- D’appolonia, D.J. Soil-bentonite slurry trench cutoffs. J. Geotech. Eng. Div. 1980, 106, 399–417. [Google Scholar] [CrossRef]
- Cai, G.; Liu, S.; Puppala, A.J. Reliability assessment of CPTU-based pile capacity predictions in soft clay deposits. Eng. Geol. 2012, 141, 84–91. [Google Scholar] [CrossRef]
- Nartowska, E.; Podlasek, A.; Vaverková, M.D.; Koda, E.; Jakimiuk, A.; Kowalik, R.; Kozłowski, T. Mobility of Zn and Cu in Bentonites: Implications for Environmental Remediation. Materials 2024, 17, 2957. [Google Scholar] [CrossRef]
- Wang, H.; Chen, D.; Guo, R.; Tian, J.; Li, B. A Preliminary Study on the Improvement of Gangue/Tailing Cemented Fill by Bentonite: Flow Properties, Mechanical Properties and Permeability. Materials 2023, 16, 6802. [Google Scholar] [CrossRef]
- Luo, X.; Chen, Q.; Deng, C.; Luo, W.; He, Y. Low-Cyclic Reversed Loading Tests on Full-Scale Precast Concrete Composite Wall Connected by Tooth Groove and Grouted Sleeve. Materials 2024, 17, 476. [Google Scholar] [CrossRef]
- Nagaraj, T.S.; Murthy, B.R.S. A critical reappraisal of compression index equations. Geotechnique 1986, 36, 27–32. [Google Scholar] [CrossRef]
- Li, X.; Cai, G.; Puppala, A.J.; Liu, S. Compression behavior of reconstituted soils mixed with bentonite for a cutoff wall in a landfill site. Environ. Earth Sci. 2018, 77, 390. [Google Scholar] [CrossRef]
- Baligh, M.M.; Vivatrat, V.; Ladd, C.C. Cone penetration in soil profiling. J. Geotech. Eng. Div. 1980, 106, 20–32. [Google Scholar] [CrossRef]
- Lunne, T.; Robertson, P.K.; Powell, J.J.M. Cone-penetration testing in geotechnical practice. Soil. Mech. Found. Eng. 2009, 46, 237. [Google Scholar] [CrossRef]
- Sully, J.P.; Robertson, P.K.; Campanella, R.G. An approach to evaluation of field CPTU dissipation data in overconsolidated fine-grained soils. Can. Geotech. J. 1999, 36, 369–381. [Google Scholar] [CrossRef]
- Elsworth, D.; Lee, D.S. Permeability determination from on-the-fly piezocone sounding. J. Geotech. Geoenvironmental Eng. 2005, 131, 643–653. [Google Scholar] [CrossRef]
- Chai, J.C.; Agung, P.M.A.; Hino, T. Estimating hydraulic conductivity from piezocone soundings. Géotechnique 2011, 61, 699–708. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Zhang, R.; Li, Z.Y. Hydraulic conductivity and microscopic properties of sodium hexametaphosphate-amended sand-sodium-activated calcium bentonite backfill in vertical cutoff walls exposed to lead-contaminated groundwater. Acta Geotech. 2025, 20, 1235–1250. [Google Scholar] [CrossRef]
- Dong, H.H.; Wang, Z.K.; Yan, Z.Z. Centrifuge modeling of backfill consolidation in soil-bentonite cutoff walls. Can. Geotech. J. 2025, 62, 1–15. [Google Scholar] [CrossRef]
- Evans, J.C.; Fang, H.Y.; Kugelman, I.J. Containment of hazardous materials with soil-bentonite slurry walls. In Proceedings of the 6th National Conference on Management of Uncontrolled Hazardous Waste Sites, Washington, DC, USA, 4–6 November 1985; pp. 369–373. [Google Scholar]
- Xu, Y.J.; Wang, G.Q.; Li, J. Develop and implement Duncan Chang constitutive model in ABAQUS. Geotech. Mech. 2004, 25, 1032–1036. [Google Scholar]
- Shi, Y.; Guo, F.Y.; Mao, C.; Wang, X. Application of FLAC3D in Soil Consolidation Simulation. J. Tianjin Urban Constr. Univ. 2006, 12, 18–22. [Google Scholar]
- Sun, J.Z.; Gao, H. Application of ABAQUS in the Analysis of Soft Foundation Consolidation Process. In Proceedings of the National Symposium on Numerical Analysis and Analytical Methods of Geotechnical Mechanics, Beijing, China, 12–13 March 2007; pp. 11–14. [Google Scholar]
- Chai, J.C.; Sheng, D.; Carter, J.P. Coefficient of consolidation from non-standard piezocone dissipation curves. Comput. Geotech. 2012, 41, 13–22. [Google Scholar] [CrossRef]
- ASTM D2487; Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). ASTM International: West Conshohocken, PA, USA, 2017.
- Fan, Q.L.; Luan, M.T.; Yang, Q. Numerical implementation of Implicit integration algorithm for modified Cam-clay model in ABAQUS. Rock Soil Mech. 2008, 29, 269–273. [Google Scholar]
- Tong, X. Mechanical and Hydraulic Properties of Soil-Bentonite and Consolidation Behavior of Cutoff Wall. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2017. [Google Scholar]
- Li, Y.C.; Cleall, P.J.; Ma, X.F. Gas Pressure model for layered municipal solid waste landfills. J. Environ. Eng. 2012, 138, 752–760. [Google Scholar] [CrossRef]
- Malusis, M.A.; Yeo, S.; Evans, J.C. Hydraulic conductivity of model soil–bentonite backfills subjected to. Can. Geotech. J. 2011, 48, 1198–1211. [Google Scholar] [CrossRef]
- Pan, Q.; Wen, Y.D.; Chen, Y.M. Stresses in soil–bentonite slurry trench cut-off walls. Géotechnique 2015, 65, 843–850. [Google Scholar]
- Filz, G.M. Consolidation stresses in soil-bentonite backfilled trenches. In Proceedings of the 2nd International Congress on Environmental Geotechnics, Osaka, Japan, 5–8 November 1996; pp. 497–502. [Google Scholar]
- Ruffing, D.G.; Evans, J.C.; Malusis, M.A. Prediction of earth pressures in soil-bentonite cutoff walls. In GeoFlorida 2010: Advances in Analysis, Modeling & Design; ASCE Library: Reston, VA, USA, 2010; pp. 2416–2425. [Google Scholar]
- Coop, M.R.; Wroth, C.P. Field studies of an instrumented model pile in clay. Geotechnique 1989, 39, 679–696. [Google Scholar] [CrossRef]
- Chai, J.C.; Carter, J.P.; Miura, N. Coefficient of consolidation from piezocone dissipation tests. In Proceedings of the International Symposium on Lowland Technology, Bangkok, Thailand, 1–3 September 2004; pp. 1–6. [Google Scholar]
- Hossain, M.J.; Chai, J.C. Advances in soil dynamics and foundation engineering-interpreting chp value from non-standard piezocone dissipation curves. In Proceedings of the American society of civil engineers geo-shanghai, Shanghai, China, 26–28 May 2014. [Google Scholar]
- Cai, G.J.; Liu, S.Y.; Puppala, A.J. Predictions of coefficient of consolidation from CPTU dissipation tests in Quaternary clays. Bull. Eng. Geol. Environ. 2011, 30, 337–350. [Google Scholar] [CrossRef]
- Chai, J.C.; Hossain, M.J.; Yuan, D. Pore pressures induced by piezocone penetration. Can. Geotech. J. 2016, 53, 540–550. [Google Scholar] [CrossRef]
- Krage, C.P.; Dejong, J.T.; Schnaid, F. Estimation of the Coefficient of Consolidation from Incomplete Cone Penetration Test Dissipation Tests. J. Geotech. Geoenvironmental Eng. 2014, 141, 06014016. [Google Scholar] [CrossRef]
- Jones, G.A.; Van, Z.D.; Rust, E. Mine tailings characterization by piezometer cone. In Cone Penetration Testing and Experience; American Society of Civil Engineers: New York, NY, USA, 2015; pp. 303–324. [Google Scholar]
- Robertson, P.K.; Campanella, R.G. Interpretation of cone penetration tests. Part I: Sand. Can. Geotech. J. 1983, 20, 718–733. [Google Scholar] [CrossRef]
- Robertson, P.K. Soil classification using the cone penetration test. J. Geotech. Geoenvironmental Eng. 1990, 27, 984–986. [Google Scholar] [CrossRef]
- Robertson, P.K.; Sully, J.P.; Woeller, D.J. Estimating coefficient of consolidation from piezocone tests. Can. Geotech. J. 1993, 29, 539–550. [Google Scholar] [CrossRef]

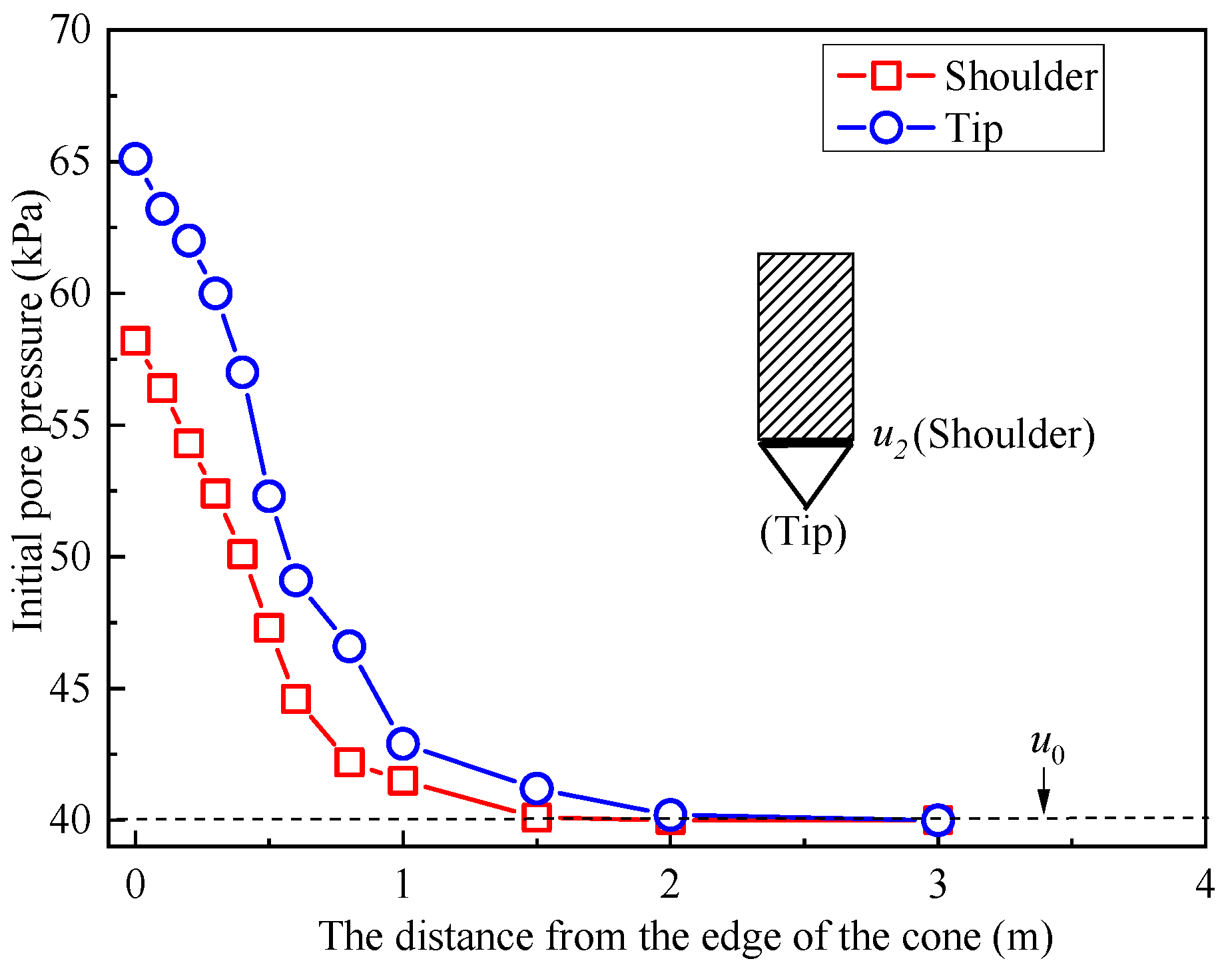
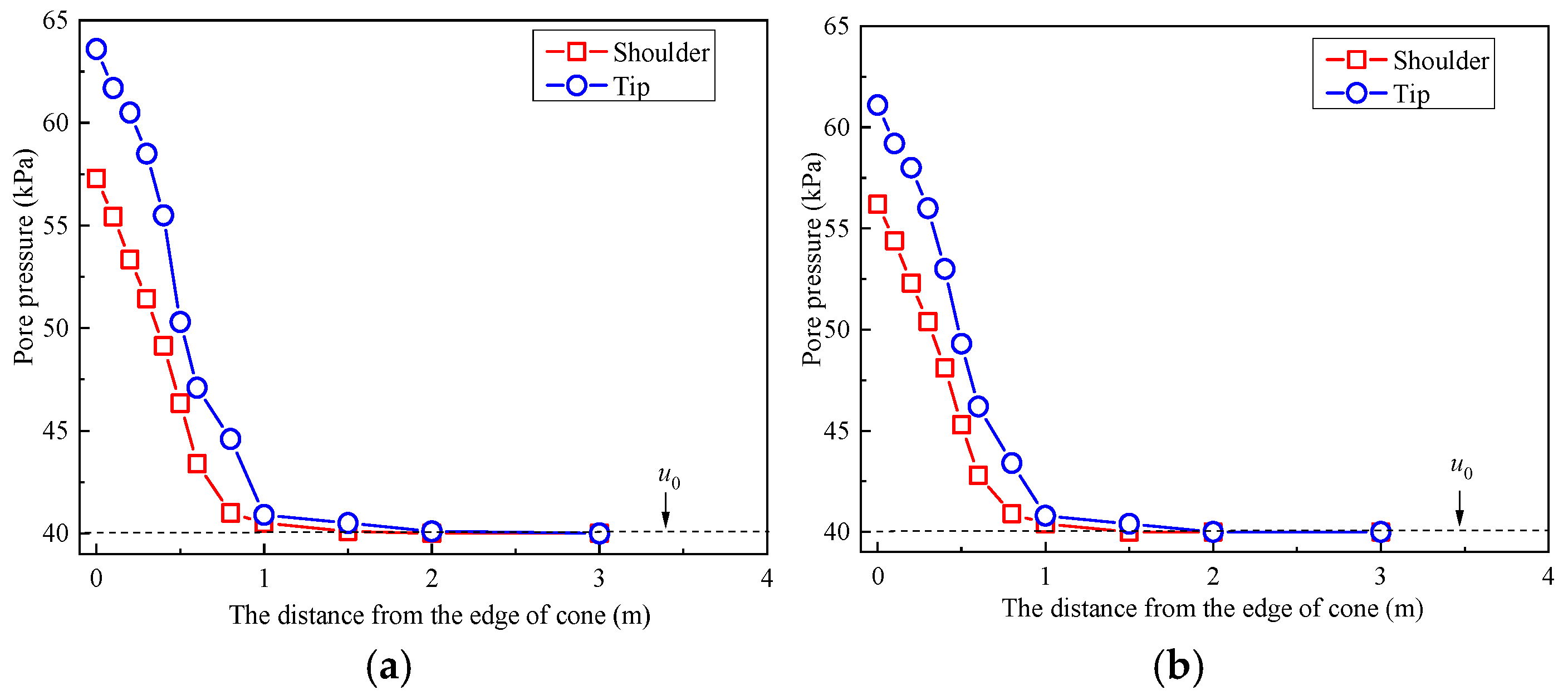
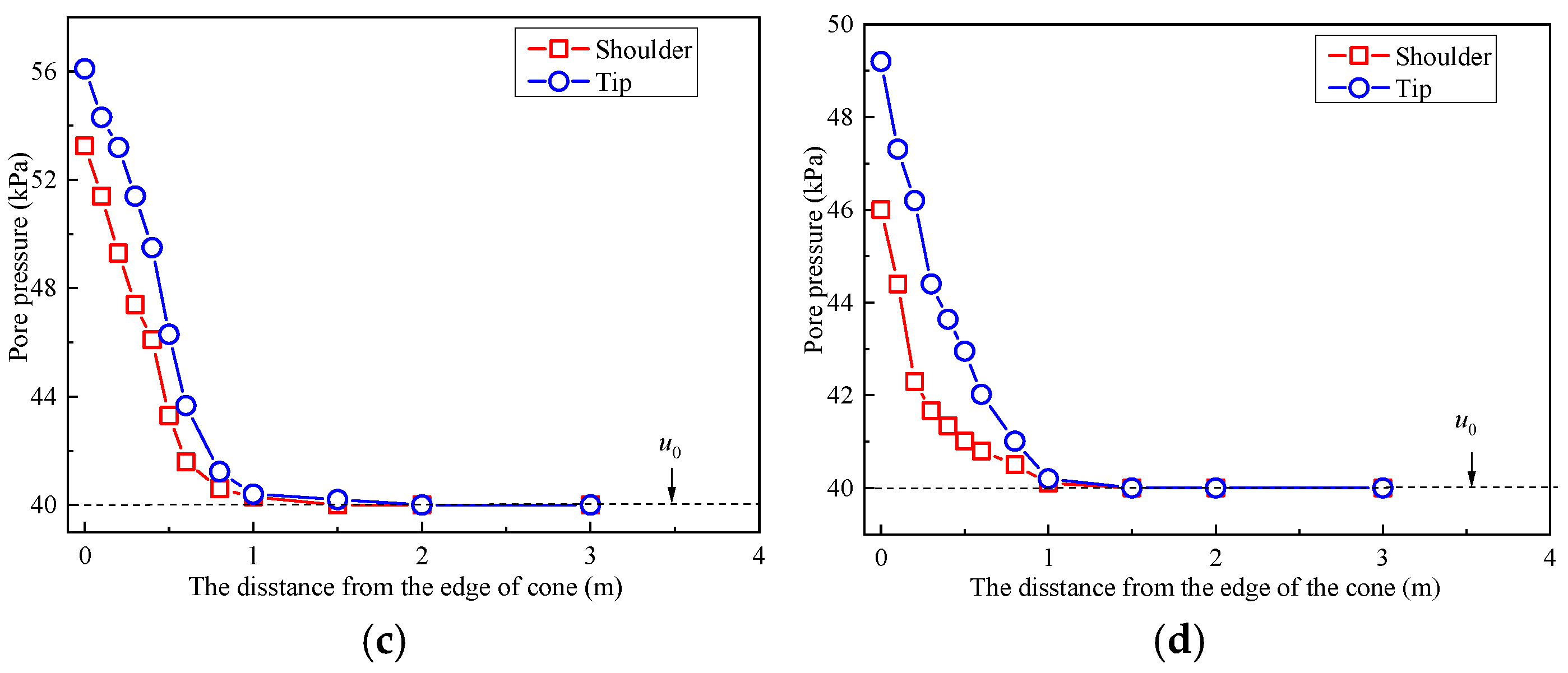
| Parameter | Size | Units | Reference |
|---|---|---|---|
| K | 0.01 | / | [26] |
| λ | 0.1 | / | [26] |
| M | 1.2 | / | [26] |
| ν | 0.33 | / | [27] |
| k0 | 0.56 | / | [26] |
| γrat | 17.7 | kN/m3 | [27] |
| γw | 10 | kN/m3 | [28] |
| kh | 4.1 × 10−8 | cm/s | [28,29] |
| Parameter | Value | Unit |
|---|---|---|
| Initial effective stress | y = 10 m: σx′ = 0, σy′ = 0 y = 0 m: σx′ = 38.5, σy′ = −77 | kPa |
| Initial pore pressure | y = 10 m: u = 0 y = 0 m: u = 90 | kPa |
| Initial pore pressure | y = 10 m: e0 = 0.96 y = 0 m: e0 = 0.54 | / |
| Initial dry density | y = 10 m: ρd = 1.28 y = 0 m: ρd = 1.42 | g/cm3 |
| Initial yield surface | y = 10 m: p′ = 0, q = 0, p0′ = 0 y = 0 m: p′ = 51, q = 38.5, p0′ = 80 | kPa |
| CPTU Types | Δui (kPa) | Δui/2 (kPa) | Δumax (kPa) | t50 (s) |
|---|---|---|---|---|
| Standard dissipation | 18.1 | 9.05 | / | 810 |
| Non-Standard dissipation | 5.49 | / | 16.4 | 305 |
| Parameter | Standard Dissipation | Non-Standard Dissipation | ABAQUS | Robertson et al., 1993 [41] |
|---|---|---|---|---|
| t50 (min) | 12.0 | 11.2 | 12.1 | 12.6 |
| kh (cm/s) | 9.3 × 10−9 | 2.7 × 10−8 | 8.5 × 10−8 | 1.2 × 10−8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Li, Y.; Yan, C.; Wang, F.; Liu, X. Comparative Evaluation of Stress Distribution and Permeability Characteristics in Bentonite Cutoff Walls Using CPTU and ABAQUS Methods. Materials 2025, 18, 3919. https://doi.org/10.3390/ma18163919
Li X, Li Y, Yan C, Wang F, Liu X. Comparative Evaluation of Stress Distribution and Permeability Characteristics in Bentonite Cutoff Walls Using CPTU and ABAQUS Methods. Materials. 2025; 18(16):3919. https://doi.org/10.3390/ma18163919
Chicago/Turabian StyleLi, Xuepeng, Yufu Li, Chao Yan, Fengyun Wang, and Xiaoyan Liu. 2025. "Comparative Evaluation of Stress Distribution and Permeability Characteristics in Bentonite Cutoff Walls Using CPTU and ABAQUS Methods" Materials 18, no. 16: 3919. https://doi.org/10.3390/ma18163919
APA StyleLi, X., Li, Y., Yan, C., Wang, F., & Liu, X. (2025). Comparative Evaluation of Stress Distribution and Permeability Characteristics in Bentonite Cutoff Walls Using CPTU and ABAQUS Methods. Materials, 18(16), 3919. https://doi.org/10.3390/ma18163919