A Review on Comfort of Pedestrian Bridges Under Human-Induced Vibrations and Tuned Mass Damper Control Technologies
Abstract
1. Introduction
- Pedestrian load modeling. Single-person walking load has significant randomness in individual weight, step frequency, gait, and other differences, and there are changes in pedestrian density and other environmental factors. Crowd loading is a more complex nonlinear role and needs to simplify the assumptions in modeling.
- Vibration response evaluation system. Existing research has been initially established to acceleration-limit-value-oriented comfort standards, avoiding sensitive frequency intervals and limiting the dynamic response control vibration, but lateral vibration comfort research is less and more concentrated in high-rise buildings. Lateral vibration also needs to be vigilant about the “load–response” nonlinear feedback triggered by the dynamics of the instability problem.
- Optimization of vibration control technology. Adjustment of structural stiffness is limited due to cost and aesthetic constraints, while a tuned mass damper (TMD) has become a mainstream in engineering due to its simple structure, high damping efficiency, and easy installation. However, a single TMD has insufficient adaptability to face broadband loading, and a multi-tuned mass damper (MTMD), although theoretically more applicable to broadband excitation, needs to balance the computational complexity of the optimization of the parameters with the feasibility of the engineering.
2. Pedestrian Load
- Periodicity: Although there are slight differences in the length and frequency of a single step of pedestrians, the inherent law of human walking determines that the walking loads are significantly periodic, and the time series of their forces show regular changes.
- Narrow-band randomness: The weight, step frequency, step length, and other parameters of different pedestrians differ, but the fluctuation range is small, resulting in a random distribution of the load parameters in a narrow interval.
- Human–bridge interaction: Pedestrians are not only the excitation source of bridge vibration but are also affected by the dynamic response of the bridge. This makes them adjust their walking posture, which in turn changes the load acting on the bridge, forming a dynamic feedback of “load–response”; at the same time, the real-time changes in the number, density, and location of pedestrians on the bridge surface make the dynamic load present a dynamic characteristic, so the crowd is very important for the accurate analysis of bridge dynamics. Meanwhile, the real-time changes in the number, density, and location of pedestrians on the bridge make the dynamic load show dynamic characteristics, so crowd load study is crucial to accurately analyze the dynamic response of bridge.
2.1. Single Pedestrian Load
2.1.1. Time-Domain Model
2.1.2. Frequency-Domain Model
2.2. Crowd Load
2.3. Provisions on Pedestrian Load in Design Codes
3. Evaluation of Human-Induced Vibration Comfort on Pedestrian Bridges
- Power interaction theory, based on some kind of model between the bridge structural motion and pedestrian walking;
- Direct resonance theory, which considers that the pedestrian excitation frequency happens to be equal to the frequency of a certain modal state of the bridge, which causes a resonance;
- Internal resonance theory, which considers that the structural nonlinearities cause different modes to enter into an internal resonance state.
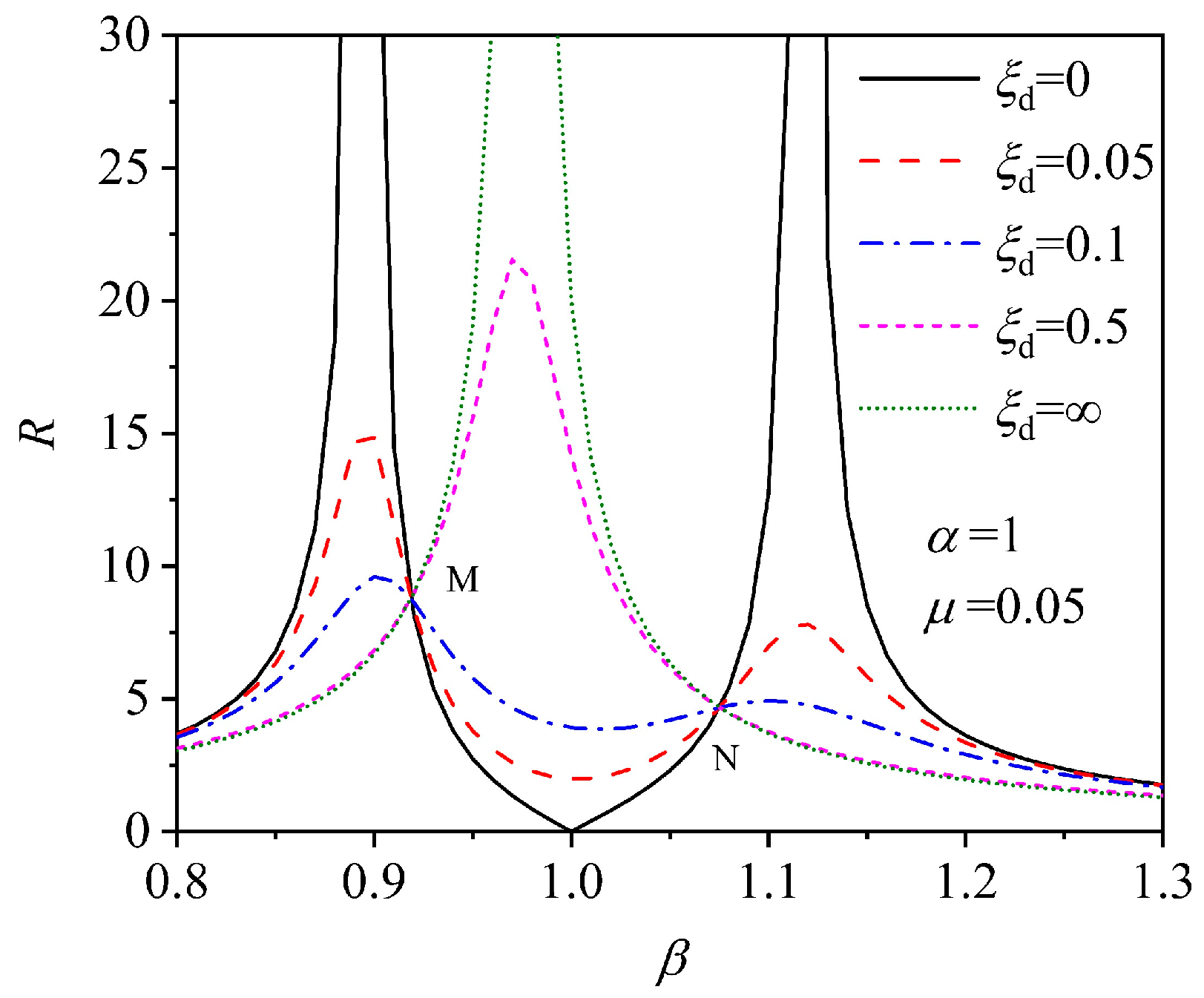
4. TMD Design for Controlling Human-Induced Vibration
5. Conclusions and Outlooks
Funding
Data Availability Statement
Conflicts of Interest
References
- Chan, H.-Y.; Mansoor, U.; Su, J.; Chen, A. Walking in the city of footbridges: Sense of community, subjective walkability and walking habits in a layered neighborhood. Travel Behav. Soc. 2025, 40, 101049. [Google Scholar] [CrossRef]
- De Lima, D.M.; Giló, B.M.d.S.; Cavalcanti, M.E.V.; Pereira, I.d.L.; de Lucena, S.S.D.; Galindo, T.A.; Bezerra, C.J.M.; Alves, I.R.d.M.; da Silva, I.S.d.S.; Medeiros, I.d.S. Vibration analysis of steel footbridges: Experimental investigation, numerical modeling and theoretical approach. Structures 2025, 72, 108250. [Google Scholar] [CrossRef]
- Bruno, L.; Venuti, F.; Nascé, V. Pedestrian-induced torsional vibrations of suspended footbridges: Proposal and evaluation of vibration countermeasures. Eng. Struct. 2012, 36, 228–238. [Google Scholar] [CrossRef]
- Wang, H.; Wang, A.; Wang, J.; Zhang, J.; Du, T.; Shen, J. Optimizing quaternary chemical additives and steel fiber dispersion in CSA cement based HPC for rapid repair engineering. Constr. Build. Mater. 2025, 489, 142265. [Google Scholar] [CrossRef]
- Gallegos-Calderón, C.; Naranjo-Pérez, J.; Renedo, C.M.C.; Díaz, I.M. A frequency-domain approach to model vertical crowd-structure interaction in lightweight footbridges. J. Sound Vib. 2023, 557, 117750. [Google Scholar] [CrossRef]
- Gonzaga, I.B.d.N.; Pfeil, M.S.; Varela, W.D. Modal parameters to estimate the dynamic response of footbridges considering the human-structure interaction. Eng. Struct. 2025, 323, 119271. [Google Scholar] [CrossRef]
- EN 1990:2002/A1:2005/AC:2010; Eurocode—Basis of Structural Design. European Commission: Brussels, Belgium, 1990.
- Sétra. Footbridge, Assessment of Vibrational Behavior of Footbridges Under Pedestrian Loading; Sétra: Paris, France, 2006. [Google Scholar]
- CJJ69-95; Technical Specification of Urban Pedestrian Overcrossing and Underpass. China Architecture & Building Press: Beijing, China, 1996.
- Andriacchi, T.P.; Ogle, J.A.; Galante, J.O. Walking speed as a basis for normal and abnormal gait measurements. J. Biomech. 1977, 10, 261–268. [Google Scholar] [CrossRef]
- Ebrahimpour, A.; Hamam, A.; Sack, R.L.; Patten, W.N. Measuring and Modeling Dynamic Loads Imposed by Moving Crowds. J. Struct. Eng. 1996, 122, 1468–1474. [Google Scholar] [CrossRef]
- Ebrahimpour, A.; Sack, R.L. Modeling Dynamic Occupant Loads. J. Struct. Eng. 1989, 115, 1476–1496. [Google Scholar] [CrossRef]
- Racic, V.; Brownjohn, J.M.W. Stochastic model of near-periodic vertical loads due to humans walking. Adv. Eng. Inform. 2011, 25, 259–275. [Google Scholar] [CrossRef]
- Chen, J.; Peng, Y.-X.; Wang, L. Experimental investigation and mathematical modeling of single footfall load using motion capture technology. Tumu Gongcheng Xuebao/China Civ. Eng. J. 2014, 47, 79–87. [Google Scholar] [CrossRef]
- Bachmann, H.; Pretlove, A.J.; Rainer, H. Dynamic Forces from Rhythmical Human Body Motions. Vibration Problems in Structures: Practical Guidelines; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Ebrahimpour, A.; Sack, R.L. Design Live Loads for Coherent Crowd Harmonic Movements. J. Struct. Eng. 1992, 118, 1121–1136. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Sato, S.; Nishioka, T.; Shiojiri, H. A study on dynamic design of pedestrian over-bridges. Trans. JSCE 1972, 4, 50–51. [Google Scholar]
- Kerr, S.C.; Bishop, N.W.M. Human induced loading on flexible staircases. Eng. Struct. 2001, 23, S0141–S0296. [Google Scholar] [CrossRef]
- Fouli, M.; Camara, A. Human–structure interaction effects on lightweight footbridges with tuned mass dampers. Structures 2024, 62, 106263. [Google Scholar] [CrossRef]
- Blanchard, J.; Davies, B.L.; Smith, J.W. Design Criteria and Analysis for Dynamic Loading of Footbridges. In Proceedings of the Symposium on Dynamic Behaviour of Bridges at the Transport and Road Research Laboratory, Crowthorne, UK, 19 May 1977. [Google Scholar]
- Bachmann, H.; Ammann, W. Vibrations in Structures: Induced by Man and Machines; International Association for Bridge and Structural Engineering: Zurich, Switzerland, 1987. [Google Scholar]
- Rainer, J.H.; Pernica, G.; Allen, D.E. Dynamic loading and response of footbridges. Can. J. Civ. Eng. 1988, 15, 66–71. [Google Scholar] [CrossRef]
- Allen, D.E.; Murray, T.M. Design criterion for vibrations due to walking. Eng. J. 1993, 30, 117–129. [Google Scholar] [CrossRef]
- Young, P. Improved floor vibration prediction methodologies. In Proceedings of the Engineering for Structural Vibration–Current Developments in Research and Practice Arup Vibration Seminar, London, UK, 1 October 2001; Institution of Mechanical Engineers: London, UK, 2001; pp. 6–13. [Google Scholar]
- Petersen, C. Dynamik der Baukonstruktionen; Springer-Verlag: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Chen, J.; Wang, L.; Peng, Y.X. Experimental investigation on Fourier-series model of walking load and its coefficients. J. Vib. Shock 2014, 33, 11–15. [Google Scholar]
- Schweizer, M.; Fina, M.; Wagner, W.; Kasic, S.; Freitag, S. Uncertain pedestrian load modeling for structural vibration assessment in footbridge design. Eng. Struct. 2024, 311, 118070. [Google Scholar] [CrossRef]
- Sim, J.; Blakeborough, A.; Williams, M.S.; Parkhouse, G. Statistical Model of Crowd Jumping Loads. J. Struct. Eng. 2008, 134, 1852–1861. [Google Scholar] [CrossRef]
- Živanović, S.; Pavić, A.; Reynolds, P. Probability-based prediction of multi-mode vibration response to walking excitation. Eng. Struct. 2007, 29, 942–954. [Google Scholar] [CrossRef]
- Ohlsson, S.V. Floor Vibration and Human Discomfort. Ph.D. Thesis, Chalmers University of Technology, Göteborg, Sweden, 1982. [Google Scholar]
- Eriksson, P.E. Vibration of Low-Frequency Floors-Dynamic Forces and Response Prediction. Ph.D. Thesis, Chalmers University of Technology, Goteborg, Sweden, 1994. [Google Scholar]
- Brownjohn, J.M.W.; Pavic, A.; Omenzetter, P. A spectral density approach for modelling continuous vertical forces on pedestrian structures due to walking. Can. J. Civ. Eng. 2004, 31, 65–77. [Google Scholar] [CrossRef]
- Ricciardelli, F. Lateral loading of footbridges by walkers. In Proceedings of the Footbridge 2005-Second International Conference, Venice, Italy, 6–8 December 2005; pp. 1–10. [Google Scholar]
- Matsumoto, Y.; Nishioka, T.; Shiojiri, H.; Matsuzaki, K. Dynamic design of footbridges. IABSE Proc. 1978, 1–15. Available online: https://www.e-periodica.ch/digbib/view?pid=bse-pe-004%3A1978%3A2%3A%3A167 (accessed on 1 May 2025).
- Wei, X.; Broeck, P.V.d.; Roeck, G.D.; Nimmen, K.V. A simplified method to account for the effect of human-human interaction on the pedestrian-induced vibrations of footbridges. Procedia Eng. 2017, 199, 2907–2912. [Google Scholar] [CrossRef]
- BS 5400-3-2000; Steel, Concrete and Composite Bridges-Code of Practice for Design of Steel Bridges. British Standards Institution: London, UK, 2000.
- Byggtjänst, S. BRO 2004 Vägverkets Allmänna Tekniska Beskrivning för Nybyggande och Förbättring av Broar; Swedish Road Administration: Borlänge, Sweden, 2004. [Google Scholar]
- ISO 10137-2007; Bases for Design of Structures—Serviceability of Buildings and Walkways Against Vibrations. ISO: Geneva, Switzerland, 2007.
- EN 03; Human Induced Vibration of Steel Structures, Design of Footbridges. Research Fund for Coal and Steel: Brussels, Belgium, 2008.
- GB/T 51228-2017; Standard for Vibration of Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Bejing, China, 2018.
- Goldman, D.E. A Review of Subjective Response to Vibratory Motion of the Human Body in the Frequency Range 1 to 70 Cycle per Second; NM-004-001; Naval Medical Research Institute: Washington, WA, USA, 1948. [Google Scholar]
- Dieckmann, D. A Study of the Influence of Vibration on Man. Ergonomics 1958, 1, 347–355. [Google Scholar] [CrossRef]
- Wright, D.T.; Green, R. Highway Bridge Vibrations—Part II: Ontario Test Programme; Report No.5; Queen’s University: Kingston, ON, Canada, 1963. [Google Scholar]
- Lenzen, K.H. Vibration of Steel Joist-Concrete Slab Floors. Eng. J. 1966, 3, 133–136. [Google Scholar] [CrossRef]
- Leonard, D.R. Human Tolerance Levels for Bridge Vibration; TRRL Report No.34; Road Research Laboratory: Crowthorne, UK, 1966. [Google Scholar]
- Smith, J.W. The Vibration of Highway Bridges and the Effects on Human Comfort. Ph.D. Thesis, University of Bristol, Bristol, UK, 1969. [Google Scholar]
- Irwin, A.W. Human response to dynamic motion of structures. Struct. Eng. 1978, 56, 237–244. [Google Scholar]
- Nakamura, S.I. Field measurements of lateral vibration on a pedestrian suspension bridge. Struct. Eng. 2003, 81, 22–26. [Google Scholar]
- Fujino, Y.; Siringoringo Dionysius, M. A Conceptual Review of Pedestrian-Induced Lateral Vibration and Crowd Synchronization Problem on Footbridges. J. Bridge Eng. 2016, 21, C4015001. [Google Scholar] [CrossRef]
- Ingólfsson, E.T.; Georgakis, C.T.; Jönsson, J. Pedestrian-induced lateral vibrations of footbridges: A literature review. Eng. Struct. 2012, 45, 21–52. [Google Scholar] [CrossRef]
- Dallard, P.; Fitzpatrick, T.; Flint, A.; Low, A.; Smith Roger, R.; Willford, M.; Roche, M. London Millennium Bridge: Pedestrian-Induced Lateral Vibration. J. Bridge Eng. 2001, 6, 412–417. [Google Scholar] [CrossRef]
- Yuan, X.B. Research on Pedestrian—Induced Vibration of Footbridge. Ph.D. Thesis, Tongji University, Shanghai, China, 2006. [Google Scholar]
- Roberts, T.M. Lateral Pedestrian Excitation of Footbridges. J. Bridge Eng. 2005, 10, 107–112. [Google Scholar] [CrossRef]
- Dey, P.; Narasimhan, S.; Walbridge, S. Reliability-based assessment and calibration of standards for the lateral vibration of pedestrian bridges. Eng. Struct. 2021, 239, 112271. [Google Scholar] [CrossRef]
- Lievens, K.; Lombaert, G.; Roeck, G.D.; Broeck, P.V.d. Comparison of TMD designs for a footbridge subjected to human-induced vibrations accounting for structural and load uncertainties. Procedia Eng. 2017, 199, 1713–1718. [Google Scholar] [CrossRef]
- Lievens, K.; Lombaert, G.; De Roeck, G.; Van den Broeck, P. Robust design of a TMD for the vibration serviceability of a footbridge. Eng. Struct. 2016, 123, 408–418. [Google Scholar] [CrossRef]
- Xu, K.; Igusa, T. Dynamic characteristics of multiple substructures with closely spaced frequencies. Earthq. Eng. Struct. Dyn. 1992, 21, 1059–1070. [Google Scholar] [CrossRef]
- Wang, D.; Wu, C.; Zhang, Y.; Li, S. Study on vertical vibration control of long-span steel footbridge with tuned mass dampers under pedestrian excitation. J. Constr. Steel Res. 2019, 154, 84–98. [Google Scholar] [CrossRef]
- Tsai, H.-C.; Lin, G.-C. Optimum tuned-mass dampers for minimizing steady-state response of support-excited and damped systems. Earthq. Eng. Struct. Dyn. 1993, 22, 957–973. [Google Scholar] [CrossRef]
- Hartog, D.J. Mechanical Vibrations; McGraw–Hill Book Company: New York, NY, USA, 1956. [Google Scholar]
- Brock, J.E. A Note on the Damped Vibration Absorber. J. Appl. Mech. 2021, 13, A284. [Google Scholar] [CrossRef]
- Ioi, T.; Ikeda, K. On the Dynamic Vibration Damped Absorber of the Vibration System. Bull. JSME 1978, 21, 64–71. [Google Scholar] [CrossRef]
- Warburton, G.B. Optimum absorber parameters for various combinations of response and excitation parameters. Earthq. Eng. Struct. Dyn. 1982, 10, 381–401. [Google Scholar] [CrossRef]
- Rana, R.; Soong, T.T. Parametric study and simplified design of tuned mass dampers. Eng. Struct. 1998, 20, S0141–S0296. [Google Scholar] [CrossRef]
- Li, Q.; Fan, J.; Nie, J.; Li, Q.; Chen, Y. Crowd-induced random vibration of footbridge and vibration control using multiple tuned mass dampers. J. Sound Vib. 2010, 329, 4068–4092. [Google Scholar] [CrossRef]
- Asami, T.; Nishihara, O.; Baz, A.M. Analytical Solutions to H∞ and H2 Optimization of Dynamic Vibration Absorbers Attached to Damped Linear Systems. J. Vib. Acoust. 2002, 124, 284–295. [Google Scholar] [CrossRef]
- Igusa, T.; Xu, K. Vibration Control Using Multiple Tuned Mass Dampers. J. Sound Vib. 1994, 175, 491–503. [Google Scholar] [CrossRef]
- Park, J.; Reed, D. Analysis of uniformly and linearly distributed mass dampers under harmonic and earthquake excitation. Eng. Struct. 2001, 23, S0141–S0296. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Harnpornchai, N. Fundamental characteristics of Multiple Tuned Mass Dampers for suppressing harmonically forced oscillations. Earthq. Eng. Struct. Dyn. 1993, 22, 51–62. [Google Scholar] [CrossRef]
- Abé, M.; Fujino, Y. Dynamic characterization of multiple tuned mass dampers and some design formulas. Earthq. Eng. Struct. Dyn. 1994, 23, 813–835. [Google Scholar] [CrossRef]
- Kareem, A.; Kline, S. Performance of Multiple Mass Dampers under Random Loading. J. Struct. Eng. 1995, 121, 348–361. [Google Scholar] [CrossRef]
- Jangid, R.S. Dynamic characteristics of structures with multiple tuned mass dampers. Struct. Eng. Mech. 1995, 3, 497–509. [Google Scholar] [CrossRef]
- Jangid, R.S.; Datta, T.K. Performance of Multiple Tuned Mass Dampers for Torsionally Coupled System. Earthq. Eng. Struct. Dyn. 1997, 26, 307–317. [Google Scholar] [CrossRef]
- Jangid, R.S. Optimum Multiple Tuned Mass Dampers for base-excited undamped system. Earthq. Eng. Struct. Dyn. 1999, 28, 1041–1049. [Google Scholar] [CrossRef]
- Li, C. Optimum multiple tuned mass dampers for structures under the ground acceleration based on DDMF and ADMF. Earthq. Eng. Struct. Dyn. 2002, 31, 897–919. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y. Optimum multiple tuned mass dampers for structures under the ground acceleration based on the uniform distribution of system parameters. Earthq. Eng. Struct. Dyn. 2003, 32, 671–690. [Google Scholar] [CrossRef]
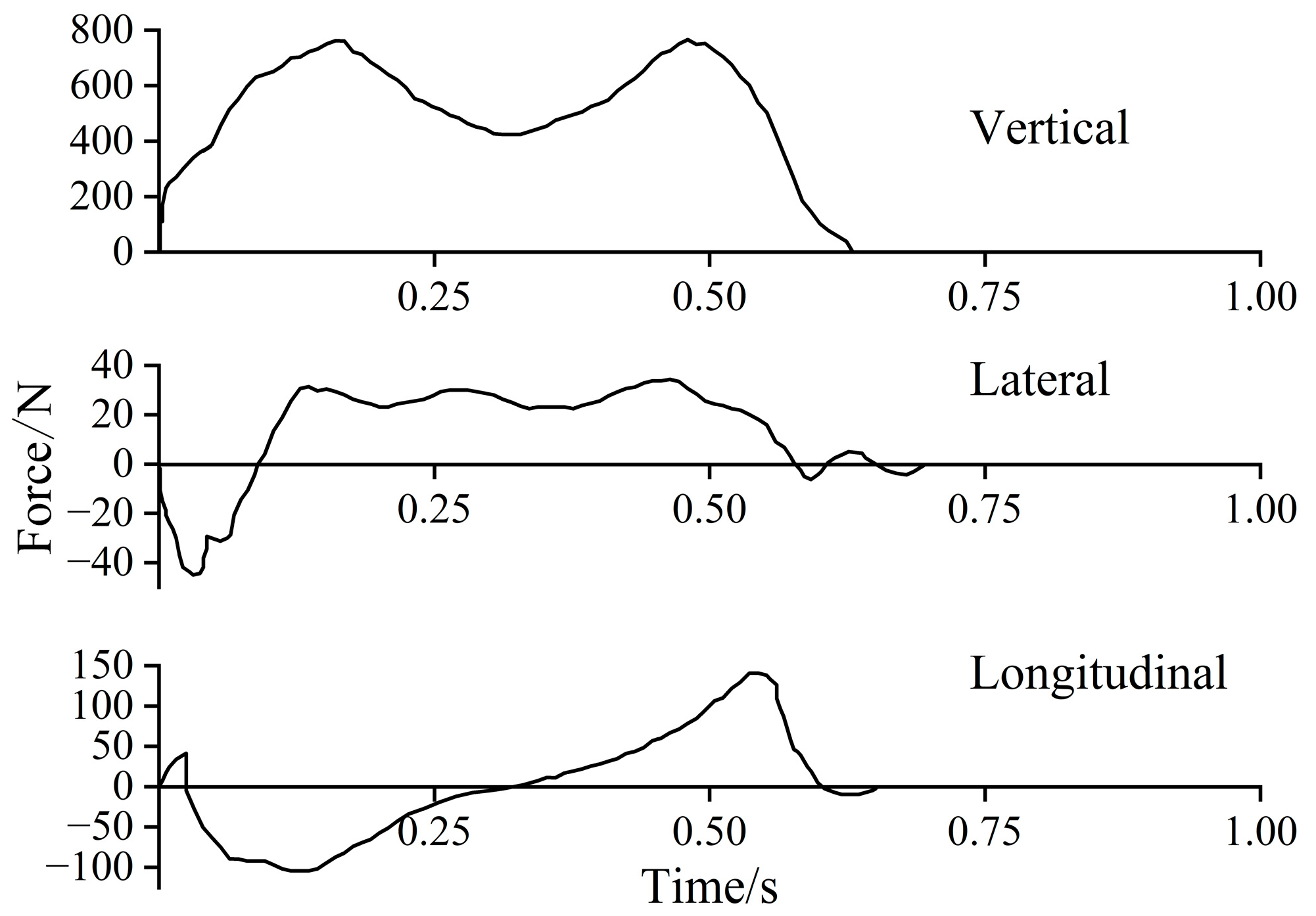
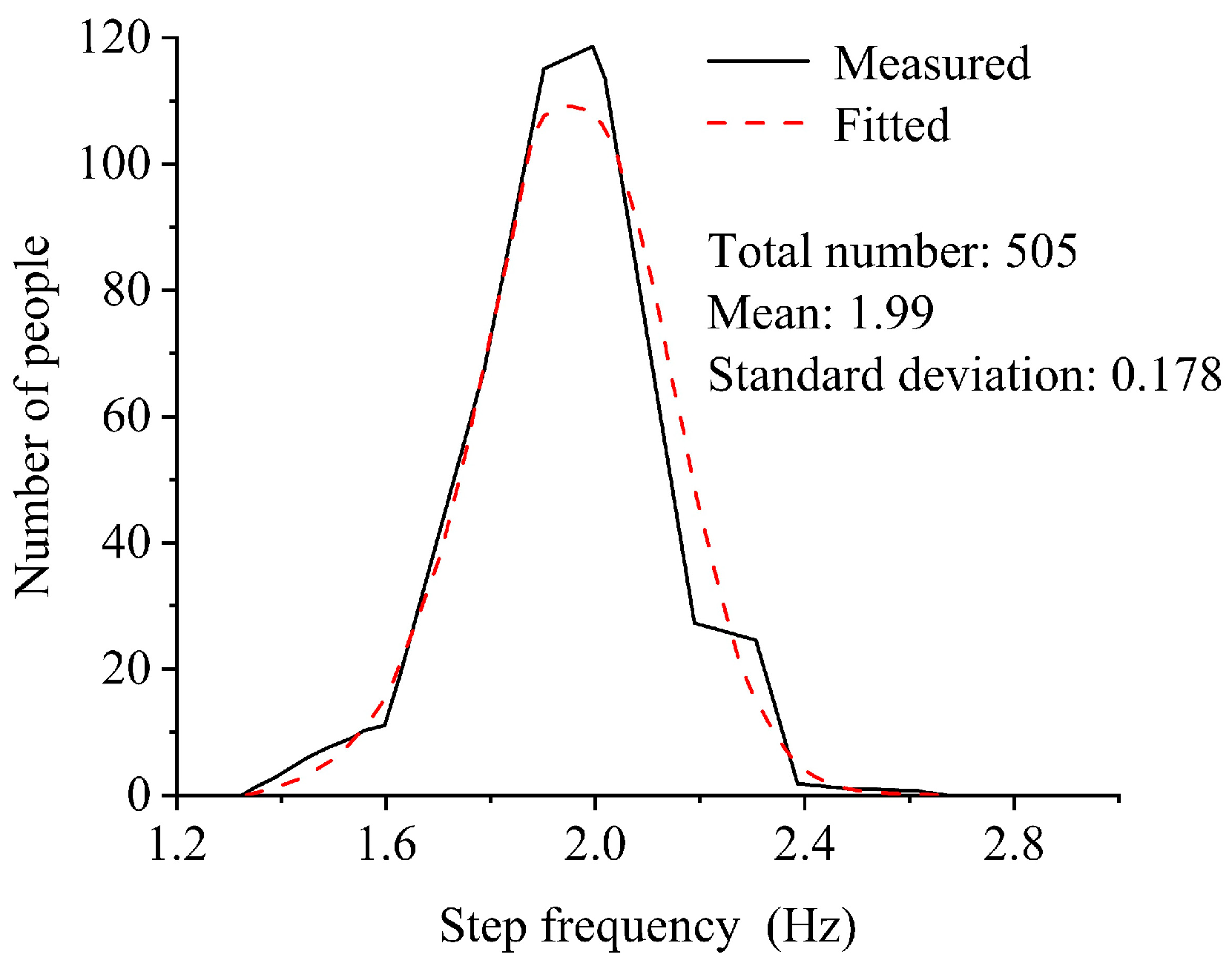

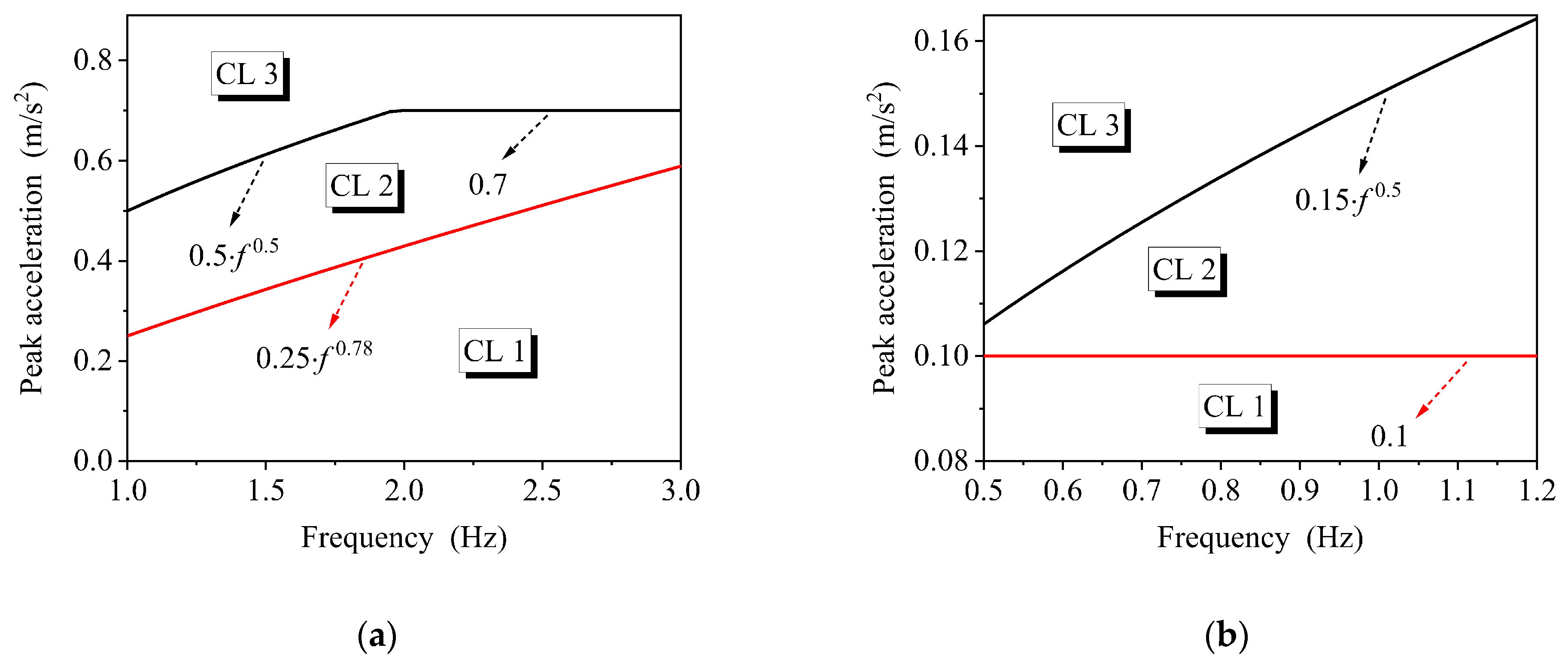


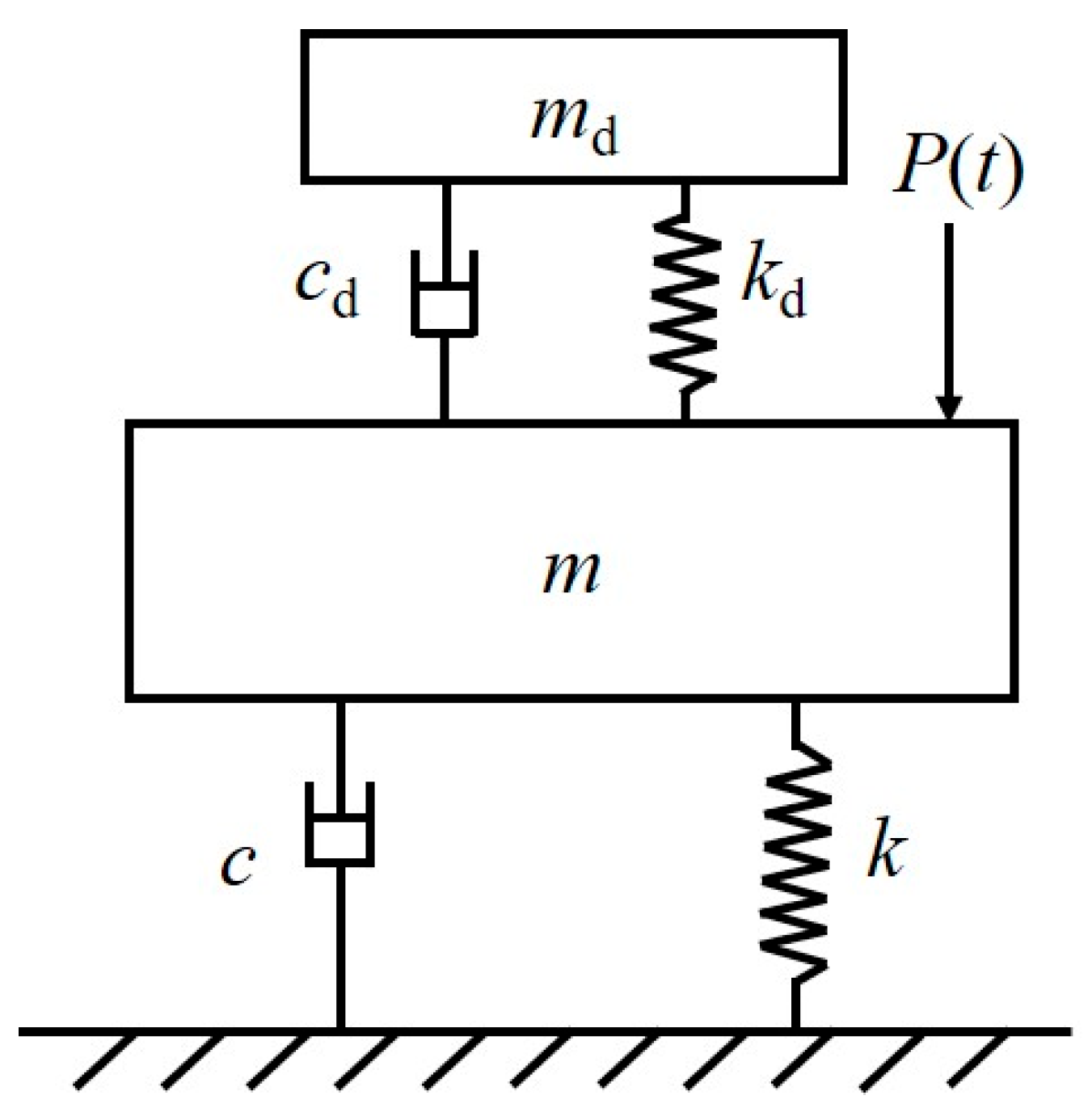

| Reference | Direction | DLF | Step Frequency |
|---|---|---|---|
| Blanchard et al. [20] | vertical | α1 = 0.257 | <4 Hz |
| Bachmann et al. [21] | vertical | α1 = 0.37, α2 = 0.1, α3 = 0.12, α4 = 0.04, α5 = 0.08 | 2 Hz |
| longitudinal | α1 = 0.039, α2 = 0.0204, α3 = 0.026, α4 = 0.083, α5 = 0.024 | 2 Hz | |
| lateral | α1 = 0.039, α2 = 0.01, α3 = 0.043, α4 = 0.012, α5 = 0.015 | 2 Hz | |
| vertical | α1= 0.4–0.5, α2 = α3 = 0.1 | 2.0–2.4 Hz | |
| Allen et al. [23] | vertical | α1 = 0.5, α2 = 0.2, α3 = 0.1, α4 = 0.05 | 1.6–2.4 Hz |
| Petersen [25] | vertical longitudinal lateral | α1 = 0.518, α2 = 0.058, α3 = 0.041 α1 = 0.408, α2 = 0.079, α3 = 0.018 α1 = 0.073, α2 = 0.138, α3 = 0.018 | 2.5 Hz 2 Hz 1.5 Hz |
| Kerr et al. [18] | vertical | α1 = −0.2649 fp3 + 1.3206 fp2 − 1.7597 fp + 0.7613, α2 = 0.07, α3 = 0.06 | - |
| Young [24] | vertical | α1 = 0.41(fp − 0.95) ≤ 0.56, α2 = 0.069 + 0.0056 fp, α3 = 0.033 + 0.0064 fp, α4 = 0.013 + 0.0065 fp | 1.0–2.8 Hz |
| Chen et al. [26] | vertical | αv1 = 0.2817 fp − 0.00792, αv2 = 0.1675, αv3 = 0.1085, αv4 = 0.0988, αv5 = 0.0783 | 1.5–2.5 Hz |
| Order | Main Harmonic | Subharmonic | |
|---|---|---|---|
| Mean | Standard Deviation | ||
| 1 | μ1 | 0.16 μ1 | 0.026 α1 + 0.0031 |
| 2 | 0.07 | 0.03 | 0.074 α1 + 0.01 |
| 3 | 0.05 | 0.02 | 0.012 α1 + 0.016 |
| 4 | 0.05 | 0.02 | 0.013 α1 + 0.0093 |
| 5 | 0.03 | 0.015 | 0.015 α1 + 0.0072 |
| Code | Load Model |
|---|---|
| BS 5400 [36] | |
| BRO 2004 [37] | |
| ISO 10137 [38] | |
| Sétra [8] | |
| EN 03 [39] | |
| GB/T 51228-2017 [40] |
| Direction | P(N) |
|---|---|
| Vertical Direction | 280 |
| Longitudinal Direction | 140 |
| Horizontal Direction | 35 |
| Comfort Level | Degree of Comfort | Vertical (m/s2) | Lateral (m/s2) |
|---|---|---|---|
| CL 1 | Maximum | ≤0.5 | ≤0.15 |
| CL 2 | Medium | 0.5–1.0 | 0.15–0.3 |
| CL 3 | Minimum | 1.0–2.5 | 0.3–0.8 |
| CL 4 | Unacceptable | >2.5 | >0.8 |
| Model | Hypothesis | μj | ξj |
|---|---|---|---|
| MTMD-1 | k1 = k2 = … = kn = kt, c1 = c2 = … = cn = ct, m1 ≠ m2 ≠ … ≠ mn, ξ1 ≠ ξ2 ≠ … ≠ ξn | ||
| MTMD-2 | m1 = m2 = … = mn = mt, ξ1 = ξ2 = … = ξn = ξt, k1 ≠ k2≠ … ≠ kn, c1 ≠ c2 ≠ … ≠ cn | ||
| MTMD-3 | m1 = m2 = … = mn = mt, c1 = c2 = … = cn = ct, k1 ≠ k2 ≠ … ≠ kn, ξ1 ≠ ξ2 ≠ … ≠ ξn | ||
| MTMD-4 | k1 = k2 = … = kn = kt, ξ1 = ξ2 = … = ξn = ξt, m1 ≠ m2 ≠ … ≠ mn, c1 ≠ c2 ≠ … ≠ cn | ||
| MTMD-5 | c1 = c2 = … = cn = ct, ξ1 = ξ2 = … = ξn = ξt, k1 ≠ k2 ≠ … ≠ kn, m1 ≠ m2 ≠ … ≠ mn |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Wu, B.; Tang, Y.; Zhang, H.; Xu, Z.; Li, G.; Lu, S. A Review on Comfort of Pedestrian Bridges Under Human-Induced Vibrations and Tuned Mass Damper Control Technologies. Materials 2025, 18, 3903. https://doi.org/10.3390/ma18163903
Zhang S, Wu B, Tang Y, Zhang H, Xu Z, Li G, Lu S. A Review on Comfort of Pedestrian Bridges Under Human-Induced Vibrations and Tuned Mass Damper Control Technologies. Materials. 2025; 18(16):3903. https://doi.org/10.3390/ma18163903
Chicago/Turabian StyleZhang, Shoukun, Baijin Wu, Yong Tang, Han Zhang, Zheng Xu, Guoqiang Li, and Shuang Lu. 2025. "A Review on Comfort of Pedestrian Bridges Under Human-Induced Vibrations and Tuned Mass Damper Control Technologies" Materials 18, no. 16: 3903. https://doi.org/10.3390/ma18163903
APA StyleZhang, S., Wu, B., Tang, Y., Zhang, H., Xu, Z., Li, G., & Lu, S. (2025). A Review on Comfort of Pedestrian Bridges Under Human-Induced Vibrations and Tuned Mass Damper Control Technologies. Materials, 18(16), 3903. https://doi.org/10.3390/ma18163903







