A Review of Pore Water Pressure Measurement Techniques in Early-Age Cement-Based Materials
Abstract
1. Introduction
2. Thermodynamic Evolution of Pore Water in Early-Age Cement-Based Materials
3. Development of Testing Methods and Instrumentation of Early-Age PWP for Cement-Based Materials
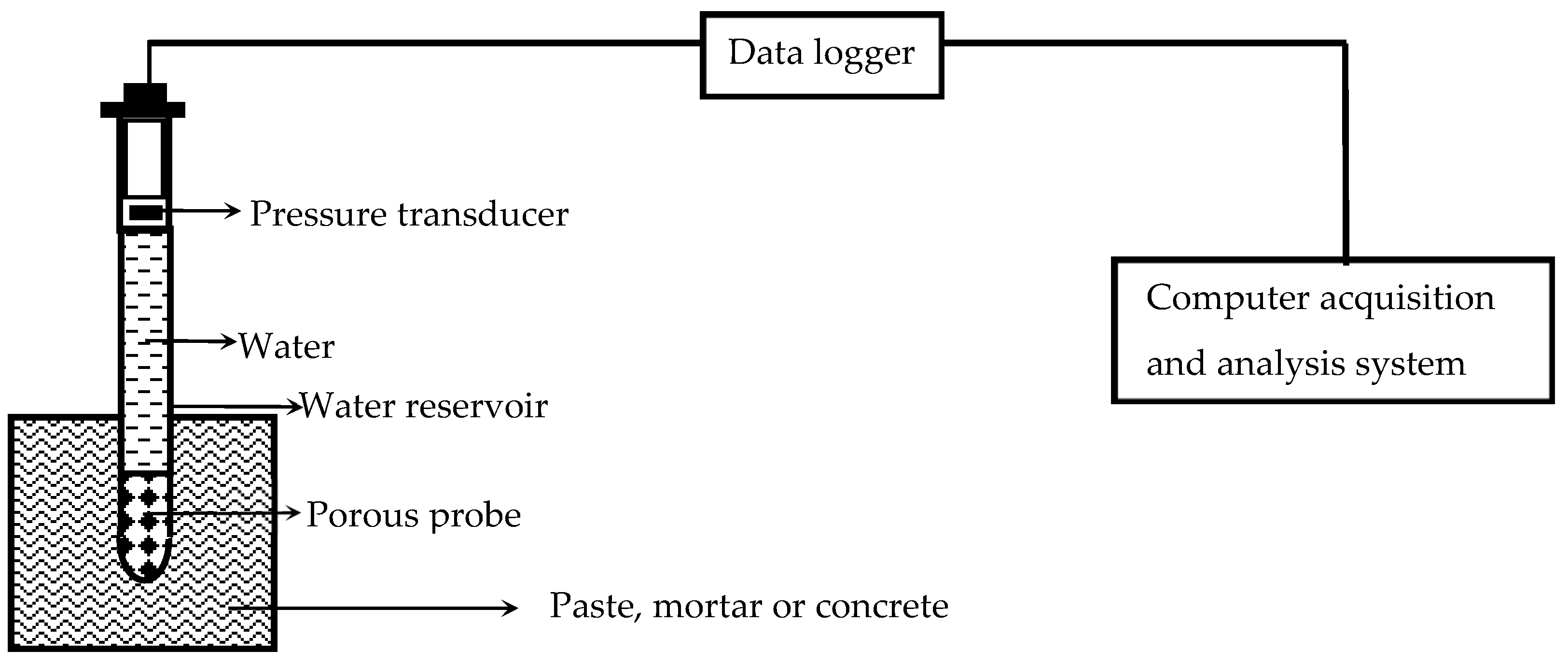
3.1. Fundamental Principles of Measurement
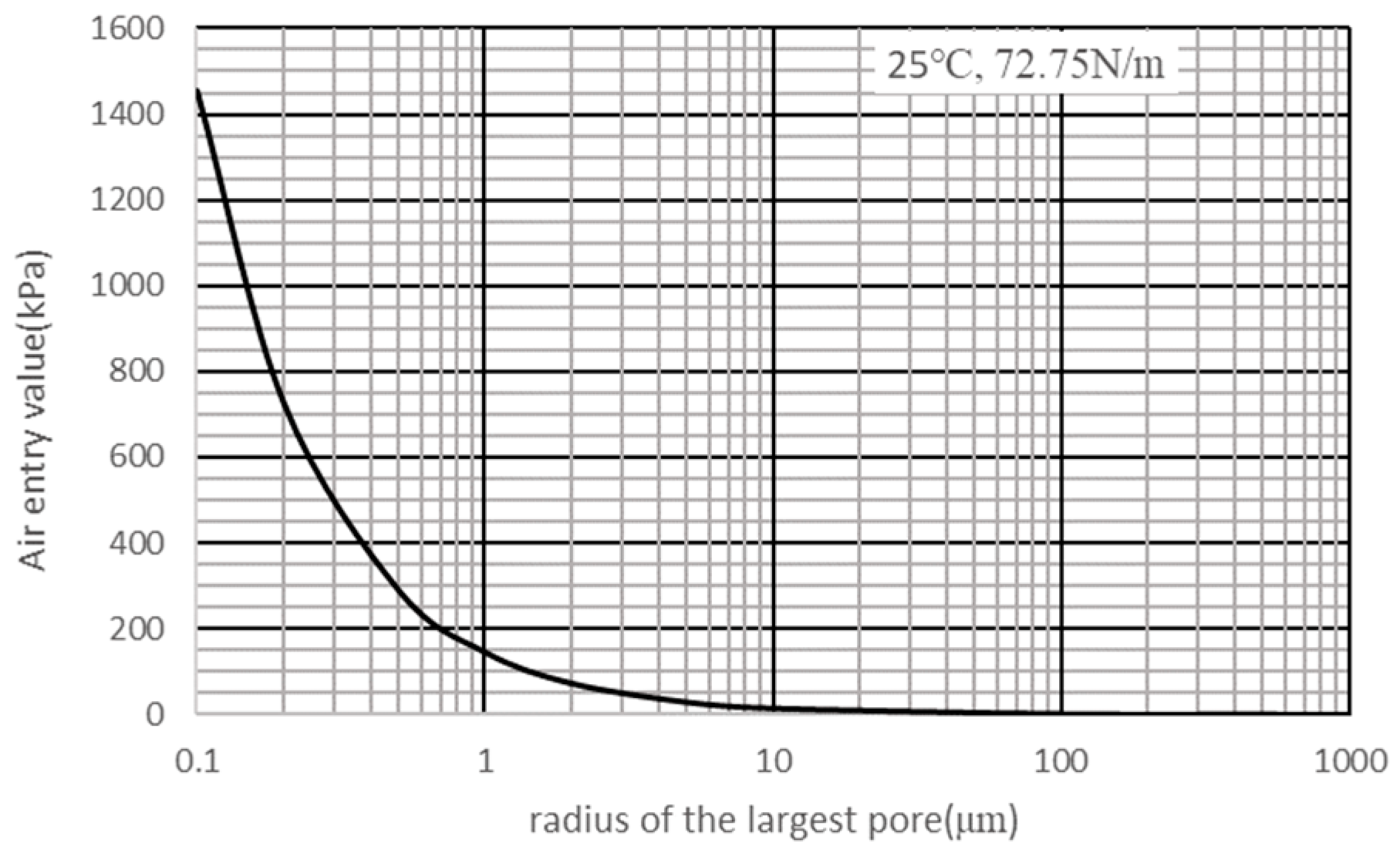
3.2. Probe Design and Measurement Range
- Probe air-ingress: Gas permeation through porous interfaces.
- Cavitation-induced nucleation: Bubble formation in the water reservoir.
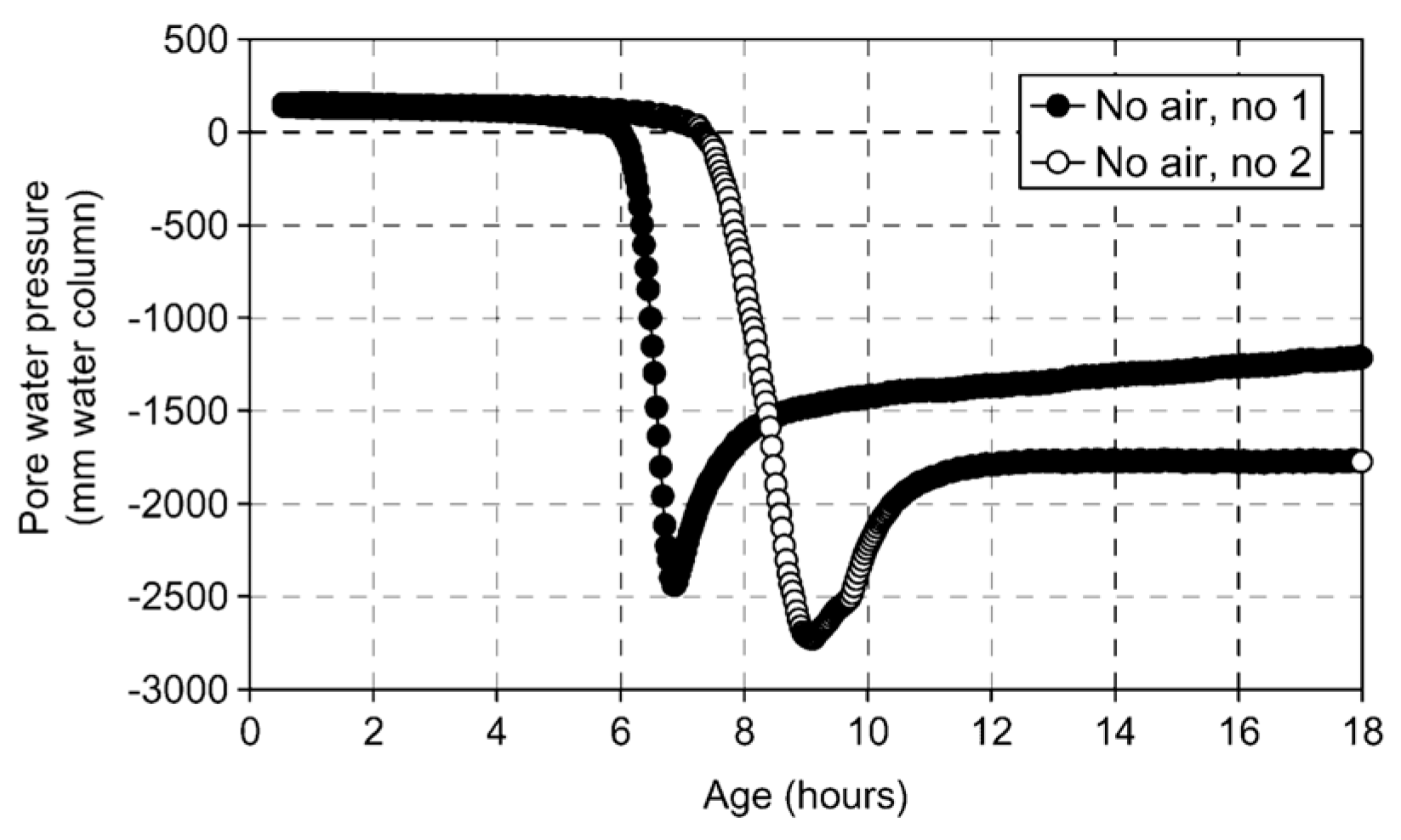
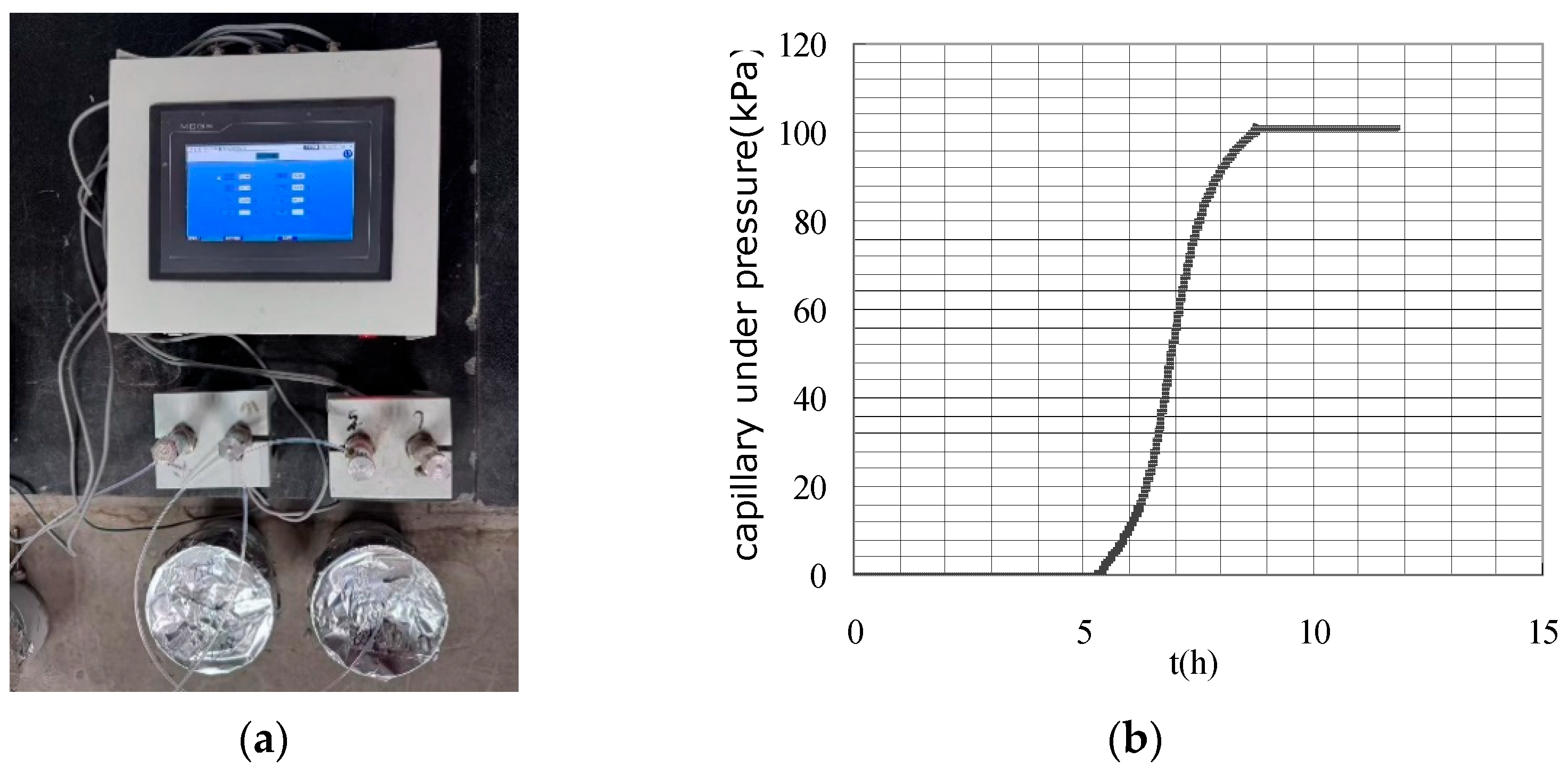
3.3. Tensiometer Implementation
3.3.1. Saturation and Calibration
- (1)
- Atmospheric pressure saturation. For probes utilizing plastic hoses, injection needles, thin metal tubes, or ordinary ceramic tips, the saturation process is relatively straightforward and involves the following steps:
- Prepare deaerated water. Boil tap water for at least 30 min to remove dissolved air, then cool it to room temperature;
- Immerse and evacuate the probe. Soak the dry probe in the deaerated water for a minimum of 3 h while concurrently applying vacuum evacuation to remove residual gases.
- (2)
- High-pressure saturation. Saturation protocols for high-capacity tensiometers (HCTs) utilizing high-AEV ceramic probes are significantly more complex due to the ceramic’s dense pore structure. Saturation is a critical prerequisite for proper HCT operation, as even minute air bubbles within the reservoir can lead to failure at pressures exceeding 100 kPa due to air compressibility. Consequently, a specialized high-pressure vacuum saturation procedure is essential. Figure 9 illustrates the high-vacuum saturation method for HCT-Cs introduced by Jamali [52]:
- Initial Vacuum Treatment: Place completely dry HCT-Cs into a saturation chamber. Connect one end of the chamber to a Pfeiffer DUO 11 two-stage rotary vane vacuum pump (capable of achieving an absolute pressure of 3.10 × 10−4 kPa) and evacuate for 1 h to eliminate residual air.
- Pressurized Water Infusion: Connect the opposite end of the chamber to a 4 MPa GDS Instruments pressure-volume controller. Apply 3000 kPa of pressure using deionized/deaerated water and maintain overnight (typically 12–16 h) to saturate the ceramic.
- Post-Saturation Handling: Remove the HCT from the saturation chamber approximately 2 h before use. Immediately immerse it in deionized water to prevent cavitation, then reset the pressure readings to 0 kPa for calibration.
3.3.2. Orientation and Embedding Depth of Probes
3.3.3. Temperature Influence
3.3.4. Field Adaptability
4. Application of Early-Age PWP Testing Methods in Cement-Based Materials
4.1. Investigating the Mechanism and Mitigation of Plastic Shrinkage Cracking in Cement-Based Materials
4.2. Characterization of Early-Age Self-Desiccation Effects and Structural Formation of Cement-Based Materials
4.3. Application of PWP Measurement in Novel and Special Concrete
5. Conclusions and Outlooks
- While sharing common measurement principles, tensiometer probe designs vary significantly across studies, leading to differences in measurement range and operational characteristics among different tensiometers. Future comparative studies among different laboratories are needed to further evaluate the repeatability and reproducibility of test results and establish a standardized methodology for this approach. Future standardization efforts must also address application-specific requirements while balancing measurement capabilities with operational feasibility.
- Under drying conditions, PWP in fresh cement-based materials demonstrates robust correlations with plastic shrinkage, tensile strength, and elastic modulus. These relationships persist across diverse material compositions and environmental conditions, establishing PWP as a reliable predictor of plastic shrinkage cracking. While reported PWP cracking thresholds vary in the literature, consensus confirms that real-time monitoring of PWP at construction sites and maintaining it within defined thresholds can effectively prevent cracking. This forms the basis for closed-loop automated fog-curing systems utilizing in-situ PWP monitoring, which have proven successful in mitigating such cracking in high-performance cement-based materials during field implementation.
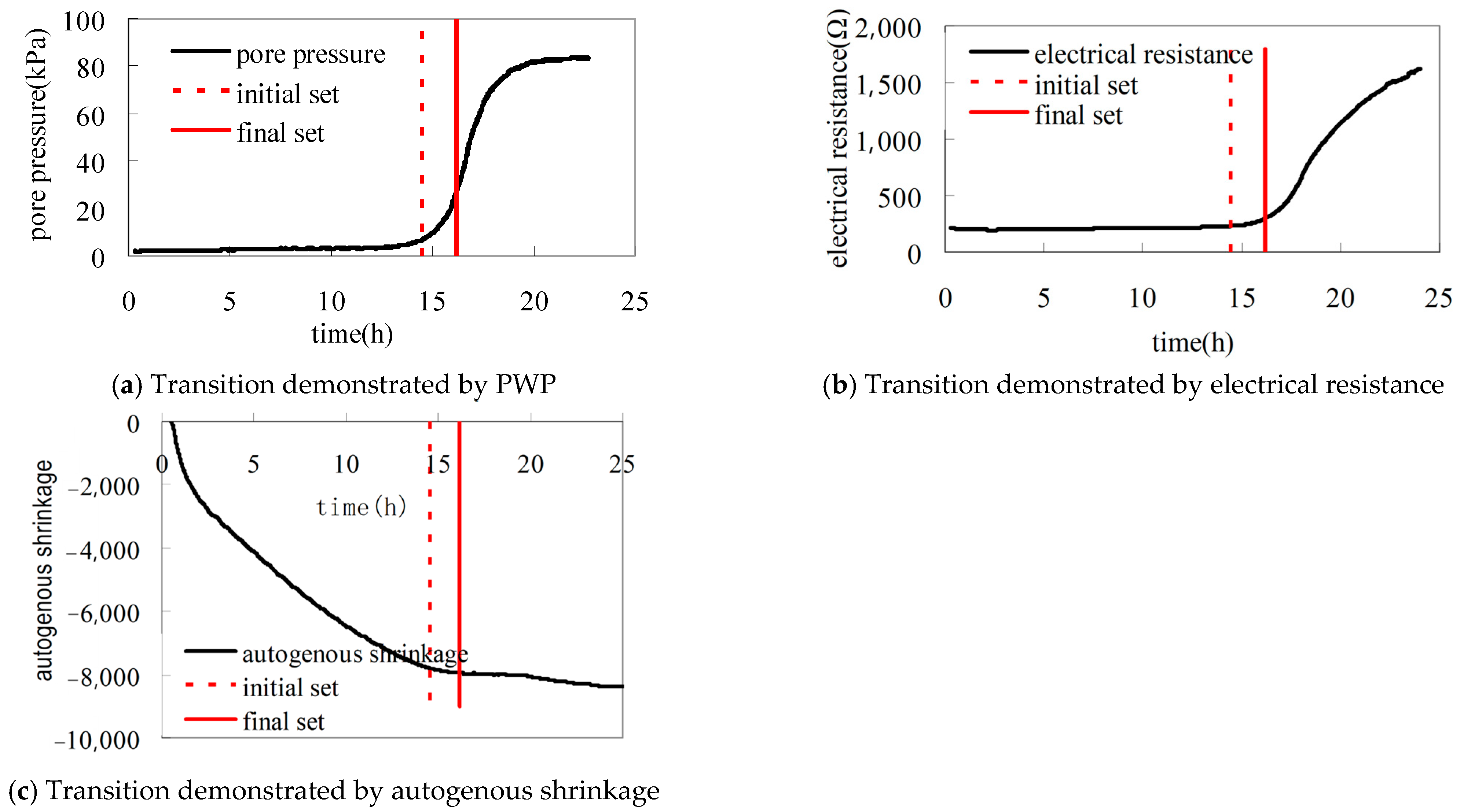
- Under sealed conditions, PWP measurement provides direct and sensitive monitoring of initial self-desiccation in cement-based materials from the moment of water addition. This approach overcomes the limitations of hygrometer methods during high-humidity stages. The measured PWP curves exhibited a distinct transition period demonstrating strong correlations with other kinds of signals like penetration resistance, electrical resistance and autogenous shrinkage etc. These correlations, combined with the capability for remote, real-time, automated, and in situ PWP monitoring, create significant potential for characterizing critical parameters, including setting time, slump retention, bleeding, slip-form friction, etc., in both laboratory and construction sites.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Powers, T.C. The Properties of Fresh Concrete; John Wiley & Sons, Inc.: New York, NY, USA, 1968. [Google Scholar]
- Kayondo, M.; Combrinck, R.; Boshoff, W. State-of-the-art review on plastic cracking of concrete. Constr. Build. Mater. 2019, 225, 886–899. [Google Scholar] [CrossRef]
- Kwak, H.-G.; Ha, S.; Weiss, W.J. Experimental and numerical quantification of plastic settlement in fresh cementitious systems. J. Mater. Civ. Eng. 2010, 22, 951–966. [Google Scholar] [CrossRef]
- Qi, C. Quantitative Assessment of Plastic Shrinkage Cracking and Its Effect on the Corrosion of Steel Reinforcement. PhD Thesis, Purdue University, West Lafayette, IN, USA, 2003. [Google Scholar]
- Uno, P.J. Plastic shrinkage cracking and evaporation formulas. ACI Mater. J. 1998, 95, 365–375. [Google Scholar] [CrossRef]
- ACI 305R-99; ACI Committee 305. Hot Weather Concreting. American Concrete Institute: Farmington Hills, MI, USA, 1999.
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstructure, Properties, and Materials, 4th ed.; McGraw-Hill Education: New York, NY, USA, 2014; pp. 61–105. [Google Scholar]
- Tazawa, E.; Miyazawa, S. Experimental study on mechanism of autogenous shrinkage of concrete. Cem. Concr. Res. 1995, 25, 1633–1638. [Google Scholar] [CrossRef]
- Igarashi, S.; Bentur, A.; Kovler, K. Autogenous shrinkage and induced restraining stresses in high-strength concretes. Cem. Concr. Res. 2000, 30, 1701–1707. [Google Scholar] [CrossRef]
- Lura, P.; Jensen, O.M.; Van Breugel, K. Autogenous shrinkage in high-performance cement paste: An evaluation of basic mechanisms. Cem. Concr. Res. 2004, 34, 139–146. [Google Scholar] [CrossRef]
- Jensen, O.M.; Hansen, P.F. Autogenous deformation and change of the relative humidity in silica fume-modified cement paste. ACI Mater. J. 1996, 93, 539–543. [Google Scholar]
- Wexler, A. Humidity and Moisture: Fundamentals and Standards; CRC Press: Boca Raton, FL, USA, 1990. [Google Scholar]
- Wiederhold, P.R. Water Vapor Measurement: Methods and Instrumentation; Marcel Dekker: New York, NY, USA, 1997. [Google Scholar]
- Sanjuan, M.A.; Toledo, R.D. Effectiveness of crack control at early age on the corrosion of steel bars in low modulus sisal and coconut fibre-reinforced mortars. Cem. Concr. Res. 1998, 28, 555–565. [Google Scholar] [CrossRef]
- Bentur, A. Introduction: Overview of Early age cracking. In Report of RILEM Technical Committee TC 181-EAS: Early Age Shrinkage Induced Stresses and Cracking in Cementitious Systems; RILEM Publications: Bagneux, France, 2007; pp. 1–11. [Google Scholar]
- Persson, B. Self-desiccation and its importance in concrete technology. Mater. Struct. 1997, 30, 293–305. [Google Scholar] [CrossRef]
- Reinhardt, H.W. (Ed.) Advanced Testing of Cementitious Materials During Setting and Hardening; RILEM Report 31; RILEM Publications: Bagneux, France, 2006; ISBN 2912143705. [Google Scholar]
- Bentz, D.P. A review of early-age properties of cement-based materials. Cem. Concr. Res. 2008, 38, 196–204. [Google Scholar] [CrossRef]
- Soleilhet, F.; Benboudjema, F.; Jourdain, X.; Gatuingt, F. Role of pore pressure on cracking and mechanical performance of concrete subjected to drying. Cem. Concr. Compos. 2020, 114, 103727. [Google Scholar] [CrossRef]
- Yao, X.; Cheng, Y. Soil Physics; Agricultural Press: Beijing, China, 1986; pp. 58–59. (In Chinese) [Google Scholar]
- Taylor, H.F.W. Cement Chemistry, 2nd ed.; Thomas Telford: London, UK, 1997; pp. 187–189. [Google Scholar]
- Bentz, D.P.; Garboczi, E.J. Percolation of phases in a three-dimensional cement paste microstructural model. Cem. Concr. Res. 1991, 21, 325–344. [Google Scholar] [CrossRef]
- Hammer, T.A. The use of pore water pressure to follow the evolution from fresh to hardened concrete. In Proceedings of the 2nd International Symposium on Advances in Concrete Through Science and Engineering, Quebec City, QC, Canada, 11–13 September 2006. [Google Scholar]
- Wittmann, F.H. On the action of capillary pressure in fresh concrete. Cem. Concr. Res. 1976, 6, 49–56. [Google Scholar] [CrossRef]
- Radocea, A. A new method for studying bleeding of cement paste. Cem. Concr. Res. 1992, 22, 855–865. [Google Scholar] [CrossRef]
- Radocea, A. A Study of the Mechanism of Plastic Shrinkage of Cementitious Materials. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 1993. [Google Scholar]
- Radocea, A. Model of plastic shrinkage. Mag. Concr. Res. 1994, 46, 125–132. [Google Scholar] [CrossRef]
- Radocea, A. Autogenous volume change of concrete at very early age. Mag. Concr. Res. 1998, 50, 107–113. [Google Scholar] [CrossRef]
- Hammer, T.A. Effect of silica fume on plastic shrinkage and pore water pressure of high-strength concretes. Mater. Struct. 2001, 34, 273–278. [Google Scholar] [CrossRef]
- Hammer, T.A. Influence of entrained air voids on pore water pressure and volume change of concrete before and during setting. Mater. Struct. 2006, 39, 801–808. [Google Scholar] [CrossRef]
- Scott, M.L.; Lane, D.S.; Weyers, R.E. Preliminary Investigation of the Relationship Between Capillary Pore Pressure and Early Shrinkage Cracking of Concrete; Research Report No. VTRC 97-R14; Virginia Transportation Research Council: Charlottesville, VA, USA, 1997. [Google Scholar]
- Esping, O.; Löfgren, I. Cracking Due to Plastic and Autogenous Shrinkage—Investigation of Early Age Deformation of Self-Compacting Concrete; Report 2005:11; Chalmers University of Technology: Gothenburg, Sweden, 2005. [Google Scholar]
- Schmidt, M.; Slowik, V. Capillary pressure controlled concrete curing in pavement construction. In Airfield and Highway Pavements 2013: Sustainable and Efficient Pavements; ASCE: Reston, VA, USA, 2013; pp. 295–306. [Google Scholar]
- Slowik, V.; Schmidt, M.; Fritzsch, R. Capillary pressure in fresh cementitious materials and identification of the air entry value. Cem. Concr. Compos. 2008, 30, 557–565. [Google Scholar] [CrossRef]
- Slowik, V.; Hübner, T.; Schmidt, M.; Villmann, B. Simulation of capillary shrinkage cracking in cement-like materials. Cem. Concr. Compos. 2009, 31, 461–469. [Google Scholar] [CrossRef]
- Holt, E.; Leivo, M. Cracking risks associated with early age shrinkage. Cem. Concr. Compos. 2004, 26, 521–530. [Google Scholar] [CrossRef]
- Holt, E. Early Age Autogenous Shrinkage of Concrete; VTT Publications 446; Technical Research Centre of Finland: Espoo, Finland, 2001; pp. 77–79. [Google Scholar]
- Tian, Q. Study on Shrinkage and Mechanism of Cementitious Materials with Low Water-Binder Ratio and High Industrial Waste Content. Ph.D. Thesis, Southeast University, Nanjing, China, 2006; pp. 101–107. (In Chinese). [Google Scholar]
- Liu, J.P.; Tian, Q.; Sun, W.; Miao, C.W.; Tang, M.S. Study on the self-desiccation effect in early-age concrete and the determination of “Time-Zero” of self-desiccation shrinkage. In Proceedings of the Volume Changes of Hardening Concrete: Testing and Mitigation, Lyngby, Denmark, 20–23 August 2006; pp. 401–410. [Google Scholar]
- Miao, C.W.; Tian, Q.; Sun, W.; Liu, J.P. Water consumption of the early-age paste and the determination of “time-zero” of self-desiccation shrinkage. Cem. Concr. Res. 2007, 37, 1496–1501. [Google Scholar]
- Miao, C.W.; Tian, Q.; Liu, J.P.; Sun, W. Testing early-age self-desiccation effect in concrete based on pore water pressure technique. J. Chin. Ceram. Soc. 2007, 35, 509–516. (In Chinese) [Google Scholar]
- Tian, Q.; Liu, J.P.; Miao, C.W.; Sun, W. Measurement of the pore water pressure of early-age cementitious materials: Significance, techniques and engineering outlooks. In Proceedings of the 1st International Conference on Microstructure Related Durability of Cementitious Composites, Nanjing, China, 13–15 October 2008; Volume 2, pp. 1439–1448. [Google Scholar]
- Tian, Q.; Wang, Y.; Guo, F.; Liu, J.P.; Miao, C.W. A smart initial curing procedure based on pore water under pressure measurement. In Proceedings of the International RILEM Conference on Use of Superabsorbent Polymers and Other New Additives in Concrete, Lyngby, Denmark, 15–18 August 2010. [Google Scholar]
- Liu, J.P.; Tian, Q.; Miao, C.W. Investigation on the plastic shrinkage of cementitious materials under drying conditions: Mechanism and theoretical model. Mag. Concr. Res. 2012, 64, 551–561. [Google Scholar] [CrossRef]
- Tian, Q.; Wang, Y.J.; Zhang, H.; Liu, J.P.; Miao, C.W. In-situ monitoring of setting of concrete based on pore water pressure measurement. In Proceedings of the 2nd International Conference on Microstructure Related Durability of Cementitious Composites, Amsterdam, The Netherlands, 11–13 April 2012. [Google Scholar]
- Wang, Y.J.; Tian, Q.; Li, H.; Sun, S.; Deng, W. The relationship between capillary pressure and tensile strength of fresh cementitious materials under water evaporation. J. Build. Eng. 2023, 78, 107678. [Google Scholar] [CrossRef]
- Liu, J.P.; Tian, Q. Early-Age Deformation and Shrinkage Crack Control in Modern Concrete; Science Press: Beijing, China, 2020; pp. 40–52. (In Chinese) [Google Scholar]
- Tian, Q.; Liu, J.P.; Zhang, H.; Wang, Y.; Guo, F.; Zhang, J. Method for Testing Setting Time of Cementitious Materials. U.S. Patent US9389216B2, 12 June 2016. [Google Scholar]
- Ghourchian, S.; Wyrzykowski, M.; Plamondon, M.; Lura, P. On the mechanism of plastic shrinkage cracking in fresh cementitious materials. Cem. Concr. Res. 2019, 115, 251–263. [Google Scholar] [CrossRef]
- Ghourchian, S.; Wyrzykowski, M.; Lura, P. A poromechanics model for plastic shrinkage of fresh cementitious materials. Cem. Concr. Res. 2018, 109, 120–132. [Google Scholar] [CrossRef]
- Jamali, A.; Mendes, J.; Nagaratnam, B.; Lim, M. A new four-stage model of capillary pressure in early age concrete: Insights from high capacity tensiometers. Cem. Concr. Res. 2022, 161, 106955. [Google Scholar] [CrossRef]
- Jamali, A.; Mendes, J.; Nagaratnam, B.; Lim, M. Monitoring of capillary pressure evolution in young age concrete using high capacity tensiometers. In SynerCrete’23, Proceedings of the International RILEM Conference on Synergising Expertise Towards Sustainability and Robustness of Cementitious Materials and Concrete Structures, Milos Island, Greece, 14–16 June 2023; RILEM Bookseries 44; Springer: Cham, Switzerland, 2023; pp. 289–300. [Google Scholar]
- Jamali, A.; Marani, A.; Railton, J.; Nehdi, M.L.; Nagaratnam, B.; Lim, M.; Mendes, J. Novel multi-scale experimental approach and deep learning model to optimize capillary pressure evolution in early age concrete. Cem. Concr. Res. 2024, 180, 107490. [Google Scholar] [CrossRef]
- Deysel, R.C. Controlling Capillary Pressure in Concrete to Prevent Plastic Shrinkage Cracking. Master’s Thesis, University of Pretoria, Pretoria, South Africa, 2022. [Google Scholar]
- Deysel, R.C. Implementing capillary pressure control measures to prevent plastic shrinkage cracking in concrete. Constr. Build. Mater. 2023, 397, 132407. [Google Scholar] [CrossRef]
- Burrows, R.W. The Visible and Invisible Cracking of Concrete; American Concrete Institute: Farmington Hills, MI, USA, 1998. [Google Scholar]
- Sayahi, F.; Emborg, M.; Hedlund, H.; Cwirzen, A.; Stelmarczyk, M. The severity of plastic shrinkage cracking in concrete: A new model. Mag. Concr. Res. 2021, 73, 315–324. [Google Scholar] [CrossRef]
- Ridley, A.M.; Burland, J.B. A new instrument for the measurement of soil moisture suction. Géotechnique 1993, 43, 321–324. [Google Scholar] [CrossRef]
- Walther, J.H.; Werder, T.; Jaffe, R.L.; Koumoutsakos, P. Cavitation in confined geometries: The role of surface interactions and nanoscale curvature. Phys. Rev. Lett. 2004, 92, 248301. [Google Scholar]
- Mendes, J.; Buzzi, O. New insight into cavitation mechanisms in high-capacity tensiometers based on high-speed photography. Can. Geotech. J. 2013, 50, 550–556. [Google Scholar] [CrossRef]
- Toll, D.G.; Lourenço, S.D.N.; Mendes, J. Advances in suction measurements using high suction tensiometers. Eng. Geol. 2013, 165, 29–37. [Google Scholar] [CrossRef]
- Mendes, J.; Buzzi, O. Performance of the University of Newcastle high capacity tensiometers. In Unsaturated Soils: Research & Applications; CRC Press: Boca Raton, FL, USA, 2020; pp. 1611–1616. [Google Scholar]
- Tarantino, A.; Mongiovì, L. Experimental procedures and cavitation mechanisms in tensiometer measurements. In Unsaturated Soil Concepts and Their Application in Geotechnical Practice; Toll, D.G., Ed.; Springer: Dordrecht, The Netherlands, 2001; pp. 189–210. [Google Scholar] [CrossRef]
- ACI 305.1-06; ACI Committee 305. Specification for Hot Weather Concreting. American Concrete Institute: Farmington Hills, MI, USA, 2007.
- Jensen, O.M. Monitoring water loss from fresh concrete. In Proceedings of the International RILEM-JCI Seminar on Concrete Durability and Service Life Planning, Ein-Bokek, Israel; 2006; pp. 197–202. [Google Scholar]
- Wang, Y.J. Study on Shrinkage Cracking Behavior and Mechanism of Ultra-High Performance Concrete. Ph.D. Thesis, Southeast University, Nanjing, China, 2023; pp. 49–53. (In Chinese). [Google Scholar]
- Lura, P. Autogenous Deformation and Internal Curing of Concrete. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2003. [Google Scholar]
- Liu, J.P.; Wang, W.; Tian, Q.; Zeng, L.; Qiao, M.; Zhao, S.; Zhu, B.; Chen, J.; Wang, Y.; Ran, Q. Test Method for Setting Time of Cement-Based Materials with Accelerating Admixture. Chinese Patent CN116429818A, 14 July 2023. (In Chinese). [Google Scholar]
- Ghourchian, S.; Butler, M.; Krüger, M.; Mechtcherine, V. Modelling the development of capillary pressure in freshly 3D-printed concrete elements. Cem. Concr. Res. 2021, 145, 106457. [Google Scholar] [CrossRef]

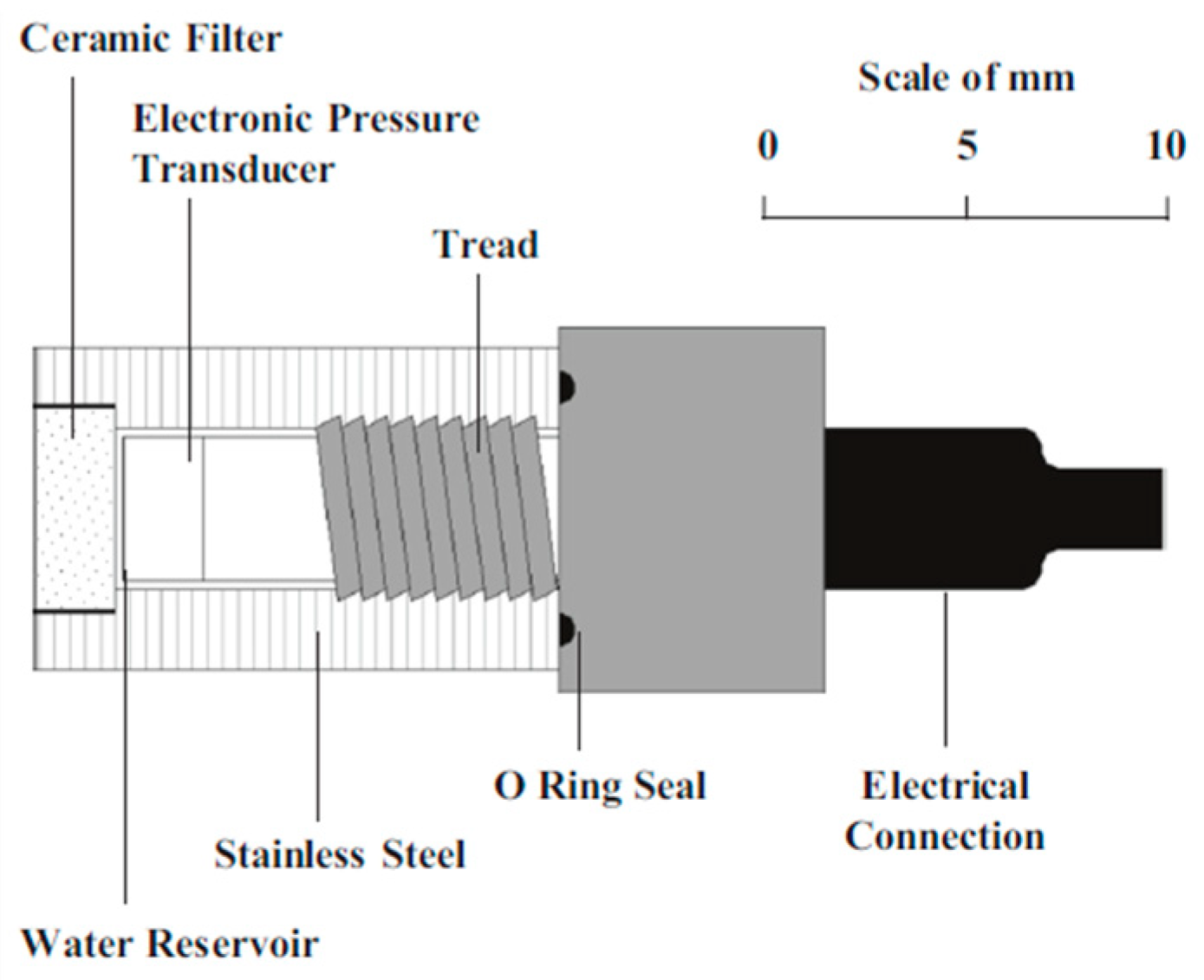






| Research Team | Research Subject | Sensor Type | Probe Orientation | Embedment Depth | Saturation Method | Peak PWP |
|---|---|---|---|---|---|---|
| Wittmann, 1976 [24] | Plastic shrinkage | Plastic tube with a paper stopper | horizontal | 7.5 cm | De-aired water saturation | 10~20 kPa |
| Radocea, 1991~1998 [25,26,27,28] | Plastic shrinkage, autogenous shrinkage and bleeding | 3 mm inner-diameter tube | vertical | 10~60 mm | De-aired water saturation | 60~80 kPa |
| Scott et al., 1997 [31] | Early-age shrinkage cracking | 5 mL syringe | vertical | 1.5 cm | De-aired water saturation | ~30 kPa |
| Hammer, 2001~2006 [23,29,30] | Early-age shrinkage cracking | 3 mm inner-diameter steel tube | vertical | 5 mm, 50 mm | De-aired water saturation | ~20 kPa |
| Liu et al., 2006~2024 [38,39,40,41,42,43,44,45,46,47,48] | Early-age shrinkage cracking | calcined porous ceramic probe | horizontal & vertical | 5~50 mm | De-aired water saturation | 80~90 kPa |
| Holt et al., 2001, 2004 [36,37] | Early-age shrinkage cracking | Type KP-2A | vertical | 3 cm, 6 cm | De-aired water saturation | 40~60 kPa |
| Slowik et al., 2008~2013 [33,34,35] | Plastic shrinkage cracking | 3 mm inner-diameter brass tube | horizontal | 4 cm | De-aired water saturation | 60~80 kPa (15 kPa for concrete) |
| Ghourchian et al., 2019 [49,50] | Plastic shrinkage | 200 kPa AEV porous ceramic probe | horizontal | 1 cm, 8.5 cm | De-aired water saturation | ~80 kPa |
| Jamali et al., 2022~2024 [52,53] | Early-age shrinkage | 1500~2000 kPa AEV HCT-C | vertical | 25~75 mm | High-pressure saturation with deionized water | 1800~2500 kPa |
| Deysel 2022~2023 [54,55] | Plastic shrinkage cracking | 300 kPa~1500 kPa AEV HCT | vertical | 32 mm | High-pressure saturation with deionized water | ~300 kPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Q.; Wang, Y.; Li, H.; Wang, Y.; Jiang, C. A Review of Pore Water Pressure Measurement Techniques in Early-Age Cement-Based Materials. Materials 2025, 18, 3875. https://doi.org/10.3390/ma18163875
Tian Q, Wang Y, Li H, Wang Y, Jiang C. A Review of Pore Water Pressure Measurement Techniques in Early-Age Cement-Based Materials. Materials. 2025; 18(16):3875. https://doi.org/10.3390/ma18163875
Chicago/Turabian StyleTian, Qian, Yang Wang, Hua Li, Yujiang Wang, and Chen Jiang. 2025. "A Review of Pore Water Pressure Measurement Techniques in Early-Age Cement-Based Materials" Materials 18, no. 16: 3875. https://doi.org/10.3390/ma18163875
APA StyleTian, Q., Wang, Y., Li, H., Wang, Y., & Jiang, C. (2025). A Review of Pore Water Pressure Measurement Techniques in Early-Age Cement-Based Materials. Materials, 18(16), 3875. https://doi.org/10.3390/ma18163875








