A Data-Driven Approach for Internal Crack Prediction in Continuous Casting of HSLA Steels Using CTGAN and CatBoost
Abstract
1. Introduction
2. Data Description and Preprocessing
2.1. Data Source and Cleaning
2.2. Feature Selection
3. Methodology
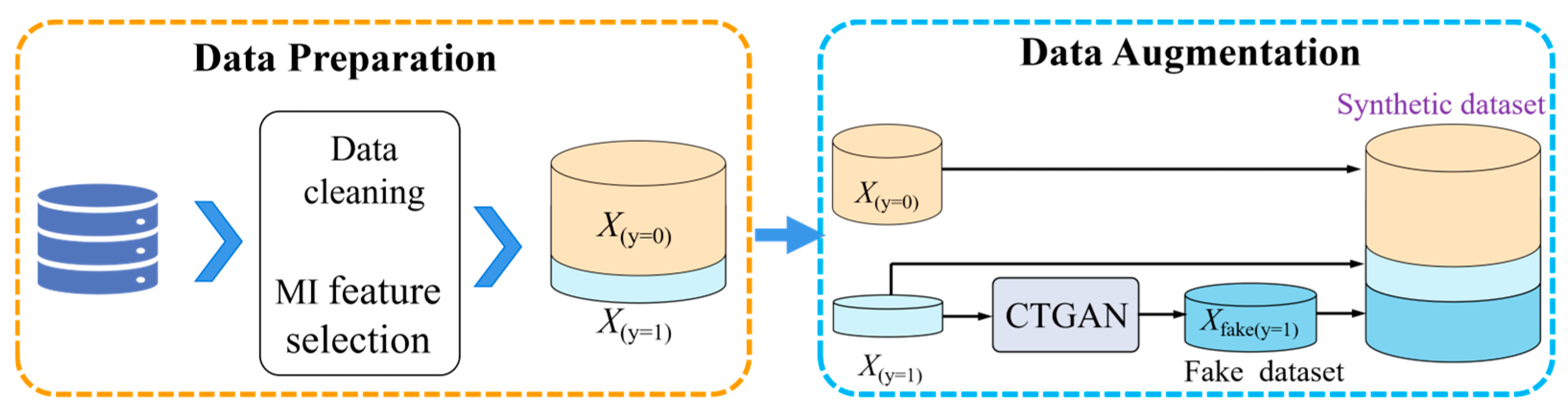
3.1. The Proposed Data Augmentation Strategy
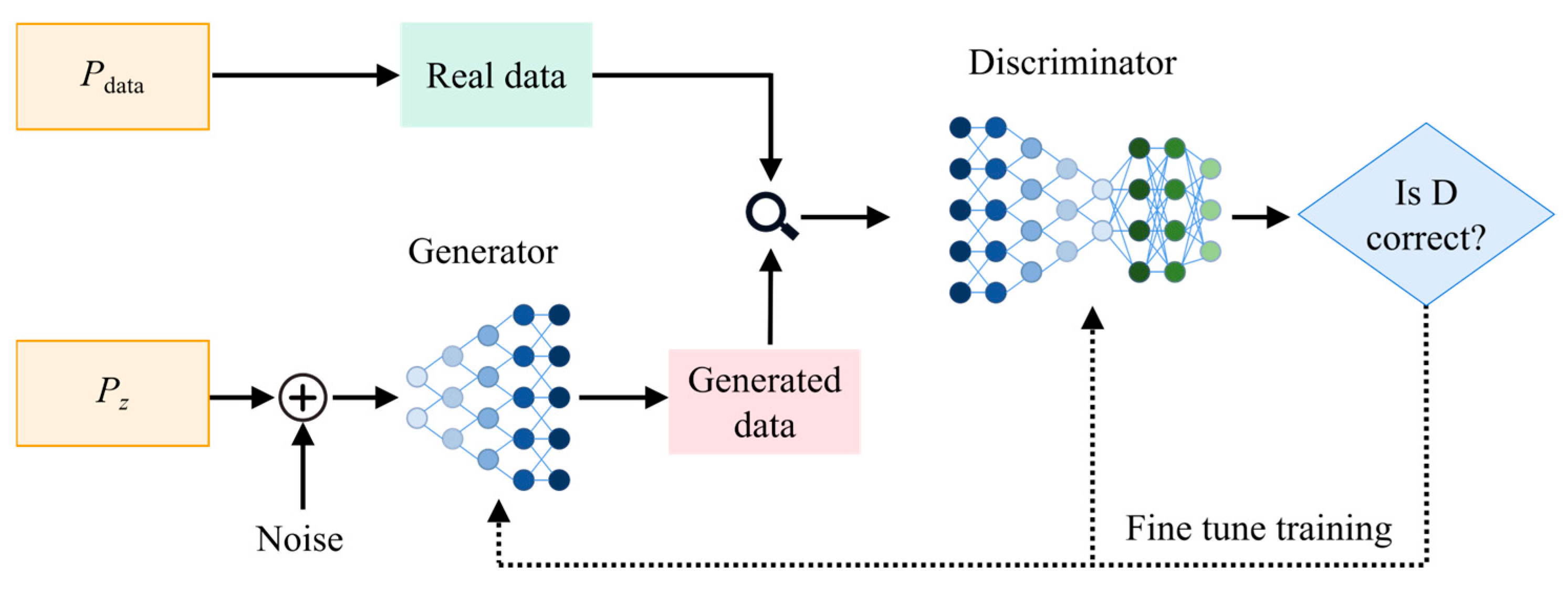
3.2. Conditional Tabular Generative Adversarial Network
3.3. Machine Learning Algorithms
4. Results and Discussions
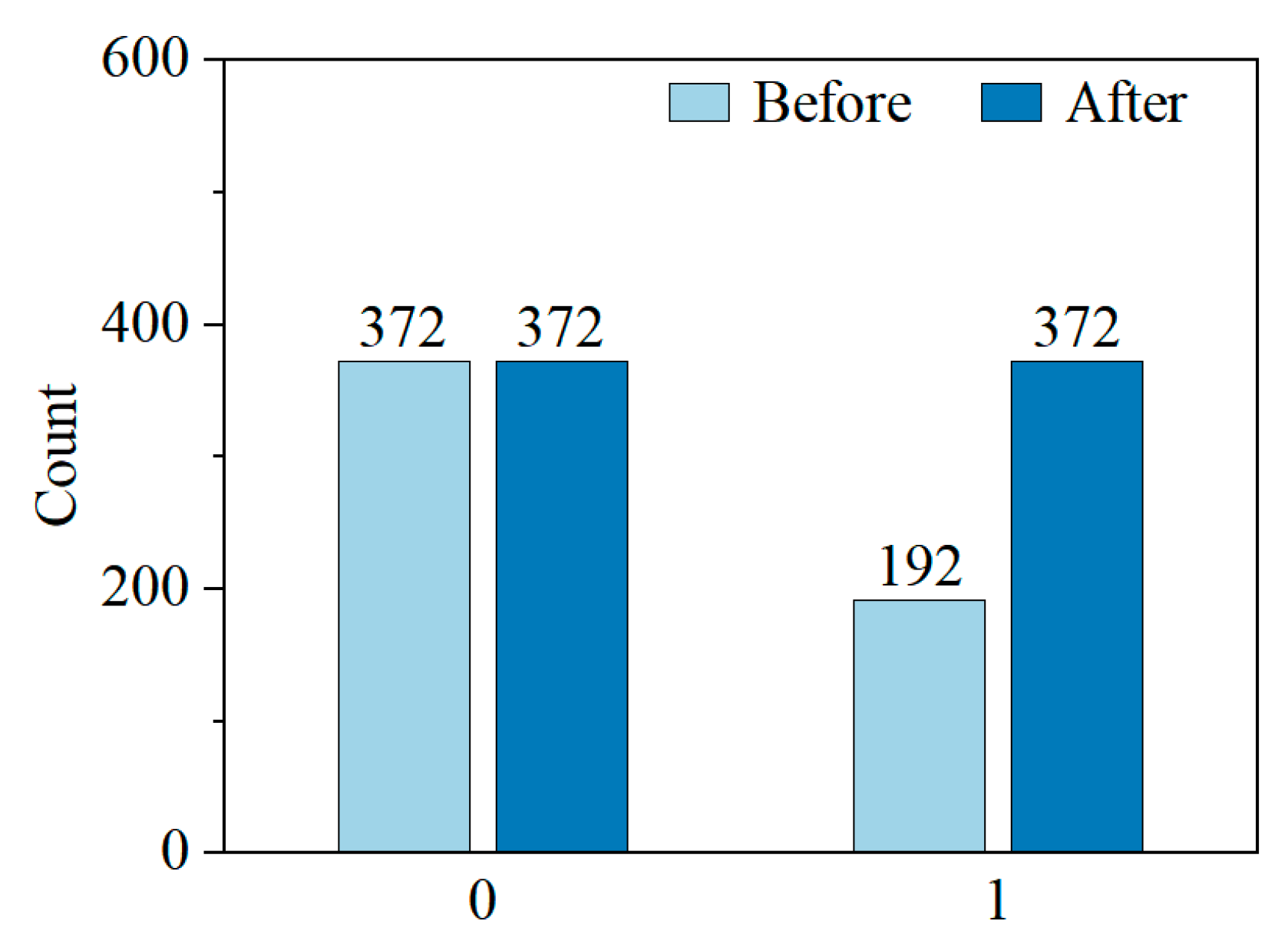
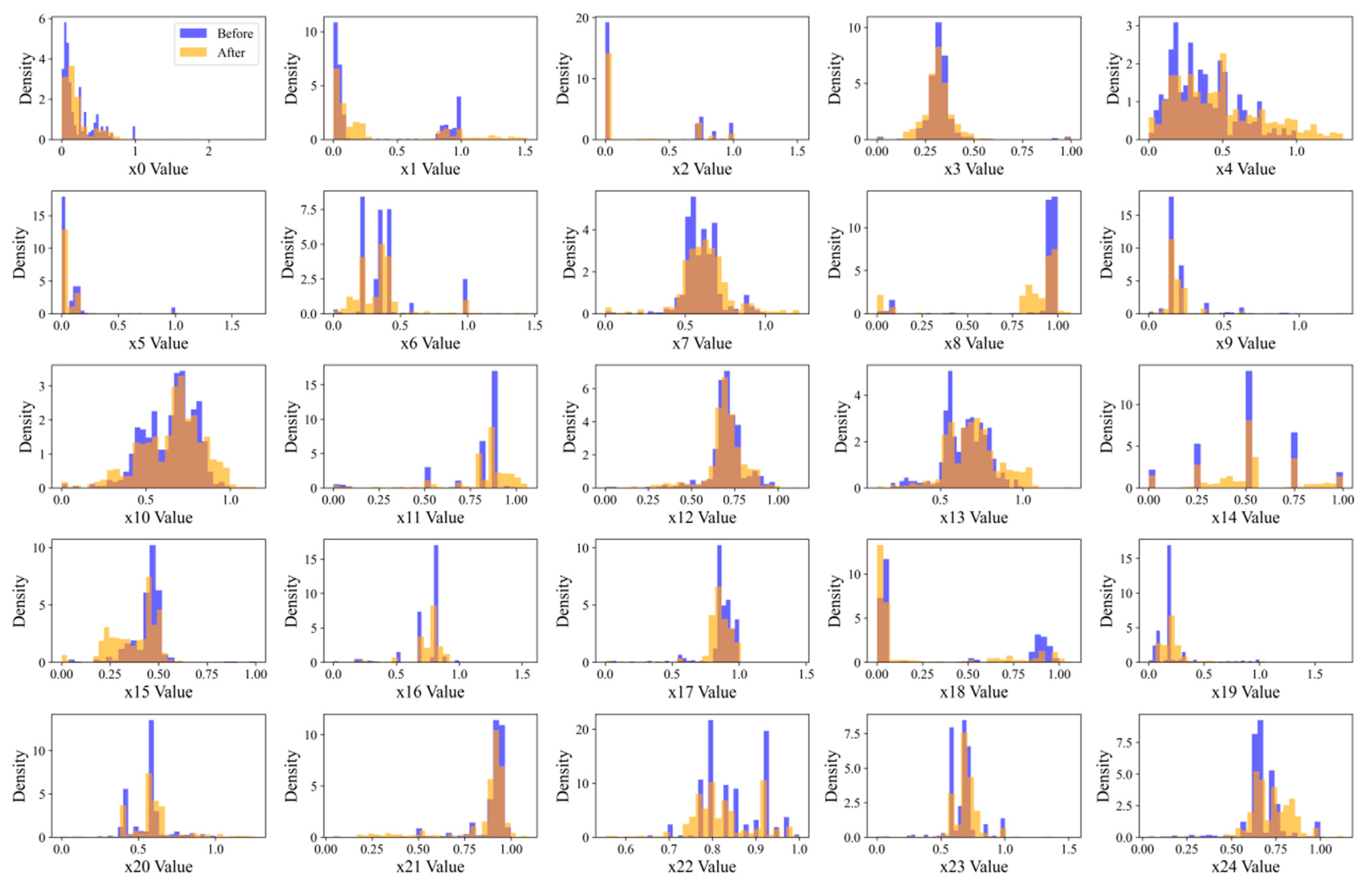
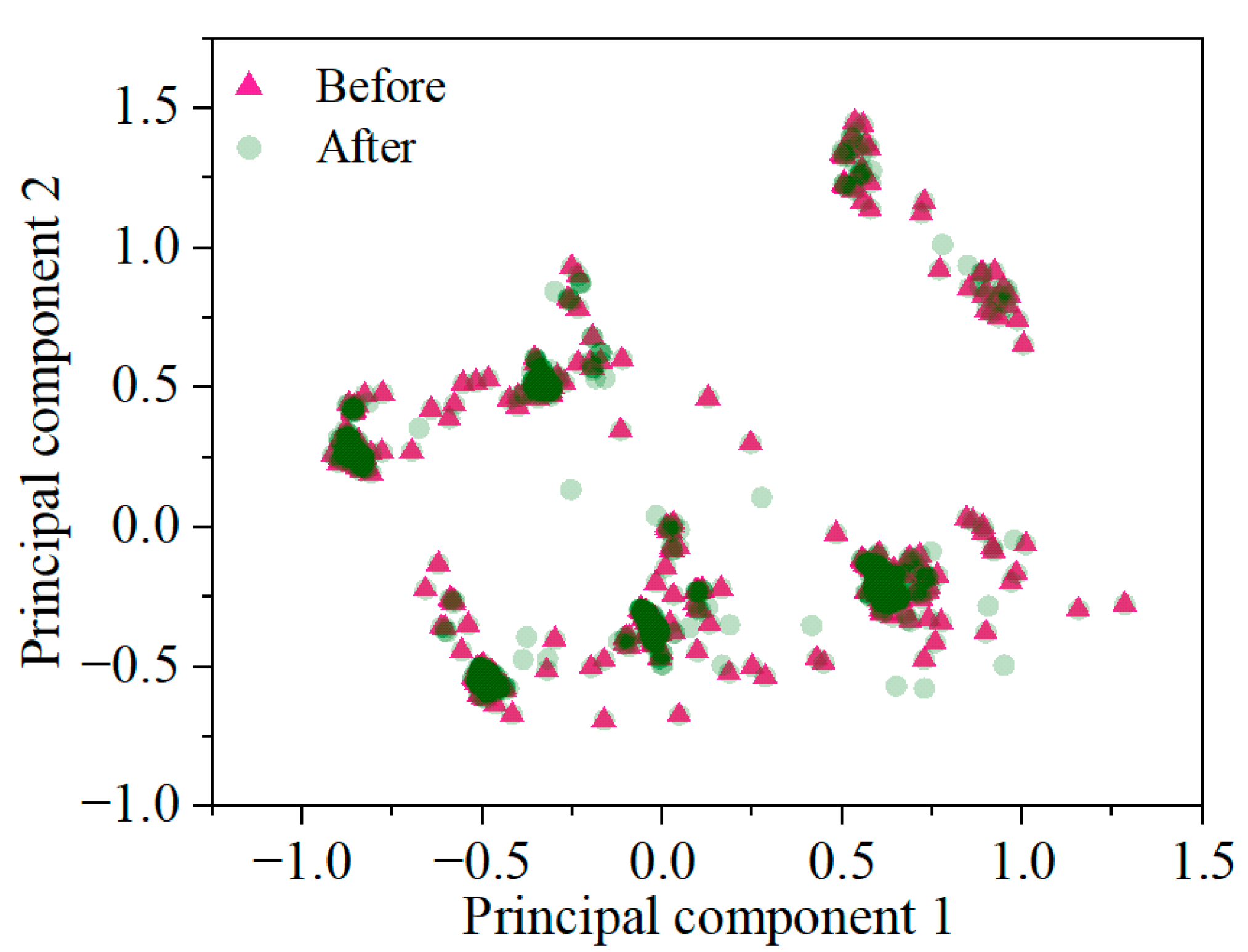
4.1. The Evaluation of the Synthetic Dataset
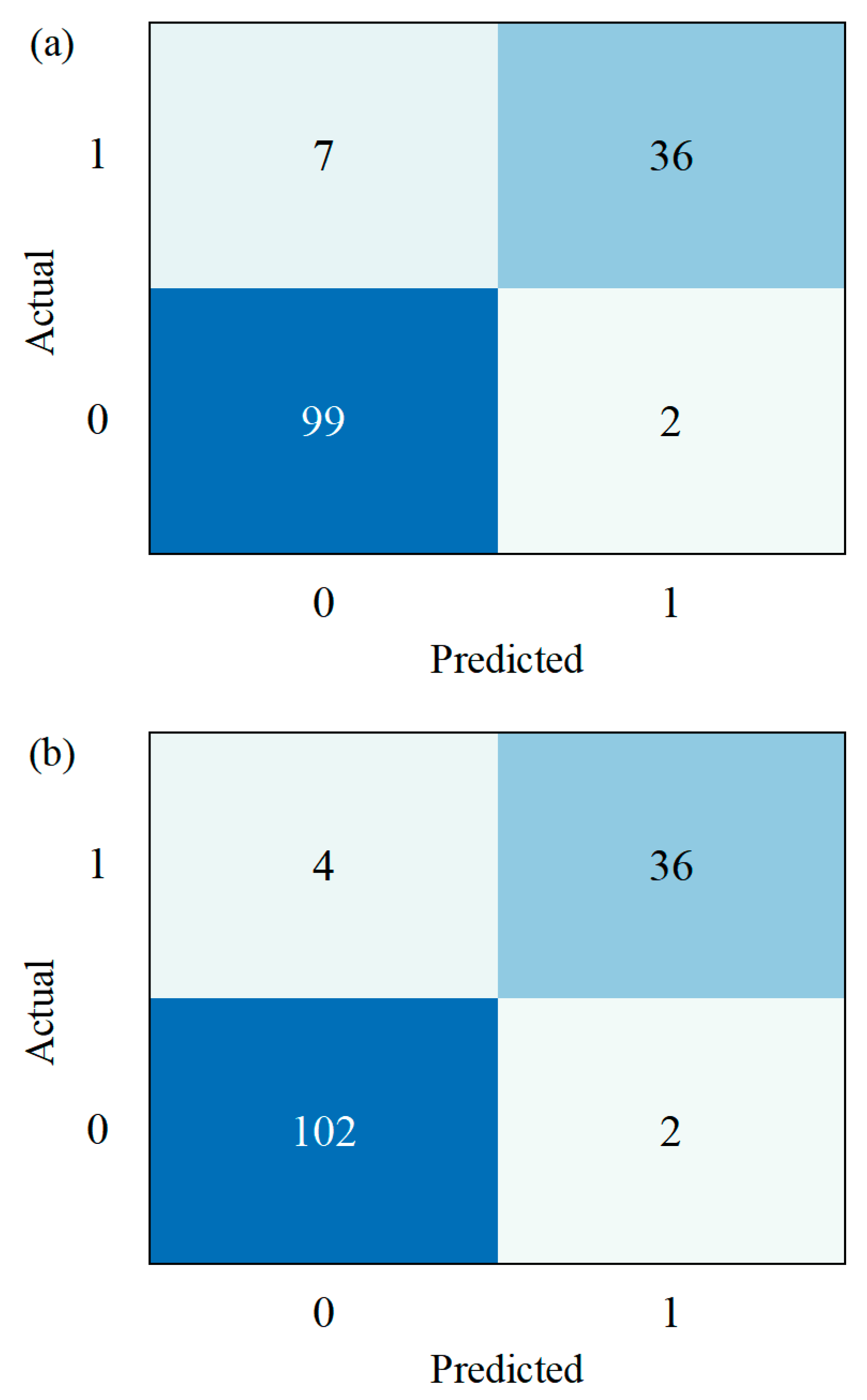
4.2. Model Prediction Results
4.3. Comparison with Other Models
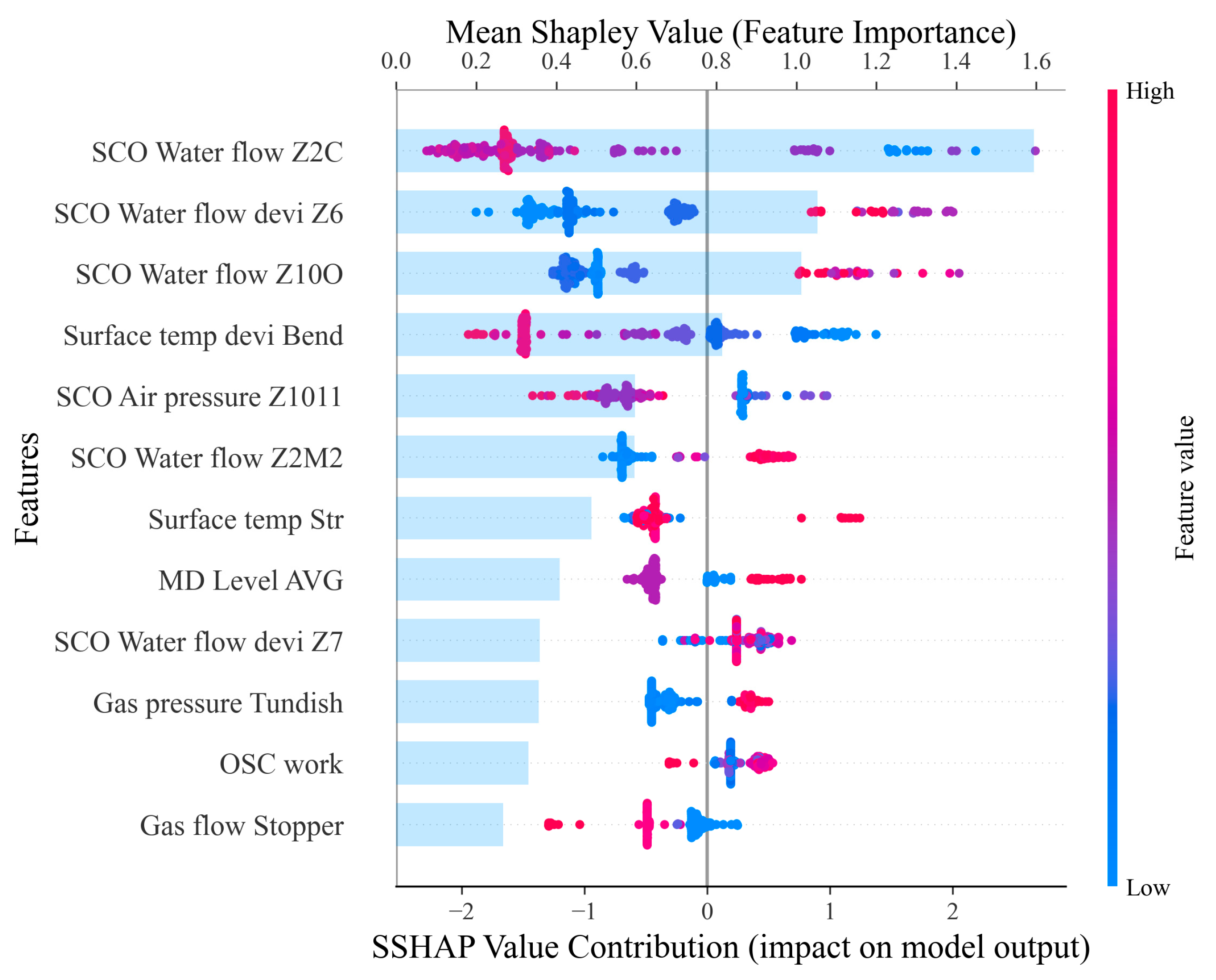
4.4. Machine Learning Explanation with SHAP
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dolzhenko, A.; Pydrin, A.; Gaidar, S.; Kaibyshev, R.; Belyakov, A. Microstructure and Strengthening Mechanisms in an HSLA Steel Subjected to Tempforming. Metals 2021, 12, 48. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, Y.; Zhang, L.; Cong, J. A Transformer and Random Forest Hybrid Model for the Prediction of Non-metallic Inclusions in Continuous Casting Slabs. Integr. Mater. Manuf. Innov. 2023, 12, 466–480. [Google Scholar] [CrossRef]
- Nellikode, S.; Murugan, S.P.; Chung, J.-H.; Lee, C.-H.; Park, H.; Kim, S.-D.; Ku, N.; Park, Y.-D. Role of M-A constituents in bainitic microstructure on crack propagation behavior in the ICCGHAZ of HSLA steels for offshore applications. J. Mater. Res. Technol. 2024, 32, 250–260. [Google Scholar] [CrossRef]
- Shen, W.; Cheng, G.; Zhang, C.; Pan, S.; Dai, L.; Liu, X. Cause Analysis of Low Tensile Plasticity in Normal Direction for Hot-Rolled Thick Plate of HSLA Steel. Steel Res. Int. 2023, 94, 2300164. [Google Scholar] [CrossRef]
- Vervynckt, S.; Verbeken, K.; Lopez, B.; Jonas, J.J. Modern HSLA steels and role of non-recrystallisation temperature. Int. Mater. Rev. 2012, 57, 187–207. [Google Scholar] [CrossRef]
- Wang, L.; Wang, S. Study on Austenite Transformation and Growth Evolution of HSLA Steel. Materials 2023, 16, 3578. [Google Scholar] [CrossRef]
- Martins, C.A.; De Faria, G.L.; Mayo, U.; Isasti, N.; Uranga, P.; Rodríguez-Ibabe, J.M.; De Souza, A.L.; Cohn, J.A.C.; Rebellato, M.A.; Gorni, A.A. Production of a Non-Stoichiometric Nb-Ti HSLA Steel by Thermomechanical Processing on a Steckel Mill. Metals 2023, 13, 405. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, J.; Wang, W.; Wang, Y.; Wang, J.; Wang, G.; Li, X. A review of research on central crack in continuous casting strand. J. Iron Steel Res. Int. 2023, 30, 1073–1089. [Google Scholar] [CrossRef]
- Kong, Y.; Chen, D.; Liu, Q.; Long, M. A prediction model for internal cracks during slab continuous casting. Metals 2019, 9, 587. [Google Scholar] [CrossRef]
- Wu, G.; Chen, T.; Chen, H.; Ji, C.; Zhu, M. The Crack Control Strategy Is Influenced by the Continuous Casting Process of Cr12MoV Steel. Steel Res. Int. 2024, 95, 2400101. [Google Scholar] [CrossRef]
- Toishi, K.; Miki, Y.; Kikuchi, N. Simulation of Crack Initiation on the Slab in Continuous Casting Machine by FEM. ISIJ Int. 2019, 59, 865–871. [Google Scholar] [CrossRef]
- Geng, M.; Ma, H.; Wang, J.; Liu, S.; Li, J.; Ai, Y.; Zhang, W. A deep learning framework for predicting slab transverse crack using multivariate LSTM-FCN in continuous casting. Expert Syst. Appl. 2025, 260, 125413. [Google Scholar] [CrossRef]
- Parlak, İ.E.; Emel, E. Deep learning-based detection of internal defect types and their grades in high-pressure aluminum castings. Measurement 2025, 242, 116119. [Google Scholar] [CrossRef]
- Ruiz, E.; Ferreño, D.; Cuartas, M.; Lloret, L.; Ruiz Del Árbol, P.M.; López, A.; Esteve, F.; Gutiérrez-Solana, F. Machine Learning Methods for the Prediction of the Inclusion Content of Clean Steel Fabricated by Electric Arc Furnace and Rolling. Metals 2021, 11, 914. [Google Scholar] [CrossRef]
- Khan, A.A.; Chaudhari, O.; Chandra, R. A review of ensemble learning and data augmentation models for class imbalanced problems: Combination, implementation and evaluation. Expert Syst. Appl. 2024, 244, 122778. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, Z.; Sun, J.; Liu, L. Machine-Learning Algorithms for Process Condition Data-Based Inclusion Prediction in Continuous-Casting Process: A Case Study. Sensors 2023, 23, 6719. [Google Scholar] [CrossRef] [PubMed]
- Shubham; Banerjee, D. Application of CNN and KNN Algorithms for Casting Defect Classification. In Proceedings of the 2024 First International Conference on Innovations in Communications, Electrical and Computer Engineering (ICICEC), Davangere, India, 24–25 October 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, Y.; Jiang, Z.; Chen, X. Interpretable Prediction Model Based on GANs–DBN Data Enhancement Strategy for Electroslag Remelting Inclusions. Metall. Mater. Trans. B 2025, 56, 2892–2906. [Google Scholar] [CrossRef]
- Zou, L.; Zhang, J.; Han, Y.; Zeng, F.; Li, Q.; Liu, Q. Internal crack prediction of continuous casting billet based on principal component analysis and deep neural network. Metals 2021, 11, 1976. [Google Scholar] [CrossRef]
- Dasari, S.K.; Cheddad, A.; Palmquist, J.; Lundberg, L. Clustering-based adaptive data augmentation for class-imbalance in machine learning (CADA): Additive manufacturing use case. Neural Comput. Appl. 2025, 37, 597–610. [Google Scholar] [CrossRef]
- Liu, D.; Zhong, S.; Lin, L.; Zhao, M.; Fu, X.; Liu, X. Deep attention SMOTE: Data augmentation with a learnable interpolation factor for imbalanced anomaly detection of gas turbines. Comput. Ind. 2023, 151, 103972. [Google Scholar] [CrossRef]
- Soomro, A.A.; Mokhtar, A.A.; Muhammad, M.B.; Saad, M.H.M.; Lashari, N.; Hussain, M.; Palli, A.S. Data augmentation using SMOTE technique: Application for prediction of burst pressure of hydrocarbons pipeline using supervised machine learning models. Results Eng. 2024, 24, 103233. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, Z.; Zhu, Y. A comprehensive survey for generative data augmentation. Neurocomputing 2024, 600, 128167. [Google Scholar] [CrossRef]
- Wang, A.X.; Chukova, S.S.; Simpson, C.R.; Nguyen, B.P. Challenges and opportunities of generative models on tabular data. Appl. Soft Comput. 2024, 166, 112223. [Google Scholar] [CrossRef]
- Du, Z.; Gao, L.; Li, X. A New Contrastive GAN With Data Augmentation for Surface Defect Recognition Under Limited Data. IEEE Trans. Instrum. Meas. 2023, 72, 1–13. [Google Scholar] [CrossRef]
- Tercan, H.; Meisen, T. Machine learning and deep learning based predictive quality in manufacturing: A systematic review. J. Intell. Manuf. 2022, 33, 1879–1905. [Google Scholar] [CrossRef]
- Zong, N.; Jing, T.; Gebelin, J.-C. Machine learning techniques for the comprehensive analysis of the continuous casting processes: Slab defects. Ironmak. Steelmak. Process. Prod. Appl. 2025, 52, 1–20. [Google Scholar] [CrossRef]
- Zhou, Q.; Qian, L.; Meng, J.; Zhao, L. The fatigue properties, microstructural evolution and crack behaviors of low-carbon carbide-free bainitic steel during low-cycle fatigue. Mater. Sci. Eng. A 2021, 820, 141571. [Google Scholar] [CrossRef]
- Cruz, F.C.; Simas Filho, E.F.; Albuquerque, M.C.S.; Silva, I.C.; Farias, C.T.T.; Gouvêa, L.L. Efficient feature selection for neural network based detection of flaws in steel welded joints using ultrasound testing. Ultrasonics 2017, 73, 1–8. [Google Scholar] [CrossRef]
- Vergara, J.R.; Estévez, P.A. A review of feature selection methods based on mutual information. Neural Comput. Appl. 2014, 24, 175–186. [Google Scholar] [CrossRef]
- Macedo, F.; Rosário Oliveira, M.; Pacheco, A.; Valadas, R. Theoretical foundations of forward feature selection methods based on mutual information. Neurocomputing 2019, 325, 67–89. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; Curran Associates Inc.: Red Hook, NY, USA, 2018; pp. 6639–6649. [Google Scholar]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
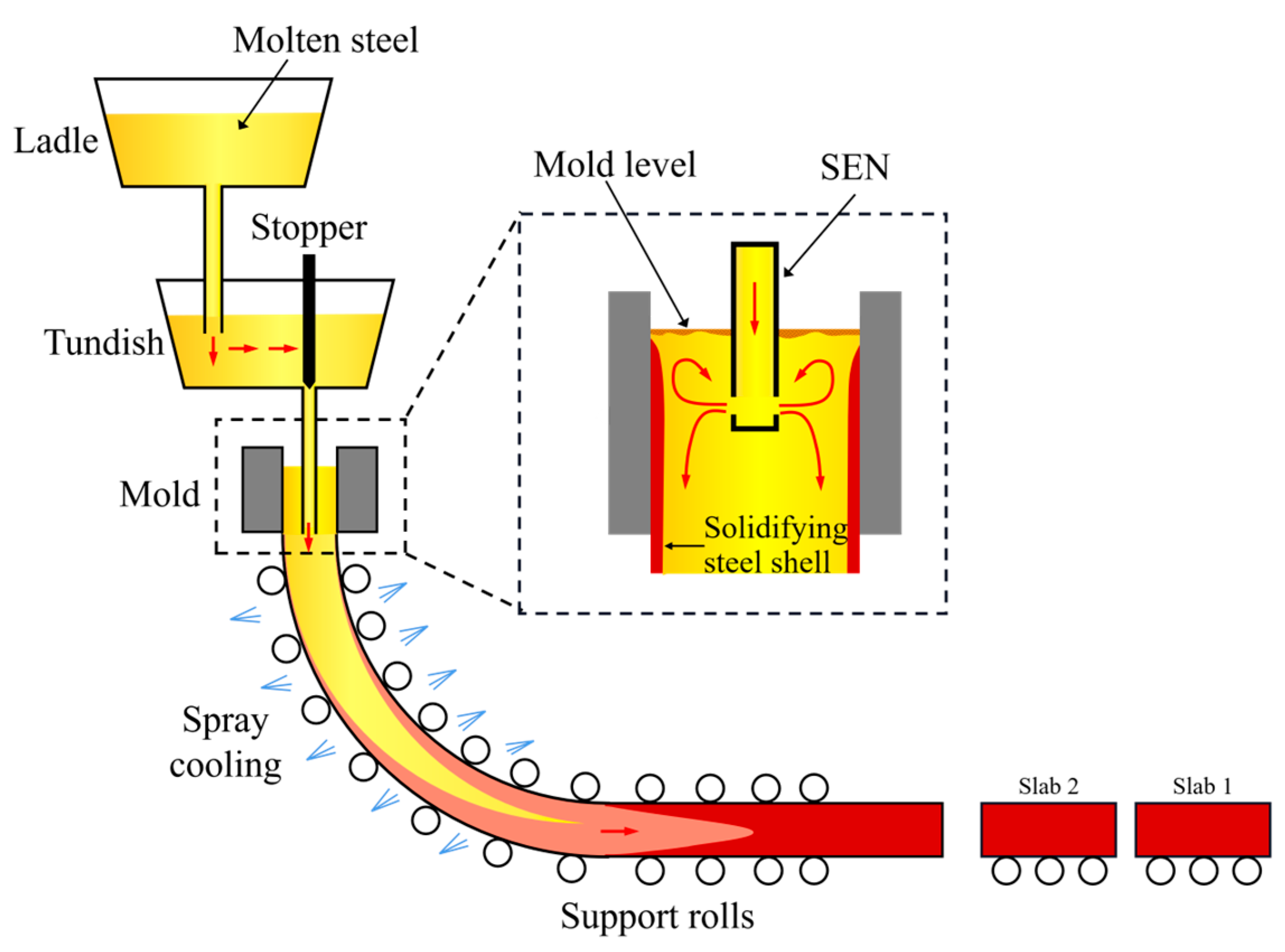


| Parameter | Unit | Value/Type |
|---|---|---|
| Metallurgical length | m | 35.1 |
| Mold height | mm | 900 |
| Mold width | mm | 870–1977 |
| Casting speed | m/min | 0.8–1.5 |
| Lubrication method | - | Mold Flux |
| Furnace capacity | ton | 200 |
| Caster radius | m | 9.1 |
| Slab thickness | mm | 230–250 |
| No. | Parameters | Unit | Description |
|---|---|---|---|
| X0 | Mn-S ratio | % | Manganese-to-sulfur ratio index in steel |
| X1 | Surface temp Str edge | °C | Straightener segment edge surface temperature |
| X2 | Gas pressure tundish | % | Gas pressure at the submerged entry nozzle tip |
| X3 | Surface temp bend | bar | Bender segment edge surface temperature |
| X4 | MD level AVG | mm | Width of continuous casting mold |
| X5 | SCO water flow Z2M2 | L/min | Secondary cooling zone Z2M2 water flow rate |
| X6 | SCO water flow Z2C | L/min | Secondary cooling zone Z2C water flow rate |
| X7 | SEN nozzle gas pressure | bar | Gas pressure in the submerged entry nozzle body |
| X8 | Gas pressure SEN | bar | Gate sealing gas pressure in the ladle/tundish/SEN. |
| X9 | OSC work | J | Oscillation energy consumption per cycle |
| X10 | SCO water flow Z1NR | L/min | Secondary cooling zone Z1NR water flow rate |
| X11 | OSC frequency | 1/min | Mold oscillation frequency |
| X12 | Casting speed cooling | m/min | Minimum casting speed at cooling segment |
| X13 | Surface temp devi bend | °C | Bender segment surface temperature deviation |
| X14 | SCO water flow Z10O | L/min | Secondary cooling zone Z10O water flow rate |
| X15 | Drive force Bend AVG | N | Average bending segment drive force |
| X16 | SCO air pressure Z1011 | bar | Secondary cooling zone Z1011 air pressure |
| X17 | TD inflow rate | ton/min | Tundish steel inflow rate |
| X18 | MCO water temp devi WF | °C | Mold cooling water temperature difference in WF loop |
| X19 | Gas flow stopper | L/min | Stopper/gate inert gas flow rate |
| X20 | SCO water flow devi Z7 | L/min | Secondary cooling zone Z7 water flow deviation |
| X21 | Surface temp Str | °C | Straightener segment surface temperature |
| X22 | Drive force Str AVG | N | Average straightener segment drive force |
| X23 | SCO water flow devi Z6 | L/min | Secondary cooling zone Z6 water flow deviation |
| X24 | Steel weight tundish | ton | Steel weight in tundish |
| Parameters | Value |
|---|---|
| Initial particle number | 20 |
| Max iterations of PSO | 50 |
| Inertia weight | 0.8 |
| Acceleration constant c1/c2 | 1.5, 1.5 |
| Iterations | 800 |
| Learning rate | 0.3 |
| Depth | 5 |
| L2 regularization | 0.6 |
| Method | Original Dataset | CTGAN | ||||||
|---|---|---|---|---|---|---|---|---|
| Acc | Pre | Rec | F1 | Acc | Pre | Rec | F1 | |
| CatBoost | 0.9169 | 0.8951 | 0.8920 | 0.8927 | 0.9239 | 0.9041 | 0.9018 | 0.9022 |
| KNN | 0.8699 | 0.8372 | 0.8231 | 0.8284 | 0.8880 | 0.8570 | 0.8555 | 0.8557 |
| SVM | 0.8131 | 0.7677 | 0.7662 | 0.7593 | 0.8145 | 0.7692 | 0.7704 | 0.7622 |
| MLP | 0.8519 | 0.9015 | 0.8211 | 0.8140 | 0.8644 | 0.8271 | 0.8297 | 0.8275 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, M.; Ma, H.; Liu, S.; Zhou, Z.; Xing, L.; Ai, Y.; Zhang, W. A Data-Driven Approach for Internal Crack Prediction in Continuous Casting of HSLA Steels Using CTGAN and CatBoost. Materials 2025, 18, 3599. https://doi.org/10.3390/ma18153599
Geng M, Ma H, Liu S, Zhou Z, Xing L, Ai Y, Zhang W. A Data-Driven Approach for Internal Crack Prediction in Continuous Casting of HSLA Steels Using CTGAN and CatBoost. Materials. 2025; 18(15):3599. https://doi.org/10.3390/ma18153599
Chicago/Turabian StyleGeng, Mengying, Haonan Ma, Shuangli Liu, Zhuosuo Zhou, Lei Xing, Yibo Ai, and Weidong Zhang. 2025. "A Data-Driven Approach for Internal Crack Prediction in Continuous Casting of HSLA Steels Using CTGAN and CatBoost" Materials 18, no. 15: 3599. https://doi.org/10.3390/ma18153599
APA StyleGeng, M., Ma, H., Liu, S., Zhou, Z., Xing, L., Ai, Y., & Zhang, W. (2025). A Data-Driven Approach for Internal Crack Prediction in Continuous Casting of HSLA Steels Using CTGAN and CatBoost. Materials, 18(15), 3599. https://doi.org/10.3390/ma18153599





