Band Gaps of Hexagonal ScN and YN Multilayer Materials
Abstract
1. Introduction
2. Materials and Methods
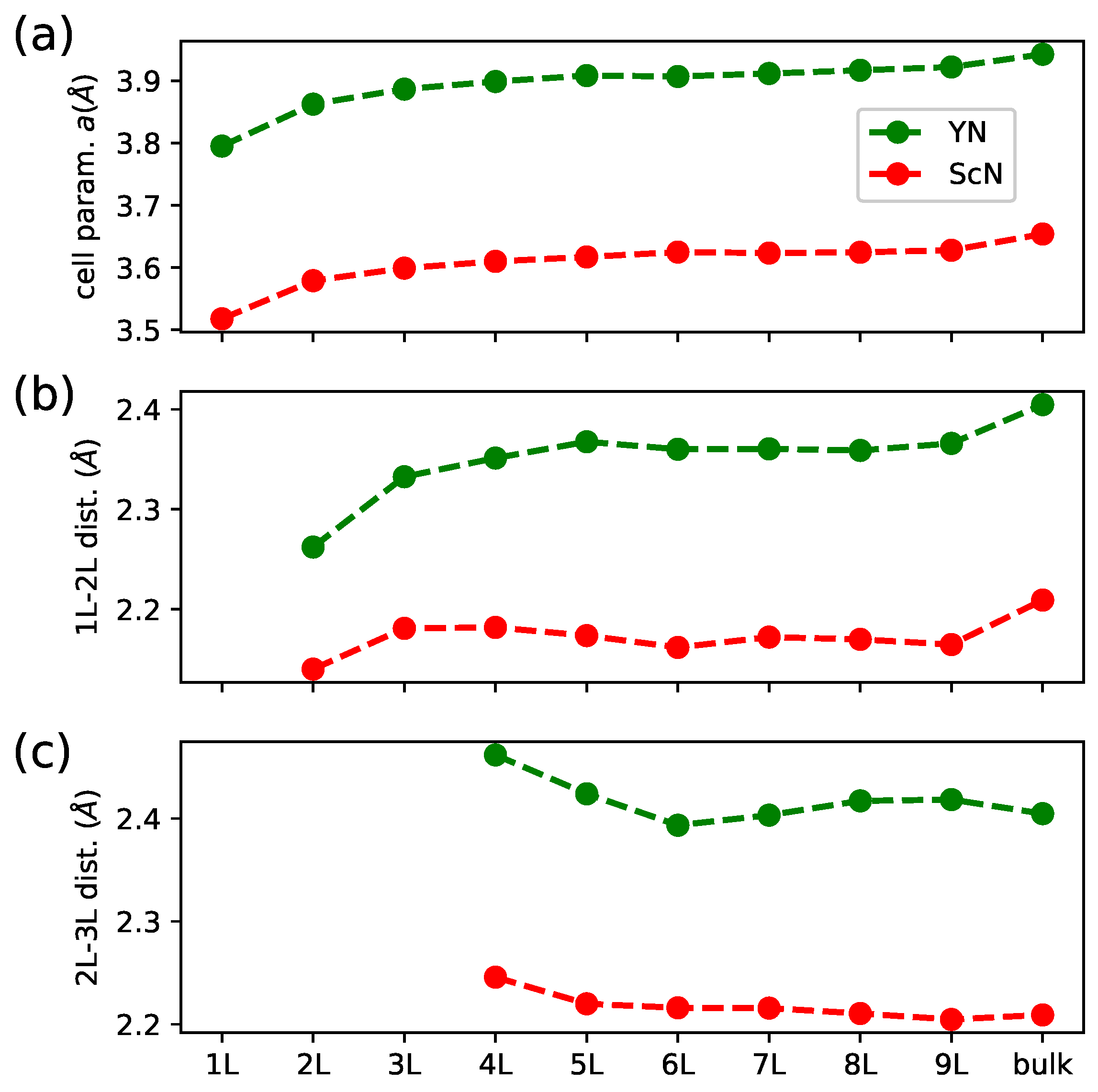
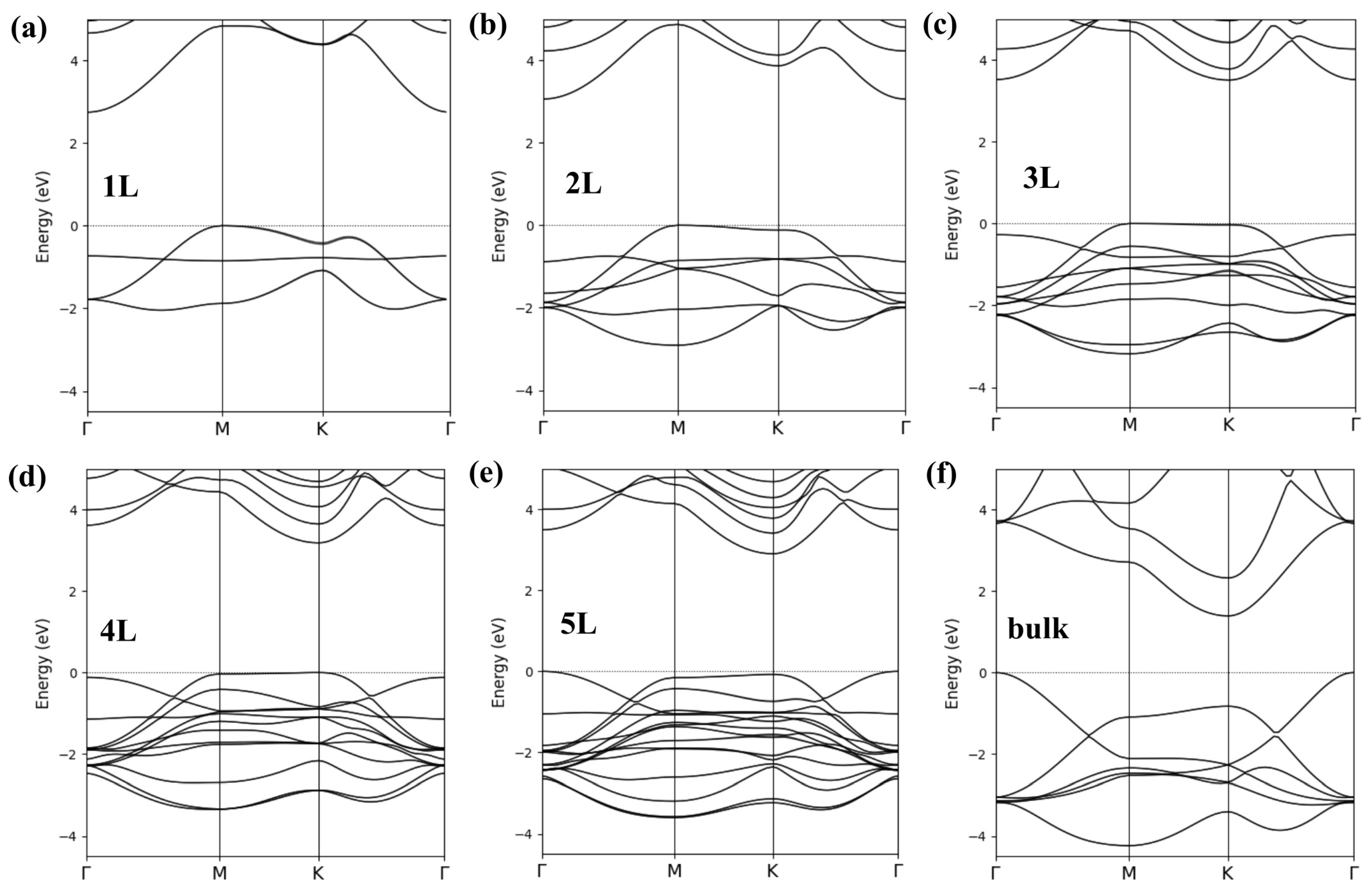
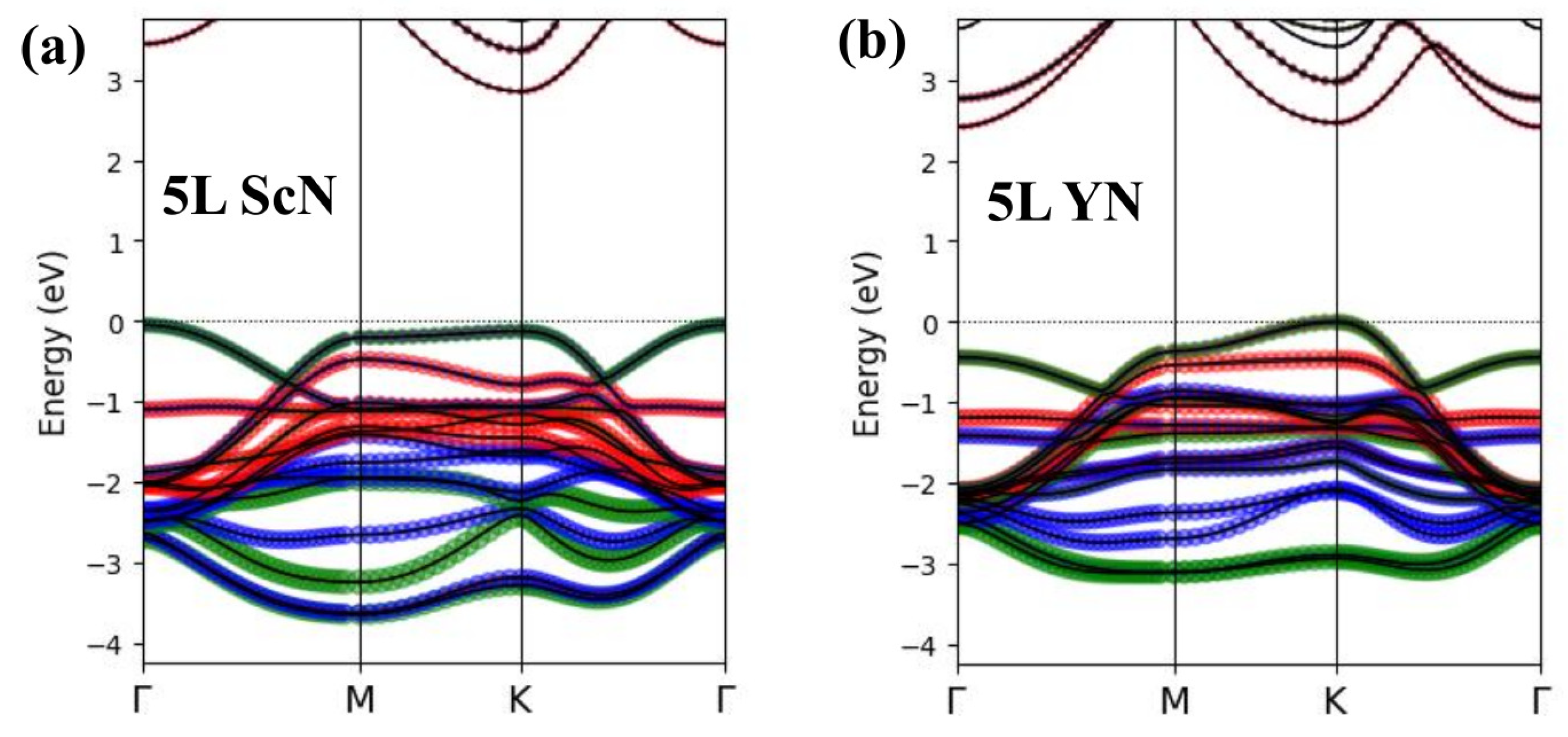
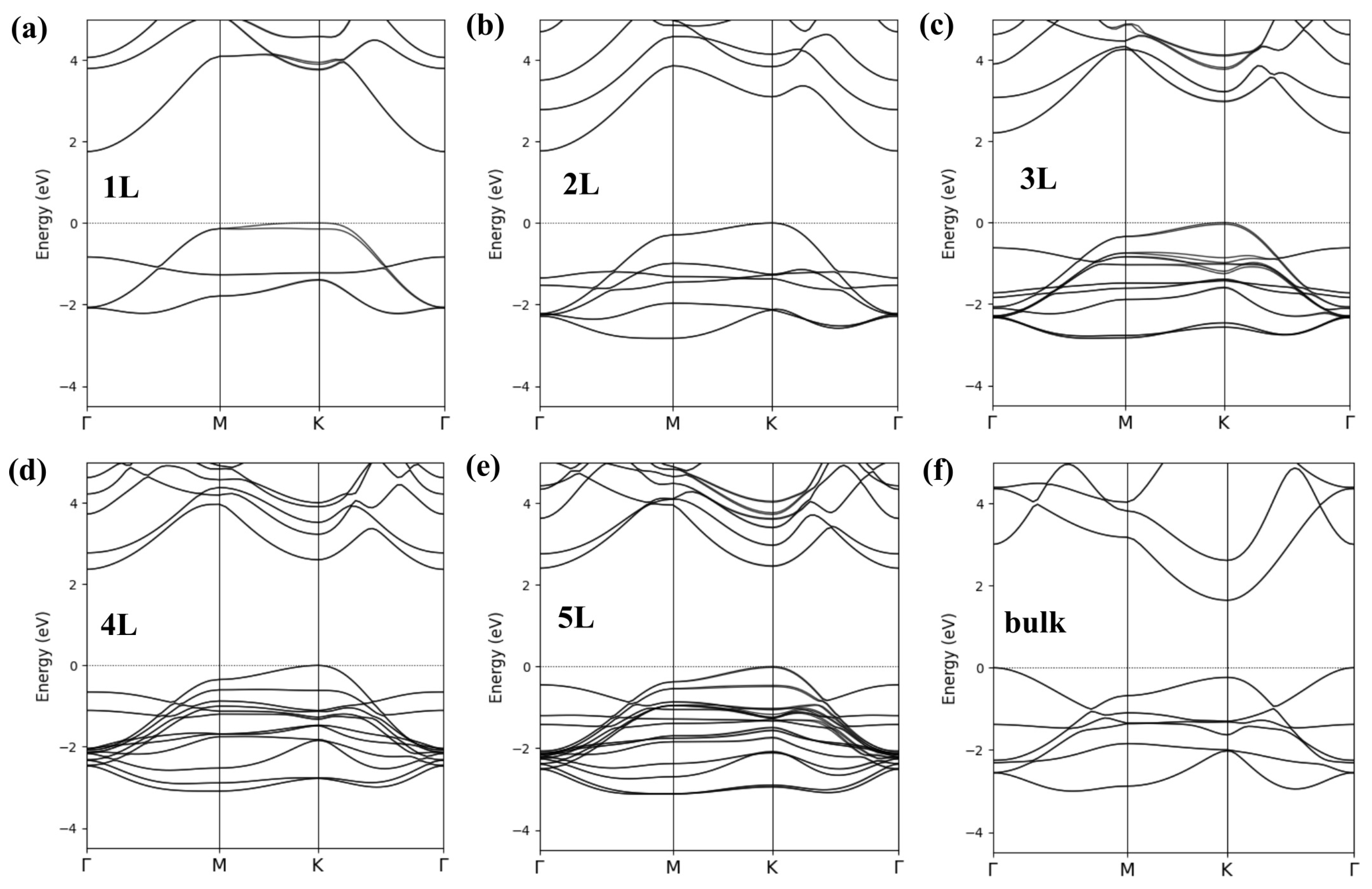
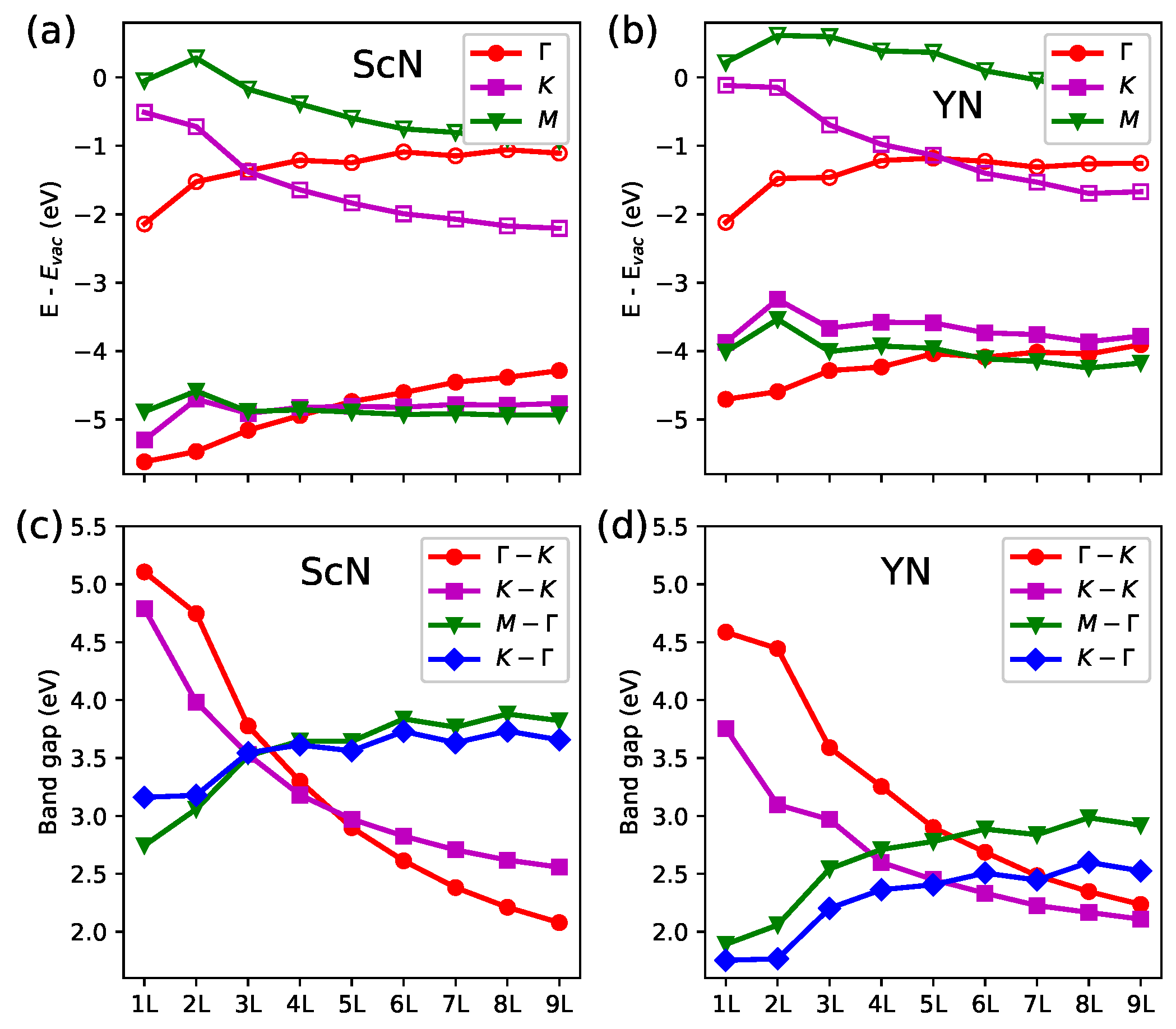
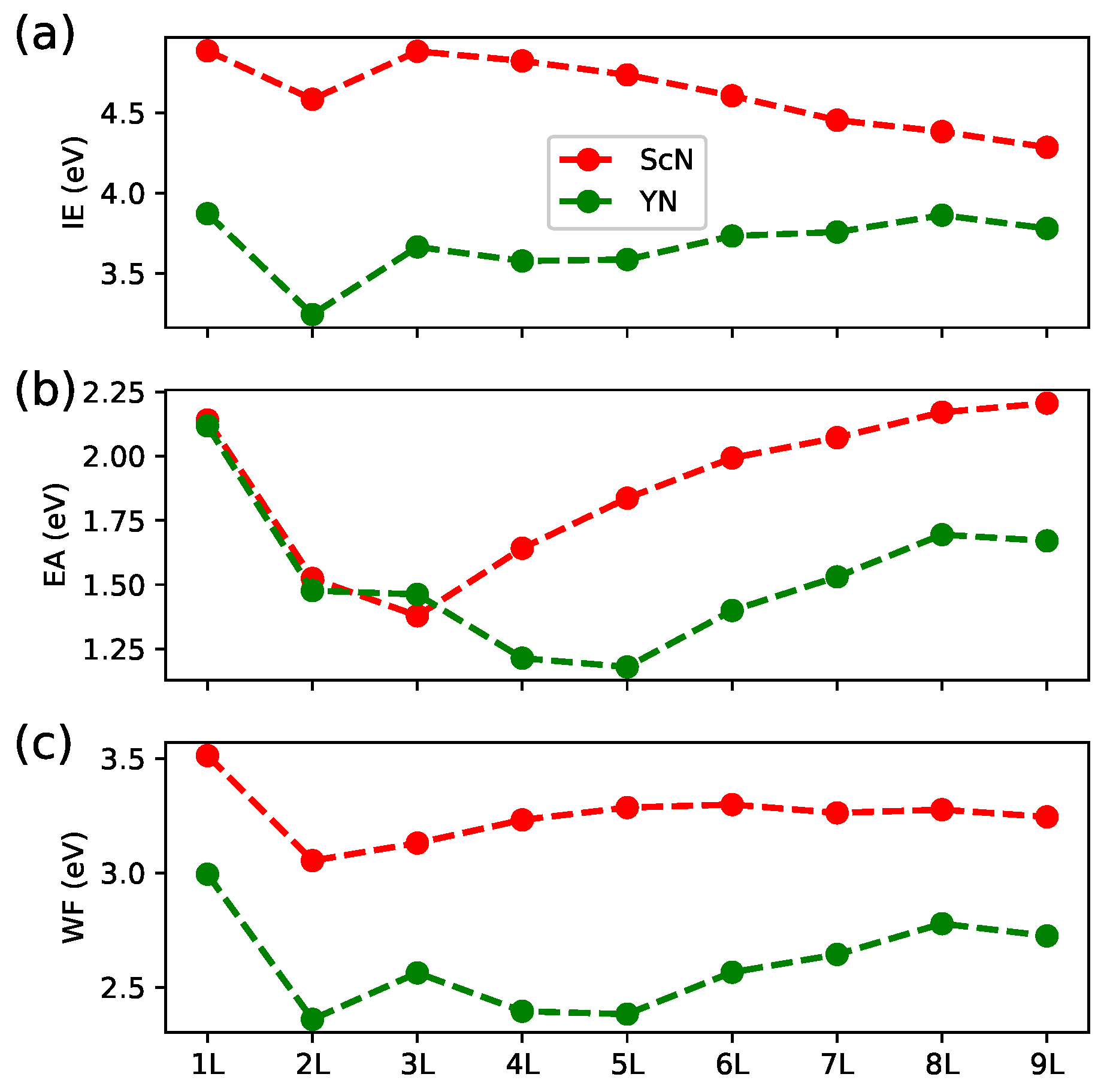
3. Results and Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Caldwell, J.D.; Aharonovich, I.; Cassabois, G.; Edgar, J.H.; Gil, B.; Basov, D.N. Photonics with hexagonal boron nitride. Nat. Rev. Mater. 2019, 4, 552. [Google Scholar] [CrossRef]
- Farrer, N.; Bellaiche, I. Properties of hexagonal ScN versus wurtzite GaN and InN. Phys. Rev. B 2002, 66, 201203(R). [Google Scholar] [CrossRef]
- Constantin, C.; Al-Brithen, H.; Haider, M.B.; Ingram, D.; Smith, A.R. ScGaN alloy growth by molecular beam epitaxy: Evidence for a metastable layered hexagonal phase. Phys. Rev. B 2004, 70, 193309. [Google Scholar] [CrossRef]
- Winiarski, M.J.; Kowalska, D. Electronic structure of REN (RE = Sc, Y, La, and Lu) semiconductors by MBJLDA calculations. Mater. Res. Express. 2019, 6, 095910. [Google Scholar] [CrossRef]
- Winiarski, M.J.; Kowalska, D.A. Crystal structure of ternary alloys of group III and rare earth nitrides by ab initio calculations. Sci. Rep. 2020, 10, 16414. [Google Scholar] [CrossRef]
- Winiarski, M.J. Electronic Structure of Ternary Alloys of Group III and Rare Earth Nitrides. Materials 2021, 14, 4115. [Google Scholar] [CrossRef] [PubMed]
- Tamleh, S.; Rezaei, G.; Jalilian, J. Stress and strain effects on the electronic structure and optical properties of ScN monolayer. Phys. Lett. A 2018, 382, 339. [Google Scholar] [CrossRef]
- Tamleh, S.; Rezaei, G.; Vaseghi, B.; Jalilian, J. Electronic structure and optical properties of two-dimensional tetragonal and hexagonal ScN monolayers: Impact of strain. J. Phys. Chem. Solids 2020, 138, 109270. [Google Scholar] [CrossRef]
- Liang, D.; Jing, T.; Deng, M.; Cai, S. Two-dimensional ScN with high carrier mobility and unexpected mechanical properties. Nanotechnology 2021, 32, 155201. [Google Scholar] [CrossRef]
- Fakhrabad, D.V.; Yeganeh, M. Investigation of the effect of lattice thermal conductivity on the thermoelectric performance of ScN monolayer. Mater. Sci. Semicond. Process. 2022, 148, 106770. [Google Scholar] [CrossRef]
- Yeganeh, M.; Fakhrabad, D.V. Piezoelectric properties in hydrofluorination surface-engineered two-dimensional ScN. Micro Nanostruct. 2022, 171, 207424. [Google Scholar] [CrossRef]
- On, V.V.; Guerrero-Sanchez, J.; Hoat, D.M. Modifying the electronic and magnetic properties of the scandium nitride semiconductor monolayer via vacancies and doping. Phys. Chem. Chem. Phys. 2024, 26, 3587. [Google Scholar] [PubMed]
- Zheng, K.; Yang, X.; Cui, H.; Yang, Q.; Ye, H.; Xiong, D.; Ingebrandt, S.; Chen, X. Intriguing electronic insensitivity and high carrier mobility in monolayer hexagonal YN. J. Mater. Chem. C 2018, 6, 4943. [Google Scholar] [CrossRef]
- Gall, D.; Stadele, M.; Jarrendahl, K.; Petrov, I.; Desjardins, P.; Haasch, R.T.; Lee, T.-Y.; Greene, J.E. Electronic structure of ScN determined using optical spectroscopy, photoemission, and ab initio calculations. Phys. Rev. B 2001, 63, 125119. [Google Scholar] [CrossRef]
- Qteish, A.; Rinke, P.; Scheffler, M.; Neugebauer, J. Exact-exchange-based quasiparticle energy calculations for the band gap, effective masses, and deformation potentials of ScN. Phys. Rev. B 2006, 74, 245208. [Google Scholar] [CrossRef]
- Ramirez-Montes, L.; Lopez-Perez, W.; Gonzalez-Garcia, A.; Gonzalez-Hernandez, R. Structural, optoelectronic, and thermodynamic properties of YxAl1−xN semiconducting alloys. J. Mater. Sci. 2016, 51, 2817. [Google Scholar] [CrossRef]
- Cherchab, Y.; Azzouz, M.; Gonzalez-Hernandez, R.; Talbi, K. First-principles prediction of the structural and electronic properties of GaxY1−xN compounds. Comput. Mater. Sci. 2014, 95, 509. [Google Scholar] [CrossRef]
- Singh, S.K.; Verma, U.P. Investigation of high pressure phase transition and electronic properties of Lutetium Nitride. J. Phys. Conf. Ser. 2015, 640, 012029. [Google Scholar] [CrossRef]
- Winiarski, M.J.; Kowalska, D.A. Electronic structure of hexagonal REN (RE = Sc, Y, and Lu) materials. Mater. Chem. Phys. 2022, 292, 126794. [Google Scholar] [CrossRef]
- Kim, H.; Choi, H.J. Thickness dependence of work function, ionization energy, and electron affinity of Mo and W dichalcogenides from DFT and GW calculations. Phys. Rev. B 2021, 103, 085404. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Lin, S.; Ye, X.; Johnson, R.S.; Guo, H. First-Principles Investigations of Metal (Cu, Ag, Au, Pt, Rh, Pd, Fe, Co, and Ir) Doped Hexagonal Boron Nitride Nanosheets: Stability and Catalysis of CO Oxidation. J. Phys. Chem. C 2013, 117, 17319. [Google Scholar] [CrossRef]
- Keum, D.H.; Cho, S.; Kim, J.H.; Choe, D.-H.; Sung, H.-J.; Kan, M.; Kang, H.; Hwang, J.-Y.; Kim, S.W.; Yang, H.; et al. Bandgap opening in few-layered monoclinic MoTe2. Nat. Phys. 2015, 11, 482. [Google Scholar] [CrossRef]
- Shi, J.; Zeng, Q.; Chen, Y.; Niu, L.; Liu, F.; Yu, T.; Suenaga, K.; Liu, X.; Lin, J. InSe monolayer: Synthesis, structure and ultra-high second-harmonic generation. 2D Mater. 2018, 5, 025019. [Google Scholar]
- Okada, M.; Sawazaki, T.; Watanabe, K.; Taniguch, T.; Hibino, H.; Shinohara, H.; Kitaura, R. Direct Chemical Vapor Deposition Growth of WS2 Atomic Layers on Hexagonal Boron Nitride. ACS Nano 2014, 8, 8273. [Google Scholar] [CrossRef] [PubMed]
- Islam, R.; Ghosh, B.; Autieri, C.; Chowdhury, S.; Bansil, A.; Agarwal, A.; Singh, B. Tunable spin polarization and electronic structure of bottom-up synthesized MoSi2N4 materials. Phys. Rev. B 2021, 104, L201112. [Google Scholar] [CrossRef]
- Ota, Y. Band alignments of graphene-like III-nitride semiconductors. Solid State Commun. 2018, 270, 147. [Google Scholar] [CrossRef]
- Wickramaratne, D.; Weston, L.; van de Walle, C.G. Monolayer to bulk properties of hexagonal boron nitride. J. Phys. Chem. C 2018, 122, 25524. [Google Scholar] [CrossRef]
- Thomas, S.; Manju, M.S.; Ajith, K.M.; Lee, S.U.; Asle Zaeem, M. Strain-induced work function in h-BN and BCN monolayers. Phys. E 2020, 123, 114180. [Google Scholar] [CrossRef]
- Schultz, T.; Schlesinger, R.; Niederhausen, J.; Henneberger, F.; Sadofev, S.; Blumstengel, S.; Vollmer, A.; Bussolotti, F.; Yang, J.-P.; Kera, S.; et al. Tuning the work function of GaN with organic molecular acceptors. Phys. Rev. B 2016, 93, 125309. [Google Scholar] [CrossRef]
- Himmerlich, M.; Krischok, S.; Lebedev, V.; Ambacher, O.; Schaefer, J.A. Morphology and surface electronic structure of MBE grown InN. J. Cryst. Growth 2007, 306, 6. [Google Scholar] [CrossRef]
- Ma, T.; Jacobs, R.; Booske, J.; Morgan, D. Work Function Trends and New Low-Work-Function Boride and Nitride Materials for Electron Emission Applications. J. Phys. Chem. C 2021, 125, 17400. [Google Scholar] [CrossRef]
| System | a (Å) | c (Å) | |
|---|---|---|---|
| ScN bulk: | |||
| GGA | 3.715 | 4.475 | 1.205 |
| D2 | 3.646 | 4.454 | 1.221 |
| D3 | 3.654 | 4.418 | 1.209 |
| LDA [19] | 3.662 | 4.416 | 1.206 |
| YN bulk: | |||
| GGA | 4.011 | 4.880 | 1.217 |
| D2 | 3.924 | 4.856 | 1.237 |
| D3 | 3.943 | 4.815 | 1.221 |
| LDA [19] | 3.965 | 4.829 | 1.218 |
| LuN bulk LDA [19] | 3.849 | 4.661 | 1.211 |
| ScN monolayer: | |||
| GGA | 3.518 | - | - |
| GGA [8] | 3.510 | - | - |
| GGA [12] | 3.520 | - | - |
| LDA [19] | 3.460 | - | - |
| YN monolayer: | |||
| GGA | 3.795 | - | - |
| LDA [19] | 3.758 | - | - |
| GGA+U [13] | 4.008 | - | - |
| LuN monolayer LDA [19] | 3.652 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winiarski, M.J. Band Gaps of Hexagonal ScN and YN Multilayer Materials. Materials 2025, 18, 2938. https://doi.org/10.3390/ma18132938
Winiarski MJ. Band Gaps of Hexagonal ScN and YN Multilayer Materials. Materials. 2025; 18(13):2938. https://doi.org/10.3390/ma18132938
Chicago/Turabian StyleWiniarski, Maciej J. 2025. "Band Gaps of Hexagonal ScN and YN Multilayer Materials" Materials 18, no. 13: 2938. https://doi.org/10.3390/ma18132938
APA StyleWiniarski, M. J. (2025). Band Gaps of Hexagonal ScN and YN Multilayer Materials. Materials, 18(13), 2938. https://doi.org/10.3390/ma18132938






